2. 中航工业西安飞行自动控制研究所, 西安 710065
2. AVIC Xi'an Flight Automatic Control Research Institute, Xi'an 710065, China
随着计算机与通信技术的发展, 分布式系统越来越多地被使用在控制系统中, 如飞行控制系统、核电站控制系统等。任务调度问题是分布式计算领域中的基本问题。有向无环图(Directed Acyclic Graph, DAG) 模型常被用来描述有约束关系的任务[1]。近年来, 针对单个DAG在多个计算资源上的调度问题研究已基本趋于成熟, DLS[2]、HEFT[3]、CPOP[4-5]等启发式算法以其较高的调度效率及较低的时间复杂度被人们所广泛接受。文献[6]提出一种基于异构计算系统的多优先级队列遗传算法(Multiple Priority Queues Genetic Algorithm, MPQGA)、文献[7]提出在异构系统中基于遗传变邻域混合调度算法(Genetic-variable Neighborhood Search Algorithm, GVNS)以及文献[8]提出基于异构多核系统的混合关键任务调度算法都是通过将启发式算法与遗传算法相结合, 对所有可行解进行随机搜索。上述算法实验结果表明, 该类算法可得到比传统启发式算法更优的调度结果。
随着用户需求的日渐复杂化, 多DAG共享一组计算资源的问题逐渐受到研究者们的广泛关注并已经取得了一些成果[9-11]。文献[12]提出将多个DAG整合成一个DAG来解决多DAG共享异构分布式资源的调度问题。由于实际任务的复杂多变, 多个DAG之间存在一定的差异, 因此多DAG调度策略存在一个公平性问题。文献[13]提出一种公平调度算法Fairness算法, 其原理是在调度队列中通过比较各DAG的相对滞后程度来决定下次调度的DAG, 该算法有效地解决了多DAG调度中的公平性问题。但在某些特殊情况时此算法也存在着一些缺陷, 例如当2个DAG滞后程度相同时, 原Fairness算法通过比较两者的剩余完成时间来决定谁优先被调度, 如此导致完成时间相对较小的DAG会被滞后调度, 导致不公平性增加; 再如当被调度DAG数大于处理机数时, 会存在由于初始阶段滞后程度较低的DAG在调度队列中得不到调度的情况, 同样也会使得调度不公平性增加。文献[14]提出LTCT算法, 解决了多个不同时间到达的DAG工作流的调度问题并得到较好的调度结果。文献[15]提出的异构分布式环境下多DAG工作流的混合调度策略, 有效解决了在不同时间上被提交的具有不同优先级的多DAG工作流之间调度的公平性问题。
针对原Fairness算法存在的问题, 本文对其进行改进, 提出一种启发式改进公平(Improved Fairness, IFairness)调度算法。在DAG选择阶段, 当2个DAG的滞后程度相同时, 采用一种新的评判指标DAG完成度作为DAG选择依据, 在计算DAG的滞后程度阶段, 将各DAG队列中即将被调度的子任务分别进行调度后, 得到的SlowdownM作为各DAG的滞后程度。
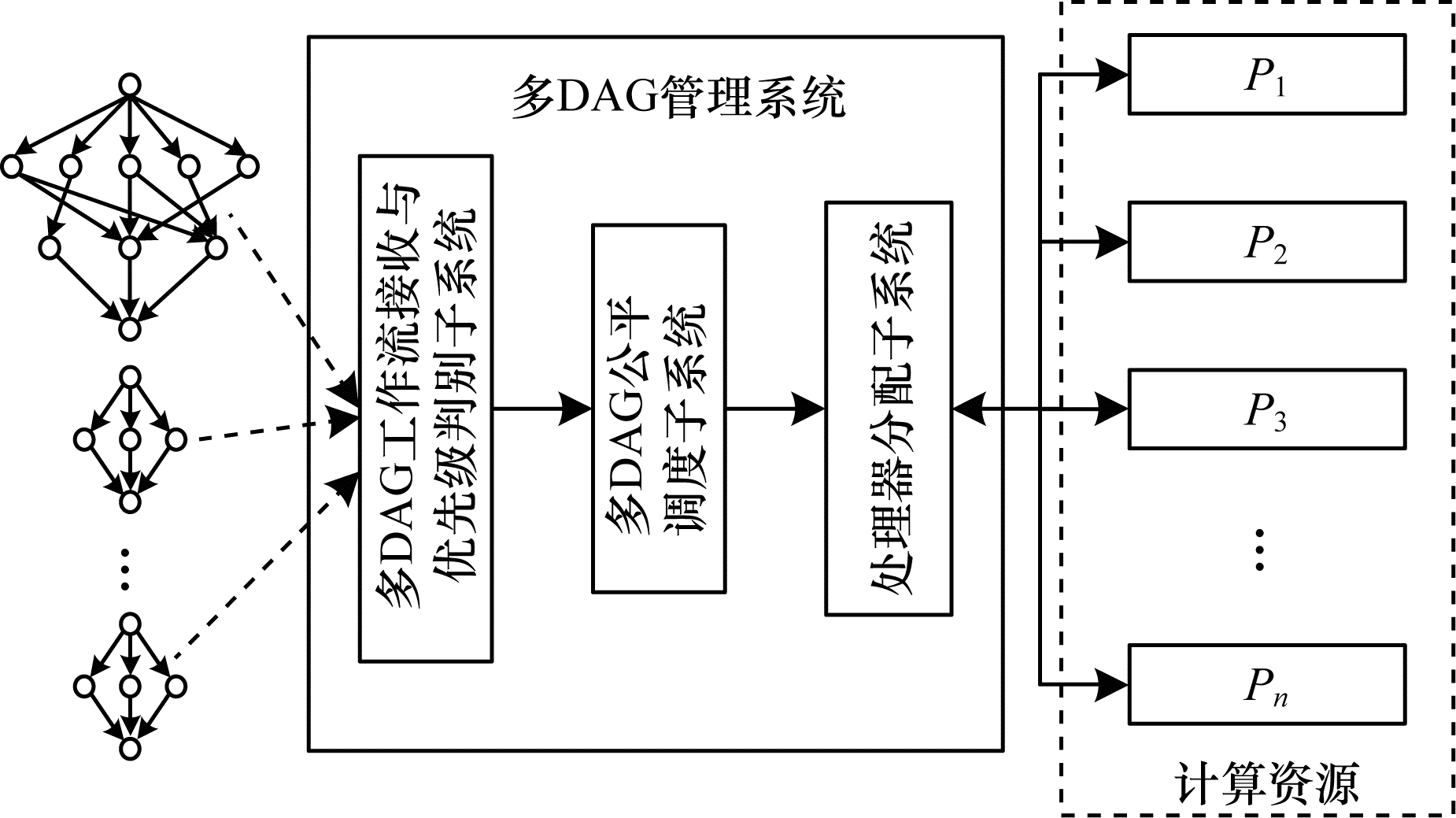
1 问题描述文献[15]提出的多DAG任务调度系统框架如图 1所示。该系统由3个部分组成, 分别是:优先级子系统负责将DAGk的子任务进行优先级分配, 针对每个DAGk生成一个优先级队列(Array, ak); 多DAG公平调度子系统负责将多DAG任务按照公平性原则进行DAG任务调度; 处理器分配子系统负责将调度队列中待调度的任务分配到相应的处理器。
|
Download:
|
| 图 1 多DAG任务调度系统模型 | |
一般地, 一个DAG可以表示为G=(V, E, C)。其中, V是任务结点集合, E是任务结点间有向边的集合, C是有向边的权值集合, 有向边(i, j)表示任务结点ni和nj之间的先后执行关系, 有向边上的权值表示任务之间数据传递的平均时间。每个DAG子任务优先级排序队列ak由向上任务权值ranku(ni)[3]确定。ranku(ni)从出口任务结点开始, 可被递归地定义为:
| $ {rank}_{u}\left(n_{i}\right)=\overline{w_{i}}+\max \limits_{n_{j} \in {succ}\left(n_{i}\right)}\left(c_{(i, j)}+{rank}_{u}\left(n_{j}\right)\right) $ | (1) |
其中, succ(ni)是后继结点集合。
当多个DAG同时被调度到一组计算资源上时, 由于资源竞争, 因此DAGk在混合调度中的完成时间很可能比单独调度的完成时间要长。
如果DAGk在单独使用资源时利用某个算法调度后和在某个混合调度算法S调度后的2个Makespan分别被表示为MOWN(k)和Mmuliti(k), 则DAGk的滞后程度定义为:
| $ Slowdown_{M}(k)=M_{\text { OWN }}(k) / M_{\text { mulitit }}(k) $ | (2) |
那么某一混合调度算法S的时间不公平性被定义为:
| $ \begin{array}{*{20}{l}} {Unfairnes{s_M}(S) = }\\ {\sum\limits_{\forall k \in A} | Slowdow{n_M}(k) - AvgSlowdow{n_M}|} \end{array} $ | (3) |
其中, A为给定的多个DAG的集合, AvgSlowdownM是所有DAG的SlowdownM的平均值, 即:
| $ AvgSlowdow{n_M} = \sum\limits_{\forall a \in A} {Slowdow{n_M}} (k)/|A| $ | (4) |
其中, |A|表示集合A的基。UnfairnessM(S)越小, 说明调度长度公平性越高。
2 改进的Fairness算法经典公平调度算法的核心是在DAG选择阶段, 该阶段总是先调度相对滞后程度最大的DAG中的任务权值ranku(ni)最大的一个任务。
本文在Fairness算法的基础上, 提出一种改进IFairness算法。下文通过文献[14]第3节的算例和图 2、图 3的调度结果来讨论改进方法。
|
Download:
|
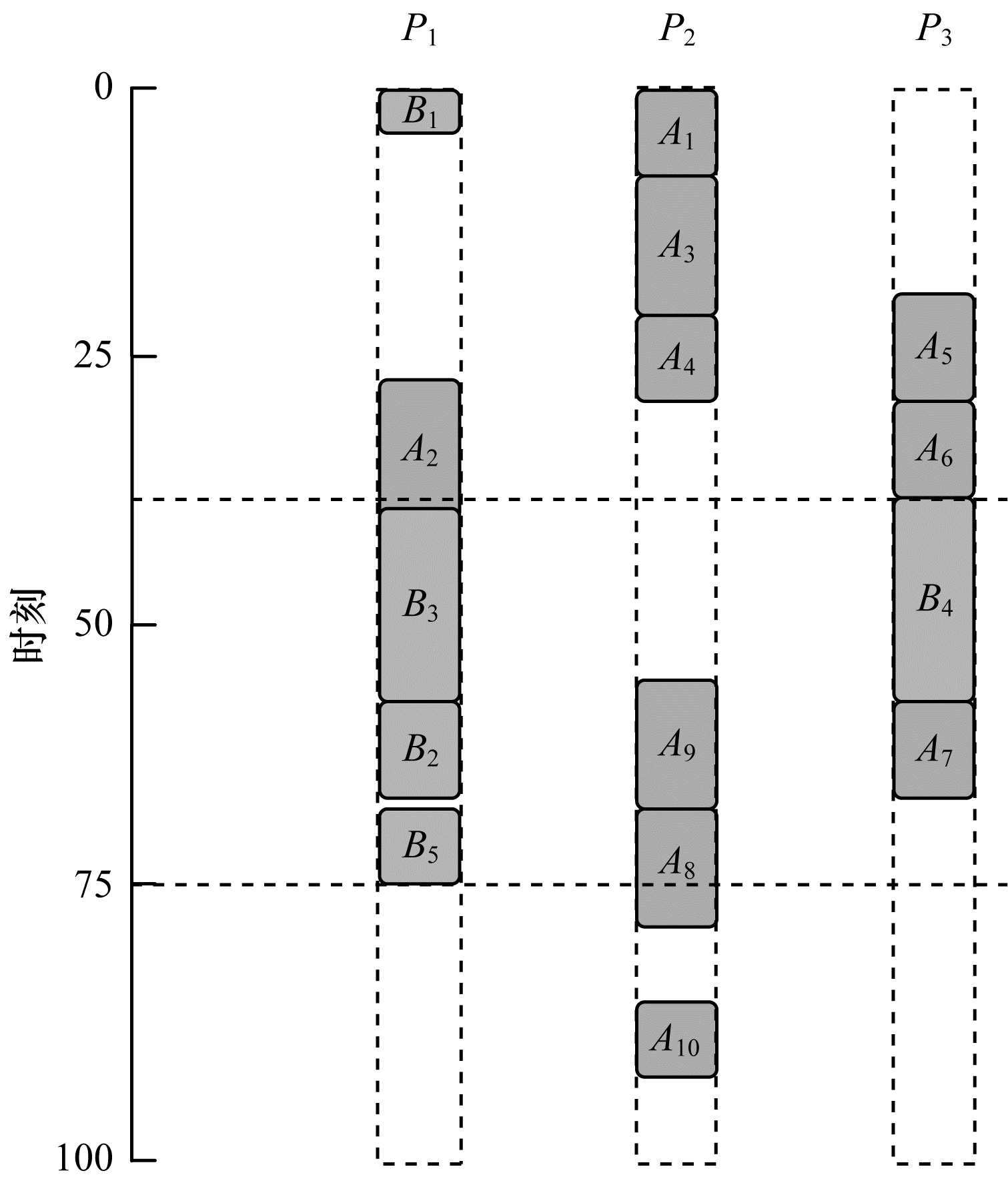
| 图 2 Fairness算法调度结果 | |
|
Download:
|
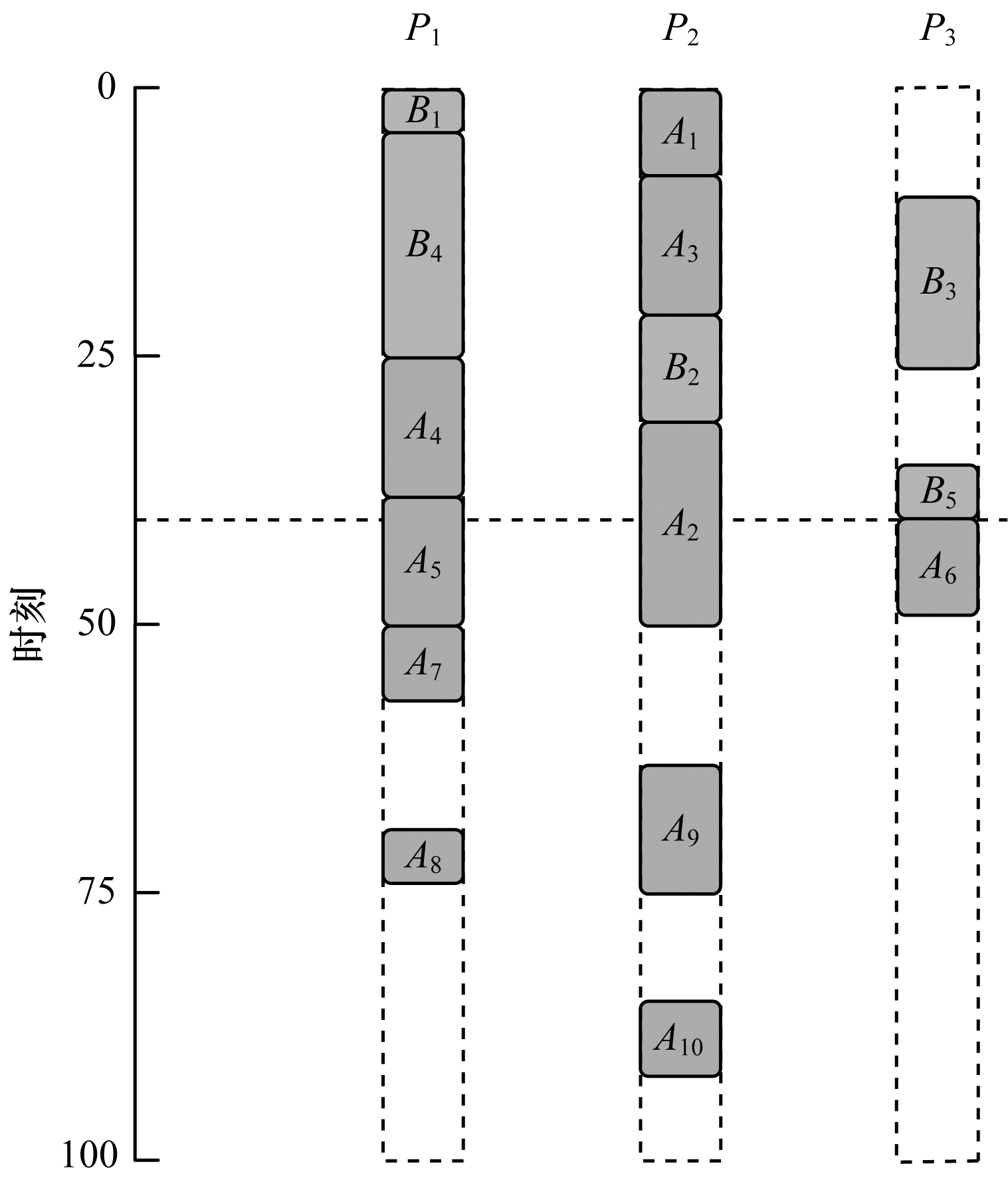
| 图 3 IFairness算法调度结果 | |
在图 2中, 系统在0时刻同时接到DAGA与DAGB到达请求调度, 此时由于DAGA与DAGB的SlowdownM都为0, 比较两者的剩余完成时间(Makespan), DAGA的剩余Makespan大于DAGB, 因此先从DAGA中选择优先级最高的任务TA1进行调度。调度结束后DAGA与DAGB的SlowdownM分别为1和0, 因此先从DAGB中选择优先级最高的任务TB1进行调度。调度结束后DAGA与DAGB的SlowdownM都为1, 由于DAGA的剩余Makespan大于DAGB, 因此先从DAGA中选择优先级最高的任务TA3进行调度。在此后的调度中, 由于DAGA与DAGB的SlowdownM都为1, 比较两者剩余Makespan时DAGA始终大于DAGB, 在调度完TA6时, DAGB的剩余Makespan大于DAGA, 此时DAGB才再次得到调度。因此, 在Fairness算法中, 当各DAG的SlowdownM相等时, Makespan相对较短的DAG可能在前期得不到调度, 这会导致其Makespan的滞后程度大于其他DAG任务。
在图 3中, 当各DAG的SlowdownM相等时, 采用完成度Cd(k)替代剩余Makespan作为DAG任务的选择的评判指标。Cd(k)的定义如下:
| $ C d(k)=f t_{\mathrm{OWN}}\left(t_{i}\right) / M_{\mathrm{OWN}}(k) $ | (5) |
其中, ftOWN(ti)为DAGk单独使用资源时调度任务ti时的完成时间, MOWN(k)为DAGk的所有任务单独在资源上调度时的执行时间, 因此0≤Cd(k)≤1。
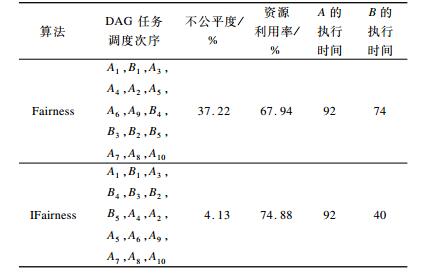
在IFairness算法中, 当各DAG的SlowdownM相等时, 比较剩余DAG的完成度Cd(k), 在集合U中将该值较小的DAG放在前面, 即完成度较小的DAG优先得到调度。针对文献[14]算例, IFairness算法的调度结果如图 3所示, 两者调度结果对比如表 1所示。由表 1可以看出, 改进算法在不公平度、资源利用率与执行时间上都比原算法有更优的调度结果。
|
下载CSV 表 1 DAGA和DAGB调度结果比较 |
此外, 本文还针对原算法的另一不足进行改进。当被调度的任务个数大于处理器个数时, 存在有任务优先被调度后但计算出较低的SlowdownM(k), 导致其后驱任务得不到调度。
本文针对上述问题进行相应的改进, 在原算法选择DAG进行调度时, 对DAGk已完成的任务ti的滞后程度进行计算并选择滞后程度最大的DAGk进行下一次调度, 即:
| $ Slowdow{n_M}(k) = {M_{{\rm{ OWN }}}}\left( {{k_{{t_i}}}} \right)/{M_{{\rm{ muliti }}}}\left( {{k_{{t_i}}}} \right) $ | (6) |
其中, MOWN(kti)表示DAGk单独使用资源时, 调度任务ti任务时的完成时间, Mmulti(kti)表示DAGk在混合调度时调度到ti任务时的完成时间。
在本文中, 采用“向后看”一步的原则, 在选择DAG进行调度时, 分别计算出各DAG中即将被调度的任务ti+1在混合调度中的完成时间, 并计算出该任务调度完成后DAGk的滞后程度, 选择滞后程度最大的DAGk为下次被调度的DAG, 即:
| $ Slowdow{n_M}(k) = {M_{{\rm{ own }}}}\left( {{k_{{t_{i + 1}}}}} \right)/{M_{{\rm{ muliti }}}}\left( {{k_{{t_{i + 1}}}}} \right) $ | (7) |
其中, Mown(kti+1)表示DAGk单独使用资源时, 调度任务ti+1任务时的完成时间, Mmulti(kti+1)表示DAGk在混合调度时调度到ti+1任务时的完成时间。算法伪代码如下所示。
算法 IFariness算法
输入 待调度的DAG集合A, 可用资源集合R, 单个DAG的时间最小化列表调度算法alg(如HEFT)
输出 集合A中所有DAG的公平混合调度方案(存储在Smulti中)
1.Procedure IFairness (A, R, alg)
2.在R的资源上用算法alg单独调度运行A中每个待调度的DAG;
3.将这些调度结果存储在Sown中;
4.将每个DAG标记为“未调度”, 放入集合U中;
5.将每个DAG的SlowdownM值置0, 并对U中的DAG根据Sown中的Makespan的值按降序排序;
6.Sown←Φ /*多个DAG混合调度结果初始为空*/
7.while U≠Φ do
8.ak←U中第1个DAG
9.ti←ak中ranku值最高的任务;
10.m←用alg调度后ti的完成时间; Smulti←ti的调度结果
11.if(ti是ak中最后一个任务)then
12.从U中删除ak;
13.else
14.For (U:ak){
/*循环遍历U中每个未调度完的DAGak*/
15.ti+1←ak中ranku值最高的任务;
16.m←用alg调度后ti+1的完成时间; Smulti←ti+1的调度结果
17.ftmulti(kti+1)←m;
18.ftOWN(kti+1)←SOWN中ti+1的完成时间;
19.SlowdownM(k)=ftown(kti+1)/ftmulti(kti+1);
20.Cd(k)=ftOWN(ti+1)/MOWN(k)
}
21.对U中的DAG按SlowdownM值升序排序;
22.if(U中存在有2个DAG的SlowdownM值相同) then
23.比较2个DAG完成度值Cd(k), 在U中将该值较小的DAG放在前面;
24.end if
25.end if
26.end while
27.return Smulti
28.end Procedure
3 仿真与结果分析为了证明算法调度效果, 本文从DAG的平均完成时间、不公平程度和计算资源利用率将本文提出的IFairness算法与原有的Fairness进行仿真对比。
3.1 DAG的调度实验本文针对2个DAG在Pnum个处理器上的调度问题, 采用IFairness算法与原有的Fairness算法在不同处理器数目上(Pnum=3, 4, 5)进行多DAG的调度。
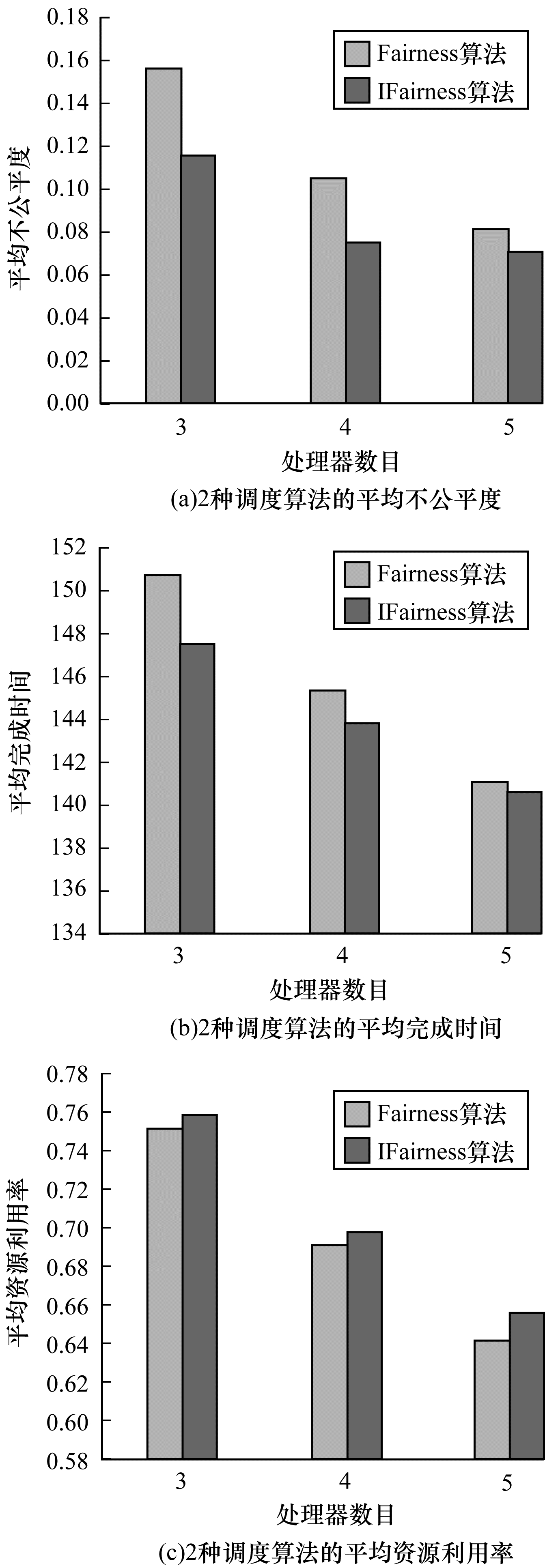
调度算法采用平均完成时间、不公平程度和计算资源利用率作为评价指标。随机生成100组DAG, 分别在3个~5个处理器上进行调度, 仿真结果如图 4所示。
|
Download:
|
| 图 4 DAG在3个~5个处理器上的调度结果对比 | |
通过以上仿真结果可以看出, 改进算法IFairness算法相比原有Fairness算法的不公平程度、平均完成时间和资源利用率都有较大的性能提升。并且通过图中DAG数目变化可以看出在计算资源较少时, 改进算法IFairness在公平性上相比Fairness算法提升较为明显, 不公平度降低了30.65%。在计算资源相对较多时, 改改进算法IFairness相比Fairness算法在资源利用率上提升较为明显, 提升了3.16%。
3.2 多个随机DAG的调度实验本文针对多个随机DAG在Pnum个处理器上的调度问题, 采用IFairness算法与原有的Fairness算法在处理器数目分别为3个~6个, 以及DAG并行调度个数分别为2、4、6、8和10的调度实验。
调度算法采用不公平程度、平均完成时间和资源利用率作为评价指标。随机生成100组DAG, 分别在3个~6个的异构处理器上进行调度, 仿真结果如图 5所示。

|
Download:
|
| 图 5 DAG在3个~6个处理器上的调度结果对比 | |
通过以上仿真结果分析可以看出, 随着DAG数目的增加, 改进算法IFairness算法相比原有Fairness算法在平均Makespan上虽提升不明显, 但总体比原算法更优。当DAG数目大于处理器数目时, 可以看出改进算法在不公平程度Unfairness降低了7.28%, 在资源利用率Utilization指标上提升了11.97%。
4 结束语本文提出一种新型公平调度算法IFairness, 该算法在DAG滞后程度相同阶段, 采用完成度替代剩余Makespan作为DAG任务的选择的评判指标, 使得调度长度相对较短的DAG可以优先得到调度, 此外在计算DAG滞后程度SlowdownM(k)阶段, 采用“向后看”一步的原则, 计算出各DAG队列中下个任务调度后的结果作为该DAG的滞后程度SlowdownM(k)。实验结果表明, IFairness在公平性、调度长度和计算资源利用率指标上相比Fairness算法具有更优的调度结果。
| [1] |
WU An, YU Han, JIN Shiyuan, et al. An incremental genetic algorithm approach to multiprocessor scheduling[J]. IEEE Transactions on Parallel and Distributed Systems, 2004, 15(9): 824-834. DOI:10.1109/TPDS.2004.38 (  0) 0)
|
| [2] |
SIH G C, LEE E A. A compile-time scheduling heuristic for interconnection constrained heterogeneous processor architectures[J]. IEEE Transactions on Parallel and Distributed Systems, 1993, 4(2): 175-187. DOI:10.1109/71.207593 (  0) 0)
|
| [3] |
TOPCUOGLU H, HARIRI S, WU M Y. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Transactions on Parallel and Distributed Systems, 2002, 13(3): 260-274. DOI:10.1109/71.993206 (  0) 0)
|
| [4] |
WU Minyou, GAJSKI D D. Hypertool:a programming aid for message-passing systems[J]. IEEE Transactions on Parallel and Distributed Systems, 1990, 1(3): 330-343. DOI:10.1109/71.80160 (  0) 0)
|
| [5] |
刘亚秋, 邵洪润, 景维鹏. 云环境下融合安全与可用性的DAG任务调度[J]. 计算机工程, 2014, 40(12): 12-18. DOI:10.3969/j.issn.1000-3428.2014.12.003 (  0) 0)
|
| [6] |
XU Yuming, LI Kenli, HU Jingtong, et al. A genetic algorithm for task scheduling on heterogeneous computing systems using multiple priority queues[J]. Information Sciences, 2014, 270(6): 255-287. (  0) 0)
|
| [7] |
WEN Yun, XU Hua, YANG Jiadong. A heuristic-based hybrid genetic-variable neighborhood search algorithm for task scheduling in heterogeneous multiprocessor system[J]. Information Sciences, 2011, 181(3): 567-581. DOI:10.1016/j.ins.2010.10.001 (  0) 0)
|
| [8] |
赵瑞姣, 朱怡安, 李联. 基于异构多核系统的混合关键任务调度算法[J]. 计算机工程, 2018, 44(2): 51-55. DOI:10.3969/j.issn.1000-3428.2018.02.008 (  0) 0)
|
| [9] |
YU Zhifeng, SHI Weisong.A planner-guided scheduling strategy for multiple workflow applications[C]//Proceedings of IEEE International Conference on Parallel Processing.Washington D.C., USA: IEEE Press, 2008: 1-8.
(  0) 0)
|
| [10] |
FHRINGER T, PRODAN R, DUAN R, et al.ASKALON: a grid application development and computing environment[C]//Proceedings of IEEE International Workshop on Grid Computing.Washington D.C., USA: IEEE Press, 2005: 10-21.
(  0) 0)
|
| [11] |
田国忠.多DAG共享资源调度的若干问题研究[D].北京: 北京工业大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10005-1014034258.htm
(  0) 0)
|
| [12] |
HONIG U, SCHIFFMANN W.A meta-algorithm for scheduling multiple DAGs in homogeneous system environments[C]//Proceedings of the 18th International Conference on Parallel and Distributed Computing and Systems.Piscataway, USA: [s.n.], IEEE Press, 2006: 147-152.
(  0) 0)
|
| [13] |
ZHAO Henan, SAKELLARIOU R.Scheduling multiple DAGs onto heterogeneous systems[C]//Proceedings of International Conference on Parallel and Distributed Processing Symposium.Washington D.C., USA: IEEE Press, 2006: 14-21.
(  0) 0)
|
| [14] |
任丰玲, 于炯, 杨兴耀. 基于最小化传输和完成时间的多DAG调度[J]. 计算机工程, 2012, 38(23): 287-290. DOI:10.3969/j.issn.1000-3428.2012.23.072 (  0) 0)
|
| [15] |
田国忠, 肖创柏, 徐竹胜, 等. 异构分布式环境下多DAG工作流的混合调度策略[J]. 软件学报, 2012, 23(10): 2720-2734. (  0) 0)
|
 2019, Vol. 45
2019, Vol. 45

