0 概述

随着互联网技术的飞速发展, 各类信息容量剧增导致严重的“信息过载”问题^[1], 一方面用户从海量数据中获取感兴趣的信息变得越来越困难, 另一方面服务方难以从海量数据中抽象出个性化的用户需求。推荐系统作为一种信息过滤系统, 能有效解决上述问题。在推荐系统中广泛使用的是基于协同过滤(Collaborative Filtering, CF)^[2]的推荐算法。该类算法基于用户对商品的评分或其他行为模式为用户提供个性化的推荐。目前协同过滤采用的主要技术包括基于邻域的方法^[3]和隐语义模型, 其中, 基于矩阵分解的隐语义模型^[4]具有较好的预测稳定性以及精确度。

文献[5]利用奇异值分解(Singular Value Decomposition, SVD)进行矩阵分解, 其主要缺点在于一开始就需要补全评分矩阵的缺失值, 即将一个稀疏矩阵转化为一个稠密矩阵后再进行分解。然而对高维稠密矩阵进行SVD分解的时间复杂度和空间复杂度都非常高。因此, 文献[6-7]分别提出基于正则化的矩阵分解(Regularized SVD, RSVD)模型和非对称矩阵分解模型(Asymmetric SVD, ASVD), 通过充分的正则化来避免过拟合, 且取得了较好的预测准确性。文献[8]提出基于信任的正则化分解模型TrustSVD, 将社会信任关系融入到推荐模型中, 有效提高了模型预测结果的准确度。文献[9]提出一种联合正则化的矩阵分解(Co-Regularized Matrix Factorization, CRMF)推荐模型, 将关联关系与社会关系相融合, 有效缓解用户的冷启动问题。SVD++模型^[7]在RSVD模型基础上融合隐式反馈信息使得预测的准确度进一步提高。

上述算法模型忽略了一个重要影响因素:用户的偏好和物品的流行度都可能会随着时间变化而改变。文献[10]提出一个基于时间依赖模型的推荐系统, 将时间因子引入到协同过滤算法中, 有效提高了推荐系统的预测准确度。但是, 在该模型引入的时间因子中, 物品偏置只与物品相关, 用户偏置只与用户相关, 导致推荐结果稳定性较差。

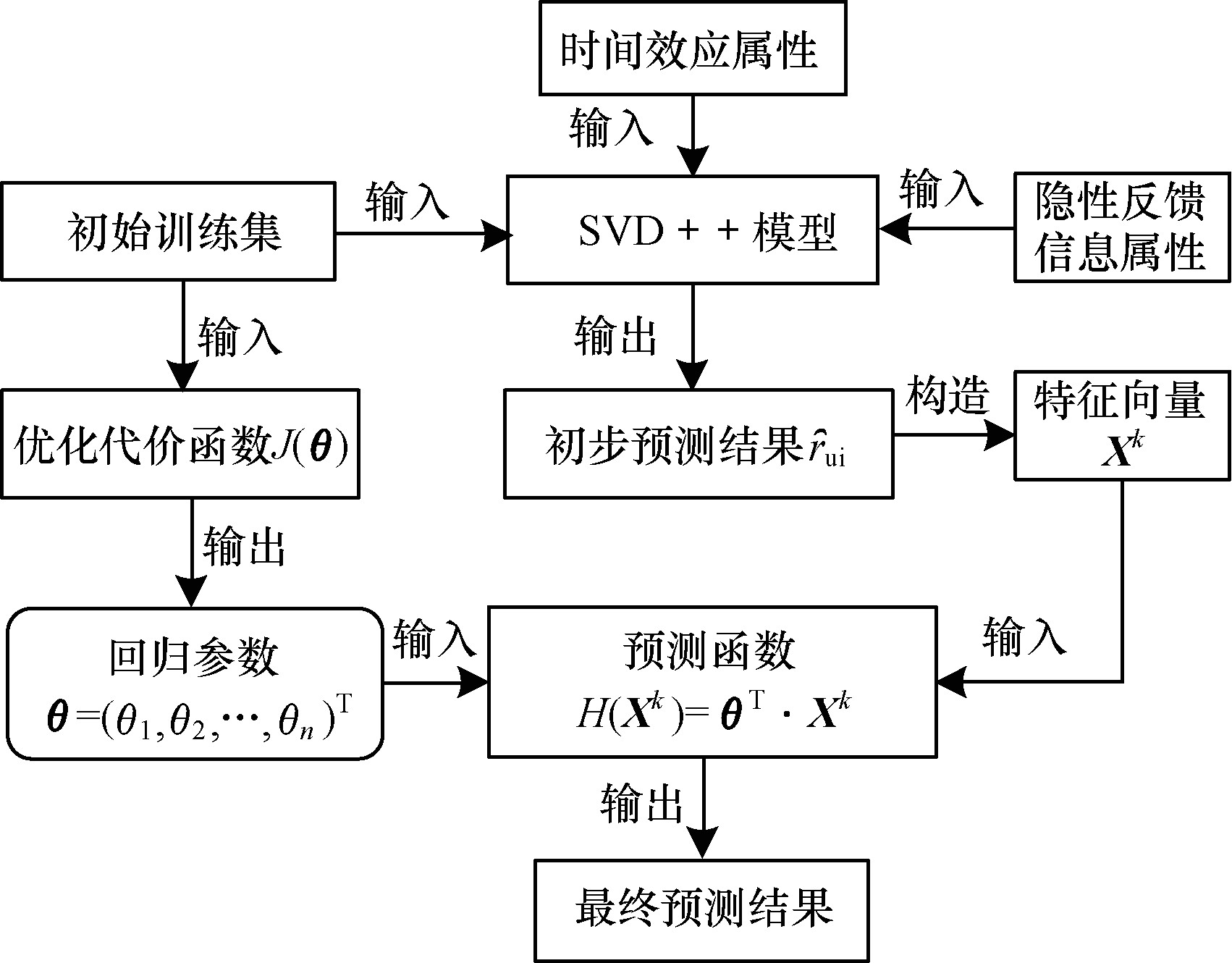
本文提出一种引入时间效应的SVD++线性回归推荐算法timeSVD++LR, 在SVD++模型的基础上引入时间效应属性, 通过对时间效应建模进一步提高预测结果的准确度, 同时根据初始预测评分构造特征向量X^k, 将原始训练数据作为线性回归模型^[11]的输入, 使用梯度下降算法^[12]优化最终代价函数, 生成一组参数θ=(θ₀, θ₁, …, θ_n)^T使得代价函数值最小, 并利用预测函数模型h_θ(X^k)=θ^TX^k求得测试集上的预测评分, 从整体上提高用户预测评分的准确性。

1 SVD++模型

SVD++模型在RSVD模型基础上融合隐式反馈信息, 使得预测的准确度进一步提高。SVD++模型的核心思想是通过隐含特征关系联系用户兴趣和项目, 将用户和项目两方面的信息融合隐式反馈信息映射到一个因子维度^[13]为f的联合隐语义空间, 用户-项目之间的交互作用被建模为该空间中的内积。

对于M个用户和N个项目, 假设评分矩阵R∈$\mathbb{R}^{M \times N}$为一个稀疏矩阵, 其中元素r_{u, i}表示用户u对项目i的评分, 对用户评分矩阵进行分解, 推导出2个分别代表用户与项目的低维潜在特征矩阵, 分别记$\boldsymbol{p} \in \mathbb{R}^{f \times M}$和$\boldsymbol{q} \in \mathbb{R}^{f \times M}$。相应地, 每一个项目i都与一个f维向量$\boldsymbol{q}_{i} \in \mathbb{R}^{f \times N}$相关, 每个用户u都与一个f维向量$\boldsymbol{p}_{u} \in \mathbb{R}^{f \times M}$相关, p_u和q_i的因子维度值f代表了该物品拥有这些因子的程度, 评分矩阵R中未知的评分$\hat{r}_{u, i}$由q_i^T·p_u来进行预测。由于在真实的模型应用中, 每个用户评分的基准线不同, 每个项目得到评分的基准线也不同, 因此引入参数μ表示训练集中所有记录评分的全局平均数; 引入用户偏置项b_u和项目偏置项b_i, 分别表示用户u和项目i与评分平均值μ的偏差。RSVD模型如式(1)所示。

$ {{\hat r}_{u,i}} = \mu + {b_i} + {b_u} + \mathit{\boldsymbol{q}}_i^{\rm{T}} \cdot {\mathit{\boldsymbol{p}}_u} $

(1)

隐式反馈信息能提供用户爱好的额外指示从而增加预测的准确度, 对于提供大量隐式反馈而仅提供少量显示反馈的用户尤其重要。为达到此目的, 为每一个项目i关联一个因子向量$\boldsymbol{y}_{i} \in \mathbb{R}^{f \times N}$, 用于根据用户评分的项目集合来表述用户特征, 由此得SVD++模型如式(2)所示。

$ {{\hat r}_{u,i}} = \mu + {b_i} + {b_{in}} + {\mathit{\boldsymbol{q}}_i}\left( {{\mathit{\boldsymbol{p}}_u} + {{\left| {R\left( u \right)} \right|}^{ - \frac{1}{2}}}\sum\limits_{j \in R\left( u \right)} {{\mathit{\boldsymbol{y}}_i}} } \right) $

(2)

其中, 集合R(u)包含用户u评分的所有项目, p_u+$|R(u)|^{-\frac{1}{2}} \sum\limits_{j \in R(u)} \boldsymbol{y}_{i}$为用户u的因子偏好程度, p_u可从显示评分记录学习得到, $|R(u)|^{-\frac{1}{2}} \sum\limits_{j \in R(u)} \boldsymbol{y}_{i}$从隐式反馈的角度出发, 由于y_i在0的附近取值, 为在观察值|R(u)|整个范围内稳定其方差, 此处用$|R(u)|^{-\frac{1}{2}}$来对其和做规范化。

2 线性回归模型

线性回归是按照给定的特征, 对其和实际值之间的组合关系进行分析, 并通过线性组合的方式来拟合真实值。对于每一条评分记录(样本k), 预测评分函数模型如式(3)所示。

$ {h_\theta }\left( {{\mathit{\boldsymbol{x}}^{\left( k \right)}}} \right) = {\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{x}}^{\left( k \right)}} = {\theta _0}x_0^{\left( k \right)} + {\theta _1}x_1^{\left( k \right)} + \cdots + {\theta _n}x_n^{\left( k \right)} $

(3)

其中, n表示特征个数, x^(k)表示样本k的特征向量。最终代价函数如式(4)所示。

$ J\left( {{\theta _0},{\theta _1}, \cdots ,{\theta _n}} \right) = \frac{1}{{2m}}\sum\limits_{k = 1}^m {{{\left( {{h_\theta }\left( {{\mathit{\boldsymbol{x}}^{\left( k \right)}}} \right) - {\mathit{\boldsymbol{y}}^{\left( k \right)}}} \right)}^2}} $

(4)

其中, J(θ₀, θ₁, …, θ_n)表示误差平方和, y^(k)表示真实值, m表示训练集的评论数总和(样本数)。代价函数用于计算参数θ=(θ₀, θ₁, …, θ_n)^T。利用梯度下降法优化代价函数J(θ₀, θ₁, …, θ_n)并求解最小值, 对θ进行求偏导操作, 解出求导部分如式(5)所示。

$ \theta _{j + 1}^k = \theta _j^k - \alpha \frac{1}{m}\sum\limits_{k = 1}^m {\left( {{h_\theta }\left( {{\mathit{\boldsymbol{x}}^{\left( k \right)}}} \right) - {\mathit{\boldsymbol{y}}^{\left( k \right)}}} \right)\mathit{\boldsymbol{x}}_j^{\left( k \right)}} $

(5)

其中, θ_j^k表示特征向量x^(k)中的第j个参数, α表示学习率, x_j^(k)表示特征向量x^(k)的第j个值。

3 timeSVD++LR推荐算法 3.1 算法原理

SVD++模型适用于对时间因子建模。通过将评分分解为各个不同项, 分别对应于不同方面的时序影响, 定义随时间变化的偏置因子^[14]:用户偏置b_u(t)和物品偏置b_i(t)。用户偏置b_u(t)体现为随着时间的变化, 用户可能会改变他们的基准评分, 例如某位过去倾向于对电影评分为3星的用户可能现在给出的评分为4星; 物品偏置b_i(t)体现为物品的流行度或许随时间变化, 例如在最新一部电影里某位演员的出现或许会导致该电影的流行或过时。在第t_ui天, 用户u对物品i的评分如式(6)所示。

$ {b_{ui}} = \mu + {b_u}\left( {{t_{ui}}} \right) + {b_i}\left( {{t_{ui}}} \right) $

(6)

其中, b_u(t_ui)和b_i(t_ui)是随时间变化的实数函数, 分别代表用户偏置b_u(t)和物品偏置b_i(t)。

$ {b_i}\left( t \right) = \left( {{b_i} + {b_{i \cdot {s_{ng}}\left( t \right)}}} \right){w_u}\left( {{t_{ui}}} \right) $

(7)

$ {b_u}\left( t \right) = \left( {{b_u} + {\alpha _u} \cdot b_u^{{\rm{is}}}\left( t \right)} \right) \cdot {z_i}\left( {{t_{ui}}} \right) $

(8)

其中, α_u表示每一个用户拥有的一个新的参数, 天数t关联一个整数S_ng(t)。对于每个用户u, 定义该用户评分日期的均值为t_u, 若u在第t天评价了一部电影, 则与该评分相关的时间偏置定义为b_u^is(t), 如式(9)所示。

$ b_u^{{\rm{is}}}\left( t \right) = {\left| {t - {t_u}} \right|^\tau }\ln \mathit{\Gamma } $

(9)

其中, τ=0.4。当t－t_u=0时, 令Γ=1, 则b_u^is(t)=0;当t－t_u>0时, 令Γ=e, 则b_u^is(t)=|t－t_u|^τ; 当t－t_u < 0时, 令Γ=e^－1, 则b_u^is(t)=-|t－t_u|^τ。

w_u(t_ui)表示物品偏置与时间相关的扩展特征, z_i(t_ui)表示用户偏置与时间相关的扩展特征, 增加参数z_i(t_ui)和w_u(t_ui)以改善由于引入时间因子带来的预测结果欠缺稳定性的问题。

$ {w_u}\left( {{t_{ui}}} \right) = {w_u} + {w_{u,t}},{z_i}\left( {{t_{ui}}} \right) = {z_i} + {z_{i,t}} $

(10)

其中w_u和z_i是稳定部分, w_{u, t}和z_{i, t}代表特定天的变化。

物品偏置b_i(t)和用户偏置b_u(t)可被分为一个固定部分和一个随时间变化的部分。通过使用随机梯度下降算法来最小化数据集上相关的平方误差函数来完成学习过程, 在SVD++算法中引入时间效应属性构造推荐模型, 用户u对物品i的初始预测评分用式(11)表示。

$ {{\hat r}_{u,i}} = {b_{ui}} + \mathit{\boldsymbol{q}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{p}}_u} + {{\left| {R\left( u \right)} \right|}^{ - \frac{1}{2}}}\sum\limits_{j \in R\left( u \right)} {{\mathit{\boldsymbol{y}}_i}} } \right) $

(11)

根据预测评分$\hat{r}_{u, i}$构造特征向量X^k, 将原始训练数据作为线性回归模型的输入, 采用梯度下降算法优化最终代价函数, 生成参数向量θ=(θ₀, θ₁, …, θ_n)^T使得代价函数值最小。将X^k和θ带入到预测模型中, 利用预测模型h_θ(X^k)=θ^TX^k求得预测评分, 从而在整体上提高用户预测评分的准确性。timeSVD++LR算法流程如图 1所示。

3.2 算法构建

从用户评分矩阵$\boldsymbol{R}_{1} \in \mathbb{R}^{M \times N}$抽取s条评分作为测试样本, 重新构造有效评分矩阵(训练集)$\boldsymbol{R} \in \mathbb{R}^{M \times N}$, r_{u, i}表示用户u对项目i的评分, r_{u, i}=－1表示未对该项目进行评分, r_{u, i}=0表示该评分作为测试集。$\boldsymbol{R} \in \mathbb{R}^{M \times N}$中评分记录数记为m(不包含0和-1的值), 表示有m个训练样本。

timeSVD++LR算法的构造步骤如下:

输入  有效评分矩阵$\boldsymbol{R} \in \mathbb{R}^{M \times N}$, 全局平均数μ, 正则化参数λ₂、λ₃、λ₄、λ₅、λ₆, 学习率γ。

输出  回归参数θ=(θ₀, θ₁, …, θ_n)^T, 最终预测评分矩阵$\hat{\hat{\boldsymbol{R}}}$。

步骤1  计算项目偏置项b_i和用户偏置b_u。

$ {b_i} = \frac{{\sum\limits_{u \in R\left( i \right)} {\left( {{r_{u,i}} - \mu } \right)} }}{{{\lambda _2} + \left| {R\left( i \right)} \right|}} $

(12)

$ {b_u} = \frac{{\sum\limits_{u \in R\left( i \right)} {\left( {{r_{u,i}} - \mu - {b_i}} \right)} }}{{{\lambda _3} + \left| {R\left( u \right)} \right|}} $

(13)

其中, R(i)表示评分了的物品i的所有用户列表, R(u)表示用户u给予评分的所有物品列表, λ₂=25, λ₃=10, 全局平均数μ表示训练集的平均评分。

步骤2  构造用户与项目的低维潜在特征矩阵$\boldsymbol{p}_{u} \in \mathbb{R}^{f \times M}$和$\boldsymbol{q}_{i} \in \mathbb{R}^{f \times N}$, 其中向量维度值代表了该物品拥有这些因子的程度。对用户偏好程度p_u加上隐式反馈信息, 如式(14)所示。

$ {{\mathit{\boldsymbol{\hat p}}}_u} = {\mathit{\boldsymbol{p}}_u} + {\left| {R\left( u \right)} \right|^{ - \frac{1}{2}}}\sum\limits_{j \in R\left( u \right)} {{\mathit{\boldsymbol{y}}_i}} $

(14)

步骤3  在矩阵因子分解方法中分别对项目偏置b_i和用户偏置b_u均加上时间效应属性, 如式(7)和式(8)所示, 用户u对物品i的初始预测评分如式(15)所示。

$ {{\hat r}_{u,i}} = \mu + {b_i}\left( {{t_{u,i}}} \right) + {b_u}\left( {{t_{u,i}}} \right) + \mathit{\boldsymbol{q}}_i^{\rm{T}} \cdot {{\mathit{\boldsymbol{\hat p}}}_u} $

(15)

为了学习模型中的参数b_i(t)、b_u(t)、p_u、q_i, 需要最小化相关联的正则化平方误差函数, 如式(16)和式(17)所示。

$ \min \sum {{{\left( {{r_{u,i}} - {{\hat r}_{u,i}}} \right)}^2}} + {\lambda _4} \cdot \varUpsilon $

(16)

$ \varUpsilon = {b_i}{\left( t \right)^2} + {b_u}{\left( t \right)^2} + \mathit{\boldsymbol{p}}_u^2 + \mathit{\boldsymbol{q}}_i^2 $

(17)

其中, 常量λ₄=0.02用来控制正则化程度, 最小化过程通过随机梯度下降算法实现。相关的预测误差记为$e_{u, i}=r_{u, i}-\hat{r}_{u, i}$, 对于给定的训练集$\boldsymbol{R} \in \mathbb{R}^{M \times N}$, 通过朝着与梯度相反的方向移动来修正参数, 如式(18)~式(21)所示。

$ {b_u}\left( t \right) \leftarrow {b_u}\left( t \right) + \gamma \cdot \left( {{e_{u,i}} - {\lambda _5} \cdot {b_u}\left( t \right)} \right) $

(18)

$ {b_i}\left( t \right) \leftarrow {b_i}\left( t \right) + \gamma \cdot \left( {{e_{u,i}} - {\lambda _5} \cdot {b_i}\left( t \right)} \right) $

(19)

$ {\mathit{\boldsymbol{q}}_i} \leftarrow {\mathit{\boldsymbol{q}}_i} + \gamma \cdot \left( {{e_{u,i}} \cdot {{\mathit{\boldsymbol{\hat p}}}_u} - {\lambda _6} \cdot {\mathit{\boldsymbol{q}}_i}} \right) $

(20)

$ {\mathit{\boldsymbol{y}}_i} \leftarrow {\mathit{\boldsymbol{y}}_i} + \gamma \cdot \left( {{e_{u,i}} \cdot {{\left| {R\left( u \right)} \right|}^{ - \frac{1}{2}}} \cdot {\mathit{\boldsymbol{q}}_i} - {\lambda _6} \cdot {\mathit{\boldsymbol{y}}_i}} \right) $

(21)

通过为每类待学习参数选择学习率γ和正则化因子λ来提高预测准确度, 本文设置γ=0.02, λ₆=0.015, λ₅=0.005。

步骤4  根据式(16)计算测试集的预测评分, 重新构建用户评分矩阵$\hat{\boldsymbol{R}}$(用测试集预测评分替代$\boldsymbol{R}_{1} \in \mathbb{R}^{M \times N}$原始测试集部分), 其中元素$\hat{r}_{u, i}$表示用户u对项目i的预测评分(针对测试集部分), 由于$\hat{\boldsymbol{R}} \neq \boldsymbol{R}$, 但$\hat{\boldsymbol{R}} \cong \boldsymbol{R}_{1} \in \mathbb{R}^{M \times N}$, 因此在timeSVD++模型基础上, 根据预测评分构造特征向量X, 进行线性回归操作进一步提高预测精度。

步骤5  重构评分矩阵$\hat{\boldsymbol{R}}$包含m个训练样本和s个测试样本, 每个样本包含n个特征, 令X^k=[x₀^(k), x₁^(k), …, x_n^(k)]^T, 1≤k≤m。令回归参数θ=(θ₀, θ₁, …, θ_n)^T, 构造预测模型h_θ(X^k)=θ^TX^k如式(3)所示, 针对m个样本, 则有h_θ(X)=θ^TX:

$ {h_\theta }\left( \mathit{\boldsymbol{X}} \right) = {\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{X}} = {\theta _0}{x_0} + {\theta _1}{x_1} + \cdots + {\theta _n}{x_n} $

(22)

步骤6  从有效评分矩阵$\boldsymbol{R} \in \mathbb{R}^{M \times N}$中选取m个初始样本评分值记为y^(k), 其中1≤k≤m, 根据式(4)构造代价函数J(θ₀, θ₁, …, θ_n), 利用梯度下降法优化代价函数使J(θ₀, θ₁, …, θ_n)最小, 得到最终求导部分解如式(23)所示。

$ {\theta _{j + 1}} = {\theta _j} - \alpha \frac{1}{m}\sum\limits_{k = 1}^m {\left( {{h_\theta }\left( {{\mathit{\boldsymbol{X}}^k}} \right) - {\mathit{\boldsymbol{y}}^{\left( k \right)}}} \right)} X_j^k $

(23)

其中, α=0.000 05表示学习率, X_j^k表示特征向量X^k的第j个值, θ_j表示第j个参数。经过多次迭代求得一组回归参数θ=(θ₀, θ₁, …, θ_n)^T。

步骤7  将回归参数θ以及测试样本特征向量X^k=[x₀^(k), x₁^(k), …, x_n^(k)]^T, 1≤k≤s, 带入到预测模型h_θ(X^k)=θ^TX^k中, 得到测试样本对应的预测评分值, 再次重构评分矩阵$\hat{\boldsymbol{R}}$, 得到最终评分矩阵$\hat{\hat{\boldsymbol{R}}} \approx R_{1} \in \mathbb{R}^{M \times N}$。

timeSVD++LR算法构造部分用到多个常量值, 针对SVD++算法, 当λ₂=25, λ₃=10, λ₄=0.02, λ₅=0.005, λ₆=0.015时^[15], 推荐算法的预测效果最好, 考虑到本文提出的算法与SVD++算法的相关性, 故选取相同的正则化参数值, 并且当学习率γ=0.02时, 在MovieLens数据集上进行测试预测结果最稳定。

4 实验与结果分析 4.1 实验设置

为测试timeSVD++LR算法的准确性, 本文将其与RSVD、SVD++、timeSVD++算法进行比较。实验采用MovieLens数据集^[16]中的MovieLens_100k数据集, 包含943名用户对1 682部电影的约100 000条评分信息(评分密度约为6.3%), 记为MovieLens_LR数据集。文献[17]对推荐系统领域内的各种不同的评价标准做了总结, 本文将采用检验推荐算法最常用的平均绝对误差(Mean Absolute Deviation, MAE)、均方根误差(Root Mean Square Error, RMSE)作为评价指标^[18]。

$ M_u^{{\rm{MAE}}} = \frac{{\sum\limits_{i = 1}^N {\left( {{X_i} - {Y_i}} \right)} }}{N} $

(24)

$ M_u^{{\rm{RMSE}}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {{X_i} - {Y_i}} \right)}^2}} }}{N}} $

(25)

其中, X_i表示timeSVD++LR算法对项目的最终预测评分, Y_i表示用户的实际评分, N表示项目的数量。MAE和RMSE的值越小, 表示算法性能越好。

由于MovieLens_LR数据集中的样本只包含用户编号、项目编号、用户评分和用户评分时间等属性, 并且用户编号和项目编号无法作为特征, 因此本文实验将timeSVD++算法得到的预测评分作为线性回归模型的特征来源, 针对样本k(用户u对项目i的评分样本)选取特征向量X^k=[x₀^(k), x₁^(k), x₂^(k), x₃^(k), x₄^(k)]^T, 其中, x₀^(k)默认为0, x₁^(k)、x₂^(k)、x₃^(k)和x₄^(k)如式(26)~式(29)所示。

$ x_1^{\left( k \right)} = \left( {{R_{u,i}} \cdot {R_{u,i}}} \right)/25 $

(26)

$ x_2^{\left( k \right)} = \left( {{R_{u,i}} + {\sigma _2}} \right) \cdot \left( {\mu + {\sigma _1}} \right)/25 $

(27)

$ x_3^{\left( k \right)} = {R_{u,i}} \cdot \left( {\mu + {\sigma _1}} \right)/25 $

(28)

$ x_4^{\left( k \right)} = {R_{u,i}} \cdot \left( {\mu + {\sigma _2}} \right)/25 $

(29)

其中, μ为全局平均数, σ₁=0.000 05、σ₂=-0.000 05为调节因子, 其作用主要是为稳定特征向量值的变化, 对整体特征向量值影响不大。

若样本k来源于训练集, 则$\hat{R}_{u, i}=r_{u, i}$; 若样本k来源于测试集, 则$\hat{R}_{u, i}=\hat{r}_{u, i}$。定义预测函数为h_θ(X^k)=θ₀+θ₁x₁^(k)+θ₂x₂^(k)+θ₃x₃^(k)+θ₄x₄^(k), 损失函数为$J(\boldsymbol{\theta})=\frac{1}{2 m} \sum\limits_{k=1}^{m}\left(h_{\theta}\left(\boldsymbol{X}^{k}\right)-\boldsymbol{y}^{(k)}\right)^{2}$, m为训练集样本数, 当J(θ)的值达到最小时, 生成回归参数θ=(θ₀, θ₁, θ₂, θ₃, θ₄)^T。将θ和测试集数据的特征向量带入到预测函数中求得测试集的预测评分。

4.2 结果分析

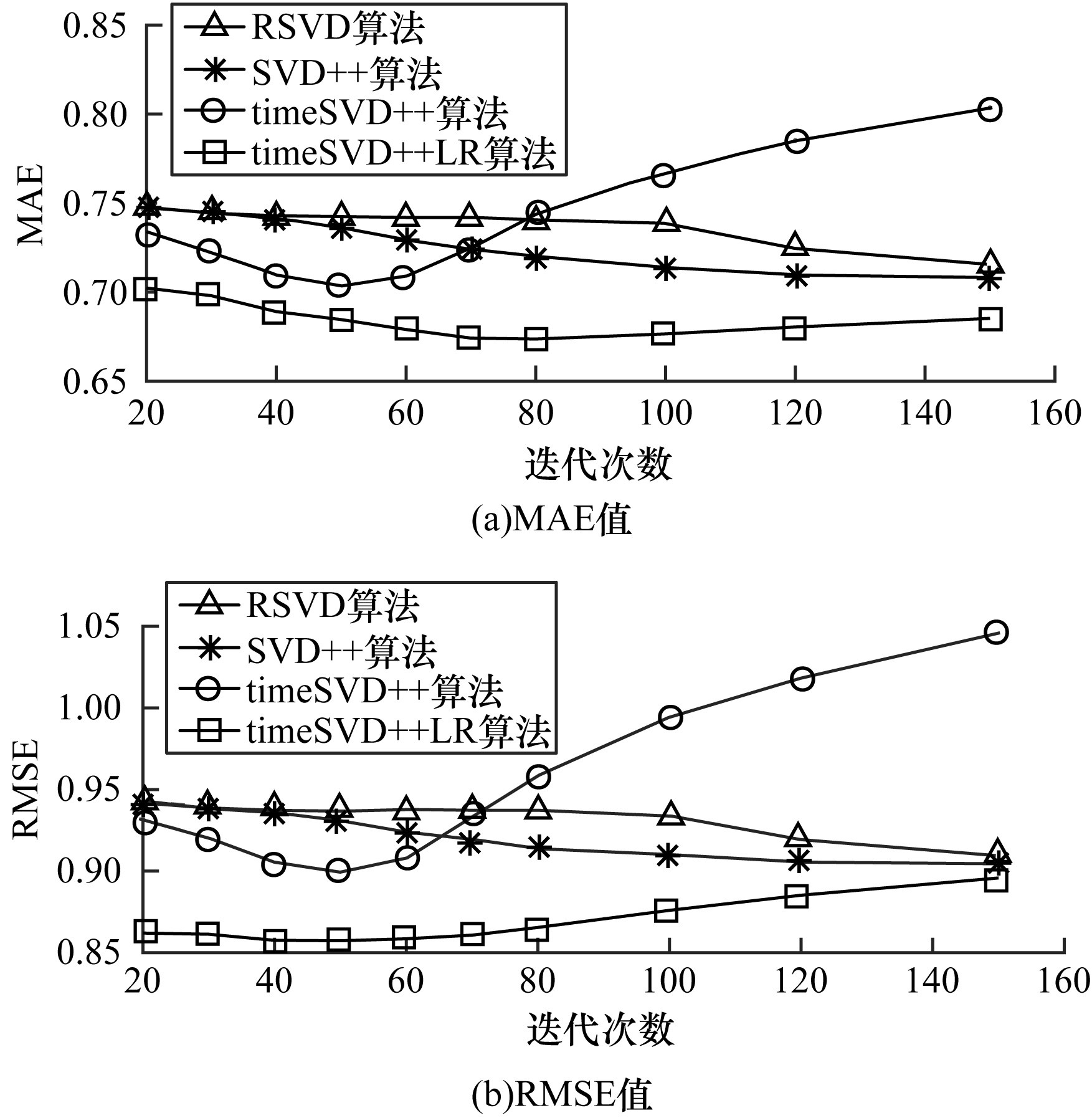
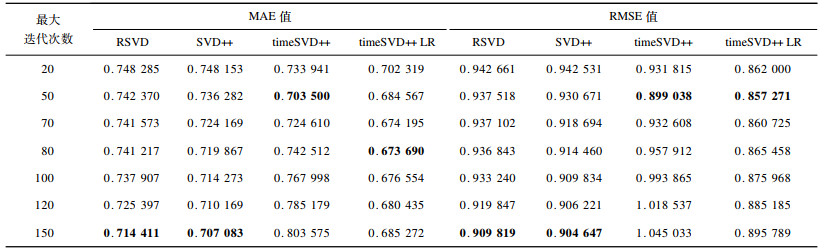
实验骤1  在MovieLens_LR数据集上测试不同最大迭代次数下算法的表现。为减弱学习率γ和因子维度f带来的影响, 令γ=0.002, f=20。在设置的最大迭代次数内, 将损失函数J(θ)所能达到的最小值对应的一组θ=(θ₀, θ₁, θ₂, θ₃, θ₄)^T值作为预测函数h_θ(X^k)的参数, 求出最终的预测分数。实验1的结果如图 2和表 1所示。在表 1中, 加粗数据为各算法的最优MAE/RMSE值。从图 2可以看出, timeSVD++LR算法的MAE、RMSE值均较其他3种算法小, 其MAE值在0.68附近波动, RMSE值保持在0.86左右。timeSVD++算法仅在SVD++算法基础上引入时间效应属性, 未进行线性回归操作, 故其MAE和RMSE值较为不稳定, 但最大迭代次数小于70左右时, 相较于RSVD和SVD++算法, 其MAE和RMSE值均相对较小, 说明在timeSVD++中引入时间效应属性在能有效提高推荐算法的预测精度。TimeSVD++LR在TimeSVD++基础上又引入线性回归操作, 还能进一步提高推荐算法稳定性。特别地, 当最大迭代次数为80时, timeSVD++LR算法模型的MAE值最小, 约为0.673 6;当最大迭代次数为50时, timeSVD++LR算法模型的RMSE值最小, 约为0.857 2。

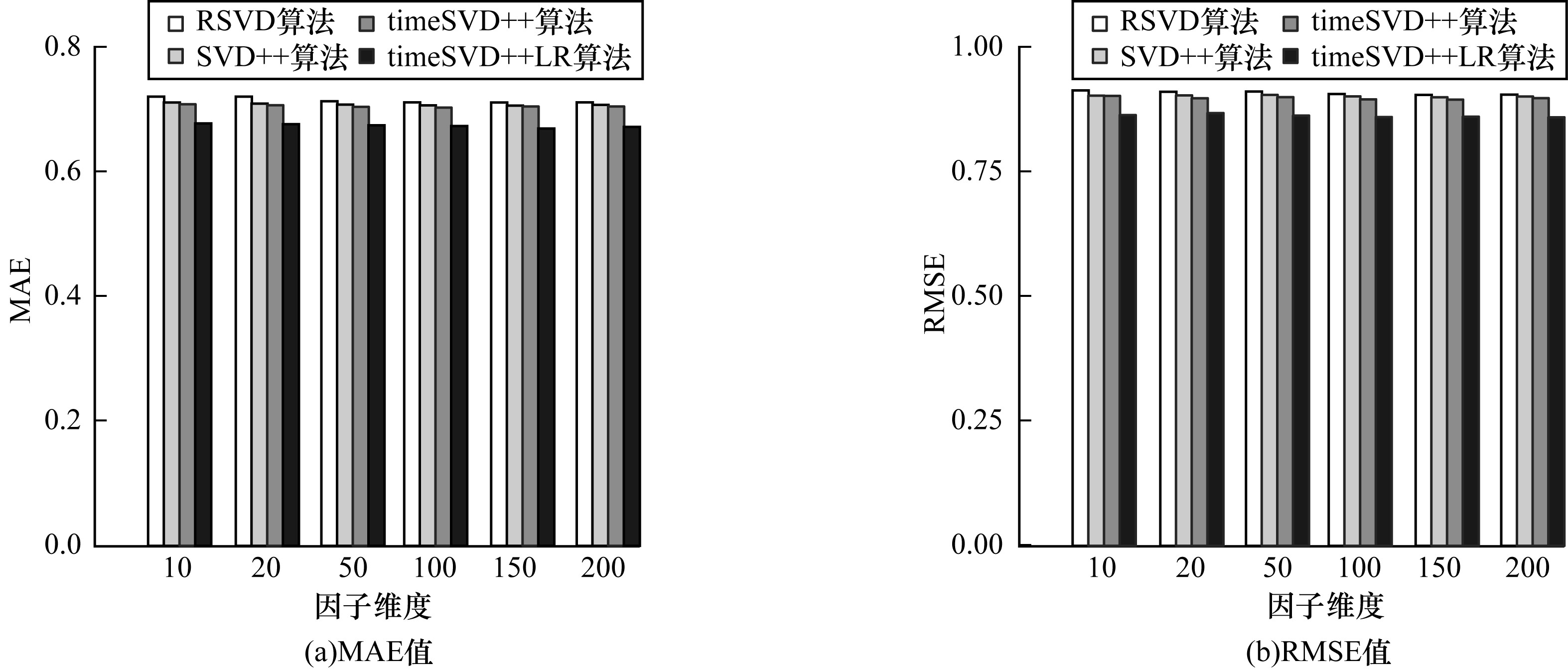
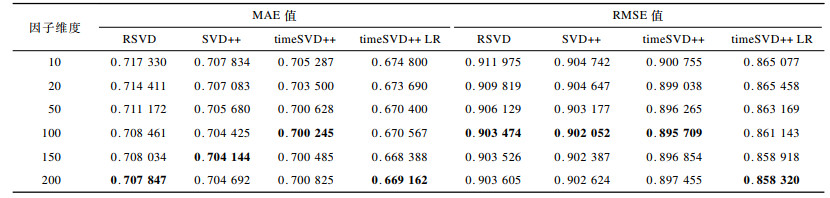
实验2  在同一数据集上测试不同因子维度f下算法的表现。4种算法模型的学习率均取γ=0.002。从表 1可知, RSVD、SVD++、timeSVD++和timeSVD++LR算法最佳最大迭代次数依次为150、150、50和80, 故在实验2中设置最大迭代次数为最佳迭代次数, 结果如图 3和表 2所示。在表 2中, 加粗数据为各算法的最优MAE/RMSE值。从图 3可看出, 在一定范围内随着因子维度的增大, 4种算法的MAE和RMSE值均逐渐减小。这说明在一定范围内因子维度的增大可提高算法的预测准确度。从表 2可看出, 当因子维度为200时, timeSVD++LR算法的RMSE值最小, 约为0.858 3, 此时MAE值约为0.669 1, 其结果均小于其他3种算法的最小RMSE和最小MAE值。

通过2组实验对比可知, 在4种算法中, timeSVD++LR算法的稳定性和预测精度较好。

5 结束语

本文提出一种引入时间效应的推荐算法timeSVD++LR。在SVD++模型基础上引入时间效应属性, 根据预测评分构造特征向量。将原始训练数据作为线性回归模型的输入, 采用随机梯度下降算法优化代价函数, 使得代价函数值最小, 生成回归参数, 并根据特征向量和回归参数求得预测评分。实验结果表明, timeSVD++LR算法的推荐准确性较RSVD、SVD++、timeSVD++算法有显著提高且推荐结果较为稳定, 同时还能较好地改善评分矩阵稀疏和扩展性弱等问题。下一步将在本文算法的基础上研究其他分类算法对推荐系统的影响。