随着计算机运算速度的提升和大数据技术的发展,自从2012年AlexNet[1]在ImageNet竞赛中获得冠军后,研究人员不断设计出更深和更复杂的深度神经网络(Deep Neural Network,DNN)模型以期获得更好的分类精度。但深度神经网络复杂的结构所需的庞大计算资源使其在实际应用中受到一定的限制,主要表现为DNN模型在资源受限的无人机、智能手机、平板电脑等硬件设备上难以进行有效部署,因此网络压缩技术应运而生。目前主流的网络压缩方法有网络剪枝[2-4]、网络参数量化[5-6]与分解[7]、网络结构轻量化设计[8]和知识蒸馏[9]等,其中网络剪枝是对网络中的冗余元素进行裁剪,是最常用的网络压缩方法之一,其能同时对卷积层和全连接层进行裁剪,尤其是结构化剪枝方法可以不受硬件条件的限制而直接达到减少网络内存占用和网络加速的目的,并且网络剪枝还可以与其他网络压缩方法进行兼容,如剪枝后的网络能通过知识蒸馏提高网络性能[10],或者利用网络结构轻量化设计进一步提升网络压缩效果[5]。
网络剪枝的核心是衡量元素的重要性并对其进行裁剪,现有算法提出的剪枝标准通常只涉及网络模型的零阶信息(参数本身信息)或一阶信息(梯度信息)[4, 11-12],并没有涉及网络二阶信息。然而,网络模型的二阶信息也是十分重要的信息,在机器学习优化任务中可以加快模型收敛速度[13]。在网络量化任务中,HAWQ算法[14]利用网络结构的二阶信息将网络不同层次量化为不同精度。在网络剪枝任务中,OBD[2]和OBS[3]算法均利用网络二阶信息,但是这2种算法需要计算Hessian矩阵,所以会消耗大量计算资源,并且OBS算法的改进版本L-OBS算法[15]依然需消耗较多的计算资源,而且这3种剪枝算法都属于非结构化剪枝算法,需要特定的硬件支持才能达到网络加速效果。
为将深度神经网络二阶信息用于网络通道剪枝,本文提出一种基于HAWQ[14]算法的结构化剪枝算法。该算法利用幂迭代法[16]获取网络通道的二阶信息,将其作为衡量通道重要性的依据并进行通道剪枝,再对剪枝后的网络进行微调得到紧凑网络,最终将本文算法运用于ResNet[17]网络与VGGNet[18]网络,并在Cifar10和Cifar100数据集[19]上进行实验验证。
1 相关工作随着深度神经网络在各行各业的深入应用,深度神经网络压缩研究也受到国内外学者的广泛关注[20]。深度神经网络剪枝算法在20世纪80年代的代表算法主要有OBD[2]和OBS[3]。HAN等人[4]于2015年对深度神经网络参数进行有效裁剪,并取得了良好的效果,该方法属于静态剪枝,即裁剪的元素不可恢复。GUO等人[21]于2016年提出动态剪枝方法,对裁剪的元素采取可恢复机制,有效提高了剪枝后的网络性能。在OBS算法的基础上,DONG等人[15]于2017年将深度神经网络的全局裁剪拓展至逐层裁剪,提出L-OBS算法。
上述剪枝算法均属于非结构化剪枝,非结构化剪枝的裁剪对象为深度神经网络参数,其虽然达到了网络稀疏效果,但需要特定的硬件支持才能达到网络加速的目的。然而,结构化剪枝可以不受硬件条件的限制,因为其剪枝对象为网络卷积核,所以可以直接达到网络加速目的。文献[11]将网络通道的L1范数作为衡量通道重要性的依据,并据此裁剪L1范数较小的通道。文献[22]依据网络下一层的输出,裁剪对输出影响较小的卷积核达到网络压缩的目的。文献[23]在原卷积核的基础上加入协同层来控制相应卷积核参与网络运算,使得最终网络结构变得复杂,但是仍可实现网络加速。文献[24]在网络通道剪枝过程中引入网络通道可恢复机制,提高网络的容错能力。文献[12]利用深度神经网络批量归一化(Batch Normalization,BN)层信息对深度神经网络进行有效剪枝,并将剪枝算法应用于YOLO网络剪枝任务中。针对网络剪枝的预训练问题,文献[25]分别对结构化剪枝与非结构化剪枝的经典算法进行深入研究,得出网络预训练并非网络剪枝中的必要步骤,引起了学业界的广泛讨论。另外,机器学习方法[10, 26]也被运用于网络剪枝任务中对网络结构实现自动化剪枝,大幅提升了网络剪枝效率。
2 结构化剪枝算法本文提出的结构化剪枝算法首先对网络进行预训练,然后利用幂迭代法[16]得到网络参数对应Hessian矩阵的主特征向量,将得到的向量用于衡量网络通道的重要性并进行通道剪枝,最后对剪枝后的网络进行再训练提高网络性能。
2.1 网络通道二阶信息获取 2.1.1 幂迭代法本文算法利用幂迭代法获取网络结构的二阶信息。幂迭代法是一种用于求解矩阵按模最大特征值(主特征值)及其对应特征向量(主特征向量)的方法。设
| $ \mathop {\lim }\limits_{k \to \infty } \frac{{{\mathit{\boldsymbol{u}}_{k, i}}}}{{{\mathit{\boldsymbol{u}}_{k - 1, i}}}} = {\lambda _1}, i = 1, 2, \cdots , n $ | (1) |
其中,uk,i是向量uk的第i个分量值[16],只要选取合适的随机向量u0,当k足够大时就可以计算P的主特征值λ1及其主特征向量uk。
2.1.2 二阶信息获取由于每层通道的参数维数很大,其对计算机存储和计算造成巨大压力,因此很难直接计算网络参数的Hessian矩阵,如对于d维的向量,得到其Hessian矩阵的复杂度为O(d2)。受HAWQ算法[14]启发,本文提出一种新的结构化剪枝算法,利用幂迭代获取网络二阶信息,其需要计算Hessian矩阵与向量的乘积。
下文对深度神经网络中网络通道参数Hessian矩阵对应的主特征向量计算进行具体介绍。假设一个网络具有LLr(
| $ L\left( {{\rm{}}\mathit{\boldsymbol{W}}{\rm{}}} \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^n l\left( {{\mathit{\boldsymbol{x}}_i}{\rm{}}, {\mathit{\boldsymbol{y}}_i}{\rm{}}, \mathit{\boldsymbol{W}}} \right) $ | (2) |
其中,
| $ \mathit{\boldsymbol{g}} = \frac{{\partial L}}{{\partial \mathit{\boldsymbol{W}}}} $ | (3) |
对于一个与梯度g维数相同的随机向量v存在式(4)成立:
| $ \frac{{\partial \left( {{\mathit{\boldsymbol{g}}^{\rm{T}}}\mathit{\boldsymbol{v}}} \right)}}{{\partial \mathit{\boldsymbol{W}}}} = \frac{{\partial {\mathit{\boldsymbol{g}}^{\rm{T}}}}}{{\partial \mathit{\boldsymbol{W}}}}\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{g}}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial \mathit{\boldsymbol{W}}}} = \frac{{\partial {\mathit{\boldsymbol{g}}^{\rm{T}}}}}{{\partial \mathit{\boldsymbol{W}}}}\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{Hv}} $ | (4) |
其中,H是损失函数L对于参数W的Hessian矩阵。式(4)成立的条件之一为向量v是随机向量,其与参数W无关。基于此,下文给出基于幂迭代法的网络Hessian矩阵主特征向量求解算法。
算法1 基于幂迭代法的网络Hessian矩阵主特征向量求解算法
输入 网络参数W、随机向量v(v与W维度相同)
输出 主特征向量V(V=v)
1.通过后向传播计算W的梯度:g=dL/dW;
2.正则化v:v=v/‖v‖;
3.For c=1,2,…,m
4.gv=gTv;
5.Hv=d(gv)/dW;
6.正则化Hv,v=Hv/‖Hv‖;
7.End For
通过算法1可以得到深度神经网络参数所对应Hessian矩阵的主特征向量。算法1的算力损耗主要为第5步,因为第5步需要求导,假设参数W维数为d,最大循环次数为m,所以求解特征向量的算法复杂度为O(md),相比于直接计算Hessian矩阵的计算复杂度O(d2),算法1的计算复杂度明显降低,其能避免直接求解网络的Hessian矩阵来获得其主特征向量,该特征向量包含二阶信息。
2.2 基于网络二阶信息的结构化剪枝算法基于网络二阶信息的结构化剪枝算法框架(第i层)如图 1所示,其中,Pi表示每一层的剪枝率,Ni+1表示输出通道数。

|
Download:
|
| 图 1 基于网络二阶信息的结构化剪枝算法框架(第i层) Fig. 1 Framework of structural pruning algorithm based on second-order information of network(the i-th layer) | |
经过算法1可以求出网络参数对应的Hessian矩阵主特征向量V,下文将具体介绍如何利用V进行深度神经网络结构化剪枝,其中Vi,j(0≤i≤LLr-1,1≤j≤Ni+1)为深度神经网络参数对应Hessian矩阵主特征向量V在第i层、第j个通道的对应值。本文结构化剪枝算法属于硬剪枝[11]算法,通道重要性的衡量依据是得出的特征向量V在对应通道Vi,j的Lp范数,计算公式为:
| $ {\left\| {{\mathit{\boldsymbol{V}}_{i, j}}} \right\|_p} = p\sqrt {\sum\limits_{n = 1}^{{N_i}} {\sum\limits_{{k_1}}^K {\sum\limits_{{k_2} = 1}^K {{{\left\| {{\mathit{\boldsymbol{V}}_{i, j}}\left( {n, {k_1}, {k_2}} \right)} \right\|}^p}} } } } $ | (5) |
其中:k1、k2分别为卷积核感受野的尺度,若为3×3卷积核,则k1=k2=3;Ni是上层卷积层的输出通道数。
硬剪枝算法需要对网络模型进行预训练,待网络模型达到较好的性能后再进行通道裁剪。因为直接裁剪后的网络性能会受到一定损耗,所以需要进行微调恢复网络性能。基于网络二阶信息的结构化剪枝算法采用预训练-剪枝-微调步骤。
算法2 基于网络二阶信息的结构化剪枝算法
输入 深度神经网络、训练数据X、剪枝率Pi
输出 紧凑的网络结构
1.初始化网络参数W;
2.对网络输入X进行训练,使网络损失函数收敛;
3.利用算法1计算W对应的Hessian矩阵主特征向量V;
4.For i=1,2,…,LLr-1
5.根据式(5)得到主特征向量V在对应通道Vi,j(1≤j≤Ni+1)中的L1范数
6.根据
7.保留被选择的通道并裁剪其余通道;
8.End For
9.获得紧凑的网络结构及其对应的参数W;
10.微调网络参数W得到最终的网络参数W*
算法2的第1步是对神经网络参数进行随机初始化;第2步是训练一个性能良好的深度神经网络用于剪枝,该步骤属于网络预训练过程;第3步可以通过算法1实现;第5步是计算特征向量的L1范数,即向量元素的绝对值之和;第6步和第7步是对网络参数进行裁剪;第4步~第9步为一个内循环过程,对深度神经网络一层通道进行裁剪;第10步是微调过程,网络微调实际上是对剪枝后的深度神经网络进行再训练,由于剪枝后深度神经网络的一些网络通道会缺失,因此网络精度会降低,需要对剪枝后的网络参数W进行微调得到性能良好的网络参数W*,计算公式为:
| $ {\mathit{\boldsymbol{W}}^*} = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_{\mathit{\boldsymbol{\bar W}}} L(\mathit{\boldsymbol{\bar W}}) $ | (6) |
在微调过程中的学习率和迭代次数均小于预训练时的学习率和迭代次数。
3 实验结果与分析本节主要介绍本文结构化剪枝算法在ResNet[17]和VGGNet[18]网络模型上的压缩效果,所有实验均基于PyTorch框架[27]。
3.1 实验数据集Cifar10数据集[19]是深度学习领域较常用的图片数据集,其常被应用于深度学习的分类任务。Cifar10数据集共分为10类,每类有6 000张图片,包括10种不同物体,每张图片为32像素×32像素的三通道RGB图片。Cifar10数据集共有50 000张训练集图片和10 000张测试集图片。
Cifar100数据集[19]是Cifar10数据集的一个衍生数据集,其所有图片均与Cifar10数据集相同。Cifar100数据集将Cifar10数据集的每类物体数据进行再划分,使原有的10类样本划分为100类样本,每类样本包含600张图片,所以Cifar100数据集可以看成Cifar10数据集的精细版本。
3.2 对比算法在实验中,将本文结构化剪枝算法与以下算法进行对比:
1)PF算法[11]。PF算法是经典的硬剪枝算法,该算法利用已训练的网络参数L1范数作为衡量通道重要性的标准并裁剪L1范数较小的通道,并对裁剪后的网络进行微调。
2)LCCL算法[23]。LCCL算法在卷积层后面加入一个低损耗的协同层来控制卷积层中相应的卷积核参与运算,其虽然达到网络加速目的,但是网络结构由此变得更加复杂。
3)Rethinking算法[25]。Rethinking算法将经典的剪枝算法进行复现,使用特殊的再训练方式对裁剪后的网络参数进行赋值,从而达到良好的网络性能。
4)SFP算法[24]。SFP算法是经典的软剪枝算法,在剪枝过程中对通道采用可恢复机制,提高了算法剪枝效果,但是其相比硬剪枝算法整个剪枝过程更长。
3.3 实验设置与性能指标本文算法在剪枝前网络模型需要进行预训练160步,初始学习率为0.1,在第80步~第120步内对学习率进行逐步衰减。微调步数为40步或80步,初始学习率设为0.001,在50%的训练步数后实施学习率衰减。算法1的最大迭代次数m取10。在VGGNet网络、ResNet56网络及ResNet110网络上,本文算法采用PF算法[11]的剪枝率。PF算法通过实验找出每个网络模型的敏感层,即对最终输出结果有很大影响的层,该算法在裁剪过程中跳过敏感层,即敏感层的剪枝率为0,其中:ResNet56网络A剪枝方式的剪枝率为10%,其跳跃层为第18层、第20层、第38层和第54层;ResNet56网络B剪枝方式的剪枝率为60%、30%和10%,其跳跃层为第16层、第18层、第20层、第34层、第38层和第54层;ResNet110网络A剪枝方式只在前期采用50%的剪枝率,其跳跃层为第36层;ResNet110网络B剪枝方式的剪枝率为50%、40%和30%,其跳跃层为第36层、第38层和第74层;VGG16网络的A剪枝方式对特定的多个卷积层采用50%的剪枝率。
网络剪枝算法的性能评价指标主要有分类准确率、参数量以及每秒浮点运算次数(Floating-point Operations Per Second,FLOPS),其中:分类准确率表征DNN模型分类结果;参数量衡量DNN所占用的计算机内存大小,参数量减少比例是剪枝后的网络与未剪枝的原始网络在网络参数量上相比减少的百分比;FLOPS是衡量网络运行速度的指标,FLOPS减少说明网络在实际运算中可以取得加速的效果,减少量越大,说明加速效果越明显。
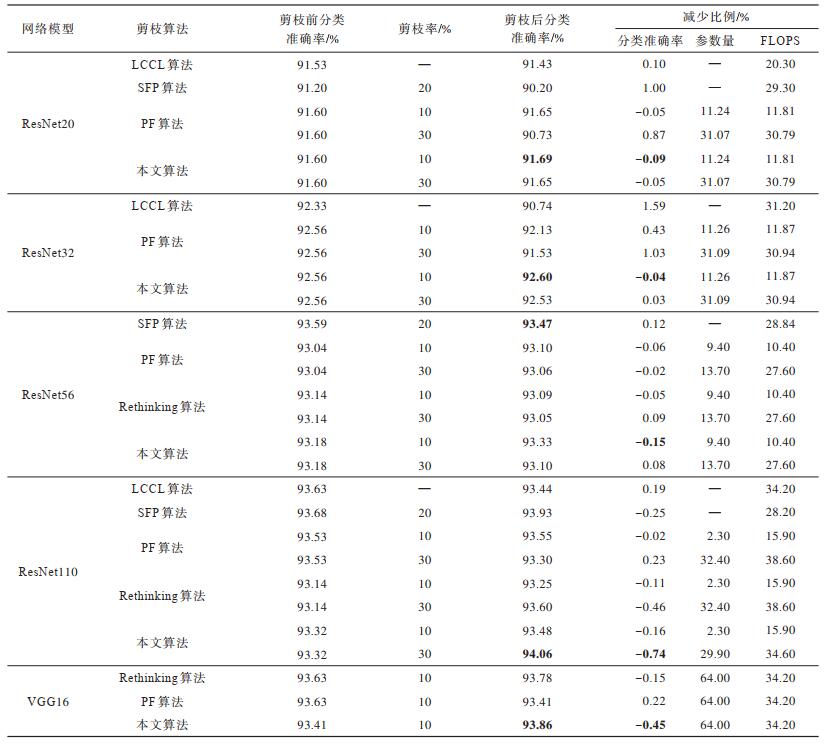
3.4 结果分析 3.4.1 Cifar10数据集上的实验结果表 1为本文算法与PF、LCCL等剪枝算法在ResNet与VGGNet网络模型上的实验结果对比,其中直接使用文献[11, 23-25]中已有对比算法的实验结果,加粗数据表示最优结果,“—”表示文献[23-24]缺少相应数据。可以看出,经过本文算法剪枝,网络结构的参数量与FLOPS均明显减少,但是网络性能未受到影响,而且在ResNet110、VGG16等网络模型上,网络性能还得到了一定的提升,具体表现为本文算法准确率在ResNet110网络模型和VGG16网络模型上分别提升了0.74%和0.45%。
|
下载CSV 表 1 5种剪枝算法在Cifar10数据集上的对比结果 Table 1 Comparison results of five pruning algorithms on Cifar10 dataset |
在相同的剪枝率下,与PF算法和Rethinking算法相比,本文算法在所有网络模型上均取得了较好的结果,说明本文算法的剪枝性能最优。在ResNet110网络模型上,本文算法相比LCCL算法在FLOPS减少比例相当的情况下,可以获得更高的分类准确率,且经过本文算法裁剪后的网络占用内存更小。在ResNet56网络模型上,在FLOPS减少比例相近的情况下,本文算法相比SFP算法分类准确率减少比例更具优势,说明其可以与软剪枝算法取得相当的剪枝性能且实现更简单。另外,从表 1可以看到,ResNet网络随着层数的加深,取得的剪枝效果也越来越好,VGG16网络经过剪枝后分类准确率也得到了一定的提升,说明随着网络层数的加深,网络中可能存在更多的冗余元素,裁剪这些冗余元素会提升分类准确率,从而论证越复杂的深度神经网络越容易裁剪这一观点。
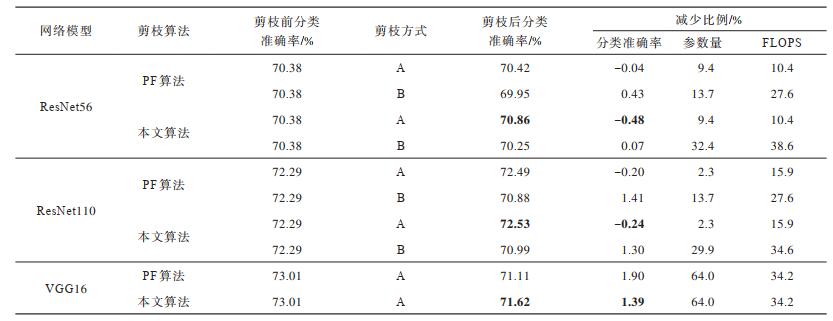
3.4.2 Cifar100数据集上的实验结果表 2为本文剪枝算法与PF算法在Cifar100数据集上的实验结果,其中加粗数据表示最优结果。由于文献[11]没有使用Cifar100数据集进行实验,因此该实验所有结果均是笔者复现的结果。根据表 2可以看出,本文算法在更复杂的分类任务中同样可以对深度神经网络进行有效裁剪,在对分类准确率没有较大影响的情况下网络模型的参数量与FLOPS都得到明显减少,但当网络模型的剪枝率较小时,其分类准确率反而得到了提升。与PF算法相比,本文算法在3个网络模型上均更具优势,说明其在更复杂的分类任务中也具有更好的剪枝性能。同时,对比网络模型在两个数据集上的实验结果,可以看出深度神经网络模型在Cifar100数据集上剪枝后的分类准确率减少比例更大,说明其对于不同复杂度的分类任务而言具有不同的冗余度,具体表现为在越复杂的分类任务中网络结构的冗余度越低。
|
下载CSV 表 2 两种硬剪枝算法在Cifar100数据集上的对比结果 Table 2 Comparison results of two hard pruning algorithms on Cifar100 dataset |
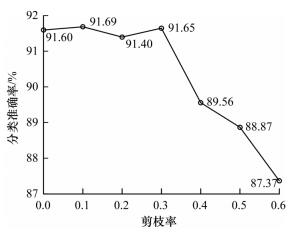
根据上述深度神经网络模型实验结果可以看出,剪枝率会对网络模型裁剪效果产生影响。为对此影响进行分析,以ResNet20网络为例对不同剪枝率下的网络模型剪枝效果进行统计,具体结果如图 2所示。由于不同网络存在不同的冗余度,对于ResNet20而言,当剪枝率为10%和30%时,有助于提升深度神经网络剪枝性能,当剪枝率大于40%时,剪枝性能会下降比较快。由此可以看出,合适的网络模型剪枝率不仅不会损耗模型性能,而且还有助于提升网络性能,然而如果网络模型剪枝率设置过大,虽然网络结构变得紧凑,但是网络性能会受到较大影响,具体表现为网络模型分类准确率大幅降低,因此如何平衡剪枝算法的剪枝率与剪枝后模型的实现效果,对于深度神经网络剪枝算法而言十分重要。
|
Download:
|
| 图 2 不同剪枝率下的DNN模型剪枝效果 Fig. 2 Pruning effect of DNN model under different pruning rates | |
本文提出一种基于深度神经网络二阶信息的结构化剪枝算法,利用幂迭代法得到经过预训练的网络模型参数Hessian矩阵的主特征向量,然后依据此向量衡量网络通道的重要性并进行通道剪枝。实验结果表明,该算法可在对原网络分类准确率影响较小的情况下实现网络参数量和FLOPS的有效裁剪。但由于本文算法目前仅在Cifar数据集上进行实验,后续可尝试使用更复杂的数据集,同时考虑与其他网络压缩方法进行融合,进一步提高深度神经网络模型的压缩效率。
| [1] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. |
| [2] |
LECUN Y, DENKER J S, SOLLA S A.Optimal single-class classification strategies[C]//Proceedings of the 19th International Conference on Neural Information Processing Systems.Cambridge, USA: MIT Press, 2007: 598-605.
|
| [3] |
HASSIBI B, STORK D G.Second order derivatives for network pruning: optimal brain surgeon[C]//Proceedings of the 2nd order derivatives for network pruning: optimal brain surgeon.Berlin, Germany: Springer, 1993: 164-171. https://www.researchgate.net/publication/2501411_Second_Order_Derivatives_for_Network_Pruning_Optimal_Brain_Surgeon
|
| [4] |
HAN S, POOL J, TRAN J, et al.Learning both weights and connections for efficient neural networks[EB/OL].[2020-02-13].https://arxiv.org/abs/1506.02626.
|
| [5] |
HAN S, MAO H, DALLY W J.Deep compression: compressing deep neural networks with pruning, trained quantization and huffman coding[EB/OL].[2020-02-13].https://arxiv.org/abs/1510.00149.
|
| [6] |
CHOI Y, ELKHAMY M, LEE J, et al.Towards the limit of network quantization[C]//Proceedings of International Conference on Learning Representations.Sydney, Australia: [s.n.], 2017: 1-8. https://www.researchgate.net/publication/311458156_Towards_the_Limit_of_Network_Quantization
|
| [7] |
ZHANG Xiangyu, ZOU Jianhua, MING Xiang, et al.Efficient and accurate approximations of nonlinear convolutional networks[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Berlin, Germany: Springer, 2015: 1984-1992. https://www.researchgate.net/publication/308867995_Efficient_and_accurate_approximations_of_nonlinear_convolutional_networks
|
| [8] |
ZHANG Xiangyu, ZHOU Xinyu, LIN Mengxiao, et al.ShuffleNet: an extremely efficient convolutional neural network for mobile devices[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Berlin, Germany: Springer, 2018: 6848-6856. https://www.researchgate.net/publication/318205093_ShuffleNet_An_Extremely_Efficient_Convolutional_Neural_Network_for_Mobile_Devices
|
| [9] |
HINTON G, VINYALS O, DEAN J.Distilling the knowledge in a neural network[EB/OL].[2020-02-13].https://arxiv.org/abs/1503.02531.
|
| [10] |
DONG Xuanyi, YANG Yi.Network pruning via transformable architecture search[C]//Proceedings of NIPS'19.Vancouver, Canada: [s.n.], 2019: 759-770. https://www.researchgate.net/publication/333337917_Network_Pruning_via_Transformable_Architecture_Search
|
| [11] |
LI H, KADAV A, DURDANOVIC I, et al.Pruning filters for efficient ConvNets[C]//Proceedings of International Conference on Learning Representation.Toulon, France: [s.n.], 2016: 1-10. https://www.researchgate.net/publication/307536925_Pruning_Filters_for_Efficient_ConvNets
|
| [12] |
YANG Minjie, LIANG Yaling, DU Minghui.YOLO pruning algorithm based on parameter subspace and scaling factor[J/OL].Computer Engineering: 1-10[2020-02-13].https://doi.org/10.19678/j.issn.1000-3428.0056932. (in Chinese) 杨民杰, 梁亚玲, 杜明辉.基于参数子空间和缩放因子的YOLO剪枝算法[J/OL].计算机工程: 1-10[2020-02-13].https://doi.org/10.19678/j.issn.1000-3428.0056932. |
| [13] |
BOYD S, VANDENBERGHE L. Convex optimization[M]. Cambridge, UK: Cambridge University Press, 2004.
|
| [14] |
DONG Z, YAO Z, GHOLAMI A, et al.HAWQ: hessian aware quantization of neural networks with mixed-precision[C]//Proceedings of 2019 IEEE/CVF International Conference on Computer Vision.Berlin, Germany: Springer, 2019: 293-302. https://www.researchgate.net/publication/339558933_HAWQ_Hessian_AWare_Quantization_of_Neural_Networks_With_Mixed-Precision
|
| [15] |
DONG X, CHEN S, PAN S.Learning to prune deep neural networks via layer-wise optimal brain surgeon[EB/OL].[2020-02-13].https://arxiv.org/abs/1705.07565v1.
|
| [16] |
BOOTH T E. Power iteration method for the several largest eigenvalues and eigenfunctions[J]. Nuclear Science and Engineering, 2006, 154(1): 48-62. |
| [17] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al.Deep residual learning for image recognition[C]//Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition.Berlin, Germany: Springer, 2016: 770-778.
|
| [18] |
SIMONYAN K, ZISSERMAN A.Very deep convolutional networks for large-scale image recognition[EB/OL].[2020-02-13].https://arxiv.org/abs/1409.1556.
|
| [19] |
KRIZHEVSKY A, HINTON G.Learning multiple layers of features from tiny images[D].Toronto, Canada: University of Toronto, 2009. https://www.researchgate.net/publication/306218037_Learning_multiple_layers_of_features_from_tiny_images
|
| [20] |
WANG Peisong.Acceleration and compression of deep neural networks[D].Beijing: University of Chinese Academy of Sciences, 2018.(in Chinese) 王培松.深度神经网络加速与压缩方法研究[D].北京: 中国科学院大学, 2018. |
| [21] |
GUO Yiwen, YAO Anbang, CHEN Yurong.Dynamic network surgery for efficient DNNs[C]//Proceedings of Advances in Neural Information Processing Systems.Barcelona, Spain: [s.n.], 2016: 1379-1387.
|
| [22] |
LUO Jianhao, WU Jianxin, LIN Weiyao.ThiNet: a filter level pruning method for deep neural network compression[C]//Proceedings of 2017 IEEE International Conference on Computer Vision.Washington D.C., USA: IEEE Press, 2017: 5068-5076. https://www.researchgate.net/publication/322058064_ThiNet_A_Filter_Level_Pruning_Method_for_Deep_Neural_Network_Compression
|
| [23] |
DONG Xuanyi, HUANG Junshi, YANG Yi, et al.More is less: a more complicated network with less inference complexity[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition.Washington D.C., USA: IEEE Press, 2017: 1895-1903. https://www.researchgate.net/publication/320971183_More_is_Less_A_More_Complicated_Network_with_Less_Inference_Complexity
|
| [24] |
YANG He, KANG Guoliang, DONG Xuanyi, et al.Soft filter pruning for accelerating deep convolutional neural networks[EB/OL].[2020-02-13].https://arxiv.org/abs/1808.06866.
|
| [25] |
LIU Zhuang, SUN Mingjie, ZHOU Tinghui, et al.Rethinking the value of network pruning[EB/OL].[2020-02-13].https://arxiv.org/abs/1810.05270.
|
| [26] |
HE Yihui, LIN Ji, LIU Zhijian, et al.AMC: AutoML for model compression and acceleration on mobile devices[C]//Proceedings of European Conference on Computer Vision.Berlin, Germany: Springer, 2018: 815-832.
|
| [27] |
PASZKE A, GROSS S, MASSA F, et al.PyTorch: an imperative style, high-performance deep learning library[EB/OL].[2020-02-13].https://arxiv.org/abs/1912.01703?context=cs.LG.
|
 2021, Vol. 47
2021, Vol. 47
