2. 中国人民解放军战略支援部队信息工程大学, 郑州 450000
2. People's Liberation Army Strategic Support Force Information Engineering University, Zhengzhou 450000, China
开放科学(资源服务)标志码(OSID):
云计算凭借其随需应变、按需即付的优势给用户带来极大的便利。为支持大规模的云服务,数据中心需开通数千台服务器和交换机。数据中心要为众多服务器和网络设备供电,因此会消耗大量能源。典型数据中心的能耗相当于25 000户家庭的能耗,每5年可能翻1番[1-2]。最近的研究结果表明,由于数据中心的服务器利用率不足会导致大量的资源被浪费,且服务器的平均利用率仅为5%~20%之间[3]。因此,在提供云服务的同时,提高数据中心的服务器利用率非常重要。
部署在服务器上的虚拟机被攻击后会影响正常服务,所以研究人员提出一种冗余备份的虚拟机策略,冗余策略能够提高云计算环境的容错性,减小对用户体验带来的影响。然而,系统组件的同质化,使得攻击者易于探测用户信息、窃取用户数据,导致云计算环境受到安全威胁[4]。2019年1月,研发人员发现WINRAR漏洞,该漏洞威胁了5亿用户的系统安全。同年10月,Android零日漏洞也被发现,该漏洞威胁了华为、三星、小米等多家电子设备的安全。基础设施异构化能够增大攻击者探测难度[5],提高云计算环境的安全性,在此基础上对虚拟机进行动态轮换能够进一步增强虚拟机安全性,通过动态改变虚拟机的部署位置和虚拟机的操作系统,避免用户虚拟机受到侧信道攻击[6]和探测攻击[7]。
然而,异构云基础设施和虚拟机轮换会带来云计算资源分配的难题[8]。一方面,由于基础设施异构化使得传统的装箱方法不再适用资源分配,供应商需考虑每一个服务器可提供的资源来实现负载均衡。另一方面,虚拟机的轮换会改变当前服务器的负载情况,如何在轮换的过程中减小负载波动值得研究。本文提出一种基于轮换策略的异构云资源分配算法,将不同的资源抽象成维度不同的向量,利用余弦定理来衡量向量之间的相似度,根据向量间的相似度进行资源分配以实现负载平衡,并在初次资源分配完成后对虚拟机选择相似度最高的服务器进行轮换。
1 相关研究云计算中的资源分配属于大规模多任务调度问题,一直是人们研究的热点。文献[9]提出一种两步式的资源分配算法,首先在云中选择一个集群,然后在集群中选择一个节点部署虚拟机,该模型使用了3个集群和6个节点,实验结果表明,选择合适的集群比选择合适的节点对资源分配的影响更大。文献[10]讨论了如何量化服务器和整个系统间的负载平衡,该研究选用贪心算法来平衡服务器之间的负载,当服务器负载超过阈值时,对该服务器上的虚拟机进行迁移,并计算迁移虚拟机后的服务器负载平衡变化值,选取最小不平衡变化值进行迁移。文献[11]根据虚拟机的状态,提出了静态虚拟机放置和动态虚拟机放置的算法,既考虑了单个服务器的资源剩余量和资源利用率,又兼顾了整体服务器的资源剩余量和资源利用率。该算法使用平面资源六边形,由代表不同资源利用类别的三角形组成。虚拟机被分配到互补资源三角形中的服务器上来平衡总体利用率。文献[12]在文献[11]的基础上提出了一种虚拟机放置互补策略。该互补策略考虑资源使用和时间使用两个方面,并认为在不同时间使用相同资源的虚拟机或在相同时间使用不同资源的虚拟机是互补的。文献[13]设计一种基于启发式正交二叉树搜索的三维装箱算法,该算法以所有叶子节点填充率最高为目标,满足了装箱的3个约束条件。文献[14]结合日常砌墙策略,提出了一种混合模拟退火算法,利用找点法和参考线规则来进行装箱,该算法能有效解决三维装箱问题。
虚拟机是一种用于模拟物理服务器的虚拟化技术。随着虚拟化的发展,虚拟机扩容和虚拟机的实时迁移为提高服务器利用率提供了两种潜在的解决方案[15-16]。虚拟机大小调整方案可以对虚拟机资源配置的细粒度进行调整。与峰值资源请求的资源调配相比,虚拟机大小调整的资源调配可以更好地利用物理资源,而计算开销可以忽略不计。实时迁移能够以无中断的方式在不同服务器之间移动正在运行的虚拟机。通过应用实时迁移和虚拟机扩容,数据中心管理器可以将虚拟机整合到更少的服务器上,以提高数据中心的能源使用率。在整合虚拟机时,可能存在虚拟机工作负载突发的情况使服务器过载[17]。虚拟机迁移通过改变底层的物理环境可以抵御云计算中的侧信道攻击,文献[18]在此基础上利用MTD技术,通过多个操作系统的轮换来增强安全性,并利用现有技术,提供了一个可行的动态防御解决方案,可以方便地部署在真实的网络环境中。不同于虚拟机迁移,该方案通过轮换删除原服务器上的虚拟机,并在新的服务器上部署新的虚拟机。测试结果表明,平台的多样性和动态性提高了系统的安全性,攻击成功率与轮换时间间隔成反比。
随着云计算的发展,越来越多的计算资源被提供给客户,如CPU、内存大小、磁盘大小、带宽等。因此,分配方法应该支持任意数量的维度[19]。同时,在保障虚拟机安全性的同时服务器的资源利用率和负载波动也应被关注。针对以上问题,本文在传统的装箱方法上做了改进,并提出一种基于轮换策略的异构云资源分配算法,主要贡献如下:
1)对底层物理设施异构化,通过异构底层物理服务器,增大攻击者探测难度,提升云计算环境安全性。
2)将影响虚拟机部署的资源抽象成向量,多维度地考虑资源分配问题,以更贴近真实的资源分配环境,同时根据虚拟机部署资源的向量与物理服务器向量间的相似度选择虚拟机,使得计算节点成本更小,能源利用率更大。
3)在每个虚拟机初次部署的同时,为每个虚拟机设置驻留时间,当到达驻留时间后根据当前服务器负载情况对虚拟机进行轮换。轮换会改变虚拟机的操作系统以及所部署的服务器位置,在提高资源利用率的同时提升了执行体的安全性。
2 问题描述虚拟机在部署时会面临服务器选择问题,由于不同的服务器负载情况可能不同,在部署时会影响云平台的整体负载情况。本文将多维异构资源的分配问题分为2个阶段:
1)初次部署虚拟机。将虚拟机部署在异构的物理服务器上,同时保证各个服务器资源利用率高和服务器间负载平衡,这本质上是一个多目标优化问题。
2)轮换已经部署好的虚拟机。轮换可以减小攻击者对虚拟机的影响,提升虚拟机安全性,但是轮换会引起服务器负载变化,所以在考虑虚拟机安全的同时,应尽量减小服务器的负载波动。
2.1 装箱问题资源分配问题通常被视为装箱问题,即在最少的箱子里放置最多的物品。云计算中影响资源分配的因素有很多,如CPU、内存大小、磁盘大小、带宽等。本文用不同的维度来表示这些因素,并对云计算中多维资源分配问题进行研究。装箱问题描述如下:有
云计算的物理基础设施是由一台台的物理服务器组成的,异构能有效提高云计算环境的安全性,但是异构的服务器之间容量不同,因此异构装箱较传统的装箱问题相比引入了新的问题。对于每台服务器均需满足以下约束条件:
| $ {P}_{j}^{\mathrm{M}}\ge {\sum\limits_{i=1}^{n}}V_{i}^{\mathrm{M}} $ | (1) |
部署在服务器
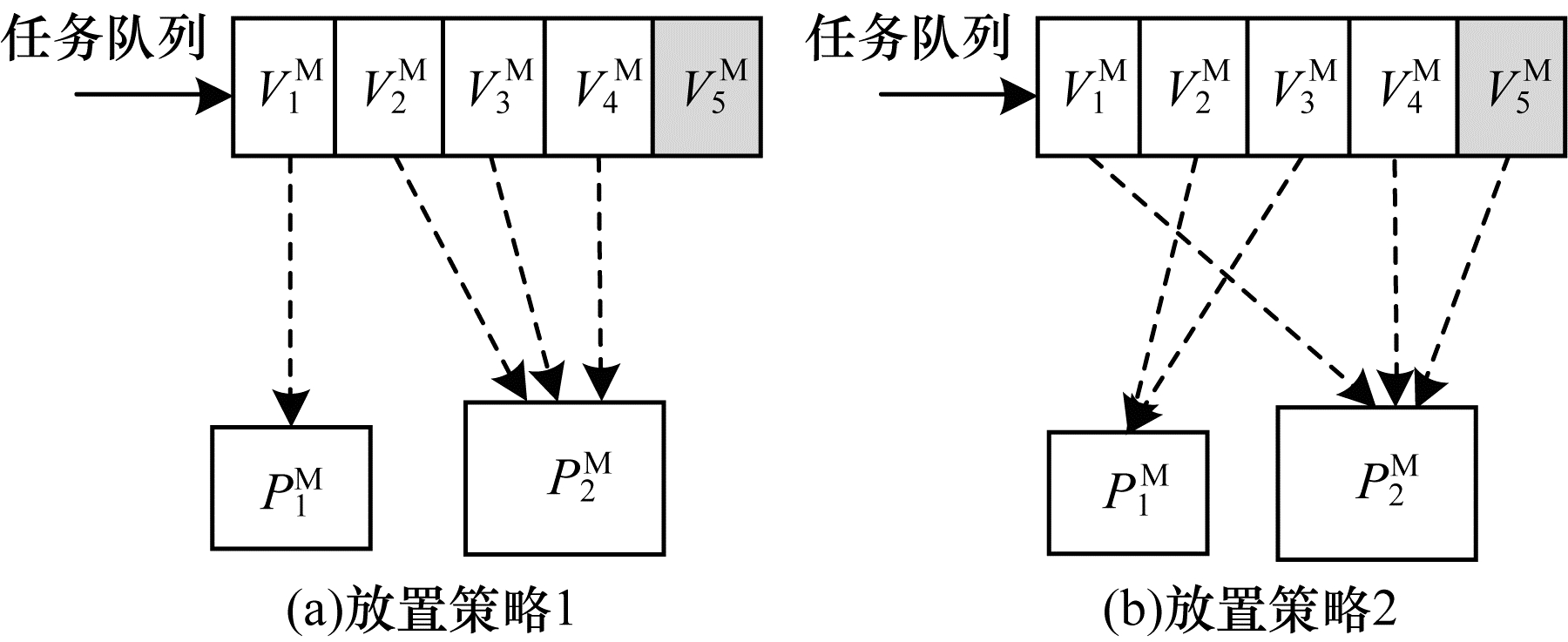
|
Download:
|
| 图 1 虚拟机放置策略 Fig. 1 Virtual machine placement strategies | |
网络攻击对网络系统的危害主要分为网络可用性危害与信息安全属性危害[20],主要体现在对可用性、机密性、完整性、不可抵赖性、认证性等安全属性的危害。由于不同的系统遇到危害时敏感性反应不同,假设攻击者只要能入侵目标主机便视为成功攻击,攻击过程的5个阶段描述如图 2所示。

|
Download:
|
| 图 2 侵入攻击阶段示意图 Fig. 2 Schematic diagram of intrusion attack phase | |
同一台物理服务器上的虚拟机之间共享资源,攻击者通过定位到目标主机所在的服务器位置,将攻击者控制的虚拟机与目标主机部署到同一台服务器上,并对目标主机发起侧信道攻击。同时,攻击者也可以探测用户虚拟机的操作系统,根据用户操作系统漏洞对目标主机进行攻击。攻击成功率
| $ P=\frac{1}{V} $ | (2) |
其中,
本节提出基于轮换策略的异构云资源分配算法,将异构云资源分配问题建模为多维装箱问题进行求解,同时提出一个资源分配利用率指标,根据该指标选择虚拟机要部署的服务器位置。
3.1 系统模型创建一台虚拟机
本节根据利用率指标来解决虚拟机布局问题。在资源分配时根据当前服务器的负载情况以及资源利用率来选择虚拟机的放置位置,参数定义如表 1所示。

|
下载CSV 表 1 参数定义 Table 1 Parameters definition |
| $ {P}_{j}^{\mathrm{M}k}={P}_{j}^{\mathrm{M}k}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}-{V}_{i}^{\mathrm{M}k}\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{t} $ | (3) |
式(3)表示服务器
| $ \mathrm{c}\mathrm{o}{\mathrm{s}}_{}\theta =\sum\limits_{l=1}^{k}\frac{{V}_{i}^{\mathrm{M}k}\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{t}\cdot {P}_{j}^{\mathrm{M}k}}{{V}_{i}^{\mathrm{M}k}\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{t}+{P}_{j}^{\mathrm{M}k}}, 1\le i\le m, 1\le j\le n $ | (4) |
| $ \begin{array}{l}{\theta }_{vp}=\mathrm{c}\mathrm{o}{\mathrm{s}}^{-1}\mathrm{ }\theta \left(\sum\limits_{l=1}^{k}\frac{{V}_{i}^{\mathrm{M}k}\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{t}·{P}_{j}^{\mathrm{M}k}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{e}}{{V}_{i}^{\mathrm{M}k}\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{t}+{P}_{j}^{\mathrm{M}k}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{u}\mathrm{e}}\right)\mathrm{ }, \\ 1\le i\le m, 1\le j\le n\end{array} $ | (5) |
资源分配问题本质上是一个多目标优化的问题,旨在提高能源效率、资源利用率、负载平衡和服务器整合。本文将云计算中的异构资源分配问题视为多维异构装箱问题,具体描述如下:有n个体积不同的虚拟机
目标函数:
| $ \mathrm{m}\mathrm{i}\mathrm{n}\sum\limits_{j=1}^{m}{P}_{j}^{\mathrm{M}k}, 1\le k\le d $ | (6) |
约束条件:
| $ \sum\limits_{i=1}^{n}{V}_{i}^{\mathrm{M}k}{x}_{ij}\le {C}_{j}^{k}{P}_{j}^{\mathrm{M}k}, 1\le j\le m, 1\le k\le d $ | (7) |
| $ \sum\limits_{j=1}^{m}{x}_{ij}=\mathrm{1, 1}\le i\le n $ | (8) |
由于虚拟机是多维资源包,本文用向量来表示虚拟机的多维资源,其中
变量说明:
约束条件:
| $ T\left({x}_{ij}^{k}\right)<t, 1\le i\le n, 1\le j\le m $ | (9) |
| $ \begin{array}{l}{P}_{j}^{\mathrm{M}k}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}=\sum\limits_{i=1}^{n}{x}_{ij}^{k}{V}_{i}^{\mathrm{M}k}\mathrm{a}\mathrm{d}\mathrm{d}-{x}_{ij}^{k}{V}_{i}^{\mathrm{M}k}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{e}, \\ 1\le j\le m\end{array} $ | (10) |
| $ \begin{array}{l}\sum\limits_{i=1}^{n}{P}_{j}^{\mathrm{M}k}=\sum\limits_{i=1}^{n}({P}_{j}^{\mathrm{M}k}+{P}_{j}^{\mathrm{M}k}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e})=\\ [{P}_{ij}^{\mathrm{M}k}+({x}_{ij}^{k}{V}_{i}^{\mathrm{M}k}\mathrm{a}\mathrm{d}\mathrm{d}-{x}_{ij}^{k}{V}_{i}^{\mathrm{M}k}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{t}\mathrm{e}\left)\right]\mathrm{ }, \\ 1\le j\le m\end{array} $ | (11) |
式(9)表示虚拟机
本文通过动态、异构的虚拟机部署方式来增强虚拟机的安全性。对于虚拟机
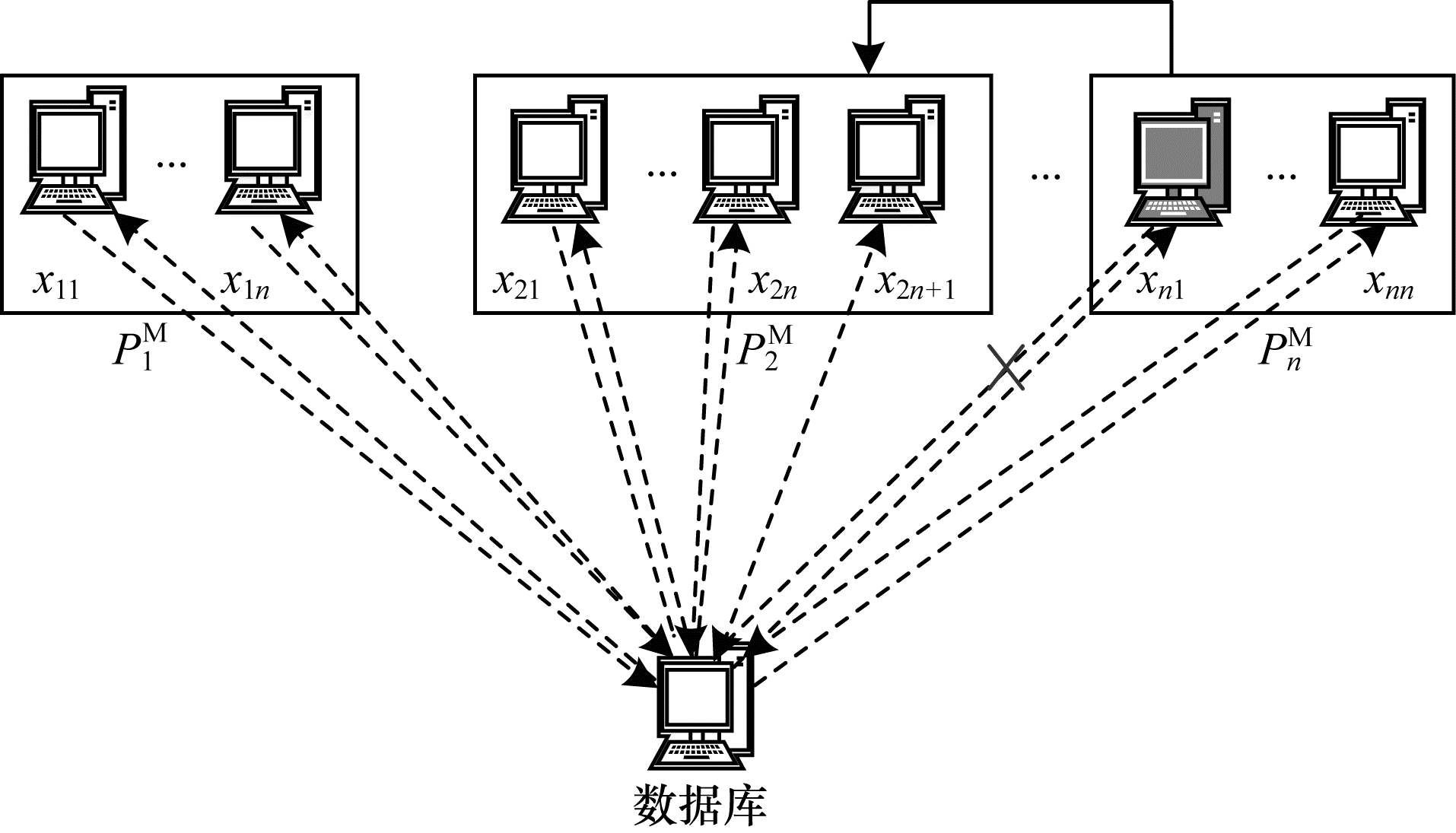
|
Download:
|
| 图 3 虚拟机轮换方法 Fig. 3 Virtual machine rotation method | |
在攻击链模型中,攻击者探测目标并发动攻击需要一定的时间,如果在攻击者探测目标信息之后及发起攻击之前对虚拟机进行轮换,就可以改变虚拟机当前的状态,使攻击者发动的攻击无效。针对攻击的特性,本文提出了一种动态轮换算法,给虚拟机设定驻留时间阈值,当虚拟机在服务器上的驻留时间到达阈值后或虚拟机状态异常时,对该虚拟机进行轮换,轮换时改变虚拟机的操作系统并将此虚拟机部署到其他的服务器上。通过动态异构虚拟机的操作系统以及底层物理环境,可以增大攻击者的探测难度,提高虚拟机的安全性。
算法1 基于轮换策略的异构云多维资源分配算法
输入 创建虚拟机时的资源需求
输出 虚拟机部署位置
1.for
2.for
3.If
4.If
5.
6.
7.
8.
9.end if
10.end if
11.update
12.else //服务器负载不为空
13.if
14.delete
15.for
16.for
17.
18.
19.
20.create
21.
22.end for
23.end for
24.update
25.end if
26.end if
27.end for
28.end for
本文根据服务器利用率指标来解决虚拟机布局问题。在资源分配时根据当前服务器的负载情况以及资源利用率来选择虚拟机的放置位置。对虚拟机
1)时间复杂度分析。当初次部署虚拟机时,没有虚拟机进行轮换。
2)安全性分析。探测攻击是攻击者常用的一种攻击手段。攻击者通过向用户发送带有恶意网址或附件的电子邮件来收集有关目标网络信息,并根据收集到的信息来判断用户的操作系统,然后利用该操作系统的漏洞发动攻击。对于攻击者来说,每次无论是否攻击成功,都能获得用户的操作系统类型,并为下次攻击做准备。攻击成功率如式(12)所示:
| $ P=\left\{\begin{array}{l}\frac{1}{V}, n=1\\ 1, n>1\end{array}\right. $ | (12) |
其中,
本文实验在Intel® CoreTM i7-4790 CPU 3.6 GHz,16 GB RAM的主机上进行,基于轮换策略的多维异构装箱算法采用C++语言编程实现,并利用Matlab工具对实验结果进行分析。攻击者已知的操作系统漏洞和防御者操作系统具有的漏洞都服从[0, 11]的均匀分布,攻击手段采用探测攻击。每个实验进行100次蒙特卡洛仿真,保证误差在合理范围内。
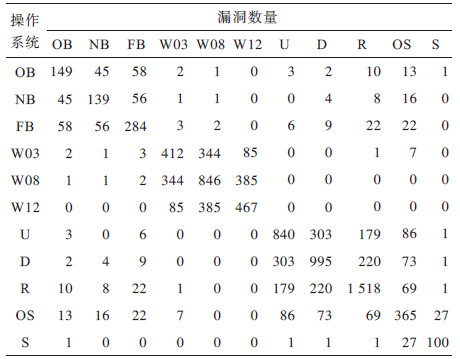
本文通过通用漏洞披露(Common Vulnerability Enumeration,CVE)公布的数据,获取了11种操作系统在1994年—2017年被公开的所有漏洞。这11种操作系统分别是OB(OpenBSD)、NB(NetBSD)、FB(FreeBSD)、W03(Windows Server 2003)、W08(Windows Server 2008)、W12(Windows Server 2012)、U(Ubuntu)、D(Debian)、R(Redhat)、OS(OpenSolaris)和S(Solaris)。表 2所示为上述系统存在的漏洞数量以及不同操作系统间存在的共同漏洞数量。
|
下载CSV 表 2 操作系统共同漏洞数量 Table 2 Number of common vulnerabilities in operating systems |
假设攻击者已获知的操作系统为
| $ P=\frac{V({I}_{i}, {I}_{j})}{V\left({I}_{j}\right)} $ | (13) |
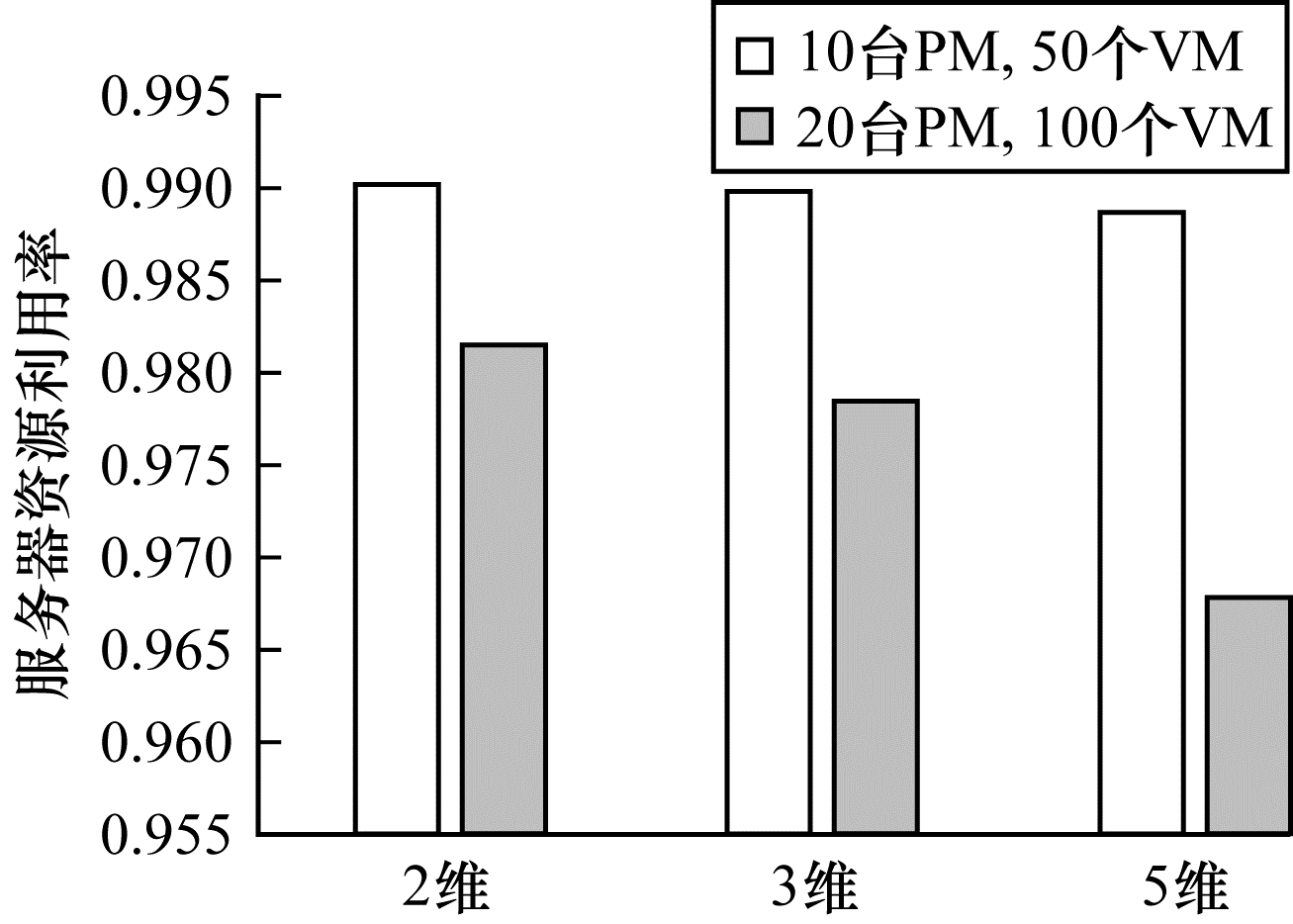
仿真实验1 不同维度下服务器资源利用率的对比实验。本实验分别对10台服务器、50个虚拟机和20台服务器、100个虚拟机这两种组合进行分析。对比这两种组合中不同维度下的服务器资源利用率情况。实验结果如图 4所示。
|
Download:
|
| 图 4 不同维度下服务器资源利用率对比 Fig. 4 Comparison of server resource utilization in different dimensions | |
从图 4可以看出,对于10台服务器和50个虚拟机的装箱实验,不同维度的服务器资源利用率不同,随着维度的升高,虚拟机的资源利用率逐渐降低。在2维时资源利用率为0.990 0,在3维时资源利用率为0.989 7,在5维时资源利用率为0.988 7;对于20台服务器和100个虚拟机,在2维时资源利用率为0.981 5,在3维资源利用率为0.978 4,在5维时资源利用率为0.967 9。通过以上实验分析结果可以看出,随着维度的增加,服务器的资源利用率会降低。
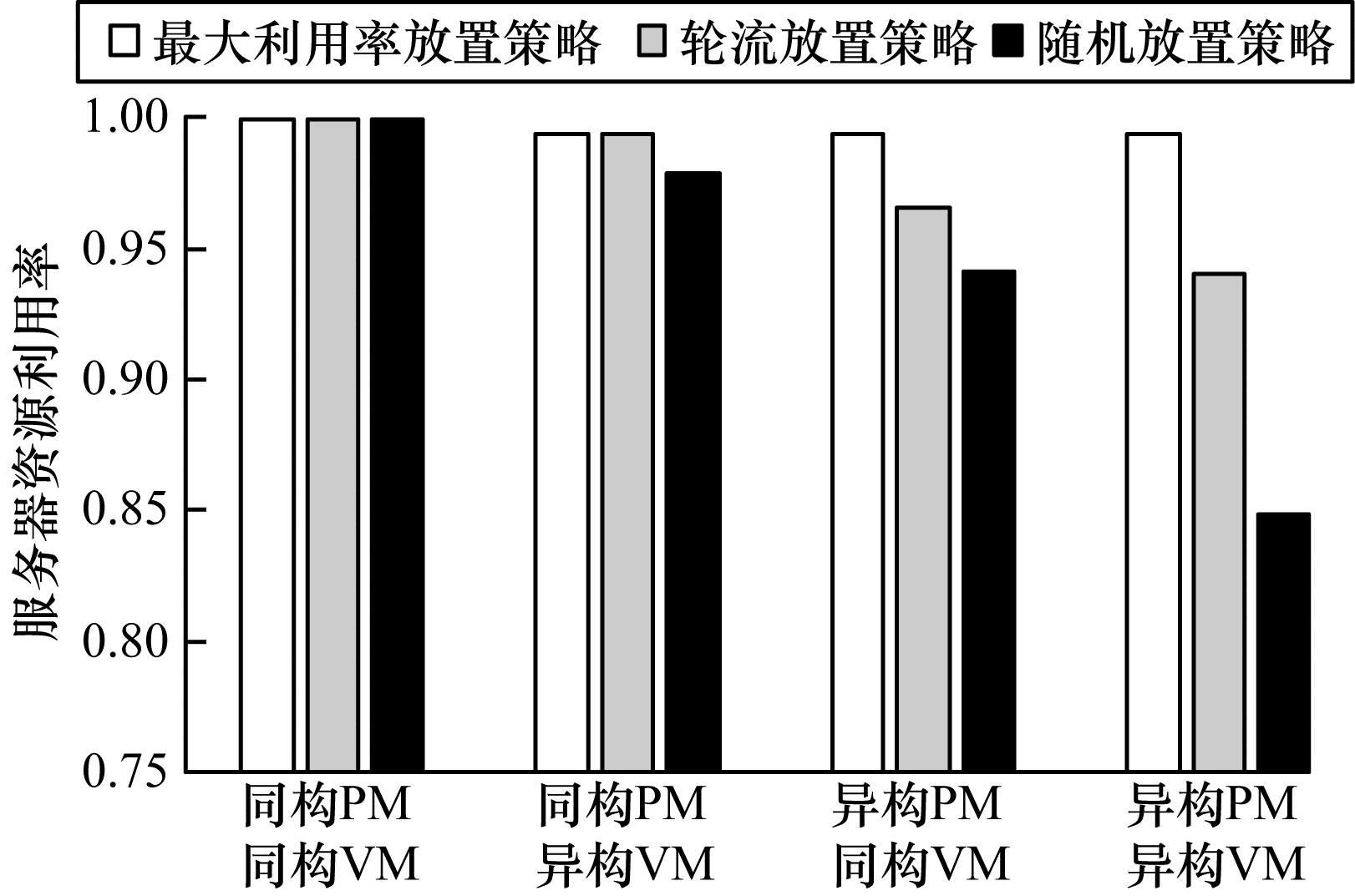
仿真实验2 不同异构程度的装箱对比实验。实验设置10台服务器、50个虚拟机进行装箱。对异构程度不同的虚拟机与服务器组合进行对比分析。4组组合分别是:同构服务器,同构虚拟机;同构服务器,异构虚拟机;异构服务器,同构虚拟机;异构服务器,异构虚拟机。将本文所使用的基于最大利用率策略与轮流放置策略、随机放置策略进行对比,如图 5所示。
|
Download:
|
| 图 5 服务器异构装箱资源利用率对比 Fig. 5 Comparison of server heterogeneous packing resource utilization | |
从图 5可以看出:当服务器与虚拟机都同构时,3种策略下的服务器平均资源利用率相同,均为0.990 0;当服务器同构、虚拟机异构时,基于最大利用率策略与轮流策略的资源利用率相同为0.993 9,随机放置策略的服务器的资源利用率为0.979 1;当服务器异构、虚拟机同构时,基于最大利用率策略下平均资源利用率最高为0.993 8,轮流策略次之,平均资源利用率为0.965 2,随机策略最差,平均资源利用率为0.941 6;当服务器异构、虚拟机异构时,基于最大利用率策略下平均资源利用率最高为0.993 8,轮流策略次之,平均资源利用率为0.940 7,随机策略最差,平均资源利用率为0.848 2。以上实验结果表明,基于利用率装箱策略在异构装箱问题中表现较好。
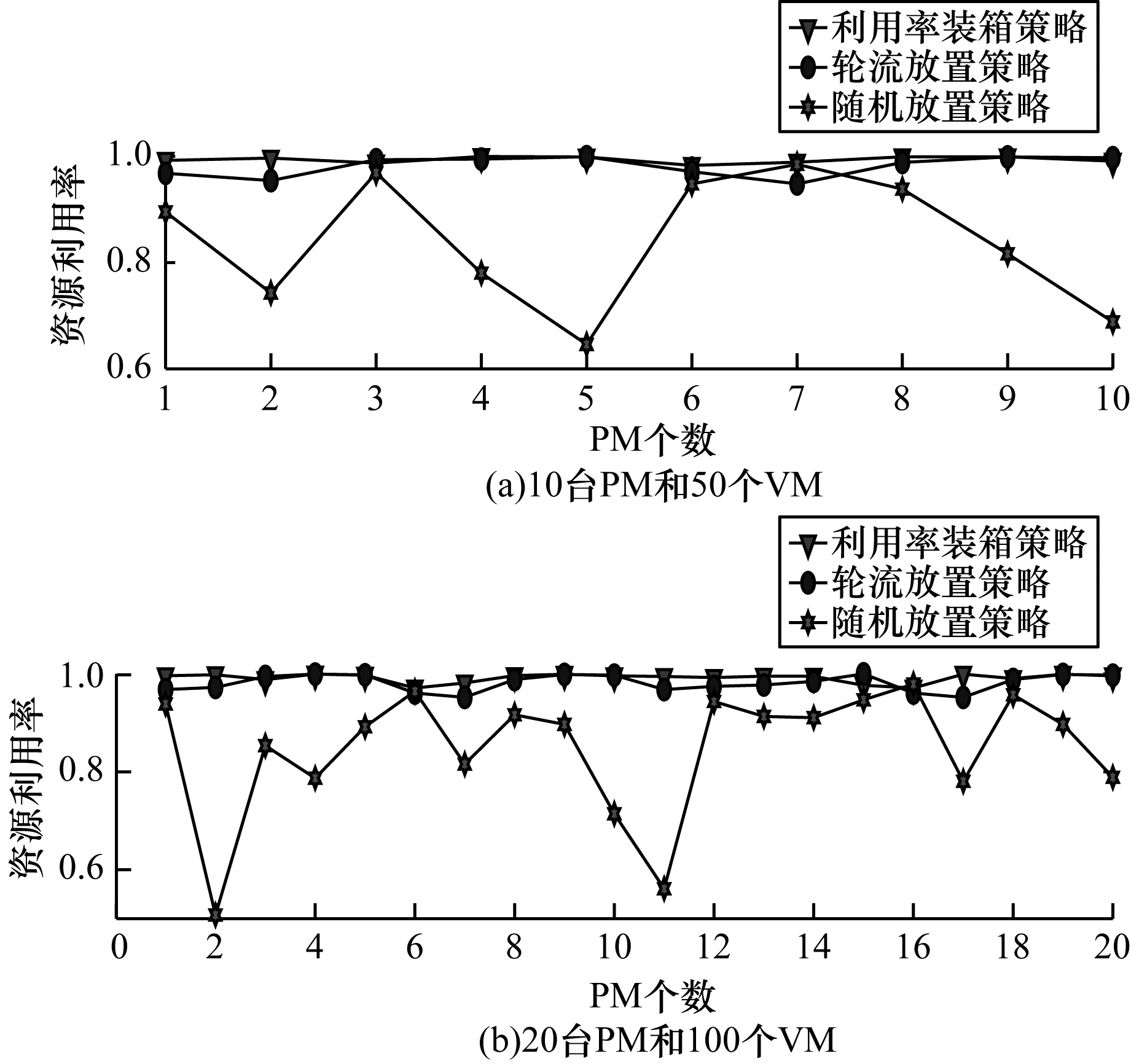
仿真实验3 不同策略下服务器利用率的对比实验。实验分为两组:一组是10台服务器,50个虚拟机;另一组是20台服务器,100个虚拟机。对比两组配置在不同虚拟机部署策略下的服务器资源利用率。
图 6所示为基于利用率装箱策略和轮流放置策略、随机放置策略的资源利用率情况。
|
Download:
|
| 图 6 不同策略下服务器资源利用率对比 Fig. 6 Comparison of server resource utilization under different strategy | |
从图 6可以看出:当服务器为10台,虚拟机为50个时,计算每台服务器的负载情况。本文使用的基于利用率装箱策略下服务器的平均资源利用率为0.993 6,差值为0.016 8,轮流放置策略的平均资源利用率为0.981 4,差值为0.051 1,随机放置策略的平均资源利用率为0.841 0,差值为0.323 0。当服务器为20台,虚拟机数量为100个时,计算每台服务器的负载情况。基于利用率装箱策略平均资源利用率为0.991 7,差值为0.028 4,轮流放置策略的平均资源利用率为0.981 6,差值为0.048 0,随机放置策略的平均资源利用率为0.848 2,差值为0.471 4。以上实验分析可得,基于利用率装箱策略能够有效提高服务器的资源利用率并减小负载波动。
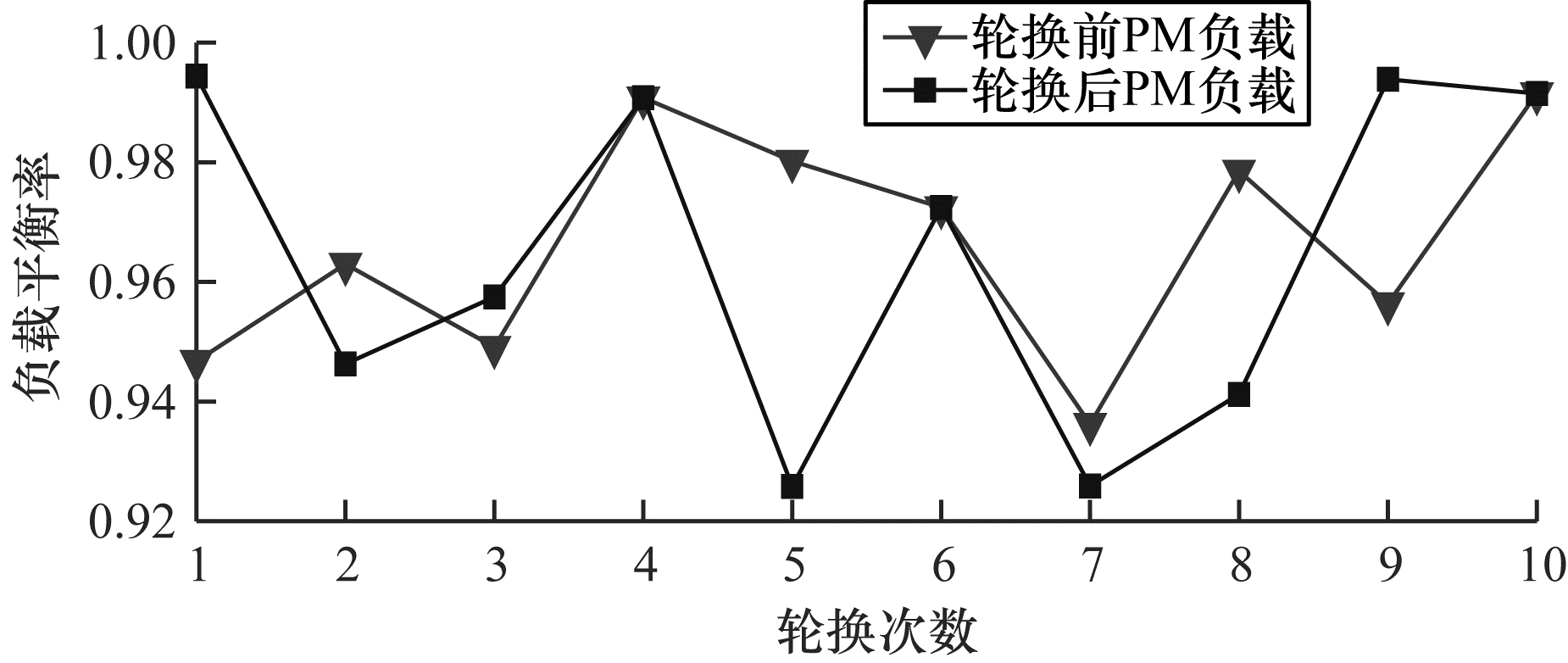
仿真实验4 轮换前后服务器负载状态对比实验。由于每个虚拟机创建的时间不同,每个虚拟机开始轮换的时间也不同,因此本实验单独考虑每个虚拟机轮换情况。首先从服务器资源池中随机选取10个虚拟机,依次进行轮换并计算轮换前后服务器负载平衡变化。
如图 7所示,轮换前服务器的平均负载平衡率为0.966 5,差值为0.055 3。进行10次轮换后服务器的平均负载平衡率为0.964 0,差值为0.068 5。通过分析实验数据可得,轮换后服务器的负载平衡率降低了0.002 5,不同服务器之间负载平衡率差值增大了0.013 5,轮换后服务器平均负载平衡降低了0.2个百分点,负载波动值增大了15.3个百分点。
|
Download:
|
| 图 7 轮换前后负载平衡率变化情况 Fig. 7 Changes in load balance rate before and after rotation | |
仿真实验5 有无轮换策略下虚拟机被攻击的对比实验。本文实验随机从操作系统库中选取1个操作系统,从物理资源池中随机选择1台服务器来部署虚拟机,操作系统服从[0, 11]均匀分布。攻击者对用户虚拟机发动探测攻击,并根据探测到的信息调整攻击策略发动下一次攻击。实验进行100次蒙特卡洛仿真,保证误差在合理范围内。
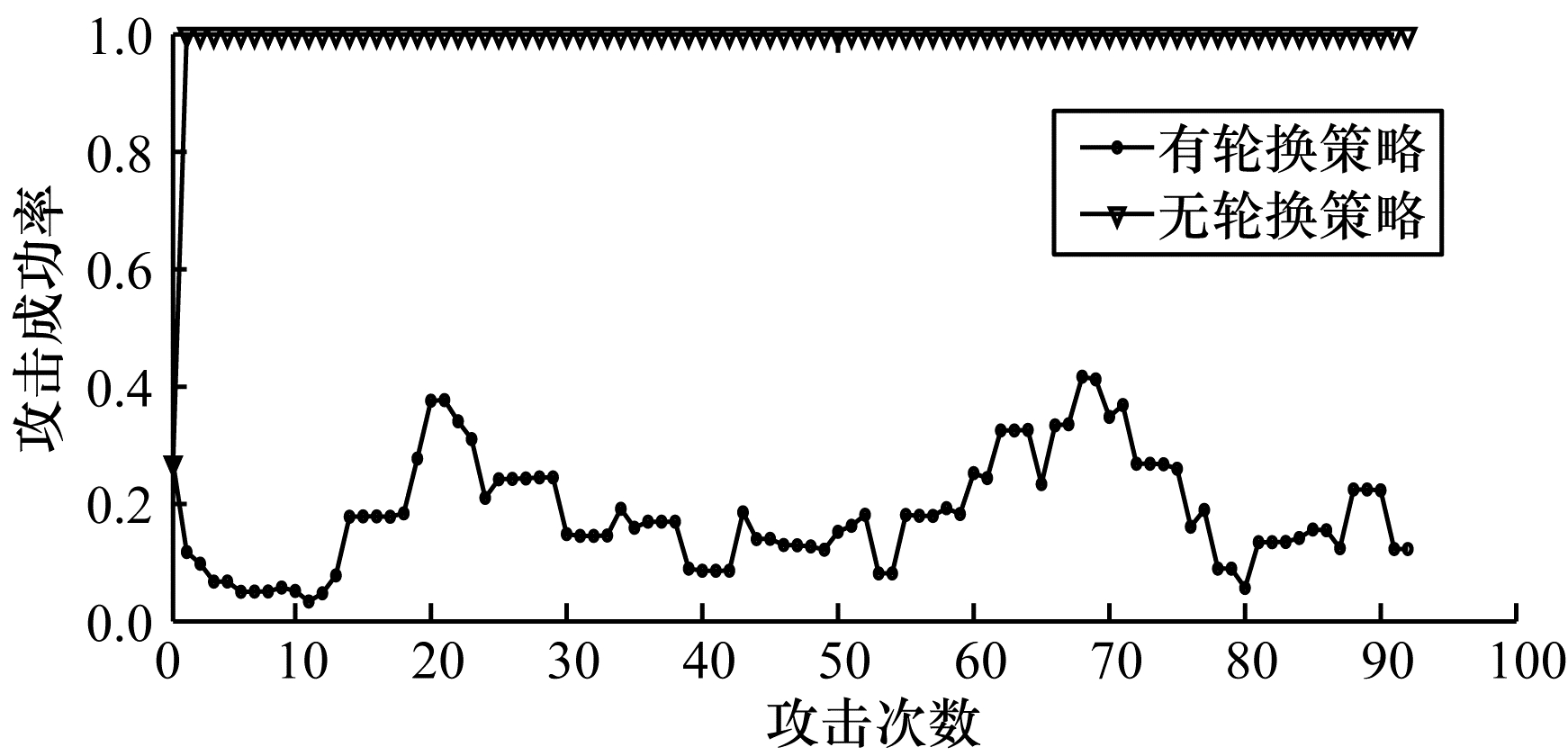
图 8所示为有无轮换策略下用户操作系统被攻击成功的概率的实验对比分析。
|
Download:
|
| 图 8 虚拟机被攻击成功的概率对比 Fig. 8 Comparison of success rate of virtual machines being attacked | |
本文针对的是探测攻击,在攻击链中攻击者先探测用户的虚拟机,根据从用户探测到的信息来判断用户的操作系统,然后根据掌握的操作系统漏洞对用户发起攻击。如图 8所示,对于非轮换策略,攻击者在首次发动攻击时,有0.27的概率能够成功攻击用户,但是第一次攻击结束后,攻击者根据探测到的信息再次发动攻击的成功率变为1。对于有轮换策略,用户在攻击者发动1次探测的时间范围内进行轮换,此时用户的操作系统已经改变,攻击者已经无法根据上次探测到的信息来确定用户的操作系统。进行100次探测攻击实验,攻击者的平均攻击成功率约为0.183 6,轮换后虚拟机的安全性提升了18.5个百分点,实验结果表明,轮换策略能够有效提高操作系统的安全性。
6 结束语云计算中的资源分配通常被建模为装箱问题。在装箱问题中,静态同构的云计算环境会威胁到虚拟机安全,动态异构的云计算环境更符合真实的资源分配情况,但也引入了新的资源分配问题。同时,由于影响资源分配的因素较多,传统的装箱方法无法解决多维的资源分配问题。针对以上问题,本文提出一种基于轮换策略的多维异构云资源分配算法。将虚拟机和服务器资源抽象为向量,并给出一种利用率指标,根据利用率指标为虚拟机选择要部署的服务器。为提高虚拟机的安全性引入了轮换策略,给每个虚拟机设定一定的驻留时间,当虚拟机在服务器上的驻留时间达到阈值或虚拟机状态出现异常后,对虚拟机进行轮换。实验结果表明,该算法在多维异构的装箱问题中具有较高的资源利用率,且能够提高虚拟机的安全性。下一步研究方向为寻找最佳轮换周期,在保证安全性的前提下尽可能减少轮换产生的开销。
| [1] |
CATAN M, COSMO R, EICHE A, et al. Aeolus: mastering the complexity of cloud application deployment[C]//Proceedings of European Conference on Service-Oriented and Cloud Computing. Berlin, Germany: Springer, 2013: 1-3.
|
| [2] |
DAYARATHNA M, WEN Y, FAN R. Data center energy consumption modeling: a survey[J]. IEEE Communications Surveys & Tutorials, 2015, 18(1): 732-794. |
| [3] |
ARMBRUST M, FOX A, GRIFFITH R, et al. A view of cloud computing[J]. Communications of the ACM, 2010, 53(4): 50-58. DOI:10.1145/1721654.1721672 |
| [4] |
WU Jiangxing. Research on cyber mimic defense[J]. Journal of Cyber Security, 2016, 1(4): 1-10. (in Chinese) 邬江兴. 网络空间拟态防御研究[J]. 信息安全学报, 2016, 1(4): 1-10. |
| [5] |
WANG Wei, ZENG Junjie, LI Guangsong, et al. Security analysis of dynamic heterogeneous redundant system[J]. Computer Engineering, 2018, 44(10): 42-45, 50. (in Chinese) 王伟, 曾俊杰, 李光松, 等. 动态异构冗余系统的安全性分析[J]. 计算机工程, 2018, 44(10): 42-45, 50. |
| [6] |
SUN Zhiyong, JI Xinsheng, YOU Wei, et al. A virtual machine dynamic migration method based on redundancy jump[J]. Computer Engineering, 2020, 46(2): 21-27, 34. (in Chinese) 孙志勇, 季新生, 游伟, 等. 一种基于冗余跳变的虚拟机动态迁移方法[J]. 计算机工程, 2020, 46(2): 21-27, 34. |
| [7] |
LI Siqi, LI Yanfei. APT attack detection based on graph algorithm[J]. Cyberspace Security, 2018, 9(6): 1-6. (in Chinese) 李斯祺, 李艳斐. 基于图算法的APT攻击检测[J]. 网络空间安全, 2018, 9(6): 1-6. DOI:10.3969/j.issn.1674-9456.2018.06.001 |
| [8] |
ZHU Wei, WANG Jun, ZHOU Xunzhao. Hospital cloud computing system based on load resource scheduling scheme balancing[J]. Computer Engineering, 2018, 44(3): 37-41, 54. (in Chinese) 朱炜, 王俊, 周迅钊. 基于负载均衡的医院云计算系统资源调度方案[J]. 计算机工程, 2018, 44(3): 37-41, 54. DOI:10.3969/j.issn.1000-3428.2018.03.006 |
| [9] |
MILLS K, FILLIBEN J, DABROWSKI C. Comparing virtual machine placement algorithms for on-demand clouds[C]//Proceedings of the 3rd IEEE International Conference on Cloud Computing Technology and Science. Washington D.C., USA: IEEE Press, 2011: 91-98.
|
| [10] |
ARZUAGA E, KAELI D R. Quantifying load imbalance on virtualized enterprise servers[C]//Proceedings of the 1st Joint WOSP/SIPEW International Conference on Performance Engineering. Washington D.C., USA: IEEE Press, 2010: 235-242.
|
| [11] |
MISHRA M, SABOO A. On theory of virtual machine placement: anomalies in existing methodologies and their mitigation using a novel vector based approach[C]//Proceedings of the 4th IEEE International Conference on Cloud Computing. Washington D.C., USA: IEEE Press, 2011: 275-282.
|
| [12] |
CHEN Lihua, SHEN Haiying. Consolidating complementary VMs with spatial/temporal-awareness in cloud datacenters[C]//Proceedings of IEEE Conference on Computer Communications. Washington D.C., USA: IEEE Press, 2014: 1033-1041.
|
| [13] |
LIU Sheng, ZHU Fenghua, LÜ Yisheng, et al. A heuristic orthogonal binary tree search algorithm for three dimensional container loading problem[J]. Chinese Journal of Computers, 2015, 38(8): 1530-1543. (in Chinese) 刘胜, 朱凤华, 吕宜生, 等. 求解三维装箱问题的启发式正交二叉树搜索算法[J]. 计算机学报, 2015, 38(8): 1530-1543. |
| [14] |
ZHANG Defu, WEI Lijun, CHEN Qingshan, et al. A combinational heuristic algorithm for the three-dimensional packing problem[J]. Journal of Software, 2007, 18(9): 2083-2089. (in Chinese) 张德富, 魏丽军, 陈青山, 等. 三维装箱问题的组合启发式算法[J]. 软件学报, 2007, 18(9): 2083-2089. |
| [15] |
LIU Haikui, JIN Hai, XU Chengzhong, et al. Performance and energy modeling for live migration of virtual machines[J]. Cluster Computing, 2013, 16(2): 249-264. |
| [16] |
ORGERIE A C, ASSUNCAO M D, LEFEVRE L. A survey on techniques for improving the energy efficiency of large-scale distributed systems[J]. ACM Computing Surveys, 2014, 46(4): 1-31. |
| [17] |
VERMA A, KUMAR G, KOLLER R. The cost of reconfiguration in a cloud[C]//Proceedings of the 11th International Middleware Conference Industrial Track. New York, USA: ACM Press, 2010: 11-16.
|
| [18] |
THOMPSON M, EVANS N, KISEKKA V. Multiple OS rotational environment an implemented moving target defense[C]//Proceedings of the 7th International Symposium on Resilient Control Systems. Washington D.C., USA: IEEE Press, 2014: 1-6.
|
| [19] |
MERGENCI C, KORPEOGLU I. Generic resource allocation metrics and methods for heterogeneous cloud infrastructures[J]. Journal of Network and Computer Applications, 2019, 146(1): 102-113. |
| [20] |
SEXTON J, STORLIE C, NEIL J. Attack chain detection[J]. Statal Analysis & Data Mining, 2015, 8(5/6): 353-363. |
 2021, Vol. 47
2021, Vol. 47
