随着传感器、无线通信网络以及GPS定位等技术的快速发展, 各种基于位置的应用产生了海量轨迹数据[1], 人们希望能够对这些海量数据进行分析, 发现潜在的分布特征和运动规律, 该需求促进了轨迹数据挖掘技术的产生与发展[2]。
轨迹数据挖掘通常需要对相似性或距离进行定义, 即度量不同轨迹之间的相似或接近程度, 从而将具有相似运动轨迹的个体划分成簇[3]。例如, 轨迹分类通过计算当前轨迹与各类别的相似度来判定轨迹所属的类别; 在预测用户目的地时, 需要计算用户当前路径与历史路径的相似程度, 以此提供可能的目的地等。
国内外专家学者对轨迹相似性度量方法进行了大量的研究和探索, 对于两条轨迹之间的相似性度量, 按照两条轨迹的轨迹点匹配时的时间匹配条件从严到松的不同要求, 度量方法大体可分为6类[4]:第1类是时间全区间相似性度量方法, 前提是两条轨迹的轨迹点数必须相同, 且对应轨迹点所处的时刻也相同, 这类方法主要有欧氏距离[5]和最小外包矩形距离[6]等; 第2类是全区间变换对应相似性度量方法, 该类方法在第1类方法的基础上, 放松了匹配的点对时刻须完全相同的限制, 这类方法的代表是动态时间规整(Dynamic Time Warping, DTW)距离[7-8]; 第3类是多子区间对应相似方法, 该类方法不要求对两条轨迹的所有轨迹点进行匹配, 而是寻找不重叠的多个相似子区间, 并将区间之间的相似性汇总成轨迹间的相似度, 此类方法能发现局部相似的时空轨迹, 其中最长公共序列[9-11]和编辑距离[12-13]是比较常用的方法; 第4类方法仅寻找两条轨迹的最大相似子区间, 用它来度量轨迹之间的相似性[4], 这类方法主要有子轨迹聚类[14-15]、时间聚焦聚类[16]、移动微聚类[17]和移动聚类[18]等; 第5类方法是单点对应相似方法, 该类方法是用某一匹配的点对的相似性代替轨迹之间的相似性, 其中历史最近距离[19]和Frechet距离[2]是最主要的两种方法; 第6类是无时间区间对应相似性度量方法, 这类方法仅考虑空间位置的相似性, 比如单向距离方法[20]和特征提取方法[21]等。
以上方法在相似性度量时大多是以时空距离为度量手段, 很少从运动方向角度刻画轨迹的相似性。考虑到移动对象的行为趋势不仅体现在行驶距离上还体现在前进方向上, 本文提出以运动方向为主导并兼顾形态距离特征的轨迹相似性度量方法, 分别采用不同的指标对距离、方向特征进行度量, 依据性能评价选取距离和方向的最优组合作为轨迹相似性度量的最终形式, 并进行实际案例分析。
1 基于距离与方向特征的轨迹相似性度量以运动方向为主导的度量方法采用方向特征与形态距离特征相结合的方式进行相似性度量。两条轨迹的方向特征相似性采用真实平均方向夹角、线性平均方向夹角、最长公共方向序列3种度量形式。轨迹的真实平均方向是该轨迹所有相邻时刻轨迹点之间真实方向的平均值, 两条轨迹的真实平均方向夹角越小表示其方向相似性越高; 轨迹的线性平均方向描述的是该轨迹的线性趋势方向, 两条轨迹的线性平均方向夹角越小表示其方向相似性越高; 轨迹的方向序列是基于轨迹相邻时刻轨迹点之间真实方向形成的方向序列, 两条轨迹的最长公共方向序列是在两条轨迹中查找具有相同方向的最长且可不连续的方向子序列, 最长公共方向序列越长表示两条轨迹的相似性越高。两条轨迹的形态距离特性相似性则采用两条轨迹的包围面积进行度量, 包围面积越小表示其相似性越高。将形态距离特征与3种方向特征分别进行组合, 通过评价多个测试数据的聚类性能, 从而选择最优的组合方式, 并将该最优组合与其他相似性度量方法的聚类效果进行对比分析。下面分别阐述形态距离度量和运动方向度量方法。设轨迹Tri={(x1i, y1i, t1i), (x2i, y2i, t2i), …, (xki, yki, tki), …, (xni, yni, tni)}, 其中, (xki, yki, tki)表示第i条轨迹中的第k个轨迹点, xki, yki)与tki分别表示该轨迹点的位置与所处时刻, n为轨迹Tri的轨迹点总数。
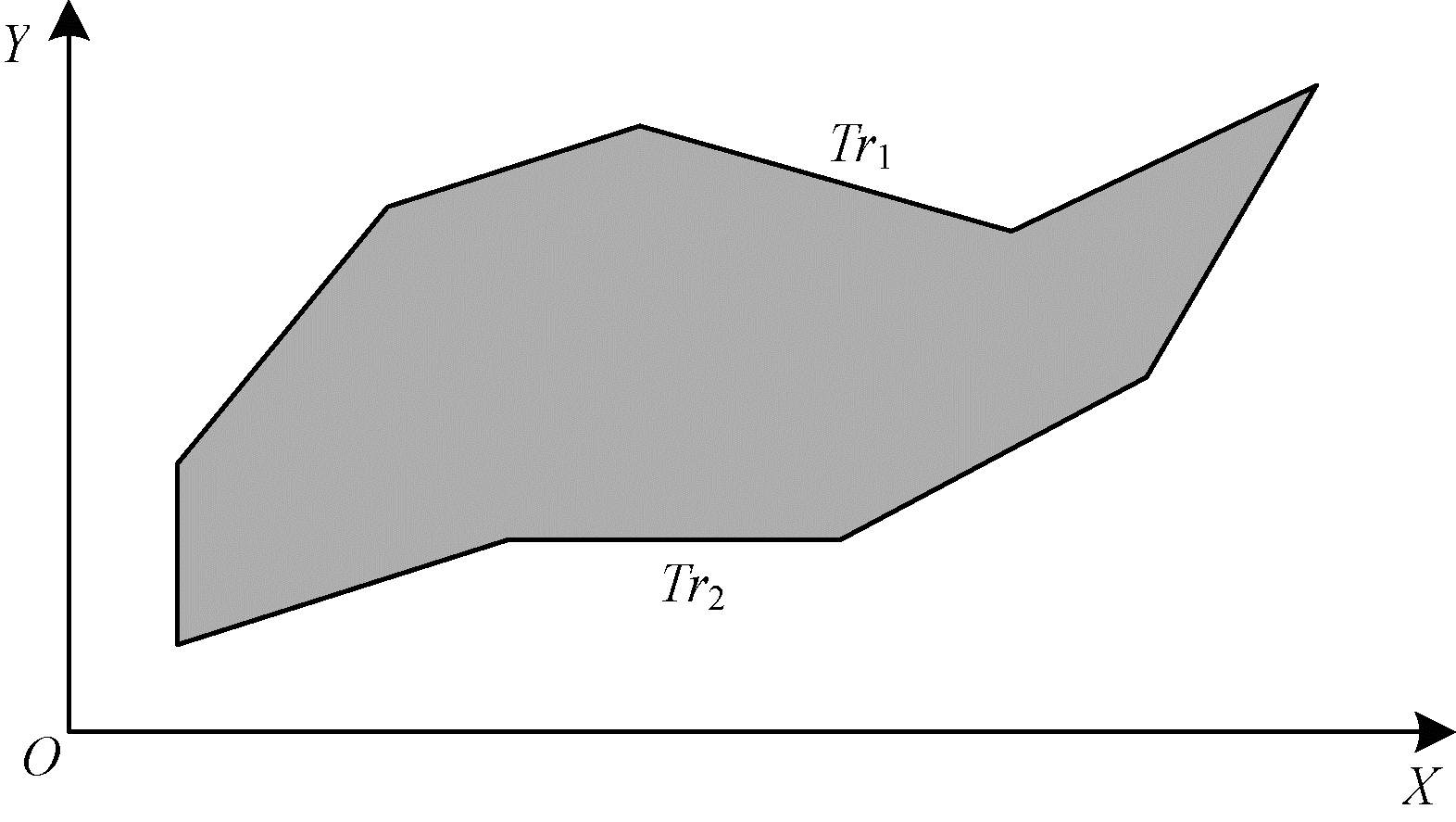
1.1 形态距离度量方法本文采用包围面积作为形态距离特征的相似性度量方法, 包围面积直接使用两条轨迹Tri与Trj围成的面积Si, j来度量序列间的相似度, Si, j越小两条轨迹越相似、接近程度越高, 包围面积是一种比较直观的度量方法, 如图 1所示, 灰色部分面积为轨迹Tr1与Tr2的包围面积S1, 2。本文采用扫描线算法对两条轨迹Tri与Trj围成的多边形进行填充, 从而得到包围面积。
|
Download:
|
| 图 1 包围面积示意图 | |
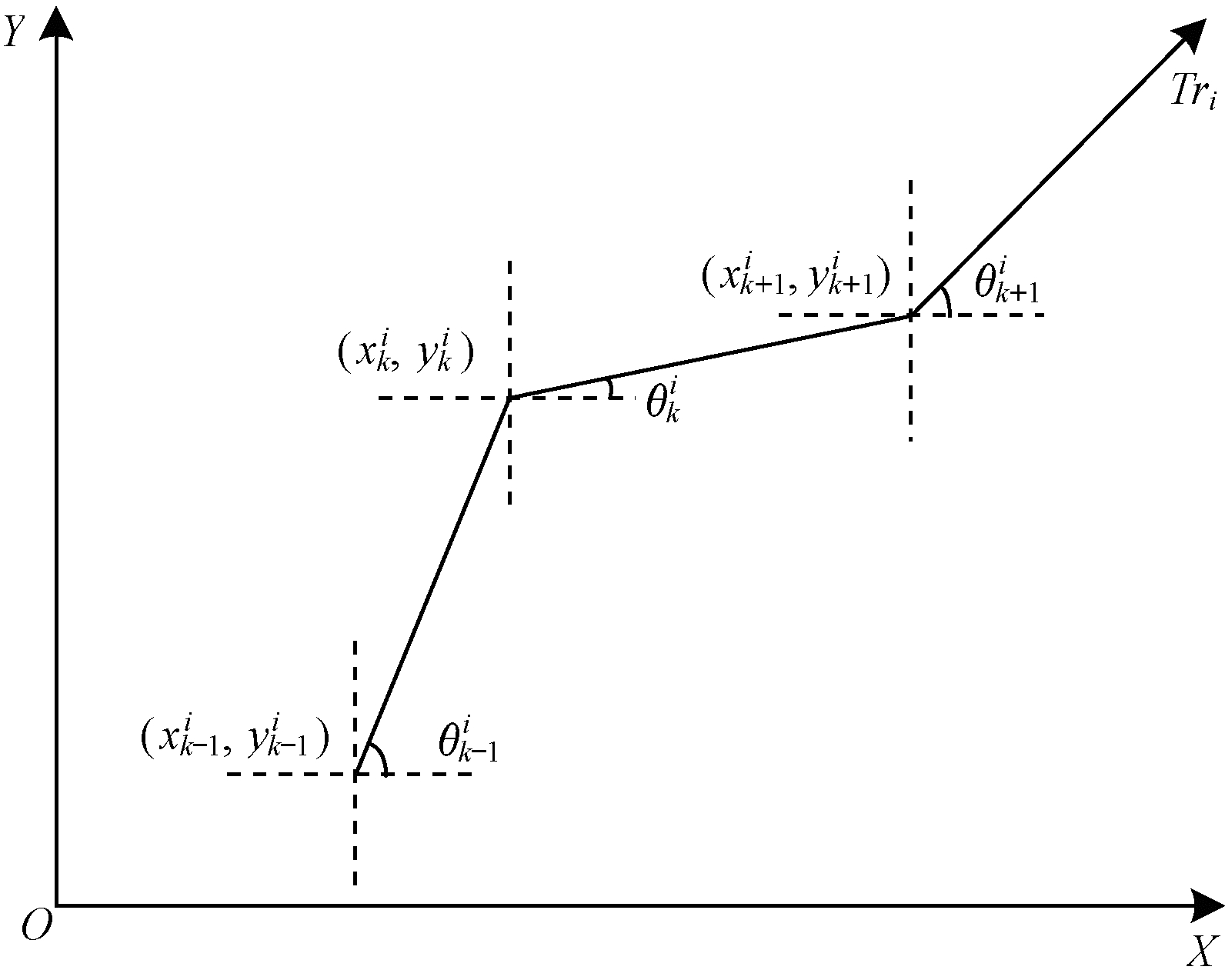
单条轨迹的真实平均方向是该轨迹所有相邻时刻轨迹点形成的轨迹段真实方向的平均值。对于轨迹Tri, 设θki表示轨迹段{(xki, yki, tki), (xk+1i, yk+1i, tk+1i)}以正东方向为基准, 按逆时针旋转得到的方向角(如图 2所示), k=1, 2, …, n-1且θki∈[0°, 360°], 则θki计算公式如下:
|
Download:
|
| 图 2 真实方向夹角示意图 | |
| $ \theta _k^i = \arctan \left( {\left| {\frac{{y_{k + 1}^i - y_k^i}}{{x_{k + 1}^i - x_k^i}}} \right|} \right) $ | (1) |
θki需根据以下不同情况进行调整:
| $ \left\{ {\begin{array}{*{20}{l}} {\theta _k^i \Leftarrow \theta _k^i,x_{k + 1}^i - x_k^i > 0\;且\;y_{k + 1}^i - y_k^i \ge 0}\\ {\theta _k^i \Leftarrow {{180}^\circ } - \theta _k^i,x_{k + 1}^i - x_k^i < 0\;且\;y_{k + 1}^i - y_k^i \ge 0}\\ {\theta _k^i \Leftarrow {{180}^\circ } + \theta _k^i,x_{k + 1}^i - x_k^i < 0\;且\;y_{k + 1}^i - y_k^i < 0}\\ {\theta _k^i \Leftarrow {{360}^\circ } - \theta _k^i,x_{k + 1}^i - x_k^i > 0\;且\;y_{k + 1}^i - y_k^i < 0} \end{array}} \right. $ | (2) |
轨迹Tri的真实平均方向角θi为各轨迹段方向角的平均值为:
| $ {\theta _i} = \left( {\sum\limits_{k = 1}^{n - 1} {\theta _k^i} } \right)/\left( {n - 1} \right) $ | (3) |
进一步地, 两条轨迹Tri与Trj的真实平均方向夹角θi, j为:
| $ {\theta _{i,j}} = \left| {{\theta _i} - {\theta _j}} \right| $ | (4) |
线性平均方向用于描述一组线要素的趋势或平均方向。对于轨迹Tri, 其线性平均方向αi是所有轨迹段(每个轨迹段视为一个线要素)的趋势方向, 计算公式如下:
| $ {\alpha _i} = \arctan \left( {\frac{{\sum\limits_{k = 1}^{n - 1} {\sin \theta _k^i} }}{{\sum\limits_{k = 1}^{n - 1} {\cos \theta _k^i} }}} \right) $ | (5) |
其中, θki即轨迹段{(xki, yki, tki), (xk+1i, yk+1i, tk+1i)}的方向角, 其含义与计算公式见1.2.1节, n为轨迹点总数。αi需根据以下不同情况进行调整:
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _i} \Leftarrow {\alpha _i},\sum\limits_{i = 1}^{n - 1} {\sin \theta _k^i} \ge 0\;且\;\sum\limits_{i = 1}^{n - 1} {\cos \theta _k^i} > 0}\\ {{\alpha _i} \Leftarrow {{180}^\circ } - {\alpha _i},\sum\limits_{i = 1}^{n - 1} {\sin \theta _k^i} \ge 0\;且\;\sum\limits_{i = 1}^{n - 1} {\cos \theta _k^i} < 0}\\ {{\alpha _i} = {{180}^\circ } + {\alpha _i},\sum\limits_{i = 1}^{n - 1} {\sin \theta _k^i} < 0\;且\;\sum\limits_{i = 1}^{n - 1} {\cos \theta _k^i} < 0}\\ {{\alpha _i} \Leftarrow {{360}^\circ } - {\alpha _i},\sum\limits_{i = 1}^{n - 1} {\sin \theta _k^i} < 0\;且\;\sum\limits_{i = 1}^{n - 1} {\cos \theta _k^i} > 0} \end{array}} \right. $ | (6) |
两条轨迹Tri与Trj的线性平均方向夹角αi, j为:
| $ {\alpha _{i,j}} = \left| {{\alpha _i} - {\alpha _j}} \right| $ | (7) |
将[0°, 360°]以30°间隔划分为不同的区间, 并将各区间分别赋予不同的固定角度值(如表 1所示), 则轨迹Tri的各轨迹段方向角θki可根据其所属的区间转化为相应的固定角度, 据此可获取轨迹Tri的方向序列Li。

|
下载CSV 表 1 不同角度区间对应的固定角度值 |
对于轨迹Tri与Trj的方向序列Li={L1i, L2i, …, Lki, …, Lni}, Lj={L1j, L2j, …, Lrj, …, Lmj}, 使用最长公共子序列(Longest Common Subsequence, LCSS)方法可获取最长公共方向序列个数li, j, 其中n、m分别为方向序列Li、Lj的方向值总数。
LCSS用来查找两个字符串之间的最长公共子字符串, 要求公共子字符串有序且连续, 之后将字符串延伸为各种序列, 查找两个序列之间的最长公共子序列, 既可要求公共子序列有序且连续, 也可要求公共子序列有序但不连续。本文使用LCSS方法在两条方向序列Li、Lj中查找具有相同方向的最长且可不连续的方向子序列, 进而得到li, j, 其递归公式如下:
| $ {l\left( {L_k^i,L_r^j} \right) = \left( \begin{array}{l} 0,k = 0{\text{ or }}r = 0\\ l\left( {L_{k - 1}^i,L_{r - 1}^j} \right) + 1,k,r > 0{\text{ and }}L_k^i = L_r^j\\ \max \left( {l\left( {L_k^i,L_{r - 1}^j} \right),l\left( {L_{k - 1}^i,L_r^j} \right)} \right)\\ k,r > 0{\text{ and }}L_k^i \ne L_r^j \end{array} \right.} $ | (8) |
其中, k=0, 1, …, n, r=0, 1, …, m。
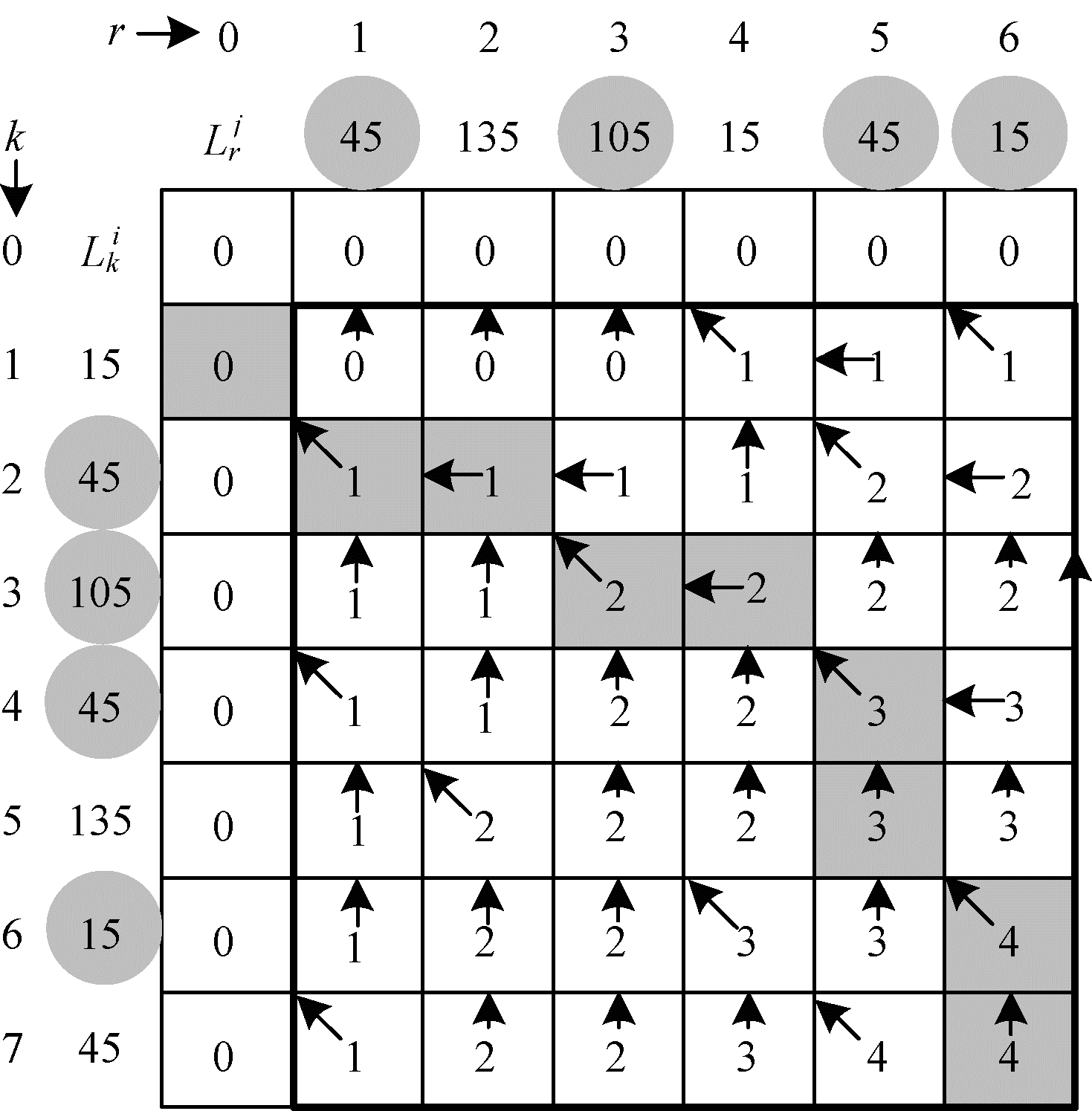
例如, 设有Lki={15, 45, 105, 45, 135, 15, 475}, Lrj={45, 135, 105, 15, 45, 15}两个方向序列, 如图 3所示, 使用LCSS递归方法得到最长公共方向序列个数li, j为4。
|
Download:
|
| 图 3 最长公共方向序列计算过程 | |
设有N条轨迹, 对任两条轨迹Tri、Trj(i, j=1, 2, …, N)分别计算包围面积Si, j、真实平均方向夹角θi, j、线性平均方向夹角αi, j、最长公共方向序列li, j, 其中, Si, j值越小表示形态距离特征相似性越高, θi, j和αi, j值越小表示方向特征相似性越高, li, j值越大表示方向特征相似性越高。对于N条轨迹, 可分别形成包围面积矩阵S=[Si, j]N×N, 真实平均方向夹角矩阵θ=[θi, j]N×N, 线性平均方向夹角矩阵α=[αi, j]N×N, 最长公共方向序列矩阵l=[li, j]N×N, 且当i=j时, Si, i=0、θi, i=0、αi, i=0、li, i=len(Tri), 其中, len(Tri)表示轨迹Tri的轨迹段个数。
对各矩阵分别进行规范化处理, 使Si, j、θi, j、αi, j、li, j的判断准则保持一致, 即值越小, 两条轨迹的相似性越高。
1) 包围面积的规范化处理, 规范化后的Sij值在[0, 1]范围内。
| $ {{S'}_{i,j}} = \frac{{{S_{i,j}} - \mathop {\min }\limits_{i,j = 1,2, \cdots ,N} \left( {{S_{ij}}} \right)}}{{\mathop {\max }\limits_{i,j = 1,2, \cdots ,N} \left( {{S_{ij}}} \right) - \mathop {\min }\limits_{i,j = 1,2, \cdots ,N} \left( {{S_{ij}}} \right)}} $ | (9) |
2) 真实平均方向夹角的规范化处理, 规范化后的θij值在[0, 1]范围内。
| $ {{\theta '}_{i,j}} = \frac{{{\theta _{i,j}} - \mathop {\min }\limits_{i,j = 1,2, \cdots ,N} \left( {{\theta _{ij}}} \right)}}{{\mathop {\max }\limits_{i,j = 1,2, \cdots ,N} \left( {{\theta _{ij}}} \right) - \mathop {\min }\limits_{i,j = 1,2, \cdots ,N} \left( {{\theta _{ij}}} \right)}} $ | (10) |
3) 线性平均方向夹角的规范化处理, 规范化后的αij值在[0, 1]范围内。
| $ {{\alpha '}_{i,j}} = \frac{{{\alpha _{i,j}} - \mathop {\min }\limits_{i,j = 1,2, \cdots ,N} \left( {{\alpha _{ij}}} \right)}}{{\mathop {\max }\limits_{i,j = 1,2, \cdots ,N} \left( {{\alpha _{ij}}} \right) - \mathop {\min }\limits_{i,j = 1,2, \cdots ,N} \left( {{\alpha _{ij}}} \right)}} $ | (11) |
4) 最长公共方向序列的规范化处理:
| $ {{l'}_{i,j}} = 1 - \frac{{{l_{i,j}}}}{{\left( {len\left( {T{r_i}} \right) + len\left( {T{r_j}} \right)} \right)/2}} $ | (12) |
其中, len(Tri)、len(Trj)分别表示轨迹Tri、轨迹Trj的轨迹段个数。因为lij≤len(Tri)且lij≤len(Trj), 所以规范化后的lij值在[0, 1]范围内。
将度量形态距离特征的包围面积与度量方向特征的真实平均方向夹角、线性平均方向夹角、最长公共方向序列分别进行组合, 从而形成3种轨迹相似性度量的组合方式:
1) 包围面积与真实平均方向夹角的组合为:
| $ Si{m_{ij}}\left( {包围面积 + 真实方向} \right) = \frac{{{S_{ij}} + {\theta _{ij}}}}{2} $ | (13) |
2) 包围面积与线性平均方向夹角的组合为:
| $ Si{m_{ij}}\left( {包围面积 + 线性方向} \right) = \frac{{{S_{ij}} + {\alpha _{ij}}}}{2} $ | (14) |
3) 包围面积与最长公共方向序列的组合为:
| $ Si{m_{ij}}\left( {包围面积 + 方向序列} \right) = \frac{{{S_{ij}} + {l_{ij}}}}{2} $ | (15) |
通过对多个测试数据集聚类结果的性能评价, 从而选择最优的相似性度量组合方式。
2 相似性度量方法性能评价 2.1 测试数据集本文采用CVRR轨迹聚类数据集[22]对基于不同轨迹相似性度量的聚类结果进行对比分析。使用3种类型的轨迹数据集:1)I5数据集, 该数据集是双向高速公路上的汽车行驶轨迹, 包含806条轨迹, 分为8类, 如图 4(a)所示; 2)LABOMNI数据集, 该数据集是人在室内的行走轨迹, 包含209条轨迹, 分为15类, 如图 4(b)所示; 3)CROSS数据集, 该数据集是模拟十字路口车辆直行与转弯的轨迹, 包含1 900条轨迹, 分为19类, 如图 4(c)所示。所有数据集均标记了每个轨迹所属的类, 可以基于轨迹相似性度量方法对这些数据集进行聚类, 进而将获得的聚类结果与数据集中标记的正确聚类进行对比, 从而评价不同轨迹相似性度量方法的聚类性能。

|
Download:
|
| 图 4 CVRR轨迹聚类测试数据集 | |
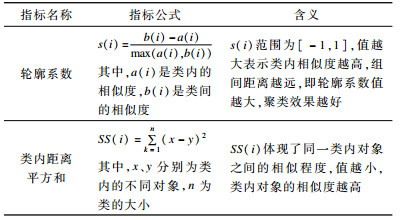
本文分别采用simij(包围面积+真实方向)、simij(包围面积+线性方向)、simij(包围面积+方向序列)>3种组合方式对测试数据集进行层次聚类分析。使用轮廓系数、类内距离平方和对聚类结果进行评价, 使用F值(F-Measure)对聚类类数识别的精度进行评价, 从而根据指标结果对3种组合方式的聚类效果进行对比。表 2为轮廓系数、类内距离平方和指标公式及其含义。
|
下载CSV 表 2 轮廓系数、类内距离平方和指标公式及其含义 |
F值计算公式如下:
| $ F = \frac{{2 \times P \times R}}{{P + R}} $ | (16) |
其中, P为正确率, R为召回率, 且P表示类标记识别正确的轨迹总数与识别出类标记的轨迹总数之比, R表示类标记识别正确的轨迹总数与数据集包含的轨迹总数之比。
下文分别为3个测试集的层次聚类评价结果:
1) I5数据集
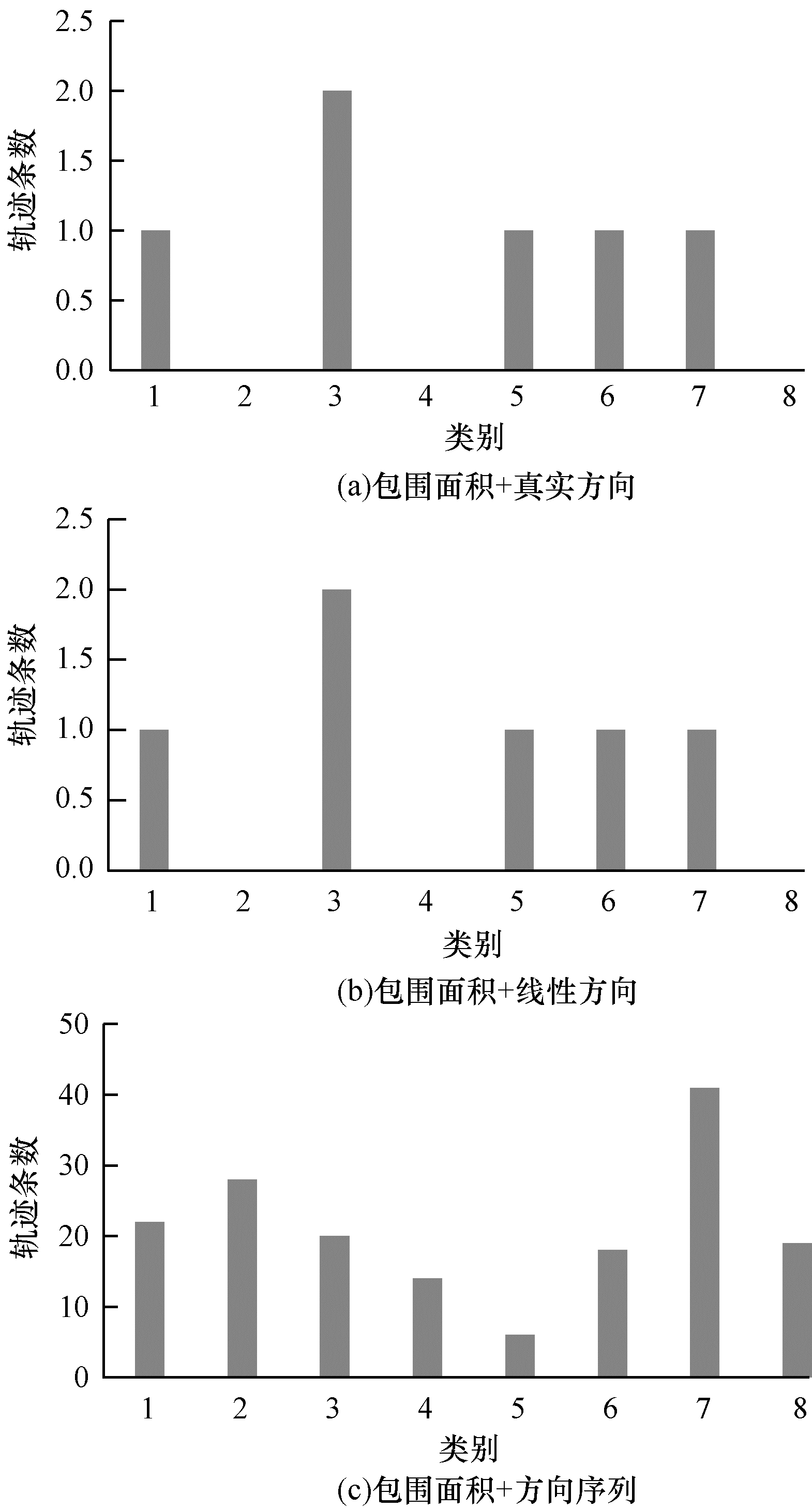
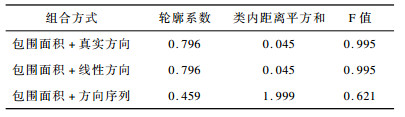
图 5统计了3种组合方式识别的各类中轨迹类标记与真实类标记不同的轨迹条数, 其中, 包围面积+真实方向、包围面积+线性方向两种组合类标记识别错误的轨迹条数较少。各组合方式评价指标结果见表 3。可以看出, 包围面积+真实方向、包围面积+线性方向两种组合方式的轮廓系数和F值较大, 类内距离平方和较小。
|
Download:
|
| 图 5 I5数据集上3种组合方式类标记识别错误的轨迹条数 | |
|
下载CSV 表 3 I5数据集上各组合聚类结果评价指标 |
2) LABOMNI数据集
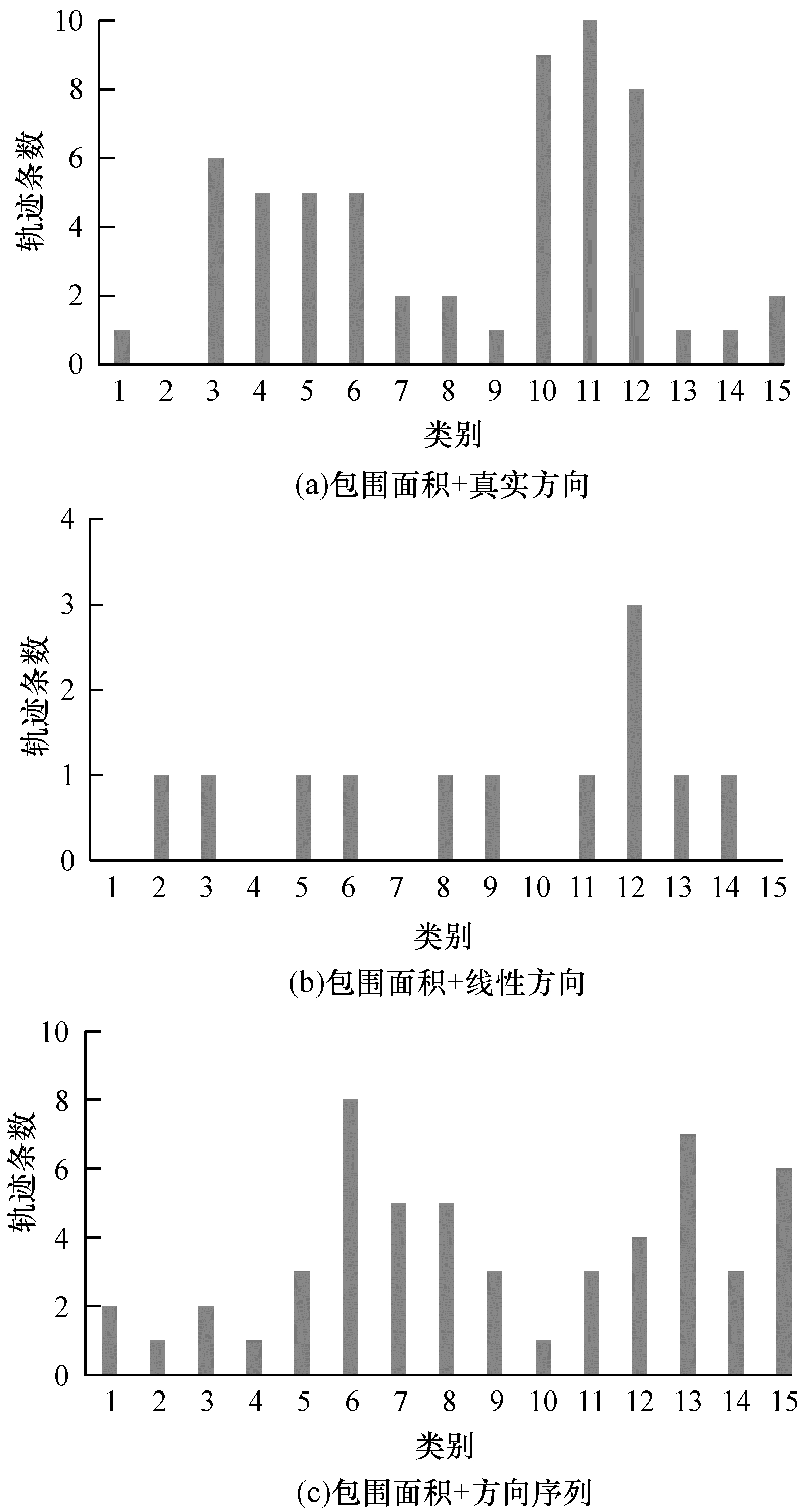
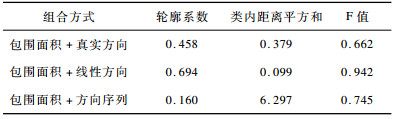
从图 6可以看出, 包围面积+线性方向组合方式类标记识别错误的轨迹条数最少。各组合方式评价指标结果见表 4。可以看出, 包围面积+线性方向的轮廓系数和F值最大, 类内聚类平方和最小。
|
Download:
|
| 图 6 LABOMNI数据集上3种组合方式类标记识别错误的轨迹条数 | |
|
下载CSV 表 4 LABOMNI数据集上各组合方式聚类结果评价指标 |
3) CROSS数据集
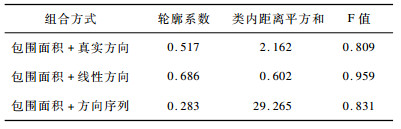
图 7表明包围面积+线性方向组合方式类标记识别错误的轨迹条数最少。各组合方式评价指标结果见表 5, 同样表明包围面积+线性方向的指标结果最优。综合3个数据集的最优组合, 本文选择包围面积+线性方向作为基于形态距离特征和方向特征的轨迹相似性度量的最优组合方式。
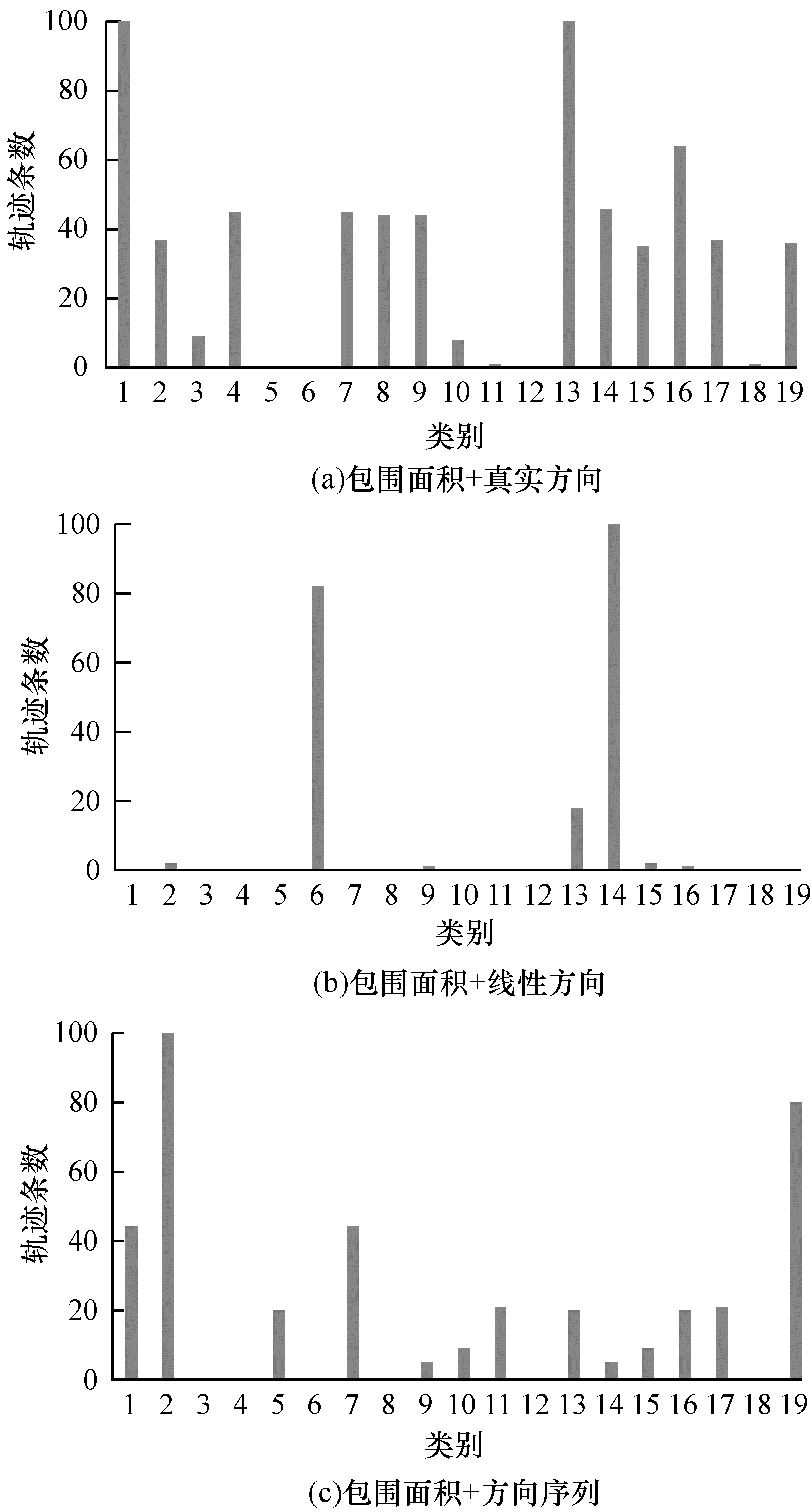
|
Download:
|
| 图 7 CROSS数据集上3种组合方式类标记识别错误的轨迹条数 | |
|
下载CSV 表 5 CROSS数据集上各组合方式聚类结果评价指标 |
使用I5、LABOMNI、CROSS这3个测试集, 将最优组合方式(包围面积与线性平均方向夹角)和经典的轨迹相似性度量LCSS方法进行对比。
1) I5数据集
采用包围面积+线性方向、LCSS方法分别对I5数据集进行层次聚类分析, 图 8(a)为聚类结果的F值, 图 8(b)为聚类得到的各类轨迹条数。可以看出, 相比于LCSS方法, 包围面积+线性方向的F值更优, 聚类得到的各类轨迹条数更贴近真实的轨迹条数。
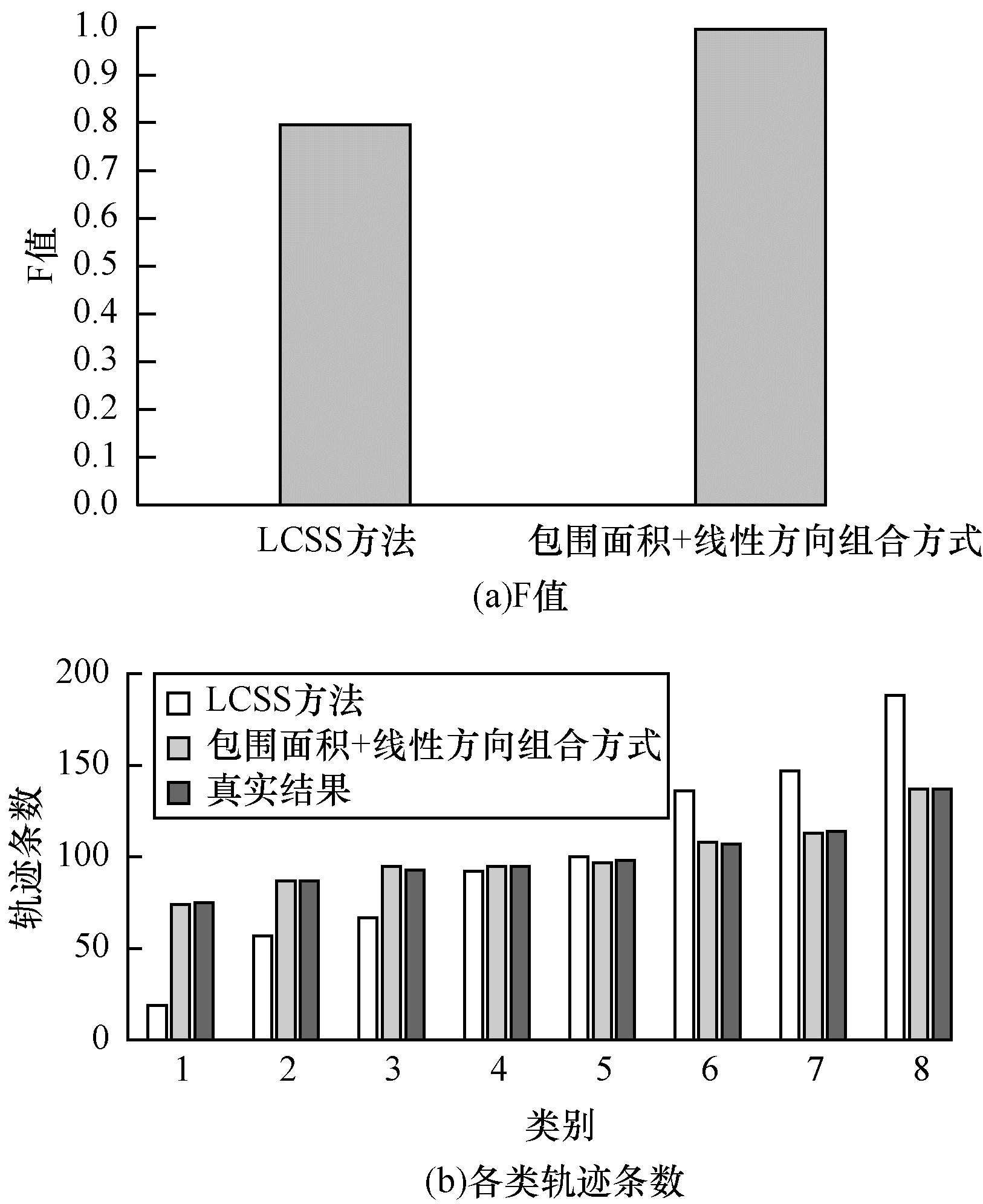
|
Download:
|
| 图 8 I5数据集上包围面积+线性方向组合方式与LCSS方法的层次聚类结果对比 | |
2) LABOMNI数据集
图 9(a)、图 9(b)的结果表明, 包围面积+线性方向的F值, 聚类得到的各类轨迹条数均优于LCSS方法。
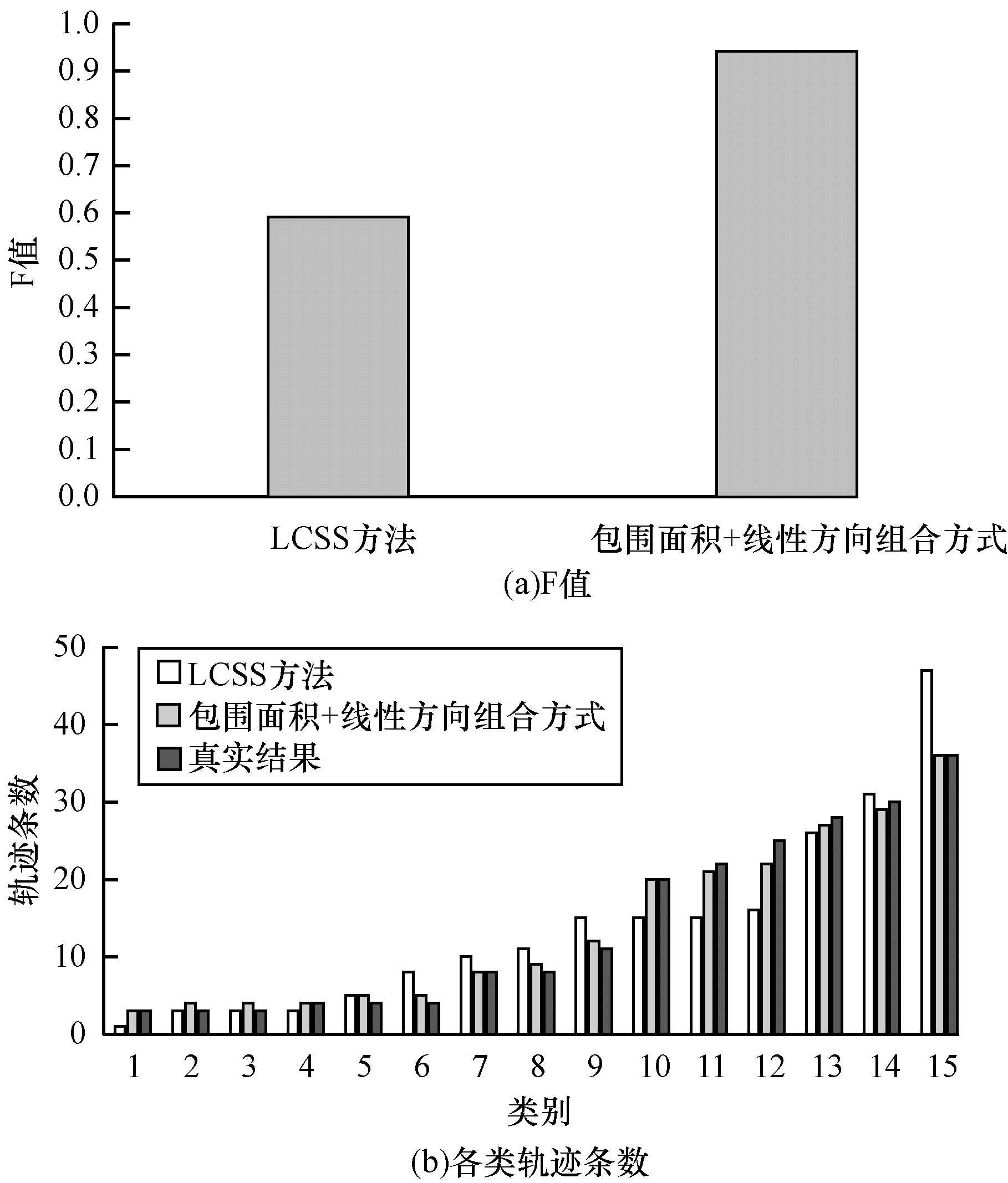
|
Download:
|
| 图 9 LABOMNI数据集上包围面积+线性方向组合方式与LCSS方法的层次聚类结果对比 | |
3) CROSS数据集
图 10(a)表明包围面积+线性方向组合方式的F值优于LCSS方法, 图 10(b)表明包围面积+线性方法组合方式得到的各类轨迹条数略优于LCSS方法。
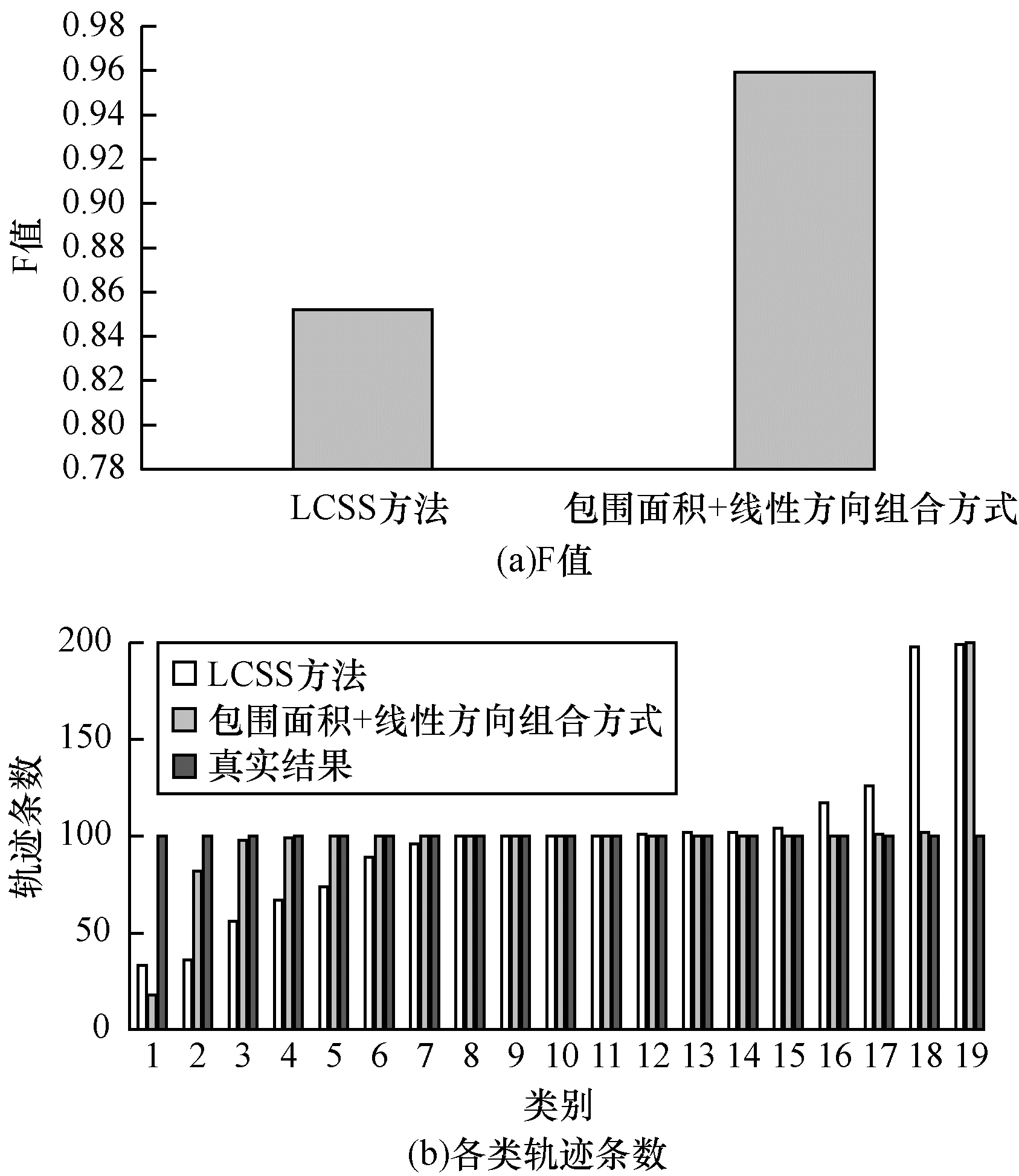
|
Download:
|
| 图 10 CROSS数据集上包围面积+线性方向组合方式与LCSS方法的层次聚类结果对比 | |
综合上述3个不同数据集的对比结果, 包围面积+线性方向组合方式作为轨迹相似性度量方法的聚类结果相较于LCSS方法的聚类结果, 准确率更优, 并且每一簇内轨迹条数更接近于真实结果, 因此认为以包围面积+线性方向组合方式作为轨迹相似性度量方法优于LCSS方法。
2.2.3 与最小外包矩形面积+线性方向的对比本文使用最小外包矩形面积代替最优组合中的包围面积, 对“包围面积+线性方向”和“最小外包矩形面积+线性方向”两种组合方式的层次聚类结果进行对比。
最小外包矩形面积指包含两条轨迹所有点集的最小外接矩形的面积(如图 11所示), 使用该矩形面积度量两条轨迹之间的距离, 面积越小表示这两条轨迹的距离越小, 接近程度越高, 从而可通过最小外包矩形面积刻画两条轨迹整体的形态距离特征。对于轨迹Tri和Trj的最小外包矩形面积可记为Si, j。
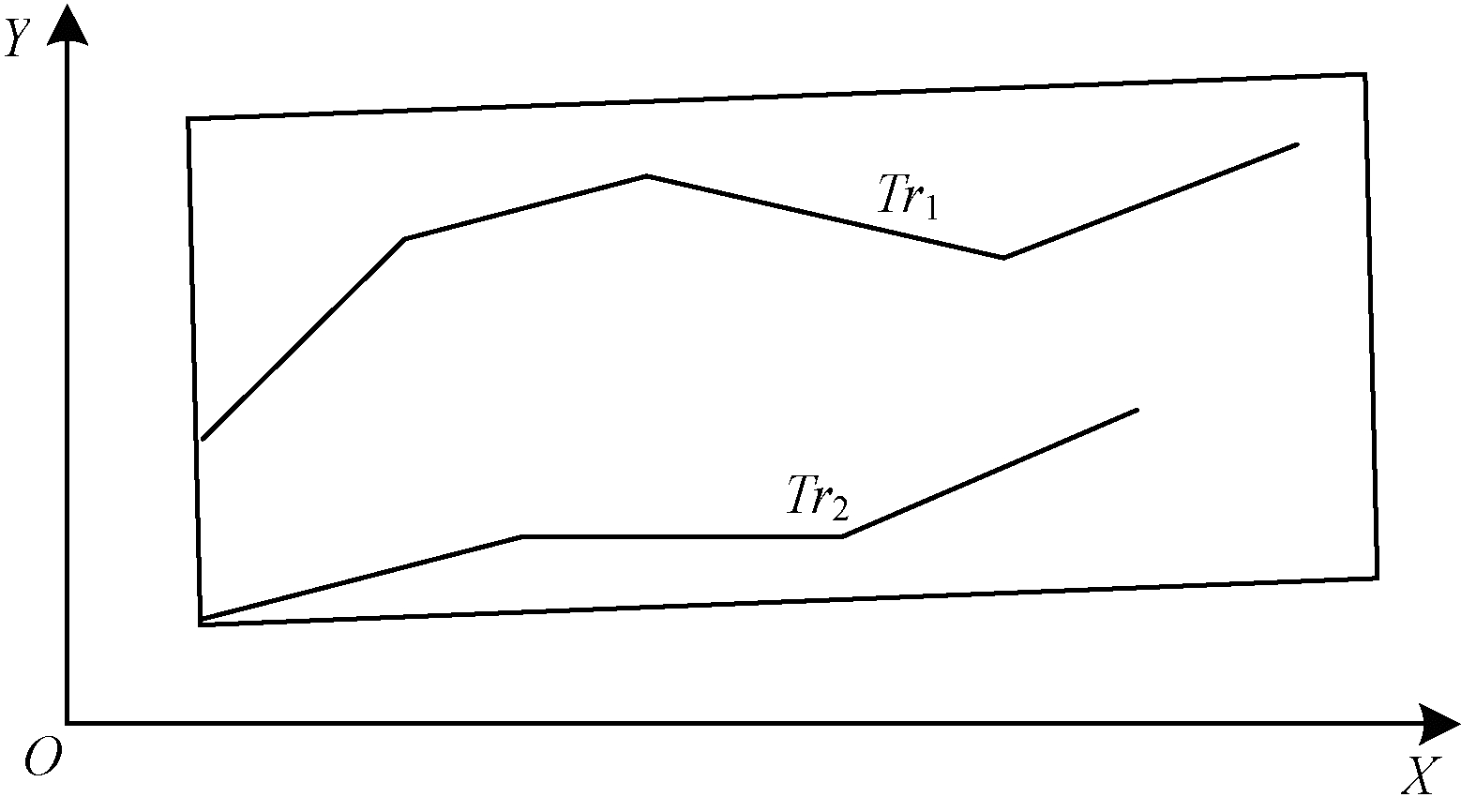
|
Download:
|
| 图 11 最小外包矩形面积示意图 | |
两种组合方式的层次聚类结果的轮廓系数、类内聚类平方和、F值见图 12, 相比于最小外包矩形面积+线性方向组合方式, 包围面积+线性方向组合方式具有更大的轮廓系数值、更小的类内距离平方和以及更接近于1的F值, 即包围面积+线性方向组合方式的聚类效果更优。
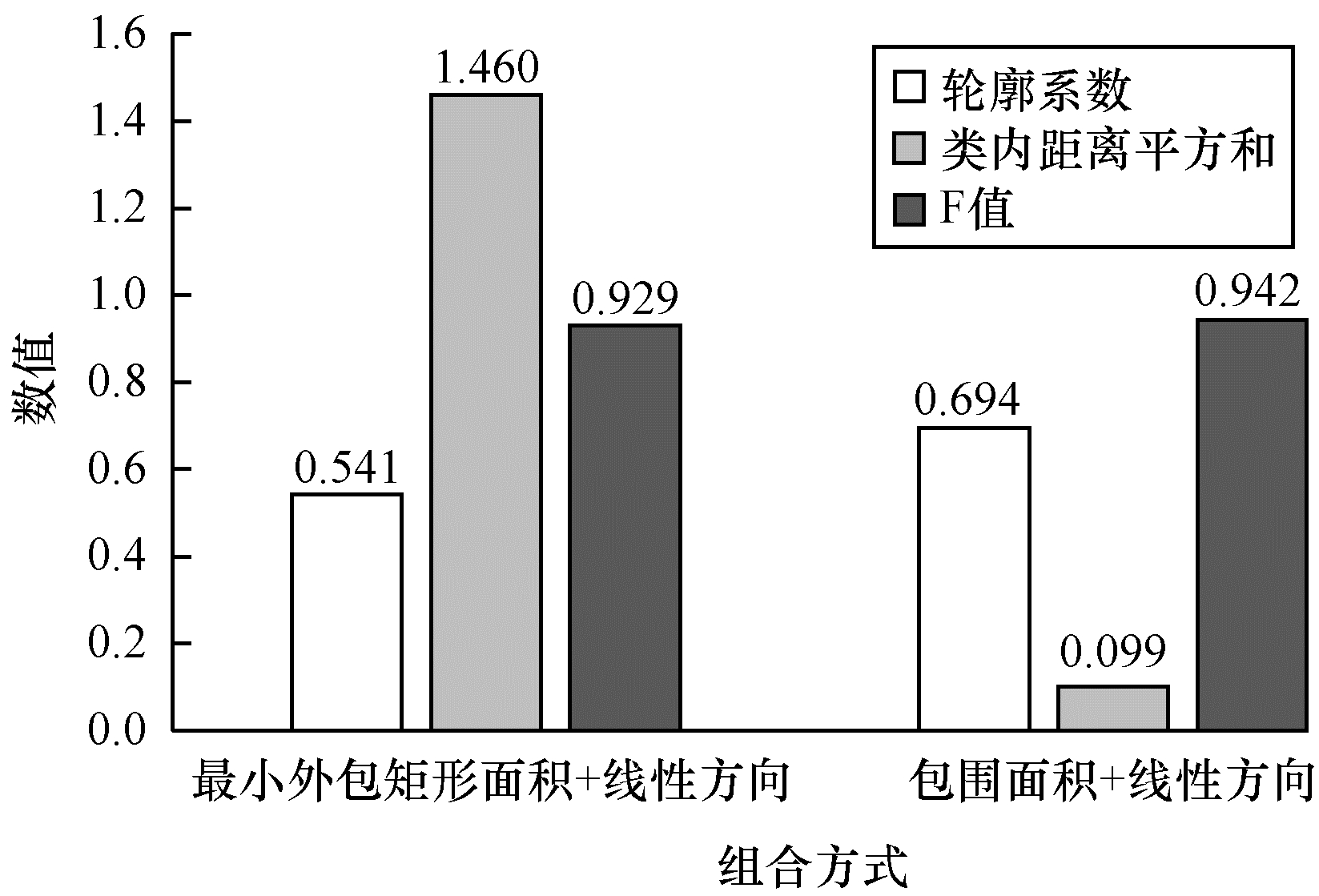
|
Download:
|
| 图 12 不同组合方式的层次聚类结果对比 | |
应用数据集为北京市33 000多辆出租车一周(2015-05-11—2015-05-17)产生的GPS轨迹数据, 共计约3.85亿条点数据, 采样间隔为60 s, 采样时间为24 h。
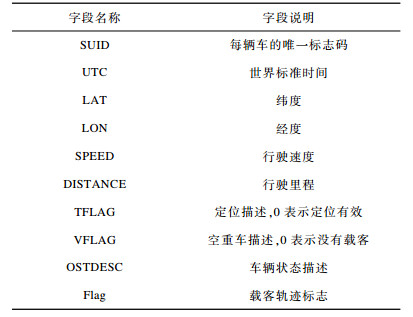
轨迹数据主要字段名称和含义如表 6所示, 经过预处理(包括噪声剔除、非载客点剔除等), 得到如图 13所示的数据, 该数据由若干载客轨迹构成, 每条轨迹仅包含载客点数据, 不同载客轨迹之间由[Flag]字段标志, 同一辆车可含有多条载客轨迹。
|
下载CSV 表 6 部分重要字段名称及其说明 |
|
Download:
|
| 图 13 载客轨迹数据 | |
从该数据集中提取行驶时间位于2015-05-11 07:00—2015-05-11 08:00的载客轨迹, 共计11 385条, 406 424个载客数据点。对选取的载客轨迹Tri(i=1, 2, …, N, N=11 385)采用simij(包围面积+线性方向)组合方式进行聚类。
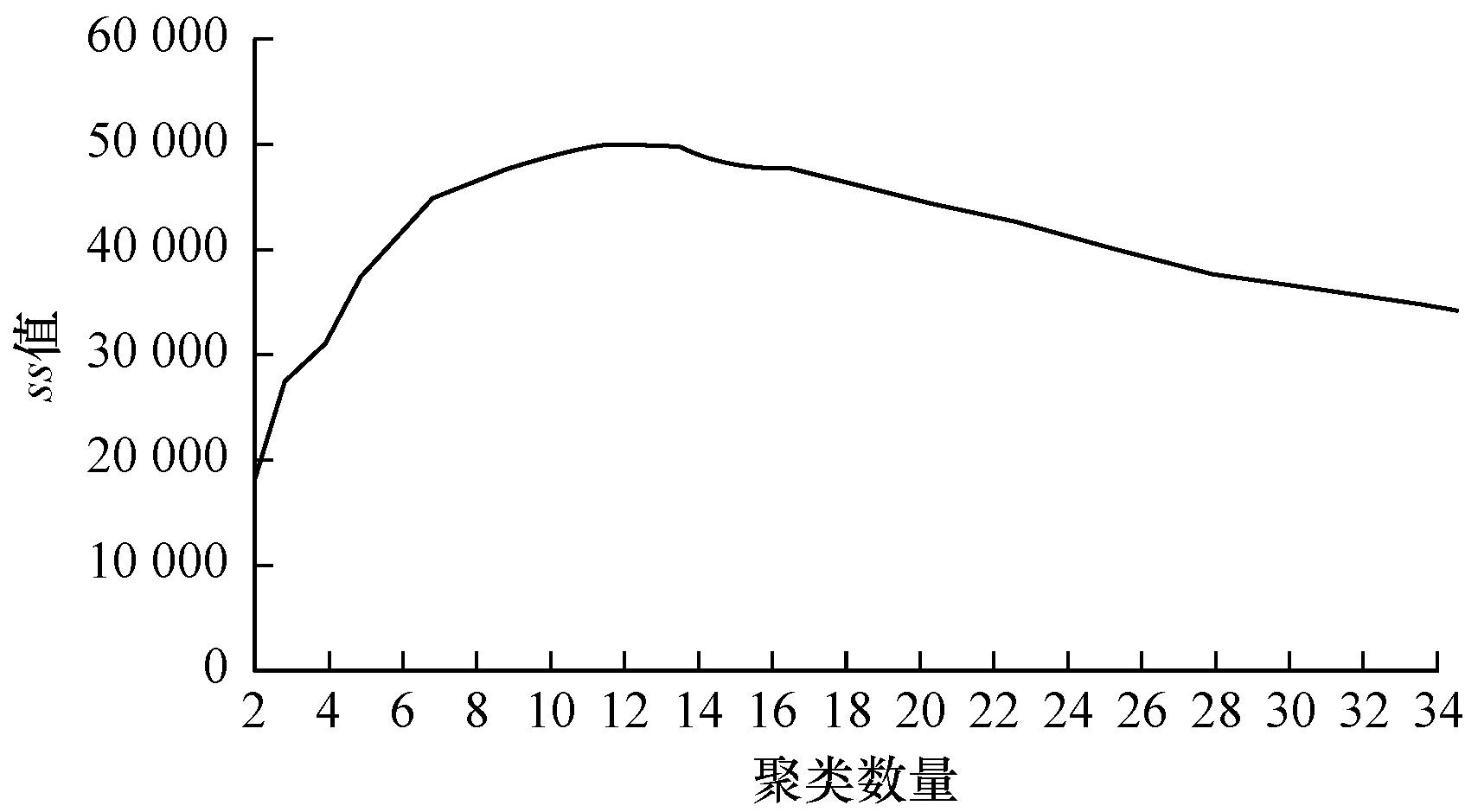
使用Calinski-Harabasz分数值确定最佳聚类数量, 如图 14所示。
|
Download:
|
| 图 14 基于Calinski-Harabasz分数值的聚类数量 | |
Calinski-Harabasz分数值ss的数学计算公式如式(17)所示。
| $ s\left( k \right) = \frac{{{\rm tr}\left( {{\mathit{\boldsymbol{B}}_k}} \right)}}{{{\rm tr}\left( {{\mathit{\boldsymbol{W}}_k}} \right)}}\frac{{m - k}}{{k - 1}} $ | (17) |
其中, m为训练集样本数, k为类别数, Bk为类别间的协方差矩阵, Wk为类内部的协方差矩阵, tr为矩阵的迹。类内部的协方差越小越好, 类间协方差越大越好, ss越大越好, 因此选择最佳聚类个数为12。
以类为对象进行分析。绘制每一类的核密度图与线性方向平均值, 如图 15所示, 黑色线表示线性方向平均值, 表明该类所有轨迹的平均方向, 深色区域表明该类主要分布区域(行政区划)。由图 15可见, 每一类轨迹的主要分布区域均以朝阳区、东城区、西城区、海淀区、丰台区为主要聚集区域, 且在东城区与西城区内, 各类的主要聚集区基本都集中在区域边界处。这些区域均在四环范围内, 北京市繁华地带, 属于二环到四环之间, 结合图 15可以发现各类的分布基本符合实际情况。此外, 有很大一部分轨迹显示经由朝阳区去往顺义区, 这些轨迹基本以机场为目的地, 由图 15(a)、图 15(c)、图 15(h)、图 15(i)、图 15(k)、图 15(l)也可以验证。

|
Download:
|
| 图 15 载客轨迹数据聚类结果的核密度图与线性方向平均值 | |
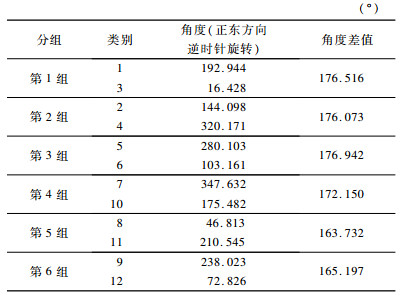
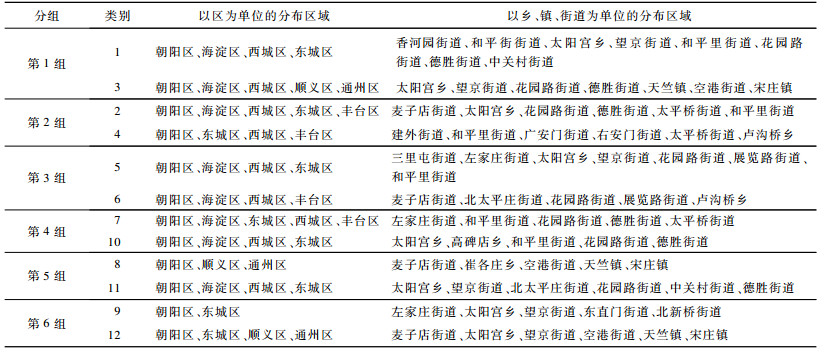
类间线性方向平均值差异较大, 可以反映本文方法效果明显, 能够对不同趋势方向的轨迹进行分类。将12类结果分为6组, 具体组合如表 7所示, 分类依据为每一组内两类结果的线性方向相反。每一组内不同类别在乡镇区域分布情况不同, 具体详见表 8。可以看出, 组内两类结果主要分布区域在行政区划上有很大相似性, 在以乡、镇、街道为单位的区域分布上有较大差异, 该差异体现在同一行政区划内的不同乡、镇、街道上, 即同一组内不同类的主要分布区域集中在相同的行政区划上, 但是并没有全部位于相同的乡、镇、街道中。
|
下载CSV 表 7 线性方向角度组合结果 |
|
下载CSV 表 8 不同类别的主要区域分布情况 |
本文提出形态距离特征与3种方向特征组合的轨迹相似性度量方法, 选出最优组合方式为包围面积与线性平均方向。将该组合方式分别与LCSS方法、最小外包矩形面积及线性平均方向组合方式进行对比验证, 发现该组合方式在性能与准确率上均表现良好。使用该组合方式对北京市出租车GPS轨迹数据进行聚类应用, 结果显示能够区分移动对象趋势方向, 验证了以移动对象运动方向为主导的轨迹相似性度量方法的有效性与准确性。由于本文在生成方向序列过程中, 采用固定阈值进行区间分割, 灵活性较差, 因此下一步可将方向序列分割阈值设置为可变参数, 选择多个阈值影响下的最优组合, 并且可结合轨迹数据与POI数据进行轨迹语义相似性度量, 实现乘客流向、主要上下车点区域的分析与识别。
| [1] |
李正欣, 张凤鸣, 李克武, 等. 一种支持DTW距离的多元时间序列索引结构[J]. 软件学报, 2014, 25(3): 560-575. (  0) 0)
|
| [2] |
SKOUMAS G, SKOUTAS D, VLACHAKI A.Efficient identification and approximation of k-nearest moving neighbors[C]//Proceedings of ACM Sigspatial International Conference on Advances in Geographic Information Systems.New York, USA: ACM Press, 2013: 264-273.
(  0) 0)
|
| [3] |
袁正午, 袁松彪. 流聚类模型及其统一表示[J]. 计算机工程, 2009, 35(16): 76-77, 80. DOI:10.3969/j.issn.1000-3428.2009.16.026 (  0) 0)
|
| [4] |
龚玺, 裴韬, 孙嘉, 等. 时空轨迹聚类方法研究进展[J]. 地理科学进展, 2011, 30(5): 522-534. (  0) 0)
|
| [5] |
KEOGH E, PALPANAS T, ZORDAN V, et al.Indexing large human-motion databases[C]//Proceedings of the 13th International Conference on Very Large Data Bases.New York, USA: ACM Press, 2004: 780-791. https://www.sciencedirect.com/science/article/pii/B9780120884698500693
(  0) 0)
|
| [6] |
ZHENG Yu, ZHOU Xiaofang. Computing with spatial trajectories[M]. Berlin, Germany: Springer, 2011.
(  0) 0)
|
| [7] |
CHEN L, ÖZSU M, ORIA V.Robust and fast similarity search for moving object trajectories[C]//Proceedings of 2005 ACM SIGMOD International Conference on Management of Data.New York, USA: ACM Press, 2005: 491-502. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.577.8494
(  0) 0)
|
| [8] |
VLACHOS M, GUNOPULOS D, DAS G.Rotation invariant distance measures for trajectories[C]//Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2004: 707-712. https://www.mendeley.com/catalogue/rotation-invariant-distance-measures-trajectories/
(  0) 0)
|
| [9] |
HERMES C, WOHLER C, SCHENK K, et al.Long-term vehicle motion prediction[C]//Proceedings of 2009 IEEE Intelligent Vehicles Symposium.Washington D.C., USA: IEEE Press, 2009: 652-657. https://ieeexplore.ieee.org/document/5164354
(  0) 0)
|
| [10] |
SAKURAI Y, YOSHIKAWA M, FALOUTSOS C.FTW: fast similarity search under the time warping distance[C]//Proceedings of the 24th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems.New York, USA: ACM Press, 2005: 326-337.
(  0) 0)
|
| [11] |
KIM J, MAHMASSANI H S. Spatial and temporal characterization of travel patterns in a traffic network using vehicle trajectories[J]. Transportation Research Part C:Emerging Technologies, 2015, 9: 375-390. (  0) 0)
|
| [12] |
曾万聃, 周敏奇, 刘云翔. 轨迹大数据的比较算法研究[J]. 吉林大学学报(信息科学版), 2016, 34(6): 792-799. DOI:10.3969/j.issn.1671-5896.2016.06.014 (  0) 0)
|
| [13] |
AGRAWAL R, FALOUTSOS C, SWAMI A.Efficient similarity search in sequence databases[C]//Proceedings of International Conference on Foundations of Data Organization and Algorithms.Berlin, Germany: Springer, 1993: 69-84. https://link.springer.com/chapter/10.1007%2F3-540-57301-1_5
(  0) 0)
|
| [14] |
LEE J G, HAN J, WHANG K Y.Trajectory clustering: a partition-and-group framework[C]//Proceedings of 2007 ACM SIGMOD International Conference on Management of Data.New York, USA: ACM Press, 2007: 593-604. https://dl.acm.org/citation.cfm?doid=1247480.1247546
(  0) 0)
|
| [15] |
LIU Jinpeng, ZHANG Yanling, LIU Gang.Partition and density-based clustering for moving objects trajectories[C]//Proceedings of the 3rd International Conference on Computer Science and Education.Washington D.C., USA: IEEE Press, 2008: 182-187.
(  0) 0)
|
| [16] |
NANNI M, PEDRESCHI D. Time-focused clustering of trajectories of moving objects[J]. Journal of Intelligent Information Systems, 2006, 27(3): 267-289. DOI:10.1007/s10844-006-9953-7 (  0) 0)
|
| [17] |
LI Yifan, HAN Jiawei, YANG Jiong.Clustering moving objects[C]//Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2004: 617-622.
(  0) 0)
|
| [18] |
BEREZANSKY M, GREENSPAN H, COHEN-OR D, et al. Segmentation and tracking of human sperm cells using spatio-temporal representation and clustering[J]. Proceedings of SPIE, 2007, 6512: 1-12. (  0) 0)
|
| [19] |
GAO Yunjun, ZHENG Baihua, CHEN Gencai, et al. Algorithms for constrained K-nearest neighbor queries over moving object trajectories[J]. Geoinformatica, 2010, 14(2): 241-276. (  0) 0)
|
| [20] |
LIN Bin, SU Jianwen. One way distance:for shape based similarity search of moving object trajectories[J]. Geoinformatica, 2008, 12(2): 117-142. (  0) 0)
|
| [21] |
PERNG C S, WANG H, ZHANG S R, et al.Landmarks: a new model for similarity-based pattern querying in time series databases[C]//Proceedings of the 16th International Conference on Data Engineering.New York, USA: ACM Press, 2000: 33-42. https://ieeexplore.ieee.org/document/839385
(  0) 0)
|
| [22] |
Trajectory analysis datasets[EB/OL].[2018-09-18].http://cvrr.ucsd.edu/bmorris/datasets/dataset_trajectory_analysis.html.
(  0) 0)
|
 2019, Vol. 45
2019, Vol. 45

 ,
,