局部图像特征点匹配是计算机视觉领域的一项基础工作, 广泛应用于对象和场景识别[1-3]、图像配准[4-5]、图像拼接[6-8]和同步定位与地图构建(Simultaneous Localization And Mapping, SLAM)[9]中。在过去的几十年中, 研究人员提出了大量的特征描述子, 如SIFT(Scale-Invariant Feature Transform)[10]具有鲁棒性高、区分力强等优点, 但描述子维度较高, 无法处理海量数据。为了减少内存消耗, 文献[11]将主成分分析(Principal Component Analysis, PCA)技术应用于梯度图像以获取特征向量, 提出PCA-SIFT描述子, 将SIFT的维度降低到36维, 提高了图像匹配的速率, 但该方法使用前需计算完整描述子, 增加了时间复杂度。现代视觉应用朝着更便携的应用设备以及更复杂的应用场景的方向发展, 浮点型描述子并不能满足实际的需求, 因此, 有必要研究出低存储、高性能的特征描述方法。
文献[12]提出BRIEF(Binary Robust Independent Elementary Feature), 随后更多二值描述子被相继提出, 如BRISK(Binary Robust Invariant Scalable Keypoints)[13]、FREAK(the Fast Retina Keypoint)[14]和LTD(Local Ternary descriptor)[15]等。与浮点型描述子相比, 这些二值描述子具有区分能力强、存储空间小、计算复杂度低等优点。然而, 它们仅运用图像的灰度大小关系进行二值编码, 虽然充分利用图像的灰度信息, 且具有实现简单的优点, 但这类描述子对图像的细微变化敏感, 容易出现误匹配。
图像的梯度特征反映了灰度的方向变化, 可提取图像轮廓信息, 比灰度特征更具有辨别能力。现有浮点型描述子SURF(Speeded Up Robust Features)[16]和MROGH(Multi-support Region Order-based Gradient Histogram)[17]都使用梯度直方图来描述图像信息, 其在几何、光照变化较大的图像中仍具有较好的鲁棒性, 但其计算复杂且生成过程耗费的存储空间较多。相应地, 二值描述子BGP(Binary Gradient Patterns)[18]因其低存储、计算简单等优点而被研究人员提出。LDB(Local Difference Binary)[19]和OSRI(Ordinal and Spatial information of Regional Invariants)[20]描述方法将梯度特征与灰度特征组合构建描述子, 其鲁棒性更好。综上所述, 尽管二值描述子具有存储空间小、计算复杂度低等优点, 然而相对于浮点型描述子, 因其极低的比特率及汉明空间的离散性, 二值描述子的表达能力有待进一步提高。
本文提出一种基于环采样的特征组合二值描述子算法。在给定的采样模式中, 将采样点的邻域以采样点为中心划分为若干个环域(最内环域为圆), 比较采样邻域内不同环域像素的灰度均值获得灰度二值向量, 计算每个采样点圆形邻域内所有像素点的高斯一阶梯度以及高斯二阶偏导数均值的绝对值, 两两对比获得梯度二值向量, 并将采样点邻域的灰度二值向量与梯度二值向量组合构成原始二值描述子。使用与FREAK[14]中类似的筛选算法将描述子的维度降至512维, 以获得性能更好的二值描述子。
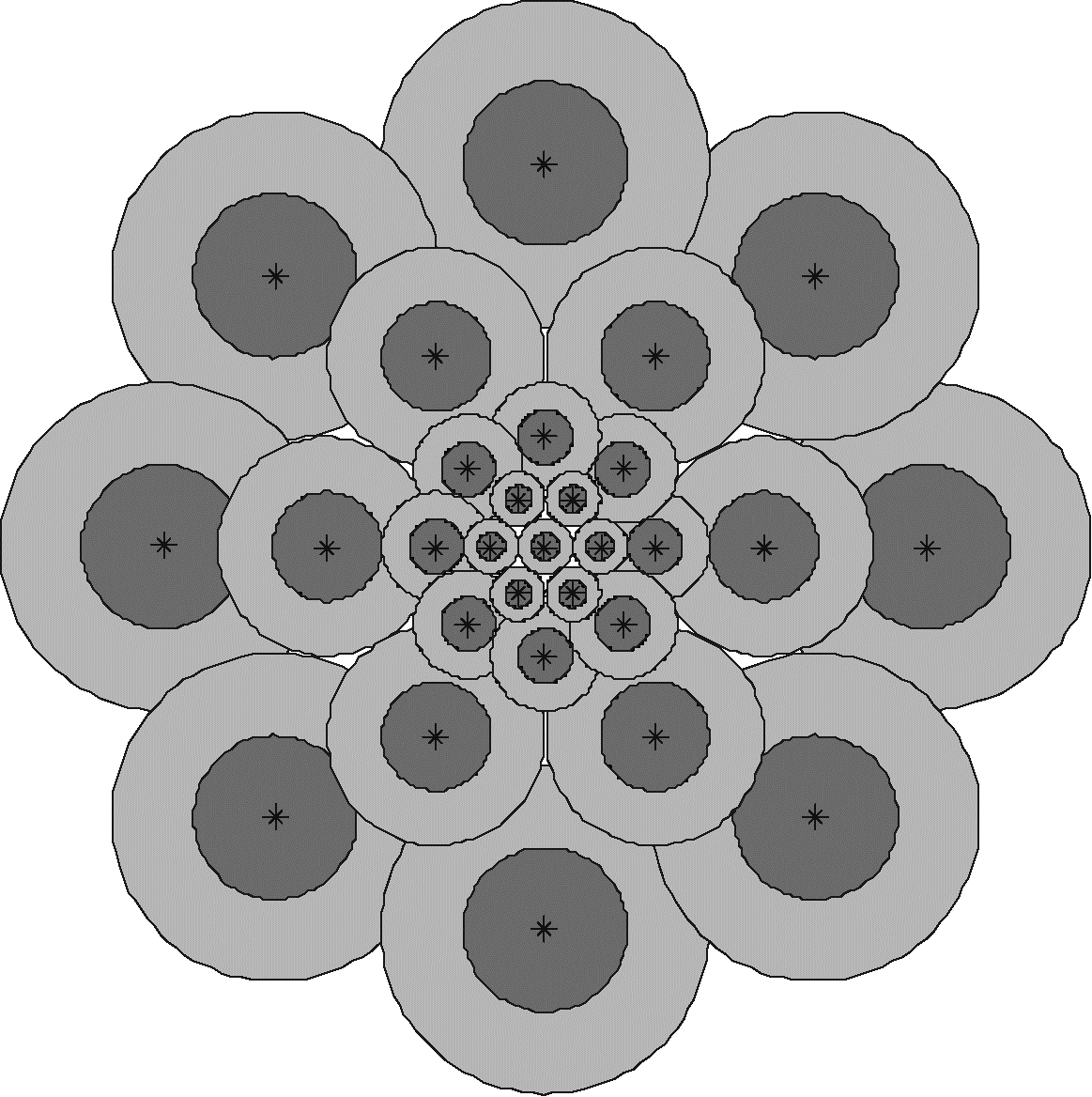
1 基于环采样模式的特征组合二值描述子本文提出的采样模型如图 1所示。与FREAK类似, 本文使用的采样模型为多同心圆环结构。从采样模型中心向外, 处在同一个同心圆环上的采样点使用尺寸相同的圆形采样邻域, 图中每个采样点都有一条实线所围成的圆形邻域, 且圆形邻域的大小与采样点的平滑滤波器尺寸相对应。为提高采样点邻域的描述能力, 将采样点圆形邻域按半径长度等份划分C+1个环域, 即1个内圆与C个外环。对于任一采样点对, 分别比较其对应环域的灰度均值获得该采样点对的灰度二值向量, 具体的二值化过程将在1.1节中详细介绍。
|
Download:
|
| 图 1 本文环采样模型 | |
为保证二值描述子的旋转不变性, 构建描述子前对每个特征点的主方向进行估计。本文通过计算特征点局部区域内所有像素的水平梯度值和垂直梯度值, 然后使用式(1)计算特征点主方向:
| $ \theta = {\rm{a}}\tan 2({g_y},{g_x}),{g_x} = \sum {dx} ,{g_y} = \sum {dy} $ | (1) |
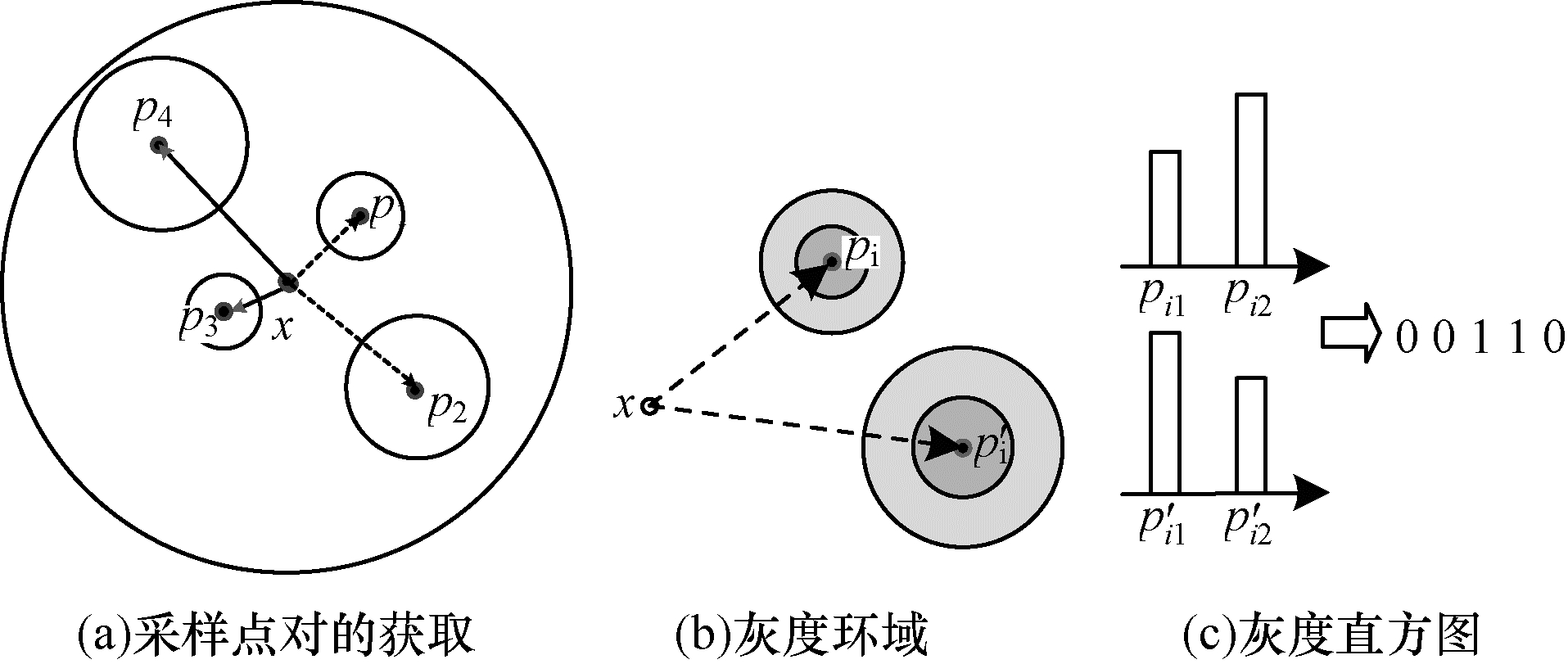
本文在编码灰度信息时使用预定义采样模型获得图像块内的采样点对, 统计所有采样点对圆形邻域内环域的灰度均值, 具体二值化过程如图 2所示。对于特征点x邻域内的任一采样点对pi和p′i, 首先计算它们环域内所有像素的灰度均值I(pij)、I(p′ij)j=1, 2, …, C+1, 然后将它们进行比较以获得二值结果, 定义灰度比较方法为:
| $ \tau \left( {{p_{ij}},p_{ij}^\prime } \right) = \left\{ {\begin{array}{*{20}{l}} {1,I\left( {{p_{ij}}} \right) < I\left( {p_{ij}^\prime } \right)}\\ {0,其他{\rm{ }}} \end{array}} \right. $ | (2) |
其中, I(pij)和I(p′ij)分别表示采样点邻域对应环域的灰度均值, 从而获得采样点对pi, p′i的灰度二值向量, 共C+1位。
|
Download:
|
| 图 2 灰度采样及二值化过程(C=1) | |
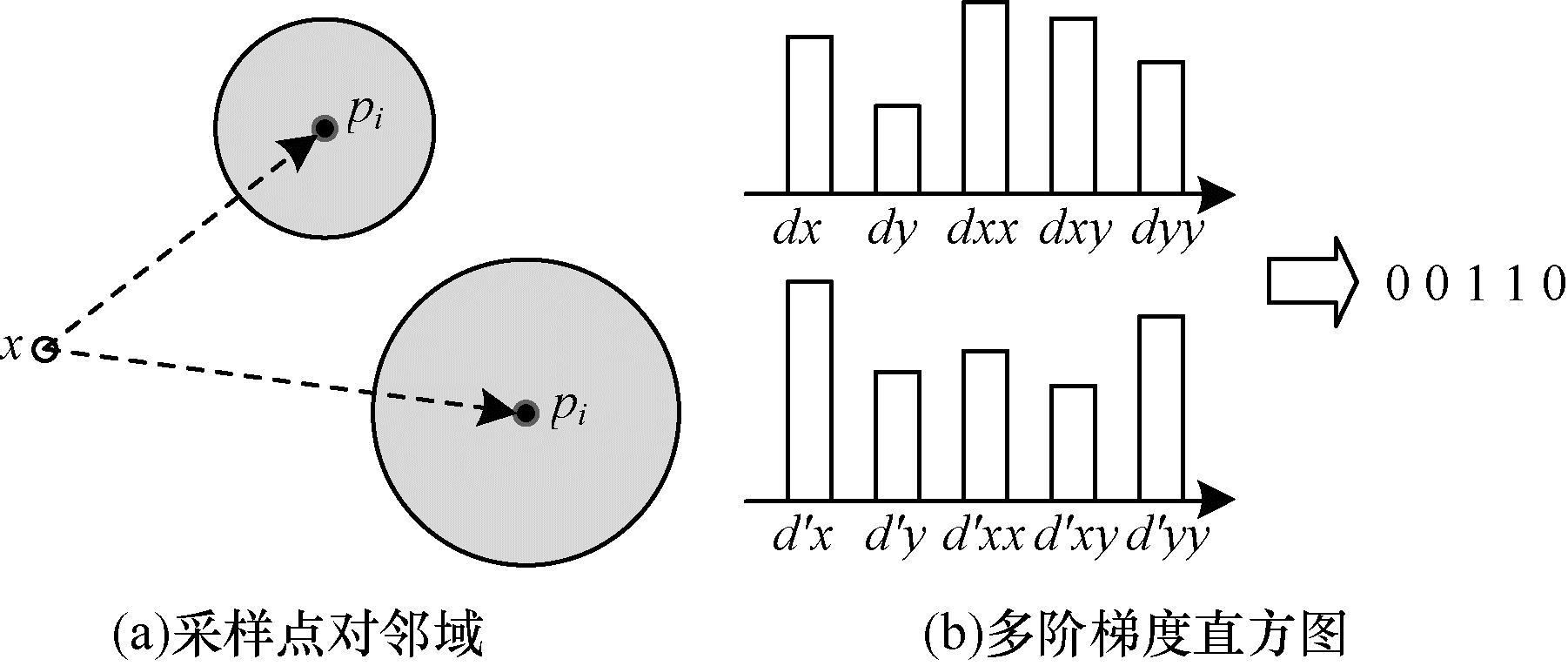
由于图像高斯一阶梯度特征不易受光照和相机变化的影响, 将其用于描述子构建, 一方面可增加描述子的信息表达能力, 另一方面也可提高描述子的鲁棒性。高斯二阶偏导数可在灰度斜坡和灰度台阶处产生双边缘响应, 强化边缘的对比度, 提高描述子的辨别力; 且高斯二阶偏导数的符号确定边缘的过渡是从亮到暗还是从暗到亮, 提取更细腻的图像边缘信息; 综上, 将梯度特征与二阶偏导数特征编码进描述子可提高其表达辨别能力。计算任一采样点对pi, p′i圆形邻域内所有像素点的一阶梯度以及二阶偏导数均值的绝对值, 进行对比获得梯度二值向量, 一阶梯度考虑垂直和水平2个分量, 二阶偏导数考虑dxx、dyy和dxy 3个分量, 共5位。定义梯度比较方法如下:
| $ \omega \left( {{d_i},d_i^\prime } \right) = \left\{ {\begin{array}{*{20}{l}} {1,G\left( {{d_i}} \right) < G\left( {d'} \right)}\\ {0,其他{\rm{ }}} \end{array}} \right. $ | (3) |
其中, G(di)和G(d′)分别表示采样点圆形邻域的一阶梯度或二阶偏导数均值的绝对值。梯度二值化具体过程如图 3所示。
|
Download:
|
| 图 3 梯度二值化过程 | |
最后, 将灰度二值向量与梯度二值向量串联, 获得采样点对(pi, p′i)的二值特征向量; 串联特征点x邻域内所有采样点对的二值特征向量, 获得特征点x的初始二值描述子。若x邻域内有N个采样点, 则存在CN2个采样点对, 故初始描述子的维数为CN2×m(m=C+1+5)。
1.2 位序号选择本文所提出的采样结构中有29个采样点, 即N=29, 将任意2个采样点组合可以产生C292=406个采样点对。这些点对中距离较近的采样点对及公用1个采样点的2个点对, 容易在图像灰度变化平缓的区域获取相似的灰度对比信息, 导致描述子冗余信息增加。因此, 需要利用特征选择策略滤除冗余位, 以生成紧凑的二值描述子, 即直接从由406×m位构成的原始二值特征向量中选择表达能力强的特征位。
本文采用与FREAK相似的特征位选择方法。首先, 构造矩阵D, 矩阵D的每一行对应于如图 4所示的数据集的14对图像中获得的一个特征点, D的行数No约为20 000, 即检测到的所有特征点的总数。矩阵的每一列表示二值对比结果0或1, 是所有采样点对的灰度和梯度对比结果中的一位。如图 5所示, 假设每一点对的二值比较结果是m位, 则列数是406×m。随后, 计算矩阵每一列的均值与常数为0.5的绝对差值(二值比特串均值越靠近0.5, 其方差越大), 差异越小表明该列具有较强的辨别能力。然后按照每一列绝对差值的大小, 从小到大对特征位进行排序。最后, 将排序后的第1个特征位放入最终筛选的集合中, 再迭代地计算待筛选的特征位与已筛选的特征位间的相关度, 将相关度低于阈值的采样点对加入到筛选集合中直到获得d个特征位, 即从长度为406×m描述子特征向量中选择最具辨别力的d位, 生成最终的二值描述子(本文d=512)。由于此特征选择策略是无监督的, 因此在每对候选匹配图像上都使用这种方法获得特征位应用于描述子的构造, 已经证明该描述子具有较好的匹配性能[21]。这在本质上类似于在线学习二值描述子[22]。

|
Download:
|
| 图 4 数据集 | |

|
Download:
|
| 图 5 位序号选择所用到的矩阵 | |
在图像匹配中, 通常使用的评价指标为召回率-查错率, 召回率recall和查错率1-precision计算公式如下:
| $ recall = \frac{{\# correct\;matches}}{{\# correspondences}} $ | (4) |
| $ 1 - precision\frac{{\# false\;\;matches}}{{\# correct\;\;matches + \# false\;\;matches}} $ | (5) |
在式(4)和式(5)中, #correct matches表示匹配结果中正确匹配点对, #correspondences表示特征点检测时重复特征点对(特征点重复即认为实际为正确匹配点对, 但可能被匹配算法匹配上, 也可能未匹配上), #false matches表示匹配结果中错误匹配点对。本文在评价特征点匹配结果时, 首先获取2个图像间的单应性矩阵H, 然后通过特征点检测算法得到左右图像中的特征点信息, 根据单应性矩阵得到重复特征点数, 即#correspondences; 接着由特征点匹配算法得到的匹配结果计算precision和recall, 绘制1-precision和recall曲线。
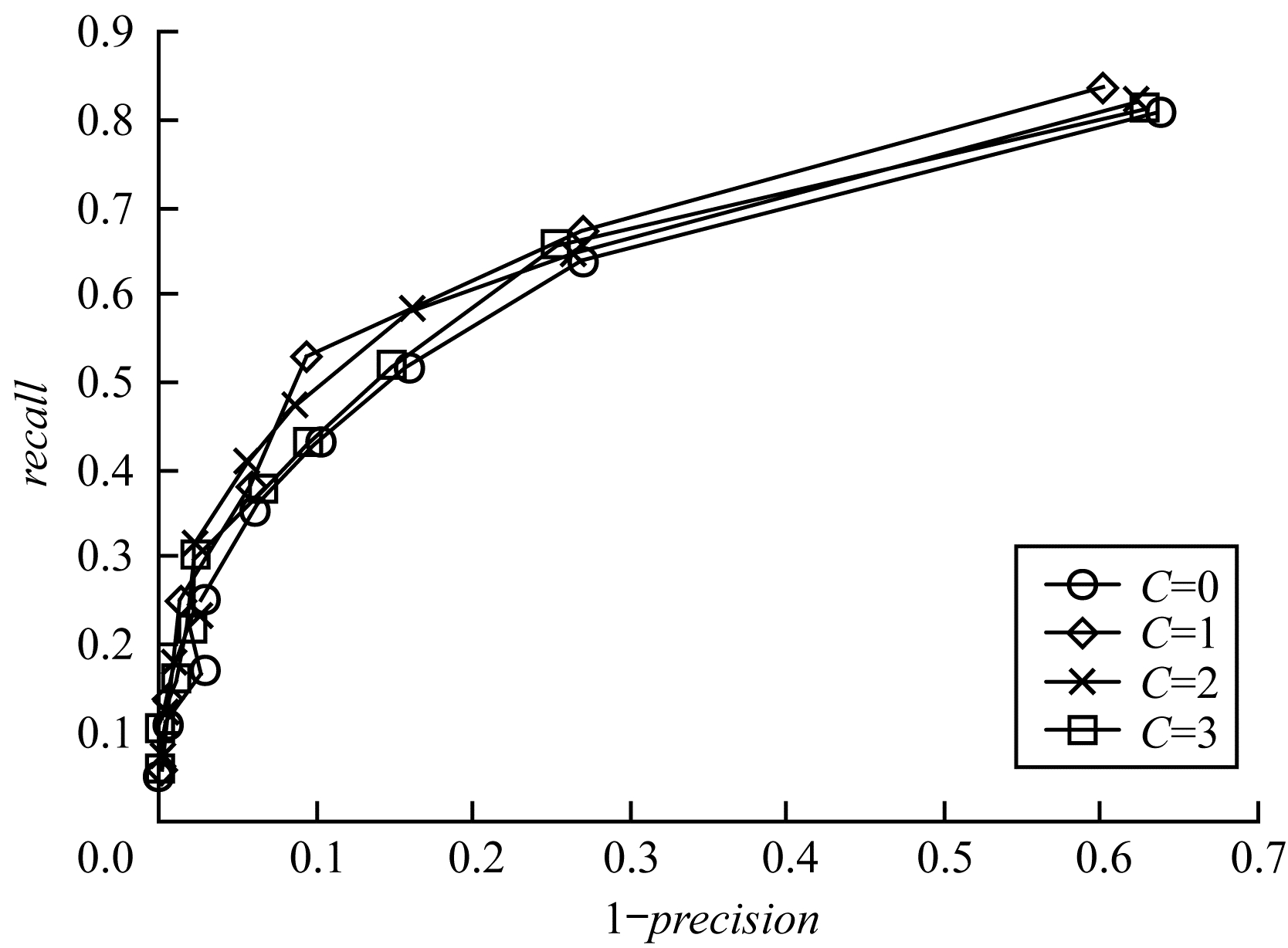
2.2 参数选择本节分析描述子中参数的设置对图像匹配性能的影响。关键参数C, 即采样点圆形邻域环域的层数。本文用如图 4所示的数据集中所有的图像(即14对图像)进行图像匹配测试确定C的取值, 这些图像对包含视角(a-g)、旋转(h-1)和光照(m-n)变换。
图 6展示了环域的层数对描述子匹配性能的影响。当C=0时, 通过统计样本点对圆形邻域内的像素灰度均值并进行对比获得二值结果。从图 6可以看出, 随着圆形邻域环的增加, 由于灰度信息分布的不同, 从而采集不同的图像特征信息, 生成描述子的性能也随着提高。但是, 当C=3时, 由于过采样引起的冗余, 性能下降, 因此最终选择C=1。
|
Download:
|
| 图 6 不同参数在图 4数据集描述子之间的平均性能比较 | |
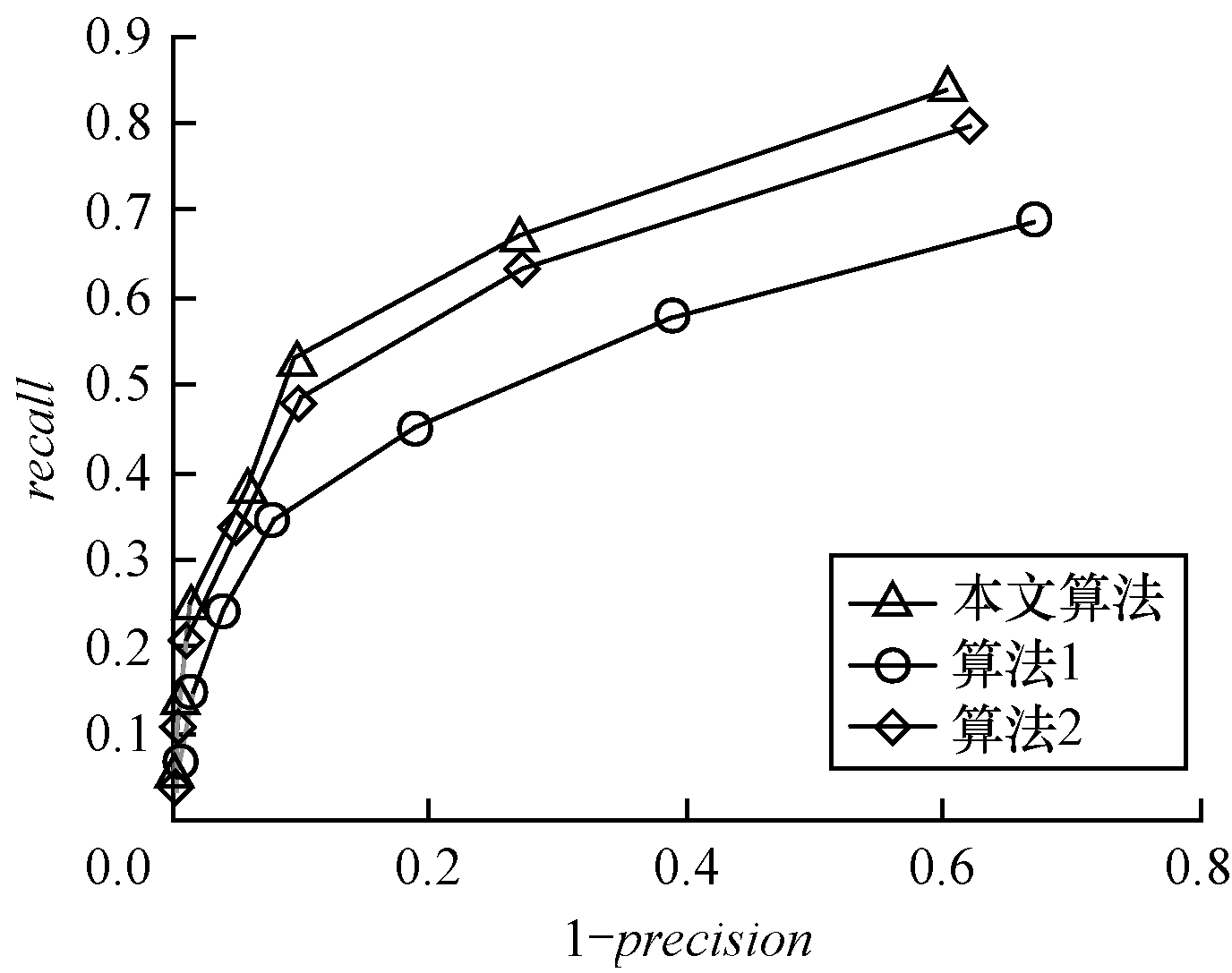
本节将C=1时获得的灰度二值向量分别与高斯一阶梯度(算法1)、高斯一阶梯度及二阶偏导数(本文算法)和高斯一阶及拉普拉斯二阶导数(算法2)进行组合获得二值描述子。为公平起见, 3种算法都使用相同的512位特征位, 使用SURF检测特征点。与灰度特征相比, 一阶梯度特征提供了更多的判别信息, 包括幅值和方向; 二阶偏导数特征增强了细节信息且具有光照不变性。如图 7所示, 本文算法的平均性能明显高于算法1, 证明了将二阶偏导数特征加入到描述子中可以改善其匹配性能; 同时将本文算法与算法2对比, 进一步证明高斯二阶偏导数的特性, 即在灰度斜坡和灰度台阶处产生双边缘响应, 强化边缘的对比度, 提高描述子的表达能力。现有的基于灰度与梯度特征的二值描述子如LDB[19]和OSRI[20], 分别比较特征点邻域内子区域的灰度和一阶梯度均值, 获得子区域的二值向量。考虑二阶偏导数特征在增强细节、强化边缘等方面的优点, 本文将高斯二阶偏导数特征参与二值描述子构建并取得了较好的结果。
|
Download:
|
| 图 7 3种算法在图 4数据集描述子之间的平均性能比较 | |
Oxford数据集是图像匹配的标准基准库, 用于评估图像特征算法的性能。图 8展示的6组基准图像序列具有不同的图像变换, 包括视角变化(graffiti和wall)、图像模糊(bikes和trees)、JPEG压缩(ubc)和光照变化(leuven)。本文使用每个序列的前5个图像, 通过将第1个图像与同一序列的其他图像匹配来测试本文描述子与其他典型特征描述算法的性能。

|
Download:
|
| 图 8 Oxford数据集 | |
本文将所提出的浮点型描述子SURF和二值型描述子FREAK、BRISK、BRIEF、LDB进行比较, 其中, BRIEF、BRISK、FREAK基于灰度特征对比得到, LDB基于灰度和梯度特征对比得到, LDB的代码从UCSB实验室[23]下载得到, 比较结果如图 9所示, 其中, SURF检测器用于检测除LDB之外的特征点。为确保公平比较, 所有方法都被调整为具有相同数量的特征点。

|
Download:
|
| 图 9 在Oxford数据集中各图像变换的实验结果 | |
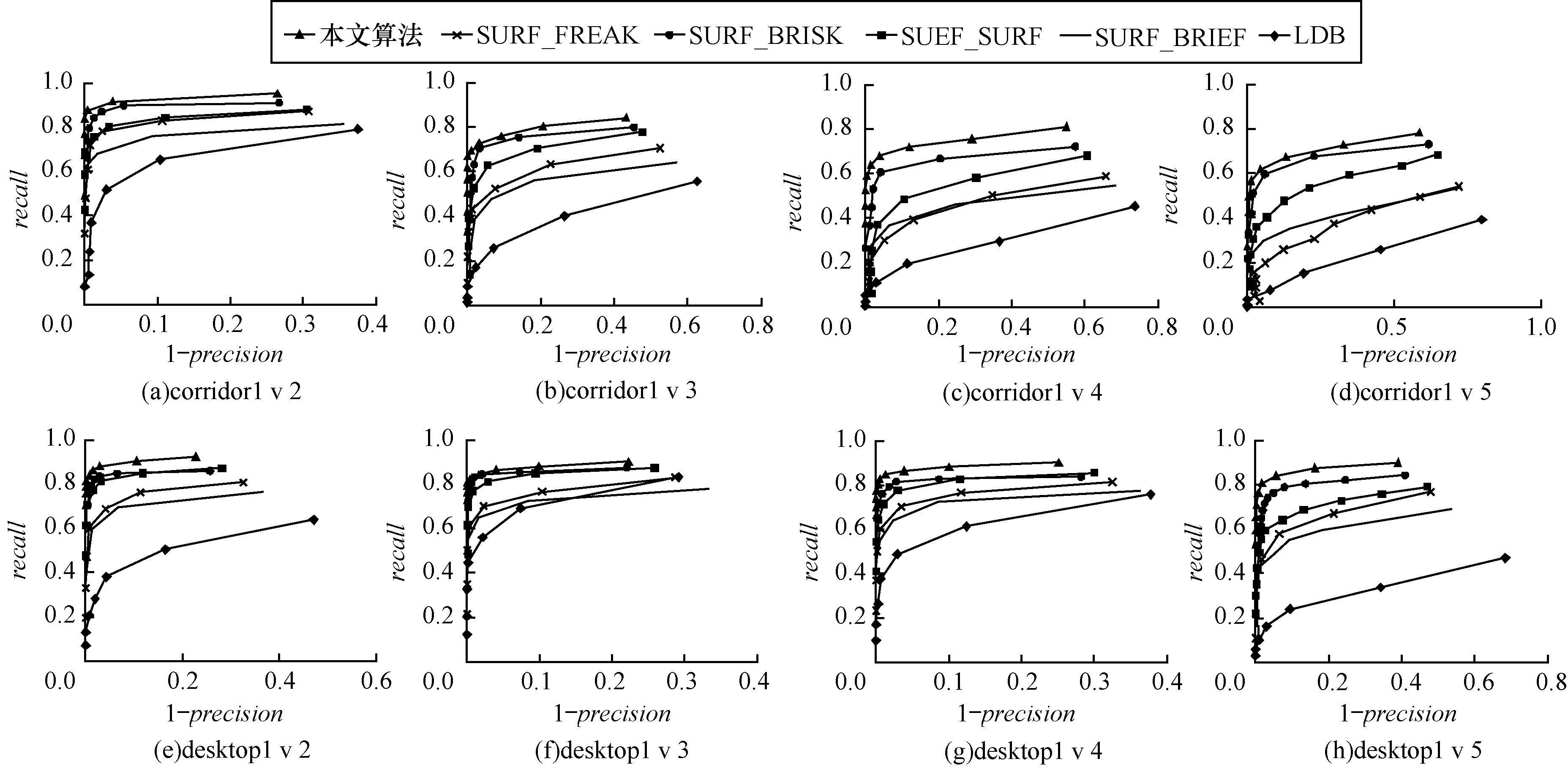
由图 9第1行、第2行可以看出, 视角变换下本文算法显示出最佳匹配性能, 而BRIEF算法匹配性能最差。这是因为处于图像较暗区域的特征点具有相似的灰度邻域, 致使BRIEF中采样点对获得的灰度对比结果相似, 描述子的鲁棒性变差, 本文通过对比环域内均值大小, 本质上将灰度分布空间进行更优的划分, 提高了相似灰度邻域的区别能力。同时, 灰度特征仅是标量, 呈现的灰度信息不具有高辨别能力, 加入梯度信息会明显提高描述子的描述力。
从图 9第3行、第4行可以看出, 在模糊变化下, 与SURF、FREAK、BRISK、BRIEF和LDB算法相比, 本文算法匹配性能较好。图像模糊对一阶梯度的计算产生较大的影响, 但本文计算图像二阶偏导数并用于描述子的构建, 可增强细节特征, 强化边缘对比度, 弥补梯度计算的缺点, 最终使描述子的整体性能得到提升。由图 9第5行JPEG压缩图像的性能曲线可以看出, 当NNDR取最大值1时, 本文描述子的查全率不低于0.85, 优于SURF、FREAK、BRISK、BRIEF和LDB描述子。SURF描述子对JPEG压缩具有一定的敏感性。
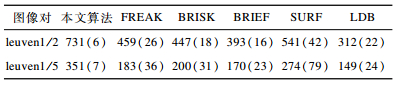
由图 9第6行可以看出, 在光照变化下, 本文描述子的匹配性能明显高于对比描述子。当NNDR取最大值时, 本文算法的查全率超过了0.95(leuven1v2), 随着光照变化程度的加深, 本文算法的查全率仍超过0.8, 而FREAK、BRISK、BRIEF、LDB和SURF算法在最好的变化情况下也只是接近于0.8。因为梯度特征不易受到光照的影响, 所以将梯度信息结合到描述子中可增强其对光照变化的鲁棒性。尤其高斯二阶偏导数特征具有增强细节以及不易受光照变化的优点, 进而获得了更好的匹配效果。表 1给出了光照条件下不同图像对的匹配结果, 与其他描述子相比, 本文算法在匹配总数上有明显提升(括号内数字为错误匹配数)。
|
下载CSV 表 1 光照图片在不同描述子之间的匹配结果 |
本节证明本文方法对复杂光照变化的鲁棒性。从Wang的网站[24]下载了一些复杂光照变化的图像序列, 如图 10所示, 与Oxford数据集中的“leuven”序列相比, 其是不同曝光时间内捕获的非线性图像序列。图 11给出了图像匹配的结果。可以看出, 本文算法的性能优于其他浮点或二值描述子, 所以本文提出的描述子具有显著的区分光照变化的能力。

|
Download:
|
| 图 10 具有复杂光照变化的图像序列 | |
|
Download:
|
| 图 11 具有复杂光照变化的图像序列实验结果 | |
本文提出一种基于环采样的特征组合二值描述子。通过特征点采样邻域内环域的划分使得灰度特征描述更细腻, 在图像一阶梯度的基础上引入图像二阶偏导数特征, 提高描述子的分辨能力和鲁棒性, 采用特征位降低描述子维度, 获得更紧凑的二值描述子。本文算法在光照变化、模糊以及JPEG压缩等方面效果较好, 但其对旋转变化较为敏感, 下一步将对图像块的主方向计算方法进行改进, 以实现二值描述子的旋转不变性。
| [1] |
YANG Xiao, WU Jianxin, YUAN Junsong. mCENTRIST:a multi-channel feature generation mechanism for scene categorization[J]. IEEE Transactions on Image Processing, 2014, 23(2): 823-836. DOI:10.1109/TIP.2013.2295756 |
| [2] |
RAMESH B, CHEN Xiang, LEE T H. Shape classification using invariant features and contextual information in the bag-of-words model[J]. Pattern Recognition, 2015, 48(3): 894-906. DOI:10.1016/j.patcog.2014.09.019 |
| [3] |
SONG Tiecheng, LI Hongliang. WaveLBP based hierarchical features for image classification[J]. Pattern Recognition Letters, 2013, 34(12): 1323-1328. DOI:10.1016/j.patrec.2013.04.020 |
| [4] |
ZHAO Haifeng, LU Ming, BU Lingbin, et al. Medical image registration based on feature points and Rényi mutual information[J]. Chinese Journal of Computers, 2015, 38(6): 1212-1221. (in Chinese) 赵海峰, 陆明, 卜令斌, 等. 基于特征点Rényi互信息的医学图像配准[J]. 计算机学报, 2015, 38(6): 1212-1221. |
| [5] |
XU Jiajia, ZHANG Ye, ZHANG He. Fast image registration algorithm based on improved Harris-SIFT descriptor[J]. Journal of Electronic Measurement and Instrumentation, 2015, 29(1): 48-54. (in Chinese) 许佳佳, 张叶, 张赫. 基于改进Harris-SIFT算子的快速图像配准算法[J]. 电子测量与仪器学报, 2015, 29(1): 48-54. |
| [6] |
ZHANG Jing, CHEN Guangxue, JIA Zhaoyang. An image stitching algorithm based on histogram matching and SIFT algorithm[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2017, 31(4): 1754-1771. |
| [7] |
DONG Qiang, LIU Jinghong, WANG Chao, et al. Image mosaic algorithm based on improved BRISK[J]. Journal of Electronics and Information Technology, 2017, 39(2): 444-450. (in Chinese) 董强, 刘晶红, 王超, 等. 基于改进BRISK的图像拼接算法[J]. 电子与信息学报, 2017, 39(2): 444-450. |
| [8] |
ZHU Zhiheng, FU Jinyang, YANG Junsheng, et al. Panoramic image stitching for arbitrarily shaped tunnel lining inspection[J]. Computer-Aided Civil and Infrastructure Engineering, 2016, 31(12): 936-953. DOI:10.1111/mice.12230 |
| [9] |
MURARTAL R, MONTIEL J M M, TARDOS J D. ORB-SLAM:a versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics, 2017, 31(5): 1147-1163. |
| [10] |
LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 215: 91-110. |
| [11] |
KE Y, SUKTHANKAR R. PCA-SIFT: a more distinctive representation for local image descriptors[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.[S.1.]: IEEE Computer Society, 2004: 506-513. http://www.researchgate.net/publication/2926479_PCA-SIFT_A_More_Distinctive_Representation_for_Local_Image_Descriptors
|
| [12] |
CALONDER M, LEPETIT V, STRECHA C, et al. BRIEF: binary robust independent elementary features[C]//Proceedings of European Conference on Computer Vision. Berlin, Germany: Springer, 2010: 778-792.
|
| [13] |
LEUTENEGGER S, MARGARITA C, ROLAND Y. BRISK:binary robust invariant scalable keypoints[J]. IEEE Computer Vision, 2011, 58(11): 2548-2555. |
| [14] |
ALAHI A, ORTIZ R, VANDERGHEYNST P. FREAK: fast retina keypoint[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D. C., USA: IEEE Press, 2012: 510-517. http://www.researchgate.net/publication/258848394_Freak_Fast_retina_keypoint
|
| [15] |
GAO Yongqiang, QIAO Yu, LI Zhifeng, et al. LTD: local ternary descriptor for image matching[C]//Proceedings of IEEE International Conference on Information and Automation. Washington D. C., USA: IEEE Press, 2014: 1375-1380. http://www.researchgate.net/publication/269329280_ltd_local_ternary_descriptor_for_image_matching
|
| [16] |
BAY H, TUYTELAARS T, VAN G L. SURF: speeded up robust features[C]//Proceedings of ECCV'06.Washington D. C., USA: IEEE Press, 2006: 404-417. http://link.springer.com/chapter/10.1007/11744023_32
|
| [17] |
FAN Bin, WU Fuchao, HU Zhanyi. Aggregating gradient distributions into intensity orders:a novel local image descriptor[J]. IEEE Computer Vision and Pattern Recognition, 2011, 32(2): 2377-2384. |
| [18] |
HUANG Weilin, YIN Hujun. Robust face recognition with structural binary gradient patterns[M]. [S.1.]: Elsevier Science Inc., 2017.
|
| [19] |
YANG Xin, CHENG K T. LDB: an ultra-fast feature for scalable augmented reality on mobile devices[C]//Proceedings of IEEE International Symposium on Mixed and Augmented Reality.[S.1.]: IEEE Computer Society, 2012: 49-57. http://www.researchgate.net/publication/261297784_LDB_An_ultra-fast_feature_for_scalable_Augmented_Reality_on_mobile_devices
|
| [20] |
XV Xianwei, TIAN Lu, FENG Jianqiang, et al. OSRI:a rotationally invariant binary descriptor[J]. IEEE Transactions on Image Processing, 2014, 23(7): 2983-2995. DOI:10.1109/TIP.2014.2324824 |
| [21] |
ROSTEN E, PORTER R B, DRUMMOND T, et al. Faster and better:a machine learning approach to corner detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(1): 105-119. DOI:10.1109/TPAMI.2008.275 |
| [22] |
BALNTAS V, TANG L, MIKOLAJCZYK K. BOLD:binary online learned descriptor for efficient image matching[J]. IEEE Computer Vision and Pattern Recognition, 2015, 41(1): 2367-2375. |
| [23] |
YANG Xin, CHENG K T. Local difference binary for ultra-fast and distinctive feature description[EB/OL].[2018-09-10].http://lbmedia.ece.ucsb.edu/research/binaryDescriptor/web_home/web_home/index.html.
|
| [24] |
WANG Zhenhua. Complex illumination datasets[EB/OL].[2018-09-10].http://zhwang.me/datasets.html.
|
 2019, Vol. 45
2019, Vol. 45

 ,
,