0 概述

目前, 5G通信已进入商用阶段, 在技术和需求的共同作用下, 其将为全行业提供万物互联的网络业务能力, 赋能互联网新业态的发展。在使能技术中, 大规模多输入多输出(Multi-Input Multi-Output, MIMO)系统利用超高天线维度挖掘空间资源, 毫米波通信通过超大带宽提升网络吞吐量, 超密集组网利用超密集基站提高频谱利用率, 由此产生海量数据, 为无线通信系统中人工智能的应用提供数据来源^[1]。而要满足未来以智能体交互为代表的业务场景, 则需要实现5G与人工智能技术的融合。

人工智能特别是深度学习在计算机视觉、自然语言处理、语音识别等领域获得巨大成功^[2], 使得无线通信领域的研究者重新思考物理层通信设计, 提出了基于自编码器的端到端优化思想, 即用全连接深度神经网络(Deep Neural Network, DNN)来表示发射端和接收端, 其中, 发射端的功率限制条件通过连接归一化层来控制, 接收端使用Softmax激活函数输出一组概率向量来确定接收到的信息, 信道则使用神经网络的一个噪声层表示^[3]。对于MIMO系统而言, 需要信道状态信息(Channel State Information, CSI)反馈和重建来执行预编码以及获得性能增益, 而且深度学习算法的计算复杂度通常较高, 其本身与经典模块中的处理方法相比优势并不明显。因此, 需要适当改变自编码器的架构和训练过程来实现端到端通信系统。

本文分析传输速率对自编码器端到端通信系统性能的影响, 推导信噪比(Signal Noise Ratio, SNR)和传输速率间的闭合表达式, 同时设计两阶段训练模式, 通过考虑真实信道的时变性对训练参数进行微调, 使系统性能得到提升。在此基础上, 提出CSI量化的方法缓解系统CSI反馈负载, 减少数据的离线训练次数, 增强神经网络的泛化性。

1 相关工作

智能无线通信系统现已成为继5G技术之后无线通信发展的主流方向。文献[3]总结了目前相关的研究成果, 并指出具有发展前景的研究方向以及若干典型范例。前期的研究兴趣主要在应用层和网络层, 如文献[4]解决了无线资源管理和分配的问题。目前, 该研究正在向物理层推进, 这种趋势特别体现在与深度学习相结合的物理层优化上。文献[5-6]认为深度学习是处理物理层通信的有效工具, 验证了深度学习在调制模式识别、信道估计、信道检测方面的可行性, 并探讨了潜在应用。文献[7]则提出一种基于深度学习的通信目标识别框架。

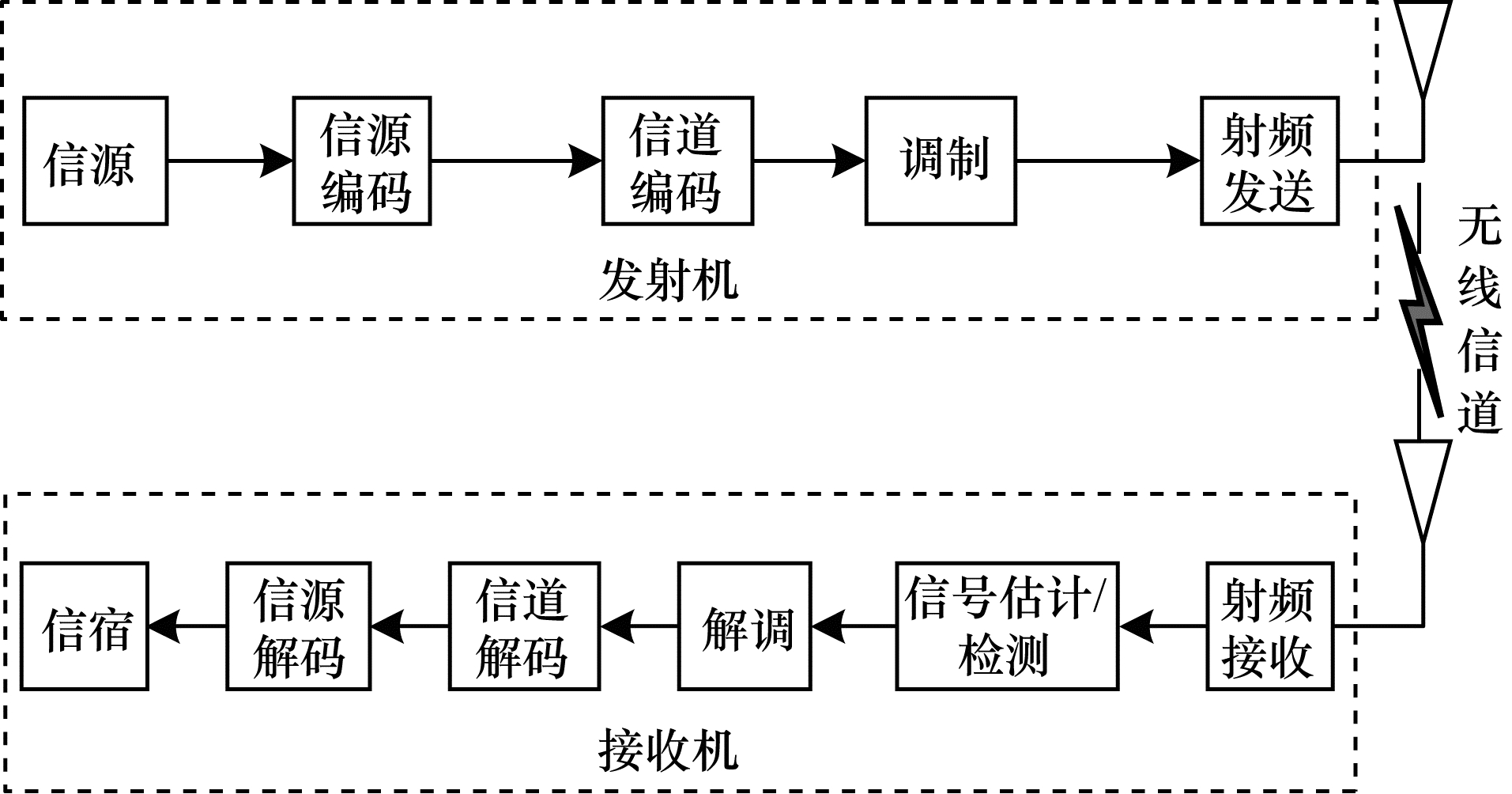
本质上, 5G的根源依旧是基于香农信息论的无线传输理论体系架构, 是在模块结构基础上设计的。一个典型的无线通信系统由发射机、无线信道和接收机组成, 具体组成模块如图 1所示。

基于深度学习的无线传输旨在改变上述通信模式, 一些研究者对无线通信系统的单个模块用深度学习方法进行优化, 例如:文献[8]在大规模MIMO射频链路受限场景下, 利用LDAMP网络对信道矩阵作二维图像处理来解决信道估计问题, 整个网络参数较少, 并且计算速度快、准确性高, 但局限于认知无线网络场景; 文献[9]提出一种高度并行的解码算法, 通过构建子块分离的深度学习极化码解码网络来减少迭代次数, 该算法是针对文献[10]只适用结构码的DNN信道解码方法的改进, 但只考虑了解码模块, 没有全面分析整个通信过程; 文献[11]为提升BP算法应用于高密度奇偶校验码(High Density Parity Check, HDPC)的性能, 通过更新分配Tanner图边缘节点的权重系数, 提出BP-DNN算法, 但其假设CSI已知, 无法有效应对信道CSI未知的情形。以上方法均遵循利用深度学习逐块优化设计的思想。

通信系统中每个模块的性能达到最佳, 并不意味着系统的整体性能是最佳的。文献[12-13]的研究结果表明, 单纯拼接多个基于迭代算法的神经网络结构并不会带来系统增益, 反而会导致更高的计算复杂度。据此, 文献[12]提出一种不同于传统模块驱动的优化思路, 其利用自编码器对估计、反馈、编码和解码过程进行全局优化, 设计端到端无线通信系统, 但该系统存在因信道未知导致反向传播计算梯度不存在的问题。文献[14]提出一种不依赖任何信道先验知识的自编码器端到端优化方案, 在收发端都用DNN代替, 并用生成对抗网络(Generative Adversarial Network, GAN)表示信道, 同时对三者迭代训练, 最终得到全局最优解。但多个DNN的训练依赖大量数据样本, 数据采集任务量大、可操作性低。

针对上述问题, 本文根据真实信道的时变特性, 提出一种基于CSI量化的方法来应对无线通信系统的瞬时CSI变化。

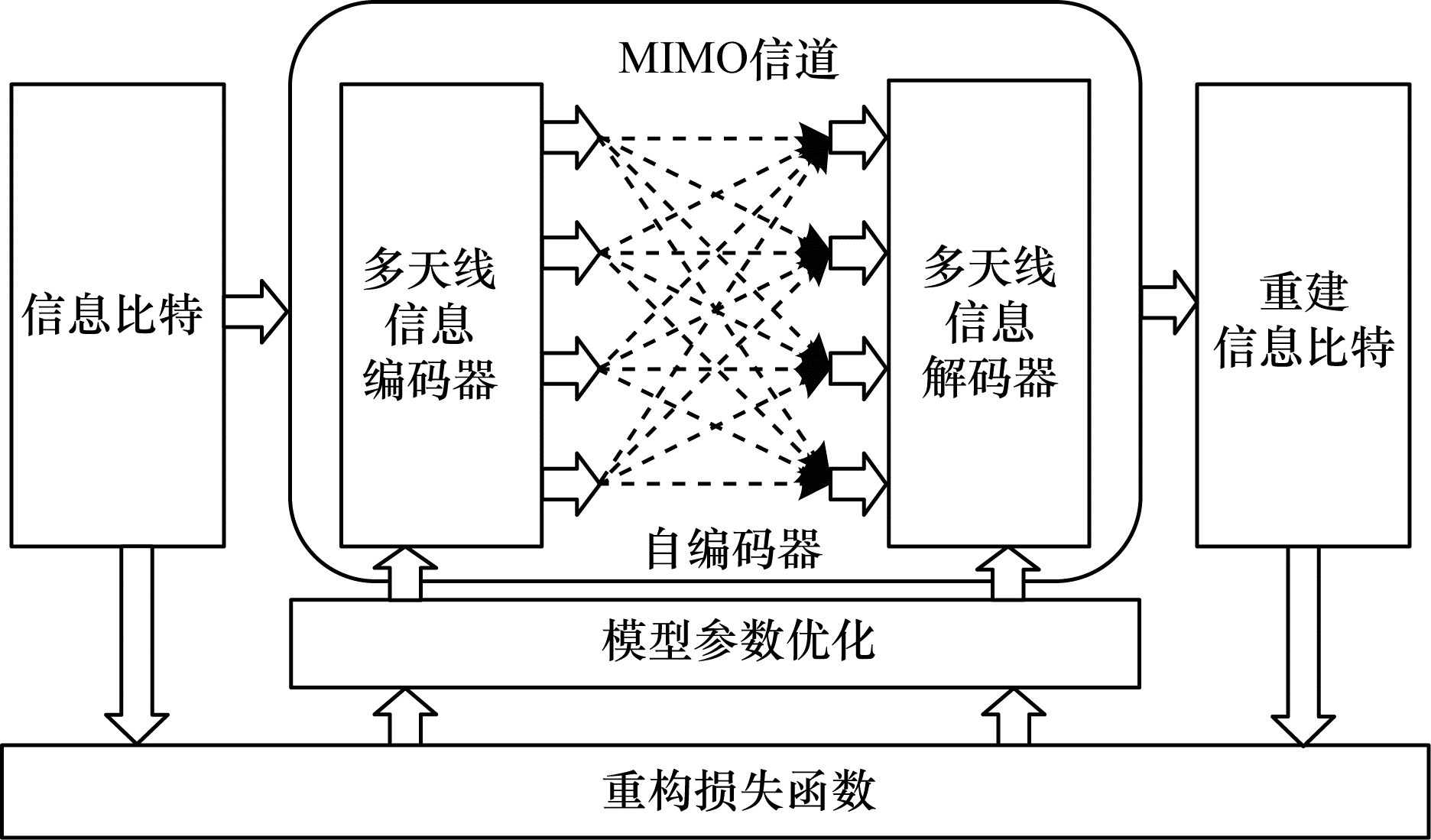
2 系统建模与信道假设 2.1 系统模型

MIMO信道自编码器端到端通信系统模型如图 2所示, 其中k bit码字s形成m_t条并行传输数据流, 这些数据流通过多天线混合信道后在接收端生成m_r条接收数据流并解码为估计消息$ \tilde s$, 则可能存在的信道数为m_t×m_r, 记为n。考虑到信道存在无线传播随机损伤, 在本文中将瑞利信道作为信道模型。

2.2 自编码器神经网络

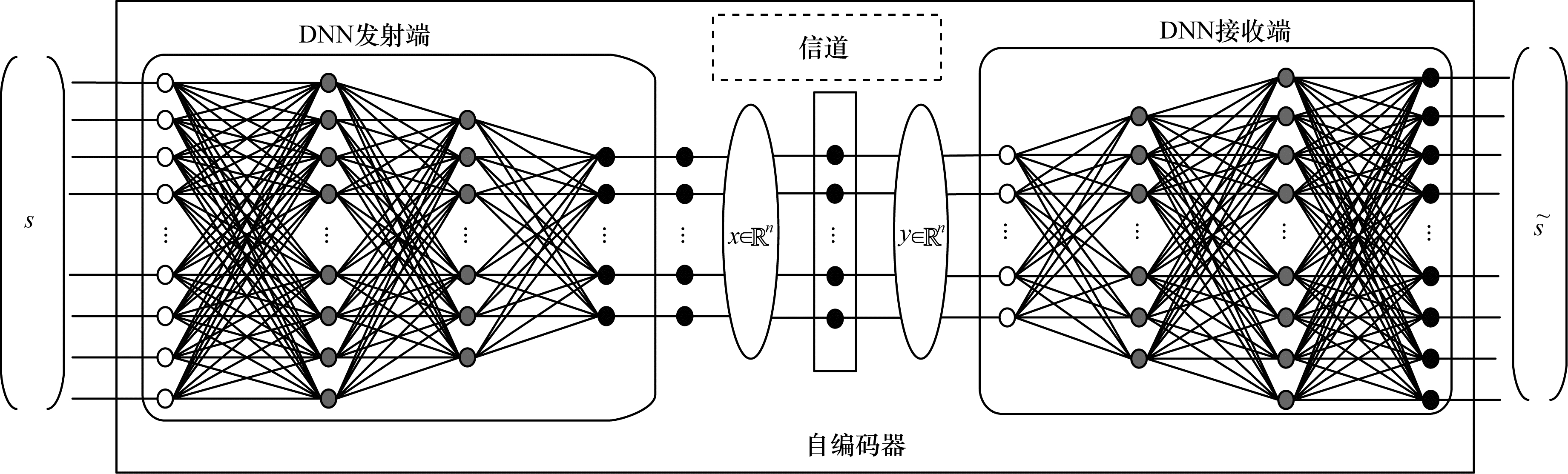
自编码器神经网络将物理层通信视作一个端到端的信号重构问题, 自编码器是一种无监督深度学习算法, 其通过学习信息的压缩形式来进行压缩信息的重构, 如图 3所示, 其中:发射端表示为全连接的DNN, 包含2个隐藏层, 码字s∈{1, 2, …, M}被编码为one-hot向量$\boldsymbol{h}_{\mathrm{s}} \in \mathbb{R}^{M} $, 即一个M维向量, 然后输入DNN, 通过归一化层来满足功率条件‖ x ‖₂²≤n, 输出为信息比特的特征表示 x; 接收端用连接一个Softmax激活函数的全连接层表示, 输出概率向量p∈(0, 1)^M, 向量的最大值的索引对应输入的估计$ {\tilde s}$。

3 基于深度学习的自编码器端到端物理层优化

本文通过与传统硬判决译码、最大似然译码方法进行对比, 验证本文方案的有效性。在此基础上, 构建两阶段训练模型。在第一阶段将信号IQ样本的同向分量和正交分量Q解耦, 形成独立的训练数据集和验证数据集; 在第二阶段对训练数据集进行微调。此外, 本文提出一种优于传统线性检测的方法, 根据量化CSI来反馈信道特性, 并将信号检测问题转化为分类问题。

3.1 自编码器端到端优化过程

在优化过程中, 用s表示发射端将k bit编码成用于传输的2^k整数码字。符号(n, k)表示2^k码字在n个信道中传输, 其传输速率可表示为R=k/n, 其中k=lb M。将s映射为期望码字值为1的one-hot向量输入神经网络, 并将输出看作一个SoftMax分类任务预测每个码字的概率。针对这样的分类任务, 可以利用梯度下降的分类交叉熵函数$ \ell_{\mathrm{CE}}$来优化网络参数, $ \ell_{\mathrm{CE}}$可表示为^[15]:

$ {\ell _{{\rm{CE}}}}(s, \tilde s) = - \frac{1}{m}\sum\limits_{i = 0}^{m - 1} {\left( {{s_i}{\mathop{\rm lb}\nolimits} {{\tilde s}_i} + \left( {1 - {s_i}} \right){\mathop{\rm lb}\nolimits} \left( {1 - {{\tilde s}_i}} \right)} \right)} $

(1)

其中, m是训练过程中的码字数。

利用随机梯度下降^[16]计算并更新权重, 具体地, 迭代计算向前传播$ \tilde{s}=f(s, \theta)$和向后传播$ \frac{{\partial \ell }}{{\partial \theta }} = \frac{{\partial {\ell _{{\rm{CE}}}}(s, f(s, \theta ))}}{{\partial \theta }}$, 其中, θ表示神经网络的权重, 使用$ \delta \omega=-\eta \frac{\partial \ell}{\partial \theta}$来更新权重, η表示学习率, tanh()为激活函数。系统的训练参数为$ (2 M+1)(M+n)+2 M$。

每一层的神经元连接结构层及输出维数如表 1所示。

实现端到端系统的关键是在接收机端准确复现发射机的输入, 即$ \tilde s = f(s, \theta )$。传输码块张量可表示为[batchsize, m_t, 2, n], 其中设置批量大小batchsize为128, m_t为传输流的大小。由此可进一步将整个训练过程描述为:

$ x=\operatorname{norm}(\operatorname{mul}(\operatorname{enc}(s, H), H), \sigma) $

(2)

其中, enc(s, H)表示消息s和信道H级联编码, mul(·)表示复数和信道H点积操作, norm(·)表示正则化操作。

因此, $ f(s, \theta )$可表示为:

$ f(s, \theta)=(\lambda H, \operatorname{dec}(\operatorname{awg}(x, \sigma))) $

(3)

其中, awg(·)表示加性高斯噪声N(0, σ), 噪声只用于向后训练的过程中。

为了量化系统的性能, 本文将块误码率(Block Error Rate, BLER)作为评估指标, 定义为^[13]:

$ {P_{\rm{e}}} = \frac{1}{M}\sum\limits_s {\Pr } (\tilde s \ne s|s) $

(4)

3.2 两阶段训练

将模型部署在真实硬件上进行无线传输时, 初始性能取决于该模型的准确性。由于在训练期间使用的信道模型与实际信道(包括尚未捕获的收发器硬件效应)之间通常存在不匹配, 因此通信性能会受到影响。笔者受迁移学习^[17]思想的启发, 提出分2个阶段进行训练, 其关键思路在于对特定信道模型进行自编码器训练(例如本文采用瑞利信道模型), 并根据从发射端获得的训练数据对接收端进行微调^[18]。

首先使用瑞利信道模型训练自编码器, 该模型应尽可能接近预期信道的行为(第一阶段)。接收端进行微调来弥补这种不匹配(第二阶段):发射端在实际信道上发送大量消息, 并在接收端获得相应的IQ样本(由信号的同向分量I和正交分量Q组成)。在此基础上, 将这些样本与相应的消息索引组合作为接收端微调的标记数据集。

在训练过程中, 为加速任务的并行计算, 将固定底层的网络结构而仅对高层进行微调, 使得神经网络提取信道特征更为高效。需要强调的是, 信道特征提取是针对信道行为而不是信道数据结构。

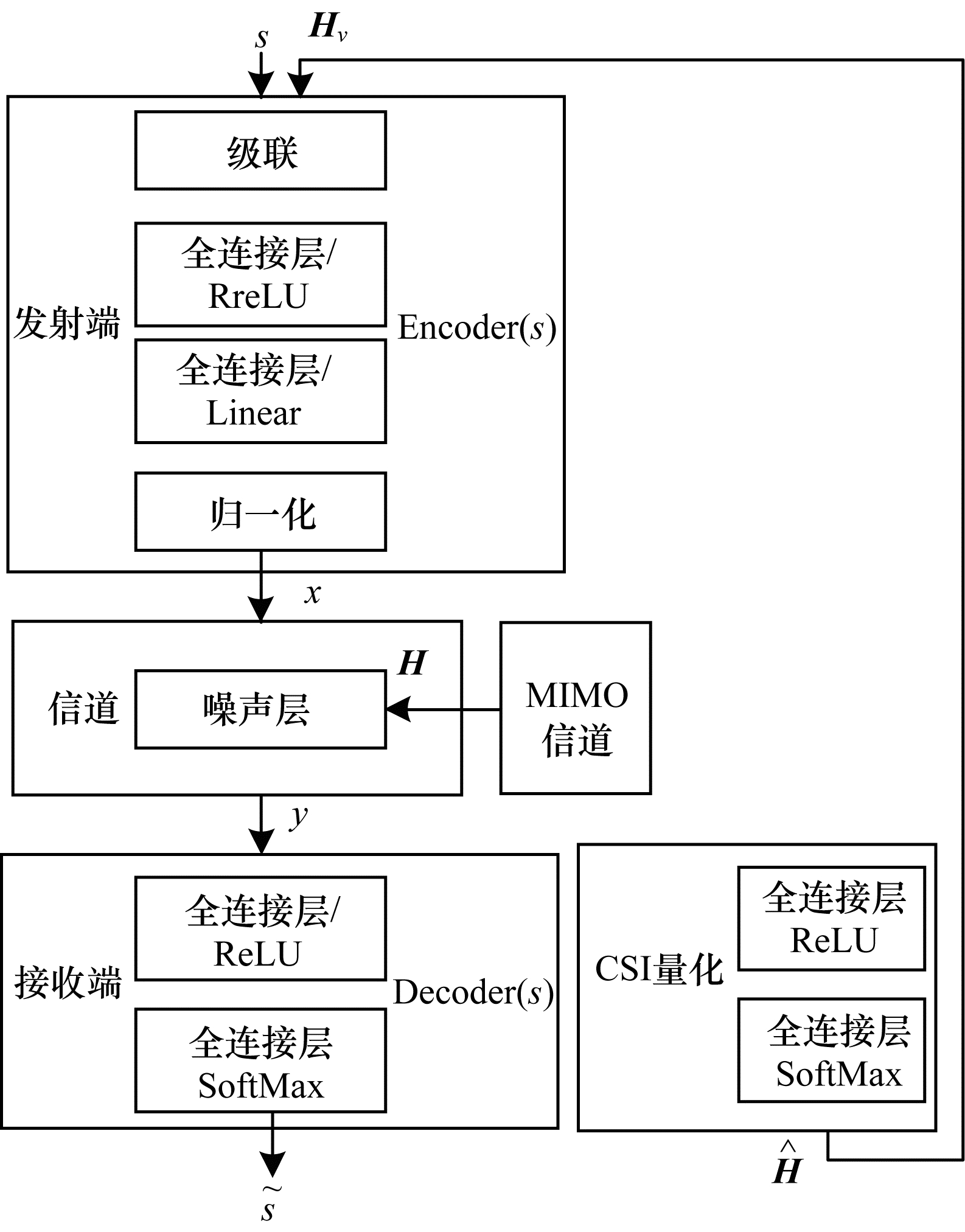
3.3 量化CSI的反馈和重建

具有量化CSI功能的网络结构模型如图 4所示。在衰落信道的条件下, 发射端无法获得每个接收端天线的CSI, 即实际通信过程中获得的CSI是不完美的。因此, 本文提出在信道编码之前将s和 H级联的方法, 这个操作使得在接收端信号检测时性能优于基本的线性检测方法, 例如迫零(Zero Force, ZF)和最小均方误差(Minimum Mean Square Error, MMSE)。

进一步地, 对CSI进行量化处理, 以便发射端能获得CSI压缩形式, 将 H量化为v bit的向量H_v, 因此, 该问题转化为2^ν值分类问题。如图 4所示, 在接收端设置一个CSI估计器, 将估计生成的${\mathit{\boldsymbol{\hat H}}} $量化为H_v并反馈给发射端。

4 数值与仿真分析 4.1 实验条件和参数设置

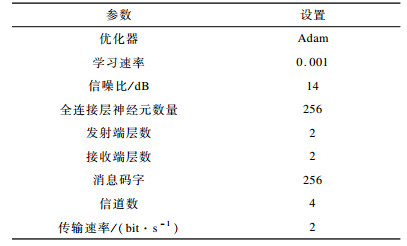
训练过程在NVIDIA TITAN X(Pascal) GPU上执行, 使用Ubuntu14.04LTS, 后端为TensorFlow支持的Keras框架。仿真实验参数初始值设置见表 2。

4.2 结果分析

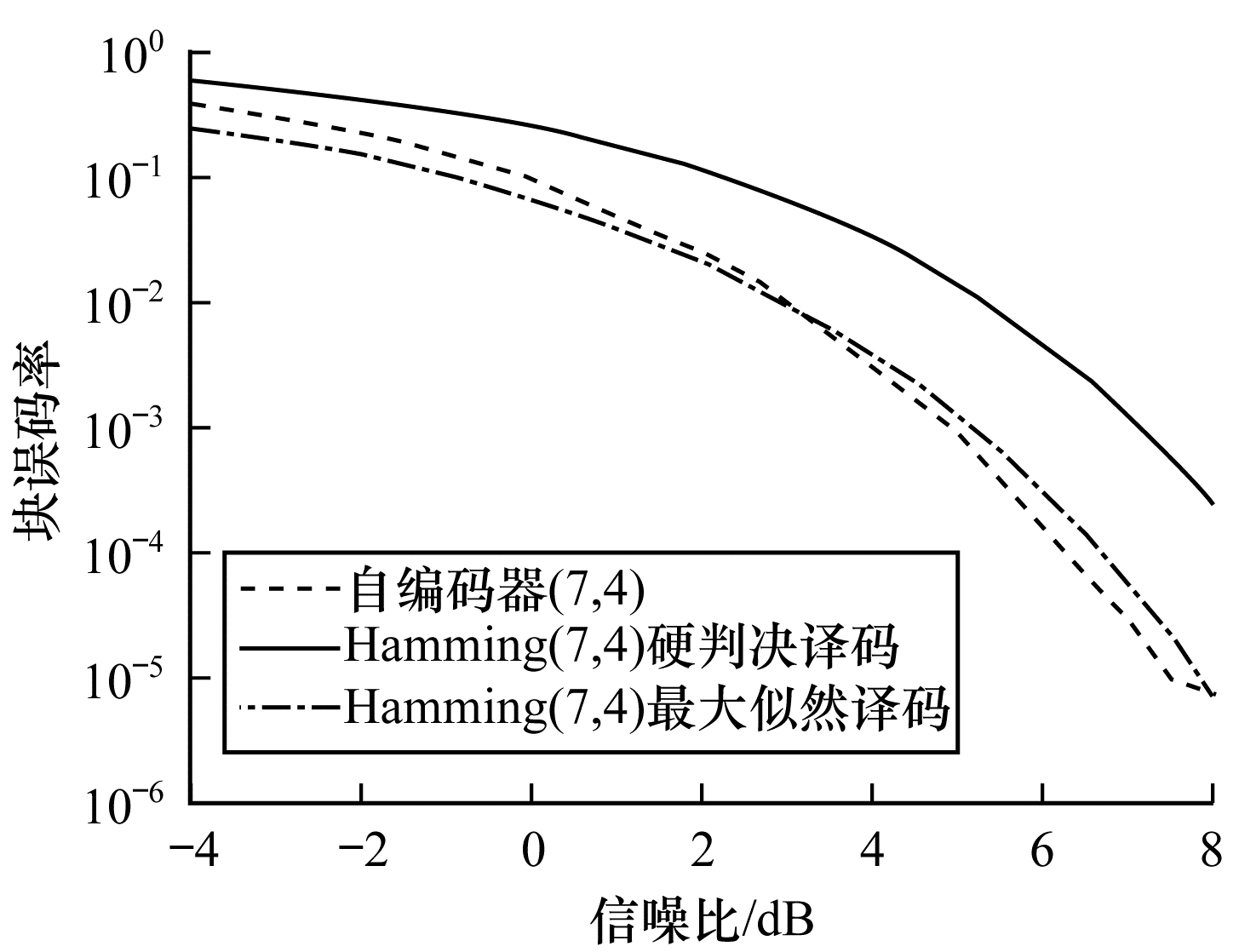
Hamming(7, 4)硬判决译码、自编码器(7, 4)、Hamming(7, 4)最大似然译码3种方案在不同信噪比下的块误码率变化曲线如图 5所示。可以看出, 自编码器端到端优化方案的性能与Hamming(7, 4)最大似然译码方案相当, 表明前者无需依赖信道的先验知识就能完成编码和解码任务, 从而验证了基于自编码器在物理层优化是可行且有效的。此外, 实验过程表明发射端使用单层的神经网络能表示信息映射传输向量的索引, 但是双层的神经网络表示会使随机梯度下降过程中更好地得到全局最优解。

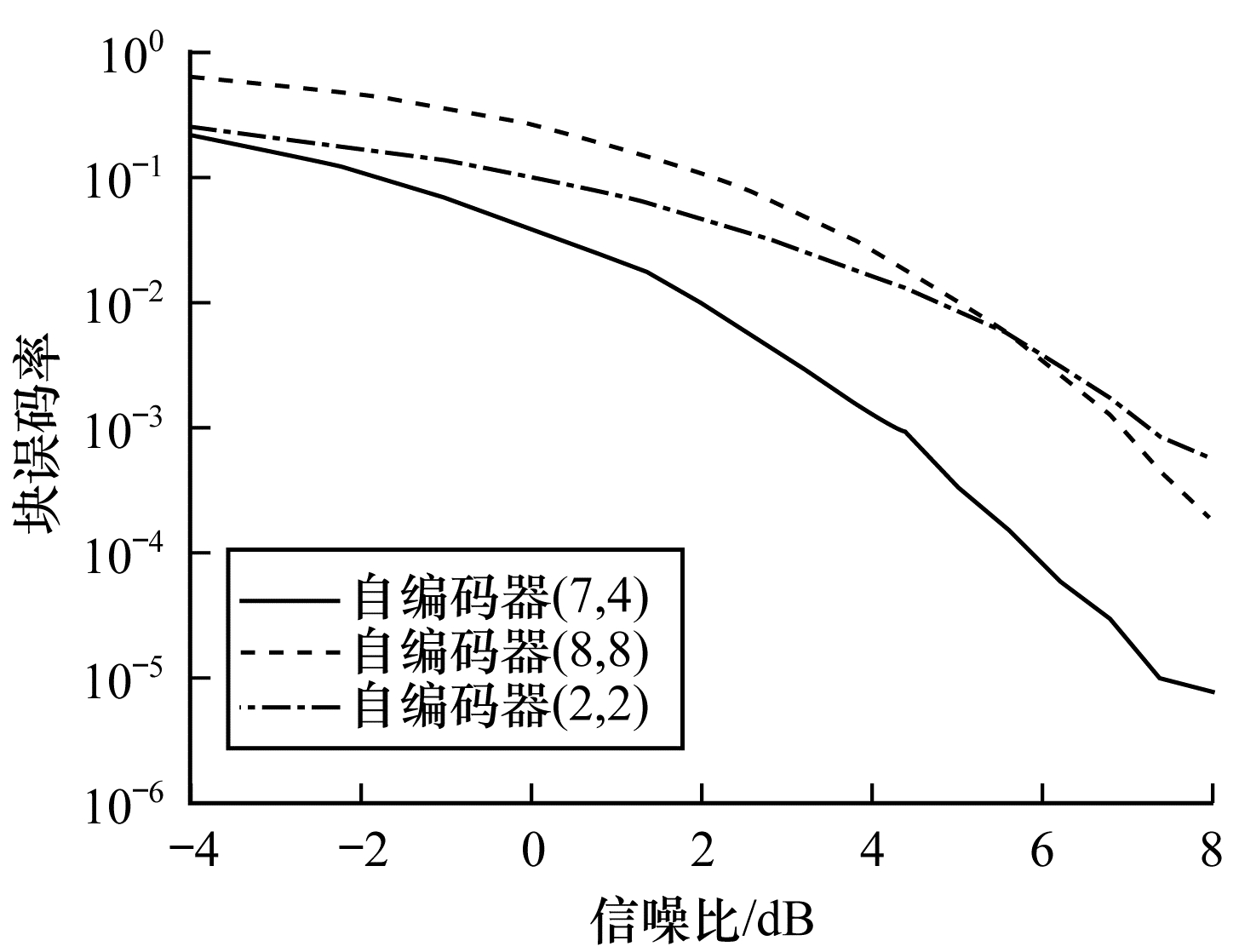
自编码器端到端系统在不同传输速率R下的变化曲线如图 6所示。通过比较R=4/7和R=1可知, 前者的性能优于后者。随着信噪比的增大, 自编码器往往能更好地学习到信道有用特性, 然而, 系统存在的强制约束(如功率条件和层数)使得自编码器的容量有限。从深度学习角度来看, R < 1意味着编码维数小于输入维数, 即欠完备自编码器, 可以学习数据分布最显著的特征。此外, 限制系统的容量意味着需要对信道特性进行稀疏表示, 这种稀疏特性有利于重构输入和降低通信系统的块误码; 另一方面, 考虑训练参数大小, 自编码器(2, 2)、(7, 4)和(8, 8)的训练参数分别为62、791和135 944, 可见信道的增加会显著增加训练参数的大小, 因此, 在设置R值时需要综合考虑功耗和性能及实际需求。

分两阶段训练和不分阶段训练对系统性能的影响如图 7所示。可以看出, 两阶段训练方法所得块误码率相比于传统方法更低。传统方法通常是将端到端系统整体训练, 而本文方法是分两阶段进行。因为分阶段的训练过程能更好地进行时延、相位的补偿, 所以能进一步提升系统性能。对于不同特定信道, 第二阶段参数微调的复杂度不同, 使得可操作性降低。尽管类似的方法在基于CNN训练特定图像上有广泛的应用, 但由于通信信道具有时变性, 因此自编码器对模型的压缩和信道提取能力仍是有限的。

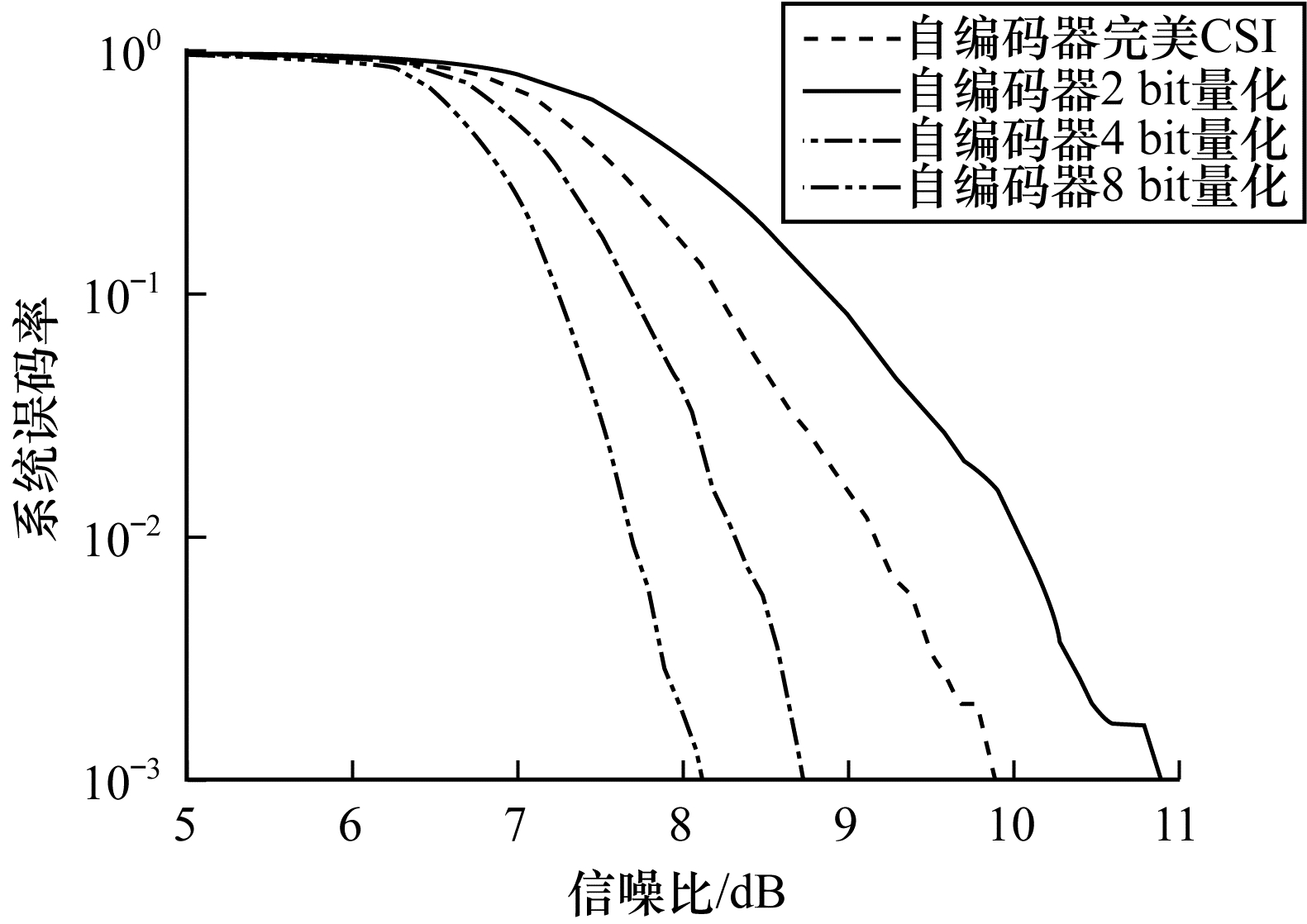
量化CSI(2 bit、4 bit和8 bit)及完美CSI在自编码器端到端系统中的性能表现如图 8所示。传统方法通常是考虑CSI已知, 即完美CSI信道, 本文方案则引入了量化CSI对实际信道进行特征提取。由图 8可知, 在低信噪比下, 量化CSI自编码器端到端性能几乎得不到提升, 而量化CSI对传统基于模块设计的通信系统在各信噪比水平下皆能得到增益。但不难看出, 当SNR≥7 dB时, CSI量化为4 bit和8 bit反馈给发射端的性能优于完美CSI, 这表明量化为2^ν bit(ν≥2)离散模型实际上有利于系统在表征信道特性时趋于收敛, 避免了对实际信道 H过拟合完全映射, 能以低开销完成CSI反馈和重建, 缓解MIMO系统中反馈负载。进一步地, 结合超密集组网(Ultra Dense Network, UDN)技术能降低密集网络需求场景的能耗。

5 结束语

本文研究基于深度学习进行自编码器端到端优化的可行性与局限性, 针对训练梯度消失和CSI反馈负载大的问题分别提出解决方案。由于深度学习需要进行大量数据训练, 因此物理层优化技术的突破关键在于系统实现复杂度和性能提升的折中, 下一步将对此进行研究。此外, 还将建立公共通信数据集并针对通信框架选择合适的训练模型。