数据挖掘技术是计算机领域和数据库领域相结合的一项热点研究课题, 而针对时间序列的分析和预测技术是数据挖掘的一个重要分支。时间序列是指在对生产和科学研究等过程中, 按照时间顺序记录得到的一系列观测值, 它是某个变量或多个变量在不同时刻所形成的随机数据, 反映了现象的发展变化规律。时间序列数据广泛存在于在工业、医药、金融、科学、物联网、电力、天文、音乐等领域中, 对这些数据进行分析能够发现时间序列数据间的关联规则、基本趋势和周期性等有价值的信息, 还能够对时间序列的未来发展状况进行预测。时间序列预测模型应用范围十分广泛, 包括金融市场预测、环境气象预测、销售业绩预测、科学数据库以及医疗诊断等领域。
对于时间序列的预测主要分为两类:未来具体值的预测和时间序列数据的短期预测, 这一过程被称为趋势预测[1]。目前基于时间序列分析的预测方法主要分为经典的统计方法、神经网络方法和机器学习等。一般的统计方法、神经网络网络方法研究都是针对未来具体值的预测, 以历史时间序列数据直接作为输入, 得到的结果也为下一个点或者之后几个点的具体预测值, 然而效果不佳, 本文实验部分也给出了利用holt-winters和长短期记忆(Long Short-Term Memory, LSTM)网络对时间序列进行回归预测的效果。对于时序数据的短期预测, 由于针对趋势预测的研究较少, 有研究人员利用机器学习方法, 例如支持向量机(SVM)、K-Means等算法对数据进行分类或者聚类, 构造分类器来预测趋势的标签, 如数据呈“上升趋势”“稳定趋势”或“下降趋势”。
为克服具体值预测结果不够准确的问题, 本文提出一种基于神经网络语言模型(Neural Network Language Model, NNLM)的时间序列短期趋势预测模型。将时间序列离散化为字符, 并使字符向量化表示m将字符的向量表示作为神经语言模型的输入, 得到下一个字符的概率分布, 取概率最大的字符即为预测的下一个最有可能的字符, 得到的字符具有一定语义, 代表预测值的范围。通过对所得输出与输入序列进行比较, 可得出“大幅下降”“小幅下降”“趋于稳定”“小幅上升”和“大幅上升”5种结果的数据走势。
1 相关工作时间序列分析的基本思想是根据系统有限长度的运行记录, 建立能够反映时间序列中所包含的动态依存关系的数学模型, 并利用该模型对系统未来的行为进行预测。对于时间序列的预测方法, 主要分为3类:1)线性模型预测方法; 2)非线性模型预测方法; 3)组合模型预测方法。线性预测模型包括线性回归模型、指数平滑模型、差分自回归滑动平均模型(ARIMA)等。非线性预测模型主要包括支持向量机(SVM)以及人工神经网络在内的深度学习方法等。组合模型预测方法就是将线性预测模型与非线性预测模型基于某种规则组合预测。
ARIMA模型以时间序列的自相关分析为基础, 是预测平稳时间序列的常用模型之一。很多研究是利用ARIMA对网络吞吐量[2]、金融[3]、天气等方面的时序数据进行分析预测。但是, 对于股票价格这类受多方面因素影响, 有非常多噪声的非稳定数据, 模型的预测效果往往较差。SVM算法对时间序列进行预测有2种不同思路:1)利用支持向量回归(SVR)预测时间序列未来的具体值[4]; 2)利用SVM预测时间序列未来的短期趋势。这也是预测时间序列2种方向, 前者为回归问题, 后者为分类问题。利用SVM、GBDT等传统机器学习算法对时间序列进行分析的研究[5]很多。
随着深度学习技术的发展, 深度学习模型越来越多地被应用于时间序列分析。在众多深度学习模型中, 循环神经网络(Recurrent Neural Network, RNN)在模型隐藏层结构设计中引入了时序的概念, 前面节点的信息会被记忆并被加入到当前节点的计算中。正是由于这一机制, 使得RNN具有了记忆能力, 前面的信息对当前节点的值都会产生影响, 可以很好地表达前后数据的依赖性。RNN模型在语音识别[6]、时间序列预测[7]等众多场景都有很好的表现。LSTM是RNN模型的变体与改进, LSTM可以有效避免RNN中的梯度消失、梯度爆炸、长期记忆能力不足等问题, 非常适合分析预测长距离时间序列和事件, 被广泛应用于故障时间预测[8]、天气预测[9]等众多典型时间序列预测场景中, 并取得了不错的效果。然而, 对于时间序列预测问题, 目前绝大多数研究都是利用RNN和LSTM直接做具体值的回归预测, 在时间序列趋势预测, 特别是与神经网络语言模型结合的趋势预测领域的应用非常有限。
神经网络语言模型是由bengio最早提出的经典模型, 模型的训练数据是一组词序列。神经网络语言模型在语音识别[10]、自然语言处理[11]等领域都取得了成功。时间序列与单词是典型的连续型数据和离散型数据, 目前, 很少有研究将神经网络语言模型与连续时间序列趋势预测相结合。
将连续型数据转化为离散数据, 并用分析离散数据的算法进行研究的实践较多。文献[12]在时间序列分段线性表示的基础上, 根据序列在不同时段的斜率变化情况, 用特殊字符来表示划分序列的分段形态模式, 从而将时间序列转换为字符串, 最后利用最长公共子序列方法计算字符串序列的距离作为时间序列的距离, 该方法与本文算法有一定的相似性, 都是将时间序列转换为离散字符串序列。但是上述研究是度量时间序列相似度, 而本文算法的目的是预测时间序列短期趋势。
对比传统的时间序列预测方法, 本文提出的方法有以下创新:
1) 不同于大多数算法直接回归预测时间序列未来具体值, 而是将连续的时间序列转换成离散事件, 与神经网络语言模型结合, 对时间序列的短期趋势进行预测。
2) 根据本文提出的时间序列离散化方法, 得到的字符表示具有更加丰富的语义信息, 可以更加直观地看出未来趋势的变化范围。
2 预测模型 2.1 预测流程本文提出的基于神经网络语言模型的时序数据趋势预测(PTTS-NNLM)算法流程如下:
1) 对输入时间序列S进行归一化, 使其均值为0, 标准差为1。
2) 对归一化后的标准化序列进行分段聚合近似(Piecewise Aggregate Approximation, PAA)转换[13]。
3) PAA后的序列通过word embedding离散化为字符串序列, 每一个字符代表对应时间段内时间序列的均值范围。
4) 深度学习模型的输入必须是数值向量, 因此, 需要将上一步得到的字符向量化表示。本文使用的词向量化表示方法是由文献[14]提出的“Distributed Representation”方法。将步骤3得到的字符串序列看作文档, 通过word2vec算法将字符转换为词向量。同时, 可以建立PAA序列与对应字符间映射的字典L。
5) 对字符串序列按输入长度进行切分, 建立训练数据集和测试数据集。输入序列通过神经网络语言模型将字典L映射为向量, 并对模型进行训练[15]。
6) 利用步骤5训练得到的神经网络语言模型对测试数据集进行预测, 并计算预测准确率。
PTTS-NNLM算法各个步骤的实现细节将在下文进行具体介绍。
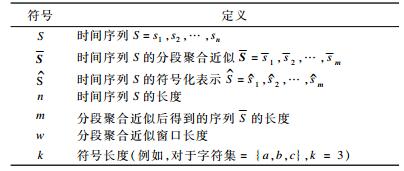
2.2 时间序列离散化时间序列离散化方法是将一个任意长度为n的时间序列按序列数据按窗口长度w缩短为任意长度m(m=n/w)的序列(m < n, 一般来说 m << n), 最后得到的符号数量大小也是一个任意整数a (a>2)。表 1为本文使用到的主要符号。
|
下载CSV 表 1 文中用到的符号 |
长度为n的时间序列S可以按窗口长度w分割, 转化为一个m维的向量
| $ {\bar s_i} = \frac{1}{w}\sum\limits_{j = w\left( {i - 1} \right) + 1}^{wi} {{s_i}} $ | (1) |
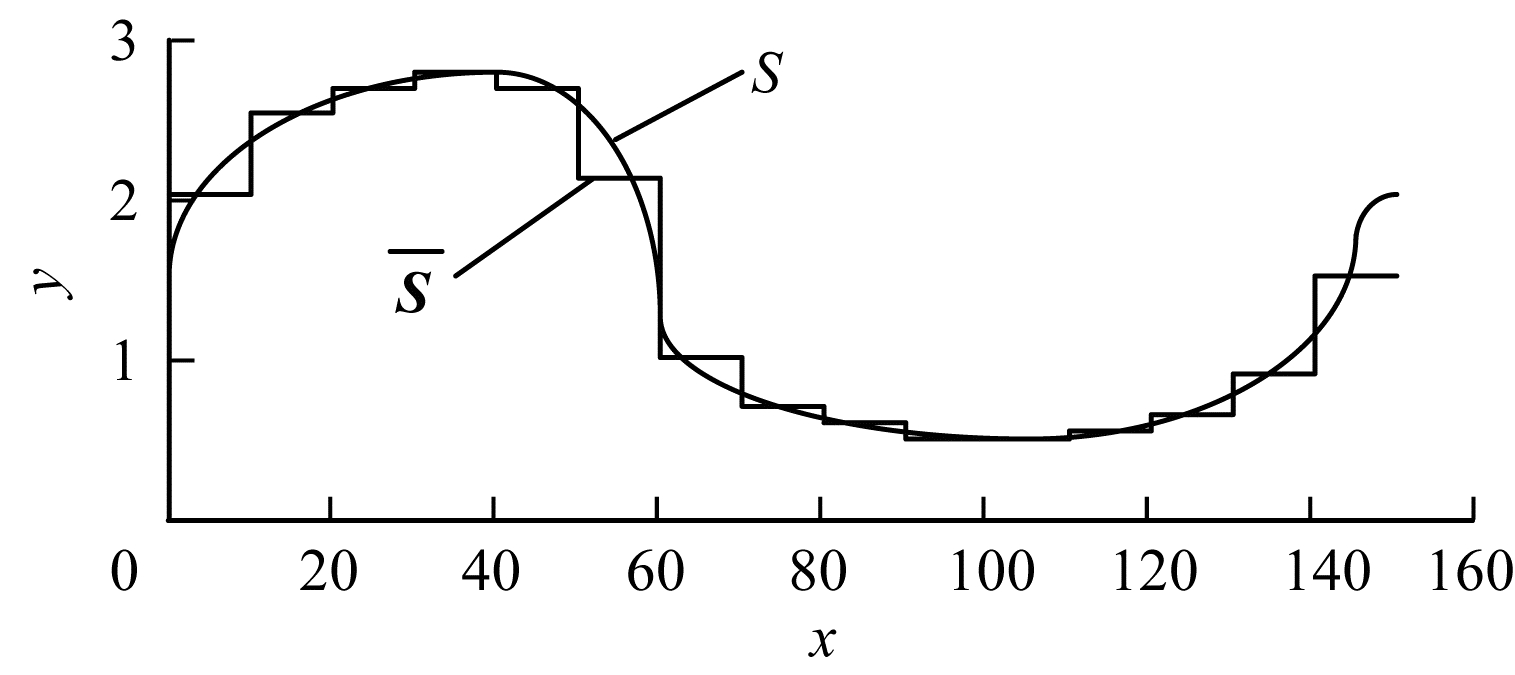
为了将时间序列从n维降为m维, 数据被等分为m段, 计算每一段数据的均值, 并将这些值的向量作为简约数据表示。如图 1所示, 通过PAA将150维时间序列降为15维。
|
Download:
|
| 图 1 时间序列通过PAA的降维 | |
时间序列做分段聚合近似的优点主要有:
1) 降维:可以使用PAA已经定义好并且得到了充分证明的降维能力, 使符号表示的维数降低。
2) 距离表示:PAA值间的差值可以对应2个字母间的数值距离。
3) 鲁棒性:减小异常数据可能给最后预测结果带来的误差。
PAA降维直观且简单, 降维效果不差于傅里叶变换和小波技术等更复杂的降维技术的效果。在将时间序PAA转换之前, 先对时间序列进行归一化, 使其均值为0, 标准差为1。
2.2.2 序列离散化将n维时间序列数据转换成m维分段聚合近似之后, 进一步转换以得到离散化字符表示, 字符的长度为k (k > 2, 例如, 对于字符集{a, b, c}, k = 3)。理想的情况是经过离散化后得到等概率的符号表示。由于归一化时间序列服从高斯分布, 可以通过不定积分确定等分高斯曲线下面积的“断点”, 即:
| $ \int_{-\infty}^{\beta_{1}} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \mathrm{d} x=1 / k $ | (2) |
| $ \int_{\beta_{i}}^{\beta_{j}} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \mathrm{d} x=1 / k $ | (3) |
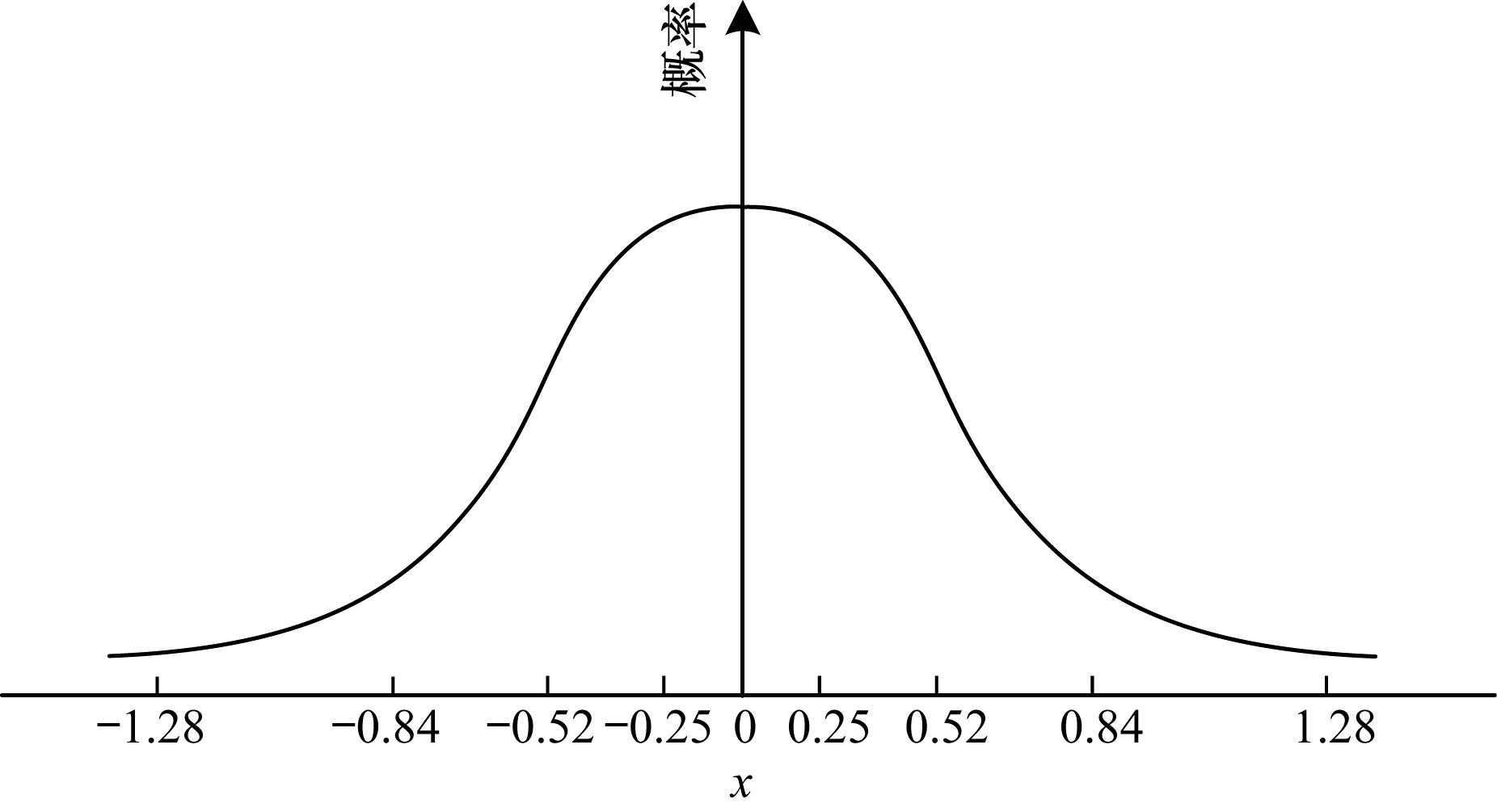
其中, β1、βi、βj分别是以k为字符集长度分割的第1、i、j个断点。以k =10为例, 通过式(2)、式(3)确定如图 2所示的-1.28、-0.84、-0.52、-0.25、0, 0.25、0.52、0.84、1.28共9个断点, 将高斯分布曲线下面积划分为10个相等的部分, 从而将PAA后的数值分布映射为a~3j 10个字母。
|
Download:
|
| 图 2 高斯分布曲线下断点分布 | |
得到了所有的断点后, 先将所有小于最小断点的分段聚合近似系数被映射为符号“a”, 所有大于最小断点而小于第2小断点的系数被映射为符号“b”, 依此类推, 将PAA降维后的序列转换成一系列由k个字符组成的字符串。
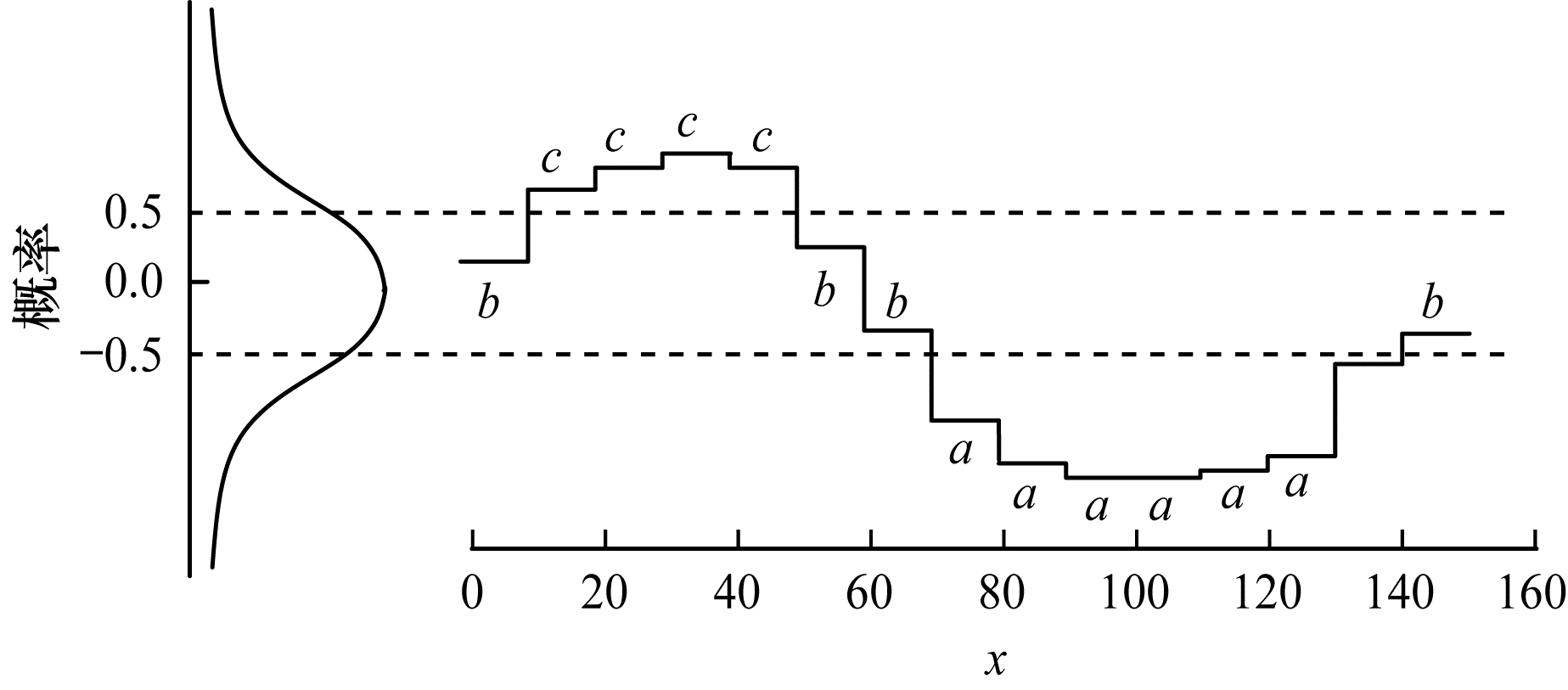
图 3所示, 假设n = 150, m = 15, k = 3, 数据首先经过PAA由150维降为15维, 再经过离散化最终得到长度为15, 由3个字符组成的有序字符串“bccccbbaaaaaab”。在实验部分, 分别选取k = 5、10、15、20, 比较字符集大小对算法预测准确率的影响。
|
Download:
|
| 图 3 时间序列被映射为字符串“bccccbbaaaaaab”的过程 | |
语言模型是自然语言处理的基础, 在机器翻译、语音识别等自然语言处理任务中有重要应用。统计语言模型的目标是在给定语句信息的情况下预测下一个词, 用公式可以表示为:
| $ \begin{aligned} p(S)=& p\left(w_{1}, w_{2}, \cdots, w_{n}\right)=\\ & p\left(w_{1}\right) \cdot p\left(w_{2} | w_{1}\right) \cdots p\left(w_{n} | w_{1}, w_{2}, \cdots, w_{n-1}\right) \end{aligned} $ | (4) |
式(4)为语言模型, 即计算一个句子S概率的模型。常用的N-gram概率语言模型采用马尔科夫假设, 即认为每个词与前面的N-1个词有关。理论上, N越大, 模型的准确度越高, 然而, N-gram模型的空间复杂度随着N的增大几乎成指数级增长。并且, 当N的取值从2到4变化时, 模型的效果提升很明显, 但是当N的取值从3变化到4时, 模型的提升效果不是很明显, 因此N一般取2或3[16]。N-gram取得了一定程度的成功, 但由于它的表达局限性, 无法解决句子的长距离依赖问题, 并不能较好描述语言。
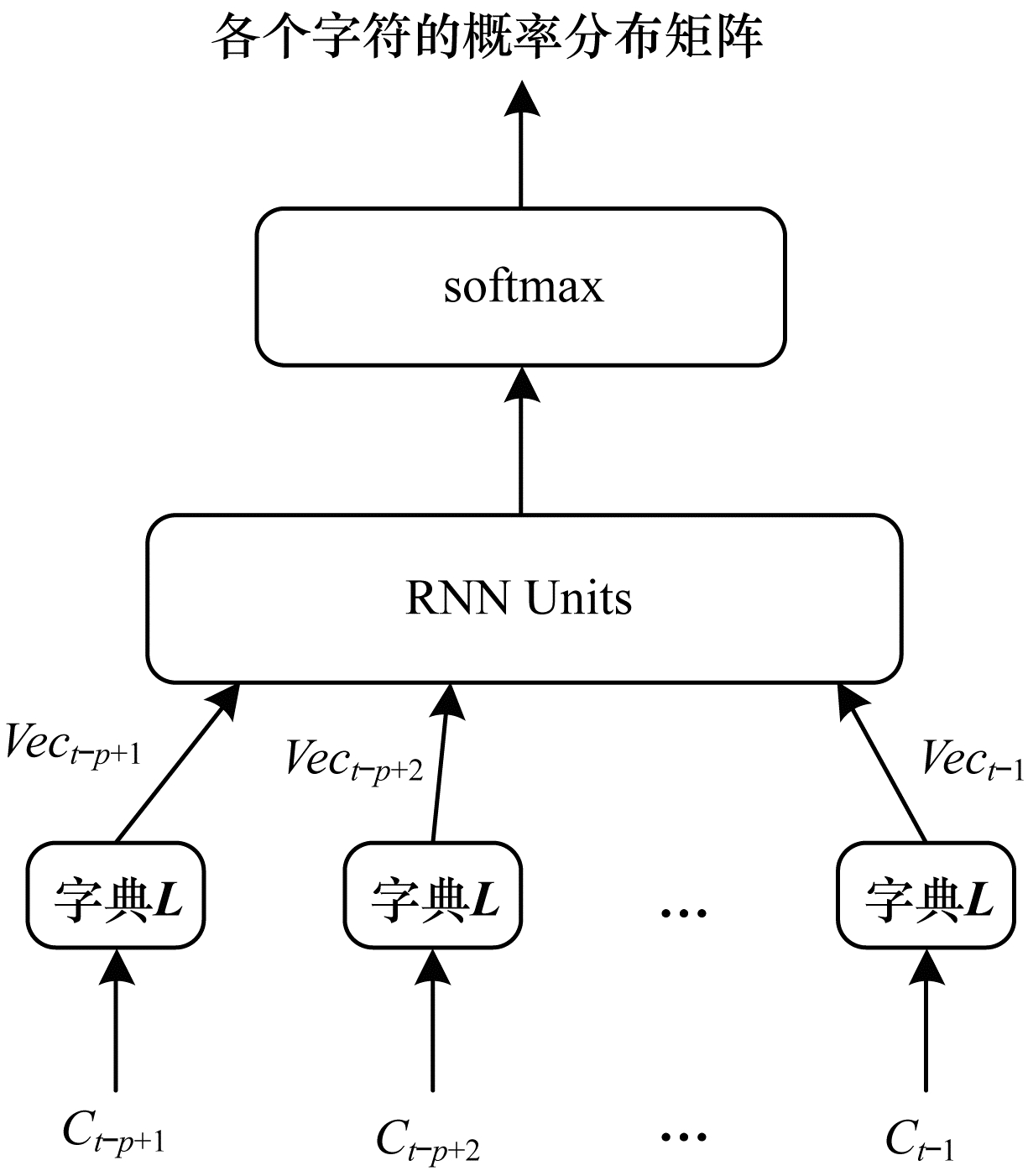
随着深度学习的不断发展, 神经网络语言模型得到了工业界和学术界越来越多的关注。相比全连接网络, 循环神经网络(RNN)同一层各个节点间也是有连接的, 当前节点的输出与前面节点的输出有关[17]。因此, 循环神经网络语言模型(RNNLM)可以获得很长的历史信息, 解决了句子的长距离依赖问题, 相比N-gram模型, RNNLM模型的效果有很大的提升。本文使用的语言模型结构如图 4所示。其中, Ci表示输入语句(Ct-p+1, Ct-p+2, …, Ct-1)中的第i个字符, 句子的长度为p。在输入层与隐藏层之间是将字符转换为对应分布式词向量的字典L, 字典L是一个k×m矩阵, 其中k为字符集的大小。每一行向量代表对应字符的词向量, m为词向量的维度。本文中字符的词向量是通过word2vec方法得到的分布式词向量[18-19]。与其他的word embedding方法相比, 如onehot方法, 分布式词向量更能体现单词在文本中的上下文语义, 意思越相近的词词向量距离就越短。
|
Download:
|
| 图 4 神经网络语言模型 | |
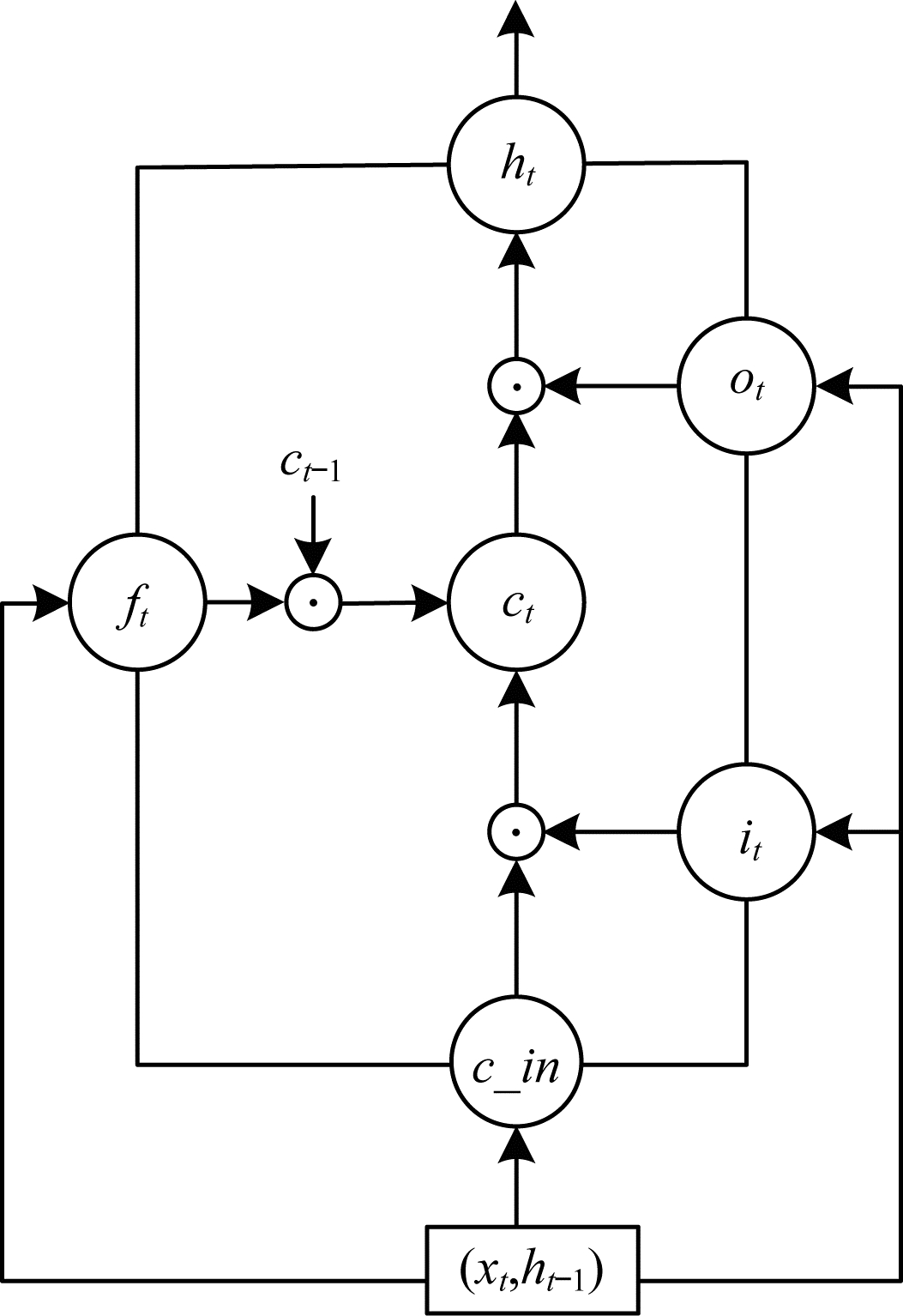
RNN部分由两层隐藏层构成, 其中每一个cell由256个LSTM单元组成, 激励函数为sigmoid函数。每个时刻t的输入为一个句子中的字符, 输出为各个字符出现在下一个位置的概率分布, 因此输入输出的维度是一样的。每次placeholder只存储一个batch的输入数据, 每次接收一个固定长度的句子。这样, 给定一个句子, 可以计算出下一个字符的概率。图 5所示为一个LSTM单元的结构。
|
Download:
|
| 图 5 循环神经网络结构 | |
图 5中心的ct 即cell, 从下方输入(ht-1, xt)到输出ht的一条线即为单元状态, xt、ht 分别为输入和输出, ct-1和ct分别代表上一时刻和当前时刻的cell值, ft、it、ot分别为LSTM中的遗忘门、输入门、输出门, LSTM可以通过门控单元决定信息是否通过或者通过的比例。
LSTM首先决定了单元状态什么信息可以保留, 遗忘门根据上一时刻的输出ht-1和当前输入xt来产生一个0~1的值ft, 通过sigmoid(σ)函数决定是否让上一时刻学到的信息Ct-1通过或部分通过。ft计算公式如下:
| $ {f_t} = \sigma \left( {{W_f} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_f}} \right) $ | (5) |
然后是产生需要更新的新信息。这一步包含两部分, 第一部分是输入门层通过sigmoid来决定多少输入部分可以通过, 第二部分通过一个tanh层生成新的单元值
| $ {i_t} = \sigma \left( {{W_i} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_i}} \right) $ | (6) |
| $ \tilde{C}_{t}=\tanh \left(W_{C} \cdot\left[h_{t-1}, x_{t}\right]+b_{C}\right) $ | (7) |
对上一个单元状态值Ct-1进行更新, 将Ct-1值乘以ft来忘掉不需要的信息, 再与需要添加更新的部分相加, 得到新的单元状态值Ct:
| $ C_{t}=f_{t} \times C_{t-1}+i_{t} \times \tilde{C}_{t} $ | (8) |
最后决定模型的输出信息。通过sigmoid函数得到一个初始输出, 使用tanh将Ct值缩放到-1~1之间, 作为输出门系数, 与初始输出相乘得到模型最后的输出:
| $ o_{t}=\sigma\left(W_{o}\left[h_{t-1}, x_{t}\right]+b_{o}\right) $ | (9) |
| $ h_{t}=o_{t} \times \tanh \left(C_{t}\right) $ | (10) |
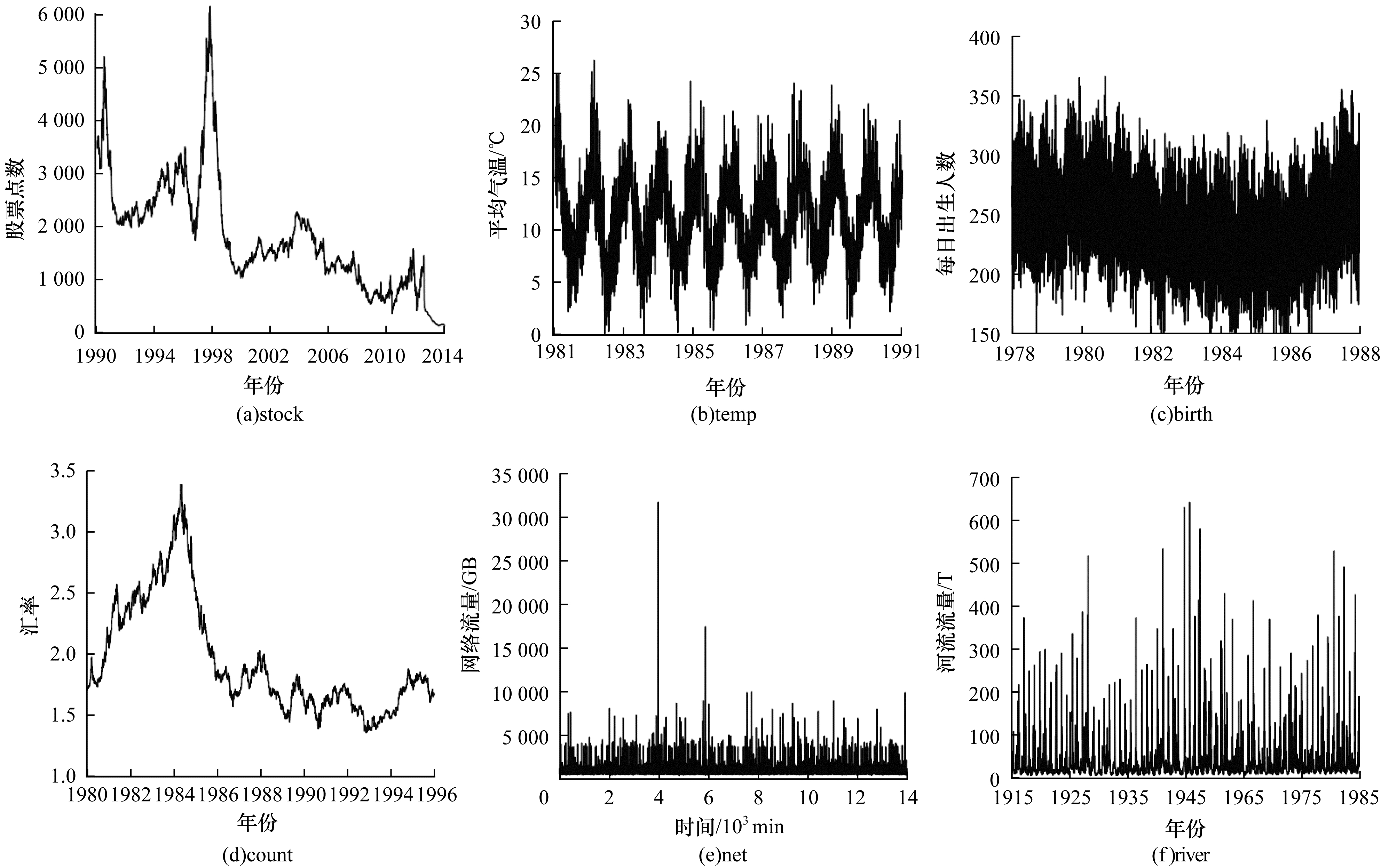
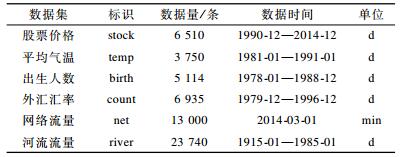
实验使用的数据出自Rob Hyndman创建的时间序列库(TSDL), 选择了其中的6个数据集, 如图 6所示, 分别为:1)某只股票每日收盘价; 2)某市每日平均气温; 3)某市每日新生儿人数; 4)我国与某国每日外汇汇率; 5)某小区某天每分钟使用网络流量; 6)saugeen河每日水流量。为了方便表示, 将6个数据集分别用英文标识表示, 对应表示方法、数据量信息和数据时间范围如表 2所示。
|
Download:
|
| 图 6 本文使用的6个时序数据集分布 | |
|
下载CSV 表 2 数据集信息 |
数据采样采用5折交叉验证法, 将每个数据集D顺序等分为5个子集Di, 每次以其中的4个数据集为训练集, 另一个为验证集, 求得验证子集的预测准确率accurracy(f; Di)(i =1, 2, 3, 4, 5), 最后的预测准确率取5个验证集的预测准确率的简单平均:
| $ {\mathop{\rm a}\nolimits} ccuracy(f;D) = \sum\limits_{i = 1}^5 {accuracy} \left( {f;{D_i}} \right) $ | (11) |
本文的评估指标为数据的短期走势范围预测准确率, 按照第2节描述的预处理方法将时间序列集离散化为k个字符, 预测下一时间窗口长度内数据的均值范围, 即预测下一个字符。将本文提出的基于神经网络语言模型的时间序列趋势预测方法(PTTS-NNLM)与传统的holt-winters、SVM、随机森林、RNN、LSTM方法, 在6个数据集上的短期趋势预测结果进行比较。使用的评价指标为准确率, 准确率accuracy的定义为:
| $ accuracy(f;D) = \frac{1}{N}\sum\limits_{k = 1}^N H \left( {f\left( {{x_k}} \right) = {y_k}} \right) $ | (12) |
其中, f为预测模型, D为预测输入数据, y为真实结果标签, H(x)为指示函数, 在x为真和假时分别取1和0。
3.2 模型实验结果本文提出的基于神经网络语言模型的时间序列趋势预测算法(PTTS-NNLM)语言模型部分的实现基于LSTM模型, 即TensorFlow实现, 输入为一个时间窗口长度的字符串, 输出为概率最大的字符, 每层神经元个数为256, 输出层维度为1, 即预测字符。本节的实验部分比较了以下4个实验参数变化时模型的效果:1)PAA降维序列数据窗口长度w分别取7、14、21、28;2)隐藏层层数分别取1、2、3;3)神经网络语言模型输入时间窗口, 即time-stamp分别取5、10、15、20、25;4)字符集大小k分别取5、10、15、20。
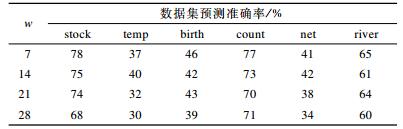
3.2.1 时间序列降维窗口长度固定模型隐藏层层数为2, 输入时间窗口大小为10, 字符集大小k为5, 模型学习率为0.001, 考察当序列降维数据窗口长度w分别取7、14、21、28, 即现实意义中的一周、两周、三周、一个月时, TSTP-NNLM算法在6个数据集上的预测准确率, 结果如表 3所示。
|
下载CSV 表 3 降维窗口w分别取7、14、21、28时的预测准确率 |
从表 3可以看出, 随着时间序列降维窗口的增大, 最后的预测准确率呈下降趋势。因此, 可以将降维时间窗口大小定为7。
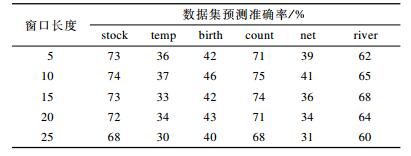
3.2.2 深度模型输入窗口长度固定时间序列降维窗口大小为7, 模型隐藏层层数为2, 字符集大小k为5, 模型学习率为0.001, 考察当语言模型输入窗口长度, 即time-stamp分别取5、10、15、20、25时, PTTS-NNLM算法在6个数据集上的预测准确率, 结果如表 4所示。
|
下载CSV 表 4 窗口长度取5、10、15、20、25时的预测准确率 |
从表 5可以看出, 当输入长度取10时, 预测准确率比取5、15、20、25时相对较高, 因此, 可以将输入长度定为10。
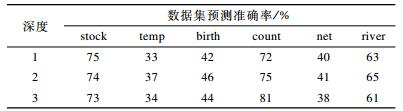
|
下载CSV 表 5 隐藏层深度为1、2、3时的预测准确率 |
固定时间序列降维窗口大小为7, 输入时间窗口大小为10, 字符集大小k为5, 模型学习率为0.001, 每层神经元个数为512, 考察当神经网络语言模型隐藏层深度分别取1、2、3时, TSTP-NNLM算法在6个数据集上的预测准确率, 结果如表 5所示。
从表 5可以看出, 隐藏层数的适当增加可以增强模型的计算能力, 提高预测准确率。然而, 层数过大不仅会导致模型冗余, 影响计算速度, 而且可能会导致过拟合, 从而使得预测准确率下降。因此, 本文神经网络语言模型的隐藏层数定为2。
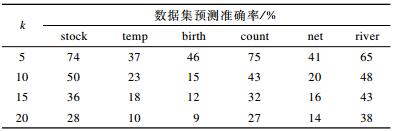
3.2.4 离散字符集大小固定时间序列降维窗口大小为7, 输入时间窗口大小为10, 神经网络语言模型隐藏层深度为2, 模型学习率为0.001, 每层神经元个数为512, 考察当字符集大小分别取5、10、15、20时, PTTS-NNLM算法在6个数据集上的预测准确率, 结果如表 6所示。
|
下载CSV 表 6 字符集大小k取5、10、15、20时的预测准确率 |
从表 6可以看出, 随着字符集长度k增大, PTTS-NNLM算法的预测准确率会逐渐下降。字符集越大, 可能产生的预测结果就会更多, 预测错误概率更高。
3.3 结果比较与评价本文选取了5种典型的传统时间序列预测算法作为对比, 分别为时间序列回归预测算法Holt-winters、SVM算法、随机森林(Random Forest)算法以及深度学习中的RNN模型和LSTM模型[20-22]。
Holt-winters算法即三次指数平滑法。指数平滑法广泛应用于时间序列预测问题, 其中, 一次指数平滑法适用于没有总体趋势和季节性的数据, 二次指数平滑法加入了趋势信息统计量, 适用于预测呈现某一特定趋势的数据, 三次指数平滑法则进一步加入了季节性信息统计量, 适用于预测具有趋势性和季节性的数据场景。Holt-winters是典型的具体值回归预测算法, 本文通过预测出的下一时间段数据均值与前面的数据PAA值比较获得趋势信息。
循环神经网络(RNN)经常用来进行时序预测或者用作语言模型的深度学习模型, LSTM模型作为RNN的变种, 解决了RNN的梯度消失、梯度爆炸和长距离记忆能力不足的问题, 非常适合时间序列预测问题。本文构建的基于RNN和LSTM的神经网络模型, 基于TensorFlow实现, 输入层时间窗口长度均为10, 隐藏层层数都为2, 每层神经元个数为256, 输出层维度为1, 即序列下一阶段的均值。
支持向量机(SVM)是机器学习中的监督学习算法, SVM最大的特点就是通过最大化几何边缘区最大化模型的泛化性能, 可以广泛应用于分类和回归问题。本文使用SVM模型是将趋势预测看做多分类问题, 预测的可能结果共k类。
随机森林为集成学习方法, 本文使用的基学习器为二叉决策树。对于随机森林方法中的参数, 定义树的最大深度h与时间窗口的大小相等, 即当时间窗口分别取10和7时, 树的最大深度分别为10和7。最大属性值的个数取树最大深度的1/3, 即当时间窗口分别取10、7时, 最大属性值的大小分别为3、2。对于决策树的数目这一属性值的确定, 分别取值2~100之间的整数计算模型的准确率。训练结果表明, 当树的数目为45时, 训练准确率最高。因此, 决策树的个数定为45。
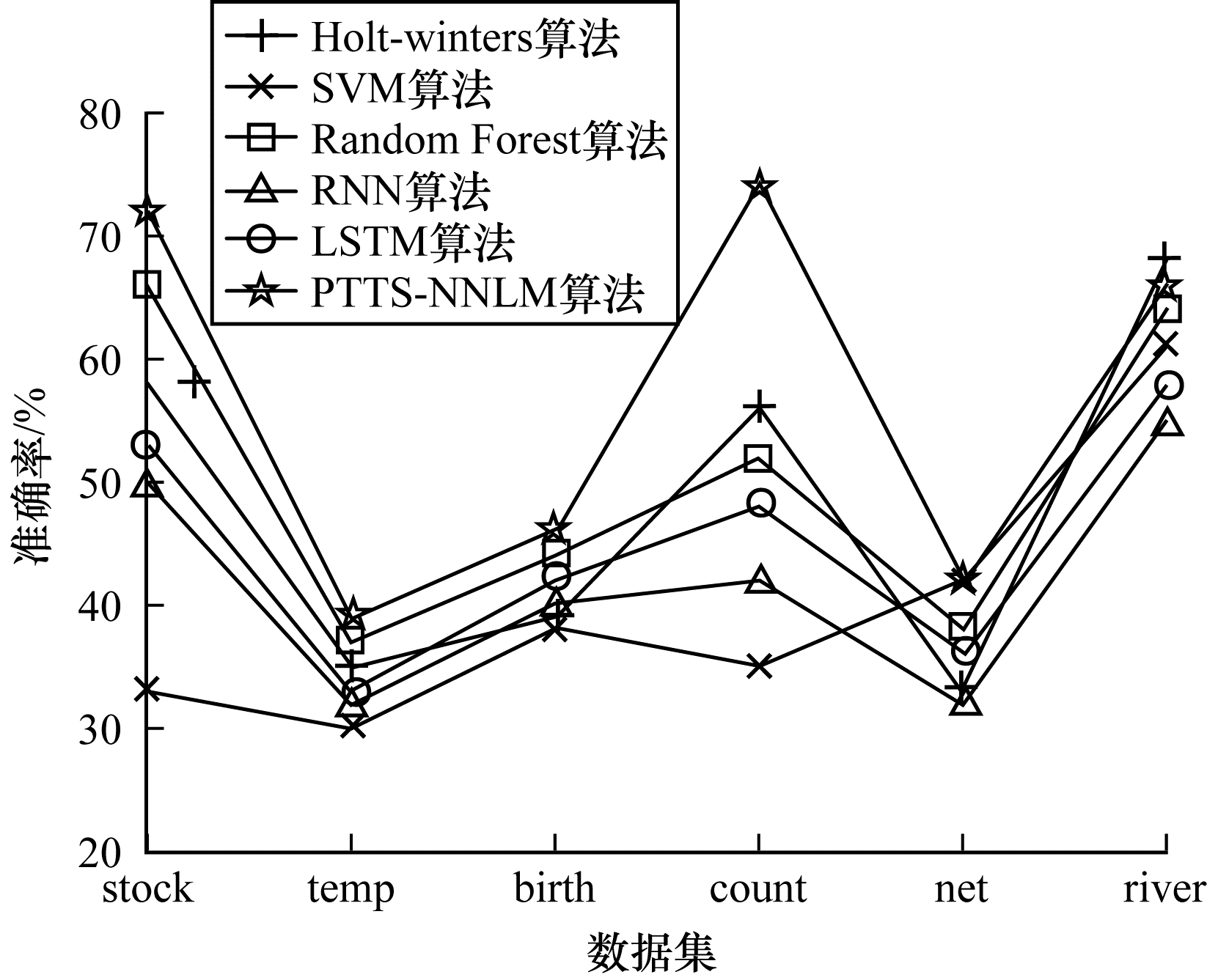
将以上5种传统算法与本文提出的算法进行比较, 并在所选取的6个数据集上进行训练, 取字符集大小k =5, 最后的预测准确率如图 7所示。
|
Download:
|
| 图 7 6种算法在6个数据集上的预测准确率对比 | |
从图 7可以看出, SVM、RNN、LSTM算法在这6个数据集上的预测效果相对较差。本文提出的PTTS-NNLM算法除了在河流流量数据上准确率略低于Holt-winters, 其他5个数据集上准确率都是最高或并列最高的, 预测准确率都较高且稳定。
4 结束语本文提出一种基于神经网络语言模型的时间序列短期趋势预测模型。将神经网络语言模型与时间序列预测相结合, 对于给定的时间序列数据, 首先进行分段降维处理, 再利用提出的离散方法将分段近似值转化为由字符组成的文本。运用word embedding方法将输入字符用具有语义信息的向量表示, 并作为神经网络语言模型的输入, 下一个时间段的字符表示作为输出, 对语言模型进行训练。实验结果表明, 相比较传统的时间序列趋势预测方法, 本文提出的短期趋势预测方法准确性有较大提升, 且由于字符表示带有语义信息, 所得到的预测结果不仅可以看出未来短期数据趋势, 还能够直接从结果中反映趋势变化程度。
| [1] |
FU Tak Chung. A review on time series data mining[J]. Engineering Applications of Artificial Intelligence, 2011, 24(1): 164-181. DOI:10.1016/j.engappai.2010.09.007 (  0) 0)
|
| [2] |
DONG Xin, Fan Weitao, GU Jun. Predicting LET througput using traffic time series[J]. ZTE Communications, 2015, 13(4): 61-64. (  0) 0)
|
| [3] |
ZHANG G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing, 2003, 50(2): 159-175. (  0) 0)
|
| [4] |
WU Jheng Long, CHANG Pei Pchann. A trend-based segmentation method and the support vector regression for financial time series forecasting[J]. Mathematical Problems in Engineering, 2012, 232: 1-20. (  0) 0)
|
| [5] |
徐国祥, 杨振建. PCA-GA-SVM模型的构建与应用研究[J]. 数量经济技术经济研究, 2011(2): 135-147. (  0) 0)
|
| [6] |
朱小燕, 王昱, 徐伟. 基于循环神经网络的语音识别模型[J]. 计算机学报, 2001, 24(2): 213-218. DOI:10.3321/j.issn:0254-4164.2001.02.016 (  0) 0)
|
| [7] |
梁振宇.基于递归神经网络的负荷预测模型与用电规划[D].广州: 华南理工大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10561-1017855832.htm
(  0) 0)
|
| [8] |
王鑫, 吴际, 刘超, 等. 基于LSTM循环神经网络的故障时间序列预测[J]. 北京航空航天大学学报, 2018, 44(4): 772-784. (  0) 0)
|
| [9] |
杨函.基于深度学习的气象预测研究[D].哈尔滨: 哈尔滨工业大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10213-1017863410.htm
(  0) 0)
|
| [10] |
黎亚雄, 张坚强, 潘登, 等. 基于RNN-RBM语言模型的语音识别研究[J]. 计算机研究与发展, 2014, 51(9): 1936-1944. (  0) 0)
|
| [11] |
GOLDBERG Y. A primer on neural network models for natural language processing[J]. Journal of Artificial Intelligence Research, 2016, 57(1): 345-420. (  0) 0)
|
| [12] |
刘芬, 郭躬德. 基于符号聚合近似的时间序列相似性符合度量方法[J]. 计算机应用, 2013, 33(1): 192-198. DOI:10.3969/j.issn.1001-3695.2013.01.049 (  0) 0)
|
| [13] |
LIN Jessica, KEOGH E J, LONARDI S, et al.A symbolic representation of time series, with implications for streaming algorithms[C]//Proceedings of International Conference on Management of Data.San Diego, USA: [s.n.], 2003: 2-11.
(  0) 0)
|
| [14] |
PACCANARO A, HINTON G E. Learning distributed representations of concepts using linear relational embedding[J]. IEEE Transactions on Knowledge and Data Engineering, 2001, 13(2): 232-244. DOI:10.1109/69.917563 (  0) 0)
|
| [15] |
BENGIO Y, DUCHARME R, VINCENT P, et al. A neural probabilistic language model[J]. Journal of Machine Learning Research, 2003, 3(6): 1137-1155. (  0) 0)
|
| [16] |
LIU Shujie, YANG Nan, LI Mu, et al.A recursive recurrent neural network for statistical machine translation[C]//Proceedings of the 52nd Meeting of the Association for Computational Linguistics.Baltimore, USA: [s.n.], 2014: 1491-1500.
(  0) 0)
|
| [17] |
MIKOLOV T, KARAFIAT M, BURGET L, et al.Recurrent neural network based language model[C]//Proceedings of IEEE Conference of the International Speech Communication Association.Washington D.C., USA: IEEE Press, 2010: 1045-1048.
(  0) 0)
|
| [18] |
LAI Siwei, LIU Kang. How to generate a good word embedding[J]. IEEE Intelligent Systems, 2016, 31(6): 5-14. DOI:10.1109/MIS.2016.45 (  0) 0)
|
| [19] |
MIKOLOV T, SUTSKEVER I. Distributed representations of words and phrases and their compositionality[J]. Neural Information Processing Systems, 2013(12): 3111-3119. (  0) 0)
|
| [20] |
GERS F A, ECK D, SCHMIDHUBER J, et al.Applying LSTM to time series predictable through time-window approaches[C]//Proceedings of International Conference on Artificial Neural Networks.Washington D.C., USA: IEEE Press, 2000: 669-676.
(  0) 0)
|
| [21] |
侯澍旻.时序数据挖掘及其在故障诊断中的应用研究[D].武汉: 武汉科技大学, 2006. http://cdmd.cnki.com.cn/article/cdmd-11915-2007090022.htm
(  0) 0)
|
| [22] |
SIVAPRAGASAM C, LIONG S, PASHA M F, et al. Rainfall and runoff forecasting with SSA-SVM approach[J]. Journal of Hydroinformatics, 2001, 3(3): 141-152. DOI:10.2166/hydro.2001.0014 (  0) 0)
|
 2019, Vol. 45
2019, Vol. 45


 ,
,