1b. 西北工业大学 计算机学院, 西安 710072;
2. 西北工业大学 太仓长三角研究院, 江苏 太仓 215400
1b. School of Computer Science, Northwestern Polytechnical University, Xi'an 710072, China;
2. Taicang Yangtze River Delta Research Institute, Northwestern Polytechnical University, Taicang, Jiangsu 215400, China
处理器锁步由2个处理器构成自监控对, 不断检查操作功能的正确性并建立故障抑制区, 防止故障蔓延到系统[1]。为提高航空、航天计算机控制等高安全关键系统的可靠性, 处理器锁步技术越来越多地被应用于上述领域[2]。处理器锁步技术作为一项安全关键计算机技术已日趋成熟并形成产品, 被应用于波音777、787等民机项目的综合模块化航电(Integrated Modular Avionics, IMA)以及Freescale、ARM等品牌的嵌入式微控制器中[3-5]。在最近的锁步技术研究中, 锁步系统不仅支持指令级位对位的对比, 还支持故障回滚和错误修复, 可靠性较高[6]。然而国内对于锁步技术, 尤其是锁步系统可靠性问题的研究较少, 因此如何建立锁步自监控处理器系统并分析锁步系统的可靠性, 已成为安全关键系统领域中一个亟待解决的问题。
广义随机Petri网(Generalized Stochastic Petri Nets, GSPN)[7]是一种高级Petri网建模工具, 不仅可以直观准确地描述系统动态故障行为, 而且可以通过状态方程、同构Markov等严格定义的数学方法对模型进行解算, 还能方便转化为仿真模型, 并通过计算机对模型进行模拟和仿真。针对锁步系统的可靠性分析问题, 本文构建锁步自监控处理器系统, 采用GSPN对该系统进行可靠性建模, 并与冗余表决可靠性模型进行对比。
1 锁步自监控系统传统的双机同步系统包含2个处理器, 一个为主处理器, 另一个为从处理器。在正常情况下, 2个处理器同时执行相同任务, 主处理器负责输出, 从处理器负责监控。当主从2个处理器结果不同时, 认为系统失效, 立即停止工作[8]。然而, 双机同步系统只能检测系统级故障, 无法实现故障定位和隔离, 也无法完成系统降级使用或故障修复[9]。
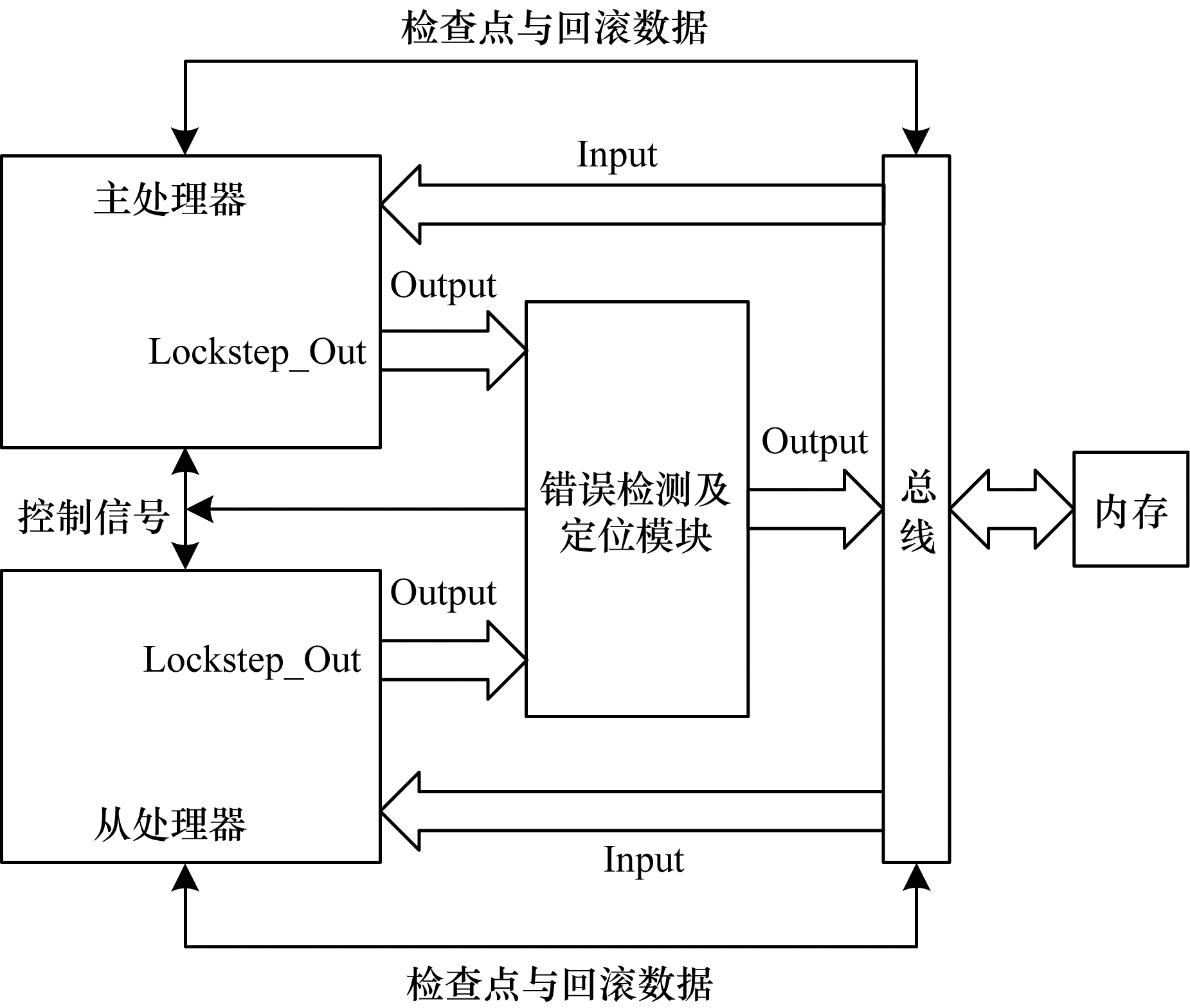
针对上述系统缺点, 本文在双机同步的基础上增加错误检查、隔离和恢复逻辑, 可以定位并恢复失效处理器的故障。锁步自监控系统架构如图 1所示。
|
Download:
|
| 图 1 锁步自监控系统架构 | |
在图 1中, 主从处理器完全独立, 总线信息经过复制后同时送入2个处理器。当处理器进行输出时, 主从处理器分别将自身的输出信号通过Lockstep_Out端口送入错误检测及定位模块, 并根据该模块返回的信息进行检查点设置或故障回滚。当进行检查点设置时, 处理器将自身的运行环境存储至固定内存中。当进行故障回滚时, 处理器根据内存中上一个检查点的运行环境信息, 重写寄存器、堆栈等信息, 完成故障回滚操作。
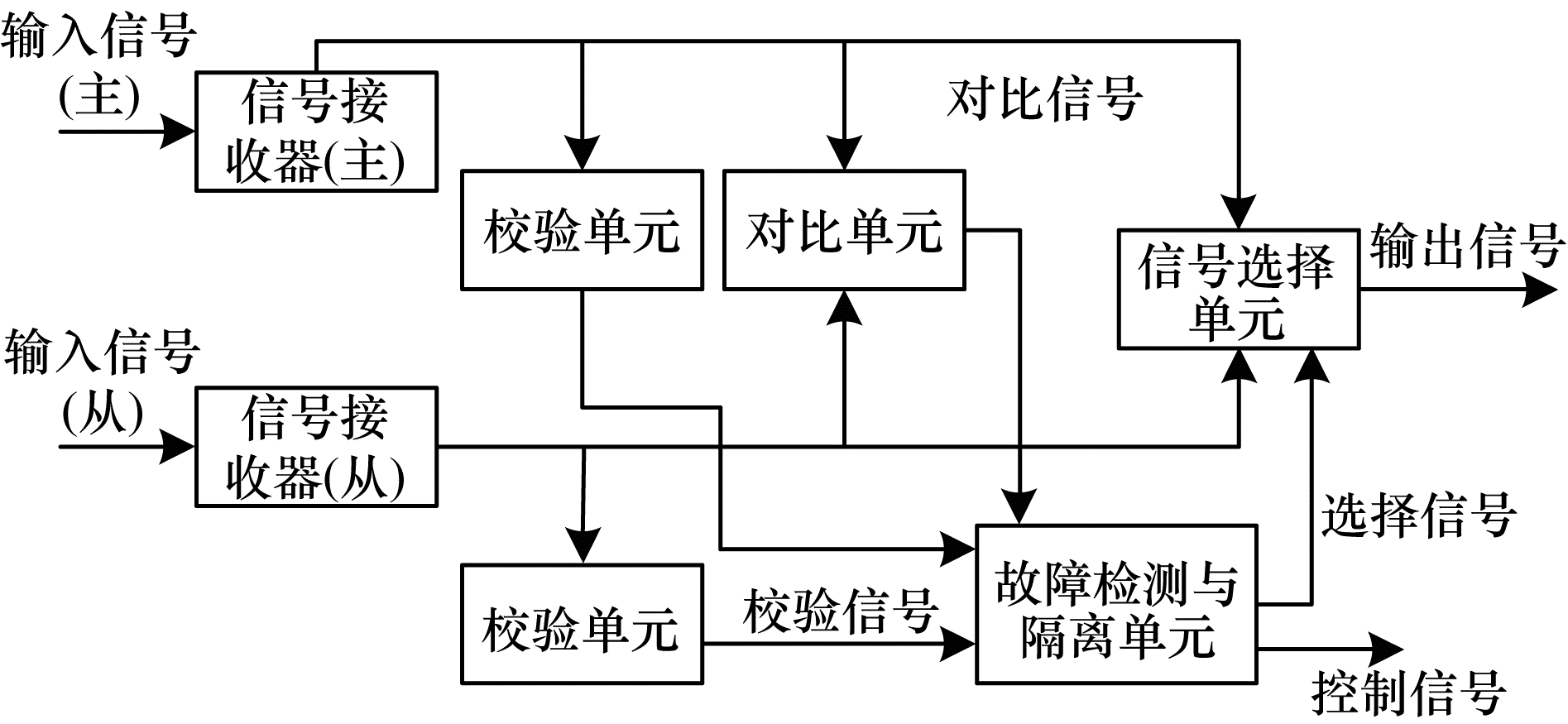
1.1 错误检测及定位错误检测及定位系统应包含信号接收单元、校验单元、对比单元、故障监测与隔离单元以及信号选择单元。错误检测及定位系统架构如图 2所示。
|
Download:
|
| 图 2 错误检测及定位系统架构 | |
在图 2中, 主从信号接收器接收信号后, 将信号分为3路, 分别送往校验单元、对比单元和信号选择单元。校验和对比结果送至故障检测与隔离单元, 该单元根据结果选择输出信号并输出控制信号。在系统工作时:
1) 若两处理器校验正确, 结果对比正常, 则系统正常工作。
2) 若单处理器校验出错, 结果对比正常, 则该路校验逻辑出错, 判定该路出现不可修复失效。系统隔离故障支路, 解除锁步, 使另一路处理器信号直接输出, 系统降级为单边工作。
3) 若主处理器校验出错, 结果对比异常, 则判定主处理器运行时出错, 发生可修复失效。系统切换主从处理器, 由新的主处理器负责信号输出, 故障处理器进入自检修复状态, 系统故障有效。
4) 若从处理器校验出错, 结果对比异常, 则判定从处理器运行时出错, 发生可修复失效。由主处理器继续负责信号输出, 故障处理器进入自检修复状态, 系统故障有效。
5) 若两处理器校验正确, 对比结果异常, 则判定两处理器失效, 或对比单元失效, 系统失效。
6) 若两处理器校验出错, 则两处理器运行出错或校验逻辑出错, 无法判别具体原因, 系统失效。
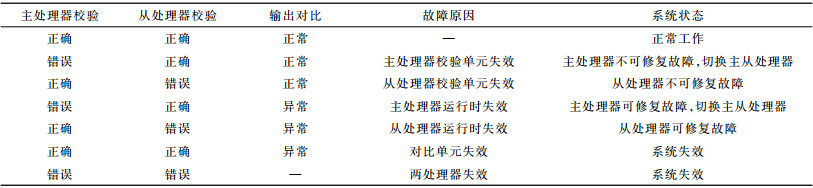
系统故障及状态如表 1所示。
|
下载CSV 表 1 系统故障及状态 |
设置检查点及系统故障恢复模块可以提高系统可靠性, 并对产生瞬时错误的处理器进行恢复[10]。本文为该系统设计检查点及系统恢复单元。该单元设计思路和工作流程如下:在处理器开始运行时, 先将寄存器重置并完成数据初始化工作, 而后等待错误检测及定位系统发来的同步控制信号。一旦同步信号到来, 系统将两CPU上下文信息统一存储在内存某处作为系统检查点, 然后同时开始执行下一条指令。在指令执行完成后, 将输出发送至错误检测及定位系统中进行自检和对比, 然后等待同步信号, 以此循环运行。
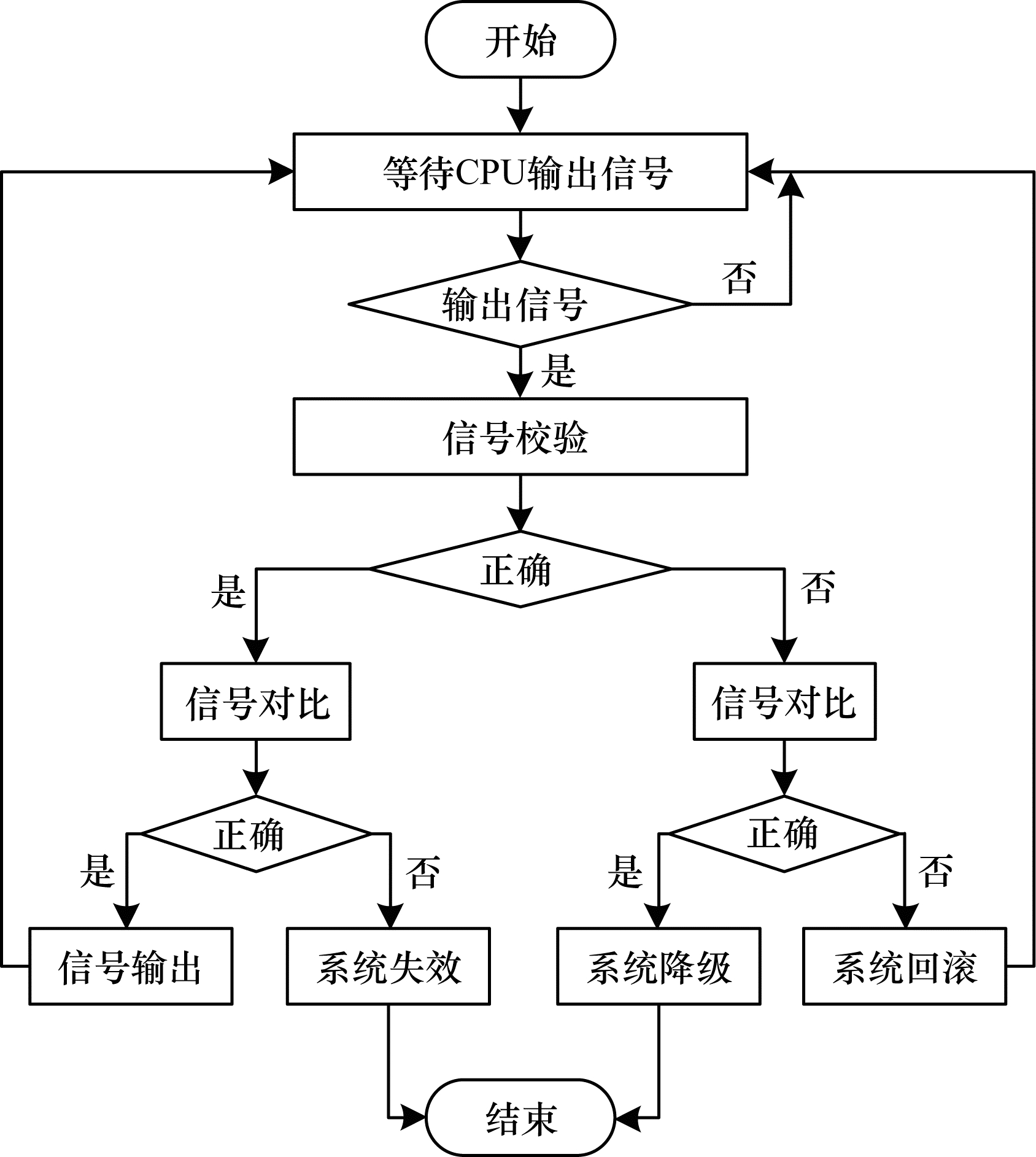
对错误检测及定位系统来说, 如图 3所示, 在接收到CPU的输出后, 先进行信号校验, 再进行信号对比, 并根据结果发送对应的控制信号给信号选择器和锁步模块, 控制系统下一步行为。
|
Download:
|
| 图 3 错误检测及定位系统工作流程 | |
当需要进行故障修复时, 回滚信号有效, 从固定内存中取出上一个检查点的无故障CPU的上下文信息, 并以此覆盖故障CPU寄存器和堆栈信息, CPU返回到距离该故障最近的正常状态开始工作, 故障修复完成。
2 建模方法 2.1 建模元素说明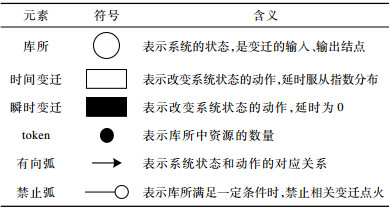
|
下载CSV 表 2 GSPN系统建模的各元素及其含义 |
在系统中, 组成系统的单元有2种失效过程:可修复失效与不可修复失效。下文分别对上述过程进行GSPN建模与分析。
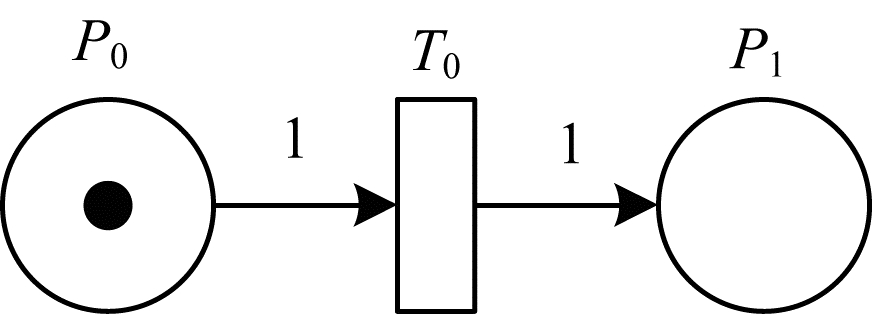
1) 不可修复失效, 即单元发生了永久性故障, 该故障不能通过系统自身修复。系统可靠性GSPN模型如图 4所示, 模型中含有2个库所和1个变迁, 库所及变迁含义如表 3所示。
|
Download:
|
| 图 4 不可修复单元的可靠性GSPN模型 | |

|
下载CSV 表 3 不可修复单元可靠性GSPN模型元素及其含义 |
在该系统中, 初始状态P0含有token, 表示系统正常工作。T0变迁表示单元故障过程, T0点火后, P0中token消失, P1中产生token, 表示单元失效。
当单元故障发生时间服从指数分布, 失效率为λ时, 系统平均无故障时间θ=
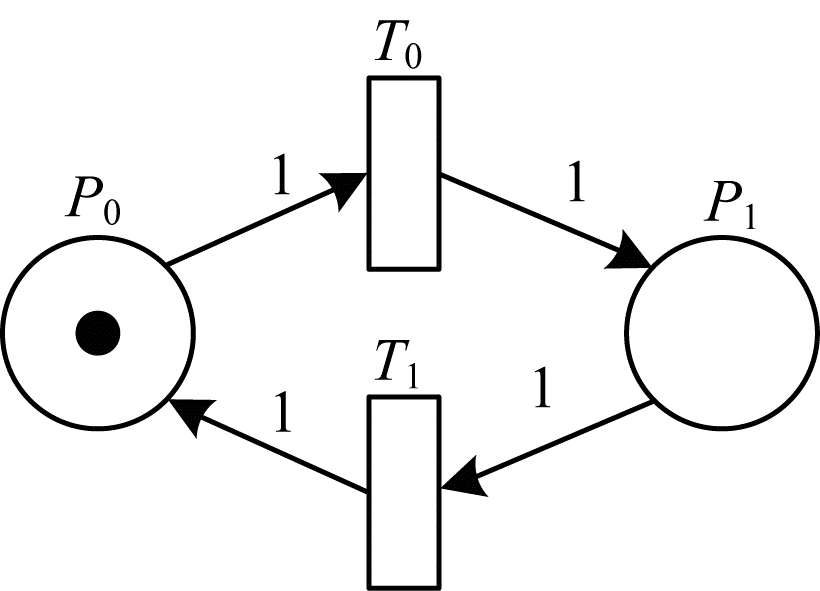
2) 可修复失效, 即单元发生暂时性故障, 该故障可以通过故障隔离和故障回滚修复。系统可靠性GSPN模型如图 5所示, 模型中含有2个库所和2个变迁, 库所及变迁含义如表 4所示。
|
Download:
|
| 图 5 可修复单元的可靠性GSPN模型 | |

|
下载CSV 表 4 可修复单元可靠性GSPN模型元素及其含义 |
在该系统中, 初始状态P0含有token, 表示系统正常工作。T0变迁表示单元故障过程, T0点火后, P0中token消失, P1中产生token, 表示单元失效。T1变迁表示系统故障修复, T1点火后, P1中token消失, P0中产生token, 表示单元恢复。T0、T1的交替点火过程表示系统故障及修复过程。
当单元故障发生及修复时间服从指数分布, 且失效率为λ、恢复率为μ时, 系统平均故障间隔时间MTBF=
为证明本文构建的锁步模型在可靠性方面的优越性, 本节将介绍一种典型的可靠性系统——冗余表决系统的GSPN模型。m/n(G)表决系统是指由n个单元组成的系统中, 至少有m个单元有效, 系统才正常工作[12]。以2/3(G)表决系统为例, 系统中包含3个同级处理器。在正常情况下, 3个处理器同时执行相同任务并将输出结果进行比较表决。当3个处理器中至少有2个处理器正常工作时, 系统正常工作; 反之, 系统失效[13]。
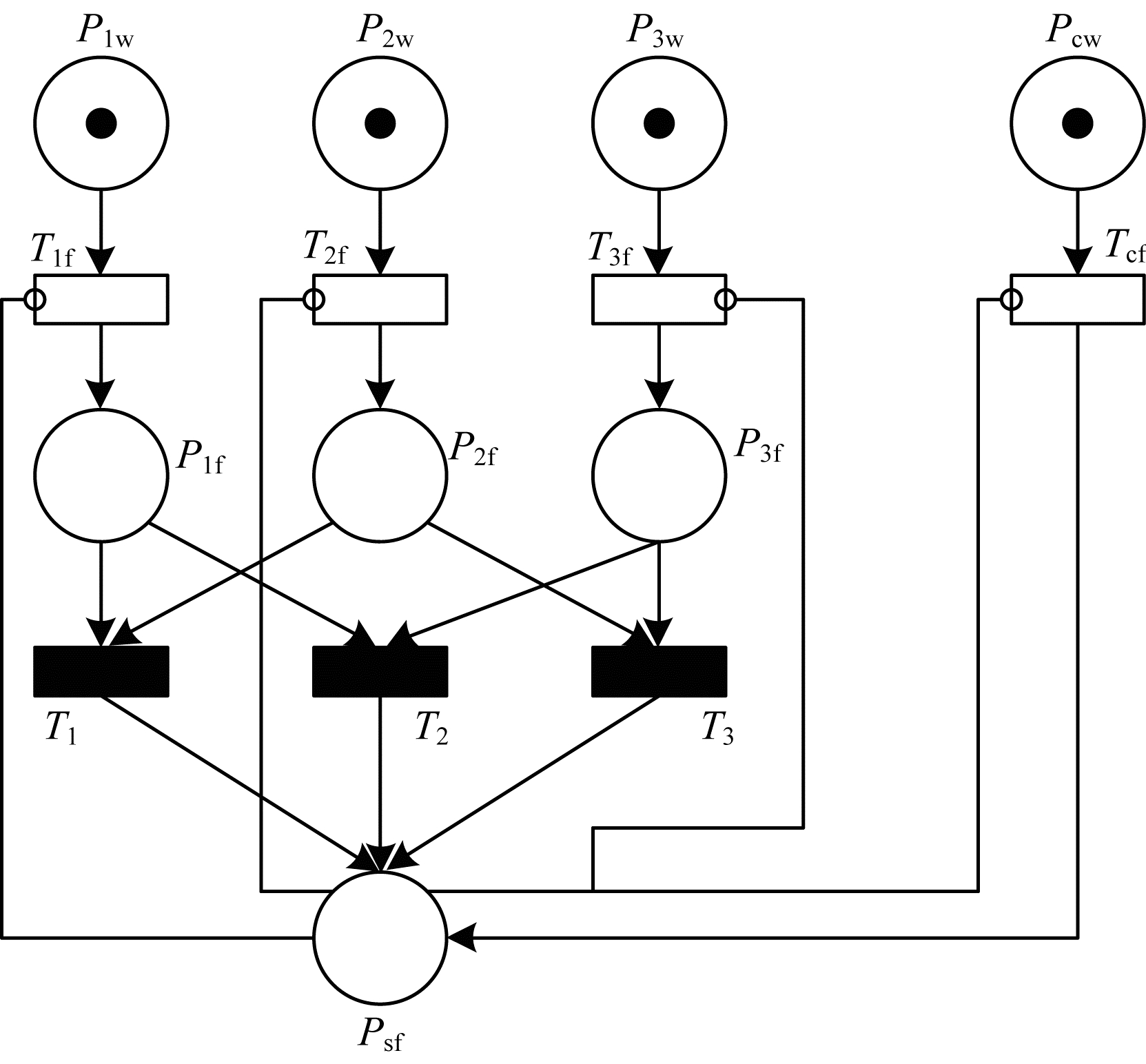
根据系统特征, 2/3(G)表决系统GSPN模型如图 6所示。
|
Download:
|
| 图 6 2/3(G)表决系统的可靠性GSPN模型 | |
在该GSPN模型的初始状态下, 库所P1w、P2w、P3w、Pcw含有token, 分别表示处理器1、处理器2、处理器3和表决单元正常工作。当变迁T1f、T2f、T3f中任意2个点火或Tcf点火时, 都会导致库所Psf中产生token, 表示系统失效。当系统失效时, 抑制弧生效, 禁止相关变迁点火, 防止系统“状态爆炸”。
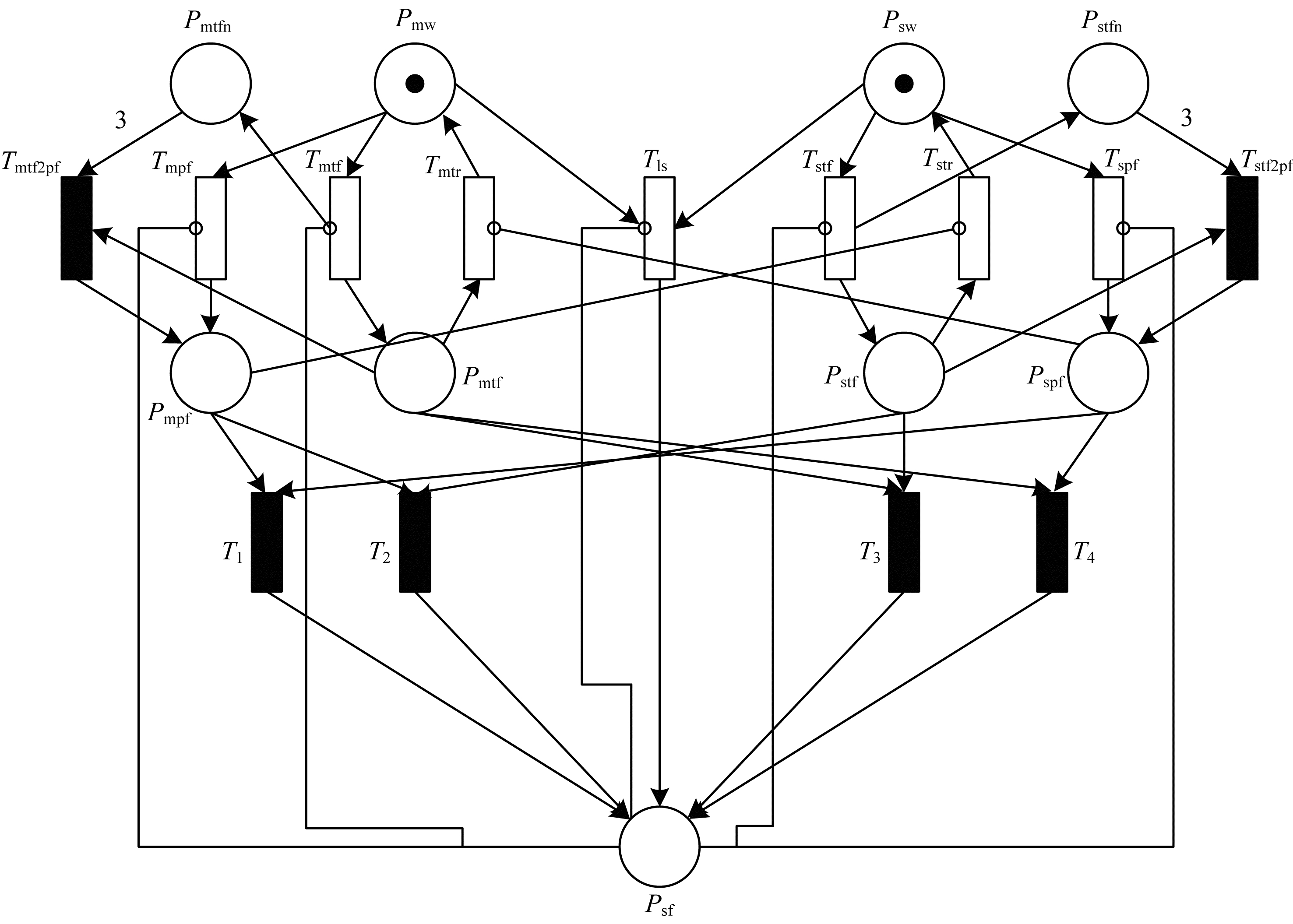
3.2 锁步自监控自修复系统GSPN模型根据锁步自监控系统特征, 可建立系统GSPN模型如图 7所示。
|
Download:
|
| 图 7 锁步自监控处理器的可靠性GSPN模型 | |
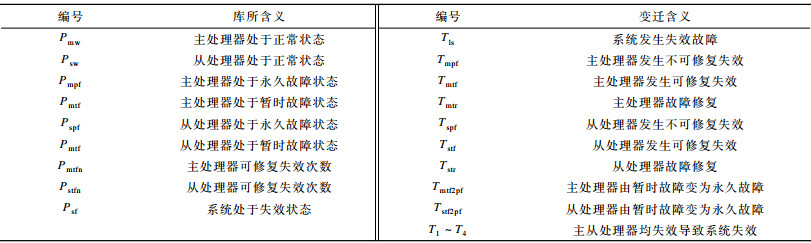
在该GSPN模型中, 使用库所表示系统状态, 如处理器的正常、失效状态。采用变迁表示改变系统状态的事件, 如故障发生、单元修复等。时间变迁中的平均实施速率λ用来表示单元故障率, μ表示维修率。瞬时变迁用来描述系统的控制过程, 如故障转化等。有向弧用于描述系统中状态与事件间的作用关系。系统库所及变迁含义如表 5所示。
|
下载CSV 表 5 系统库所及变迁含义 |
模型中除了有向弧F(Pmtfn, Pmpf)和F(Pstfn, Pspf)的弧权为3外, 其余所有弧权均为1, 这是由于当处理器发生多次可修复失效后, 系统不再认为该处理器可靠, 因此强制其进入故障状态。在波音777飞控系统中, 故障检测单元在检测到一个模块连续3个周期均故障的情况下, 可判定该模块进入永久故障状态[14]。
模型中的抑制弧F(Pmpf, Tstr)、F(Pspf, Tmtr)表示当主处理器或从处理器发生故障时, 另一个处理器自修复功能失效。其他抑制弧表示当系统失效时, 未失效单元不再失效, 防止系统“状态爆炸”。
模型的工作过程为:在初始状态下, 库所Pmw和库所Psw含有token, 表示主从处理器均正常, 系统正常工作。在经过某个随机时间后, 假设主处理器发生不可修复失效, 则变迁Tmpf点火, 库所Pmw中token消失, Pmpf中产生token, 表示主处理器进入永久故障状态, 从处理器信号校验后直接输出, 系统降级使用。此时不论从处理器发生何种失效, 均会导致瞬时变迁T1或T2点火, Psf中产生token, 系统失效。
若主处理器发生可修复失效, 则变迁Tmtf点火, 库所Pmw中token消失, Pmtf和Pmtfn中产生token, 分别表示主处理器处于暂时故障状态和发生可修复失效的次数, 主处理器进入自检修复状态, 从处理器代替主处理器功能。此时, 若主处理器修复成功, 则变迁Tmtr点火, 库所Pmtf中token消失, Pmw中产生token, 表示主处理器状态正常, 系统恢复双机锁步状态。反之, 若从处理器在主处理器修复完成前失效, 则系统中2个处理器均失效, 变迁T3或T4点火, 系统失效。
若系统中任意处理器发生可修复失效的次数超限(该模型中阈值为3), 即库所Pmtfn或Pstfn中的token数达到3个, 则认为该处理器不再可靠, 变迁Tmtf2pf或Tstf2pf点火, 强制该处理器进入永久故障状态。同时, 若两处理器发生失效故障, 则变迁Tls点火, 库所Psf中产生token, 系统失效。
4 GSPN模型分析 4.1 实验环境与参数设置SPNP软件包是由美国Duke大学TRIVEDI教授的研究小组研发的一个可视化且较成熟的GSPN分析求解软件[15]。GSPN模型的重要特性, 如变迁的实施概率、禁止弧和弧权等都可以在该软件中描述, 而且该软件对GSPN模型的状态空间大小没有限制, 使其可以应用于大型复杂系统的模型分析。
在本文建立的GSPN模型中, 所有时间变迁的平均实施速率均服从指数分布, 因此模型同构于一个Markov网络, 可以使用SPNP软件的数字分析方式进行精确分析。设置软件的最大迭代次数为2 000次, 数字精确度为10-6。
本文将对上述模型进行2个实验:实验1通过设置处理器相关的故障维修参数得到系统可靠度指标, 并与冗余表决系统、单处理器系统进行对比。冗余表决系统各元件故障及维修参数如表 6所示, 锁步系统各元件故障和维修参数如表 7所示。实验2在实验1的基础上, 分别改变元件的可修复失效故障率、不可修复故障率和可修复故障容忍值, 并将结果进行对比, 以期获得锁步自监控系统的可靠性设计。

|
下载CSV 表 6 冗余表决系统元件故障参数 |
|
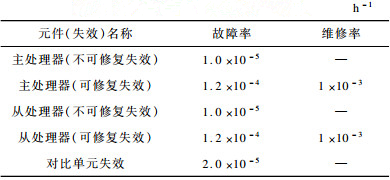
下载CSV 表 7 锁步系统元件故障及维修参数 |
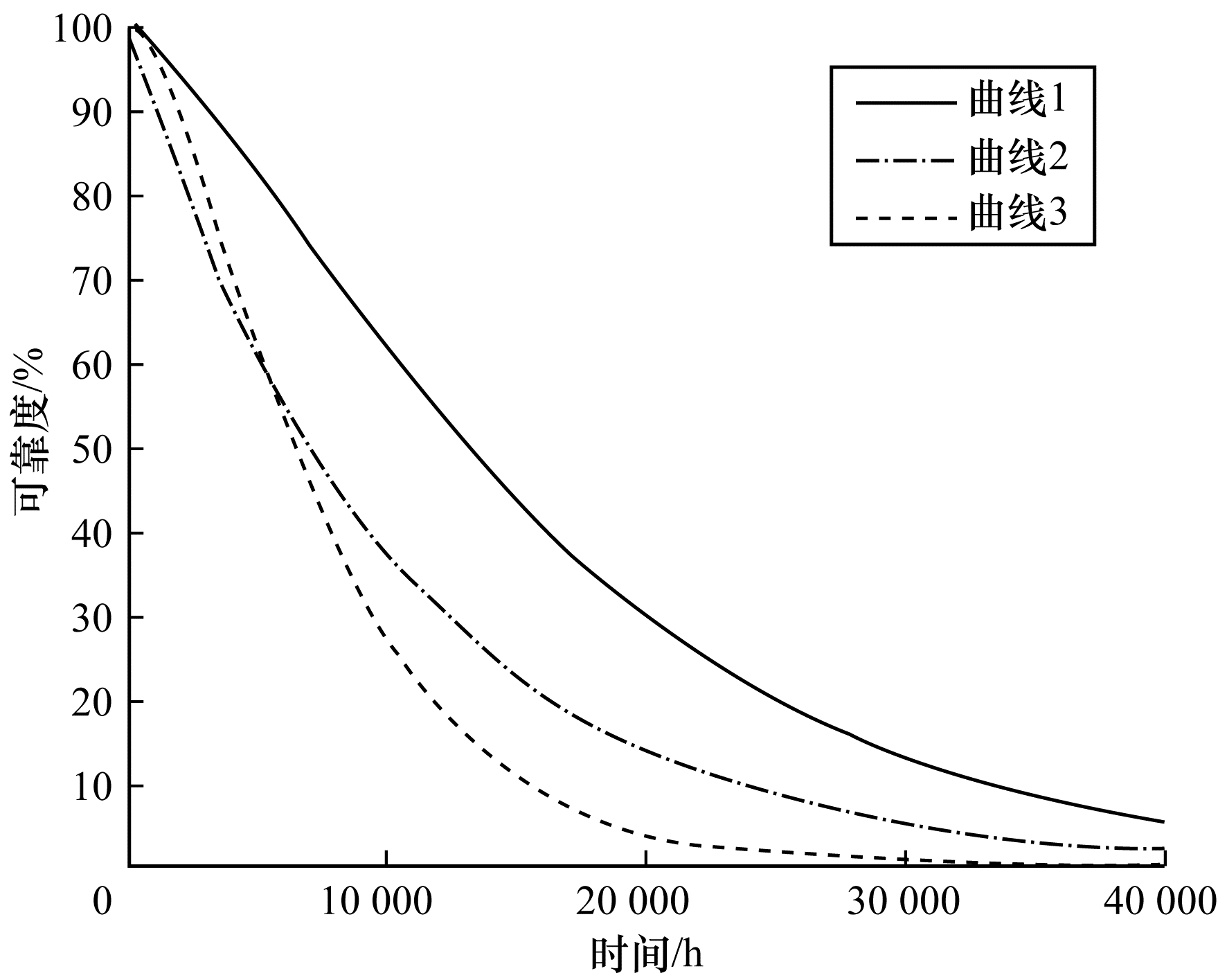
对于实验1的锁步系统, 将GSPN模型中库所Pmw和Psw的初始token值设为1, 时间变迁的参数按表 7进行设置, 弧F(Pmtfn, Pmpf)和F(Pstfn, Pspf)的权重设置为3, 当库所Psf中产生token时, 表示系统失效。分析范围为0 h~40 000 h, 精度为100 h, 模型可靠度函数R(t)如图 8所示。
|
Download:
|
| 图 8 实验1模型可靠度对比结果 | |
在图 8中, 曲线1表示上文建立的锁步系统可靠度函数, 曲线2表示单处理器系统可靠度函数(处理器失效率λ=1.2×10-4/h), 曲线3表示2/3(G)表决系统可靠度函数, 系统参数见表 7。
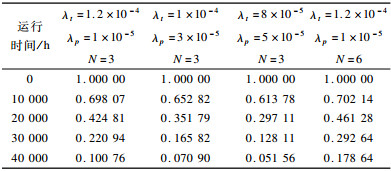
对于实验2, 在实验1的基础上, 分别改变锁步系统的处理器可修复故障率λt、不可修复故障率λp和可修复故障阈值N的参数值, 其余条件不变。系统可靠度与运行时间的关系如表 8所示, 对应的模型可靠度函数R(t)如图 9所示。
|
下载CSV 表 8 不同参数下系统可靠度与时间的关系 |
|
Download:
|
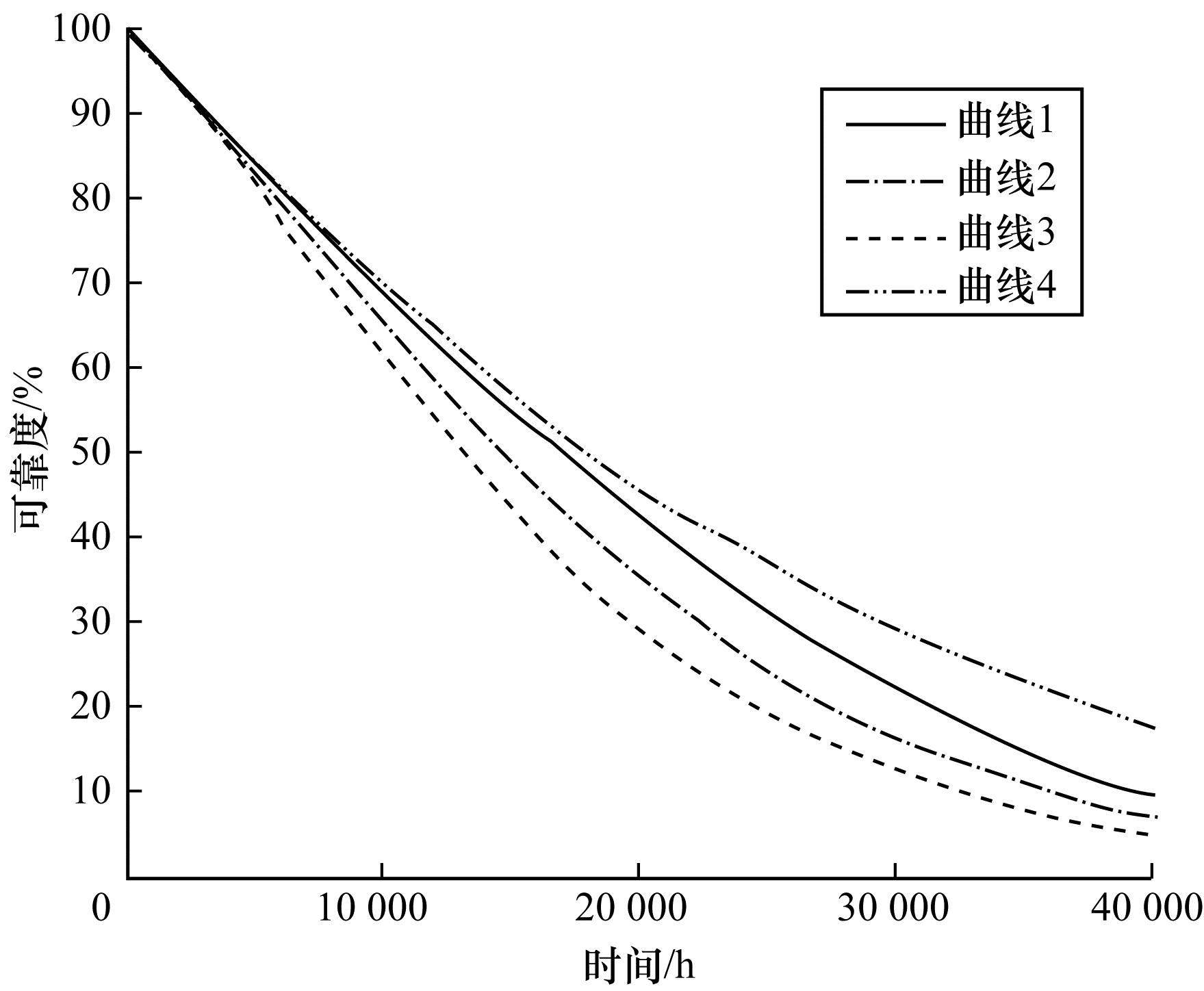
| 图 9 实验2模型可靠度对比结果 | |
在图 9中, 曲线1~曲线4分别表示表 8第1行中第2列~第5列参数对应的系统可靠度函数R(t)。
综合实验1和实验2可以得到如下结论:
1) 锁步自监控处理器系统(称为锁步系统)的可靠度随时间增加逐渐减小, 最终衰减至0。从图 8可以看出, 在单处理器失效率相同的情况下(λ=1.2×10-4/h), 锁步系统的可靠度始终高于单处理器和2/3(G)表决系统, 在系统运行至10 000 h时, 锁步系统的可靠度比单处理器和2/3(G)表决系统分别高出136%和73%, 证明采用锁步自监控及故障回滚技术可以显著提高系统可靠性, 并有效增加系统平均无故障时间。
2) 增加处理器可恢复失效阈值可以提高系统可靠性。这种变化在系统运行初期并不显著, 是由于初期处理器的失效次数难以达到设定阈值, 而阈值改变带来的影响在系统运行至30 000 h左右比较明显, 因此在可接受的范围内增加该阈值, 可以在系统运行中后期使可靠性明显提高。
3) 在处理器失效率相同的情况下, 不可修复失效的概率越高, 系统可靠性越低。在该锁步系统中, 处理器不可修复失效主要是由校验单元的失效产生, 由于该单元相当于串联接入系统, 对可靠性的影响较大, 因此在其他条件相同的情况下, 提高处理器校验单元的可靠性有助于系统可靠性的提升。
5 结束语本文以锁步处理器系统为研究对象, 以广义随机Petri网为建模工具, 建立锁步自监控处理器系统的可靠性模型, 有效描述了该系统的故障行为和状态迁移。在建立模型的基础上, 通过SPNP软件描绘了系统可靠度随时间的变化曲线, 与典型的可靠性模型进行对比, 并分析系统各参数变化对整体系统可靠度的影响。实验数据验证了模型及分析方法的有效性。下一步将研究锁步双核同时失效的情况, 增加异构锁步的校验, 提高锁步故障自检能力。
| [1] |
付爱英, 周晶晶. 基于Lockstep的容错技术的研究[J]. 科技广场, 2012(7): 70-73. DOI:10.3969/j.issn.1671-4792.2012.07.019 (  0) 0)
|
| [2] |
YEH Y C B.Triple-triple redundant 777 primary flight computer[C]//Proccedings of Aerospace Applications Conference.Washington D.C., USA: IEEE Press, 1996: 293-307. https://www.researchgate.net/publication/3626737_Triple-triple_redundant_777_primary_flight_computer
(  0) 0)
|
| [3] |
FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J]. Journal of Guidance Control and Dynamics, 2009, 32(2): 401-416. (  0) 0)
|
| [4] |
DE OLIVEIRA A B, TAMBARA L A, KASTENSMIDT F L.Applying lockstep in dual-core ARM cortex-a9 to mitigate radiation-induced soft errors[C]//Proceedings of the 8th Latin American Symposium on Circuits and Systems.Washington D.C., USA: IEEE Press, 2017: 1-4.
(  0) 0)
|
| [5] |
REORDA M S, VIOLANTE M, MEINHARDT C, et al.A low-cost SEE mitigation solution for soft-processors embedded in systems on pogrammable chips[C]//Proceedings of Conference on Design, Automation and Test in Europe.New York, USA: ACM Press, 2009: 352-357.
(  0) 0)
|
| [6] |
HERNANDEZ C, ABELLA J. Timely error detection for effective recovery in light-lockstep automotive systems[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2015, 34(11): 1718-1729. DOI:10.1109/TCAD.2015.2434958 (  0) 0)
|
| [7] |
郭鹏. 基于Petri网的飞机复杂系统可靠性分析方法研究[J]. 航空工程进展, 2016, 7(2): 174-180. (  0) 0)
|
| [8] |
DEVILLERS R, VALMARI A.Application and theory of petri nets and concurrency[C]//Proceedings of International Conference on Applications and Theory of Petri Nets and Concurrency.Berlin, Germany: Springer, 2016: 79-85.
(  0) 0)
|
| [9] |
SONDON S, MANDOLESI P, MASSON F, et al.A dual core low power microcontroller with open MSP430 architecture for high reliability lockstep applications using a 180 nm high voltage technology node[C]//Proceedings of the 4th Latin American Symposium on Circuits and Systems.Washington D.C., USA: IEEE Press, 2013: 1-4.
(  0) 0)
|
| [10] |
ABATE F, STERPONE L, LISBOA C A, et al. New techniques for improving the performance of the lockstep architecture for SEEs mitigation in FPGA embedded processors[J]. IEEE Transactions on Nuclear Science, 2009, 56(4): 1992-2000. DOI:10.1109/TNS.2009.2013237 (  0) 0)
|
| [11] |
陈克伟, 董利霞, 李丹. 基于GSPN的网络系统动态可靠性建模方法[J]. 计算机测量与控制, 2012, 20(4): 239-242. (  0) 0)
|
| [12] |
SHIN K G, HAGBAE K. A time redundancy approach to TMR failures using fault-state likelihoods[J]. IEEE Transactions on Computer, 1994, 43(10): 1151-1162. DOI:10.1109/12.324541 (  0) 0)
|
| [13] |
KRISHNAN R, SOMASUNDARAM S. Reliability analysis of repairable consecutive-k-out-of-n:G systems with sensor and repairmen[J]. International Journal of Quality and Reliability Management, 2013, 28(8): 894-908. (  0) 0)
|
| [14] |
MILLER F P, VANDOME A F, MCBREWSTER J, et al. Boeing 777[J]. Flying, 2010, 345(2): 414-418. (  0) 0)
|
| [15] |
TRIVEDI K S, CIARDO I G.SPNP: stochastic petri net package-version 5.0[C]//Proceedings of the 3rd International Workshop on Petri Nets and Performance Models.Washington D.C., USA: IEEE Press, 2007: 142-151.
(  0) 0)
|
 2019, Vol. 45
2019, Vol. 45







