卷积神经网络(Convolutional Neural Networks, CNN)主要用于计算机视觉领域。近年来, CNN的性能大幅提升, CNN模型的分类准确率从84.7%增长至96.5%。2016年, 在ImageNet比赛的图像目标检测任务中, 前5名的队伍大多采用ResNet/Inception网络, 并融合Faster R-CNN框架[1]。自动驾驶公司Momenta研发团队提出SE(Squeeze and Excitation)架构[2], 其识别错误率为2.3%。SE架构在引入较少的计算量和参数量的情况下, 可大幅提升现有CNN模型的性能, 从而将人工应用于更广泛的领域, 例如自动驾驶汽车[3]、智能手机[4]和无人机[5]等。
然而, CNN的计算复杂度较高, 模型参数量较多。例如, AlexNet需要1.4 GOPS来处理单个224像素×224像素的图像, 并且其模型参数所占容量达到61 MB, 这对于计算及存储资源有限的移动端设备来讲是难以达到的。CNN的压缩是有效的解决途径之一, 以自动驾驶为例, 特斯拉会周期性地更新用户汽车中的模型, 对模型进行压缩会使频繁更新的可行性更高, 提高更新速度, 改善用户体验。同时, 模型压缩有利于提升推理速度, 从而保证自动驾驶的实时性推理。此外, 移动设备受到电池电量的限制, 运行大的神经网络模型需要足够的带宽和能量。以现场可编程门阵列(Field Programmable Gate Array, FPGA)为例, 其片上存储约为10 MB, 放不下完整的网络权值。如果模型压缩后能存储到片上静态随机存储器上, 其消耗的能量比从片外动态随机存储器存取数据的耗能少。因此, 神经网络的压缩非常重要。
目前已有很多神经网络的压缩方法。文献[6]基于神经网络的线性结构, 通过低秩近似来减少参数量。文献[7]利用奇异值分解来减少权重数量。文献[8]使用哈希函数将连接权重随机分组到哈希表中以减少参数的位宽。文献[9]使用L2最小误差来量化神经网络。文献[10-11]通过剪枝、量化以及Huffman压缩实现对神经网络的深度压缩。文献[12]将网络删减、参数共享相结合来对CNN进行压缩。文献[13]采用动态定点量化方法缩短权重数据的位宽, 以压缩CNN。网络精馏、网络分解等方法也能实现对神经网络的压缩[14]。
针对神经网络模型在权值量化后个别元素组成的子串重复出现的情况, 本文基于文献[11]的剪枝和量化方法, 利用LZW(Lempel-Ziv-Welch)编码算法, 以单个字符的ASCII码为中间承接变量, 把重复子串转化为简短信息, 以达到压缩模型容量的目的。
1 压缩方法及过程描述神经网络一般包含较多参数[15], 造成计算以及存储资源的浪费。对于参数冗余的情况, CNN模型可从直接降低模型精度和直接进行剪枝2个角度压缩模型容量。
1.1 CNN模型容量压缩策略直接降低模型精度可压缩CNN模型的容量, 在caffe[16]深度学习框架中, CNN模型的参数以32位浮点的方式进行存储和计算, 若能降低单个权值的有效位数, 就可以压缩模型容量。通过分析发现, CNN中卷积层以及全连接层的参数大多介于-1~1之间, 位于0值周围。LeNet-5网络模型各层权值的范围如表 1所示。
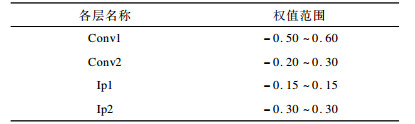
|
下载CSV 表 1 LeNet-5权值分布情况 |
LeNet-5模型的权值介于-0.50~0.60之间, 有效位在小数位上, 为此可以把定点数(不包含符号位)全部用于存储小数部分, 直接把小数点放置在有效位的前一位。如简化为8位定点, 就用8 bit来存储32位浮点对应的前8位小数。由于神经网络一般为深层网络, 各层的参数量不同, 扮演的角色以及重要程度也不同。在降低精度时可以分层考虑, 例如把卷积层参数转化为8位, 把全连接层参数转化为10位。
由于最初的输入特征图是浮点形式的, 计算得到的输出结果也是浮点形式的, 不能直接把连接权重转换为定点形式, 因此本文综合考虑浮点数在计算机中的存储格式以及定点数的意义, 提出将伪代码1(C++形式)的浮点转化为“伪定点”的方式。该“伪定点”具有浮点数的形式, 但是可以表达定点数的意义。
32位浮点在计算机中存储的最高位为符号位, 其后8位为经过偏差修正的指数位, 剩下的23位为小数位。伪代码1实现了转8位定点, 通过tmp=*(int*)v语句获取浮点数的32位二进制形式。在将浮点数的二进制形式还原为具体小数时, 32位浮点数会在小数点前添1, 使小数位变为24位。若指数偏差值(exp)为-8, 则小数点向左移动8位, 即小数点后有7位是0, 第8位是1。如果把32位浮点的23位小数部分全部置0, 就可以达到和定点数相同的意义。若exp大于-8, 则小数点移动后前8位小数不会全部为0, 通过tmp=tmp & (0xffffffff << (23-exp-8))语句截取前8位小数而丢弃后面的小数位, 使8位定点数只包含小数点后8位小数的含义。若exp小于-8, 该代码的浮点转定点未能完全实现, 这是因为32位浮点数的小数点在移位前, 会在小数点前自动添1且添加的1无法消除, 不能变为0。32位浮点转8位定点的具体过程如算法1所示。
算法1 32位浮点转8位定点算法
#define EXP_BIT 0x7f800000
int main()
{
float *v=& va; //va为待转化32位浮点数
tmp=*(int*)v;
exp=((tmp & EXP_BIT) >> 23)-127;
if(exp<=-8)
{
tmp=tmp & (0xffffffff << 23);
}
else
{
tmp=tmp & (0xffffffff << (23-exp-8));
}
}
通过把不重要的权值直接置0进行剪枝也可以压缩模型容量, 重要权值与不重要权值主要根据其绝对值来进行区分[17]。在修剪连接权值后, 神经网络中的某些神经元可能没有输入或者输出, 这些神经元就失去了存在的意义, 也应该减掉。由于神经网络在训练过程中要进行反向传播和梯度计算, 某些理应被减掉的神经元由于没有输入或者输出, 反向传播计算梯度时为0, 不会对其他神经元造成影响, 相当于从神经网络中剔除, 因此不需要对这些神经元进行人为剪枝。此外, 剪枝过程不是一次性完成的, 必须重新训练且剪枝比例(阈值)要逐渐加大, 以保证剪枝效果。
1.2 权值k-means聚类量化在神经网络模型压缩模型容量后, 结合k-means算法进行聚类量化。首先要设置量化个数, 确定量化中心。量化中心的初始化方法有很多, 其中线性平均初始化的效果较好[11]。然后采用k-means聚类, 使权值聚集在最近的初始量化中心, 把聚类簇中心值作为新的量化中心, 如此迭代直到聚类中心不能更新或者小于某个范围, 具体过程如算法2(C++形式)所示。
算法2 权值k-means聚类量化算法
//检测是否达到聚类要求
if (fabs(mPreD-mCurD) / mPreD < 0.001) break;
//给每个权值选择最近的聚类中心
for (int n=0;n < nWeights; n++) //nWeights为进行//聚类的权值数目
{
for (int k=0;k < nCluster; k++)//nCluster为聚类中//心数目
{
distance=fabs(cWeights[n]-cCentro[k]); //cWeights[n]//为权值, cCentro[k]为聚类中心值
if (distance < mindistance)
mindistance=distance;
cLabel[n]=k; //cLabel[n]为权值聚类后标签
}
cDistance[n]=mindistance; //cDistance[n]为权值到聚//类中心的距离
}
//累加聚类后权值到聚类中心的总距离
for (int n=0;n < nWeights; n++)
{
mCurD=mCurD + cDistance[n];
}
//聚类中心更新
for (int n=0;n < nWeights; n++)
{
ptrC[cLabel[n]]+=cWeights[n];
ptrS[cLabel[n]]+=1;
}
for (int k=0;k < nCluster; k++)
{
cCentro[k]=ptrC[k];
cClusterSize[k]==ptrS[k];
cCentro[k]/=cClusterSize[k]; //得出新的聚类中心
}
在聚类量化后增加一个查找表, 神经网络的权值用聚类中心值代替, 可减少每个权值的有效位数。例如, 权值量化到32个区间, 则量化结果可以用5 bit表示, 实现进一步压缩。在量化后, 前向计算的每个权值用对应的聚类中心代替, 通过后向传播计算每个类内的权值梯度, 聚类中心的更新同文献[11]。然而, 聚类中心的更新存在以下问题:
1) 对于剪枝后的模型, 如果剪枝足够充分, 0值附近是没有权值的, 则在k-means的线性平均初始化后, 0值周围的聚类中心存在没有权值聚集的情况, 该聚类中心也不会更新。
2) 同问题1)的情形类似, 极大值或极小值周围的权值很少, 有可能导致某些聚类中心不能进行权值聚集和更新。具体情况如图 1所示。
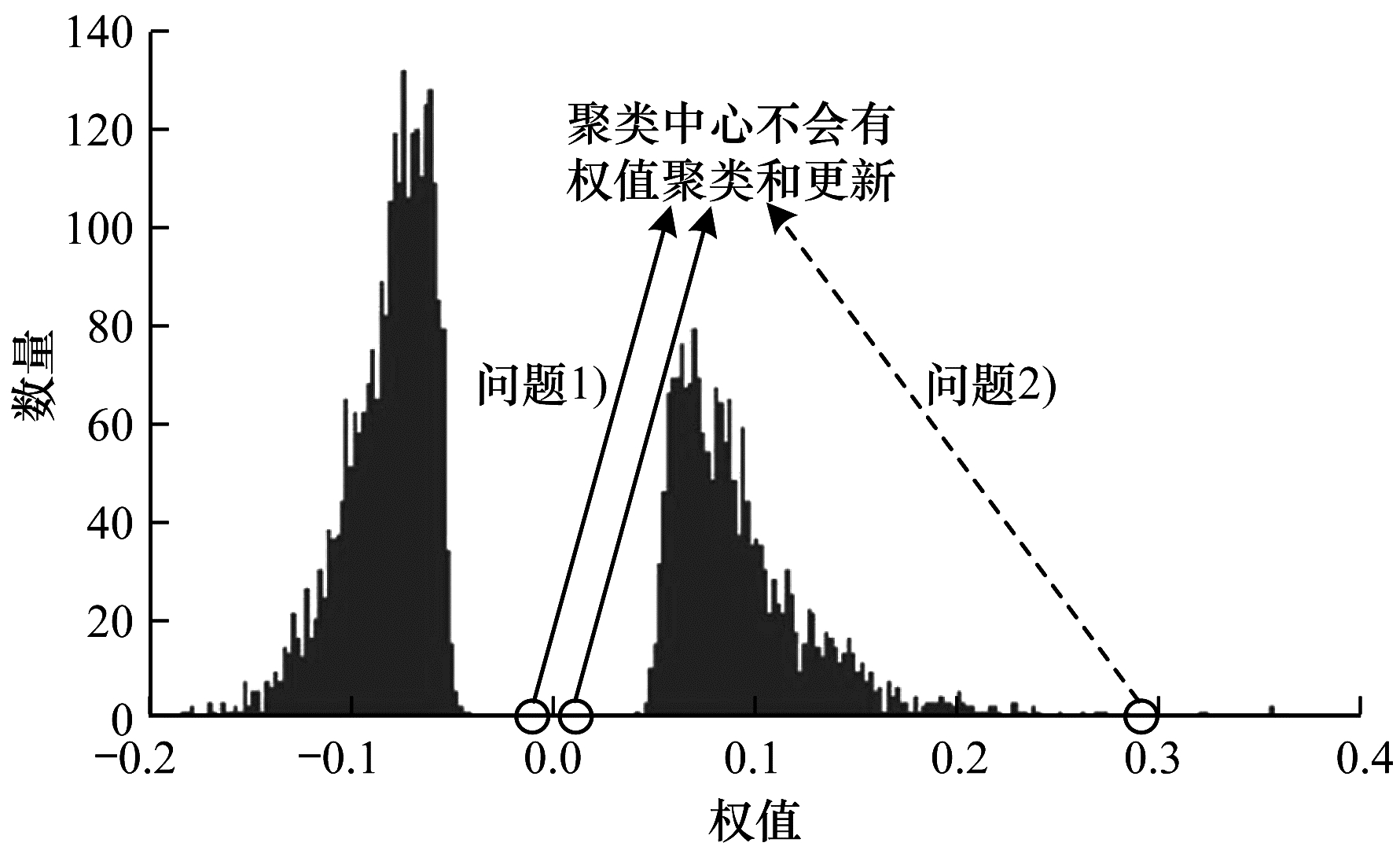
|
Download:
|
| 图 1 LeNet-5的Conv2层权值分布及聚类情况 | |
针对上述问题, 可以在聚类完成后剔除这些没有权值聚集的聚类中心, 进一步减少聚类中心的数量。
1.3 基于LZW编码的压缩方法LZW编码算法的基本过程如下:提取待压缩文件数据中的不同字符, 并基于这些字符创建一个初始编码表, 即字典。将每个新出现的字符串添加到编码表中, 用一个数字来表示相应的字符串, 压缩文件只存数字, 如果某一字符串再次出现在后续待压缩序列中, 可用相应的数字来代替。随着压缩过程的进行, 动态构建编码表并逐渐增大。在解码时, 从已编码的数据中还原编码表, 待解压缩完成后, 将其丢弃。与量化、Huffman等压缩方法相比, 压缩文件中重复子串出现的次数越多, LZW编码压缩的效果就越好。
经分析, AlexNet、Vgg、Googlennet、LeNet-5等网络模型剪枝后的大部分值为0, 量化时只对非0值进行操作。0值直接赋予一个标签号(例如-1), 则量化结果会有大量由-1组成的子串出现, 符合LZW的特点。根据文献[11], 将LeNet-5卷积层和全连接层的非0值分别量化为8 bit(256个量化值)和5 bit(32个量化值), 量化后卷积层权重的标签号为-1~255共257个, 全连接层权重标签号为-1~31共33个。LZW编码初始化的编码表一般只定义单个字符, 比如数字0~9、字母a~z, 采用单字节编码系统ASCII码的方式, 以0~255来表示单个字符。为得到最佳压缩效果, 本文在初始化编码表之前加入新的映射, 以全连接层的33个标签号为例, 把标签号加上某个数后作为ASCII码使用。例如, -1映射为单个字符@, 10映射为单个字符K, 25映射为Z, 则原数据-1/-1/10/25/10会映射为@@KZK组成的字符串, 其长度缩短。然后, 以映射后的33个字符建立初始编码表。LZW压缩编码过程如算法3(python形式)所示, 解压缩过程与此相反, 不再赘述。
算法3 LZW压缩编码算法
def compress():
dict_size=33
dictionary=dict((chr(int(i)+65), int(i)) for i in xrange(dict_size))
w=""
result=[]
s=""
f=open("量化后的权值文件")//每行只有一个权值//标签
for line in f:
c=line.strip(‘\n’)
s=s + str(chr(int(c)+65))
for c in s:
wc=w + c
if wc in dictionary:
w=wc
else:
result.append(dictionary[w])
dictionary[wc]=dict_size
dict_size +=1
w=c
if w:
result.append(dictionary[w])
return result
本文LZW编码压缩方法相对于Huffman压缩方法[11]最主要的特点如下:Huffman方法作用于非0值, 而这些非0值的存储与计算都采用稀疏矩阵的格式, 导致计算过程中寻址过程复杂, 耗时较长; LZW编码方法作用于含0值的全体权值, 不需要稀疏矩阵, 因此其计算速度更快。
2 实验结果与分析 2.1 2种容量压缩策略的结果对比为了对比2种CNN模型容量压缩策略的效果, 本文首先把浮点数转换为各种长度的定点数并测试模型的准确率。本文实验在ubuntu16.04操作系统下进行, 基于caffe(源码为C++语言)深度学习框架, 具体修改位于src/caffe/layers/文件夹下的conv_layer.cpp(卷积层)和inner_product_layer.cpp(全连接层)的2个.cpp文件, 在ComputeBlobMask函数中加入算法1所示的32位浮点转定点片段。本文浮点转定点的操作分层进行, 转换并训练微调完一层后再继续下一层的转换操作。
表 2所示为浮点转为各种长度的定点数后的模型准确率。在表 2中, 准确率项有2个数值, 括号前的数值表示转化后不经过重新训练的准确率, 括号内的数值表示经过训练后所能达到的准确率, 下同。从表 2可以看出, 在定点位数下降到8位时准确率基本维持不变, 当下降为7位时无论是否进行下一步训练, 全连接层的准确率都明显下降, 尤其在转换Ip1后, 下降幅度较大。对于卷积层, 在定点位数为5时的准确率明显下降, 说明卷积层和全连接层对于精度降低的敏感程度不同。为此, 本文将全连接层的位数设为8, 对卷积层进行不同位数的定点转换, 然而效果并不好, 具体结果如表 3所示。因此, 对于浮点转定点这一方法, 各层权值最小可转化为8位定点。
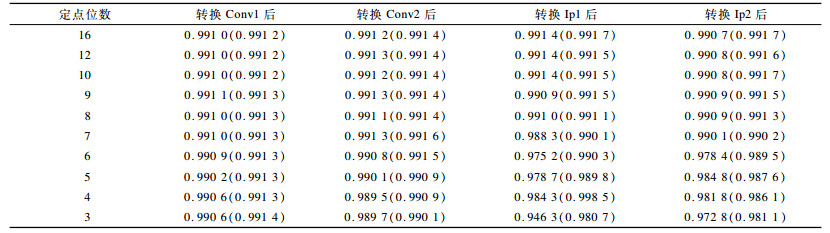
|
下载CSV 表 2 浮点转定点后的模型准确率对比 |

|
下载CSV 表 3 卷积层量化为不同精度时的模型准确率对比 |
由文献[11]可知, 对于直接剪枝, LeNet-5的权值数量可以减少90%以上而不降低精度。本文复现了文献[11]的实验过程, 权值数量能减少90.5%而不降低准确率。与直接减少精度的方法相比, 直接剪枝的方法小数位能减少到8位, 加上符号位一共9位, 压缩比小于4, 因此, 剪枝方式的压缩比更高。
本文也尝试把2种方法结合起来使用, 但其效果较差。例如, 以一定的剪枝比例剪枝后模型没有精度衰减, 然后把权值转化为20位定点数时, 模型的准确率仍在0.99以下。究其原因, 剪枝把小于一定阈值的权值置为0, 本文的浮点转定点方法会适当缩小权值, 其原因为:剪枝舍弃了较小的权值, 把部分阈值较小的权值直接裁剪掉; 浮点转定点抛弃了权值的尾巴部分而保留了主干部分, 对每个权值都适当修剪。两者都减少了模型容量, 舍弃了神经网络连接权值中的细小枝节, 结合起来会因为抛弃太多内容而使准确率下降。
2.2 k-means聚类量化结果在量化部分, 文献[11]和本文复现的实验都能在没有精度损失的情况下把LeNet-5模型的卷积层量化为8位, 而把全连接层量化为5位。另外, 本文在浮点转定点后加入量化过程也能达到卷积层8位和全连接层5位的结果。总体来讲, 无论是剪枝后的模型还是转定点后的模型, 量化后的准确率基本不变。但是, 采用k-means聚类剪枝后的模型在进行线性初始化后, 部分聚类中心没有权值聚类到其周围, 如图 2所示。在图 2中, Ip1的中间4个聚类中心没有权值聚集, 可以丢弃。
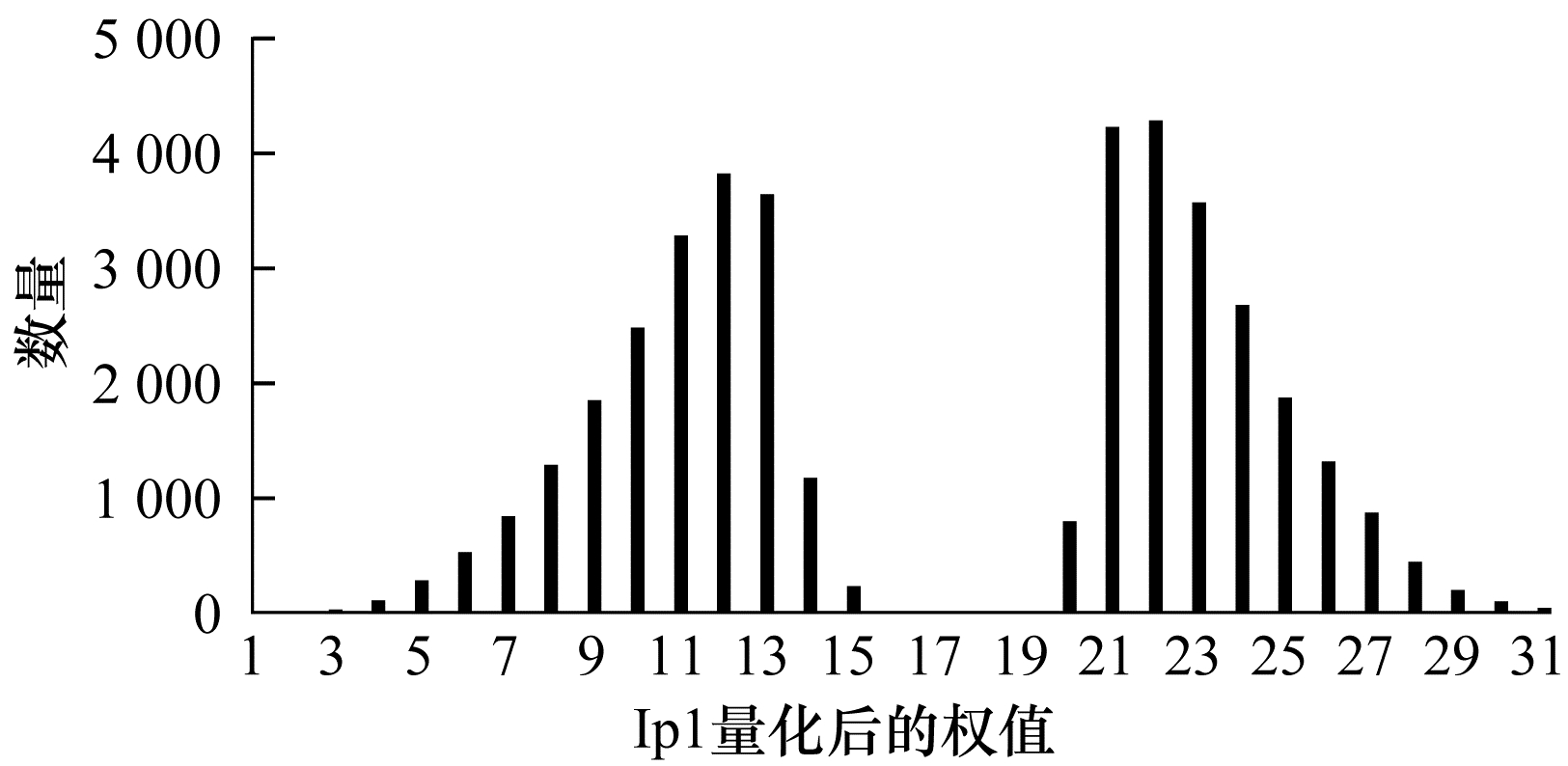
|
Download:
|
| 图 2 LeNet-5网络Ip1层量化后的权重分布 | |
在转定点并量化之后, 由于没有大量子串重复出现, LZW编码的效果不理想。直接对剪枝并量化后的非零值进行LZW编码效果也不好, 在具体实验过程中, Ip1层剪枝量化后的非0值大约有40 000个, 每个数值占5 bit, 经过LZW编码后长度为14 685, 但编码结果中的最大值为14 477, 需要16 bit, LZW编码的压缩作用很小。在对剪枝量化后的整体进行编码时, 压缩效果较明显, 具体情况如表 4所示。

|
下载CSV 表 4 LeNet-5网络各层编码前后的结果对比 |
由表 4可以看出, 除了Conv1外, 其他层都压缩为原来的一半以下, 效果较明显。总的压缩比依据编码前后的总位数来计算, 计算过程如下:
| $ \frac{{4\ 000 + 200\ 000 + 2\ 000\ 000 + 25\ 000}}{{4\ 120 + 71\ 331 + 456\ 060 + 11\ 682}} = 4.103\ 5 $ |
即可以压缩为原来的24.37%。文献[11]只对剪枝后的非0值进行量化, 并以紧凑的存储方式CSC(Compressed Sparse Column)或CSR(Compressed Sparse Row)来存储稀疏网络, 本文将LZW直接作用于全部参数, 相比之下本文方法少了一级寻址过程, 计算速度更快。剪枝加量化可以压缩为:
| $ \frac{{(0.25 + 25 + 400 + 5) \times 32}}{{(0.25 + 25) \times 8 + (400 + 5) \times 5}} = 6.18 $ |
在剪枝、量化、LZW编码后, 最终压缩比可以达到6.18×4.10=25.338, 略小于文献[11]所能达到的39。但文献[11]的Huffman编码存储稀疏权值的索引以及计算时寻址的过程较繁琐, 本文直接对全体权值进行操作, 过程简单且速度更快, 是压缩比和计算速度的折中选择。
3 结束语本文提出基于LZW编码的CNN压缩方法, 对剪枝、浮点转定点这2种模型容量压缩策略进行分析, 采用k-means聚类量化, 并引入LZW编码方式。实验结果表明, 在剪枝、量化、LZW编码后, 该方法的压缩比可达25.338, 且计算速度较快。下一步将把该方法应用于AlexNet、Vgg等大型网络中, 验证其压缩效果。
| [1] |
深度学习大讲堂.ILSVRC2016目标检测任务回顾: 图像目标检测[EB/OL].[2018-07-01].https://www.leiphone.com/news/201701/u3D5QnJbS9khm0VT.html.
(  0) 0)
|
| [2] |
HU Jie, LI Shen, SUN Gang.Squeeze-and-excitation networks[EB/OL].[2018-07-01].https://arxiv.org/pdf/1709.01507.pdf.
(  0) 0)
|
| [3] |
BOJARSKI M, TESTA D D, DWORAKOWSKI D, et al.End to end learning for self-driving cars[EB/OL].[2018-07-01].https://arxiv.org/pdf/1604.07316.pdf.
(  0) 0)
|
| [4] |
FANG Shihau, FEI Yuxaing, XU Zhezhuang, et al. Learning transportation modes from smartphone sensors based on deep neural network[J]. IEEE Sensors Journal, 2017, 17(18): 6111-6118. DOI:10.1109/JSEN.2017.2737825 (  0) 0)
|
| [5] |
GANDHI D, PINTO L, GUPTA A.Learning to fly by crashing[C]//Proceedings of 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems.Washington D.C., USA: IEEE Press, 2017: 3948-3955.
(  0) 0)
|
| [6] |
DENTON E, ZAREMBA W, BRUNA J, et al.Exploiting linear structure within convolutional networks for efficient evaluation[C]//Proceedings of International Conference on Neural Information Processing Systems.Cambridge, USA: MIT Press 2014: 1269-1277.
(  0) 0)
|
| [7] |
NOVIKOV A, PODOPRIKHIN D, OSOKIN A, et al.Tensorizing neural networks[EB/OL].[2018-07-01].https://arxiv.org/pdf/1509.06569.pdf.
(  0) 0)
|
| [8] |
CHEN Wenlin, WILSON J T, TYREE S, et al.Compressing neural networks with the hashing trick[EB/OL].[2018-07-01].https://arxiv.org/pdf/1504.04788.pdf.
(  0) 0)
|
| [9] |
ANWAR S, HWANG K, SUNG Wonyong.Fixed point optimization of deep convolutional neural networks for object recognition[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing.Washington D.C., USA: IEEE Press, 2015: 1131-1135.
(  0) 0)
|
| [10] |
HAN Song.Efficient Methods and Hardware for Deep Learning[D].San Francisco, USA: Stanford University, 2017.
(  0) 0)
|
| [11] |
HAN Song, MAO Huizi, DALLY W J.Deep compression: compressing deep neural networks with pruning, trained quantization and huffman coding[EB/OL].[2018-07-01].https://arxiv.org/pdf/1510.00149.pdf.
(  0) 0)
|
| [12] |
韩云飞, 蒋同海, 马玉鹏, 等. 深度神经网络的压缩研究[J]. 计算机应用研究, 2018, 35(10): 2894-2897. DOI:10.3969/j.issn.1001-3695.2018.10.003 (  0) 0)
|
| [13] |
蔡瑞初, 钟椿荣, 余洋, 等. 面向"边缘"应用的卷积神经网络量化与压缩方法[J]. 计算机应用, 2018, 39(9): 2449-2454. (  0) 0)
|
| [14] |
雷杰, 高鑫, 宋杰, 等. 深度网络模型压缩综述[J]. 软件学报, 2018, 29(2): 251-266. (  0) 0)
|
| [15] |
DENIL M, SHAKIBI B, DINH L, et al.Predicting parameters in deep learning[C]//Proceedings of the 26th International Conference on Neural Information Processing Systems.New York, USA: ACM Press, 2013: 2148-2156.
(  0) 0)
|
| [16] |
JIA Yangping, SHELHAMER E, DONAHUE J, et al.Caffe: convolutional architecture for fast feature embedding[C]//Proceedings of ACM International Conference on Multimedia.New York, USA: ACM Press, 2014: 675-678.
(  0) 0)
|
| [17] |
HAN Song, JEFF P, JOHN T, et al.Learning both weights and connections for efficient neural networks[C]//Proceedings of Annual Conference on Neural Information Processing Systems.Cambridge, USA: MIT Press, 2015: 1135-1143.
(  0) 0)
|
 2019, Vol. 45
2019, Vol. 45

