2. 北京联合大学 机器人学院, 北京 100027
2. College of Robotics, Beijing Union University, Beijing 100027, China
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种全天候、全天时的高分辨率微波遥感成像雷达, 广泛应用于地球遥感、海洋研究、资源勘探和灾情预报等领域[1]。近几年由于无人机技术的快速发展, 机载SAR成为测绘困难地区实现全天候、全天时快速成像的主要遥感手段[2-4]。然而, SAR采集的原始数据量相当庞大, 若将数据直接传输再由主机端进行处理, 则对于设备的传输速度要求过高, 因此机载SAR的实时处理至关重要[5-6]。同时, 由于机载SAR计算资源有限, 分析过程可能需要大量时间, 因此降低了无人机对外界环境的响应能力[7]。
为权衡无人机的性能和功耗问题, 对嵌入式机载设备提出了更高要求, 虽然利用专用芯片、现场可编程门阵列(Field Programmable Gate Array, FPGA)、数字信号处理(Digital Signal Processing, DSP)等专用硬件的性能优化方案具有较大优势, 但研发成本也很高。通过移动ARM GPU对通用计算进行加速是近几年在嵌入式平台新兴的优化方案, 能够降低额外的硬件成本与功耗, 且通用性和可移植性强[8], 此外, 在并行加速计算中具有较大的性能优势, 可提供高于CPU数十倍甚至数百倍的计算性能[9]。但由于嵌入式ARM GPU硬件资源的限制, 导致目前传统GPU平台上的优化方法无法应用于嵌入式ARM GPU, 因此其意味着需要投入更多专门的工作来进行嵌入式ARM GPU优化。可见, 嵌入式ARM GPU优化研究具有重要意义。
目前, 研究人员对于机载SAR已开展了大量的研究工作。文献[10]通过GPU对无人机SAR成像的性能进行加速。文献[11]在具有GPU和CPU的异构平台上设计并实现机载SAR处理系统。文献[12]提出基于图像的新GPU光线跟踪方法进行单静态SAR双反射仿真。文献[13]设计异构CPU-GPU框架, 解决了无人机拍摄的高清视频检测成本过高问题。文献[14]通过GPU并行加速来提高SAR成像目标检测效率。文献[15]在多个GPU平台上通过反投影进行多通道SAR处理。文献[16]在配备Tegra K1的片上系统上进行完全聚焦SAR算法并行优化以实现算法实时处理。然而, 国内外关于SAR并行算法的通用性研究较少, 由于不同硬件平台需对算法进行针对性优化及改进, 因此会增加软件算法人员的工作量和移植难度。本文在ARM Mali-T860 GPU异构计算平台上, 提出基于OpenCL的多视处理算法、旋转放缩算法和图像量化算法的并行优化策略, 以提升SAR算法整体性能。
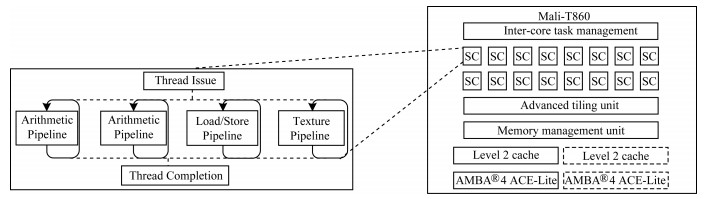
1 ARM Mali-T860 GPU架构Mali-T860是一款由ARM公司研发设计的Midgard架构的最高性能GPU, 如图 1所示。该GPU可扩展至16个连通着色器核心(Shader Core, SC)。在每个核心中包含2个算术流水线、1个数据读写流水线和1个纹理流水线。每个算术流水线是基于单指令多数据(Single Instruction Multiple Data, SIMD), 指令可同时对多个数据元素进行操作。数据读写流水线对RAM进行读写操作, 纹理流水线负责所有与纹理相关的内存访问。Mali Midgard GPU中的算术管道基于SIMD样式矢量化, 指令可同时对多个数据元素进行操作[17]。
|
Download:
|
| 图 1 ARM Mali-T860 GPU架构 Fig. 1 ARM Mali-T860 GPU architecture | |
多视处理是早期对SAR图像相干斑进行处理的技术[18]。本文采用的多视处理技术对合成孔径的多普勒带宽进行分割, 孔径被分割后各自成像(出现多视), 然后将叠加后的各子视图进行平均处理[19]。但是, 多视处理技术的前提是每一个子视图必须观测相同的地物, 几乎是同时且没有辐射失真, 还需要使用相同的极化方式和频率。
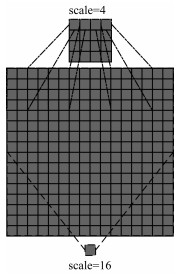
根据多视参数(scale)将图像按行和列取均值输出, 例如scale=4, 其中scale需选取2~16中的偶数, 因此本文选取4和16作为scale的值。如图 2所示, 图像按行x和列y每4个像素取均值输出为1个像素F(x′, y′), 图像整体缩小为原图像的1/16, 如式(1)~式(3)所示:
| $ {{x^\prime } = x \div {\rm{ scale }}} $ | (1) |
| $ {{y^\prime } = y \div {\rm{ scale }}} $ | (2) |
| $ F\left( {{x^\prime }, {y^\prime }} \right) = \left[ {\sum\limits_{j = 0}^{{\rm{scale }}} {\sum\limits_{i = 0}^{{\rm{scale }}} f } (x + i, y + j)} \right] \div {\rm{ scal}}{{\rm{e}}^2} $ | (3) |
|
Download:
|
| 图 2 scale为4和16时的多视处理 Fig. 2 Multi-view processing with scales of 4 and 16 | |
多视处理算法中每个结果数据都需要访存scale×scale个数据并进行均值计算, 数据和数据之间不存在依赖关系, 具有良好的并行性。但该算法在读取不同行数据时, 无法保证数据地址的连续性, 这是导致算法性能下降的原因之一, 其优化重点为提高访存带宽的利用率。
2.2 旋转放缩旋转放缩作为图像几何变换中最复杂的操作, 广泛应用于军事、航空、生物医学等领域[20]。由于在图像旋转放缩的过程中需要使用浮点运算, 原始图像为整数像素坐标(x, y), 变换为目标图像的位置坐标并非整数, 反之亦然。因此, 图像旋转变换包括坐标的几何运算和对运算结果的插值处理两方面, 并且根据选择的插值方法不同, 得到的旋转效果也不同。
输入算法所需参数输出矩阵的行Orow、列Ocol、角度a和放缩比例s, 计算原图像中心位置(xmid, ymid)与输出图像中心位置(xoutMid, youtMid), 如式(4)~式(7)所示:
| $ {{x_{{\rm{mid}}}} = \frac{{{i_{{\rm{row}}}}}}{2} - 1} $ | (4) |
| $ {{y_{{\rm{mid}}}} = \frac{{{i_{{\rm{col}}}}}}{2} - 1} $ | (5) |
| $ {{x_{{\rm{ outMid }}}} = \frac{{{o_{{\rm{row}}}}}}{{2 \times s}} - 1} $ | (6) |
| $ {{y_{{\rm{ outMid }}}} = \frac{{{O_{{\rm{col}}}}}}{{2 \times s}} - 1} $ | (7) |
在图像放缩过程中, 首先计算旋转角度后对应到原图位置, 坐标转换以放缩后的图像中心为原点, 如式(8)和式(9)所示。其次计算旋转前坐标, 获取4个角点坐标, 如式(10)所示。最后进行双线性插值计算, 如式(11)~式(17)所示:
| $ \begin{array}{*{20}{l}} {x_i^\prime = ({y_i} \div s - {y_{{\rm{ outMid }}}}) \times {\rm{sin}}{\kern 1pt} {\kern 1pt} a + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({x_i} \div s - {x_{{\rm{ outMid }}}}) \times {\rm{sin}}{\kern 1pt} {\kern 1pt} a + {x_{{\rm{ mid }}}}(i = 0,1, \cdots ,n)} \end{array} $ | (8) |
| $ \begin{array}{*{20}{l}} {y_i^\prime = ({y_i} \div s - {y_{{\rm{ outMid }}}}) \times {\rm{cos}}{\kern 1pt} {\kern 1pt} a + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({y_i} \div s - {y_{{\rm{ outMid }}}}) \times {\rm{cos}}{\kern 1pt} {\kern 1pt} a + {y_{{\rm{ mid }}}}(i = 0,1, \cdots ,n)} \end{array} $ | (9) |
| $ {x_1} = \left\lfloor {{x^\prime }} \right\rfloor ,{x_2} = \left\lceil {{x^\prime }} \right\rceil ,{y_1} = \left\lfloor {{y^\prime }} \right\rfloor ,{y_2} = \left\lceil {{y^\prime }} \right\rceil $ | (10) |
| $ {{Q_{11}} = ({x_1},{y_1})} $ | (11) |
| $ {{Q_{12}} = ({x_1},{y_2})} $ | (12) |
| $ {{Q_{21}} = ({x_2},{y_1})} $ | (13) |
| $ {{Q_{22}} = ({x_2},{y_2})} $ | (14) |
| $ {f({R_1}) = \frac{{{x_2} - {x^\prime }}}{{{x_2} - {x_1}}} \times f({Q_{11}}) + \frac{{{x^\prime } - {x_1}}}{{{x_2} - {x_1}}} \times f({Q_{21}})} $ | (15) |
| $ {f({R_2}) = \frac{{{x_2} - {x^\prime }}}{{{x_2} - {x_1}}} \times f({Q_{12}}) + \frac{{{x^\prime } - {x_1}}}{{{x_2} - {x_1}}} \times f({Q_{22}})} $ | (16) |
| $ {F(x,y) = \frac{{{y_2} - {y^\prime }}}{{{y_2} - {y_1}}} \times f({R_1}) + \frac{{{y^\prime } - {y_1}}}{{{y_2} - {y_1}}} \times f({R_2})} $ | (17) |
旋转放缩算法需要计算每个图片像素处理前后的坐标位置F(x, y), 所有像素坐标计算并不存在数据依赖关系, 具有较好的并行度, 但每个像素都存在密集计算, 并且该算法在双线性插值计算中存在较多的条件分支, 其优化重点为简化计算及对条件分支的优化。
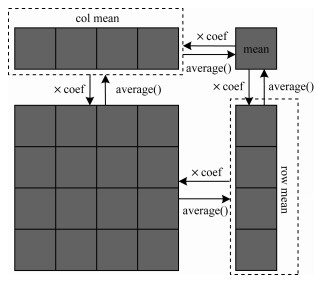
2.3 图像量化图像量化是图像处理领域的一项基本技术, 其可以在保证图像颜色失真度较小的前提下, 将含有丰富颜色信息的图像用少数的代表色进行表示[21], 如图 3所示。图像量化等级(coef)多, 所得图像层次丰富, 灰度分辨率高, 图像质量好, 但数据量会增加; 图像量化等级少, 图像层次欠丰富, 灰度分辨率低, 会出现假轮廓现象, 图像质量变差, 但数据量会降低。
|
Download:
|
| 图 3 图像量化过程 Fig. 3 Image quantization process | |
在图像量化过程中, 需要求矩阵的行均值Rmean、列均值Cmean、全均值M以及结果像素F(x, y), 如式(18)~式(21)所示:
| $ {{R_{{\rm{ mean }}}}(y) = \left[ {\sum\limits_{i = 0}^{{\rm{ row }}} {f({x_i},y)} } \right] \div {\rm{col}}} $ | (18) |
| $ {{C_{{\rm{ mean }}}}(x) = \left[ {\sum\limits_{i = 0}^{{\rm{ col }}} {f(x,{y_i})} } \right] \div {\rm{ row }}} $ | (19) |
| $ M = \left[ {(\sum\limits_{i = 0}^{{\rm{ col }}} {{R_{{\rm{ mean }}}}} (i)) \div {\rm{col}} + (\sum\limits_{i = 0}^{{\rm{ row }}} {{C_{{\rm{ mean }}}}} (i)) \div {\rm{ row }}} \right] \div 2 $ | (20) |
| $ F(x,y) = M \times {\rm{coef}} \div {R_{{\rm{ mean }}}}(x) \div {C_{{\rm{ mean }}}}(y) $ | (21) |
图像量化算法是典型的访存密集型算法, 算法执行过程中需要计算行均值、列均值以及全均值, 至少需要对所有像素访存两次, 并且结果矩阵的运算也需要对所有像素进行一次访存, 这将极大增加算法执行时间。该算法优化重点为提高访存效率并减少重复数据访存。
3 算法优化策略 3.1 多视处理算法优化策略ARMMali-T860 GPU基于SIMD设计, 即将数据以向量形式存储, 再通过一条指令对整个向量进行运算。该GPU寄存器为128位的向量化设计, 每执行1次SIMD向量操作, 相当于连续4次float/integer或2次double操作。向量化效果基本与并行化效果相一致, 且理论上性能是普通标量运算的4倍, 提高了访存带宽利用率。
3.2 旋转放缩算法优化策略旋转放缩算法是典型的计算密集型算法, 由于该算法的每个数据都需要反复计算输入和输出图像的中心坐标、旋转角度的正弦值和余弦值等参数, 而且这些参数由初始输入决定, 因此优化策略将这些参数由CPU进行计算, 再以常量参数输入GPU, 以此简化并行算法中各线程的流水线计算。
在双线插值计算中存在的4条分支会导致线程间负载不均衡。算术逻辑单元(Arithmetic and Logic Unit, ALU)支持4次mul操作和3次add操作的点积计算, 计算周期为7 FLOPS, 因此将双线插值计算转换成2阶矩阵点积, 通过条件分支将不符合条件的参数置0, 在保证结果正确的情况下实现所有线程的负载均衡, 具体公式如式(22)~式(27)所示:
| $ {{t_1} = \left\{ {\begin{array}{*{20}{l}} {(f({Q_{11}}),0),{x_1} = {x^\prime }}\\ {(0,f({Q_{12}})),{x_1} \ne {x^\prime }} \end{array}} \right.} $ | (22) |
| $ {{t_2} = \left\{ {\begin{array}{*{20}{l}} {(f({Q_{21}}),0),{x_1} = {x^\prime }}\\ {(0,f({Q_{22}})),{x_1} \ne {x^\prime }} \end{array}} \right.} $ | (23) |
| $ {{v_0} = ({x_2} - {x^\prime },{x^\prime } - {x_1})} $ | (24) |
| $ {{v_1} = (({y_2} - {y^\prime }) \times {v_0},({y_2} - {y^\prime }) \times {v_0})} $ | (25) |
| $ {{v_2} = ({t_1},{t_2})} $ | (26) |
| $ F(x,y) = \left\{ {\begin{array}{*{20}{l}} {{v_0} \cdot {t_1},{y_1} = {y^\prime }}\\ {{v_1} \cdot {v_2},{y_1} \ne {y^\prime }} \end{array}} \right. $ | (27) |
旋转放缩算法中存在较多的条件判断语句, 这些条件判断语句主要是为了区分不同元素在双线性插值中的运算。由于不同的分支运算存在差异, 将导致线程间的负载不均衡, 因此为减少条件分支, 使用A=B?C:D语句代替if…else…语句是减少动态指令的主要方式。
3.3 图像量化算法优化策略SIMD向量操作对于数据对齐有较高的要求, 因此首先考虑col均值运算, 通过一次读入4个行元素提高访存效率, 再基于线程并行折半求和, 最终计算得出当前列的平均值。
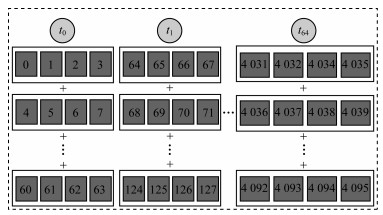
row均值计算采用for循环逐个累加所得保证线程连续寻址, 但是每个work_group中仅有一个线程, 因此如何在开启大量线程的同时满足线程的连续寻址是row归约提升性能的关键。通过增加work_group线程数以提升整体处理性能, 这样虽然会导致不同线程的跨步寻址问题, 但是能保证每个线程连续寻址。如图 4所示, 以4 096×4 096的矩阵规模为输入, 每个work_group开启64个线程, 每个线程负责累加64个数据, 然后输出64×4 096的临时矩阵, 最后在计算所有元素的均值步骤中得出列均值。实验结果表明, row规约优化对于计算所有元素均值的kernel增加了0.8 ms~0.9 ms的时间开销, 但对于计算列均值的kernel减少了5 ms的时间开销。
|
Download:
|
| 图 4 row mean规约优化 Fig. 4 row mean reduction optimization | |
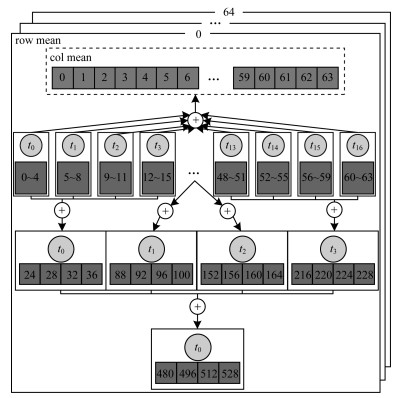
由于col与row均值的求解过程中存在一定的数据重复, 如求解col与row均值的kernel需要读取当前行的值, 因此将col与row归约的两个kernel合并为一个kernel。单个线程每次读入的4个行元素可用于求解当前col均值, 同时用于累加以求出row均值的4个行元素。以数据规模为4 096×4 096为例, 得出64×4 096的预处理矩阵, 4 096×1的row均值矩阵。求解全均值的kernel进一步计算预处理矩阵得出col均值矩阵, 如图 5所示。
|
Download:
|
| 图 5 col mean和row mean的kernel合并 Fig. 5 Kernel merge of col mean and row mean | |
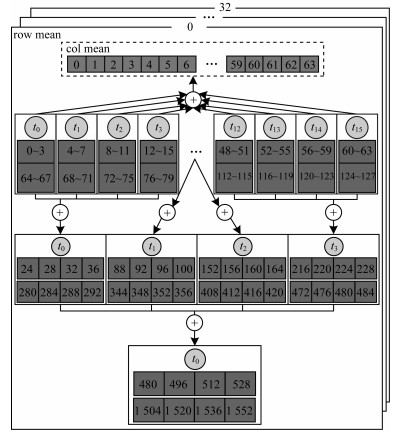
kernel合并后每个线程一次读取4个数据, 即每个work_group一次读取64个数据(每个work_group开启16个线程)。在此基础上, 为进一步提高带宽利用率, 每个线程执行两次读取, 即每个work_group一次读取128个数据, 如图 6所示。
|
Download:
|
| 图 6 访存优化 Fig. 6 Memory access optimization | |
本文选择ARM Mali-T860 GPU平台和Cortex-A53(1.8 GHz) CPU平台, ARM Mali-T860 GPU性能配置如表 1所示。

|
下载CSV 表 1 ARM Mali-T860 GPU性能配置 Table 1 Performance configuration of ARM Mali-T860 GPU |
本文设定数据规模为512×512~4 096×4 096, 通过优化算法的加速比衡量计算性能提升效果, 确保测试精度。
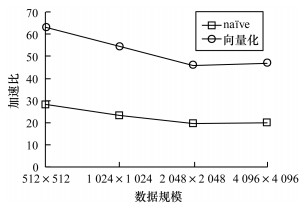
4.2.1 多视处理算法性能分析如图 7所示, naïve为多视处理算法的GPU初始版本, 向量化表示经过向量化处理的多视处理算法, scale=4时多视处理算法优化后取得了45倍~62倍的性能提升。可以看出, 随着数据规模的增大, 加速比不断减小, 算法优化效果有所下降, 主要原因为开启的线程资源大于实际硬件的线程数, 所有任务必须通过线程的上下文切换实现, 但上下文切换的过程中存在数据延时情况。
|
Download:
|
| 图 7 多视处理算法优化效果(scale=4) Fig. 7 Optimization effect of multi-view processing algorithm(scale=4) | |
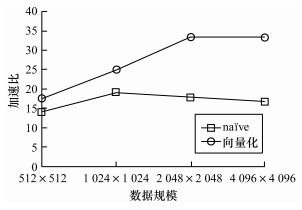
如图 8所示, scale=6时多视处理算法优化后取得了17倍~33倍的性能提升。可以看出, 随着数据规模的增大, 算法加速比不断增加, 优化效果越发明显, 主要原因为单个线程处理数据量的增加, 即单线程流水线变长, 可有效缓解多视处理算法对于线程数量的需求。
|
Download:
|
| 图 8 多视处理算法优化效果(scale=16) Fig. 8 Optimization effect of multi-view processing algorithm(scale=16) | |
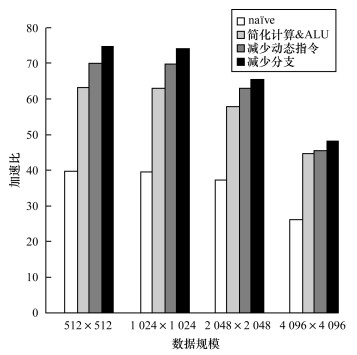
如图 9所示, naïve表示旋转放缩算法的GPU初始版本, 简化计算 & ALU、减少动态指令和减少分支分别表示经过简化计算 & ALU、减少动态指令和减少分支的旋转放缩算法, 旋转放缩算法优化后取得了48倍~74倍的性能提升。
|
Download:
|
| 图 9 旋转放缩算法优化效果(a=30°、s=1.5) Fig. 9 Optimization effect of rotation scaling algorithm (a=30°、s=1.5) | |
可以看出, 在数据规模为1 024×1 024和512×512时, 加速比基本相同, 随着数据规模的进一步增加, 算法优化效果有所下降, 其主要影响因素为:1)旋转放缩算法是计算密集型算法, 具有较好的并行性, kernel执行时间由单线程执行时间决定; 2)Mali-T860 GPU平台线程数量有限, 若开启线程数超过硬件本身, 则需要通过上下文切换来完成所有任务。同时, 笔者对旋转放缩算法进行SIMD向量操作, 但算法性能仍有所下降, 其主要原因为每个线程处理单个数据的运算流水线已经满载, 向量化操作会进一步增加计算量。
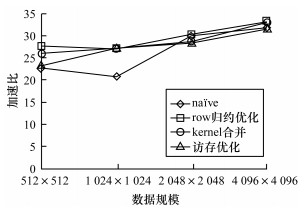
4.2.3 图像量化算法性能分析如图 10所示, naïve表示图像量化算法的GPU初始版本, row归约优化、kernel合并和访存优化分别表示经过row归约优化、kernel合并和访存优化的图像量化算法, 图像量化算法优化后取得了31倍~33倍的性能提升。
|
Download:
|
| 图 10 图像量化算法优化效果(coef=35) Fig. 10 Optimization effect of image quantization algorithm (coef=35) | |
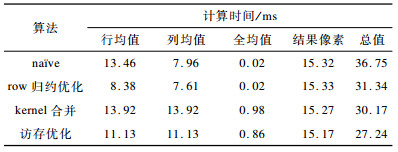
可以看出, 在数量规模为512×512和1 024×1 024时, row归约优化的加速比相比naïve有所下降, 但随着数据规模的增加, row归约优化的加速效果越发明显, 其主要因素为:1)在row归约优化后, row均值kernel会生成一个临时矩阵, 需要在全均值kernel中做进一步计算, 这就造成了一部分额外访存开销; 2)随着数据规模的增大, 线程计算量不断增加, 线程计算开销隐藏了访存延迟。数据规模为4 096×4 096时的图像量化算法计算时间消耗如表 2所示。
|
下载CSV 表 2 图像量化算法计算时间消耗(数据规模为4 096×4 096) Table 2 Computing time consumption of image quantization algorithm(data size is 4 096×4 096) |
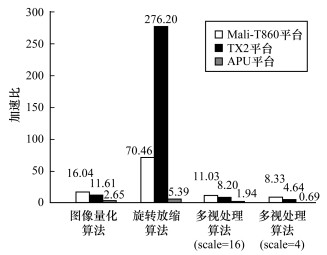
如图 11所示, 分别将本文算法在NVIDIA Tegra X2(TX2)和AMD RyzenTM Embedded V1000(APU)上进行实现, 可以看出算法优化效果为:APU>TX2>Mali-T860, 但各平台运行程序时的功耗为:APU>TX2>Mali-T860(如表 3所示), 因此综合考虑该性能差距为可接受。TX2的旋转放缩算法性能远低于其他平台, 其主要原因为TX2硬件不支持点积计算, 通过软件实现的点积操作不能达到性能提升的效果。
|
Download:
|
| 图 11 不同嵌入式异构GPU平台上的算法优化效果(数据规模4 096×4 096) Fig. 11 Algorithm optimization effect on different embedded heterogeneous GPU platforms(data size is 4 096×4 096) | |

|
下载CSV 表 3 不同嵌入式异构GPU平台上的程序执行功耗 Table 3 Power consumption of executing programs on different embedded heterogeneous GPU platforms |
传统ARM嵌入式平台的CPU无法满足机载SAR的计算需求, 因此ARM CPU+GPU的嵌入式异构多核平台应运而生。本文充分利用嵌入式ARM Mali-T860 GPU平台的计算能力, 通过对机载SAR成像处理中的多视处理、旋转放缩和图像量化算法设计并行优化策略实现算法加速。实验结果表明, 与基于CPU的SAR成像算法相比, 基于ARM Mali-T860 GPU优化后的多视处理、旋转放缩和图像量化算法整体性能更好。后续将考虑在NVIDIA Tegra X2和AMD RyzenTM Embedded V1000平台上对机载SAR成像过程中的多视处理、旋转放缩和图像量化算法做进一步性能优化, 更好地权衡SAR算法的性能和功耗问题。
| [1] |
HUANG Guoman, CHENG Chunquan, ZHAO Zheng, et al. Technology and application of airborne SAR remote sensing mapping[J]. Science of Surveying and Mapping, 2019, 44(6): 105-113. (in Chinese) 黄国满, 程春泉, 赵争, 等. 机载SAR遥感测图技术及应用[J]. 测绘科学, 2019, 44(6): 105-113. |
| [2] |
LI Lan, CHEN Erxue, LI Zengyuan, et al. Multi-baseline InSAR tomographic estimation method of forest aboveground biomass[J]. Forestry Science, 2017, 53(11): 85-93. (in Chinese) 李兰, 陈尔学, 李增元, 等. 森林地上生物量的多基线InSAR层析估测方法[J]. 林业科学, 2017, 53(11): 85-93. |
| [3] |
ZHAO Xianbin, YAN Wei, KONG Yi, et al. Application of normalized radar cross section with incident angle in airborne SAR detection images[J]. Chinese Journal of Geophysics, 2015, 58(6): 1869-1880. (in Chinese) 赵现斌, 严卫, 孔毅, 等. 机载SAR探测图像中归一化雷达截面随入射角变化规律应用[J]. 地球物理学报, 2015, 58(6): 1869-1880. |
| [4] |
DUPONT Q F M, CHUA D K H, TASHRIF A, et al. Potential applications of UAV along the construction's value chain[J]. Procedia Engineering, 2017, 182: 165-173. DOI:10.1016/j.proeng.2017.03.155 |
| [5] |
GAO Xiangwu, HUANG Guangmin, YANG Ruliang. Fast positioning method and analysis of positioning accuracy for airborne SAR targets[J]. Modern Radar, 2004, 26(9): 7-10. (in Chinese) 高祥武, 黄广民, 杨汝良. 机载SAR目标快速定位方法和定位精度分析[J]. 现代雷达, 2004, 26(9): 7-10. |
| [6] |
LIU Yunlong, LI Yilei, ZHOU Liangjiang, et al. A fast geometric precision correction algorithm for airborne SAR[J]. Journal of Radar, 2016, 5(4): 419-424. (in Chinese) 刘云龙, 李焱磊, 周良将, 等. 一种机载SAR快速几何精校正算法[J]. 雷达学报, 2016, 5(4): 419-424. |
| [7] |
GONG Ruohao.Image codec parallel optimization based on embedded mobile GPU[D].Chengdu: Southwest Jiaotong University, 2015.(in Chinese) 龚若皓.基于嵌入式移动GPU的图像编解码并行优化[D].成都: 西南交通大学, 2015. |
| [8] |
TOMOIAGA R, STRATULAT M.AES performance analysis on several programming environments, operating systems or computational platforms[C]//Proceedings of the 5th International Conference on Systems and Networks Communications.Washington D.C., USA: IEEE Press, 2010: 172-176.
|
| [9] |
GONG Ruohao, YANG Bin. Parallel optimization method of 2D floating-point matrix operation based on Mali T604 GPU[J]. Microcontrollers & Embedded Systems, 2015, 15(5): 43-46. (in Chinese) 龚若皓, 杨斌. Mali T604 GPU的二维浮点矩阵运算并行优化方法[J]. 单片机与嵌入式系统应用, 2015, 15(5): 43-46. |
| [10] |
XU Zhiwei, ZHU Daiyin. High-resolution miniature UAV SAR imaging based on GPU Architecture[J]. Journal of Physics:Conference Series, 2018, 1074(1): 1-22. |
| [11] |
WU Zheng, LIU Yabo, ZHANG Lei, et al. Highly efficient synthetic aperture radar processing system for airborne sensors using CPU+GPU architecture[J]. Journal of Applied Remote Sensing, 2015, 9(1): 197-223. |
| [12] |
BALZ T, STILLA U. Hybrid GPU-based single- and double-bounce SAR simulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(10): 3519-3529. DOI:10.1109/TGRS.2009.2022326 |
| [13] |
LI Maowen, TANG Linbo, HAN Yuqi, et al.Heterogeneous CPU-GPU moving targets detection for UAV video[C]//Proceedings of the 9th International Conference on Digital Image Processing.[S.l.]: International Society for Optics and Photonics, 2017: 1-11.
|
| [14] |
CUI Zongyong, QUAN Hongbin, CAO Zongjie, et al. SAR target CFAR detection via GPU parallel operation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(12): 4884-4894. DOI:10.1109/JSTARS.2018.2879082 |
| [15] |
OTTEN M, VLOTHUIZEN W, SPREEUW H, et al.Real-time processing of multi-channel SAR data with GPUs[C]//Proceedings of 2016 European Radar Conference.Washington D.C., USA: IEEE Press, 2016: 65-68.
|
| [16] |
RADECKI K, SAMCZYNSKI P, KULPA K, et al.A real-time focused SAR algorithm on the Jetson TK1 board[EB/OL].[2019-09-15].https://www.spiedigitallibrary.org/conference-proceedings-of-spie/10004/1/A-real-time-focused-SAR-algorithm-on-the-Jetson-TK1/10.1117/12.2241209.short.
|
| [17] |
ARM® MaliTM GPU OpenCL version 3.10 developer guide[EB/OL].[2019-09-15].https://static.docs.arm.com/100614/0310/arm_mali_gpu_opencl_developer_guide_100614_0310_00_en.pdf?_ga=2.112119492.1926375158.1569594046-1113341207.1521090777.
|
| [18] |
LU Zili, JIA Xin, ZHU Weigang, et al. Study on SAR image despeckling algorithm[J]. Journal of Ordnance Equipment Engineering, 2017, 38(6): 110-114. (in Chinese) 鲁自立, 贾鑫, 朱卫纲, 等. SAR图像相干斑抑制方法综述[J]. 兵器装备工程学报, 2017, 38(6): 110-114. |
| [19] |
ZHU Bo, LIU Tao. Performance evaluation in subaperture measurement of synthetic aperture radar[J]. Ship Electronic Engineering, 2016, 36(2): 46-49. (in Chinese) 朱博, 刘涛. 合成孔径雷达多视处理方法性能评估[J]. 舰船电子工程, 2016, 36(2): 46-49. |
| [20] |
ZENG Wenfeng, LI Shushan, WANG Jiang'an. Translation, rotation and scaling in image registration based on affine transformation model[J]. Infrared and Laser Engineering, 2001, 30(1): 18-20. (in Chinese) 曾文锋, 李树山, 王江安. 基于仿射变换模型的图像配准中的平移、旋转和缩放[J]. 红外与激光工程, 2001, 30(1): 18-20. |
| [21] |
SU Qinghua.Optimization methods of color image quantization model and its application in crack images[D].Wuhan: Wuhan University of Technology, 2013.(in Chinese) 苏清华.图像颜色量化模型优化方法及其在裂纹图像中的应用[D].武汉: 武汉理工大学, 2013. |
 2020, Vol. 46
2020, Vol. 46

 ,
,