近年来, 随着计算机技术的飞速发展, 各个行业都收集到大量的数据, 而在这些大量数据背后隐藏着很多重要的信息, 为了更好地利用这些数据对用户进行精准定位或者为用户提供个性化服务, 推荐系统应运而生。该系统经过多年的积累和沉淀已成功应用于在线视频、社交网络和电子商务等诸多领域。协同过滤技术是在推荐系统中应用较成功的技术, 同时, 聚类分析也是一种重要的技术手段。协同过滤技术是解决信息过载的有效方法之一[1-3], 而聚类分析是研究物以类聚的一种科学有效的方法, 它可以使得原始无分类、无规律以及错综复杂的数据反映出一定的规律性或特殊的分类性。文献[4]提出将数据挖掘中的K-means++聚类算法应用于入侵检测系统。为避免K-means++聚类算法陷入局部最优, 研究人员采用集成聚类来优化聚类算法, 如文献[5]利用优势集搜索方法在聚类集成中找出超簇, 并找到聚类集成结果。同时, 研究人员采用人工蜂群算法来优化协同过滤算法中使用的聚类算法。人工蜂群算法是一种新颖的基于群智能的全局优化算法, 它属于群智能算法的一种。如文献[6]多次使用欧式距离进行聚类, 利用Bagging进行集成学习来改变聚类, 以提高聚类效果。文献[7]在传统人工蜂群算法[8-9]上进行改进, 提出一种基于回溯搜索的人工蜂群算法, 该算法对图像进行处理时, 其精度和收敛速度都明显提高。虽然上述算法都在一定程度上提高了聚类效果, 但是在聚类时并没有充分有效地挖掘数据集的信息, 因此在进行推荐时会出现数据稀疏[3]和冷启动等问题。
针对上述问题, 本文提出一种改进的聚类集成联合相似度推荐算法。采用K-means++算法进行聚类, 并利用改进的蜂群算法优化K-means++聚类中心, 使用集成方法对聚类进行集成, 从而得出最佳聚类结果。同时, 在数据集Iris、Red Wine、Australia与MovieLens上验证聚类集成算法的收敛时间和误差均值。采用联合相似度算法计算同类用户间的相似度, 并在MovieLens数据集上验证本文算法的推荐效果。
1 聚类的个性化推荐 1.1 蜂群优化联合相似度算法本文算法依据用户的历史行为信息构造出用户评分矩阵。利用用户的评分信息和用户属性信息进行聚类, 并采用改进的蜂群算法对聚类中心进行优化, 使得算法能够解决局部最优的问题, 进而提高聚类效果。在此基础上, 依据评价聚类标准CH(Calinski-Harabasz)对改进聚类算法进行评估, 通过对训练数据集进行多次K-means++聚类, 利用Bagging方法集成聚类结果, 并采用一致性函数进行引导聚合, 得到聚类结果k。在同一类别中采用联合相似度算法计算该类别中的邻居用户。为找到效果最佳的相似度算法, 本文对多种相似度算法进行对比, 从而找到最优搭配相似度。根据相似度值的排序找出与目标用户邻近的集合, 再通过对最邻近集合中用户对项目的评分数据加权得到对未知项目的评分, 将计算得到的评分数据用来预测目标用户对未知项目的评分, 将得到的评分与设置阈值相比较, 当其大于设置阈值时, 则将其推荐给用户; 否则, 不能将其推荐给用户。
1.1.1 K-means++聚类算法为解决K-means++算法初始点比较敏感的问题, 本文选用K-means++聚类算法对初始值进行改进。K-means++聚类算法的描述如下:
输入 无标记的训练集合U{X1, X2, …, Xi}, Xi(i=1, 2, …, k)表示随机挑选一个用户作为第i个聚类中心点
输出 聚类的数目k
步骤1 在所有集合中随机挑选一个用户作为第一个聚类中心点X1。
步骤2 对于数据中的每一个点Xi, 计算其与已经选择的聚类中心的最近聚类中心距离A(Xi)=argmin‖Xi-Xa‖22, i=1, 2, …, k。
步骤3 如果A(Xi)点较大, 则很有可能被选择作为一个新的聚类中心点。
步骤4 重复步骤2和步骤3, 直至选出k个聚类中心, 聚类结束。
1.1.2 改进的人工蜂群算法由于K-means++算法对数据进行聚类时, 得到的聚类中心的计算大多依赖于前面得到的聚类中心, 使得在进行大规模数据计算时受到限制, 为解决该问题, 本文采用人工蜂群算法对K-means++算法进行优化, 但是传统的人工蜂群算法会使聚类中心受到局部限制, 因此本文采用改进的人工蜂群算法对聚类中心进行优化, 这样不仅可以对数据进行全面优化, 而且还可以解决因全局变量变化引起的局部受限问题。改进的人工蜂群算法主要分为以下4个阶段:
1) 改进初始化。由于传统的人工蜂群算法中初始值的设置是随机产生的, 为了提高算法的性能, 本文对生成初始值的随机方式进行改进, 具体如下所示:
| $ {x_{ij}} = {x_{{\rm{mi}}{{\rm{n}}_j}}} + {\rm{random}} [0,1]({x_{{\rm{ma}}{{\rm{x}}_j}}} - {x_{{\rm{mi}}{{\rm{n}}_j}}}) $ | (1) |
2) 改进引领蜂。为了寻找在不同时期对种群的调整方式, 本文对引领蜂进行线性搜索, 使得算法能够动态调整蜜蜂的采蜜领域范围, 线性调整公式如下所示:
| $ {d_s} = - {d_{{\rm{min}}}} + ({\rm{MCN}} - g)({d_{{\rm{min}}}} - {d_{{\rm{max}}}})/{\rm{MCN}} $ | (2) |
| $ {\varphi _{ij}} = {d_s} - 2 \times {d_s} \times {\rm{ rand}} ( - 1,1) $ | (3) |
其中, MCN表示最大迭代次数, g表示当前迭代次数, dmin和dmax分别代表邻域的最小范围和最大范围。在每次迭代过程中, 对式(3)中的φij进行更新。
在线性调整公式中, 前期g值较小, ds值变大, 则范围就越大, 蜂群可以在较大邻域内进行搜索; 后期g值变大, ds值变小, 则范围就越小, 蜂群可以在该邻域内进行细致搜索。
蜜源更新是引领蜂依据其记忆中的食物源位置进行邻居搜索, 并找到食物源附近的更好食物源。当引领蜂找到一个食物源之后会评估其适应度值, 采用式(4)来确定邻居食物源:
| $ {v_{ij}} = {x_{ij}} + a{\varphi _{ij}}({x_{ij}} - {x_{kj}}) $ | (4) |
其中, a是随机数, 且k≠i, j=(1, 2, …, D), φij为随机数且φij∈(-1, 1), xij代表产生的新位置。
由式(4)可知蜜源搜索的新解, 它的全局搜索能力较好, 但是其局部搜索能力较差。因此, 将在搜索策略中引入自适应步长, 在搜索中利用新的搜索策略对xij和目前最佳解xbest(ij)进行搜索, 进而提高局部搜索策略的效率, 其中, 加强局部邻域搜索的表达式为:
| $ \begin{array}{*{20}{l}} {{v_{ij}} = \lambda {x_{ij}} + (1 - \lambda ){x_{{\rm{ best }}(ij)}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{ij}}((1 - \lambda )({x_{{\rm{ best }}(ij)}} - {x_{kj}}))} \end{array} $ | (5) |
其中,
3) 改进跟随蜂。为使聚类效果的紧凑度和分离度更加明显, 本文选用适应度函数, 使得类内聚类效果更加紧凑, 类间分离度更加明显。假设Ci代表第i个聚类的数据集合, Ii表示第i类的聚类中心, 也就是一个蜜源。适应度函数设计为:
| $ {J_i} = \sum\limits_{v \in {C_i}} {{{\left\| {v,{I_i}} \right\|}^2}} $ | (6) |
其中, v∈Ci是Ci中的元素。
| $ {f_i} = \frac{{{\rm{C}}{{\rm{N}}_i}}}{{{J_i}}} + \frac{{{\rm{CK}}}}{M} $ | (7) |
其中, fi表示蜜源Ii的适应度值, CNi=Ci, 也就是Ci中的元素个数, Ji是第i类Ci中的数据到聚类中心Ii的距离之和, CK表示聚类中心到其他聚类中心的距离之和,
当所有的引领蜂搜索完成时, 引领蜂会将蜜源信息和其对应的适应度给跟随蜂, 跟随蜂根据式(8)中的概率计算每个引领蜂被跟随的概率, 概率表达式为:
| $ {P_i} = \frac{{{f_i}}}{{\sum\limits_{i = 1}^{{\rm{SN}}} {f(i)} }} $ | (8) |
其中, fi是蜜源xi对应的适应度值, 适应度值的大小与蜜源被选择的概率大小成正比, SN为训练样本的个数。
4) 侦查蜂搜索。当某个食物源对应的计数器中的数值大于某个预先设置的阈值时, 可以认为当前食物源已经耗尽, 放弃该食物源, 相应的引领蜂变为侦查蜂, 采用式(8)在可行解空间内随机产生新的食物源。
1.1.3 改进的蜂群聚类算法改进的蜂群聚类算法的具体步骤为:步骤1 假设引领蜂和跟随蜂的数量相同, 且都为训练样本个数SN, 设置最大迭代次数为MCN, 设置控制参数limit和类别数k。
步骤2 蜂群初始化, 随机产生{Z1, Z2, …, ZSN}个初始蜂群, 并根据式(7)计算各个蜜蜂的适应度值。
步骤3 对适应度值进行排序, 将一半适应度范围作为引领蜂, 一半适应度范围作为跟随蜂。引领蜂利用式(5)进行邻域搜索得到新蜜源, 如果新蜜源的适应度大于旧蜜源的适应度, 则把旧蜜源替换为新蜜源; 否则, 仍保持不变。当全部引领蜂完成邻域搜索时, 利用式(8)计算概率Pi。
步骤4 根据步骤3得出的概率Pi和轮盘赌法则来判断此处引领蜂的适应度, 得出的概率越大则表明引领蜂i的适应度越大, 且被跟随蜂选择的机率就越大。当跟随蜂对引领蜂选择完成时, 按照式(5)对引领蜂进行邻域搜索, 并将搜索到的位置作为新蜜源位置。
步骤5 将搜索到的蜜源位置初始化为聚类中心, 对数据集进行一次K-means++迭代聚类, 根据最近邻原则进行聚类划分, 并找出各聚类中心更新蜂群。
步骤6 在迭代limit次后, 如果引领蜂的所在位置不变, 则将引领蜂变为侦察蜂, 并按式(5)产生一个新的蜜源。
步骤7 若迭代次数达到MCN, 则算法结束, 并输出最后的聚类中心; 否则, 转向步骤3, 且limit=limit+1。
步骤8 基于以上改进的蜂群优化K-means++聚类结果可以找到相对应的值, 但是该结果不一定是最优解, 因此要使用评估聚类算法对结果进行评估, 将簇内的稠密程度和簇间的离散程度即轮廓系数作为该聚类算法的评估标准, 它是一种评价聚类效果的方式。本文选用Calinski-Harabasz Index轮廓系数[10]来计算每一个聚类中心聚类结果的轮廓系数。Calinski-Harabasz Index轮廓系数的计算方法如下所示:
| $ S(k) = \frac{{ {\rm{tr}} ({\mathit{\boldsymbol{A}}_k})}}{{ {\rm{tr}} ({\mathit{\boldsymbol{B}}_k})}}\frac{{(m - k)}}{{(k - 1)}} $ | (9) |
其中, m表示训练样本集中聚类的数目, k表示当前聚类数目, Ak表示类与类之间的协方差矩阵, Bk表示每个类内部数据的协方差矩阵, tr表示Ak类和Bk类构成矩阵的迹。式(9)表明tr(Bk)的值越小越好, 而tr(Ak)的值越大越好, 这样得出的结果S越好, 且其对应的k值越精确, 聚类结果更加精确。
1.1.4 改进的蜂群聚类集成算法本文使用Bagging并行集成学习方法进行聚类集成。集成学习的主要思想是使用不同的方法改变原始训练样本的分布, 从而构建多个不同的分类器, 并将这些分类器线性组合得到一个更强大的分类器作为最后的决策。
使用改进的蜂群优化K-means++聚类算法生成K个基聚类成员, 利用Bagging对K个基聚类成员进行集成, 并使用投票法对基聚类成员进行聚类集成。聚类集成的基本思想是在数据范围内进行有放回的再抽样, 假设样本容量为n, 原数据中每个数据被抽到的概率相等, 且为1/n, 即为bootstrap样本。
改进的蜂群聚类集成算法的步骤为:
步骤1 假设初始训练数据集数量为n, 每次从训练数据集中使用bootstraping方法抽取b(b < n)个训练样本(在数据集中, 有些数据很有可能被多次抽到, 而有些数据可能一次也没有被抽到), 抽取K轮, 得到K个训练集(K个训练集之间是相互独立的)。
步骤2 将K个训练样本分别采用改进的蜂群聚类基学习器单独进行训练, 将初始训练数据集和聚类数建立为一个n×K的矩阵, 该矩阵用于记录对每个训练样本聚类类别的投票, 其中, cij表示第i个基学习器的第j个聚类中心。
步骤3 为判断每个训练样本的最终聚类类别, 本文根据步骤2建立的矩阵, 按照投票法则进行判断。训练样本的最终类别是由票数最多的类别决定的, 如果某个类别的投票数相同, 则随机选择一个类别作为该样本的最终聚类类别。
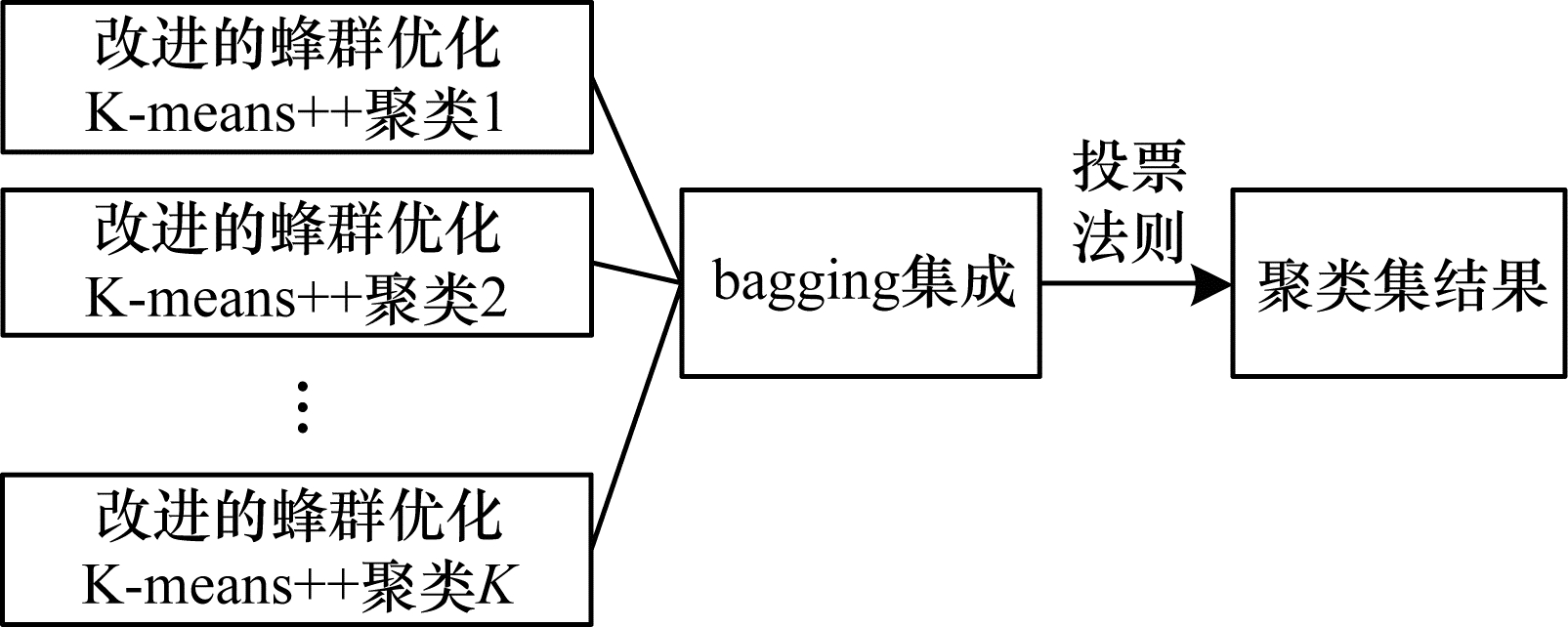
根据改进的蜂群优化聚类集成算法对数据集进行聚类运算, 能够得到Kn, 即用户n的K个类簇, 假设为Fn。改进的蜂群优化聚类集成如图 1所示。
|
Download:
|
| 图 1 改进的蜂群优化聚类集成 Fig. 1 Clustering ensemble optimized by improved bee colony | |
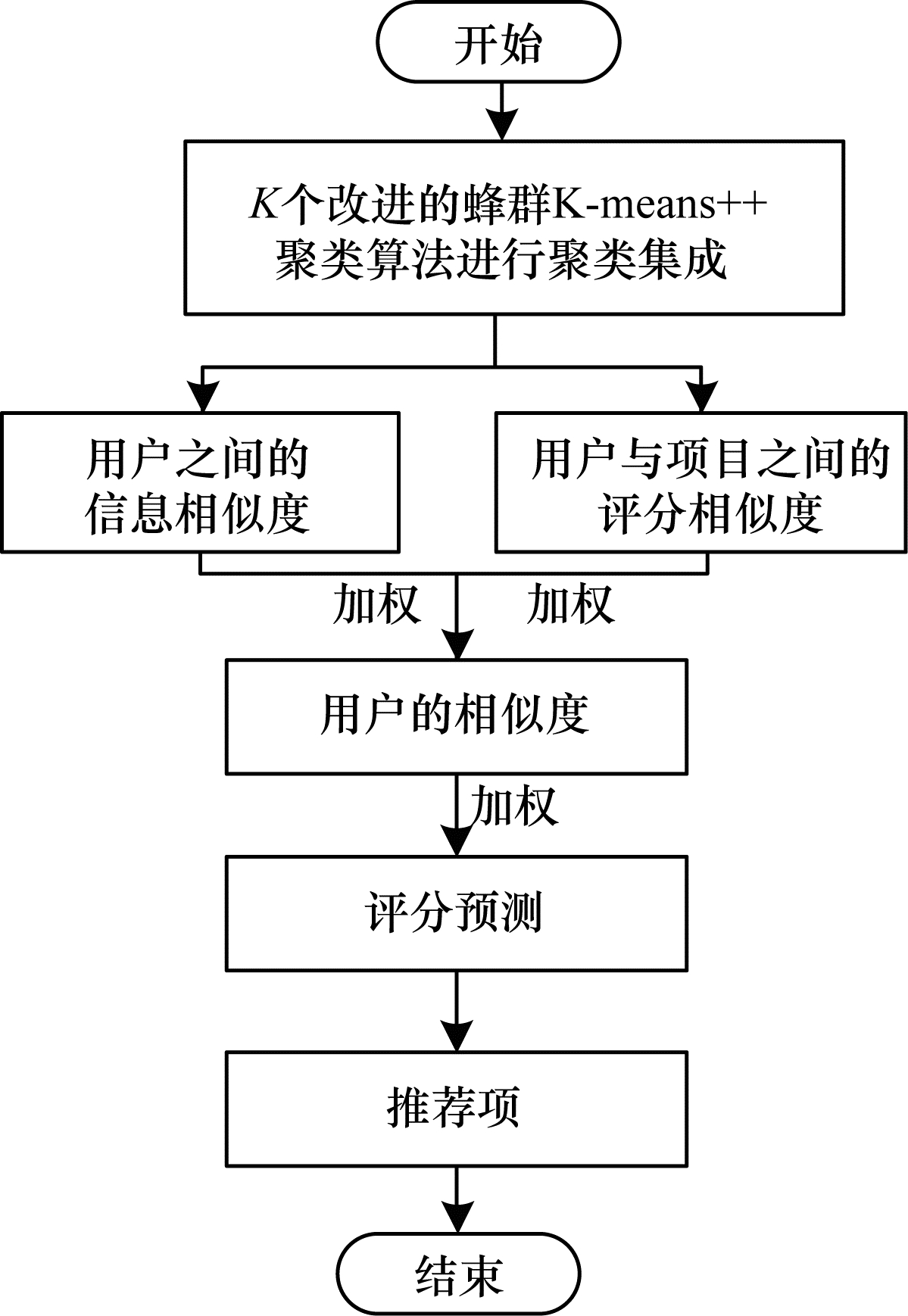
改进的蜂群优化聚类集成联合相似度推荐算法流程如图 2所示。
|
Download:
|
| 图 2 本文算法流程 Fig. 2 Procedure of the proposed algorithm | |
改进的蜂群聚类集成算法假定原始数据集包含n个数据对象, 一次聚类集成需要循环t次, 每次聚类的数目为k, 基聚类成员个数为K。K-means++算法每次迭代的时间复杂度为O(k×n×t), 算法通过集成聚类集成K个改进的蜂群优化聚类算法, 其总时间复杂度为O(K×n×t×k)。
1.3 用户联合相似度计算传统的个性化推荐算法在用户历史行为记录较少的情况下, 很难准确找到有效信息并将信息推荐给用户, 导致其推荐性能下降。针对上述问题, 在同一类中, 本文将用户与用户之间的相似度和用户行为相似度进行线性联合作为联合相似度, 在2种相似度中采用调节参数使得相似度达到最优。相似度表达形式为:
| $ {\rm{sim}} (x,y) = {\rm{sim}}{ _1}(x,y) + {\rm{sim}}{ _2}(x,y) $ | (10) |
其中, sim(x, y)表示用户x与用户y的相似度, sim1(x, y)表示用户x与用户y的属性相似度, sim2(x, y)表示用户的行为相似度。
将肯德尔相关系数(Kendall)与皮尔逊算法相联合作为本文的相似度算法, 其中, 肯德尔相关系数[11]主要用来测量在同一类别中2个用户之间的相似度值, 其表达形式为:
| $ {\rm{sim}}{ _1}(x,y) = \frac{{C - D}}{{\frac{1}{2}N(N - 1)}} $ | (11) |
其中, x, y表示用户, C表示用户x与用户y拥有一致性属性的个数(同增或者同减的属性个数), D表示用户x与用户y拥有不一致的属性个数(即属性不是同时增加, 也不是同时减少), N表示用户x与用户y的元素个数(假设用户x与用户y的元素个数相同),
为了防止在同一类别中未被用户评分的项目被忽略, 本文采用皮尔逊相关系数[12]来描述同一类别中用户评分间的相似程度。皮尔逊相关系数表达形式为:
| $ {\rm{sim}}{(x,y)^\prime } = \frac{{\sum\limits_{s \in {s_{xy}}} {({r_{xs}} - \overline {{r_x}} )} ({r_{ys}} - \overline {{r_y}})}}{{\sqrt {\sum\limits_{s \in {s_{xy}}} {{{({r_{xs}} - \overline {{r_x}} )}^2}} } \sqrt {\sum\limits_{s \in {s_{xy}}} {{{({r_{ys}} - \overline {{r_y}})}^2}} } }} $ | (12) |
其中, x, y表示用户,
在同一类别中为预测某用户对某项目的评分, 需要考虑与该用户兴趣相似的用户对该项目的评分。本文采用基于邻域[13]的评分预测方法进行评分预测, 利用改进的蜂群优化K-means++聚类集成算法对用户进行聚类得到k个类别, 然后在同一个簇内计算用户的加权联合相似度, 并将相似度值按照大小进行排序, 取出相似度最高的前n项作为邻域, 再预测用户对未知项目的评分, 其表示方法为:
| $ {R_{xi}} = \overline {{R_x}} + \frac{{\sum\limits_{y \in s(x,k) \cap n(i)} { {\rm{sim}} } (x,y)({r_{yi}} - \overline {{r_y}})}}{{\sum\limits_{y \in s(x,k) \cap n(i)} | {\rm{sim}} (x,y)|}} $ | (13) |
其中, Rxi表示用户x对项目i的预测评分[14-15],
为验证本文算法的有效性与可行性, 选用Iris、Red Wine、Australia与MovieLens100K数据集进行聚类算法的测试, 并采用K-means++聚类算法与改进的蜂群聚类集成算法对上述数据集进行处理。本文选用MovieLens网站提供的电影评分数据集对推荐算法的召回率和精度进行实验[16]。实验使用的数据是MovieLens100K数据集, 其中包括943位用户对1 682部电影的100 000个评分, 该数据集对各个类别电影的评分值为1~5, 考虑到实际仿真的效率, 实验将数据集划分为训练数据集和测试数据集, 其中, 80%的数据集作为训练集, 剩余的20%数据集作为测试集, 这样可以减少偶然因素带来的不利影响, 保证实验的精确性。
2.2 评价指标推荐算法的评价指标有多种, 准确度、多样性及新颖性等都可以用来评价推荐算法的推荐质量, 本文采用准确度来度量推荐质量的好坏。评价推荐算法的准确度[17-18]比较常用的指标有平均绝对误差(Mean Absolute Error, MAE)[19]、精度(Precision)与召回率(Recall), MAE是用来衡量推荐给用户的准确性, 能更好地反映预测值误差的实际情况, 且MAE越小, 则推荐算法的准确度越高[20], MAE的计算方法为:
| $ {\rm{MAE}} = \frac{1}{m}\sum\limits_{i = 1}^m | {x_i} - {y_i}| $ | (14) |
其中, xi表示为某用户对项目的预测评分集合, 设为{x1, x2, …, xm}, yi表示用户对所有项目的实际评分集合, 设为{y1, y2, …, ym}。
精度是用户对某一项目的推荐所占的比例, 其计算方法为:
| $ {{P_i} = \frac{{{X_i}(L)}}{L}} $ | (15) |
| $ {P = \frac{1}{n}\sum\limits_{i = 1}^n {{P_i}} } $ | (16) |
其中, Xi(L)表示推荐列表中实际用户看过的项目数量, L表示该聚类的推荐列表长度。
召回率是对正确推荐项目的一种衡量, 其计算方法为:
| $ {\rm{Recall}} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{N_r^i}}{{N_p^i}}} $ | (17) |
其中, Nri是对聚类用户的推荐列表中实际被用户选择的电影数量, Npi表示某个用户看过的所有电影数量。
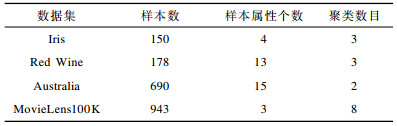
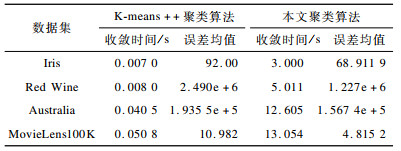
2.3 实验结果与分析实验1 为验证本文提出的聚类算法优于K-means++聚类算法, 在相同条件下, 对本文聚类算法和K-means++聚类算法的收敛时间和聚类误差均值进行比较。利用不同的数据集来验证本文聚类算法的聚类效果更优。对于不同的数据集, 设置不同规模大小的蜂群, 具体如表 1所示, 且设置最大迭代次数为1 000, limit次数为100。本文聚类算法与K-means++聚类算法对数据集的聚类结果对比如表 2所示。从表 2可以看出, 虽然K-means++聚类算法的收敛速度较快, 但是聚类衡量数值的变化较大, 因此不同实验选择不同的初始聚类中心, 对实验结果的影响较大。同时, K-means++聚类算法容易受初始聚类中心的影响, 使算法陷入局部最优。本文采用改进的蜂群优化聚类集成算法, 虽然增加了时间的复杂度和聚类属性, 但是降低了聚类误差的幅度, 解决了K-means++聚类算法的缺点, 进而改善了聚类效果, 使聚类效果更加稳定。同时, 在时间复杂度允许的范围内提高了聚类效果, 使聚类效果更加精确, 且可以在无监督的情况下进行精确划分, 更好地挖掘数据间的关系。
|
下载CSV 表 1 聚类实验的数据集信息 Table 1 Dataset information of clustering experiment |
|
下载CSV 表 2 2种算法对数据集的聚类结果对比 Table 2 Comparison of clustering results of two algorithms for dataset |
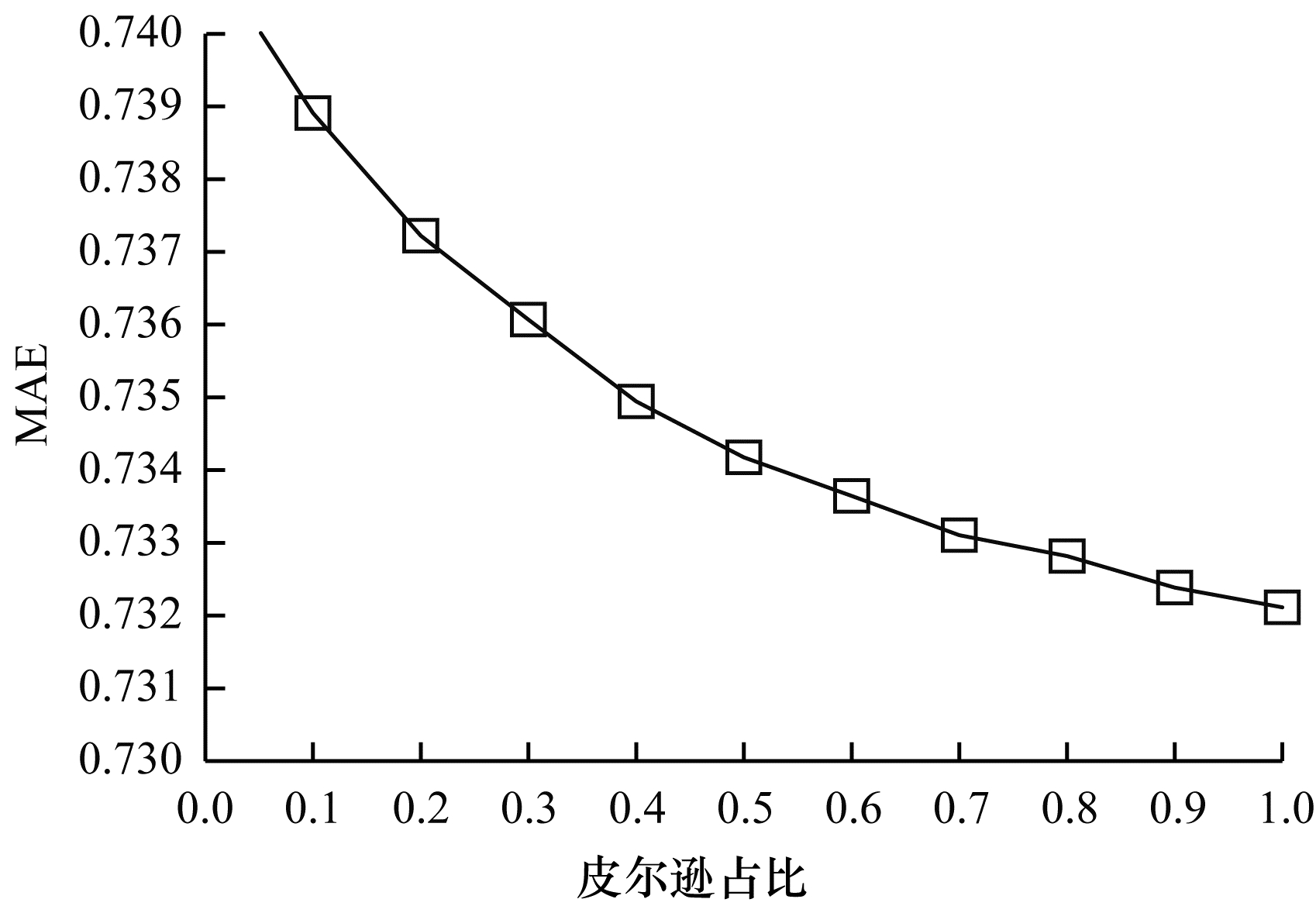
实验2 在相同条件下, 实验通过比较本文联合相似度算法和其他相似度算法的平均绝对误差, 来验证本文联合相似度算法优于单个相似度算法和其他联合相似度算法。本文选用MovieLens100K数据集进行实验, 并根据实验1得出的MovieLens100K数据集聚类结果进行相关的实验验证。图 3表示基于用户的皮尔逊相似度和杰卡德相似度联合的MAE。从图 3可以看出, 采用皮尔逊和杰卡德相联合的相似度, 在MAE最低时与杰卡德的单独相似度等效。因此单个相似度算法优于该联合相似度算法, 且需要改用其他联合相似度算法使相似度结果达到最优。
|
Download:
|
| 图 3 杰卡德和皮尔逊联合相似度的MAE Fig. 3 MAE of joint similarity of Jaccard and Pearson | |
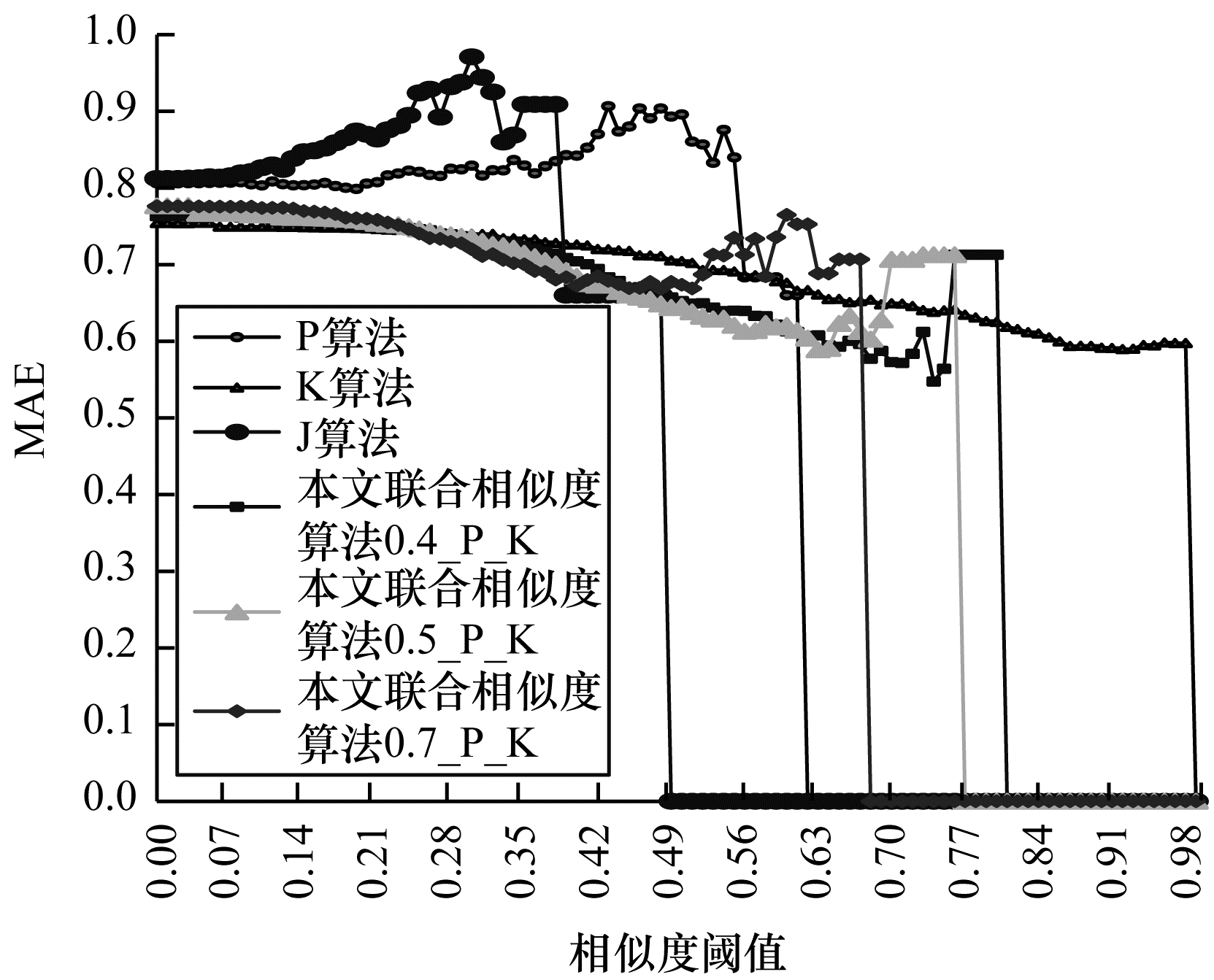
经过大量的实验验证了肯德尔和皮尔逊联合相似度算法优于其他相似度算法, 结果如图 4所示, 其中, P表示皮尔逊算法, K表示肯德尔算法, J表示杰卡德算法, 0.5_P_K表示皮尔逊所占比例是0.5, 0.7_P_K表示皮尔逊所占比例是0.7。从图 4可以看出, 本文算法比各种相似度算法的MAE小, 且当皮尔逊占0.4权重、阈值取0.75时, 肯德尔和皮尔逊联合相似度算法的MAE达到最低。结合图 3和图 4可知, 本文提出的肯德尔和皮尔逊联合相似度算法, 比单独的皮尔逊相似度算法、肯德尔相似度算法、杰卡德相似度算法以及杰卡德和皮尔逊进行联合得到的相似度算法的MAE均低, 因此本文提出的联合相似度算法具有可行性。
|
Download:
|
| 图 4 不同相似度算法的MAE Fig. 4 MAE of different similarity algorithms | |
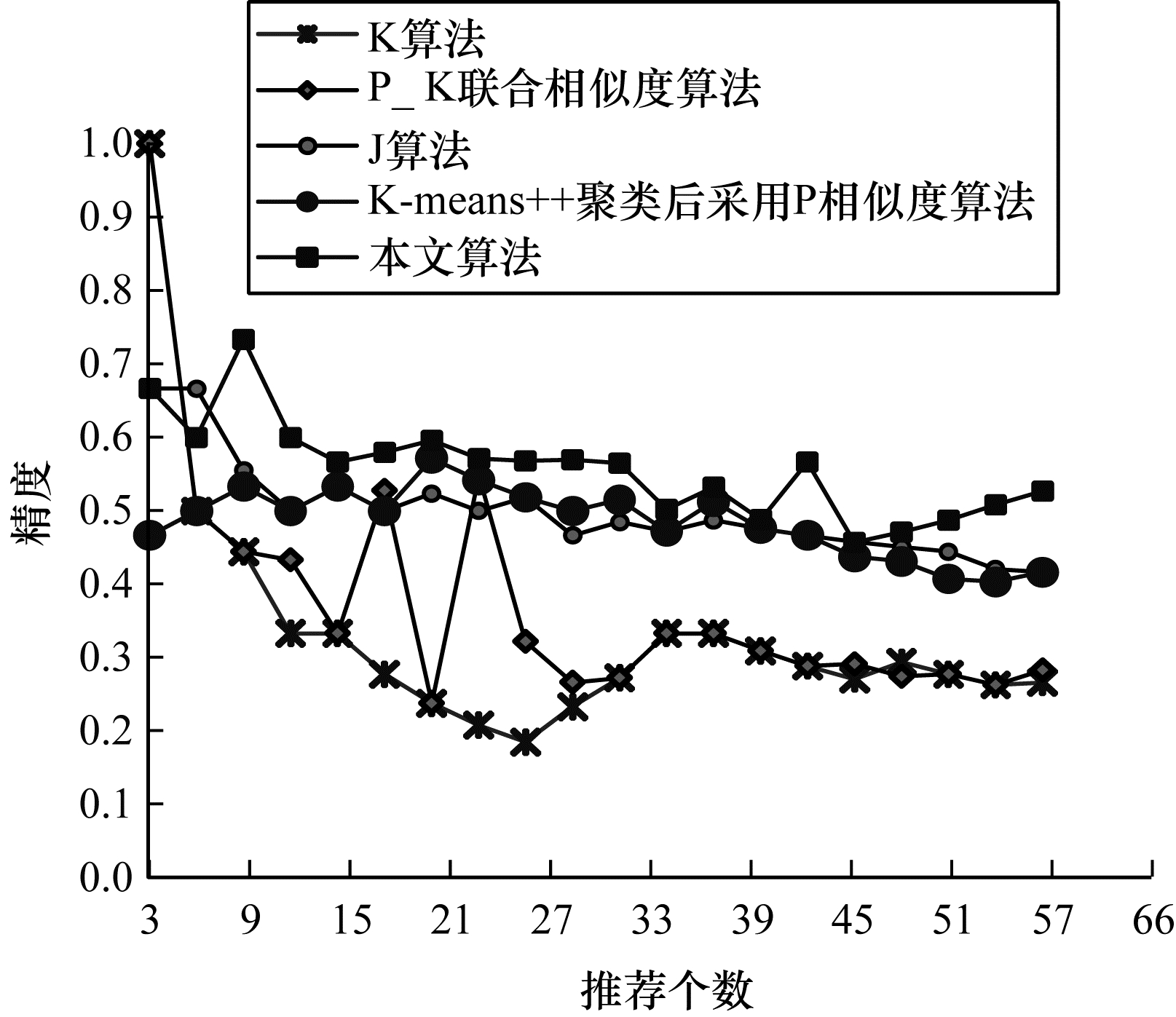
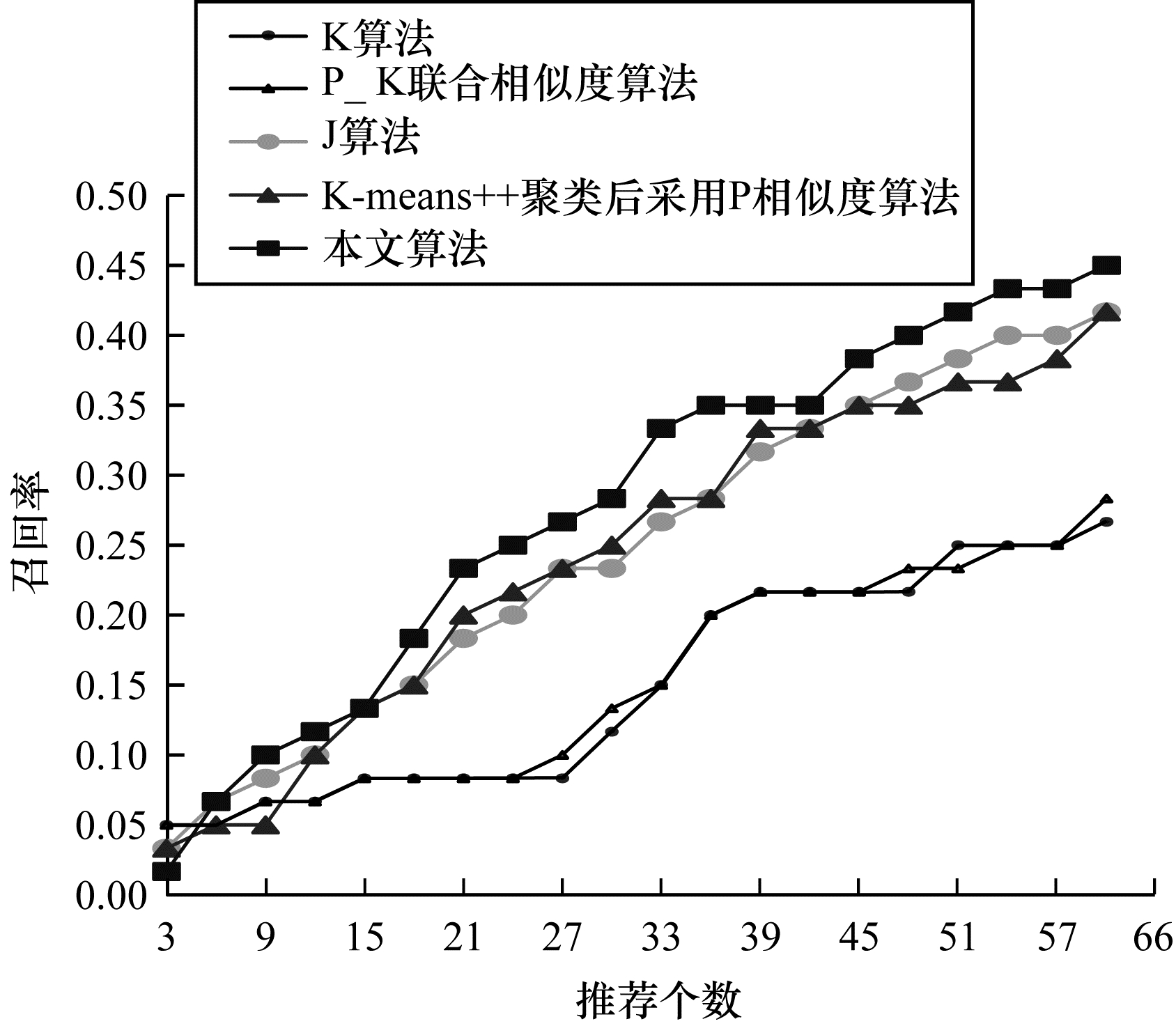
实验3 为验证本文算法的有效性, 在相同参数条件下, 实验比较了本文算法和其他算法的精度以及召回率。由实验2的结果可以确定, 联合相似度算法优于单个相似度算法, 且当皮尔逊占0.4权重、阈值取0.75时, 肯德尔和皮尔逊联合的相似度算法达到最优, 因此将其作为本文联合相似度算法进行实验。本文算法对精度与召回率的影响分别如图 5、图 6所示。从图 5可以看出, 当推荐个数大于6时, 本文提出的聚类集成联合相似度推荐算法的精度高于其他相似度算法, 因此, 可以根据推荐个数的不同选择不同的推荐方法, 从而提高精度。从图 6可以看出, 当推荐个数大于6时, 本文算法的召回率优于其他算法, 因此, 本文算法优于其他4种个性化推荐算法。
|
Download:
|
| 图 5 不同算法的精度 Fig. 5 Precision of different algorithms | |
|
Download:
|
| 图 6 不同算法的召回率 Fig. 6 Recall rate of different algorithms | |
综上所述, 改进的蜂群优化聚类集成联合相似度推荐算法比其他相似度算法以及只有聚类集成算法的精度和召回率都要高, 且MAE相对较小, 因此, 本文推荐算法不仅考虑到用户的基本属性特征, 还考虑到项目的属性特征, 这样一方面可以提高本文推荐算法的精度和召回率, 另一方面又降低了本文算法的MAE, 同时在一定程度上缓解了数据稀疏问题, 使得本文推荐算法达到最佳效果。
3 结束语传统的协同过滤算法在数据稀疏的情况下, 不能及时准确地为用户推荐其所需项目, 且传统的K-means++聚类协同过滤算法也不能找到最优的k值, 从而无法实现最佳推荐。为此, 本文提出改进的蜂群优化聚类集成联合相似度推荐算法。该算法不仅可以缓解推荐算法中的数据稀疏性问题, 而且有效提高了推荐质量, 还解决了K-means++聚类不佳等问题, 改善初始聚类中心不稳定的缺点。下一步将对基于项目聚类的联合相似度推荐算法进行改进, 利用改进的蚁群算法对项目信息进行聚类, 以提高推荐算法的准确性和可行性。
| [1] |
YANG Wenjuan, JIN Zixin. The research on collaborative filtering algorithm based on clustering[J]. Computer Knowledge and Technology, 2018, 14(16): 185-188. (in Chinese) 杨文娟, 金子馨. 基于聚类的协同过滤算法的研究[J]. 电脑知识与技术, 2018, 14(16): 185-188. |
| [2] |
SHI Yansong. Research on personalized recommendation system based on big data[J]. Telecom World, 2019, 26(4): 81-82. (in Chinese) 石岩松. 基于大数据的个性化推荐系统研究[J]. 通讯世界, 2019, 26(4): 81-82. |
| [3] |
HOU Yaozu.Research on collaborative filtering recommenda-tion algorithm based on two-stage joint hashing technology[D].Hefei: Anhui Agricultural University, 2018.(in Chinese) 候耀祖.基于两阶段联合哈希技术的协同过滤推荐算法研究[D].合肥: 安徽农业大学, 2018. |
| [4] |
CHEN Lishan. Research on intrusion detection system based on K-means clustering algorithm[J]. Journal of Kunming University, 2017, 39(3): 58-62. (in Chinese) 陈丽珊. 基于K-means聚类算法的入侵检测系统研究[J]. 昆明学院学报, 2017, 39(3): 58-62. |
| [5] |
ZHOU Bing, LI Fei, HOU Weizhao, et al. Dominant set fuzzy clustering ensemble based on cluster filtering[J]. Computer & Network, 2019, 45(7): 61-64. (in Chinese) 周冰, 李飞, 侯位昭, 等. 基于簇过滤的优势集模糊聚类集成[J]. 计算机与网络, 2019, 45(7): 61-64. |
| [6] |
LI Shan, ZHANG Huaxiang. Ensemble clustering method based on Bagging[J]. Computer Engineering and Design, 2010, 31(1): 164-166. (in Chinese) 李杉, 张化祥. 基于Bagging的聚类集成方法[J]. 计算机工程与设计, 2010, 31(1): 164-166. |
| [7] |
GUO Wenyan, ZHOU Jirui, ZHANG Jiaojiao. Image enhancement algorithm based on improved artificial bee colony[J]. Computer Engineering, 2017, 43(11): 261-271. (in Chinese) 郭文艳, 周吉瑞, 张姣姣. 基于改进人工蜂群的图像增强算法[J]. 计算机工程, 2017, 43(11): 261-271. |
| [8] |
WANG Shuwei, GUO Xiuping, LIU Jia. An efficient hybrid artificial bee colony algorithm for disassembly line balancing problem with sequence-dependent part removal times[J]. Engineering Optimization, 2019, 51(11): 1920-1937. DOI:10.1080/0305215X.2018.1564918 |
| [9] |
XI Wanqiang, WANG Yaoyao, CHEN Bai, et al. Iterative learning control of robot based on artificial bee colony algorithm[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ:Journal of Systems and Control Engineering, 2019, 233(9): 1221-1238. DOI:10.1177/0959651818824202 |
| [10] |
KAUFMAN L, ROUSSEEUW P J. Finding groups in data:an introduction to cluster analysis[J]. Applied Statistics, 1991, 40(3): 486-487. DOI:10.2307/2347530 |
| [11] |
DING Chuchu, SUN Ting, ZOU Xin, et al. Epileptic brain network analysis based on Kendall's improved synchronization algorithm[J]. Journal of Physics:Conference Series, 2018, 1053(1): 1-5. |
| [12] |
HERLOCKER J L, KONSTAN J A, TERVEEN L G, et al. Evaluating collaborative filtering recommender systems[J]. ACM Transactions on Information Systems(TOIS), 2004, 22(1): 5-53. DOI:10.1145/963770.963772 |
| [13] |
CALINSKI T, HARABASZ J. A dendrite method for cluster analysis[J]. Communications in Statistics-Simulation and Computation, 1974, 3(1): 1-27. DOI:10.1080/03610917408548446 |
| [14] |
CHEN S Y, STEM M, CERULLO M, et al. Predicting the risk of readmission from dehydration after ileostomy formation:the dehydration readmission after ileostomy prediction score[J]. Diseases of the Colon and Rectum, 2018, 61(12): 1410-1417. DOI:10.1097/DCR.0000000000001217 |
| [15] |
ZHANG P, BIGIO B, RAPAPORT F, et al. PopViz:a Webserver for visualizing minor allele frequencies and damage prediction scores of human genetic variations[J]. Bioinformatics, 2018, 34(24): 4307-4309. DOI:10.1093/bioinformatics/bty536 |
| [16] |
LI Yuanbo, CAO Han. Collaborative filtering recommendation algorithm based on PCA dimension reduction[J]. Computer Technology and Development, 2016, 26(2): 26-30. (in Chinese) 李远博, 曹菡. 基于PCA降维的协同过滤推荐算法[J]. 计算机技术与发展, 2016, 26(2): 26-30. |
| [17] |
CACHEDA F, CARNEIRO V, FERNANDEZ D, et al. Comparison of collaborative filtering algorithms; limitations of current techniques and proposals for scalable, high-performance recommender systems[J]. ACM Transactions on the Web, 2011, 5(1): 161-171. DOI:10.1145/1921591.1921593 |
| [18] |
LALCHANDANI U R, SAHAI V, HERSBERGER K, et al. A radiologist's guide to response evaluation criteria in solid tumors[J]. Current Problems in Diagnostic Radiology, 2019, 48(6): 576-585. DOI:10.1067/j.cpradiol.2018.07.016 |
| [19] |
BOURASC, TSOGKAS V.Clustering to deal with the new user problem[C]//Proceedings of the 15th International Conference on Computational Science and Engineering.Washington D.C., USA: IEEE Press, 2012: 58-65.
|
| [20] |
MA Hongwei, ZHANG Guangwei, LI Peng. Survey of collaborative filtering algorithms[J]. Journal of Chinese Computer Systems, 2009, 30(7): 1282-1288. (in Chinese) 马宏伟, 张光卫, 李鹏. 协同过滤推荐算法综述[J]. 小型微型计算机系统, 2009, 30(7): 1282-1288. |
 2020, Vol. 46
2020, Vol. 46
