2. 大连外国语大学 语言智能研究中心, 辽宁 大连 116044
2. Research Center for Language Intelligence, Dalian University of Foreign Languages, Dalian, Liaoning 116044, China
在知识图谱中, 知识表示为三元组 < 头实体, 关系, 尾实体>(即RDF三元组)的形式, 使得知识能够得到结构化处理[1]。人们必须为知识图谱应用设计各种基于图形的方法, 然而知识图谱中的知识不能作为完备的知识, 尤其是在大规模知识图谱上下文中, 需要不断补充其中的实体关系进行知识图谱补全[2]。同时, 现有的知识图谱均以三元组的形式表示知识, 这限定了知识必须包含头实体、关系和尾实体三部分, 但实际上三元组并不是适合所有知识的表示方式。例如管理员想查找某学生的导师A的博士论文, 但是已有知识库中并没有导师A的博士论文, 必须得到一个不完全的三元组 < A, 博士论文, ?>, 要补全这个三元组, 必须补充知识库。按照知识图谱的规则, 这个不完全三元组无法加入现有的知识图谱, 只能在以后通过扩充知识库的方式来补全成完整的三元组后加入。因此, 研究保存不完全三元组的方法, 实现知识图谱的动态补全, 是一个具有研究意义的问题。
RDF三元组中关系本身的特性会对头尾实体进行限制。例如句子“Lennon was murdered by Champan outside the Dakota on Dec.8.1980”中蕴含的三元组为 < Chapman, kill, Lennon>, 其中关系“kill”决定了头尾实体都属于“人”这类实体, 属于地理位置这类的实体“Dakota”则可以被排除。
在多数知识图谱中, 关于实体有简明的描述[3], 这些丰富的语义信息对实体非常重要。以FreeBase中的三元组(William Shakespare, book/author/works_written, Romeo and Juliet)为例, 头实体“William Shakespare”含有描述“William Shakespare was an English poet, playwright, and actor…”, 尾实体“Romeo and Juliet”含有描述“Romeo and Juliet is a tragedy written by William Shakespare early in his career…”, 这些描述对三元组的补全具有重要作用。
本文提出一个运用实体描述的知识图谱补全方法, 即基于半边的多层卷积模型(Half-edged based Multilayer Convolution Model, HMCM)。该模型利用实体描述和关系自身可以对实体类别进行限制的特性组成半边,以保存缺失头实体或尾实体的不完全三元组。在此基础上, 通过将对应类别的半边相结合,减少输入三元组的数量,再把候选的不完全三元组代入卷积神经网络(Convolutional Neural Network, CNN)进行知识图谱补全。
1 相关工作 1.1 知识图谱补全针对知识图谱补全问题, 研究者提出了较多的方法[4-6], 如基于结构与文本联合表示的知识图谱补全方法[4]和基于双层随机游走的关系推理算法[6]等。学习知识嵌入的代表模型有距离模型、单层神经网络模型、能量模型、双线性模型、矩阵分解模型和翻译模型等[7]。张量神经网络模型[8]和基于文档特征的向量空间模型[9]在现有模型中加入多层神经网络来进行知识图谱的补全。文献[10-11]通过类比实验发现, 词向量空间的平移不变现象普遍存在于词汇的语义关系和句法关系中。对此, 文献[12]进一步提出翻译模型TransE。然而该模型解决一对一关系的问题效果较好, 但无法应对一对多、多对一和多对多关系的问题。文献[13]提出TransH模型, 通过将关系建模为超平面, 并将h和t投影到关系特定超平面, 从而让实体在不同的关系中扮演不同的角色, 以解决TransE存在的问题。文献[14]提出的TransR模型在不同的语义空间中模拟实体和关系, 并在学习嵌入时将实体从实体空间映射到关系空间。文献[15]则提出一种基于多步关系路径的表示学习模型PTransE。文献[16]提出的DSKG模型利用循环神经网络实现了知识图谱的补全和实体预测。文献[17]提出的DKRL模型用CBOW和卷积神经网络把实体的描述运用到三元组的补全中。文献[18]提出的ProjE模型关注实体与关系之间的联系, 不需要预训练, 参数规模小, 并且预测能力强。文献[19]提出的ConMask模型先以计算实体和关系语义相似度的方法对错误的三元组进行屏蔽, 再进行补全工作, 大幅减少了训练时间。
1.2 半边图文献[20]介绍了半边原理及其在知识图谱中的应用。该文指出半边是一个基本概念, 其将资源视为顶点和资源属性信息表示为半边, 不同顶点的半边依据可结合性而结合成为边, 表示资源属性之间的关联关系。此后, 文献[21-22]介绍了半边在本体和因子图中的应用, 文献[23]则证明了半边图在大规模图形数据库相似性搜索和高性能查询处理方面的优势。
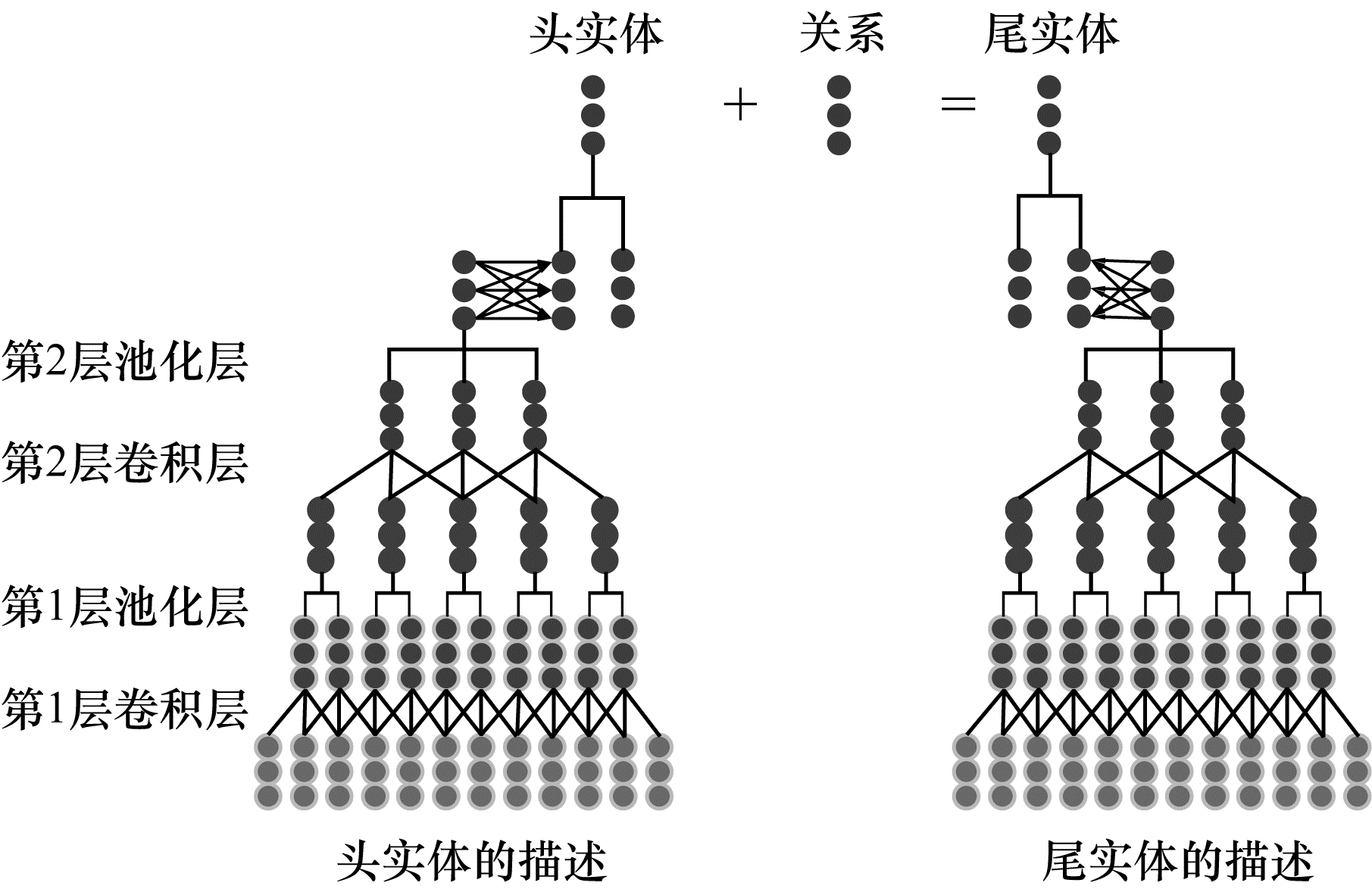
2 基于半边的多层卷积模型本文提出基于半边的多层卷积模型HMCM。该模型通过使用实体和关系约束组成两种半边, 并根据结合规则使之相互结合, 得到候选三元组集。对于需要补全的缺失三元组, 在候选三元组集中查找对应的候选三元组代入CNN进行补全。本文模型的整体结构如图 1所示, 其利用两个两层的卷积神经网络, 分别对头实体的描述和尾实体的描述进行训练。在此基础上, 将训练得到的实体描述表示与实体结构表示相结合, 使用TransE模型进行实体和关系的补全。
|
Download:
|
| 图 1 HMCM模型结构 Fig. 1 HMCM model structure | |
以图的顶点表示实体, 以边表示关系, 是知识表示的常用方法。这种方法将顶点和边作为不可分割的原子概念。半边即是针对这一问题提出的概念,
其定义[17]如下:
定义1(半边) 半边是描述资源属性的概念, 资源有若干属性, 对应于一个顶点有若干个半边。半边具有以下特点:
1) 一个半边属于某个顶点, 且分为不同的半边类型。半边类型由资源特征属性决定。
2) 半边之间相互独立, 即属性之间相互独立, 但半边与其他的半边可以相互结合。资源特征属性之间的关联关系, 表示何种类型的两个半边可以结合, 称为半边结合类型。
3) 每个半边有一个数值性度量值, 称为半边权值, 一般取大于0的实数, 与资源属性的载荷情况成反比, 即半边权值越大, 资源属性的载荷越小。
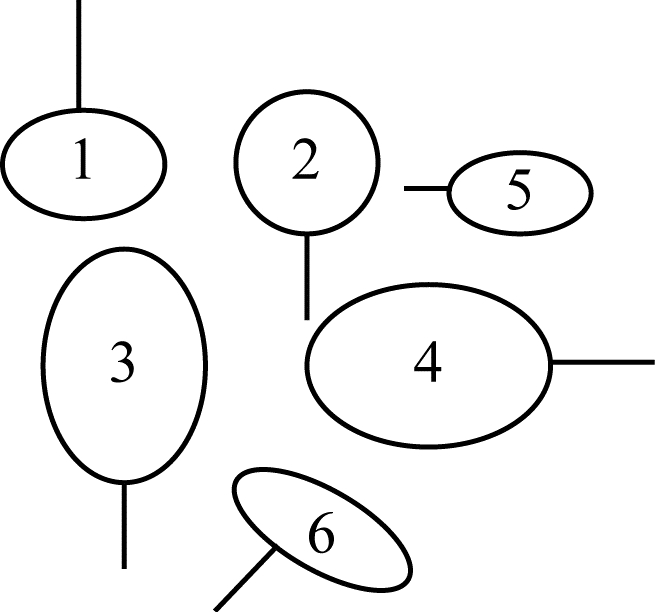
图 2展示了常见半边的形态。
|
Download:
|
| 图 2 半边示意图 Fig. 2 Schematic diagram of half-edge | |
参考半边的定义, 结合知识图谱中三元组的特性, HMCM所使用的三元组半边定义如下:
定义2(三元组半边) 三元组半边为知识图谱补全所使用的特殊半边, 分为头结点半边和尾结点半边两种, 每个顶点均只有一个半边与其相连。三元组半边符号定义如下:
1) 头结点半边HE1={Hh, Rh, csm}。其中:Hh={h, Wh}代表顶点, 由三元组中的头实体h和该实体的描述Wh组成; Rh={r, rs}代表与顶点相连的半边, 由三元组中的关系r和该关系所连接的头尾结点类别rs组成; csm为实体描述与关系的相似度得分。
2) 尾结点半边HE2={Tt, Rh, csm}。其中:Tt={t, Wt}代表顶点, 由三元组中的尾实体t和该实体的描述Wt组成; Rh与csm定义与头结点半边中相同。
使用上述两种半边, 即可得到HMCM所使用的半边集HE={HE1, HE2}。
2.2 半边的实现与结合 2.2.1 半边的实现给定三元祖(h, r, t)∈T, 其中, h, t∈E代表实体;
定义实体类别S={s1, s2, …, sn}, 其中每个实体h(或t)都有自己的类别{si, si+1, …, sj}, 或是人, 或是位置等。对关系r追加候选实体类别rs={sh, st}, 其中, sh是关系r所连接的头实体类别, st是其尾实体类别。例如关系father的候选实体类rs={s1, s1}, s1为生物类的实体集, 这可以解释为生物的父亲一定是生物。因此, 那些逻辑上错误的三元组(比如某人的父亲是某个地理位置)就可以被过滤掉。
最后处理实体的描述。先从描述文本中删除所有停用词, 再标记所有短语并将这些短语视为单词。这些描述单词的集合定义为Wh=[w1, w2 …, wi], 即词向量wi是实体h的一个描述单词。
通过以上符号可以定义三元组的两种半边HE1和HE2, 如式(1)和式(2)所示:
| $ {\rm{HE}}1 = \left\{ {\mathit{\boldsymbol{h}}, \mathit{\boldsymbol{r}}, {\rm{rs}}, {\mathit{\boldsymbol{W}}_{\rm{h}}}, {\rm{csm}}} \right\} $ | (1) |
| $ {\rm{HE}}2 = \left\{ {\mathit{\boldsymbol{t}}, \mathit{\boldsymbol{r}}, {\rm{rs}}, {\mathit{\boldsymbol{W}}_{\rm{t}}}, {\rm{csm}}} \right\} $ | (2) |
其中, 实体h(或t)和该实体的描述Wh(或Wt)为顶点, 关系r为半边, 候选实体类rs和csm为半边的权值。csm是实体的描述与关系相似度得分, 其定义如式(3)所示:
| $ {\mathop{\rm csm}\nolimits} = \frac{1}{i}\sum\limits_{x = 1}^i {\left( {a\frac{{{\mathit{\boldsymbol{w}}_x}*\mathit{\boldsymbol{r}}}}{{\left\| {{\mathit{\boldsymbol{w}}_x}} \right\|*\parallel \mathit{\boldsymbol{r}}\parallel }}} \right)} $ | (3) |
其中, a是大于1的常数, 用于缓和求平均值所造成的相似度差距缩小的现象。
2.2.2 半边的结合设实体集E中的两个实体h和t, 若h∈HE1, t∈HE2, HE1.r=HE2.r, 并满足式(4):
| $ |{\rm{HE}}1 \cdot {\mathop{\rm csm}\nolimits} - {\rm{HE}}2 \cdot {\mathop{\rm csm}\nolimits} | > c $ | (4) |
其中, c为设定阈值。三元组 < h, r, t>是一个补全的候选三元组, 由此得到候选三元组的集合HRT, 如式(5)所示:
| $ {\rm{HRT}} = \left\{ {\begin{array}{*{20}{l}} {\left\langle {{\mathit{\boldsymbol{h}}_i}, {\mathit{\boldsymbol{r}}_j}, {\mathit{\boldsymbol{t}}_k}} \right\rangle \mid {\mathit{\boldsymbol{h}}_i} \in {\rm{HE}}1, {\mathit{\boldsymbol{t}}_k} \in {\rm{HE}}2}\\ {{\rm{HE}}1.\mathit{\boldsymbol{r}} = {\rm{HE}}2.\mathit{\boldsymbol{r}} = {\mathit{\boldsymbol{r}}_j}}\\ {|{\rm{HE}}1 \cdot {\rm{csm}} - {\rm{HE}}2 \cdot {\rm{csm}}| > c} \end{array}} \right. $ | (5) |
HRT将被用于进行实体和关系预测。
2.2.3 实体预测与关系预测对于实体预测, 即缺失一个头实体或尾实体的三元组, 首先使用其中的实体和关系组成半边, 在HRT中选择满足该半边的候选三元组, 再将这些候选三元组代入HMCM进行补全。
同理, 对于关系预测, 可在HRT中得到同时含有已知头尾实体的三元组集合, 再使用HMCM进行补全。
2.3 卷积神经网络卷积神经网络(CNN)是一种广泛应用于图像的高效模型, 其对某些自然语言处理任务和关系分类任务非常有效[17]。同时, CNN也可以用于关系分类任务[24-25]。鉴于实体描述词汇量大、信息环境复杂、推理规则不明确等特点, 本文模型需要一个具有良好的容错能力且并行处理能力和自学习能力、运行速度快、自适应能力强的模型来进行训练, 而卷积神经网络正符合此需求。
参考DKRL模型, HMCM使用两层的卷积神经网络, 第1层池化层为max-pooling层, 第2层池化层为mean-pooling层, 具体描述如下:
在卷积层中, 设Zi为第i个卷积层的输出, Xi为第i个卷积层的输入, 大小为k的卷积窗滑过Xi中的输入向量以得到Xi(k)。在第1个卷积层中, X1是实体的描述向量(x0, x1, …, xn)。因此, 卷积层的第i层输出向量如式(6)所示:
| $ {\mathit{\boldsymbol{Z}}_i} = \sigma \left( {{\mathit{\boldsymbol{W}}_i}{\mathit{\boldsymbol{X}}_i} + {\mathit{\boldsymbol{b}}_i}} \right) $ | (6) |
其中,
模型的第1层输入为头实体和尾实体对应的描述单词集Wh和Wt, 即X1=Wh(或X1=Wt)。
卷积层之后使用池化层来缩小CNN的参数空间和滤波器噪声。卷积层的输出向量被分成多个大小为nL的非重叠窗口。对于第1层池化层, 选取每个窗口的最大值以构成新的向量。nL-max-pooling得到nL大小的窗口内输入向量中最大的特征值, 如式(7)所示:
| $ {\mathit{\boldsymbol{X}}_2} = \max \left( {{\mathit{\boldsymbol{Z}}_{{n_{\rm{L}}} \times i}}, {\mathit{\boldsymbol{Z}}_{{n_{\rm{L}}} \times (i + 1)}}, \cdots , {\mathit{\boldsymbol{Z}}_{{n_{\rm{L}}} \times (i + 1) - 1}}} \right) $ | (7) |
nL-max-pooling可以缩小nL次特征表示的大小, 降低CNN编码器的复杂性和参数学习的成本。然而, 一些描述非常复杂, 不同的句子可能表示信息的不同方面, 仅使用max-pooling会导致大量的信息丢失。对此, 第2个池化层使用mean-pooling以减少信息丢失, 使所有包含不同本地信息的输入向量都能对最终实体嵌入有贡献, 并可以在反向传播期间进行更新, 所得特征值如式(8)所示:
| $ {\mathit{\boldsymbol{X}}_3} = \sum\limits_{i = 1}^m {\frac{{{\mathit{\boldsymbol{Z}}_{2i}}}}{m}} $ | (8) |
最终结果通过一层全连接神经网络与第2层池化层相连, 输出结果为与实体结构向量同维的向量, 记为实体的描述向量。
使用卷积神经网络训练得到的实体描述表示与实体结构表示组合形成最终的实体表示hc、tc。基于描述的实体表示记为hd、td, 基于结构的实体记为hs、ts, 则hc和tc的计算公式如式(9)和式(10)所示:
| $ {{\mathit{\boldsymbol{h}}_c} = \frac{{{\mathit{\boldsymbol{h}}_{\rm{s}}} + {\mathit{\boldsymbol{h}}_{\rm{d}}}}}{2}} $ | (9) |
| $ {{\mathit{\boldsymbol{t}}_{\rm{c}}} = \frac{{{\mathit{\boldsymbol{t}}_{\rm{s}}} + {\mathit{\boldsymbol{t}}_{\rm{d}}}}}{2}} $ | (10) |
最后使用TransE模型进行实体和关系预测, 如式(11)所示:
| $ S = \left\| {{\mathit{\boldsymbol{h}}_{\rm{c}}} + \mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{t}}_{\rm{c}}}} \right\| $ | (11) |
由于已经使用半边筛选了实体的类别, 此处实体的输入量仅为某个类中实体的数量, 因此可缩短运行时间。
2.4 损失函数选择TransE的损失函数作为训练目标, 如式(12)所示:
| $ \begin{array}{l} L = \sum\limits_{(\mathit{\boldsymbol{h}}, \mathit{\boldsymbol{r}}, \mathit{\boldsymbol{t}}) \in T} {\sum\limits_{\left( {{\mathit{\boldsymbol{h}}^\prime }, {\mathit{\boldsymbol{r}}^\prime }, {\mathit{\boldsymbol{t}}^\prime }} \right) \in {T^\prime }} {\max } } \left\{ {\gamma + \left| {{\mathit{\boldsymbol{h}}_{\rm{c}}} + \mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{t}}_{\rm{c}}}} \right| - } \right.\\ \;\;\;\;\left. {\left| {\mathit{\boldsymbol{h}}_c^\prime + \mathit{\boldsymbol{r}} - \mathit{\boldsymbol{t}}_{\rm{c}}^\prime } \right|, 0} \right\} \end{array} $ | (12) |
在式(12)中, γ是边际超参数, γ>0, T′是训练集T的负例的集合, 如式(13)所示:
| $ \begin{array}{l} {T^\prime } = \left\{ {\left( {{\mathit{\boldsymbol{h}}^\prime }, \mathit{\boldsymbol{r}}, \mathit{\boldsymbol{t}}} \right)\left| {{\mathit{\boldsymbol{h}}^\prime } \in E \cup \left( {\mathit{\boldsymbol{h}}, {\mathit{\boldsymbol{r}}^\prime }, \mathit{\boldsymbol{t}}} \right)} \right|{\mathit{\boldsymbol{r}}^\prime } \in } \right.\\ \left. {\;\;\;\;\;\;R \cup \left( {\mathit{\boldsymbol{h}}, \mathit{\boldsymbol{r}}, {\mathit{\boldsymbol{t}}^\prime }} \right)\mid {\mathit{\boldsymbol{t}}^\prime } \in E} \right\} \end{array} $ | (13) |
T′为三元组中头实体、尾实体或关系被另一个实体或关系随机替换所组成的错误三元组集。如果三元组已经在T中, 则不会将其视为负样本。由于h和t有两种表示(基于结构的表示和基于描述的表示), 因此在基于边距的得分函数中, 实体的表示是基于结构表示和基于描述表示的平均值。
2.5 算法描述HMCM算法伪代码如下:
算法1 HMCM算法
输入 三元组T={(h, r, t)}, 每个实体对应的描述Wh
for e in E://在实体和关系之间组合, 形成半边
for r in R:
if (e.s==rs.sh):
csm=a*(Wh*r)/(||Wh||*||r||); HE1.append(h, r, csm)
if (e.s==rs.st):
csm=a*(Wt*r)/(||Wt||*||r||); HE2.append(t, r, csm)
else:continue
for i in HE1://按照结合规则进行半边的结合, 利用c
//进行筛选
for j in HE2:
if(|i.csm-j.csm|>c):HRT.append(< h, r, t>)
for < h, r, t> in HRT://实体描述代入CNN得到最终
//的实体向量
hd=Wh→CNN; hc=(hs+hd)/2
td=Wt→CNN; tc=(ts+td)/2
(hc, r, tc)→TransE//最终结果代入TransE模型
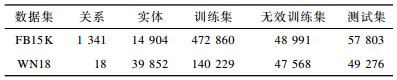
3 实验与结果分析本文实验的数据集使用FB15K和WN18, 这两个数据集均是从典型的大型知识库中提取的数据集, 可用于评估知识图谱补全模型。为确认每个实体都能进行基于描述表示学习的训练, 从数据集中删除了部分实体和包含这些实体的所有三元组。处理后的FB15K和WN18数据集的数据分布如表 1所示。其中:FB15K训练集有472 860个三元组、14 904个实体和1 341个关系, 测试集有57 303个三元组; WN18中训练集有140 229个三元组、39 852个实体和18个关系, 测试集有49 276个三元组。
|
下载CSV 表 1 FB15K和WN18的数据分布 Table 1 Data distribution of FB15K and WN18 |
训练模型采用多次实验来寻找最佳的参数设置, 其中, 实体和关系维度n分别为50、80和100, 学习率λ分别为0.000 5、0.001 0和0.002 0, 边缘参数γ分别为0.5、1.0、1.5和2.0。第1个池化层使用4-max-pooling。
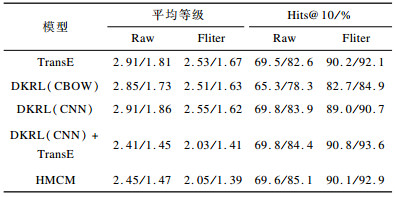
使用正确实体的平均等级和排在前10名(实体)或第1名(关系)的正确率这两种指标对模型性能进行评价, 同时参照文献[13], 遵循Raw和Filter 2个评估标准并对比CBOW模型和CNN模型, 得到实体预测和关系预测的比较结果, 如表 2和表 3所示, 表中数据均以FB15K/WN18的形式列出。

|
下载CSV 表 2 实体预测结果对比 Table 2 Comparison of entity prediction results |
|
下载CSV 表 3 关系预测结果对比 Table 3 Comparison of relation prediction results |
可以看出, HMCM与DKRL(CNN)+TransE在平均等级和Hits@10上显著优于TransE和CBOW。在实体预测方面, HMCM略优于DKRL, 而在关系预测方面, DKRL模型相对占优。这表明在基于结构补全方面, HMCM与DKRL都没有优于TransE。这是由于TransE在结构补全方面较为优秀, 而DKRL和HMCM都是在TransE的基础上进行优化, 并没有对其进行较大改进, 因此, 相比之下优势并没有非常大, 但相较于DKRL, HMCM对实体和关系的组合进行了一定限制, 提高了精确度, 因此, 在实体预测方面HMCM更占优。而对于关系预测, HMCM对结构与描述做了平均处理, 削弱了关系描述中隐藏的语义对于关系预测的作用, 导致预测关系的能力变弱。同时由于在半边的结合规则中, 关系是非常重要的一环, 缺失关系对半边的结合精确度有所影响, 因此HMCM的预测能力与DKRL相差无几。为对此进行改进, 后续将从实体的描述中发掘头尾实体之间的联系来加强关系预测的能力, 弥补其不足。
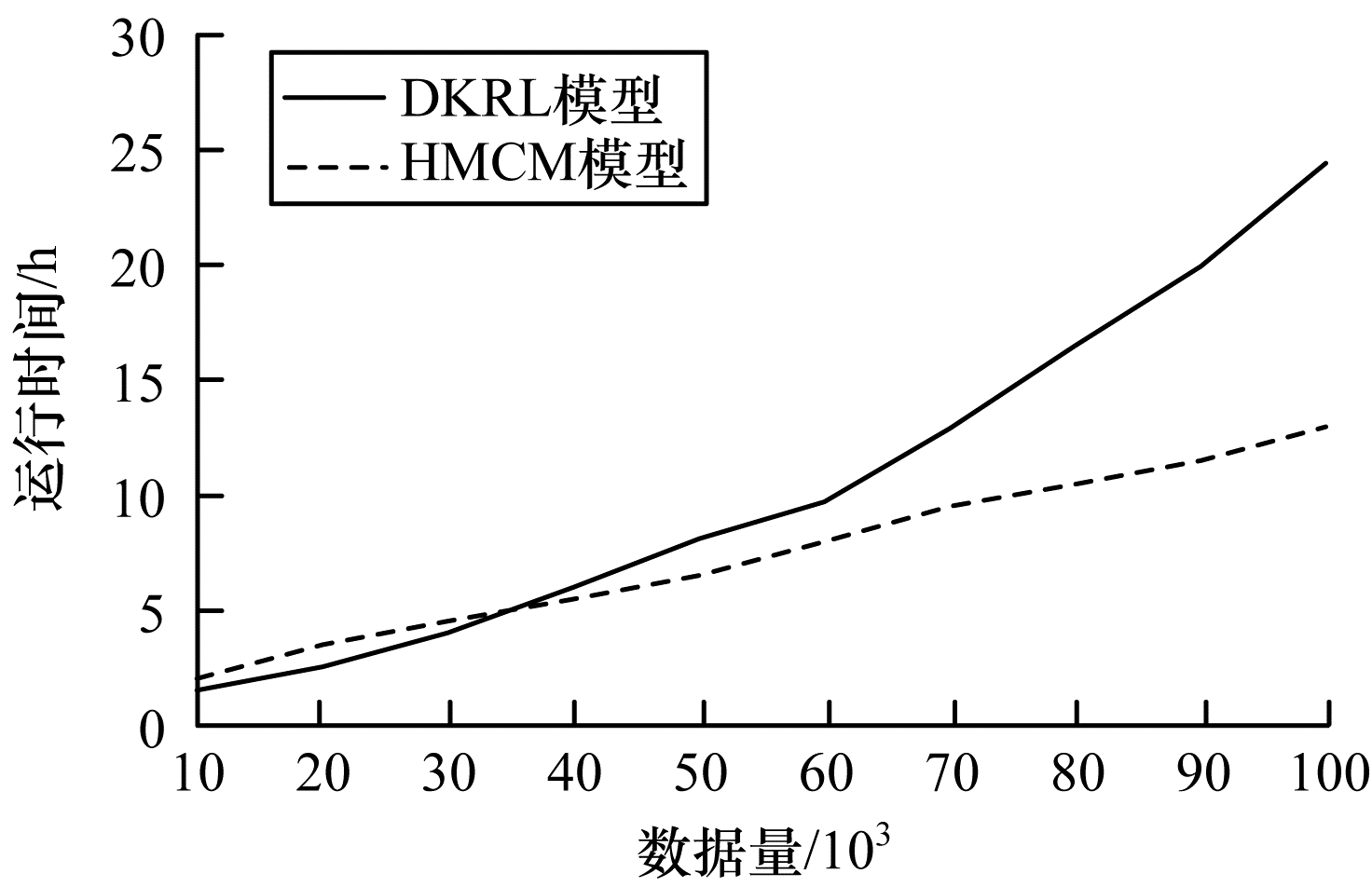
从训练集中选取100 000个数据对DKRL和HMCM分别进行测试, 记录模型运行时间, 如图 3所示。可以看出, 当数据量较少时, HMCM的效率略低于DKRL, 而随着数据量不断增长, HMCM的运行效率逐渐比DKRL高。这是因为HMCM将三元组的范围扩展为半边, 这虽然能发现潜在语义关系, 但也一定程度上扩大了搜索范围, 因此, 当数据量较少时, 其补全效率比DKRL略低, 而随着数据量的增长, HMCM中半边的作用逐渐体现, 数据过滤效果逐渐增强, 因此, 运行时间也较DKRL越来越少。
|
Download:
|
| 图 3 DKRL模型与HMCM模型的运行时间对比 Fig. 3 Comparison of running time by DKRL model and HMCM model | |
此外, HMCM把不完全的三元组以半边的形式加以暂存, 这让只能通过补充知识库才能进行补全的三元组在后续补全工作中可以使用现有的半边来加快补全进程, 避免了不必要且重复的遍历工作, 从而实现知识图谱的动态补全。
4 结束语本文提出HMCM模型, 通过引入半边优化具有实体描述的知识图谱学习, 使用深度卷积神经网络提取实体描述的语义, 并将描述与结构相结合进行知识图谱补全。实验结果表明, 该模型在实体预测和关系预测中均能达到预期目标, 并且在知识图谱的动态补全方面具有优势。但HMCM模型仅考虑表示学习的实体描述, 而未将其他类型的文本信息运用到模型中。此外, 模型中虽然引入了半边来提高补全的精度, 但是人工标记关系和实体分类依然耗时耗力。针对以上不足, 下一步将对模型进行优化, 完成实体的自动分类, 同时对关系的约束进行定义, 进一步探索时变半边图与知识图谱结合的方法。
| [1] |
SINGHAL A.Introducing the knowledge graph: things, not strings[EB/OL].[2019-07-08].http://googleblog.blog-spot.ie/2012/05/introducing-knowledge-graph-things-not.html.
|
| [2] |
XU Zenglin, SHENG Yongpan, HE Lirong, et al. Review on knowledge graph techniques[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(4): 589-606. (in Chinese) 徐增林, 盛泳潘, 贺丽荣, 等. 知识图谱技术综述[J]. 电子科技大学学报, 2016, 45(4): 589-606. |
| [3] |
WANG Hui, YU Bo, HONG Yu, et al. Web information extraction system based on knowledge graph[J]. Computer Engineering, 2017, 43(6): 118-124. (in Chinese) 王辉, 郁波, 洪宇, 等. 基于知识图谱的Web信息抽取系统[J]. 计算机工程, 2017, 43(6): 118-124. |
| [4] |
BAO Kaifang, GU Junzhong, YANG Jing. Knowledge graph completion method based on jointly representation of structure and text[J]. Computer Engineering, 2018, 44(7): 205-211. (in Chinese) 鲍开放, 顾君忠, 杨静. 基于结构与文本联合表示的知识图谱补全方法[J]. 计算机工程, 2018, 44(7): 205-211. |
| [5] |
WANG Fei, LIU Jingping, LIU Bin, et al. Survey on construction of code knowledge graph and intelligent software development[J]. Journal of Software, 2020, 31(1): 47-66. (in Chinese) 王飞, 刘井平, 刘斌, 等. 代码知识图谱构建及智能化软件开发方法研究[J]. 软件学报, 2020, 31(1): 47-66. |
| [6] |
LIU Qiao, HAN Minghao, JIANG Liuyi, et al. Two-tier random walk based relational inference algorithm[J]. Chinese Journal of Computers, 2017, 40(6): 1275-1290. (in Chinese) 刘峤, 韩明皓, 江浏祎, 等. 基于双层随机游走的关系推理算法[J]. 计算机学报, 2017, 40(6): 1275-1290. |
| [7] |
LIU Zhiyuan, SUN Maosong, LIN Yankai, et al. Knowledge representation learning:a review[J]. Journal of Computer Research and Development, 2016, 53(2): 247-261. (in Chinese) 刘知远, 孙茂松, 林衍凯, 等. 知识表示学习研究进展[J]. 计算机研究与发展, 2016, 53(2): 247-261. |
| [8] |
SOCHER R, CHEN D, MANNING C D, et al.Reasoning with neural tensor networks for knowledge base completion[C]//Proceedings of the 26th International Conference on Neural Information Processing Systems.New York, USA: ACM Press, 2013: 926-934.
|
| [9] |
NEELAKANTAN A, ROTH B, MCCALLUM A.Compositional vector space models for knowledge base completion[EB/OL].[2019-07-08].https://arxiv.org/pdf/1504.06662.pdf.
|
| [10] |
MIKOLOV T, CHEN K, CORRADO G, et al.Efficient estimation of word representations in vector space[EB/OL].[2019-07-08].https://arxiv.org/pdf/1301.3781.pdf.
|
| [11] |
MIKOLOV T, SUTSKEVER I, CHEN K, et al.Distributed representations of words and phrases and their compositionality[C]//Proceedings of International Conference on Neural Information Processing Systems.[S.l.]: Curran Associates Inc., 2013: 3111-3119.
|
| [12] |
BORDES A, USUNIER N, GARCIA-DURAN A, et al.Translating embeddings for modeling multi-relational data[C]//Proceedings of International Conference on Neural Information Processing Systems.[S.l.]: Curran Associates Inc., 2013: 2787-2795.
|
| [13] |
WANG Zhen, ZHANG Jianwen, FENG Jianlin, et al.Knowledge graph embedding by translating on hyperplanes[C]//Proceedings of the 28th AAAI Conference on Artificial Intelligence.[S.l.]: AAAI, 2014: 1-5.
|
| [14] |
LIN Yankai, LIU Zhiyuan, SUN Maosong, et al.Learning entity and relation embeddings for knowledge graph completion[C]//Proceedings of the 29th AAAI Conference on Artificial Intelligence.[S.l.]: AAAI, 2015: 1-5.
|
| [15] |
LIN Yankai, LIU Zhiyuan, LUAN Huanbo, et al.Modeling relation paths for representation learning of knowledge bases[EB/OL].[2019-07-08].https://arxiv.org/pdf/1506.00379v2.pdf.
|
| [16] |
GUO Lingbing, ZHANG Qingheng, GE Weiyi, et al.DSKG: a deep sequential model for knowledge graph completion[C]//Proceedings of China Conference on Knowledge Graph and Semantic Computing.Berlin, Germany: Springer, 2018: 65-77.
|
| [17] |
XIE Ruobing, LIU Zhiyuan, JIA Jia, et al.Representation learning of knowledge graphs with entity descriptions[C]//Proceedings of the 30th AAAI Conference on Artificial Intelligence.New York, USA: ACM Press, 2016: 2659-2665.
|
| [18] |
SHI B, WENINGER T.ProjE: embedding projection for knowledge graph completion[C]//Proceedings of the 31st AAAI Conference on Artificial Intelligence.[S.l.]: AAAI, 2017: 1236-1242.
|
| [19] |
SHI B, WENINGER T.Open-world knowledge graph completion[C]//Proceedings of the 32nd AAAI Conference on Artificial Intelligence.[S.l.]: AAAI, 2018: 1-5.
|
| [20] |
CHEN Tuanqiang, WANG Zhengming. Time-varying half-edge graph:a novel topology model for attributed relationships of Internet resources[J]. Journal of Computer Applications, 2007, 27(3): 512-513. (in Chinese) 陈团强, 王正明. Internet资源属性关系的新拓扑模型——时变半边图[J]. 计算机应用, 2007, 27(3): 512-513. |
| [21] |
LASTRA-DÍAZ J J, GARCÍA-SERRANO A, BATET M, et al. HESML:a scalable ontology-based semantic similarity measures library with a set of reproducible experiments and a replication dataset[J]. Information Systems, 2017, 66: 97-118. DOI:10.1016/j.is.2017.02.002 |
| [22] |
HOFFMANN C, ROSTALSKI P. Linear optimal control on factor graphs-a message passing perspective-[J]. IFAC-PapersOnLine, 2017, 50(1): 6314-6319. DOI:10.1016/j.ifacol.2017.08.914 |
| [23] |
ZHAO Peixiang.Similarity search in large-scale graph data-bases[M]//ZOMAYA A Y, SAKR S.Handbook of big data technologies.Berlin, Germany: Springer, 2017: 507-529.
|
| [24] |
ZENG Daojian, LIU Kang, LAI Siwei, et al.Relation classification via convolutional deep neural network[C]//Proceedings of the 25th International Conference on Computational Linguistic.Dublin, Ireland: [s.n.], 2335-2344.
|
| [25] |
ZHANG Dongxu, YUAN Bin, WANG Dong, et al.Joint semantic relevance learning with text data and graph knowledge[C]//Proceedings of the 3rd Workshop on Continuous Vector Space Models and Their Compositionality.[S.l.]: ACL, 2015: 32-40.
|
 2020, Vol. 46
2020, Vol. 46
