2. 航天宏康智能科技(北京)有限公司, 北京 100048
2. Aerospace Hongkang Intelligent Technology(Beijing) Co., Ltd., Beijing 100048, China
随着人工智能技术的不断发展, 多智能体协同控制在军事应用中取得了重大突破[1-2], 以无人机、无人车[3]和无人水面艇等为代表的无人智能体在执行军事作战中的侦察、护航、打击等任务时[4-6]通常以追踪问题为基础开展研究。而在现代战场环境下, 由于任务和环境的复杂性, 一般需要多个作战智能体协同完成对多个动态运动目标的追踪任务, 因此智能体面对动态变化的战场态势, 如何进行任务分工及采取何种行动策略将会影响智能体的作战质量和作战效率。
针对多目标追踪问题, 学者们进行了大量研究并取得一定的成果。文献[7]提出一种合作团队追踪单一运动目标的方法, 针对运动目标位置估计的不确定性, 最大限度地缩小目标可到达空间。仿真结果表明, 在位置不确定的情况下, 该方法能通过追踪智能体捕获目标。文献[8]提出基于轨迹集和随机有限集的多目标追踪问题求解方法, 通过多对象密度函数确定测量值的贝叶斯轨迹分布, 其中包含所有轨迹的信息。
强化学习主要解决智能决策问题, 其目前在单智能体决策领域取得了较大成功, 如AlphaGo、AlphaGo Zero等。针对团队最优决策问题, 学者们主要通过基于价值函数和概率这两种方法将单智能体强化学习扩展到多智能体强化学习。文献[9-11]基于价值函数的方法, 采用Q-learning、DQN和IQL算法并结合奖励函数, 仿真模拟了在完全协作、完全竞争及非完全协作/竞争环境下多个智能体的性能表现。但是, 当环境较复杂及智能体规模较大时, 上述算法的稳定性和可扩展性较差, 且难以应对较大的连续动作空间, 无法输出离散状态动作值。文献[12-14]基于概率的方法提出深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)算法, 在动作输出方面通过网络拟合策略函数并直接输出动作值, 可应对更大的动作空间以及连续动作的输出。针对上述方法存在的学习时间长、实时性差等问题, 本文提出一种基于多智能体协同强化学习的多目标追踪方法(Multi-Target Tracking method based on Multi-Agent Collaborative Reinforcement Learning, MTT-MACRL)。
1 多目标追踪问题 1.1 问题描述多目标追踪问题涉及追踪和目标智能体两方面, 其主要的研究目标为多个自主追踪智能体的协同追踪策略[15-17]。目前, 关于追踪问题的描述不一, 本文将追踪问题定义为:假设在相同的有限二维空间内存在np个追踪智能体, 则追踪智能体集合P=P1, P2, …, Pnp, 假设在相同有限二维空间内存在ne个目标智能体, 则目标智能体集合E=E1, E2, …, Ene, 追踪智能体和目标智能体统称为智能体A, A=P∪E。OPi(i=1, 2, …, np)代表追踪智能体Pi的中心, OEj(j=1, 2, …, ne)代表目标智能体Ej的中心, VPi(i=1, 2, …, np)代表追踪智能体Pi的运动速度, VEj(j=1, 2, …, ne)代表目标智能体Ej的运动速度。
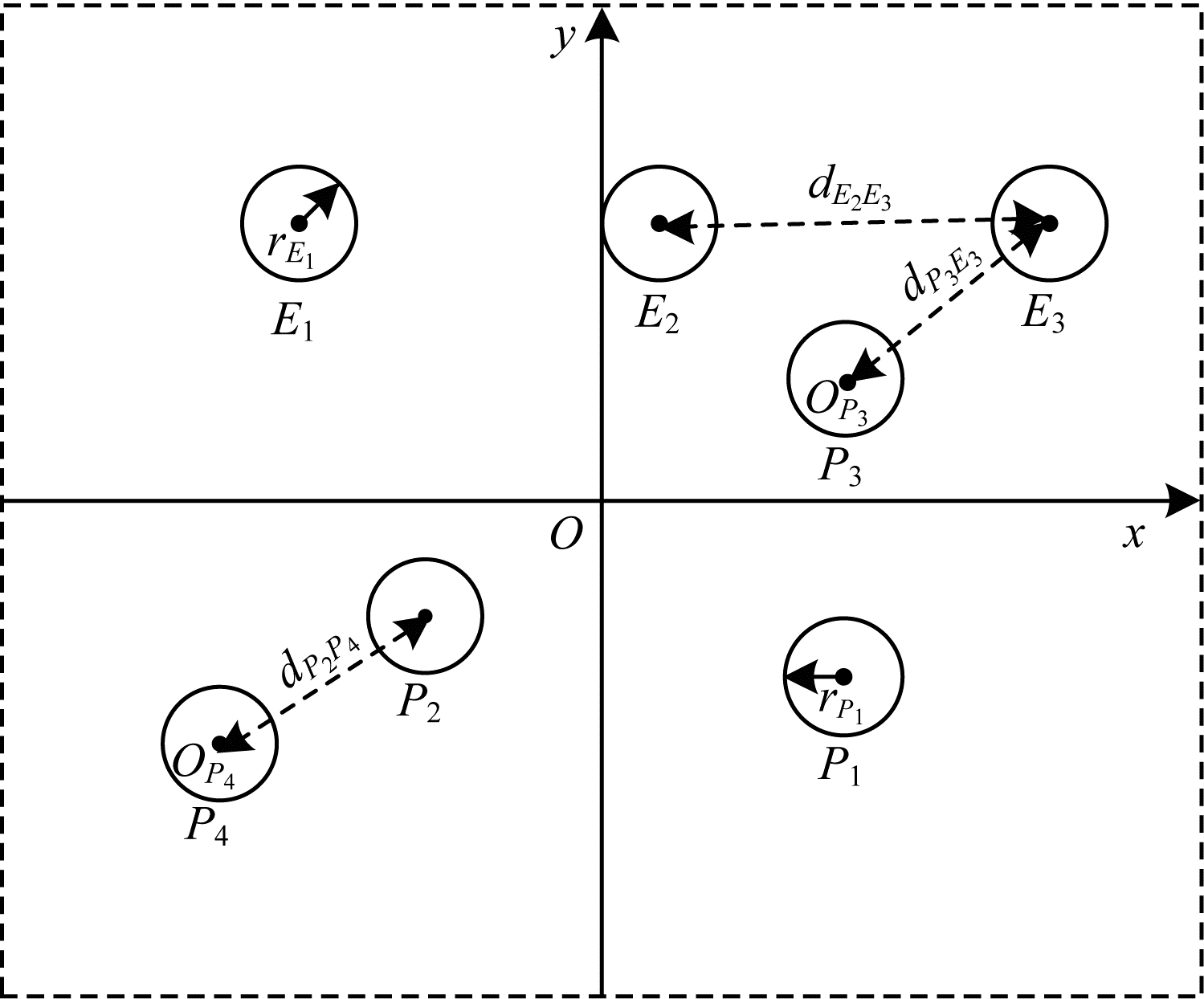
在时刻t∈T(T=1, 2, …)内所有智能体同时运动, 时刻t智能体在环境中的位置近似看作其中心位置, 即追踪智能体的位置Xp(t)=(xp1(t), x2p(t), …, xpnp(t)), 目标智能体的位置Xe(t)=(xe1(t), xe2(t), …, xene(t)), rPi(i=1, 2, …, np)代表追踪智能体Pi的半径, rEj(j=1, 2, …, ne)代表目标智能体Ej的半径, dPiEj(i=1, 2, …, np, j=1, 2, …, ne)代表追踪智能体Pi与目标智能体Ej的距离, dEjEk(j=1, 2, …, ne, k=1, 2, …, ne)代表目标智能体Ej与Ek的距离, dPiPk(i=1, 2, …, np, k=1, 2, …, np)代表追踪智能体Pi与Pk的距离。dPiEj≤rPi+rEj表示追踪智能体Pi成功追到目标智能体Ej, dPiPk≤rPi+rPk表示追踪智能体Pi与Pk相撞, dEjEk≤rEi+rEk表示目标智能体Ej与Ek相撞。在所有智能体中, 某一个智能体可以知道其他智能体的位置、相对距离及运动速度, 多智能体追踪问题的简易示意图如图 1所示。
|
Download:
|
| 图 1 多智能体追踪示意图 Fig. 1 Schematic diagram of multi-agent tracking | |
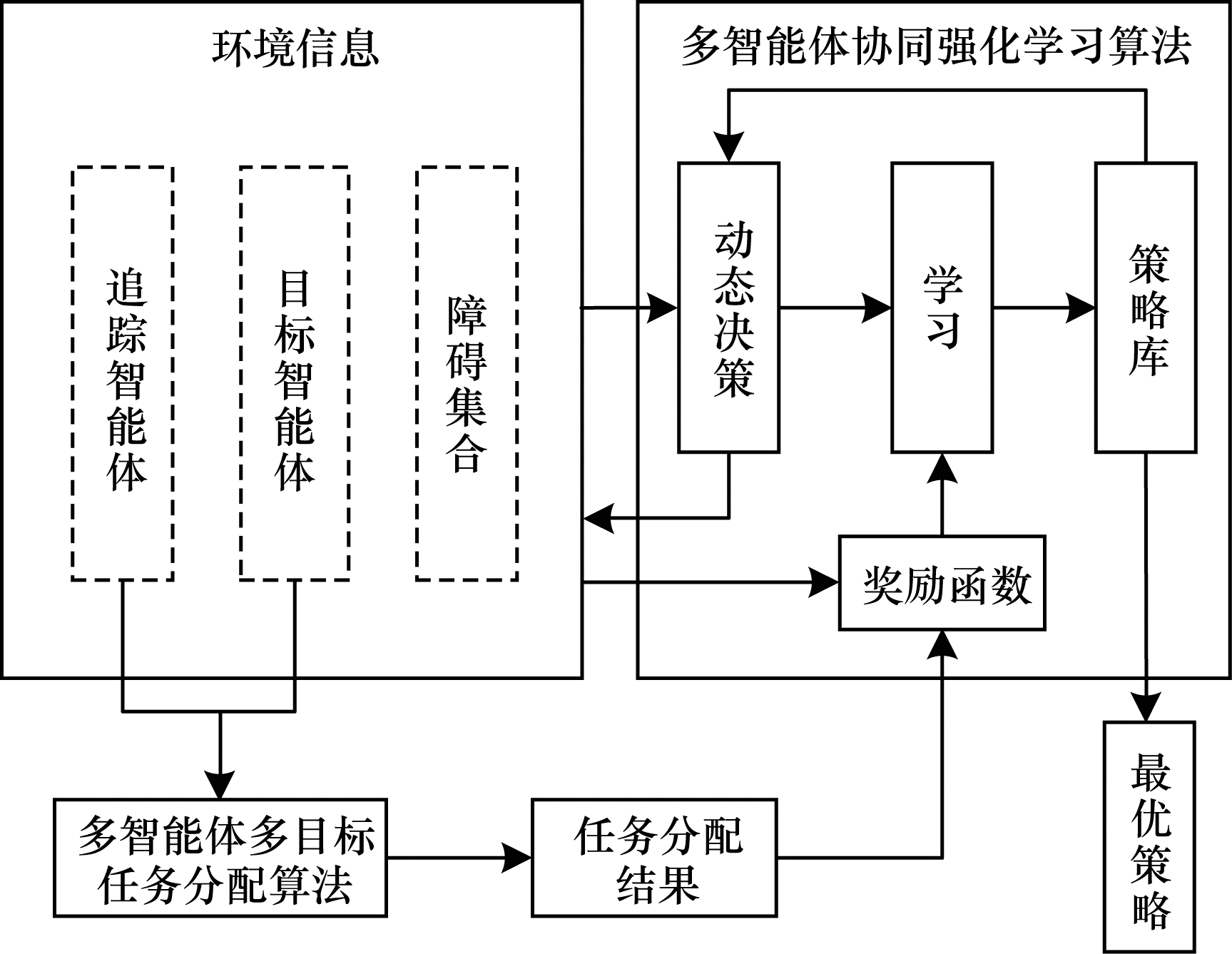
多目标追踪方法主要包括环境建模、任务分配和追踪策略学习3个方面, 具体框架如图 2所示。先对追踪智能体、目标智能体、障碍数量及位置等环境信息进行建模, 将追踪智能体、目标智能体作为多智能体多目标任务分配算法的输入, 经过计算得到各个智能体的任务分配结果。根据各个智能体的任务分配结果和环境信息, 对其进行奖励函数设置。在每一个时间步长中, 各个智能体根据观察到的环境信息采取相应行动作用于环境, 使得环境的状态发生变化, 同时通过奖励函数从环境中获得奖励反馈并进行学习更新策略, 然后多个智能体根据观察新的环境状态采取行动从中获得奖励再进行学习。重复上述过程, 通过不断优化决策并更新策略库得到最优策略或较优策略。
|
Download:
|
| 图 2 多目标追踪方法框架 Fig. 2 Framework of multi-target tracking method | |
在多智能体多目标追踪问题中, 多个智能体需要通过协调与协作完成对多个运动目标的追踪任务。本文假设多个智能体之间能够进行交流与通信, 同时可获取各个运动目标的位置, 以缩短目标智能体的总追踪路径为优化目标, 根据参与任务的智能体数目与运动目标数目建立以下任务分配模型:
1) 当追踪智能体数目与目标智能体数目相同时, 即np=ne, 其数学模型为:
| $ \begin{array}{*{20}{l}} {\min D = \sum\limits_{i = 1}^{{n_{\rm{p}}}} {\sum\limits_{j = 1}^{{n_{\rm{e}}}} {{d_{{P_i}{E_j}}}} } {x_{{P_i}{E_j}}}}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}\sum\limits_{j = 1}^{{n_{\rm{e}}}} {{x_{{P_i}{E_j}}}} = 1, i = 1, 2, \cdots , {n_{\rm{p}}}}\\ {\quad \sum\limits_{i = 1}^{{n_{\rm{p}}}} {{x_{{P_i}{E_j}}}} = 1, j = 1, 2, \cdots , {n_{\rm{e}}}}\\ {{x_{{P_i}{E_j}}} = 0{\rm{ 或 }}1, i = 1, 2 \cdots , {n_{\rm{p}}}, j = 1, 2, \cdots , {n_{\rm{e}}}} \end{array} $ |
其中, D代表追踪智能体对于目标智能体的总追踪路径;
2) 当追踪智能体数目小于目标智能体数目时, 即np < ne, 其数学模型为:
| $ \begin{array}{*{20}{l}} {\min D = \sum\limits_{i = 1}^{{n_{\rm{p}}}} {\sum\limits_{j = 1}^{{n_{\rm{e}}}} {{d_{{P_i}{E_j}}}} } {x_{{P_i}{E_j}}}}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}\sum\limits_{j = 1}^{{n_{\rm{e}}}} {{x_{{P_i}{E_j}}}} = 1, i = 1, 2, \cdots , {n_{\rm{p}}}}\\ {\quad \sum\limits_{i = 1}^{{n_{\rm{p}}}} {{x_{{P_i}{E_j}}}} \le 1, j = 1, 2, \cdots , {n_{\rm{e}}}}\\ {{x_{{P_i}{E_j}}} = 0{\rm{ 或}}1, i = 1, 2 \cdots , {n_{\rm{p}}}, j = 1, 2, \cdots , {n_{\rm{e}}}} \end{array} $ |
3) 当追踪智能体数目大于目标智能体数目时, 即np>ne, 其数学模型为:
| $ \begin{array}{*{20}{l}} {\min D = \sum\limits_{i = 1}^{{n_{\rm{p}}}} {\sum\limits_{j = 1}^{{n_{\rm{e}}}} {{d_{{P_i}{E_j}}}} } {x_{{P_i}{E_j}}}}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}\sum\limits_{j = 1}^{{n_{\rm{e}}}} {{x_{{P_i}{E_j}}}} = 1, i = 1, 2, \cdots , {n_{\rm{p}}}}\\ {\quad \sum\limits_{i = 1}^{{n_{\rm{p}}}} {{x_{{P_i}{E_j}}}} \le 1, j = 1, 2, \cdots , {n_{\rm{e}}}}\\ {{x_{{P_i}{E_j}}} = 0{\rm{ 或 }}1, i = 1, 2 \cdots , {n_{\rm{p}}}, j = 1, 2, \cdots , {n_{\rm{e}}}} \end{array} $ |
多智能体多目标任务分配算法具体步骤如下:
步骤1 初始化追踪智能体数目np、各个追踪智能体的位置Xp(t0)、目标智能体数目ne以及各个目标智能体的位置Xe(t0)。
步骤2 依次计算追踪智能体与每个目标智能体之间的距离dPiEj组成距离效益矩阵D, 计算公式为:
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{d_{{P_1}{E_1}}}}&{{d_{{P_1}{E_2}}}}& \cdots &{{d_{{P_1}{E_{{n_{\rm{e}}}}}}}}\\ {{d_{{P_2}{E_1}}}}&{{d_{{P_2}{E_2}}}}& \cdots &{{d_{{P_2}{E_{{n_{\rm{e}}}}}}}}\\ \vdots & \vdots &{}& \vdots \\ {{d_{{P_{{n_{\rm{p}}}}}{E_1}}}}&{{d_{{P_{{n_{\rm{p}}}}}{E_2}}}}& \cdots &{{d_{{P_{{n_{\rm{p}}}}}{E_{{n_{\rm{e}}}}}}}} \end{array}} \right] $ |
步骤3 当追踪智能体数目np等于目标智能体数目ne时转步骤4;当追踪智能体数目np小于目标智能体数目ne时转步骤5;当追踪智能体数目np大于目标智能体数目ne时转步骤6。
步骤4 运用匈牙利算法根据距离效益矩阵D对多个智能体的任务分配模型进行求解, 转步骤7。
步骤5 虚拟增加(ne-np)个追踪智能体, 采用加边补零法将该非标准指派问题转化为标准指派问题, 并利用匈牙利算法对多个智能体的任务分配模型进行求解, 转步骤7。
步骤6 虚拟增加(np-ne)个目标智能体, 采用加边补零法将该非标准指派问题转化为标准指派问题, 并利用匈牙利算法对多个智能体的任务分配模型求解, 转步骤7。
步骤7 输出多个追踪智能体的任务分配结果, 算法结束。
2.2 多智能体协同强化学习算法 2.2.1 状态和动作设置在多智能体追踪问题中, 每个智能体的行为都会导致环境状态的改变进而影响其他智能体的行动。多个智能体之间存在合作关系或竞争关系, 每个智能体所获得的回报不仅与自身动作有关, 而且与其他智能体的动作有关[18-20]。
在本文二维平面空间的多目标追踪问题中, 任意时刻的状态可以表示为s={X, V}, 其中, X表示各个智能体的初始位置及障碍等的位置信息, V表示各个智能体的运动速度。智能体的动作空间为智能体在二维平面空间(x, y)中任意方向移动的距离。
2.2.2 奖励函数设置奖励函数的设置直接影响智能体的学习效果和学习效率。在本文多目标追踪问题中, 追踪智能体的奖励函数设置与其任务分配结果有关, 可以根据rt=ωTmt确定, 即奖励值r是一组带权重的分解奖励之和。假设有np个追踪智能体追踪ne个目标智能体, 得到实时的距离效益矩阵D。根据多智能体多目标任务分配算法求解得出各个追踪智能体的任务分配结果, 假设追踪智能体Pi追踪目标Ej, 则追踪智能体Pi的奖励函数设置为:rPi=r1+r2+r3+r4, 其中, r1表示与其他追踪智能体Pj发生碰撞,
对于目标智能体Ei而言, 其奖励函数rEi=ra+rb+rc+rd, 其中:ra表示与其他目标智能体Ej发生碰撞,
本文采用多智能体多目标任务分配算法和多智能体协同强化学习算法进行多目标追踪, 其核心工作包括:1)根据环境中各个追踪智能体以及目标智能体的位置信息, 运用多智能体多目标任务分配算法确定多个智能体的任务分配结果; 2)根据不同智能体的任务分配结果以及环境中的其他信息(如障碍位置、环境边界等)设计相应的学习模型, 多个智能体与仿真环境交互并将其经验数据存储至样本池中, 然后从样本池中随机取出一定数量的样本进行学习同时更新策略。在多个智能体的学习任务中, 所有智能体的策略由参数θ={θ1, θ2, …, θn}确定, 其策略集合π={π1, π2, …, πn}, 则单智能体i的期望收益梯度为:
| $ \begin{array}{*{20}{l}} {{\nabla _{{\theta _i}}}J\left( {{\theta _i}} \right) = {E_{s \sim p\mu , {a_i}\sim{\pi _i}}}\left[ {\nabla {\theta _i}{{\log }_a}{\pi _i}\left( {{a_i}\mid {o_i}} \right) \cdot } \right.}\\ {\left. {Q_i^\pi \left( {s, {a_1}, {a_2}, \cdots , {a_n}} \right)} \right]} \end{array} $ | (1) |
其中, Qiπ(s, a1, a2, …, an)表示联合动作值函数, 状态s(s=(o1, o2, …, on))包含所有智能体的观测值, 将其与所有智能体的联合动作(a1, a2, …, an)同时作为输入, 而输出为单智能体i的Q值。结合确定性策略梯度, 单智能体i的期望收益梯度为:
| $ \begin{array}{*{20}{l}} {{\nabla _{{\theta _i}}}J\left( {{\mu _i}} \right) = {E_{s, a\sim M}}\left[ {{\nabla _{{\theta _i}}}{\mu _i}\left( {{a_i}\mid {o_i}} \right) \cdot } \right.}\\ {\left. {{\nabla _{{a_i}}}Q_i^\mu \left( {s, {a_1}, {a_2}, \cdots , {a_n}} \right)\mid {a_i} = {\mu _i}\left( {{o_i}} \right)} \right]} \end{array} $ | (2) |
其中, M表示样本池, 其记录了所有智能体的经验数据。联合动作值函数Qiμ按式(3)进行更新:
| $ \ell \left( {{\theta _i}} \right) = {E_{s, a, r, s'}}\left[ {{{\left( {Q_i^\mu \left( {s, {a_1}, {a_2}, \cdots , {a_n}} \right) - y} \right)}^2}} \right] $ | (3) |
其中:
| $ y = {r_i} + \gamma Q_i^{{\mu ^\prime }}\left( {{s^\prime }, a_1^\prime , a_2^\prime , \cdots , a_n^\prime } \right)\mid a_j^\prime = \mu _j^\prime \left( {{o_j}} \right) $ | (4) |
多目标追踪的具体步骤如下:
1) 参数初始化, 设置环境的范围边界及追踪智能体、目标智能体及障碍的数量、位置、速度等信息以及样本池M的容量K和总训练回合数N。
2) 根据任务目标设置智能体的奖励函数和动作空间。
3) 设置初始训练回合数Episode=0、最小取样样本数Ns和已存储样本池数量Nb。
4) 判断训练回合数Episode是否小于N, 如果是, 则执行下一步; 否则算法结束。
5) 根据当前状态st, 每个智能体遵循当前策略选择动作ai。
6) 执行动作a=(a1, a2, …), 各个智能体得到奖励值ri, 同时达到新的状态st+1。
7) 存储(st, a, r, st+1)至样本池M, Nb←Nb+1。
8) 判断Ns是否小于Nb, 若是, 则跳转至步骤11;否则执行步骤9。
9) 对于每个智能体而言, 随机从样本池M中取Ns个样本, 根据式(4)计算yj, 并利用式(2)和式(3)分别更新actor网络和critic网络。
10) 更新目标网络。
11) 赋值更新st←st+1, 训练回合数Episode←Episode+1, 返回步骤4。
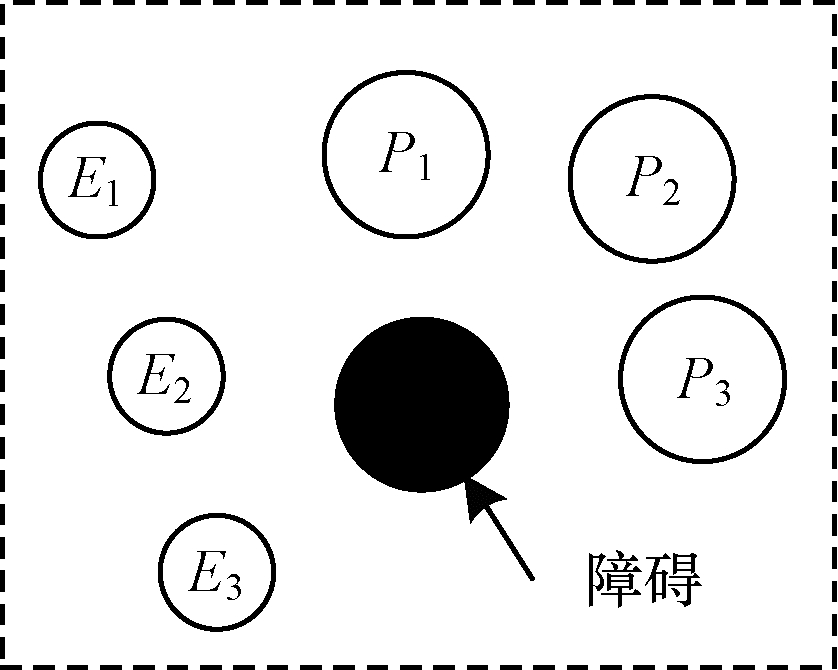
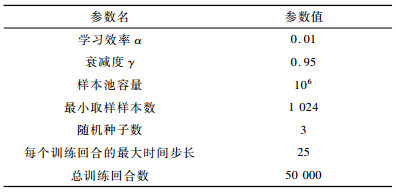
3 实验结果与分析 3.1 实验设置为验证本文MTT-MACRL方法的可行性和有效性, 在同一实验环境下将本文MTT-MACRL方法与DDPG方法[14]和MADDPG方法[21]进行对比。实验场景设置如图 3所示, 实验环境为连续的二维平面空间, 其中存在3个追踪智能体、3个目标智能体和1个障碍, 在同一离散时间内3个追踪智能体与3个目标智能体同时运动, 由于目标智能体被限制在该环境中, 因此追踪智能体可以追踪到目标智能体。在上述实验场景中的参数设置如表 1所示。
|
Download:
|
| 图 3 实验场景 Fig. 3 Experimental scene | |
|
下载CSV 表 1 参数设置 Table 1 Parameter setting |
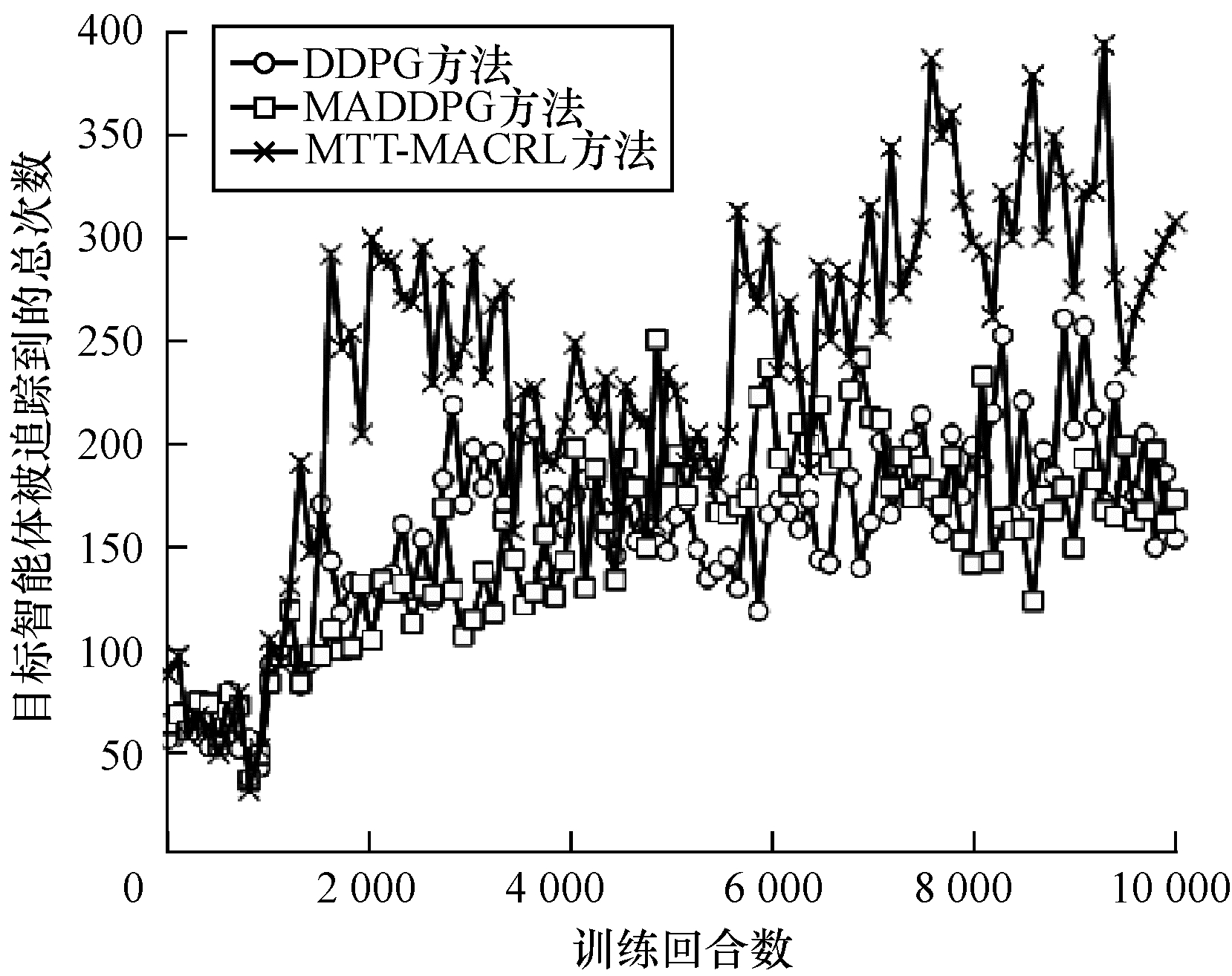
在多智能体追踪问题中, 追踪智能体主要学习如何快速接近目标智能体以完成对多个目标智能体的追踪任务。图 4为10 000个训练回合中, DDPG方法[14]、MADDPG方法[21]以及本文MTT-MACRL方法的目标智能体在平均每100个训练回合中被追踪到的总次数与训练回合数的关系。
|
Download:
|
| 图 4 目标智能体被追踪到的总次数 Fig. 4 The total number of times the target agent has been tracked | |
可以看出, 在10 000个训练回合中, 本文MTT-MACRL方法平均每100个训练回合成功追踪到目标智能体的总次数为239次, DDPG方法和MADDPG方法平均每100个训练回合成功追踪到目标智能体的总次数分别为158次、153次。当平均每100个训练回合成功追踪到目标智能体的总次数达到145次时, 运用本文MTT-MACRL方法、DDPG方法和MADDPG方法至少分别需要进行2 500个、8 000个和7 600个训练回合。综上所述, 本文MTT-MACRL方法相比其他两种方法, 学习速度更快, 能够根据智能体的位置快速执行有效策略, 且实时性更好。
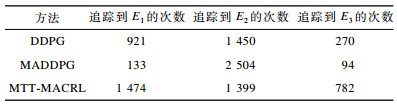
3.2.2 有效性验证为验证本文MTT-MACRL方法的有效性, 将其与DDPG方法和MADDPG方法的学习策略分别在上述场景中进行3次实验。在每次实验中, 追踪智能体和目标智能体的位置为随机生成, 每个训练回合的最大时间步长为50步, 共进行1 000个回合的测试, 并统计3次实验中每个目标智能体被追踪到的次数以及所有目标智能体被追踪到的总次数, 具体情况如表 2~表 4所示。

|
下载CSV 表 2 第1次实验中追踪到目标智能体的总次数 Table 2 total number of times the target agent has been tracked in the first experiment |
|
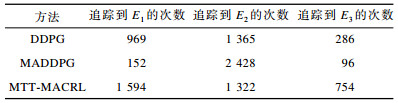
下载CSV 表 3 第2次实验中追踪到目标智能体的总次数 Table 3 The total number of times the target agent has been tracked in the second experiment |
|
下载CSV 表 4 第3次实验中追踪到目标智能体的总次数 Table 4 The total number of times the target agent has been tracked in the third experiment |
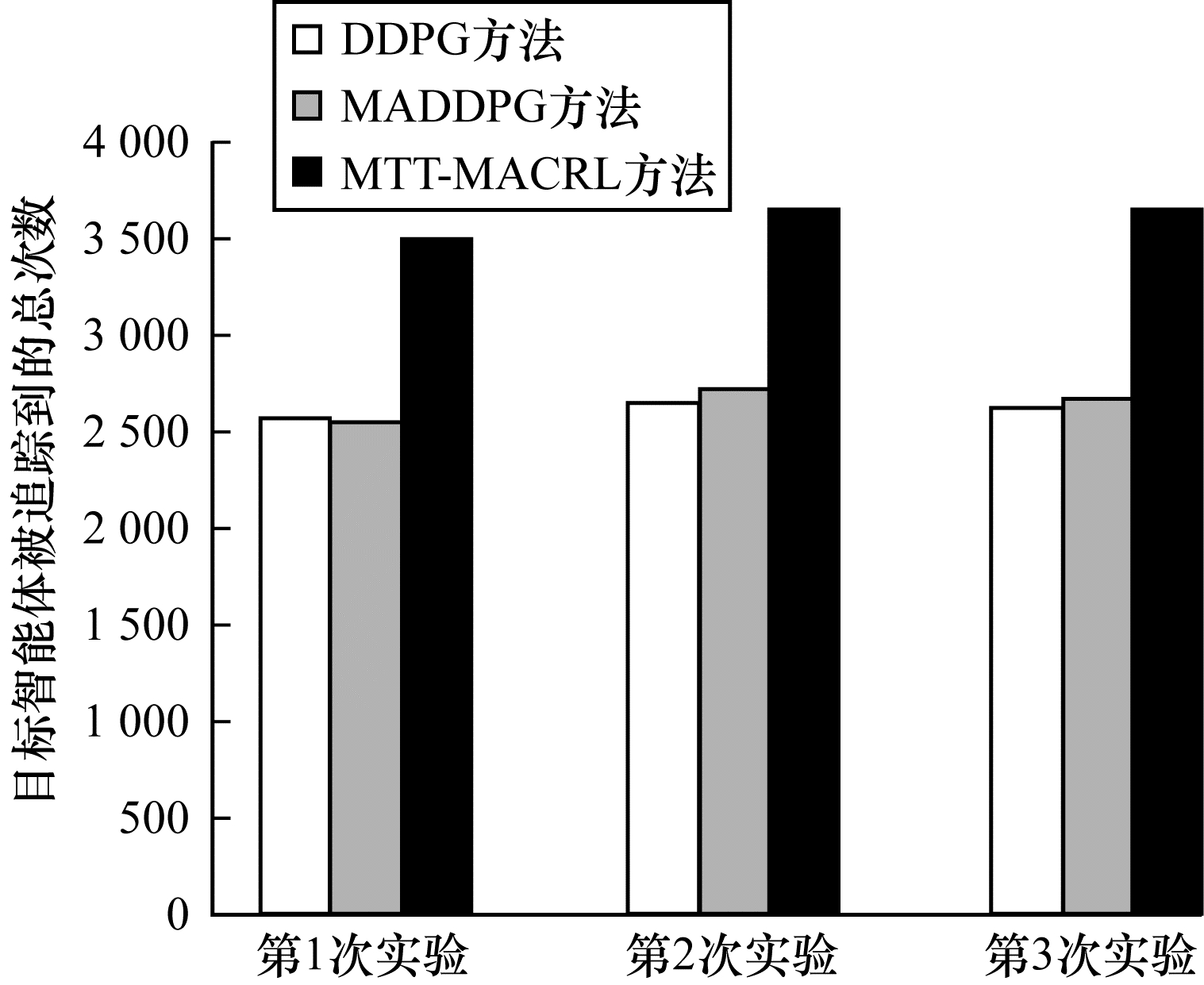
在3次实验中, 采用DDPG方法、MADDPG方法以及本文MTT-MACRL方法得到目标智能体被追踪到的总次数如图 5所示。可以得出, 利用DDPG方法、MADDPG方法和本文MTT-MACRL方法平均每次实验追踪到目标智能体的总次数分别为2 605次、2 650次和3 605次。本文MTT-MACRL方法对于目标智能体的成功追踪次数相比DDPG方法和MADDPG方法分别提高了38.39%和36.04%。
|
Download:
|
| 图 5 3次实验中目标智能体被追踪到的总次数 Fig. 5 The total number of times the target agent has been tracked in three experiments | |
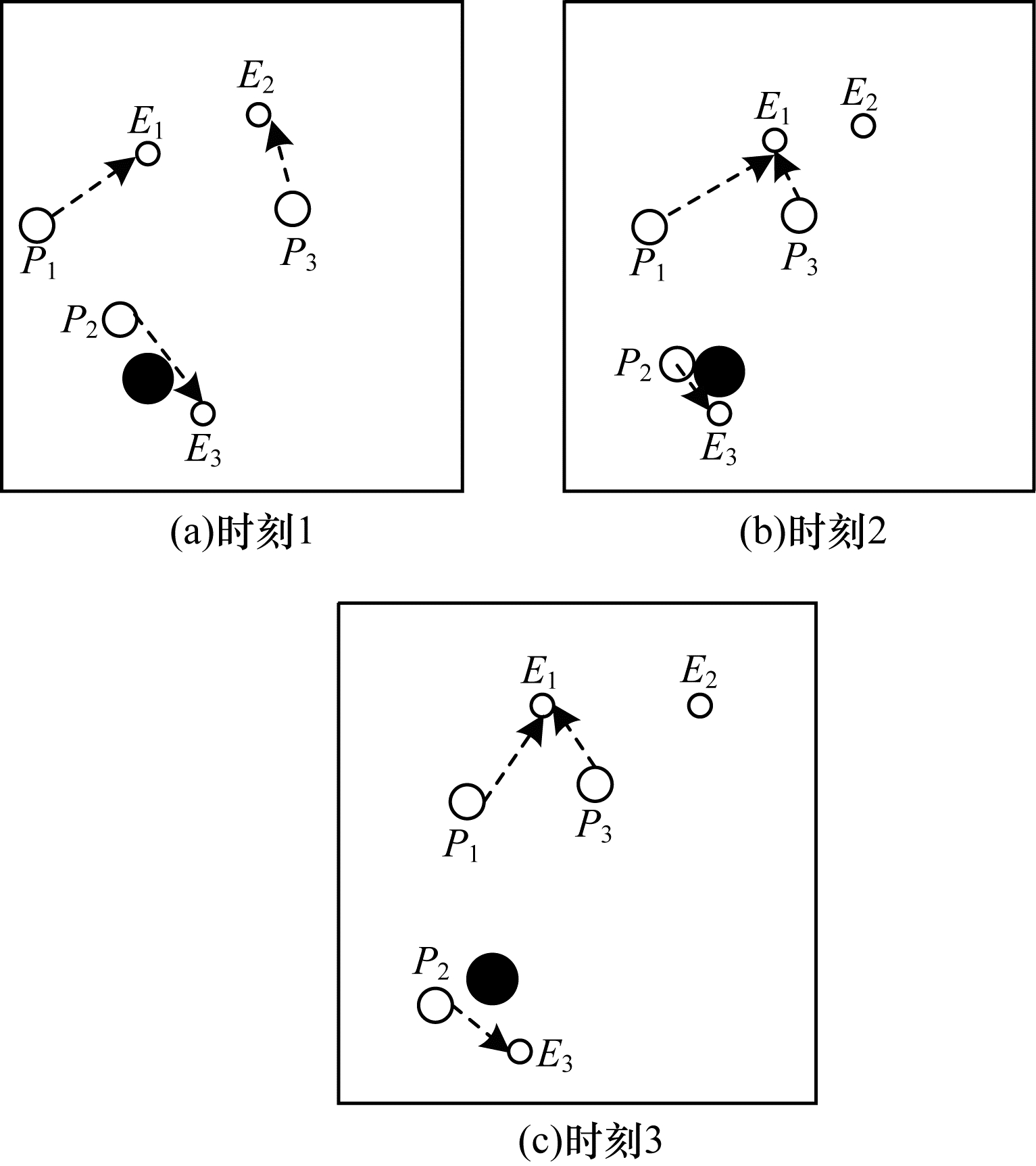
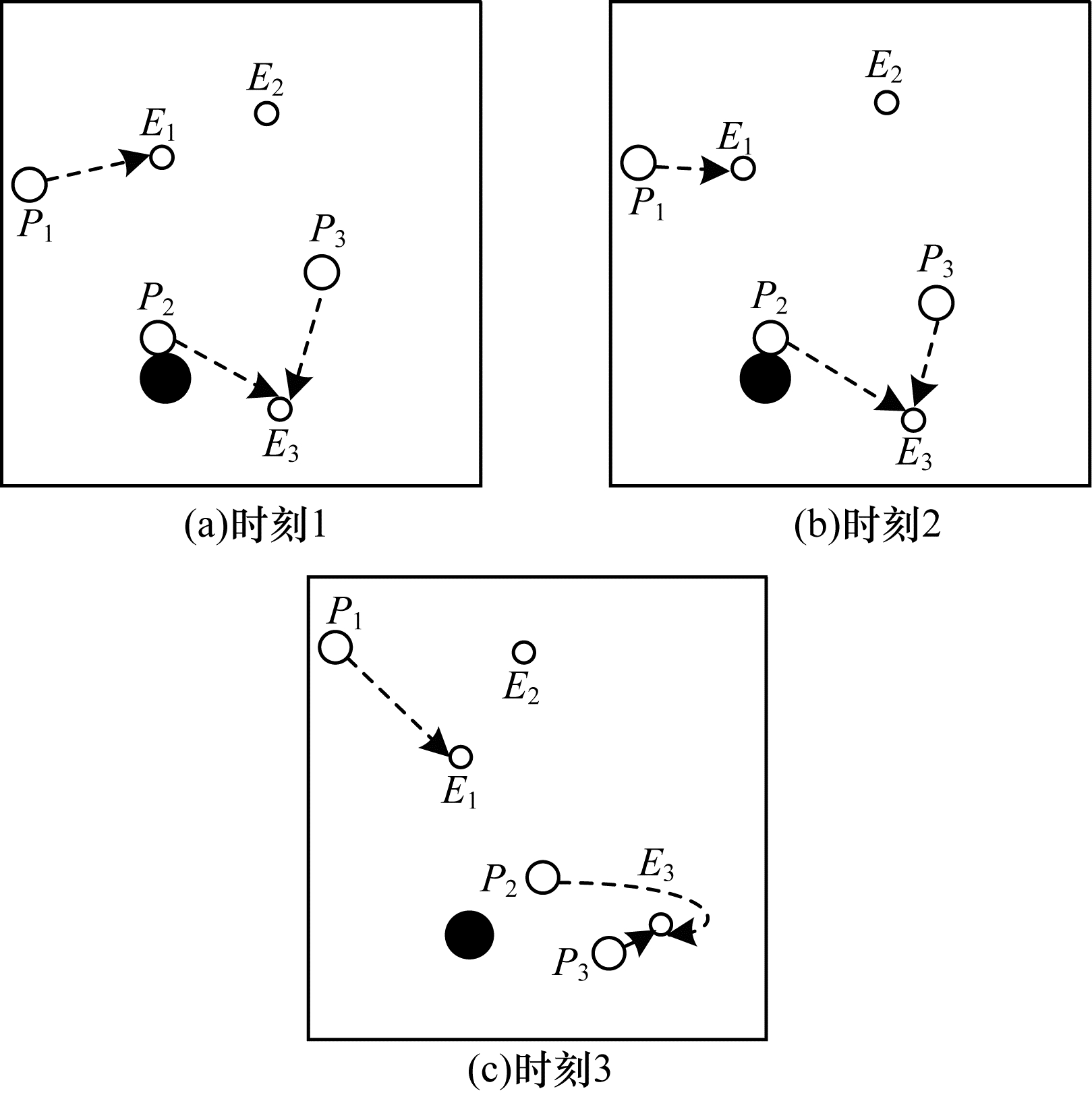
通过DDPG方法和MADDPG方法得到不同时刻追踪智能体及目标智能体的位置分布情况, 如图 6和图 7所示。可以看出, 多个追踪智能体未进行相互合作且出现了多个目标智能体同时追踪同一个目标智能体的情况, 因此造成某一个目标智能体无智能体追踪, 不能快速有效地完成追踪任务。
|
Download:
|
| 图 6 DDPG方法在不同时刻的智能体位置分布情况 Fig. 6 The distribution of agent position of DDPG method at different moments | |
|
Download:
|
| 图 7 MADDPG方法在不同时刻的智能体位置分布情况 Fig. 7 The distribution of agent position of MADDPG method at different moments | |
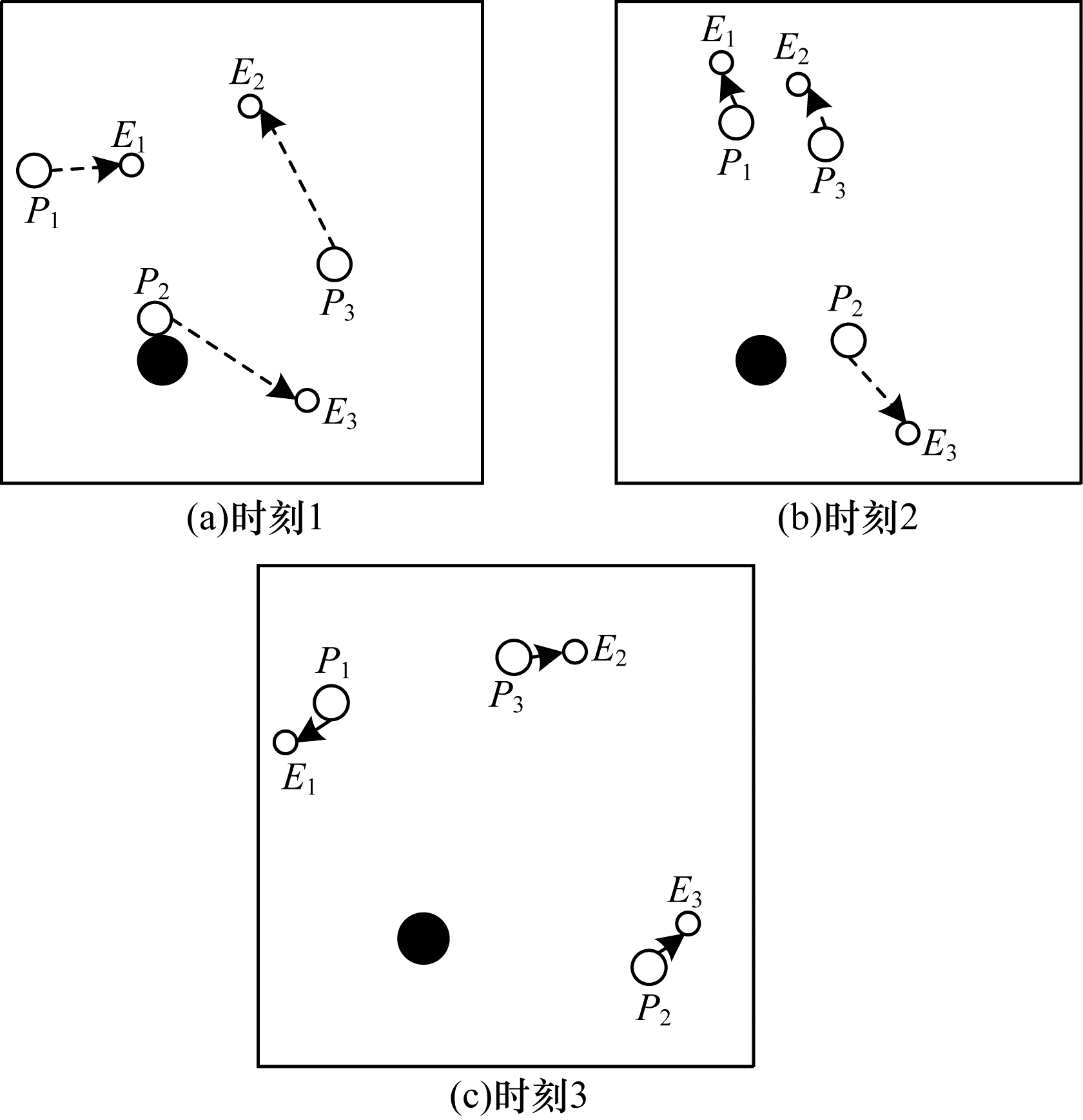
通过本文MTT-MACRL方法得到不同时刻追踪智能体及目标智能体的位置分布情况, 如图 8所示。可以看出, 多个追踪智能体经过学习训练能够与其他智能体相互协作进行任务分配, 保证一个追踪智能体对应一个目标智能体。同时, 根据追踪智能体与目标智能体的位置信息能够实时更新任务分配情况, 保证参与追踪任务的智能体的总追踪路径最短。
|
Download:
|
| 图 8 MTT-MACRL方法在不同时刻的智能体位置分布情况 Fig. 8 The distribution of agent position of MTT-MACRL method at different moments | |
本文提出一种基于多智能体协同强化学习的多目标追踪方法。根据追踪和目标智能体数目及其位置信息建立任务分配模型, 运用匈牙利算法对其进行求解得到多个追踪智能体的任务分配情况, 并结合环境信息为多个追踪智能体设置奖励函数, 同时通过多智能体协同强化学习算法使其在复杂环境中不断重复执行探索-积累-学习-决策过程, 最终从经验数据中学习决策策略完成多目标追踪任务。实验结果表明, 与DDPG方法和MADDPG方法相比, 本文方法的学习速度更快, 且多个智能体通过相互协作能更有效地追踪目标智能体。
| [1] |
LAMINI C, FATHI Y, BENHLIMA S.Collaborative Q-learning path planning for autonomous robots based on holonic multi-agent system[C]//Proceedings of the 10th International Conference on Intelligent Systems: Theories and Applications.Washington D.C., USA: IEEE Press, 2015: 1-6.
|
| [2] |
HAJDUK M, SUKOP M, HAUN M.Agent approach to multi-agent systems[M]//HAJDUK M, SUKOP M, HAUN M.Studies in systems, decision and control.Berlin, Germany: Springer, 2018: 21-22.
|
| [3] |
HAN Xiangmin, BAO Hong, LIANG Jun, et al. An adaptive cruise control algorithm based on deep reinforcement learning[J]. Computing Engineering, 2018, 44(7): 32-35. (in Chinese) 韩向敏, 鲍泓, 梁军, 等. 一种基于深度强化学习的自适应巡航控制算法[J]. 计算机工程, 2018, 44(7): 32-35. |
| [4] |
YU H L, MEIER K, ARGYLE M, et al. Cooperative path planning for target tracking in urban environments using unmanned air and ground vehicles[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(2): 541-552. |
| [5] |
YANG P, TANG K, LOZANO J A, et al. Path planning for single unmanned aerial vehicle by separately evolving waypoints[J]. IEEE Transactions on Robotics, 2015, 31(5): 1130-1146. DOI:10.1109/TRO.2015.2459812 |
| [6] |
ZHOU Hailing, KONG Hui, WEI Lei, et al. Efficient road detection and tracking for unmanned aerial vehicle[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 297-309. DOI:10.1109/TITS.2014.2331353 |
| [7] |
SHAH K, SCHWAGER M.Multi-agent cooperative pursuit-evasion strategies under uncertainty[M]//CORRELL N, SCHWAGER M, OTTE M.Distributed autonomous robotic systems.Berlin, Germany: Springer, 2019: 451-468.
|
| [8] |
GARCIA-FERNANDEZ A F, SVENSSON L. Multiple target tracking based on sets of trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(3): 1685-1707. DOI:10.1109/TAES.2019.2921210 |
| [9] |
SOUIDI M E H S, SIAM A, PEI Z Y, et al. Multi-agent pursuit-evasion game based on organizational architecture[J]. Journal of Computing and Information Technology, 2019, 27(1): 1-11. |
| [10] |
DUAN Yong, XU Xinhe. Research on multi-robot cooperation strategy based on multi-agent reinforcement learning[J]. Systems Engineering-Theory & Practice, 2014, 34(5): 1305-1310. (in Chinese) 段勇, 徐心和. 基于多智能体强化学习的多机器人协作策略研究[J]. 系统工程理论与实践, 2014, 34(5): 1305-1310. |
| [11] |
GUPTA J K, EGOROV M, KOCHENDERFER M.Cooperative multi-agent control using deep reinforcement learning[C]//Proceedings of International Conference on Autonomous Agents and Multiagent Systems.Berlin, Germany: Springer, 2017: 66-83.
|
| [12] |
WEI E, WICKE D, FREELAN D, et al.Multiagent soft Q-learning[C]//Proceedings of 2018 AAAI Spring Symposium Series.Palo Alto, USA: AAAI Press, 2018: 1-10.
|
| [13] |
FOERSTER J, FARQUHAR G, AFOURAS T, et al.Counterfactual multi-agent policy gradients[EB/OL].[2019-08-01].https://arxiv.org/abs/1705.08926.
|
| [14] |
LILLICRAP T, HUNT J, PRITZEL A, et al.Continuous control with deep reinforcement learning[EB/OL].[2019-08-01].https://arxiv.org/abs/1509.02971.
|
| [15] |
YAN Yalin.Research on multi-robot pursuit-evasion problem based on game theory[D].Harbin: Harbin Engineering University, 2014.(in Chinese) 晏亚林.基于博弈论的多机器人追捕问题的研究[D].哈尔滨: 哈尔滨工程大学, 2014. |
| [16] |
FANG Baofu, PAN Qishu, HONG Bingrong, et al. Constraint conditions of successful capture in multi-pursuers vs one-evader games[J]. Robot, 2012, 34(3): 282-291. (in Chinese) 方宝富, 潘启树, 洪炳镕, 等. 多追捕者-单-逃跑者追逃问题实现成功捕获的约束条件[J]. 机器人, 2012, 34(3): 282-291. |
| [17] |
ZHANG Xu, LI Ling, JIA Leilei. Research and simulation of multi-robot pursuit and escape strategy based on differential game[J]. Equipment Manufacturing Technology, 2015(9): 9-12. (in Chinese) 张旭, 李玲, 贾磊磊. 基于微分博弈的多机器人追逃策略研究及仿真[J]. 装备制造技术, 2015(9): 9-12. |
| [18] |
DU Wei, DING Shifei. Overview on multi-agent reinforcement learning[J]. Computer Science, 2019, 46(8): 1-8. (in Chinese) 杜威, 丁世飞. 多智能体强化学习综述[J]. 计算机科学, 2019, 46(8): 1-8. |
| [19] |
ZHANG Yue.Research on multi-agent deep reinforcement learning methods and applications[D].Xi'an: Xidian University, 2018.(in Chinese) 张悦.多智能体深度强化学习方法及应用研究[D].西安: 西安电子科技大学, 2018. |
| [20] |
WANG Weixun, HAO Jianye, WANG Yixi, et al.Towards cooperation in sequential prisoner's dilemmas: a deep multiagent reinforcement learning approach[EB/OL].[2019-08-01].https://arxiv.org/abs/1803.00162.
|
| [21] |
LOWE R, WU Y, TAMAR A, et al.Multi-agent actor-critic for mixed cooperative-competitive environments[C]//Proceedings of Advances in Neural Information Processing Systems.Berlin, Germany: Springer, 2017: 6379-6390.
|
 2020, Vol. 46
2020, Vol. 46
