时间序列数据[1-2]是指随着时间进行变化的一系列数据, 通常存在于日志数据中, 例如某天的CPU、硬盘使用率、某个地区一年的温度等。这些数据由物联网中的传感器进行采集, 并上传至服务器作为每天的日志数据。数据科学家将其作为基础数据, 查询并分析该数据从而得出结果来进一步优化目标。时间序列数据具有数据格式单一、数据种类复杂、数据之间关联性强等特点。关于时间序列的查询通常需要构建索引, 索引构建方法主要有B+树[3-4]、布隆过滤器[5]、solr搜索服务器[6]。对于时间序列而言, 大部分时间上相邻的时间序列数据具有较强的关联性, 单条数据的索引不适用于时间序列数据。文献[7]在无序的基于LSM树[8-9]数据存储上对观测的时间序列数据进行存储索引, 将时间序列数据按照时间划分成一块块固定长度的分段并且进行查询。该方法可以使用较小的代价就能完成对时间序列数据的快速访问, 但由于其是固定分段, 因此没有考虑时间序列本身的特征, 缺乏灵活性, 在进行范围查询时, 获取的无关数据量较多, 查询效率较低。
本文提出一种基于动态分段的时间序列索引DSI。该索引将一条时间序列根据自身数据特点, 设置相应的限制参数进行分段, 形成数据长度不同的分段。对于分段查询, 使用区间树对分段块进行搜索并通过主键查询数据。
1 相关知识 1.1 时间序列的基本定义时间序列T是采集到的时间长度为m的数据, 可表示为T={t1, t2, …, tm-1, tm}, 按照一定的时间间隔采集时间序列中的数据t1、t2, 相邻点的时间差值相等。
1.2 时间序列的局部性时间序列数据存储一般是以采集数据的时间作为主键, 依据采集时间进行排序, 相邻数据具有一定的关联性。因为使用者读取某一时间数据后, 很有可能继续读取相邻时间段的数据, 所以读取时间序列数据时不只是读取一条数据, 而是连续读取一段时间序列数据, 为创建分段索引提供了理论依据。
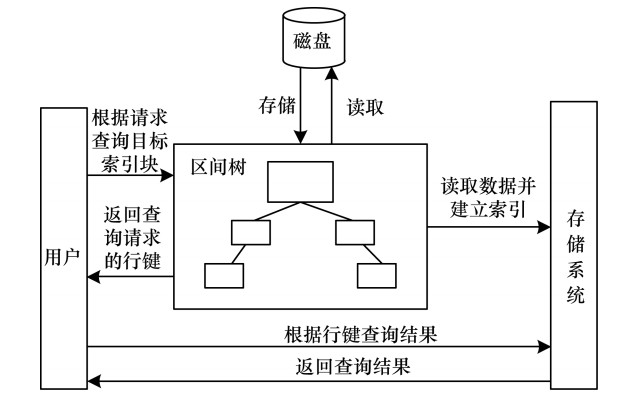
2 DSI索引 2.1 索引查询框架在数据查询时, 首先向索引查询框架(如图 1所示)输入请求, 索引查询框架根据请求确定目标数据块, 然后返回目标索引块的行键, 最后用户根据行键存储系统中查询的目标数据。
|
Download:
|
| 图 1 索引查询框架 Fig. 1 Index query framework | |
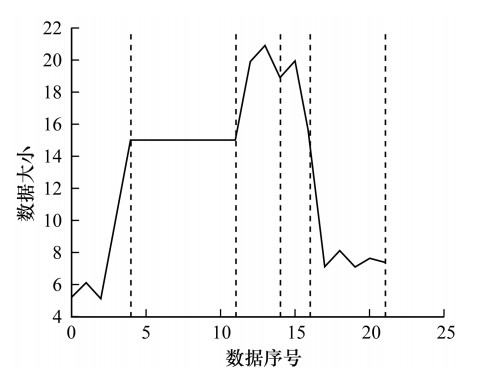
DSI是根据时间序列数据目标字段的值进行动态切分的一种索引。相对于将数据划分为相同长度的数据块索引来说, DSI根据数据值之间的关系进行切分及索引, 能够减少无效数据的读取, 提升读取效率。在图 2中, 两条虚线之间的数据为一个数据段。每个数据段包含数据的个数不同, 算法根据时间序列数据的特性, 在数据点之间差异大、数据波动大的地方, 例如一条时间序列的波峰和波谷区间, 减少相应的段长度。对于数据波动较少的地方增加相应的段长度, 同时对于数据频度较小, 即数据出现次数较小的数据段减少相应的数据段长度, 从而提升有效数据的读取量。
|
Download:
|
| 图 2 索引数据块的动态划分 Fig. 2 Dynamic segmentation of indexed data blocks | |
DSI索引主要包含索引块和区间树两部分。由于时间序列的数据值随时间的变化而变化, 因此根据时间将存储在存储系统中的每个时间序列段划分为一个个更小的数据段。
| $ R=\left\{\left[r_{1}, r_{2}\right), \left[r_{2}, r_{3}\right), \cdots, \left[r_{m-1}, r_{m}\right)\right\} $ | (1) |
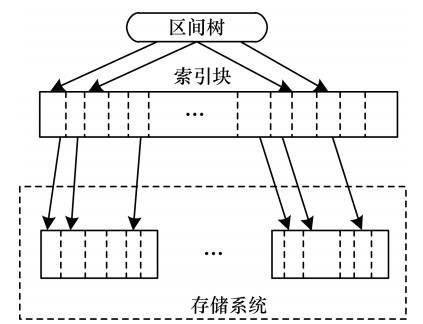
其中, R为一个索引块集合, rm表示时间序列中第m个点的主键, [rm-1, rm)定义为左闭右开的区间。当用户进行范围查询时, 给出一个查询区间。将查询区间和索引序列段上信息进行对比, 如果符合条件, 则表明时间序列数据段是用户所需的数据, 因此提取整个数据块。图 3为索引整体结构。在存储系统中, 根据主键查询存储系统中的数据, 将时间序列根据其自身特点划分为一个个逻辑数据块。在索引层中, 为每一个逻辑数据块创建一个相应的索引块, 该块包含了描述逻辑数据块的信息, 然后使用区间树获取索引块。
|
Download:
|
| 图 3 索引整体结构 Fig. 3 Overall structure of index | |
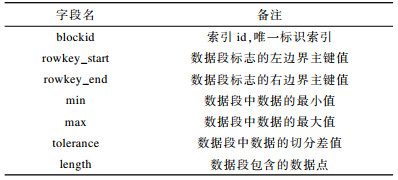
一条索引块表示的数据块可能包含成百上千条数据, 也可能包含几十条数据, 根据时间序列数据的特点确定, 因此需找到一个合适的方法对这些数据进行切分。对于每一个目标数据块, 把目标块中的最大值和最小值作为索引的关键信息。这样既能节省索引空间, 又能在一定程度上保持查询准确率。因此, 对于每一个索引块, 可将其看作[min, max]区间。对于区间查询来说, 区间查询的左右端点构成的区间与索引块区间相交, 该块是需要查询的数据块。同时, 由于描述信息简单, 因此当有大量数据插入时, 索引建立速度也较快。表 1详细介绍了索引中各字段的数据构成, 其中tolerance字段表示该索引代表的数据块中数据值的差值, 该差值用于下文中索引块的生成。
|
下载CSV 表 1 索引块字段表 Table 1 Field table of indexed blocks |
根据上文描述可知, 数据之间的差值越小, 代表数据之间的波动越小。数据之间的差值越大, 数据值之间的波动越大, 则应该切分成不同的数据段。但对于每一类时间序列数据, 由于数量之间的差异, 因此对于不同的时间序列数据块的切分不同, 需要用户指定差值E。同时, 根据差值E确保每个数据段中的数据之间的差值小于差值E。
推论1 对于一个普通的时间序列t[i:j], 要保证时间序列t[i:j]不被切分, 只需保证该时间序列数据的最大值和最小值的差值小于E即可, 证明如下:
| $ \operatorname{range}[i ; j]=\max t[k]-\min t[k] \leqslant E, i \leqslant k \leqslant j $ | (2) |
证明 时间序列t[i:j]中的任意2个数据a、b存在
综上所述, 确保每个数据段中数据之间的差值小于E, 只需找到数据段的最大值和最小值进行切分。同时, 借助于APCA[10-11]思想, 动态划分时间序列, 基于此, 本文提出一种不定长的时间序列分块划分算法。
算法1 时间序列分块划分算法
输入 时间序列T, 基准差值E>0, 差值级别count
输出 索引集合indexList
1.indexList ← {}
2.初始化minValue, maxValue, lastTol
3.计算T的标准差和均值mean, stdv
4.map← splitTolerance(mean, E, stdv, count)
5.for each data t[i] in T do
6.tol← min(map.get(t[i]), lastTol)
7.If max(maxValue, t[i])-min(minValue, t[i])>tol
//生成索引块并加入到索引集合中
8.indexBlock←generateIndexBlock()
9.indexList.add(indexBlock)
10.重置minValue, maxValue, lastTol
11.else
12.minValue←min(minValue, t[i])
13.maxValue←max(maxValue, t[i])
14.lastTol←tol
15.end if
16.end for
17.return indexList
由算法1可知, 该算法的输入为时间序列T, 用户的输入差值E以及用户划分的差值级别count, 用户对于不同数值大小的数据切分差值也不同。输出为切分的块, 即索引集合。首先初始化各参数值, 其中, minValue代表当前段的最小值, maxValue代表当前段的最大值, lastTol代表上一个相邻的索引(第1行、第2行)。然后计算出时间序列的数据均值mean以及标准差stdv, 便于下文不同数值数据进行级别划分赋予相应差值。在得到均值及标准差后, 根据均值、标准差以及基准差值生成相应的差值项(第3行)。函数splitTolerance根据不同数据值产生不同的差值, 由一个键值对形式的集合map进行保存。遍历时间序列T中的每项值t[i], 首先获取当前t[i]在map中对应的差值, 然后和上条数据的差值lastTol对比并取较小值。根据推论1, 用当前段的最大值减去最小值确定是否超过当前差值, 如果超过差值则进行索引块的建立(第4行)。接着为下一个索引块重置minValue、maxValue、lastTol(第5行~第10行)。反之, 保留当前差值, 即赋值给lastTol, 同时将minValue、maxValue和t[i]比较更新最小值和最大值(第12行~第14行)。
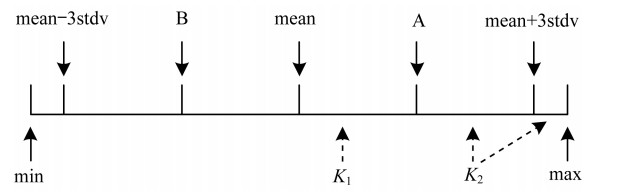
splitTolerance是根据差值进行切分的函数, 输入参数为差值级别count、均值mean、标准差stdv及基准差值E。在现实数据中, 存在异常数据及极端数据。拉伊达法则[12]表明均值mean范围上下的3个标准差stdv的数据范围内能够涵盖接近99%的数据, 同时数据数值和mean值越接近, 数据频度越大。图 4为一个count值为2的区间划分结果。首先设立一个以mean值为中心, 范围为[mean-3stdv, mean+3stdv]的区间。count等于2代表将[mean, mean+3stdv]平均分成两份, 从而产生2个区间[mean, A]和[A, mean+3stdv], 同一区间内的数据差值一样。距离中心值越近的区间, 该区间的差值越大, 区间[mean, A]和[A, mean+3stdv]产生了2个差值K1, K2。[mean, A]区间距离mean值更近, 因此差值K1大于K2。K1值为基准差值E, K2值为E/2。对于[mean+3tdv, max]特殊区间中点差值, 则使用相邻区间的差值, 在本例中为K2的值。同理, 如果count为n, 则在n个切分区间中的第i(K1≤i≤n)个区间差值数据为E/i, [mean+3tdv, max]的区间数据为E/n。因为mean值左边部分与右边部分是对称的, 所以不再赘述。
|
Download:
|
| 图 4 数据差值判断 Fig. 4 Judgment of data difference | |
本文主要利用区间树进行索引块的快速查找, 区间树是由动态集合维护的红黑树, 是一种自平衡的二叉树, 主要用于对区间数据的查询, 区间树由红色节点和黑色节点构成, 因此对n个节点区间的插入和删除都能在O(lg n)时间内完成。区间树的结构如表 2所示。区间树每个节点主要由五部分构成:左右端点left和right, left是一个实数值, right是一个键值对形式的集合; 左右孩子区间树节点指针node_L和node_R, 分别指向左右孩子区间树节点; NodeMax, 代表当前节点及子树节点的左右端点的最大值。在表 2中, 第2条数据id为2, 左端点数据为8, 右端点是一个键值对集合, 包含有关键字为9及关键字为20的键值对元素, 同时左子节点是id为3的节点, 右子节点不存在。当前节点以及子树的最大值NodeMax为20。

|
下载CSV 表 2 区间树结构 Table 2 Interval tree structure |
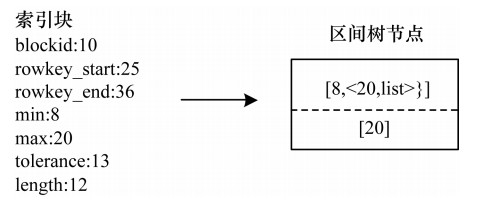
在建立区间树时, 需先了解如何将一个索引块节点转化为一个区间树节点。在查询区间树时, 主要是通过比较区间树节点的左端点与右端点进行查询, 因此当构造区间树时, 将获得的索引块的min值作为区间树的左端点left, max值作为区间树的右端点right的一部分。由于区间树可能出现左右端点一致的情况, 造成很多的冗余节点, 因此将区间树的右端点转化为一个有序集合。需要注意的是, 该有序集合是一个键值对形式的集合, 键是每一个索引块的max值, 而值是一个链表形式的集合list, list中存储的是索引块的rowkey_start起始主键和rowkey_end结束主键等关键信息, 因此左端点相同的数据都在同一个区间树节点中。图 5为索引块到区间树节点的转化表示, 对于一个blockid为10的索引块, 索引块的min值为8, max值为20, 将min值作为区间树节点的左端点, max值作为区间树节点的右端点, 同时NodeMax值为max值。
|
Download:
|
| 图 5 索引块到区间树的转化过程 Fig. 5 Conversion process of indexed blocks to interval trees | |
相对于传统将每一个索引块都独立为一个树节点的方法, 区间树查询将左端点相同的索引块进行融合, 根据NodeMax剪枝以及右端点有序的特点, 减少查询目标数据时的比较次数。在区间树的建立过程中, 输入已划分好的索引块, 每个索引块都有一个min值和max值, 只需将索引块转化为区间的节点数据即可。首先初始化一个区间树, 并获取树的根节点, 然后初始化一个临时节点。对于索引块集合的每一索引块, 先将其转化为区间树节点。其中索引块的max值为区间节点的NodeMax值, 将根节点的NodeMax值和当前的NodeMax进行对比, 取两者较大的值来更新根节点的NodeMax值。接着使用当前插入节点和根节点的左端点进行比较, 如果左端点小于根节点的左端点, 则继续和根节点的左子树进行比较。如果2个左端点相等则将该节点加入当前节点的存储集合中, 并取2个节点的NodeMax值的较大值为新的NodeMax值, 表示这2个节点共用一个树节点; 否则与根节点的右子树节点进行比较。如果不存在left值相同的节点, 则在叶子节点中创建一个新的区间节点。最后根据红黑树的性质进行树旋转操作来保持整个树的平衡。旋转操作的详细过程可参见文献[13-14]。
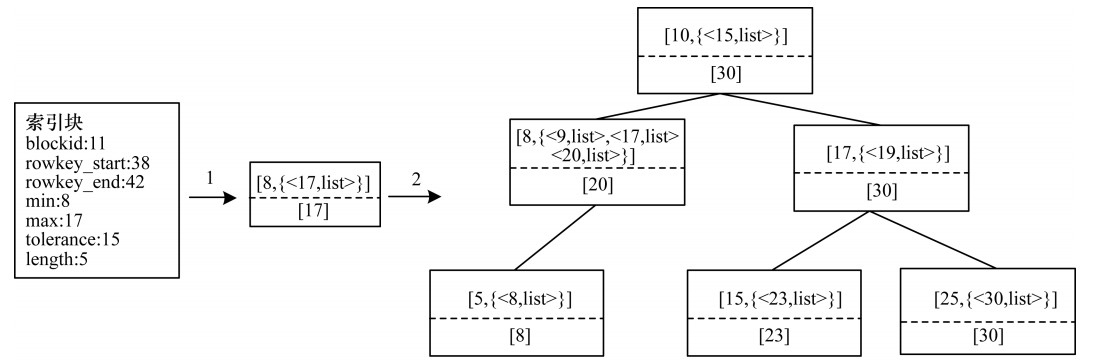
图 6为索引块节点在区间树中的插入过程, 其中右半部分的区间树根据表 2构建而成。在每一个区间树节点中, 虚线上半部分代表了该节点的左右端点, 虚线下半部分表示该节点的NodeMax值。将blockid为11的索引块转化为left为8、right键值对集合中键为17的一个区间树节点, NodeMax的值为17。由于区间树以左端点为关键字进行排序, 因此插入节点的left值(8)和根节点left值(10)进行比较, 由于插入节点的left值小于根节点left值, 因此进一步遍历根节点的左子节点。在遍历左子节点时, 发现有left为8的区间节点, 便插入该节点中。由于右端点right是一个有序集合, 其中key包含9和20等数值, 在对右端点键为17的数据进行插入时, 只需找到第一个大于17的数据插入到该数据中。在本例中, 插入到键为20的元素前。
|
Download:
|
| 图 6 区间树的插入过程 Fig. 6 Insertion process of interval trees | |
索引块存在于区间树节点中, 先从区间树中找出索引块。对于区间树的查询[15-17], 除了图 7中两种区间树查询没有命中的情况, 即查询区间的左端点大于区间节点的右端点和区间节点的左端点小于查询节点的右端点, 其余都是需要查询的目标线段。在图 7中, 细实线为查询的目标区间, 粗实线为区间树中的区间。
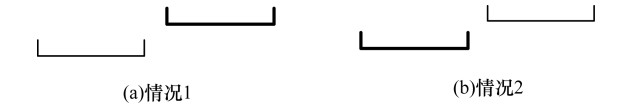
|
Download:
|
| 图 7 区间树查询不命中的情况 Fig. 7 Cases where interval tree queries do not hit | |
在获得目标区间后, 遍历区间树中的每个节点, 给出索引块的查询算法, 其中输入为区间树根节点t、查询区间[left, right]、区间集list。
算法2 索引查询算法RecursiveSearch
//区间树左端点不大于查询区间右端点两者才有交集
1.if t!=NIL and t.leftpoint < =right
//返回区间树右端点第一个大于查询区间左端点的位置
2.start < -findFirst(t.rightpoint, left)
//将该位置开始一直到有序集合末尾数据都加入list
3.list.add(t.rightpoint, start)
4.end if
5.leftchild < -t.leftchild; rightchild < -t.rightchild
6.if leftchild!=NIL and
7.leftchild.NodeMax>=left
8.RecursiveSearch(leftchild, left, right, list)
9.end if
10.if rightchild!=NIL and
11.rightchild.NodeMax>=left
12.RecursiveSearch(rightchild, left, right, list)
13.end if
该算法是一个递归算法, 输入为区间树根节点t, 查询区间[left, right]以及用于存放数据的集合list, 主要是对区间树中的节点进行遍历, 先判断该节点是否存在图 7(a)的情况, 即查询的区间右端点right小于区间树节点的左端点t.leftpoint。如果满足该情况, 则可以把当前节点排除(第1行)。对于图 7(b)的情况, 因为区间树右端点t.rightpoint是一个集合, 则只要判断区间树的右端点集合t.rightpoint中是否有数据大于查询区间的左端点left即可, 因为区间树的右端点集合t.rightpoint依次递增, 只需找到右端集合t.rightpoint中第一个大于查询区间的左端点left即可。调用findFirst函数找到右端点集合元素key中第一个大于查询区间左端点left, 并返回键值对序号start(第2行)。由于区间树的右端点t.rightpoint中的key集合是有序的, 从start开始的位置一直到集合末尾右端点集合元素中的key都大于查询区间左端点left, 这些集合元素都满足查询要求, 因此从start位置开始到集合末尾位置的数据都加入到list(第3行)。由于无需比较每一个节点集合中所有数据, 因此在一定程度上提高了查询效率。接着判断左子节点leftchild的NodeMax值是否大于查询区间左端点left, 左子节点leftchild的NodeMax代表了当前左子树的节点最大值。如果NodeMax不大于查询区间左端点left, 则满足图 7(b)的情况, 可进一步进行剪枝(第6行~第9行)。如果不满足, 则继续以相同方式遍历右子节点rightchild(第10行~第13行)。总体来说, 通过多个索引段的融合排序以及NodeMax剪枝, 可使整个区间树查询算法效率得到进一步提升。本质上该算法是对二叉树的遍历, 二叉树的遍历时间复杂度为O(n), 总的时间复杂度为O(n), n为区间节点个数。由于区间树节点具有NodeMax属性, 同时区间树节点的右端点是有序的, 因此在进行查询时一定程度上减少了查询比较次数, 最终的时间复杂度应远小于O(n), 空间复杂度为O(1)。
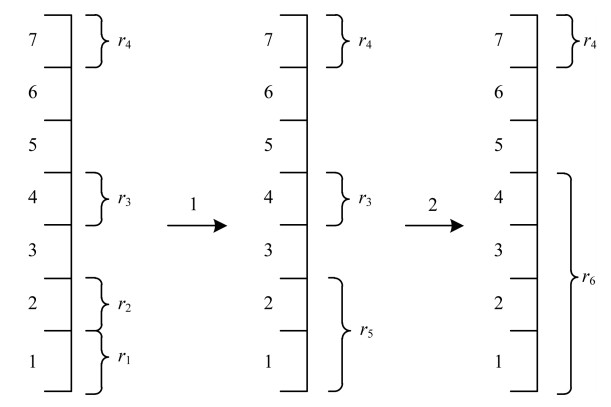
2.5.2 查询结果优化对于一个区间查询请求, 可能返回很多的索引段。因此需要进一步缩减结果, 文献[18-19]使用层次聚类算法将多个结果集合进行聚类进一步减少结果数。图 8展示了将查询出的时间序列结果进行层次聚类的过程, 候选集为4个聚类, 需要聚合成2个聚类。左边数字为时间序列块, 右边数字为候选集结果聚类r。首先计算所有结果集中两两聚类之间的距离。找出聚类集中距离最小的2个聚类集r1、r2, 距离最小代表 2个聚类融合引入的无关数据量最少。将r1、r2进行融合变成r5, 接着进一步融合, 计算r3、r4、r5中距离最小的2个聚类, 因为r3、r4融合需要引入序号为5、6的不相关时间序列数据段, 而r5、r6融合需要仅引入序号为3的不相关时间序列数据段, 代价较小, 因此将r5、r3融合成r6。
|
Download:
|
| 图 8 层次聚类过程 Fig. 8 Hierarchical clustering process | |
算法3展示了层次聚类的具体过程, 输入数据为结果集合list, 目标聚类数count, 先将list中的每一项转化为一个cluster(第1行), 然后对cluster中的每两项进行两两距离计算, 由于是对区间进行层次聚合, 因此选取的距离函数是找到2个聚类中的区间最小距离(第2行、第3行)。在每次合并后, 就减少一个聚类个数, 如果聚类个数达到要求则返回; 否则继续进行下一轮聚类(第4行)。总体来说, 本文方法是以牺牲一定的查询精准度来获取更少的结果集, 其每次只保存最小距离值, 因此空间复杂度为O(1), 而需要计算出两两聚类的距离, 时间复杂度为O(n3), n为当前聚类个数。
算法3 层次聚类算法
输入 结果集list、聚类个数count
输出 目标聚类个数listclusters
1.将list中的每一项转化成为一个cluster, 得到cluster的集合listclusters
2.对listclusters中的每一项, 两两计算距离
3.找到距离最小的2个聚类, 合并聚类
4.判断当前cluster个数是否小于count, 若大于count则返回步骤2, 若小于count则进行步骤5
5.返回结果集listclusters
3 实验 3.1 实验环境实验在单台计算机上运行, 处理器为Intel Core i7-4710 2.5 GHz, 内存大小为24 GB, 操作系统为64位Windows 7, JDK版本为1.8.0 _152。
3.2 实验数据实验数据主要来自于CMOP[20]观测数据和股票数据2个数据集。CMOP观测数据来自于传感器测量出的温度数据, 数据时间范围为2008年12月1日至2011年11月30日, 数据量约为3 000万, 温度数据平缓、波动较小。股票数据主要是来源于沪深股市300支股票的一档挂单数据(通过电脑进行买卖的股票数据), 数据时间范围为2013年3月1日至2013年12月31日, 数据量约为600万, 该数据相对温度数据震荡、波动较大。本文对比方法为基于固定分段的时间序列查询索引CRI[7]。
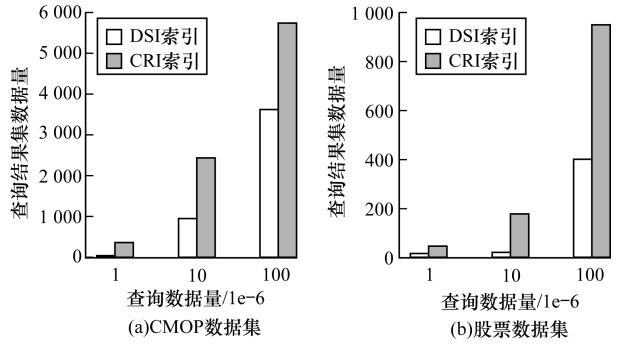
3.3 实验结果 3.3.1 相同量级数据集下的数据查询效果为保证实验公平性, 在索引块数量一致的情况下进行相同数据的查询。DSI和CRI的查询效率如图 9所示。横坐标为进行查询的数据区间实际包含数据的条数, 纵坐标为查询到的结果集的数据量。在CMOP数据集中, 对实际包含数据量为30、300、3 000的数据区间进行查询, 最终返回索引所标记的数据量。由于数据查询是以块的方式进行, 因此查询到的数据总量越少, 代表查询到的数据包含的无关数据量越少, 查询精度越高。由图 9可以看出, DSI效果优于CRI, 且由于股票数据的波动较大, 因此对此目标查询区间, DSI能够有效识别并划分区间。
|
Download:
|
| 图 9 相同量级数据集下查询效率对比 Fig. 9 Comparison of query efficiency between datasets of equivalent size | |
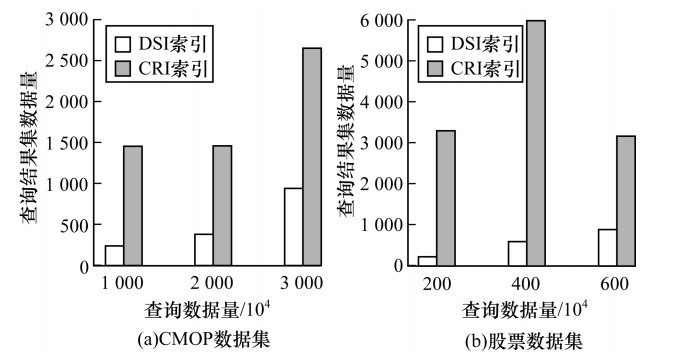
在DSI和CRI产生的索引块数量一致的情况下, 图 10展示了不同数据总量下的查询效率, 在CMOP数据集和股票数据集中, 查询数据量是总数的10-4, 对于总的数据量为3 000万的数据集, 查询数据量为10-4, 即查询包含3 000条的数据区间, 由此可知, 查询到的总数据量小的索引的无关数据少, 效率高。可以看出, DSI仍优于CRI, 主要原因在于DSI是根据目标查询数据的分布来动态切分数据。在该过程中, DSI关注了数据分布, 而CRI是静态划分, 仅记录最大值和最小值, 因此在查询时经常访问到包含极端值的块, 从而导致查询到的无关数据较多, 数据量增加。对于DSI动态查询, 极端值根据差值被切分成不同的段, 从而不影响正常的数据查询。
|
Download:
|
| 图 10 不同量级数据集下的查询效率对比 Fig. 10 Comparison of query efficiency between datasets of different sizes | |
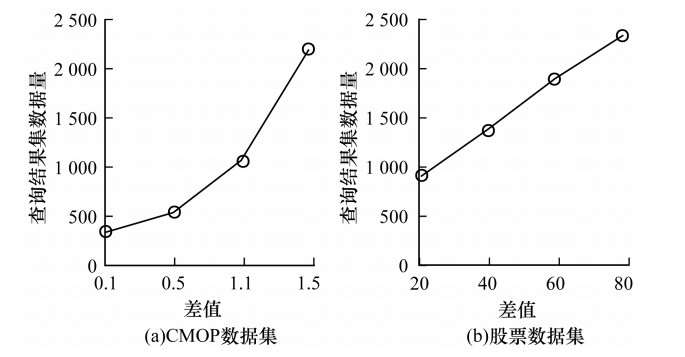
图 11为对3 000万CMOP观测数据、600万股票数据的查询结果。每一类数据都是调整不同差值后, 对各自相同数据区间进行查询。对于股票数据而言, 当差值数据为20、40、60、80时,对应的数据总块数分别为1.39×106、6.9×105、3.5×105、1.9×105。随着差值的增加, 数据总块数逐渐减少, 但查询数据逐渐增多。随着差值的减少, 数据总块数增加, 在查询目标块数时需要花费更多时间, 但查询无关数据少。对于较平缓的CMOP观测数据, 当差值数据为0.1、0.5、1.1、1.5时,对应的数据总块数分别为2.79×106、4.8×105、1.6×105、1.1×105。随着数据总块数的减少,查询出的数据也相对减少。
|
Download:
|
| 图 11 数据差值对查询结果的影响 Fig. 11 Impact of data difference on query results | |
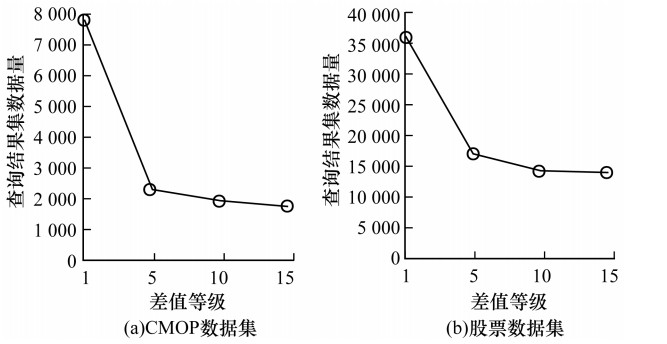
图 12是不同差值等级对查询结果的影响。对于CMOP感测数据而言,当差值等级为1、5、10、15时,对应的数据总块数分别为2.5×104、2.6×105、7.5×105、1.09×106;对于股票数据而言,当差值等级为1、5、10、1.5时,对应的数据总块数分别为3.8×105、8.7×105、1.43×106、1.65×106。由此可知, 随着差值等级值的变大, 产生的索引块数会变多。在差值逐渐变大的过程中, 早期对提升数据查询精准度有一定的影响, 随着差值增大到一定程度时, 例如CMOP数据和股票数据差值在15时, 索引块数变多, 但查询精度并没有明显提升, 因此选取一个合适的差值等级至关重要。
|
Download:
|
| 图 12 差值等级对查询结果的影响 Fig. 12 Impact of difference level on query results | |
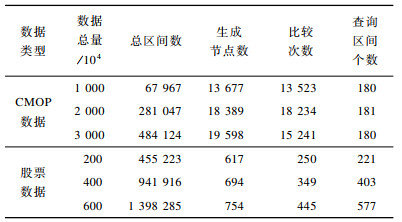
表 3是区间树查询的效率结果。第2行~第4行是温度数据的区间查询情况。对于第2行数据来说, 生成总区间段是67 967个, 由于利用红黑树节点的left值进行排序, 相同left值会加入到同一节点, 因此生成的节点数大幅减少, 同时, 每个树的右边节点是一个根据right值排好的键值对集合, 在查询时无需对区间树节点right值集合中的每一个值进行判断, 只需找到树集合中大于查询区间的左端点的第一个值即可, 后续节点不用判别是否相交, 便可直接加入。同时, 每个节点还有NodeMax值, 通过NodeMax值算法能在一定程度上减少查询时与区间树节点的比较次数。在67 957个区间中, 查询180个区间, 只需与区间树节点进行13 523次比较。对于股票数据, 由于数据波动大但范围小, 因此生成的节点数比较少。由以上结果可知, 区间树查询在一定程度减少了区间遍历的次数。
|
下载CSV 表 3 区间树查询效率 Table 3 Interval tree query efficiency |
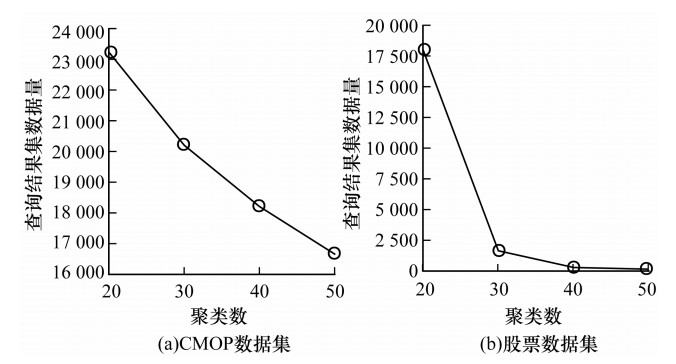
图 13为层次聚类算法对查询结果的影响, 显示了3 000万CMOP数据集和600万股票数据集对于10 000条数据及200条数据的查询情况。由此可知, 随着聚类数的增加, 查询结果集的冗余数逐渐变少, 但对于用户来说, 结果集变多, 将耗费更多的时间去查看其中结果, 因此用户需根据不同数据的特点选择合适的结果集。
|
Download:
|
| 图 13 层次聚类算法对查询结果的影响 Fig. 13 Impact of hierarchical clustering algorithm on query results | |
本文针对时间数据的局部性特点, 提出基于动态分段的时间序列值查询索引, 用户根据数据特点通过动态分段提升查询效果, 并使用层次聚类算法解决结果集过多的问题。实验结果表明, 本文索引的查询效率优于传统时间序列索引。但层次聚类需要用户手动设置, 因此下一步可将层次聚类的参数改为自动设置, 减少查询冗余, 同时根据不同时间序列数据的特点调整辅助参数, 进一步提升查询性能。
| [1] |
JIA Pengtao, HE Huacan, LIU Li, et al. Overview of time series data mining[J]. Application Research of Computers, 2007, 24(11): 15-18. (in Chinese) 贾澎涛, 何华灿, 刘丽, 等. 时间序列数据挖掘综述[J]. 计算机应用研究, 2007, 24(11): 15-18. |
| [2] |
KEOG E. On the need for time series data mining benchmarks:a survey and empirical demonstration[J]. Data Mining and Knowledge Discovery, 2003, 7(9): 349-371. |
| [3] |
LONG Yu, WU Shangyuan, GAO Qian, et al. Design and implementation of large data hybrid index based on B+ tree[J]. Automation & Instrumentation, 2018(9): 67-69. (in Chinese) 龙禹, 吴尚远, 高骞, 等. 基于B+树的电力大数据混合索引设计与实现[J]. 自动化与仪器仪表, 2018(9): 67-69. |
| [4] |
LI Xianhui, REN Cuihua, YUE Menglong. A distributed real time database index algorithm based on B+tree and consistent hashing[J]. Procedia Engineering, 2011, 24: 171-176. |
| [5] |
HUANG Can, FANG Xusheng, ZHANG Chaoquan, et al. Split counting Bloom filter and its application in Hbase secondary index[J]. Computer System Application, 2016, 25(3): 119-123. (in Chinese) 黄璨, 方旭昇, 张朝泉, 等. 分片计数布隆过滤器及其在Hbase二级索引的应用[J]. 计算机系统应用, 2016, 25(3): 119-123. |
| [6] |
WANG Wenxian, CHEN Xingshu, WANG Haizhou, et al. A secondary index scheme of big data in HBase based on Solr[J]. Netinfo Security, 2017(8): 39-44. (in Chinese) 王文贤, 陈兴蜀, 王海舟, 等. 一种基于Solr的HBase海量数据二级索引方案[J]. 信息网络安全, 2017(8): 39-44. |
| [7] |
WANG S, MAIER D. Lightweight indexing of observational data in log-structured storage[J]. Proceedings of the VLDB Endowment, 2014, 7(7): 529-540. |
| [8] |
SEARS R, RAMAKRISHNAN R.bLSM: a general purpose log structured merge tree[C]//Proceedings of ACM SIGMOD International Conference on Management of Data.New York, USA: ACM Press, 2012: 217-228. https://dl.acm.org/doi/10.1145/2213836.2213862
|
| [9] |
O'NEIL P, CHENG E, GAWLICK D, et al. The Log-Structured Merge-tree(LSM-tree)[J]. Acta Informatica, 1996, 33(4): 351-385. |
| [10] |
GUHA S, KOUDAS N, SHIM K. Approximation and streaming algorithms for histogram construction problems[J]. ACM Transactions on Database Systems, 2006, 31(1): 396-438. |
| [11] |
HUNG N Q V, JEUNG H, ABERER K. An evaluation of model-based approaches to sensor data compression[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(11): 2434-2447. |
| [12] |
LI Rui, WANG Huizhong, FENG Jianwen. Application of pauta criterion in temperature acquisition system based on LabVIEW[J]. Computer Measurement and Control, 2018, 26(6): 207-210. (in Chinese) 李蕊, 王慧忠, 冯建文. 改进拉伊达准则在LabVIEW温度采集系统中的应用[J]. 计算机测量与控制, 2018, 26(6): 207-210. |
| [13] |
MA Botao, SUN Peng, ZHU Xiaoyong, et al. Overviews on research of red-black tree algorithm[J]. Journal of Network New Media, 2018, 7(4): 56-62. (in Chinese) 马博韬, 孙鹏, 朱小勇, 等. 红黑树算法研究综述[J]. 网络新媒体技术, 2018, 7(4): 56-62. |
| [14] |
CHEN Yihui, LONG Zhaohua. Applying red-black tree in RFID tag file system[J]. Computer Engineering and Design, 2016, 37(10): 2837-2843. (in Chinese) 陈毅辉, 龙昭华. 红黑树在RFID标签文件系统中的研究与应用[J]. 计算机工程与设计, 2016, 37(10): 2837-2843. |
| [15] |
SFAKIANAKIS G, PATLAKAS I, NTARMOS N, et al.Interval indexing and querying on key-value cloud stores[EB/OL].[2019-01-18].http://eprints.gla.ac.uk/83136/.
|
| [16] |
KOLOVSON C, STONEBRAKER M.Segment indexes: dynamic indexing techniques for multi-dimensional interval data[C]//Proceedings of 1991 ACM SIGMOD International Conference on Management of Data.New York, USA: ACM Press, 1991: 138-147. https://dl.acm.org/doi/10.1145/119995.115807
|
| [17] |
WANG Wei, WANG Yujun, SHI Baile. Dynamic interval index structure in constraint database systems[J]. Journal of Computer Science and Technology, 2000, 15(6): 542-551. |
| [18] |
CHANG Jinming, WANG Honglei. Indoor location algorithm based on hierarchical clustering and Bayseian[J]. Computer Era, 2019(2): 5-8. (in Chinese) 常津铭, 王红蕾. 基于层次聚类和贝叶斯的室内定位算法[J]. 计算机时代, 2019(2): 5-8. |
| [19] |
ZHANG Qianjun. Multi-radar data fusion based on time series clustering[J]. Telecommunication Engineering, 2019, 59(2): 145-150. 张乾君. 基于时间序列聚类的多雷达数据融合[J]. 电讯技术, 2019, 59(2): 145-150. |
| [20] |
Center for caostal margin observation & observation[EB/OL].[2019-01-18].http://www.stccmop.org/datamart.
|
 2020, Vol. 46
2020, Vol. 46
