近年来, 锂离子电池作为便携式能源, 因其相对于镍氢、铝酸等其他类型电池的明显优势而迅速普及, 锂离子电池具有重量较轻、高化学反应性、高能量密度(高达23 Wh/kg~70 Wh/kg)等优点, 其不需要完全放电即可充电, 没有任何不利影响(无记忆效应), 且自放电率较低, 在不使用时可以更好地保持电量, 并具有更长的生命周期(在3 000次循环时提供80 %容量)。这些特点使其成功应用于众多领域中并发挥了重要作用, 如消费电子产品(手机、笔记本电脑等)、汽车行业中的混合动力及电动汽车、混合动力飞机、可再生能源(太阳能和风能)和太空探索等领域。迄今为止, 锂离子电池已经被公认为是一个标准电源, 而且其性能还在持续提高。
然而, 锂离子电池在其充电和放电循环期间会经历不可逆过程, 例如, 会形成固体电解质中间相(Solid-electrolyte Interphase, SEI), 这严重影响电池的电化学反应[1]。不可逆过程会导致持续的容量衰减, 最终导致电池故障, 如不及时采取更换或维护等安全措施, 可能会造成灾难性后果。因此, 目前关于锂离子电池技术的主要研究热点仍然是在改进锂离子电池系统的性能和可靠性方面[2]。为进行合理的充放电管理并满足应用中的高可靠性要求, 对使用过程中的剩余使用寿命(Remaining Useful Life, RUL)预测的研究已经成为锂离子电池系统中故障预测和健康管理(Prognostics and Health Management, PHM)的热点和挑战性问题。
PHM任务一般分为数据的获取、数据的预处理和特征的选择、健康指标(Health Indicators, HI)的构建、剩余使用寿命的预测和不确定性问题的处理等步骤。数据的获取是通过在设备上安装传感器, 得到一些原始的测量数据。数据的预处理和特征的选择通过数据的获取得到原始数据, 对原始信号进行分析可以得到选取的特征, 并进行压缩和选择, 使其最大限度地保留原始的数据信息。健康指标的构建是运用信号处理技术、人工智能技术等对数据的特征进行处理, 得到单一的特征或者融合的多个特征作为HI。RUL的预测是整个流程中最重要的也是最关键的任务[3], 它的目的是得到从预测开始到设备寿命结束的时间长度。不确定性问题的处理是将RUL的点估计预测变为区间估计预测, 使RUL预测的结果具有不确定表达能力。
本文具体介绍锂离子电池RUL的4种预测方法, 即基于机理模型的方法、基于数据驱动的方法、基于机理模型和数据驱动融合的方法和基于数据驱动的模型融合的方法, 分析基于数据驱动的各种RUL预测方法的优缺点, 对未来的研究热点进行总结, 并给出合理的建议。
1 锂离子电池的RUL预测方法电池的RUL是指从当前时刻到电池的健康状态(SOH)达到0 %, 即寿命终止时刻(End Of Life, EOL)的剩余时间或循环次数[4]。针对电池RUL的预测方法有很多, 然而, 由于存在数据的不可用性和电池模型的复杂性等问题, 目前还没有所谓的最佳的预测电池RUL的通用模型。本文将RUL预测方法分为4类:
1) 根据被预测对象自身的物理、化学或经验等系统机理模型构建的RUL预测方法。
2) 不需要特定系统机理模型, 完全依据历史特征数据构建的数据驱动的RUL预测方法。
3) 上面两类方法的混合, 即基于机理模型的方法与基于数据驱动的方法相结合的方法。
4) 基于数据驱动的模型融合的方法。
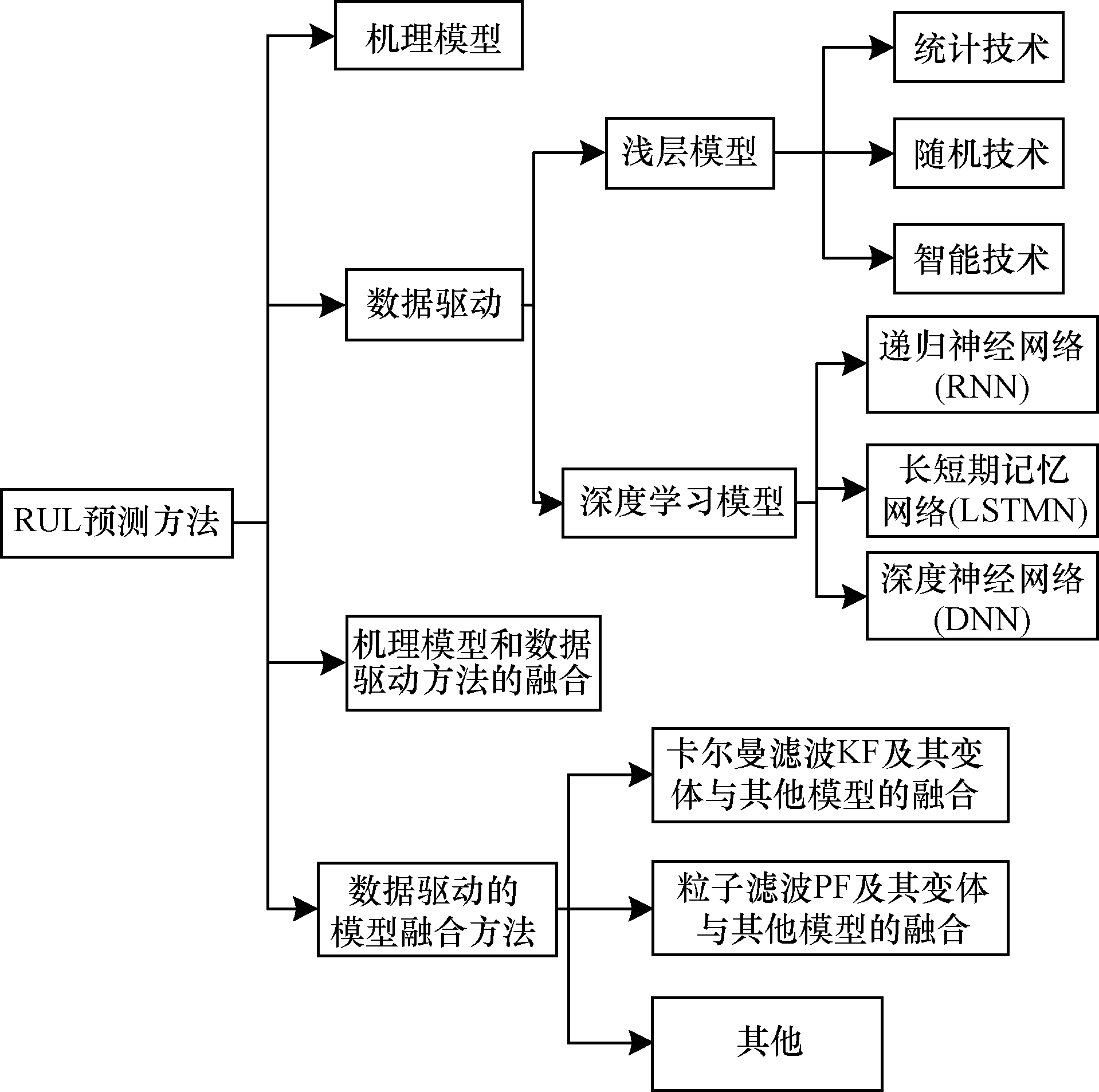
以上4类方法又可以分为离线和在线2种情况, 一般对于有大量历史数据并且实时性要求不高的场合多数采用离线模型, 离线模型可以对大量的历史数据进行充分的训练提高模型的准确率, 而对于实时性要求较高的场合, 不太适合利用大量历史数据进行离线学习, 多数采用在线模型对实时数据进行学习, 锂电子电池RUL预测方法如图 1所示。
|
Download:
|
| 图 1 锂离子电池的RUL预测方法 Fig. 1 RUL prediction method for lithium-ion batteries | |
基于机理模型的方法侧重于通过建立影响电池寿命的退化过程的物理模型来识别可观察量与感兴趣指标之间的对应关系。例如, 文献[5]考虑了锂离子电池电阻退化的经验指数增长模型, 使用标准粒子滤波(PF)和重采样技术测量描绘不同时间间隔的系统健康状态的退化数据。文献[6]用2种经验指数模型进行预测, 利用PF优化模型相关参数得到了较好的效果。文献[7]采用简化的等效电路模型, 应用高斯-厄米特粒子滤波器(Gauss-Hermite Particle Filter, GHPF)技术跟踪容量衰减趋势并预测未来的容量值, 这是PF技术的一个扩展。文献[8]利用GHPF技术估计电池荷电状态, 不仅提高了估计精度, 而且减少了采样粒子的数量, 降低了算法复杂度。文献[9]开发了基于统一粒子滤波(Unified Particle Filter, UPF)的退化模型来预测锂离子电池的RUL, 提出的模型在预测RUL时具有比PF方法更好的精度, 误差小于5 %。文献[10]提出了基于球形立方粒子滤波(Spherical Cubature Particle Filter, SCPF)的状态空间模型来检验26个锂离子电池的RUL, 所提出的模型在预测精度方面优于PF方法。
以上基于机理模型的RUL预测方法可以在相对稳定的外部条件下较好地提高预测的准确性, 但是模型的准确性很容易受到可变电流和温度的影响, 而且在不同外部条件情况影响下, 很难获得准确的机理模型。
3 基于数据驱动的方法数据驱动方法旨在通过基于可用数据自适应建立的一些近似模型来映射上述机理模型的输入数据与输出数据之间的关系, 如统计模型、神经网络(Neural Networks, NN)、高斯过程回归、支持向量回归、模糊推理等, 这些数据驱动的近似模型按照采用的技术不同大致可以划分为统计技术、随机技术和智能技术。
3.1 浅层模型浅层模型包含以下3种技术:
1) 统计技术
自回归统计模型(Auto-Regressive Model, AR)及其变体一般是通过建立线性模型来处理时间序列问题, 将未来的状态值视为过去的状态值和随机误差的线性函数。文献[11]提出了一种非线性退化自回归(ND-AR)时间序列模型用于锂电池的RUL预测, 并且使用正则化PF处理不确定性问题。文献[12]将ARMA模型用于锂电池的RUL预测中, 结合经验模式分解(Empirical Mode Decomposition, EMD)将全局退化趋势和健康状态(SOH)分离, 从而得到RUL和SOH。
卡尔曼滤波(KF)和粒子滤波(PF)也是2个非常重要的统计方法, 它们不仅在机理模型的RUL预测中发挥着重要的作用, 而且在基于数据驱动的方法中也有较好的应用。KF的思想是用已知的数据来预测未来的数据, 但是受到的噪声影响必须是高斯噪声。由于加入了噪声的因素, 因此比马尔科夫模型(Markov Model, MM)更加接近现实的情况, 预测的曲线与实际的曲线更加的吻合。文献[13]提出了基于无味卡尔曼滤波(Unscented Kalman Filter, UKF)方法用来对锂电池进行RUL预测。文献[14]提出了一种基于非线性时间序列预测模型和UKF算法相结合的新的RUL预测方法, 由UKF和短期容量递归更新电池模型的状态, 所提出的模型具有比EKF更高的准确性和可靠性。文献[15]提出了基于Lebesgue采样的扩展卡尔曼滤波器(LS-EKF)用于对锂电池的RUL预测。为了进一步提高预测的精度, 相关的研究人员开始研究粒子滤波器。
粒子滤波(PF)算法的思想来自于蒙特卡洛思想, 简单来说, 即用事件的频率来近似表达事件的概率。PF主要的优点是能够以现在的数据预测未来的相关数据, 而且数据的分布可以是任意的, 不局限于高斯分布, 比卡尔曼滤波器更加符合相关的实际情况。文献[16]将粒子滤波技术结合核平滑(Kernel Smoothing, KS)方法用于锂电池的RUL预测, 该方法可以同时估算退化模型中的退化状态和未知参数, 通过实验得到所提出的方法比传统的PF方法表现更好。文献[17]提出了一种基于马尔科夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)的改进无味粒子滤波器(Improved Unscented Particle Filter, IUPF)的锂离子电池RUL预测方法, 该方法利用MCMC解决UPF算法中的样本贫化问题。文献[18]提出了基于量子粒子群优化(Quantum Particle Swarm Optimization, QPSO)算法的粒子滤波用于锂电池的RUL预测, 通过与传统基于PSO算法的PF方法的对比, 表现出了较好的结果。文献[19]提出的SVR-PF改进了标准PF具有的粒子贫化效应的缺点, 实验结果表明所提出的SVR-PF比PF具有更好的电池状态的估计能力和RUL预测能力。文献[20]提出一种基于马尔科夫链蒙特卡罗(Monte Carlo Markov Chain, MCMC)的无迹粒子滤波改进算法, 更加全方面地克服了标准PF所具有的粒子退化问题, 相关的实验结果表明, 该方法在RUL的预测上具有更高的预测精度。
2) 随机技术
高斯过程(Gaussian Process, GP)是具有联合多元高斯分布的随机变量的累积损伤过程。文献[21]将GP和PF相结合, 把不同条件下的数据融合作为GP模型分布学习的输入, 最后用PF完成对锂电池RUL的预测。文献[22]提出一种多尺度高斯过程回归(Multiscale Gaussian Process Regression, MGPR)用来对锂电池进行RUL预测, 实验结果表明, 该方法比传统的GPR有更好的效果。文献[23]提出了一种基于高斯过程混合(Gaussian Process Mixture, GPM)的新型RUL预测方法, 它的主要思想是:分别将不同的轨迹段与不同的GPR模型拟合, 从而用于处理多模态问题, GPM还可以产生预测的置信区间, 实验结果表明, 该方法优于传统的GPR。
维纳过程(Wiener Process)是描述布朗运动(Brownian Motion)的模型, 它是一个马尔科夫过程, 是经常使用的随机过程模型。文献[24]采用具有测量误差(WPME)的维纳过程开发一种新的RUL预测方法, 该方法使用最大似然估计来提高参数的估计效率, 使用多个实例验证了模型的有效性。
随机过程可以更好地评估锂离子电池的健康退化过程。然而, 当算法考虑随机电流、时变温度和自放电特性的影响时, 实现精确预测仍然是一个挑战。
3) 智能技术
SVM的优势在于只需要少量的训练数据, 由SVM训练最终得到的支持向量决定了计算量的大小, 即在一定程度上降低了维度灾难的问题。文献[25]采用支持向量回归(Support Vector Regression, SVR)技术实现在电池接近EOL时预测准确的RUL。文献[26]提出了基于灵活支持向量回归(Flexible Support Vector Regression, F-SVR)的非迭代预测模型和基于支持向量回归SVR的迭代多步预测模型, 用于锂电池的RUL预测, 能够将低维度的数据用作输入, 得到较好的预测结果。文献[27]提出了相等充电电压差的时间间隔(Time Interval of an Equal Charging Voltage Difference, TIECVD)和相等放电电压差的时间间隔(Time Interval of an Equal Discharging Voltage Difference, TIEDVD)2个新的健康指标, 结合特征向量选择和SVR对锂电池的RUL进行预测。
虽然SVM(或SVR)表现较好, 但是它不适用于大数据的处理, 而且对RUL的估计是点估计。下文介绍的相关向量机(Relevance Vector Machine, RVM)不仅训练所需要的时间短, 而且获得的RUL估计是概率估计, 得到了相关研究人员的青睐。
文献[28]将放电电压样本熵(Sample Entropy, SampEn)特征用作RVM的输入, 用来预测锂电池的RUL。文献[29]提出了一种稀疏贝叶斯学习方法, 将充电电压和电流用作RVM的输入来估算可植入医疗设备锂电池的RUL, 所提出的方法在实时RUL预测中表现出色。文献[30]提出了一种仅需要锂离子电池工作参数的HI提取和优化框架, 用于电池退化建模, 其中RVM用作RUL估计。文献[31]提出了一种基于RVM算法的容量退化模型用于预测锂离子电池RUL, 取得了不错的预测结果。文献[32]提出RVM的方法进行锂离子电池的RUL预测, 给出了RUL的置信区间, 充分考虑了不确定性的问题, 将得到的结果与EKF对比, 绝对误差平均值和均方根误差平均值均低1 %。文献[33]提出一种融合多个核函数构建RVM预测模型的方法, 实验结果表明, 所提出的方法平均绝对误差和均方根误差都小于最优的单核相关向量机预测方法。
3.2 深度学习模型3.1节的浅层模型的方法虽然在锂电池RUL的预测上精度高, 但是都不能处理大量的数据, 限制了其在现实中的应用, 近年来深度学习方法逐渐开始应用, 对于大数据的处理正是它们的特点和优势。
递归神经网络(Recurrent Neural Network, RNN)在处理时间序列数据上有着独特的优势, 而且RNN能够将先前的信息存储到记忆单元并且运用到现在的相关任务中。文献[34]将锂电池阻抗谱数据输入到自适应RNN中用于锂电池的RUL预测。文献[35]将RNN运用到电动车和混合动力车辆的锂电池RUL预测上, 得到了较好的效果。虽然RNN表现优秀, 但是由于其本身网络结构带来的梯度消失和梯度爆炸问题很难解决, 相关的研究人员将研究转向了它的变体——长短期记忆网络(Long Short-Term Memory, LSTM)。
LSTM将所有的信息通过门结构进行处理, 遗忘门的功能是决定是否保留信息, 输入门的功能是更新细胞状态, 输出门的作用在于确定下一个隐藏状态的值。LSTM的门机制避免了梯度消失和梯度爆炸的问题。文献[36]提出基于长短期记忆网络LSTM的模型来预测RUL, 使用了各种锂离子电池在不同的电流速率和温度下的实验数据对模型进行验证, 该模型不依赖离线训练数据, 取得了较为满意的RUL预测结果。
深度神经网络(Deep Neural Networks, DNN)是深度学习中的一个基础模型。文献[37]采用DNN预测电池的SOH和RUL, 并与其他机器学习算法, 如线性回归(Linear Regression, LR)、k-近邻(k-Nearest Neighbors, k-NN)、支持向量机(SVM)和人工神经网络(ANN)进行比较, 取得了更好的预测结果。
深度学习模型虽然具有处理大数据的能力, 并且具有比浅层模型更强的学习能力, 但它同样存在缺乏对预测结果不确定性的分析。
4 机理模型与数据驱动模型的混合方法混合方法旨在尽可能地结合上述基于机理模型和基于数据驱动的两类方法, 试图克服各类方法的局限性, 从而通过更好地利用所有可用信息来提高诊断和预测的准确性。文献[38]开发了一个基于DS理论(Dempster-Shafer Theory, DST)和贝叶斯蒙特卡罗(Bayesian Monte Carlo, BMC)的双指数经验退化模型来预测RUL, DST用于初始化训练数据集的参数, BMC用来更新模型的参数。文献[39]介绍了植入式医疗设备中锂离子电池的故障预测研究, 采用混合数据驱动和机理模型的方法来进行寿命预测, 它由2个模块组成, 稀疏贝叶斯学习用于从电荷相关特征推断容量(数据驱动模块), 递归贝叶斯过滤用于更新经验容量衰减模型(机理模型模块)。文献[40]结合布朗运动的退化模型和PF进行锂电池RUL的预测, 通过与GPR相比, 该方法具有更好的性能和更稳健的预测结果。文献[41]结合指数模型和PF算法对锂电池进行RUL预测, 与ARIMA等算法相比具有更高的预测精度。文献[42]将减少了参数数量的双指数经验模型结合PF算法, 其中PF算法用于跟踪电池容量的衰退过程, 实验结果表明, 该方法具有更高的RUL预测精度。
5 基于数据驱动的模型融合方法第4节的方法虽然预测精度很高, 但是在实际应用中可能表现的不是很出色, 由于对锂电池的RUL的估计具有重大的意义, 预测精度越高, 带来的损失就越小, 节省的资金就越多。因此,相关的研究人员在近些年开始尝试使用模型融合的方法进行RUL预测。这里的模型融合不限定模型的类型, 前文中总结的第3类混合方法特指机理模型和数据驱动模型的混合, 与此不同, 本节的模型融合为纯数据驱动模型之间的融合。
因为基于融合的方法结合了2个甚至多个方法的优点, RUL预测精度得到了较大的提升。文献[43]提出将扩展卡尔曼滤波器(EKF)和基于非线性尺度退化参数的自回归(Nonlinear Scale Degradation Parameter based Autoregressive, NSDP-AR)模型融合用于锂电池的RUL预测, 实验结果表明, 该方法相较于ND-AR结合EKF的RMSE和MAE值均有下降, 由于EKF的性能要优于其他的滤波器方法,因此所提出的方法降低了对经验模型的依赖, 提高了RUL预测的精度。文献[44]将RVM和KF相结合, 提升了RVM长期预测的性能, 通过在PCoE电池数据集上的实验, 将RVM的RUL-Error由0.140 6降低到0.031 2, 而且MAE和RMSE均有较大幅度的下降(MAE下降到原来的30 %, RMSE下降到原来的21.5 %)。通过在卫星电池数据集上的实验可以看出, 随着训练的数据集变长, 能够获得更好的拟合效果, 验证了所提方法能够改善RVM长期预测的能力。文献[45]结合无味卡尔曼滤波器(UKF)、经验模式分解(Empirical Mode Decomposition, CEEMD)和相关向量机(RVM)来预测锂离子电池的RUL, 实验结果表明, 与单一的UKF和RVM相比, 提出的方法能够得到更具鲁棒性的预测结果, 而且实现了在锂离子电池放电电流不同的情况下, 能得到相较于传统方法更具有鲁棒性和准确的RUL预测结果。文献[46]提出SVR和PF融合的方法用于锂电池的SOH和RUL预测, 通过与标准的PF进行对比实验, 当随机变量用于产生初始粒子时与提高RUL的阈值时,SVR-PF比标准PF都要更加拟合实际的RUL曲线, 产生更好的预测结果。
为了解决传统的AR模型在训练中参数不能更新, 且在长期的预测过程中难以获得PF测量函数的问题, 文献[47]提出了一种IND-AR模型结合PF算法的方法, 该方法利用非线性劣化因子和迭代参数更新方法来改善长期预测性能, 将预测的结果用作PF的测量函数, 同时利用PF计算不确定性问题。此方法可适用于小样本数据下的非线性退化情况, 实验结果表明了所提出方法具有良好的预测精度。文献[48]通过结合AE的深度神经网络显著地提高了在PCoE上的RUL预测精确度。首先用具有AE模型的多维特征提取方法来表示电池健康退化, 然后使用DNN进行RUL预测。实验结果表明,与Bayesian Regreesion、LR以及SVR进行对比, 该方法RMSE值分别降低5.26 %、5.34 %、4 %, 预测的精度分别提升了4.26 %、5.34 %、4 %, 融合模型相较于单一的模型具有更高的预测精度和更低的RMSE值。针对锂离子电池数据集的劣化特性, 文献[49]将小波去噪(Wavelet Denoising, WD)方法和混合高斯过程函数(Hybrid Gaussian Process Function Regression, HGPFR)融合对锂电池进行RUL预测, 其中WD用于减少噪声的影响, 实验结果表明,所提出的模型比HGPFR模型的错误率, RMSE以及MAPE分别降低2.3 %、75.4 %、78.1 %, 比GPR降低了6 %、75.8 %、80.5 %, 充分说明了所提出方法的优越性。为了在少量数据的情况下精确预测电池的RUL, 文献[50]将RVM和PF相结合用于锂电池的RUL预测, 其中,RVM用于基于有限的可用数据进行特征提取以初始化老化模型。然后, 应用PF进一步更新模型参数以获得精确的老化模型并预测电池的故障时间, 实验结果表明, 在训练数据为整个退化数据的30 %的情况下, 所提出的方法能够精确预测RUL, 减少了整体所需要的时间。针对传统的PF方法的不足, 文献[51]提出了一种RVM、PF和AR模型融合的锂离子电池RUL预测的方法, 通过与PF的对比实验结果表明MAE和RMSE都有明显下降, 预测结果较PF略有提升, 证明了此方法的有效性。
另外一种混合策略是将EKF或PF算法中表示系统的动态行为状态方程或测量方程的机理模型替代为数据驱动的合适模型。例如, 文献[52]提出了扩展卡尔曼滤波(EKF)和离线训练的神经网络的组合模型, 而文献[53]使用粒子滤波器代替EKF。这些方法基于以下考虑:基于机理模型和替代模型都需要在一些可用的观察数据的基础上识别合适的模型参数。然而, 机理模型的分析推导非常耗时, 替代模型则不需要任何机理分析推导, 计算速度更快, 特别是对于数值模型而言, 这一点特别适合实时应用。文献[54]利用粒子滤波和多层感知器(Multi Layer Perceptron, MLP)神经网络提出了一个的实时的RUL预测框架, 其中MLP用于替换PF的测量方程。总体来说, 基于融合的方法基本上为该领域目前最优的方法, 代表了对锂电池RUL预测的最高水平。
6 方法对比与未来展望本文对基于数据驱动的RUL预测方法的优缺点进行比较, 如表 1所示。可以看出, AR虽然是点估计, 但是结合PF能够处理不确定性问题。KF的相关变体虽然预测的精度较KF有所提升, 但是仅考虑了高斯噪声。PF及其变体的数据分布更加广泛, 解决了KF的不足, 并且相关的改进SVR-PF方法解决了传统PF的样本贫化的问题。GPR和Winner相较于前面的方法, 更加贴合大数据环境下的高维数据的特点, 但是只能处理小样本的数据, 而且长期的预测结果较差, 相关的变体例如GPM只提供预测的置信区间。基于AI的相关技术解决了GPR和Winner不能使用过去数据的问题, 但是其中的SVM和RVM不能处理大量的数据, 而且SVM是点估计。RVM的区间估计解决了SVM点估计的问题, 但是RVM的预测性能严重依赖于核函数的选择, 相关的变体例如融合多个核函数构建的RVM解决了单一核函数的选择对预测结果的影响, 提高了预测的精度。深度学习的模型解决了浅层模型不能处理大量数据的缺点, 但是RNN会出现梯度消失和梯度爆炸的问题, LSTM通过门机制解决了RNN的上述问题。通过结合机理模型和数据驱动模型, 能够解决上述模型的部分问题, 但是上述的模型都有进一步提升的空间, 这就催生了基于数据驱动的融合模型, 该融合模型因为结合了多种方法, 预测精度相较于单一的数据驱动模型有较大的提升, 基于数据驱动的融合模型将单一的模型结合其他的方法进行改进, 能够更好地模拟退化的趋势, 明显提升RUL预测结果, 表明了融合模型的优越性。

|
下载CSV 表 1 基于数据驱动的各种RUL预测方法优缺点对比 Table 1 Comparison of advantages and disadvantages of varous RUL prediction method based on data driven |
总体而言, 无论是基于机理模型还是基于数据驱动的RUL预测方法都有各自不同的要求和适用场景, 两者也有不同的优点和缺点。数据驱动的模型是由基于经验寿命数据和系统运行的历史数据构建的, 优点是不需要复杂物理系统的真实机理表达公式, 模型不复杂, 更容易应用到实际应用中, 缺点是需要大量的经验数据才能构建高精度模型, 这些模型并不代表实际的系统, 它需要收集更多的数据来学习从而理解真实的系统行为。机理模型则理解系统的物理规则, 具有描述系统的确切公式, 优点是精度更高, 因为它的模型是建立在实际(或接近实际)的物理系统之上的, 代表一个真实的系统, 可以更真实地观察和判断模型, 缺点是高度复杂, 需要大量的计算时间/资源, 不太适合在实际应用中使用, 还有就是在包含不可测变量的大型复杂系统的情况下很难建立准确的机理模型。混合方法可以克服基于模型的方法和数据驱动方法各自的缺点。而基于模型融合的RUL预测方法并不特指混合方法, 也就是说不限定模型的类型, 可以是纯数据驱动的模型融合, 基于模型融合的RUL预测已经成为提高锂离子电池RUL预测性能的研究热点。
在未来的研究中, 应该关注以下5个方面:
1) 目前的工作大多数在单一工况和几种工况下进行预测, 很少考虑到温度和其他外界因素的综合影响, 未来可以将相关的工作集中于多种工况、多种因素影响下的锂离子电池RUL的预测。
2) 进一步研究基于数据驱动的融合模型的方法, 同时要注重对不确定性问题的处理, 改进相关的算法以提高预测的精度。
3) 目前对锂离子电池的RUL的预测方法进展较慢, 方法比较固定, 未来可以其他的领域如NLP中借鉴相关的方法来处理, 例如最新的TCN等。
4) 在未来的研究中, 希望能在动态操作或者运行的条件下, 对相关设备的锂离子电池组进行RUL的预测。
5) 现有的研究只关注SOH、RUL或者电池故障的检测, 希望未来能形成从锂离子电池的生产、使用状态的日常与异常监测到故障的诊断与RUL的预测以及对应的维护策略、废旧锂离子电池的回收与再利用等整体的流程。
7 结束语本文总结了近年来锂离子的RUL预测方法, 对RUL预测的基于机理模型、基于数据驱动、基于机理模型与数据驱动融合和基于数据驱动的模型融合4种方法进行综述, 并对比分析其优缺点, 给出目前的研究热点和建议。下一步将研究关于锂电池RUL预测的基于数据驱动的组合方法并借鉴相关领域的方法, 进一步提高锂离子电池RUL预测的准确率。
| [1] |
PINSON M B, BAZANT M Z. Theory of SEI formation in rechargeable batteries:capacity fade, accelerated aging and lifetime prediction[J]. Journal of the Electrochemical Society, 2012, 160(2): 243-250. |
| [2] |
KHUMPROM P, YODO N. A data-driven predictive prognostic model for lithium-ion batteries based on a deep learning algorithm[J]. Energies, 2019, 12(4): 21-32. |
| [3] |
WAAG W, FLEISCHER C, SAUER D U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles[J]. Journal of Power Sources, 2014, 258: 321-339. DOI:10.1016/j.jpowsour.2014.02.064 |
| [4] |
XING Y, MA E W M, TSUI K L, et al. Battery management systems in electric and hybrid vehicles[J]. Energies, 2011, 4(11): 1840-1857. DOI:10.3390/en4111840 |
| [5] |
AN D, CHOI J H, KIM N H. Prognostics 101:a tutorial for particle filter-based prognostics algorithm using Matlab[J]. Reliability Engineering and System Safety, 2013, 115: 161-169. DOI:10.1016/j.ress.2013.02.019 |
| [6] |
SU X, WANG S, PECHT M, et al. Prognostics of lithium-ion batteries based on different dimensional state equations in the particle filtering method[J]. Transactions of the Institute of Measurement and Control, 2017, 39(10): 1537-1546. DOI:10.1177/0142331216642836 |
| [7] |
HU C, JAIN G, TAMIRISA P, et al. Method for estimating capacity and predicting remaining useful life of lithium-ion battery[J]. Applied Energy, 2014, 126: 182-189. DOI:10.1016/j.apenergy.2014.03.086 |
| [8] |
LI Bin, PENG Kai, LI Guidan. State-of-charge estimation for lithium-ion battery using the Gauss-Hermite particle filter technique[J]. Journal of Renewable and Sustainable Energy, 2018, 10(1): 141-155. |
| [9] |
MIAO Qiang, XIE Lei, CUI Hengjuan, et al. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique[J]. Microelectronics Reliability, 2013, 53(6): 805-810. DOI:10.1016/j.microrel.2012.12.004 |
| [10] |
WANG D, YANG F, TSUI K L, et al. Remaining useful life prediction of lithium-ion batteries based on spherical cubature particle filter[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(6): 1-10. DOI:10.1109/TIM.2016.2560398 |
| [11] |
LIU D, LUO Y, LIU J, et al. Lithium-ion battery remaining useful life estimation based on fusion nonlinear degradation AR model and RPF algorithm[J]. Neural Computing and Applications, 2014, 25(3/4): 557-572. |
| [12] |
ZHOU Yapeng, HUANG Miaohua. Lithium-ion batteries remaining useful life prediction based on a mixture of empirical mode decomposition and ARIMA model[J]. Microelectronics Reliability, 2016, 65: 265-273. DOI:10.1016/j.microrel.2016.07.151 |
| [13] |
HE W, WILLIARD N, CHEN C, et al. State of charge estimation for electric vehicle batteries using unscented Kalman filtering[J]. Microelectronics Reliability, 2013, 53(6): 840-847. DOI:10.1016/j.microrel.2012.11.010 |
| [14] |
ZHENG Xiujuan, FANG Huaijing. An integrated unscented Kalman filter and relevance vector regression approach for lithium-ion battery remaining useful life and short-term capacity prediction[J]. Reliability Engineering and System Safety, 2015, 144: 74-82. DOI:10.1016/j.ress.2015.07.013 |
| [15] |
YAN Wuzhao, ZHANG Bin, WANG Xiaofeng, et al. Lebesgue-sampling-based diagnosis and prognosis for lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2015, 63(3): 1804-1812. |
| [16] |
HU Y, BARALDI P, DI M F, et al. A particle filtering and kernel smoothing-based approach for new design component prognostics[J]. Reliability Engineering and System Safety, 2014, 134: 19-31. |
| [17] |
ZHANG X, MIAO Q, LIU Z. Remaining useful life prediction of lithium-ion battery using an improved UPF method based on MCMC[J]. Microelectronics Reliability, 2017, 75: 288-295. DOI:10.1016/j.microrel.2017.02.012 |
| [18] |
YU Jingsong, MO Baohua, TANG Diyin, et al. Remaining useful life prediction for lithium-ion batteries using a quantum particle swarm optimization-based particle filter[J]. Quality Engineering, 2017, 29(3): 536-546. DOI:10.1080/08982112.2017.1322210 |
| [19] |
DONG Hancheng, LING Mingxiang, WANG Changhong, et al. Lithium-ion battery state-of-health estimation and remaining useful life prediction[J]. Transactions of Beijing Institute of Technology, 2015, 35(10): 1074-1078. (in Chinese) 董汉成, 凌明祥, 王常虹, 等. 锂离子电池健康状态估计与剩余寿命预测[J]. 北京理工大学学报, 2015, 35(10): 1074-1078. |
| [20] |
LIU Yajiao, LIU Zhenze, SONG Chenhui. Improved particle filter algorithm for RUL prediction of lithium-ion batteries[J]. Journal of Jilin University(Information Science Edition), 2018, 36(2): 173-177. (in Chinese) 刘亚姣, 刘振泽, 宋晨辉. 基于改进粒子滤波的锂离子电池RUL预测[J]. 吉林大学学报(信息科学版), 2018, 36(2): 173-177. DOI:10.3969/j.issn.1671-5896.2018.02.009 |
| [21] |
LI Fan, XU Jiuping. A new prognostics method for state of health estimation of lithium-ion batteries based on a mixture of Gaussian process models and particle filter[J]. Microelectronics Reliability, 2015, 55(7): 1035-1045. DOI:10.1016/j.microrel.2015.02.025 |
| [22] |
HE Yijun, SHEN Jiani, SHEN Jifu, et al. State of health estimation of lithium-ion batteries:a multiscale Gaussian process regression modeling approach[J]. AIChE Journal, 2015, 61(5): 1589-1600. DOI:10.1002/aic.14760 |
| [23] |
LI L L, WANG P C, CHAO K H, et al. Remaining useful life prediction for lithium-ion batteries based on Gaussian processes mixture[J]. PIOS One, 2016, 11(9): 13. |
| [24] |
TANG Shengjin, YU Chuangqiang, WANG Xue, et al. Remaining useful life prediction of lithium-ion batteries based on the wiener process with measurement error[J]. Energies, 2014, 7(2): 520-547. DOI:10.3390/en7020520 |
| [25] |
PATIL M A, TAGADE P, HARIHARAN K S, et al. A novel multistage support vector machine based approach for lithium-ion battery remaining useful life estimation[J]. Applied Energy, 2015, 159: 285-297. DOI:10.1016/j.apenergy.2015.08.119 |
| [26] |
WANG Shuai ZHAO Lingling, SU Xiaohong, et al. Prognostics of lithium-ion batteries based on battery performance analysis and flexible support vector regression[J]. Energies, 2014, 7(10): 6492-6508. DOI:10.3390/en7106492 |
| [27] |
ZHAO Qi, QIN Xiaoli, ZHAO Hongbo, et al. A novel prediction method based on the support vector regression for the remaining useful life of lithium-ion batteries[J]. Microelectronics Reliability, 2018, 85: 99-108. DOI:10.1016/j.microrel.2018.04.007 |
| [28] |
WIDODO A, SHIM M C, CAESARENDRA W, et al. Intelligent prognostics for battery health monitoring based on sample entropy[J]. Expert Systems with Applications, 2011, 38(9): 11763-11769. DOI:10.1016/j.eswa.2011.03.063 |
| [29] |
HU C, JAIN G, SCHMIDT C, et al. Online estimation of lithium-ion battery capacity using sparse Bayesian learning[J]. Journal of Power Sources, 2015, 289: 105-113. DOI:10.1016/j.jpowsour.2015.04.166 |
| [30] |
LIU Datong, ZHOU Jianbao, LIAO Haitao, et al. A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2015, 45(6): 915-928. DOI:10.1109/TSMC.2015.2389757 |
| [31] |
WANG D, MIAO Q, PECHT M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model[J]. Journal of Power Sources, 2013, 239: 253-264. DOI:10.1016/j.jpowsour.2013.03.129 |
| [32] |
LI Sai, PANG Xiaoqiong, LIN Huilong, et al. RUL prediction for lithium-ion batteries based on relevance vector machine[J]. Computer Engineering and Design, 2018, 39(8): 2682-2686. (in Chinese) 李赛, 庞晓琼, 林慧龙, 等. 基于相关向量机的锂离子电池剩余寿命预测[J]. 计算机工程与设计, 2018, 39(8): 2682-2686. |
| [33] |
LIU Yuefeng, ZHAO Guangquan, PENG Xiyuan. A lithium-ion battery remaining using life prediction method based on multi-kernel relevance vector machine optimized model[J]. Acta Electronica Sinica, 2019, 47(6): 1285-1292. (in Chinese) 刘月峰, 赵光权, 彭喜元. 多核相关向量机优化模型的锂电池剩余寿命预测方法[J]. 电子学报, 2019, 47(6): 1285-1292. DOI:10.3969/j.issn.0372-2112.2019.06.015 |
| [34] |
LIU J, SAXENA A, GOEBEL K, et al.An adaptive recurrent neural network for remaining useful life prediction of lithium-ion batteries[C]//Proceedings of Annual Conference on Prognostics and Health Management Society.Portland, USA: [s.n.], 2010: 1-9.
|
| [35] |
EDDAHECH A, BRIAT O, BERTRAND N, et al. Behavior and state-of-health monitoring of lithium-ion batteries using impedance spectroscopy and recurrent neural networks[J]. International Journal of Electrical Power and Energy Systems, 2012, 42(1): 487-494. DOI:10.1016/j.ijepes.2012.04.050 |
| [36] |
ZHANG Yongzhi, XIONG Rui, HE Hongwen, et al. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 1-10. DOI:10.1109/TVT.2018.2848579 |
| [37] |
KHUMPROM P, YODO N. A Data-driven predictive prognostic model for lithium-ion batteries based on a deep learning algorithm[J]. Energies, 2019, 12(4): 1-21. |
| [38] |
HE W, WILLIARD N, OSTERMAN M, et al. Prognostics of lithium-ion batteries based on dempster-shafer theory and the Bayesian Monte Carlo method[J]. Journal of Power Sources, 2011, 196(23): 10314-10321. DOI:10.1016/j.jpowsour.2011.08.040 |
| [39] |
HU C, YE H, JAIN G, et al. Remaining useful life assessment of lithium-ion batteries in implantable medical devices[J]. Journal of Power Sources, 2018, 375: 118-130. DOI:10.1016/j.jpowsour.2017.11.056 |
| [40] |
DONG Guangzhong, CHEN Zonghai, WEI Jingwen, et al. Battery health prognosis using brownian motion modeling and particle filtering[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8646-8655. DOI:10.1109/TIE.2018.2813964 |
| [41] |
ZHANG Lijun, MU Zhongqiang, SUN Changyan. Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter[J]. IEEE Access, 2018, 6: 17729-17740. DOI:10.1109/ACCESS.2018.2816684 |
| [42] |
ZHANG Ning, XU Kaidong, WANG Kai, et al. Research on prediction of the remaining useful life of lithium-ion batteries based on particle filtering[J]. Chinese High Technology Letters, 2017, 27(8): 699-707. (in Chinese) 张凝, 徐皑冬, 王锴, 等. 基于粒子滤波算法的锂离子电池剩余寿命预测方法研究[J]. 高技术通讯, 2017, 27(8): 699-707. DOI:10.3772/j.issn.1002-0470.2017.08.003 |
| [43] |
LIU De, GUO Li, PANG Jie, et al.A fusion framework with nonlinear degradation improvement for remaining useful life estimation of lithium-ion batteries[C]//Proceedings of IEEE Annual Conference of the Prognostics and Health Management Society.Washington D.C., USA: IEEE Press, 2013: 598-607.
|
| [44] |
SONG Yuncheng, LIU Datong, HOU Yandong, et al. Satellite lithium-ion battery remaining useful life estimation with an iterative updated RVM fused with the KF algorithm[J]. Chinese Journal of Aeronautics, 2018, 31(1): 31-40. DOI:10.1016/j.cja.2017.11.010 |
| [45] |
CHANG Yang, FANG Huajing, ZHANG Yong. A new hybrid method for the prediction of the remaining useful life of a lithium-ion battery[J]. Applied Energy, 2017, 206(15): 1564-1578. |
| [46] |
DONG Hancheng, JIN Xiaoning, LOU Yangbing, et al. Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter[J]. Journal of Power Sources, 2014, 271: 114-123. DOI:10.1016/j.jpowsour.2014.07.176 |
| [47] |
SONG Yucheng, LIU Datong, YANG Chen, et al. Data-driven hybrid remaining useful life estimation approach for spacecraft lithium-ion battery[J]. Microelectronics Reliability, 2017, 75: 142-153. DOI:10.1016/j.microrel.2017.06.045 |
| [48] |
REN Lei, ZHAO Li, HONG Sheng, et al. Remaining useful life prediction for lithium-ion battery:a deep learning approach[J]. IEEE Access, 2018, 6: 50587-50598. DOI:10.1109/ACCESS.2018.2858856 |
| [49] |
PENG Yu, HOU Yandong, SONG Yuchen, et al. Lithium-ion battery prognostics with hybrid Gaussian process function regression[J]. Energies, 2018, 11(6): 1420. DOI:10.3390/en11061420 |
| [50] |
ZHANG Yognzhi, XIONG Rui, HE Hongwen, et al. Validation and verification of a hybrid method for remaining useful life prediction of lithium-ion batteries[J]. Journal of Cleaner Production, 2019, 212: 240-249. DOI:10.1016/j.jclepro.2018.12.041 |
| [51] |
LIU Yuefeng, ZHAO Guangquan. A fusion prediction method of lithium-ion battery cycle-life[J]. Chinese Journal of Scientific Instrument, 2015, 36(7): 1462-1469. (in Chinese) 刘月峰, 赵光权. 锂离子电池循环寿命的融合预测方法[J]. 仪器仪表学报, 2015, 36(7): 1462-1469. DOI:10.3969/j.issn.0254-3087.2015.07.003 |
| [52] |
CHARKHFARD M, FARROKHI M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF[J]. IEEE Transactions on Industrial Electronics, 2011, 57(12): 4178-4187. |
| [53] |
DAROOGHEH N, BANIAMERIAN A, MESKIN N, et al.A hybrid prognosis and health monitoring strategy by integrating particle filters and neural networks for gas turbine engines[C]//Proceedings of Conference on Prognostics and Health Management.Austin, USA: [s.n.], 2015: 1-6.
|
| [54] |
CADINI F, SBARUFATTI C, CANCELLIERE F, et al. State-of-life prognosis and diagnosis of lithium-ion batteries by data-driven particle filters[J]. Applied Energy, 2019, 235: 661-672. DOI:10.1016/j.apenergy.2018.10.095 |
 2020, Vol. 46
2020, Vol. 46
