0 概述

随着计算机技术的快速发展和网络数据的海量增加, 云存储技术成为云计算不可或缺的一部分, 它允许用户把大量的数据外包存储在云中, 从而减少用户存储空间管理和计算的成本, 但此时外包数据的安全也受到极大威胁, 不可信的云存储提供者可能为了利益而篡改或删除数据, 也有可能因为硬件/软件故障而造成数据丢失。因此, 用户需要确认存储在云中的数据是未被篡改且被云存储器完整存储的^[1]。

为有效验证外包数据的完整性, 研究者相继提出很多审计方案。当用户想要检验数据的完整性时, 第三方审计者(Third Party Auditor, TPA)能够代替用户在不下载所有数据的前提下对数据进行完整性的检验。如果TPA在执行审计过程中没有删除用户的任何秘密值, 则称为公开审计。文献[2]提出公开审计的方案, 而为提高性能和安全性, 文献[3-5]提出了新的审计方案，文献[3]方案支持无需第三方审计者帮助的公开审计，且不会向第三方审计者泄露用户的隐私信息，文献[4]提出一种灵活的分布式存储完整性审计机制，文献[5]提出一种安全的云存储系统支持保护隐私的公开审计方案。此外，文献[6-8]方案则是在前人所做工作基础上的改进。文献[6]针对半可信的第三方审计者，提出一种用户可以与云服务提供者进行交互，由用户自己完成数据完整性验证的方案, 文献[7]提出一种改进的基于LBT树形认证结构的数据完整性公开审计方案，文献[8]提出已知数据伪造改造的概念，利用基于等级的认证跳表设计了相应的改进方案。之后, 针对动态群组隐私保护的审计方案^[9-10]和面向公有云及多管理者群组的公开审计方案^[11]相继被提出。上述审计方案都是基于传统的公钥密码体制, 由证书授权方产生用户的公私钥对, 通过绑定用户的公钥来产生对应的私钥, 而产生的证书都是由证书授权方管理, 会出现证书管理问题, 包括密钥的分发、存储、撤销和认证, 并且密钥生成中心(Key Generation Center, KGC)有能力产生任何实体的签名, 有可能会泄露用户的身份信息。针对证书管理问题, 一系列基于身份的公开审计方案^[12-14]被提出。文献[12]提出一种新的基于身份的聚合签名公开审计方案，解决了存储用户在上传数据前需要先颁发证书从而产生巨大成本的问题，并在其安全模型下是可证明安全的, 文献[13]采用一种有效的基于证书的公钥设置密钥管理方案，将基于身份的聚合签名与公开验证相结合，构造了可证明数据完整性协议，减少了TPA单个任务的审计时间, 文献[14]则提出针对多个云环境的基于身份的审计方案。

然而, 上述方案都存在密钥托管问题, 用户的私钥完全是由KGC产生, 而KGC有可能不是完全可信的, 可能会泄露用户的隐私信息。在这种情况下, 该问题可以通过设定KGC是完全可信的实体而得以解决, 这在文献[15-16]的方案中有所体现。文献[17]提出了无证书的公开审计(Certificateless Public Key Cryptography, CLPKC)的概念。在CLPKC中, 用户的私钥包含两部分, 一部分是由用户自己生成的, 另一部分是由KGC生成的。因此, CLPKC解决了传统公钥密码体制中的证书管理和密钥托管问题。基于先前的工作, 文献[18]提出了新的签名机制——无证书签名机制, 该机制由无块验证和同态认证来实现, 是首个通过无证书签名产生的无证书公开审计方案。该方案的提出解决了传统密码体制中的证书管理问题和基于身份公开审计中的密钥托管问题, 但其签名方案不能抵抗第一类型攻击, 即攻击者可以在他的意愿下替换用户的公钥, 并且当用户出现恶意行为时, 不支持用户追踪的功能。

本文提出一种无证书的公开审计方案, 采用同态技术完成多用户的审计请求, 从而减少计算量, 提高审计效率。同时利用ELGamal体制对恶意用户身份进行追踪, 以保证数据和签名用户身份的隐私性。

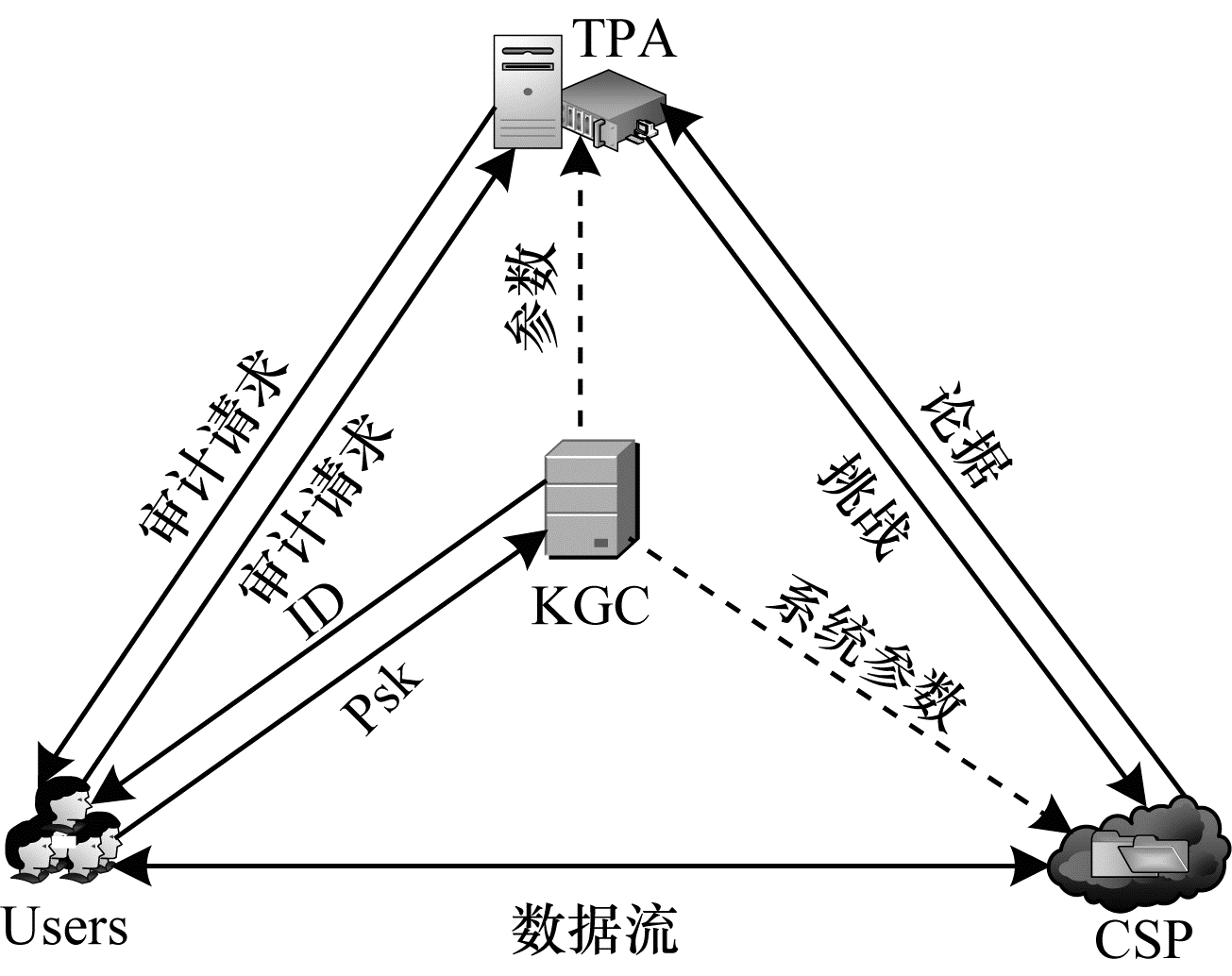
1 系统模型和安全模型 1.1 系统模型

本文方案的系统模型如图 1所示, 其中包含4个实体:KGC, TPA, 云存储器提供者(Cloud Server Provider, CSP), 群组用户(Users)。每类实体的主要功能描述如下:

1) KGC:KGC是完全可信的, 它生成系统主密钥、公共参数以及产生用户和群管理者的部分公私钥对。

2) TPA:TPA是完全可信的, 它负责验证存储在CSP中数据的完整性, 在验证过程中不会获得任何具体的数据信息。

3) CSP:CSP是半可信的, 它提供足量的存储空间和检索功能, 但同时它是好奇的, 并会在多种动机的促使下返回错误的数据, 造成机密数据的泄露。

4) Users:群组用户包含一个群管理者和其他用户, 管理者具有注册和追踪用户的权利, 通过管理者完成注册的用户, 可以访问和更新共享数据。

1.2 安全模型

在本文方案中, CSP是半可信的, 因此, 可能会遭受到来自内部或外部的攻击; 审计方案的安全模型是由敌手$\mathcal{A}$和挑战者F之间的游戏定义的, 而该游戏是基于CDH困难性问题。挑战游戏有以下阶段:

1) 初始化阶段:挑战者F执行初始化阶段, 产生系统公共参数pp和系统主密钥msk, 然后将公共参数pp发送给敌手$\mathcal{A}$, 保留主密钥msk。

2) 询问阶段:敌手$\mathcal{A}$可以向挑战者F做多次询问, 包括密钥提取询问和签名生成询问。

(1) 密钥提取询问:挑战者F接收到询问的身份信息ID_i, 通过执行运算, 将(ID_i, x_i, pk_i)发送给敌手$\mathcal{A}$。

(2) 签名生成询问:挑战者F接收到询问的身份信息ID_i, 数据块m_i和数据块id_i, F执行签名生成算法, 将{σ_i, C_{i, 1}, C_{i, 2}}_{i∈[1, n]}发送给$\mathcal{A}$。

3) 输出结果:敌手$\mathcal{A}$输出伪造的签名{σ_i, C_{i, 1}, C_{i, 2}}_{i∈[1, n]}, 若能通过签名验证, 则$\mathcal{A}$赢得挑战游戏, CDH困难问题被攻破。

1.3 设计目标

本文方案需要满足以下性质:

1) 公开审计:公开审计者可以在不检索整篇数据的前提下验证共享数据的完整性。

2) 正确性:公开验证者可以正确验证共享数据的完整性。

3) 不可伪造性:只有群组用户可以产生有效、共享数据的原始数据(如签名)。

4) 身份的隐私性:公开审计者在对共享数据块的审计过程中不能区分签名者的身份信息。

5) 批量审计:公开审计可以满足多个数据块的一次性验证需求, 提高审计效率。

6) 追踪性:当群管理者发现群组用户有恶意的访问行为时, 可以使用追踪权限找到该用户。

2 预备知识 2.1 双线性运算

设p为大素数, G₁是阶为p的乘法循环群, g是G₁的生成元。定义一个双线性映射e:G₁×G₁=G₂满足以下3个性质^[20]:

1) 双线性:对于∀a, b∈$\mathbb{Z}$_p^*, g₁, g₂∈G₁, 都有e(g₁^a, g₂^b)=e(g₁, g₂)^ab。

2) 非退化性:存在∀P, Q∈G₁, 使e(P, Q)≠1。

3) 可计算性:对于∀P, Q, 可以通过多项式时间算法来计算e(P, Q)。

2.2 困难性问题

本文方案的安全性证明基于以下困难性问题:

定义1  Computational Diffie-Hellman(CDH)问题。对于2个随机数a、b, 已知(g, g^a, g^b), 计算g^ab的值是困难的, 其中G₁是q阶的循环群, g是G₁的生成元。

定义2  Decisional Diffie-Hellman(DDH)问题。给定(g, g^a, g^b, g^c), 没有任何的多项式运算可以判定g^c=g^ab, 其中a, b, c∈$\mathbb{Z}$_p^*, G₁是q阶的循环群, g是G₁的生成元。

定义3  Discrete Logarithm(DL)问题。输入g, g^a∈G₁(a∈$\mathbb{Z}$_p), 输出a, DL假设在G₁中计算是不可行的, 在G₁中解决DL问题是困难的。

2.3 椭圆曲线上的ElGamal加密体制

本文方案使用有效的群签名以获得数据完整性的审计, 通过群签名嵌入椭圆曲线上的ElGamal加密体制来保护群组用户的私钥。椭圆曲线上的ElGamal加密体制安全是基于DDH困难性问题而成立的, 其加密过程描述如下:

1) 初始化:G₁是阶为素数q的乘法循环群, g为G₁的生成元。随机数x∈$\mathbb{Z}$_q是加密者的私钥, pk=g^x∈G₁是其对应的公钥。

2) 加密阶段:给定消息m∈G₁, 加密者首先随机选择暂时密钥y∈$\mathbb{Z}$_q, 计算C₁=g^y∈G₁, C₂=m·pk^y, 将(C₁, C₂)作为密文返回值。

3) 解密阶段:解密者加密私钥x, 通过计算C₂/C₁^x而得到明文m。

3 无证书公开审计方案 3.1 单用户情形

本文可证明安全的无证书公开审计方案包括以下9个运算阶段。

1) 初始化(Setup)阶段。输入安全参数λ, 由KGC生成系统参数, 其中, G₁是阶为素数q的循环群, g是G₁的生成元; 存在双线对运算e:G₁×G₁→G_T, 存在2个抗碰撞的哈希函数h:(0, 1)^*→$\mathbb{Z}$_p^*, H:(0, 1)^*→G₁。KGC随机选择α∈$\mathbb{Z}$_q^*作为系统主密钥, 计算系统公钥P_pub=g^α, 公共参数PP={g, G₁, G_T, h, H, P_pub}。

2) 密钥生成(KeyGen)阶段。用户U_i将自己的ID_i发送给KGC, KGC根据用户发送的身份信息生成用户的部分私钥psk_1i=H(ID_i)^α, 部分公钥pk_i=H(ID_i), 群管理者的部分私钥psk_1m=H(ID_m)^α, 部分公钥pk_m=H(ID_m), KGC通过安全信道将psk_1i和psk_1m分别发送给用户和群管理者; 用户和群管理者在接收KGC发送的psk_1i和psk_1m后, 随机选择t_i, t_m∈$\mathbb{Z}$_q^*, 生成私钥psk_2i=H(ID_i)^αt_i, psk_2m=H(ID_m)^αt_m; T_i=H(ID_i)^t_i, T_m=H(ID_m)^t_m分别作为用户和群管理者的公钥; 群管理者随机选择d∈$\mathbb{Z}$_q^*作为自己的专属私钥, 计算得到用户的公钥D_i=H(ID_i)^t_id, 群管理者的公钥D_m=H(ID_m)^t_md和D=g^d。

3) 用户注册(UserEnroll)阶段。用户U_i将自己的身份信息ID_i发送给群管理者, 群管理者根据用户U_i的ID_i和公钥{T_i}_{i∈[1, n]}建立用户列表List, 完成用户的注册。

4) 签名生成(SignGen)阶段。数据拥有者(Data Owner)将数据存储在CSP中, 将数据M划分成n个数据块, 即M={m₁, m₂, …, m_n}, m_l∈$\mathbb{Z}$_q; 对每个数据块产生对应的签名, 用户U_i随机选择k_i∈$\mathbb{Z}$_q^*, 计算得到V_i=g^k_i, h_l=g^h(id_l), l=1, 2, …, n, 其中id_l是数据的标签名, 生成对应的签名值:C_{l, 1}=g^k_im_l, C_{l, 2}=H(ID_i)^t_iD^k_im_lσ_l=h_l^k_iH(ID_i)^αt_i=g^h(id_l)k_iH(ID_i)^αt_im_l。将签名值{σ_l, C_{l, 1}, C_{l, 2}}_{l∈[1, n]}发送给CSP存储进行后续验证。

5) 签名验证(SignVerify)阶段。CSP接收到用户上传的签名值{σ_l, C_{l, 1}, C_{l, 2}}_{l∈[1, n]}后对其进行验证。验证式(1)是否成立。若等式成立, 则签名有效; 若不成立, 则签名无效, 需重新生成对应签名。

$ e\left( {{\sigma _l}, g} \right) = e\left( {{h_l}, {V_i}} \right)e\left( {T_i^{{m_l}}, {P_{{\rm{pub}}}}} \right) $

(1)

6) 挑战生成(ChalGen)阶段。TPA在接收到用户发送的审计请求后, 向CSP发送挑战消息。TPA从n个数据块中选取c个数据块, 其中c∈[1, n], j∈[1, c], 对每个j随机选择ρ_j∈$\mathbb{Z}$_q^*, 产生挑战消息chal={j, ρ_j}_j∈c, 并将chal={j, ρ_j}_j∈c发送给CSP。

7) 证据生成(ProofGen)阶段。CSP接收到TPA发送的挑战消息chal={j, ρ_j}_j∈c后, 计算出与之对应的证据:$E = \sum\limits_{j \in c} {{m_j}{\rho _j}} $, $\sigma = \prod\limits_{j \in c} {\sigma _j^{{\rho _j}}} $, 而后将生成的证据proof={E, σ}发送给TPA进行验证。

8) 证据验证(ProofVerify)阶段。TPA接受到CSP发送证据proof={E, σ}后, 对CSP生成的证据进行验证。若式(2)成立, 则表示数据被CSP正确持有; 否则, 数据可能被篡改或丢失。

$ e\left( {\sigma , g} \right) = e\left( {V_i^{\sum\limits_{j \in c} {h\left( {{\rm{i}}{{\rm{d}}_j}} \right){\rho _j}} }, g} \right)e\left( {T_i^E, {P_{{\rm{pub}}}}} \right) $

(2)

9) 用户追踪(Trace)阶段。如果用户存在恶意的访问行为或上传不合法的数据情况, 群管理者可以行使追踪权限, 用专属私钥d进行追踪, 查询到该用户的身份信息并将其从注册用户名单中删除, 更新用户列表List, 并将更新后的用户列表发送给CSP, CSP删除与之对应存储的签名值, 使其不能通过签名验证, 从而保证签名的有效性。如果有新的用户想要加入群组, 可以通过群管理者进行注册加入。重新对撤销用户生成签名标签的数据块签名, 生成新的签名, 签名验证过程与之前一致。在群管理者行使追踪权限时, 用专属私钥d进行追踪, 通过下式进行验证:

$ {T_i} = \frac{{{C_{l, 2}}}}{{C_{l, 1}^d}} = \frac{{H{{\left( {{\rm{I}}{{\rm{D}}_i}} \right)}^{{t_i}}} \cdot {D^{{k_i}{m_l}}}}}{{{{\left( {{g^{{k_i}{m_l}}}} \right)}^d}}} = H{\left( {{\rm{I}}{{\rm{D}}_i}} \right)^{{t_i}}} $

(3)

3.2 多用户情形

当出现多个用户发送审计请求时, TPA可以在同一时间完成审计。若给定m个用户U_i, i=1, 2, …, m, 每个用户需要审计的数据块数目为n_i, 对应的数据块标识符为id_{i, j}。TPA向CSP发送审计挑战为:chal={j, ρ_{i, j}}, j=1, 2, …, n_i。

CSP产生对应的证据:${\sigma _i} = \prod\limits_{j = 1}^{{n_i}} {\sigma _{i, j}^{{\rho _{i, j}}}} $, $\sigma = \prod\limits_{i = 1}^m {{\sigma _i}} $, ${E_i} = \sum\limits_{j = 1}^{{n_i}} {{m_{i, j}}} {\rho _{i, j}}$, 之后将生成的证据proof={σ, E₁, E₂, …, E_m}发送给TPA进行验证。

TPA接收到CSP发送证据proof={σ, E₁, E₂, …, E_m}后, 验证下式是否成立:

$ e\left( {\sigma , g} \right) = e\left( {\prod\limits_{i = 1}^m {V_i^{\sum\limits_{j = 1}^{{n_i}} {h\left( {{\rm{i}}{{\rm{d}}_{i, j}}} \right){\rho _{i, j}}} }, g} } \right)e\left( {\prod\limits_{i = 1}^m {T_i^{{E_i}}} , {P_{{\rm{pub}}}}} \right) $

(4)

4 正确性分析与安全性证明 4.1 正确性分析

定理1  给定共享数据块和对应的合法签名, TPA可以检验共享数据的完整性。

证明  本文方案的正确性基于式(1)和式(2)。基于双线性对的性质, 式(1)和式(2)的验证过程分别如式(5)和式(6)所示:

$ \begin{array}{l}e\left(\sigma_{1}, g\right)=e\left(g^{h\left(\mathrm{id}_{i}\right) k_{i}} H\left(\mathrm{ID}_{i}\right)^{\alpha t_{i} m_{1}}, g\right)= \\ e\left(g^{h\left(\mathrm{i} \mathrm{d}_{i}\right) k_{i}}, g\right) e\left(H\left(\mathrm{ID}_{i}\right) \alpha t_{i} m_{1}, g\right)= \\ e\left(g^{k_{i}}, g^{h\left(\mathrm{id}_{i}\right)}\right) e\left(H\left(\mathrm{ID}_{i}\right) t_{i} m_{i}, g^{\alpha}\right)= \\ e\left(h_{i}, V_{i}\right) e\left(T_{i}^{m_{1}}, P_{\mathrm{pub}}\right)\end{array} $

(5)

$ \begin{array}{*{20}{l}} {e(\sigma , g) = e\left( {\prod\limits_{j \in c} {\sigma _j^{{\rho _j}}} , g} \right) = }\\ {e\left( {\prod\limits_{j \in c} {{{\left[ {{g^{h(ij)}}{k_i}H{{\left( {{\rm{I}}{{\rm{D}}_i}} \right)}^{{\alpha _i}{m_j}}}} \right]}^{{\rho _j}}}} , g} \right) = }\\ {e\left( {\prod\limits_{j \in c} {{g^{h\left( {{\rm{i}}{\omega _j}} \right){k_i}{\rho _j}}}} , g} \right)e\left( {\prod\limits_{j \in c} H {{\left( {{\rm{I}}{{\rm{D}}_i}} \right)}^{\alpha {t_i}{m_j}{\rho _j}}}, g} \right) = }\\ {e\left( {{g^{{k_i}}}, g_{jec}^{\Sigma h\left( {{\rm{i}}{\omega _j}} \right){\rho _j}}} \right)e\left( {T_i^{\Sigma _m^\prime c_j^\prime {\rho _j}}, g} \right) = }\\ {e\left( {V_{{i_i}}^\Sigma \frac{{{\Sigma _i}}}{{{c^{h\left( {{{\rm{i}}_i}} \right)}}}}} \right) = } \end{array} $

(6)

若式(1)和式(2)成立, 则公开验证者认为共享数据是完整的。上述通过验证式(1)和式(2)的正确性, 证明了本文方案的正确性。

对于多用户情形的批审计, 式(4)验证过程如式(7)所示:

$ \begin{array}{l} e(\sigma , g) = e\left( {\prod\limits_{i = 1}^m {{\sigma _i}} , g} \right) = \prod\limits_{i = 1}^m e \left( {\prod\limits_{j = 1}^{{n_i}} {\sigma _{i, j}^{{\rho _{i, j}}}} , g} \right) = \\ \prod\limits_{i = 1}^m {\left[ {e\left( {\prod\limits_{j = 1}^{{n_i}} {{g^{h\left( {{\rm{i}}{{\rm{d}}_{i, j}}} \right){k_{{\rho _{i, j}}}}}}} , g} \right)e\left( {\prod\limits_{j = 1}^{{n_i}} H {{\left( {{\rm{I}}{{\rm{D}}_i}} \right)}^{\alpha {t_i}{m_{i, j}}{\rho _{i, j}}}}, g} \right)} \right]} = \\ \prod\limits_{i = 1}^m {\left[ {e\left( {\prod\limits_{j = 1}^{{n_i}} {V_i^{h\left( {{\rm{i}}{{\rm{d}}_{i, j}}} \right){\rho _{i, j}}}} , g} \right)e\left( {\prod\limits_{j = 1}^{{n_i}} H {{\left( {{\rm{I}}{{\rm{D}}_i}} \right)}^{{t_i}{m_{i, j}}{\rho _{i, j}}}}, {g^\alpha }} \right)} \right]} = \\ \prod\limits_{i = 1}^m {\left[ {e\left( {V_i^{\sum\limits_{j = 1}^{{n_i}} h \left( {{\rm{i}}{{\rm{d}}_{i, j}}} \right){\rho _{i, j}}}, g} \right)} \right.} \left. {e\left( {T_i^{\sum\limits_{j = 1}^{{n_i}} {{m_{i, j}}} {\rho _{i, j}}}, {P_{{\rm{pub}}}}} \right)} \right] = \\ e\left( {\prod\limits_{i = 1}^m {V_i^{\sum\limits_{j = 1}^{{n_i}} h \left( {{\rm{i}}{{\rm{d}}_{i, j}}} \right){\rho _{i, j}}}} , g} \right)e\left( {\prod\limits_{i = 1}^m {T_i^{{E_i}}} , {P_{{\rm{pub}}}}} \right) \end{array} $

(7)

4.2 安全性证明

定理2  CDH困难性假设在G₁中成立, 则任何多项式敌手在本文方案下伪造签名在计算上是不可行的。

证明  如文献[5, 17]中所述, 使用无证书签名方案的标准安全模型应考虑2种类型的敌手, 分别称为Ⅰ型敌手和Ⅱ型敌手, 具有不同的攻击能力。这2类敌手的详细定义如下:

1)Ⅰ型敌手:该类型的敌手无法询问KGC的主密钥, 但能够用其选择的值替换任何实体的公钥(敌手具有此能力的原因为无证书签名方案中没有涉及到证书管理)。

2)Ⅱ型敌手:该类型的敌手可以询问KGC的主密钥, 但不能替换任何实体的公钥(敌手的成功询问表明无证书签名方案中存在秘钥托管问题)。

下文将证明, 如果Ⅰ型敌手或Ⅱ型敌手能够用审计方案生成一个伪造签名, 那么就存在一个能够解决G₁中CDH困难问题的算法F, 这与G₁中的CDH问题在计算上不可行的假设相矛盾。

1) 考虑Ⅰ型敌手的情况。敌手$\mathcal{A}$_Ⅰ:基于审计方案的构造, 为在F算法模拟的安全游戏中生成伪造的签名, $\mathcal{A}$_Ⅰ需要向F算法请求5种不同运行阶段的查询, 包括系统初始化查询、hash-Ⅰ查询、部分私钥提取查询、hash-Ⅱ查询和签名查询。同时, 敌手能够在游戏中进行公钥替换。在这个游戏中, hash-Ⅰ可以看作是一个随机预言模式。算法F模拟游戏如下:

(1) 初始化查询:敌手$\mathcal{A}$_Ⅰ询问系统的初始化阶段。F算法设置P_pub=g^a, 输出并将整个系统参数PP={g, G₁, G_T, h, H, P_pub}返回到$\mathcal{A}$_Ⅰ。

(2) hash-Ⅰ查询:$\mathcal{A}$_Ⅰ询问签名者标识的hash-Ⅰ结果。F选择一个随机的r∈$\mathbb{Z}$_q, 然后抛硬币。硬币显示1, 则概率为p, 否则为0。如果掷币结果为1, 则F设置H(ID_s)=p^r∈G₁; 如果掷币结果为0, 则F设置H(ID_s)=(p^r)^b∈G₁。最后, F将H(ID_s)的结果返回给$\mathcal{A}$_Ⅰ。由于G₁是一个循环群, a是$\mathbb{Z}$_q的一个随机元素, p^r和(p^r)^b都是G₁的元素, p^a和(p^r)^b在G₁中具有相同的分布, 因此, 根据F返回的H(ID_s)的结果, $\mathcal{A}$_Ⅰ无法区分掷币的结果。

(3) 部分私钥提取查询:$\mathcal{A}$_Ⅰ询问签名者身份ID_s上的部分私钥。如果前一个$\mathcal{A}$_Ⅰ查询中相应的掷币结果为1, F将部分私钥输出为psk_s=H(ID_s)^r; 在相应的hash-Ⅰ查询中随机选取r; 否则, F将输出⊥。

(4) 公钥替换:根据敌手$\mathcal{A}$_Ⅰ的假设, 敌手$\mathcal{A}$_Ⅰ可以替换任何实体的公钥。具体地, $\mathcal{A}$_Ⅰ首先生成一个随机的x_s∈$\mathbb{Z}$_p^*, 并将签名者的公钥设置为pk_s=H(ID_s)^x_s。然后, $\mathcal{A}$_Ⅰ将(ID_m, x_s, pk_s)发送给到F, F将记录这个密钥替换, 以便之后的使用。

(5) hash-Ⅱ询问:$\mathcal{A}$_Ⅰ请求对签名者身份ID_s返回hash-Ⅱ查询结果, 该签名者的公共密钥为pk_s, 数据块m和数据块id_i。F输出h_i=g^h(id_i), 并将结果返回给$\mathcal{A}$_Ⅰ。

(6) 签名询问:$\mathcal{A}$_Ⅰ通过提交hash-Ⅱ询问返回的结果V_i, 请求数据块m和数据块标识id_i上签名者的签名。如果前一个hash-Ⅰ询问中对应的掷币结果为1, 那么F输出的签名为σ_i=h_i^k_iH(ID_i)^αx_s, 在相应的hash-Ⅰ查询中随机选取r; 否则, F输出⊥。最终, $\mathcal{A}$_Ⅰ输出一个伪造的签名σ。在此基础上, F知道该伪造的对应hash-Ⅰ询问结果是H(ID_s)=(p^b)^r, 而伪造的结果是σ_i=h_i^k_i(H(ID_i)^ab)^r。显然, F可以通过计算得出p^ab。这意味着如果$\mathcal{A}$_Ⅰ成功伪造一个签名, 那么F就能够解决G₁中的CDH问题。

2) 考虑Ⅱ型敌手的情况。由算法F模拟的安全游戏中生成伪造签名, 敌手还需要请求不同类型的询问, 包括初始化询问、hash-Ⅰ查询、部分私钥提取查询、hash-Ⅱ查询和签名查询。与Ⅰ型敌手的游戏不同, F应该将主密钥返回给$\mathcal{A}$_Ⅱ, 但是, $\mathcal{A}$_Ⅱ不能执行公钥替换。在此游戏中, hash-Ⅱ被视为一个随机预言模式。在给定p、p^a和p^b的情况下, 算法F模拟游戏如下:

(1) 初始化询问:$\mathcal{A}$_Ⅱ对初始化阶段进行询问。F生成随机数λ∈$\mathbb{Z}$_p作为主密钥和公共参数PP={g, G₁, G_T, h, H, P_pub}。然后, F将主密钥和公共参数返回给$\mathcal{A}$_Ⅱ。

(2) hash-Ⅰ查询:$\mathcal{A}$_Ⅱ询问签名者身份ID的hash-Ⅰ结果。F计算pk_s=H(ID_s), 并将pk_s的结果返回给$\mathcal{A}$_Ⅱ。

(3) 部分私钥提取询问:$\mathcal{A}$_Ⅱ询问签名者身份ID上的部分私钥。F将部分私钥计算为psk_s=H(ID_s)^rλ, 并将询问结果返回给$\mathcal{A}$_Ⅱ。作为第Ⅱ类敌手的定义, $\mathcal{A}$_Ⅱ不能执行公钥替换。F将pk设置为签名者的公钥。

(4) hash-Ⅱ询问:$\mathcal{A}$_Ⅱ对签名者身份、签名者公钥、数据块m和数据块标识进行hash-Ⅱ询问的结果。F生成一个随机的r∈$\mathbb{Z}$_p, 并进行掷币游戏。硬币显示1, 概率为p_c, 否则为0。如果掷币结果显示1, F设置h_i=g^h(id_i)=p^r; 如果掷币结果为0, F设置h_i=g^h(id_i)=(p^b)^r。最后, F将h_i=g^h(id_i)的结果返回给$\mathcal{A}$_Ⅱ。由于G₁是循环群, r是$\mathbb{Z}$_p的一个随机元素, p和p^b都是G₁的元素, p^r和(p^b)^r在G₁中具有相同的概率分布, 因此$\mathcal{A}$_Ⅱ不能根据F返回的hash-Ⅱ询问结果来区分掷币游戏的结果。

(5) 签名询问:$\mathcal{A}$_Ⅱ询问数据块m和数据块标识id上的签名。如果上一个hash-Ⅱ询问中的相应掷币结果为1, 则F输出的签名为σ_i=h_i^k_i(H(ID_i)^a)^r。否则, F输出⊥。然后, $\mathcal{A}$_Ⅱ输出一个伪造的签名σ。最后, F知道该伪造的对应hash-Ⅰ询问结果是H(ID_s)=(p^b)^r, 而伪造的结果是σ_i=h_i^k_i(H(ID_i)^ab)^r。显然, F可以通过计算得出p^ab。这意味着如果$\mathcal{A}$_Ⅱ成功伪造一个签名, 那么F就能够解决G₁中的CDH问题。

综上所述, 如果$\mathcal{A}$_Ⅰ或$\mathcal{A}$_Ⅱ能够成功伪造签名, 那么F就能够解决G₁中的CDH问题, 这与G₁中CDH问题在计算上不可行的假设相矛盾。因此, 在本文方案中生成签名的伪造在计算上是不可行的。

定理3  只要DL假设成立, 半可信的云存储服务器在本文方案下生成伪造的审计证明在计算上是不可行的。

证明  如定理2所证明的, 对于不可信云, 如果G₁上的CDH问题是困难的, 则在本文提出的机制下伪造签名是不可行的。在本文中, 除了试图在每个数据块上计算伪造签名来生成伪造的审计证明之外, 如果不可信的云可以赢得下面的安全游戏(称为Game1), 则它可以伪造损坏的共享数据的审计证明。安全游戏描述如下:

Game1一个公开的验证者向云服务器发送一个审计挑战chal={j, ρ_j}_j∈c, 基于正确的共享数据M生成的审计证明应该是proof={E, σ}, 它能够通过式(2)的验证。不可信云生成证据为proof′={E′, σ′}是基于损坏的共享数据M′, 其中M≠M′且为非零的。如果基于损坏的共享数据M′的无效证据可以成功地通过验证, 则不可信云将获胜; 否则, 它会失败。

下文将证明如果不可信云可以赢得Game1, 那么就能找到解决G₁中的DL问题的方案, 这与DL假设中G₁中的DL问题在计算上是不可行的相矛盾。假设不可信云可以赢得Game1, 根据式(2)得到:

$ e\left( {{\sigma ^\prime }, g} \right) = e\left( {V_i^{\sum\limits_{j \in c} h \left( {{\rm{i}}{{\rm{d}}_j}} \right){\rho _j}}, g} \right)e\left( {T_i^{{E^\prime }}, {P_{{\rm{pub}}}}} \right) $

proof′={E′, σ′}是一个正确的审计证明。

定理4  在公共审计过程中, 公开验证者识别共享数据块c中所有签名者的身份的概率至多为$\frac{1}{d^{c}}$。

证明  对于算法A, 在一个数据块上揭示签名者身份信息的概率是1/d, 因为选择的c个数据块的签名是独立的, 其中c∈[1, n], 公开验证者能区分共享数据中选择的c个数据块的所有签名者身份的总概率最多为1/d^c。

在本文方案中, 公开验证者知道共享数据中的每个数据块都是由用户各自签名的, 因为它需要用户的公共密钥来验证整个共享数据的正确性。然而, 它不能区分每个特定数据块上的签名者是谁。因此, 公开验证者在揭示私有信息方面不具有特殊的优势, 例如在共享数据中对较多的数据块进行签名时, 或者特定的数据块经常被不同的组员频繁修改时, 公开验证者均不能有效地分辨出签名者具体的身份。根据上文对方案的正确性分析, 证明了本文方案支持数据隐私保护。

定理5  假设一个审计证明proof={E, σ}, 只要DL假设成立, 对于公开验证者来说, 揭示本文机制下共享数据中的任何私有数据在计算上是不可行的。

证明  如果生成的证据包含的元素$E = \sum\limits_{j \in c} {{m_j}} {\rho _j}$, $\sigma = \prod\limits_{j \in c} {{{\left( {{g^{h\left( {{\rm{i}}{{\rm{d}}_i}} \right){k_i}}}H{{\left( {{\rm{I}}{{\rm{D}}_i}} \right)}^{\alpha {t_i}}}} \right)}^{{\rho _j}}}} $是关于数据块m_j中所有元素的线性组合, 则直接发送到公开验证者, 公共验证者可以在收集充足数量的线性组合之后通过求解线性方程来获取数据的内容。为保存私有数据, 以随机数作为计算组合元素。公共验证者则用本文提出的方案审计共享数据的完整性。为能够求解线性方程组, 公共验证者必须知道σ、E的值。然而, 给定签名私钥psk_2i=H(ID_i)^αt_i, 计算t_i与解决G₁中的DL问题一样困难, 这在计算上是不可行的。因此, 给出E和σ, 公共验证者不能直接获得数据块中所有元素的任何线性组合, 并且不能揭示共享数据M中的任何私有数据。

5 性能分析 5.1 计算开销

在计算开销方面, 将本文方案与文献[18]方案进行分析对比, 如表 1所示。其中, T_exp表示指数运算所需的时间, T_mul表示乘法运算所需的时间, T_pair表示双线性对运算所需的时间, T_hash表示Hash运算所需的时间, T_m表示幂运算所需的时间, d表示签名的用户数, c表示挑战的数据块数目, n表示数据分块数, s表示每个数据块中包含的子数据块数。从表 1可以看出, 文献[18]方案主要是支持无证书的公共审计方案, 但没有签名认证和用户追踪, 其计算开销随着数据块的增多而增大, 开销远大于本文方案。本文方案支持签名验证、多数据块的批量审计和用户追踪, 而在多用户的情形下, 审计时间没有太多的增加, 且计算开销比文献[18]方案小。

5.2 通信开销

为检验云存储中数据的完整性, 公开审计者需要将审计挑战发送给云存储, 之后云存储将审计证据发送给公开审计者。|q|是$\mathbb{Z}$_q中元素的大小, |G₁|是群G₁中元素的大小。具体对比结果如表 2所示。

5.3 实验结果

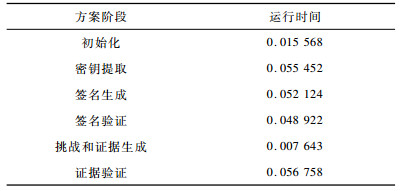
本文采用模拟实验来评估方案的计算开销和通信开销。实验测试环境为:Inter i5-7200U CPU2.50 GHz, 8 GB内存, Windows10×64操作系统, 采用Pairing Based Cryptography(PBC)(http://crypto.stanford.edu./pc/)在Visual C++ 6.0中编译实现。本文方案中主要阶段的运行时间如表 3所示。

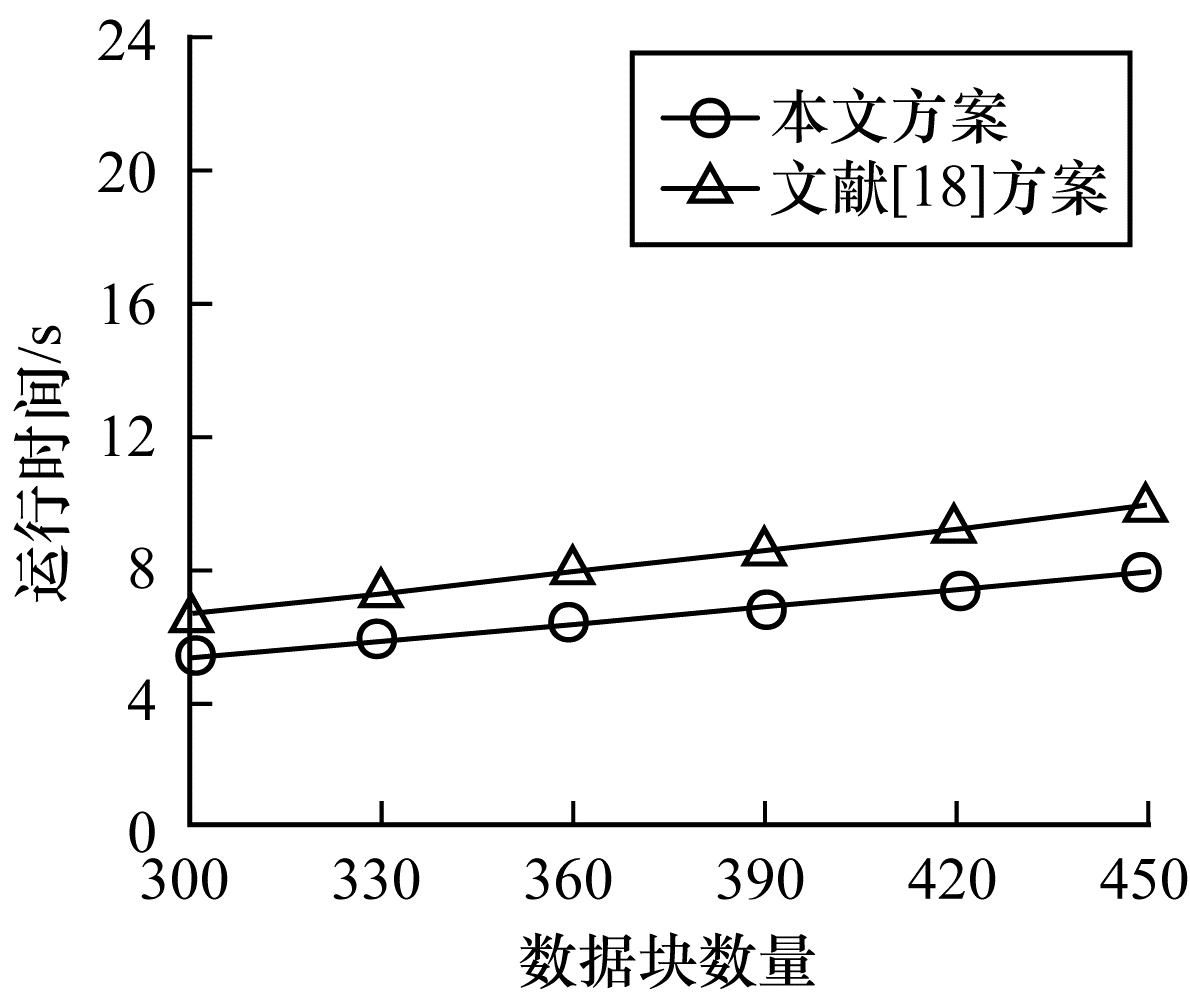
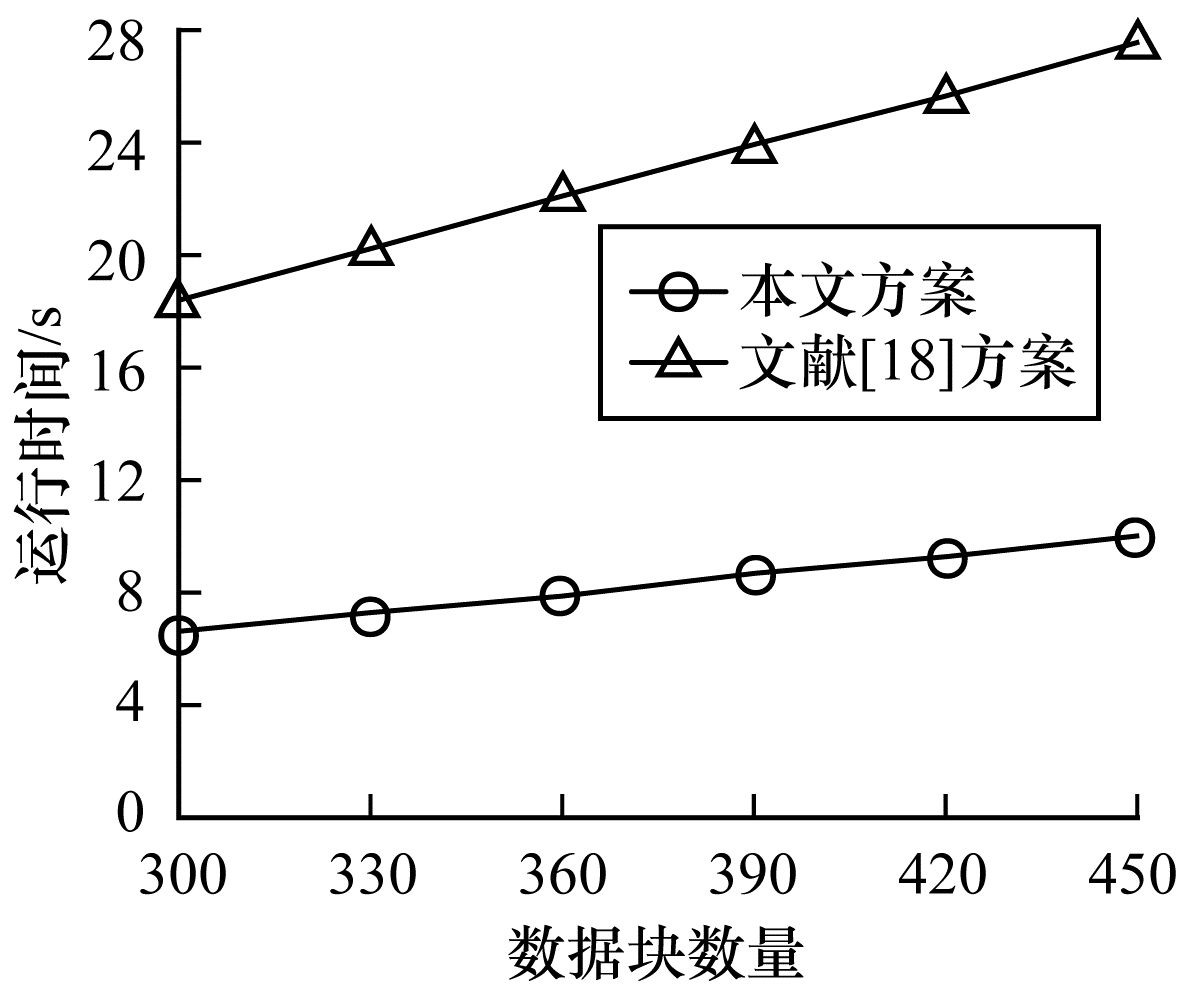
基于本文方案与文献[18]方案计算开销和通信开销的对比, 图 2和图 3分别给出了选择不同数量的数据块时签名生成阶段和证据验证阶段运行时间的对比。

本文方案和文献[18]方案都是基于无证书的公开审计方案, 因此在证据验证阶段的运行时间相同, 但本文方案在签名生成阶段和证据验证阶段的运算时间均少于文献[18]方案, 从而减少了计算开销, 节约了计算成本, 提高了效率。

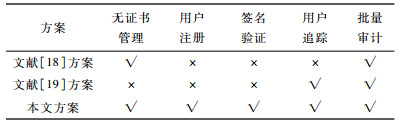
5.4 功能对比

将本文方案与文献[18-19]方案的主要功能进行对比, 如表 4所示。其中, √表示支持该功能, ×表示不支持该功能。

从表 4可以看出, 文献[18-19]和本文方案同时具有批量审计的功能, 但前2种方案不支持用户注册和签名验证, 且文献[18]方案不支持用户追踪, 文献[19]方案未解决证书管理问题。由此可知，本文方案实现的功能更为全面，不仅解决了传统密码体制中的证书管理问题，而且也实现了批量审计和用户追踪功能。

6 结束语

本文提出一种无证书的共享数据公开审计方案, 解决了公钥密码体制中出现的证书管理问题, 能够进行多用户多数据块的批量审计, 并通过ELGamal体制支持群管理者对群组用户身份的追踪。安全性分析和实验结果表明, 该方案基于CDH、DDH和DL困难性问题, 实现了签名的不可伪造性和身份的隐私保护性, 是安全高效的。下一步将研究具有动态群组用户隐私保护功能的公开批量审计方案。