2. 矿山数字化教育部工程研究中心, 江苏 徐州 221116
2. Mine Digitization Engineering Research Center of Minstry of Education, Xuzhou, Jiangsu 221116, China
心脏胸外按压作为基本的紧急救助措施, 要求施救者的动作具有较高的准确度, 以获得良好的急救效果, 同时避免潜在的二次伤害。对于成年人的心脏按压, 按压深度是否在5 cm~6 cm之间是评判按压规范有效的重要标准之一。传统胸外按压深度测量运用最多的主要是对加速度二次积分得到距离, 如文献[1]使用惯性导航算法和加速度计监测胸部按压深度以及文献[2]提出的加速度二次积分测量胸外按压深度方法等。但在实际应用中, 考虑到噪声的影响以及存在积分时延, 上述方法存在积分漂移、误差累积等问题[3]。
根据前期研究的实验数据观察, 当物体为有规律的往复运动时, 会产生有规律的加速度波形。当胸外心脏按压规范有效时, 波形相似度较高; 当按压距离差距超过5 mm时, 波形与标准距离波形显示具有明显差异; 当按压中间出现较大抖动和按压间歇过长时, 其波形显示与标准波形也存在着明显差异, 这说明其波形信号的识别分类过程具有可学习的特征, 可以利用人工智能的方法进行学习并分类[4], 从而达到物体往复运动距离评估的目的。
卷积神经网络具备强大的特征提取能力, 已广泛应用于图像识别与目标检测领域。目前, 已有部分学者研究利用卷积神经网络处理波形信号分类任务, 如文献[5]利用卷积神经网络对天然地震波形信号的识别分类研究以及文献[6]利用卷积神经网络识别雷达波形等, 然而他们都需要大量标签数据作为训练集, 而在胸外心脏按压急救过程中需要在短时间内连续多次按压, 难免存在测距遮挡、抖动等问题, 同时在多数情况下按压测距难以达到毫米级的高精度, 从而较难得到大量高可信度的数据标签。为此, 本文提出一种基于加权方差的弱监督学习策略, 对实验中缺失或者可信度低的数据标签进行修正, 并通过建立卷积神经网络的加速度波形识别分类模型, 对急救中胸外心脏按压的波形进行评估。
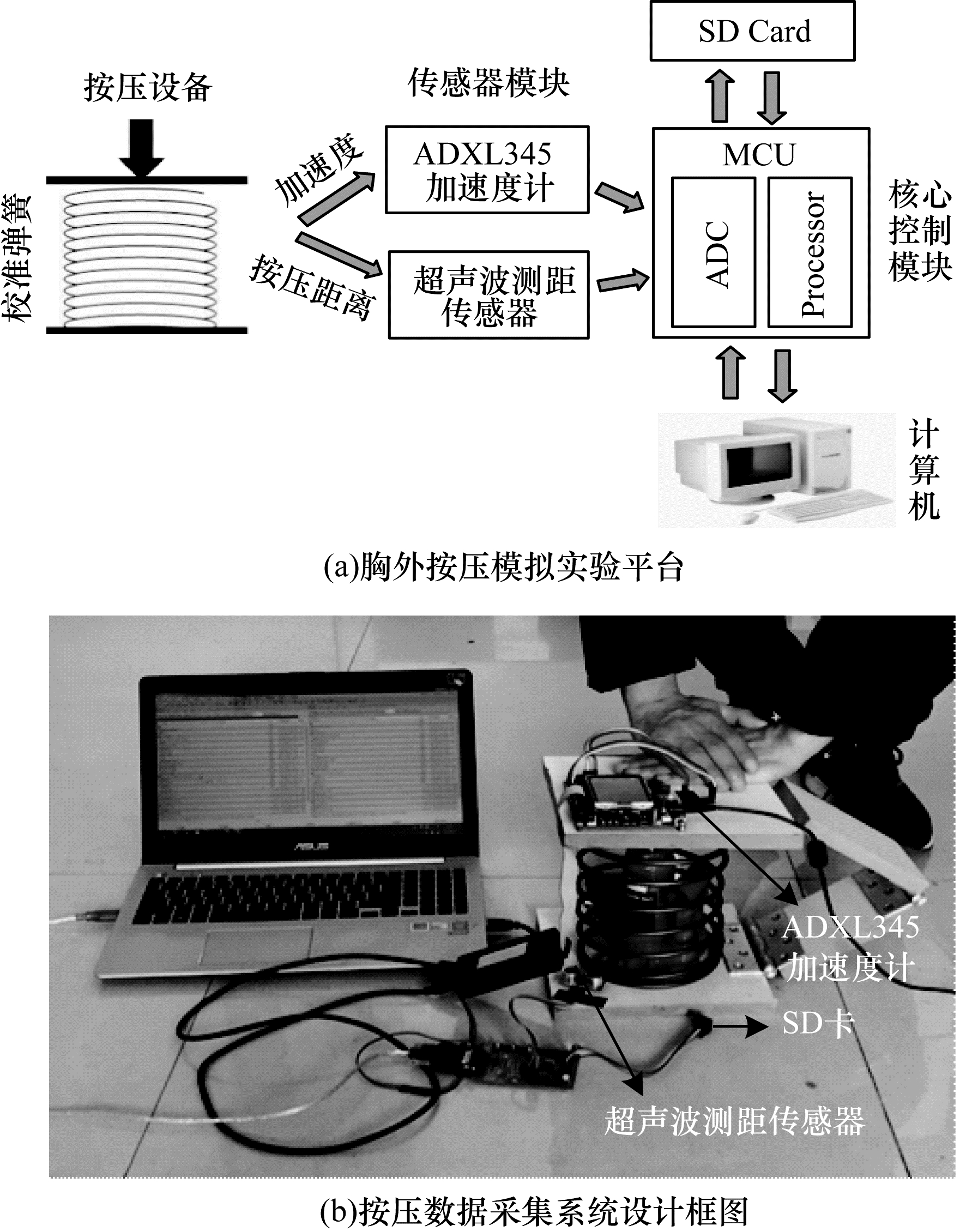
1 实验平台与数据采集图 1(a)所示为本文设计的胸外按压仿真数据采集平台的基本架构, 用以构建胸外按压加速度的数据集。该系统由按压设备、传感器模块和按压控制模块3个部分组成。通过操作按压设备模拟心脏胸外按压动作, 传感器模块由超声波测距传感器和加速度传感器组成, 前者采集按压深度, 以便得到初始的数据标签, 后者采集加速度数据, 然后交由核心控制模块进行数据分析、波形预处理、控制与存储。在硬件配置方面, 本文使用三轴加速度计ADXL345和所提供的三轴加速传感器MMA7361, 其具有低功耗、高抗震的优点[7]; 数据存储设备选用SD卡, 容量大, 体积小, 因不存在活动部件, 其可靠性显著高于硬盘。实地采集场景如图 1(b)所示。实际数据采集过程中的部分参数如表 1所示。
|
Download:
|
| 图 1 实验数据采集系统 Fig. 1 Experimental data acquisition system | |

|
下载CSV 表 1 数据生成与采集过程的有关参考值 Table 1 Related reference values for data generation and acquisition process |
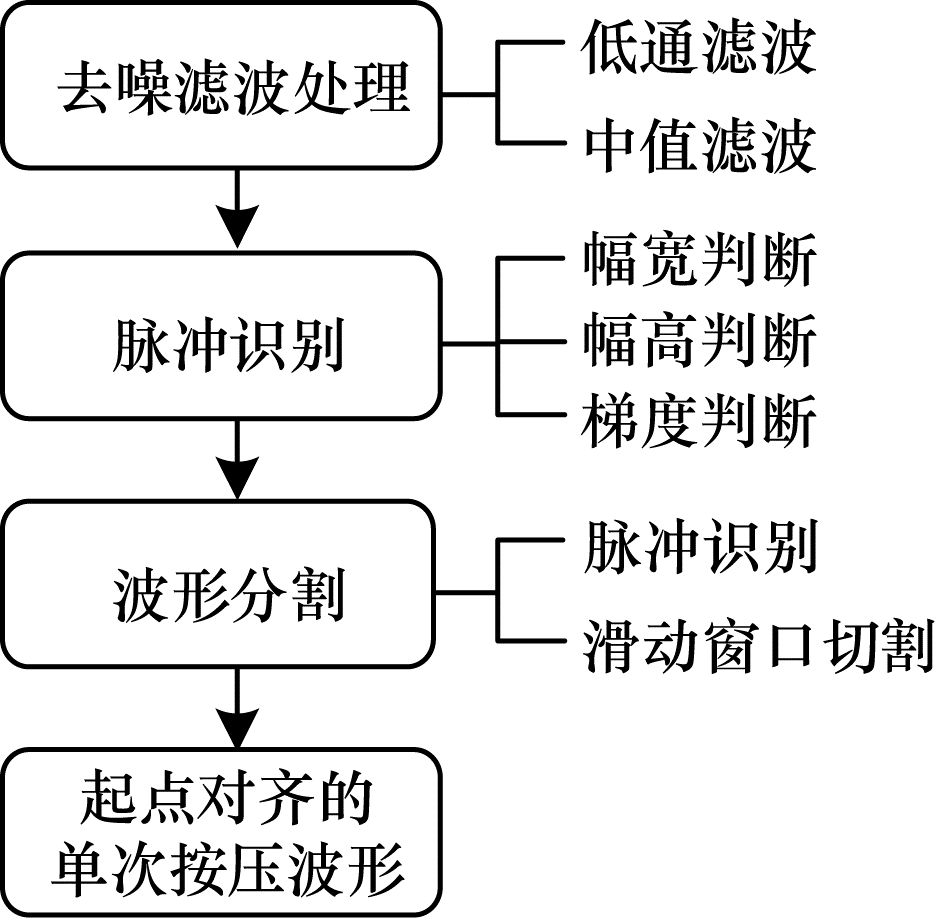
直接由传感器输出的原始波形数据规律性较弱, 掺杂有操作失误和电磁干扰导致的大量噪声。另一方面, 单一批次采集得到的多个波形数据之间不存在标准界限, 信息粒度过大, 很难对其进行有效建模和分析, 需要从中截取出单个波形进行后续研究。整合上述步骤, 形成数据预处理流程, 主要包括噪声抑制、脉冲波形定位及分割等操作, 如图 2所示。
|
Download:
|
| 图 2 数据预处理过程 Fig. 2 Data preprocessing process | |
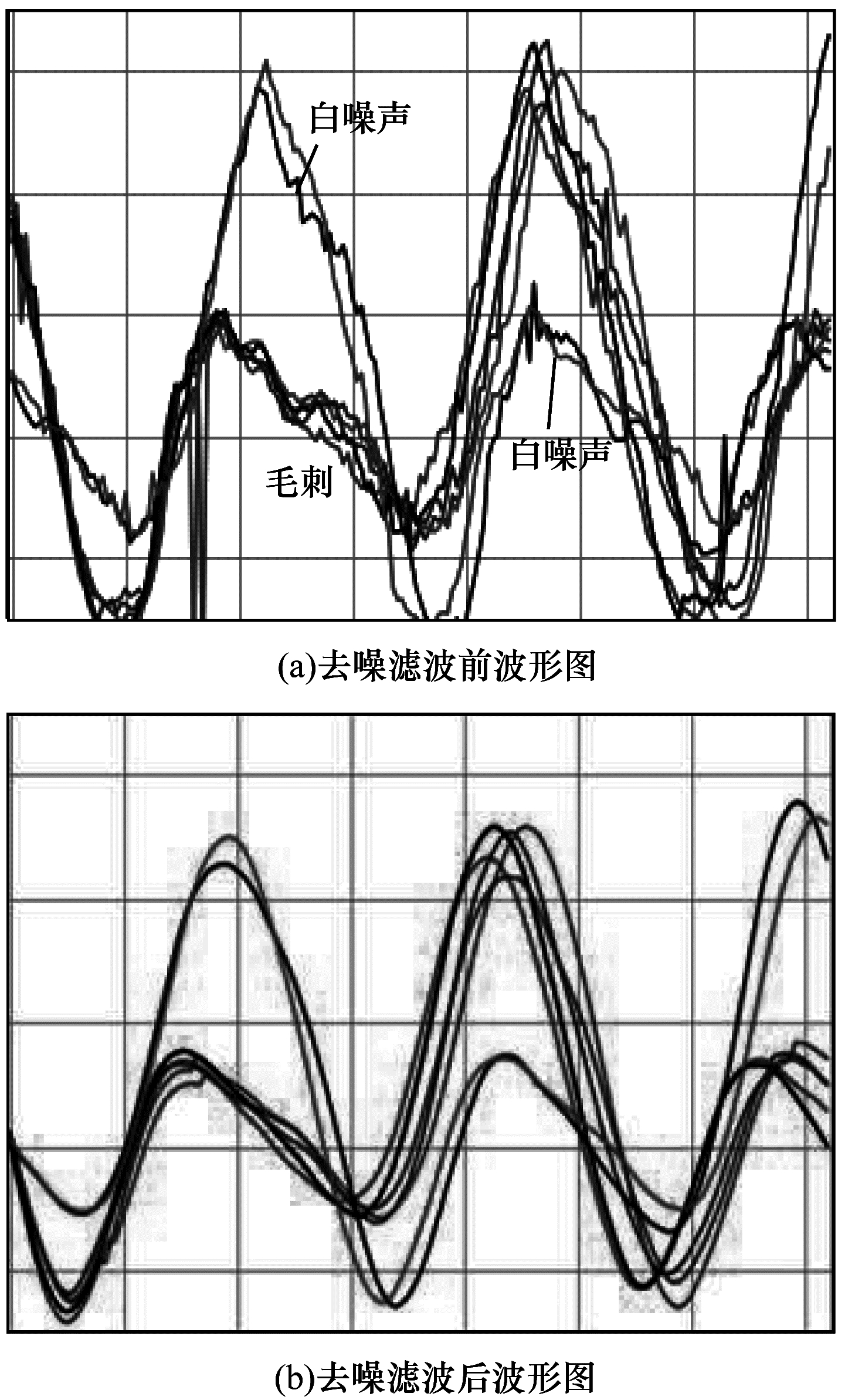
图 3(a)所示为直接通过传感器采集得到的按压加速度波形的可视化结果, 可以清晰地看出其中存在大量白噪声和毛刺, 为数据分析和后续的波形分类带来很多偶然性因素。因而本文先后采取低通控辐滤波和中值滤波对原始数据进行去噪滤波处理, 前者过滤不合适的白噪声和锤击异常[8], 后者对周期性干扰有良好的抑制作用, 平滑度高[9], 滤波后效果如图 3(b)所示。
|
Download:
|
| 图 3 去噪滤波前后对比 Fig. 3 Comparison before and after denoising filtering | |
经过滤波处理的数据虽然具备了可利用的规律性, 但是大量波形相互连接构成的长序列数据给后续的特征提取和学习造成了很大困难, 因而需要识别并定位其中每一次按压的波形作为按压效果评估的基本单元。本文根据波形的梯度值和振幅大小识别出单个波形, 在截取波形时采用滑动窗口方法, 共分为4个步骤:
步骤1 创建滑动窗口A、B, 分别存放传感器采样的原始数据和滤波后的波形数据。
步骤2 设置波形曲线的突变阈值为重力加速度的21%, 扫描步骤1中2个滑动窗口中的数据。
步骤3 从检测到的B突变点和A突变点所间隔的区域中选取优化点作为起点, 对窗口A幅宽进行切割, 直至下一次突变作为终止点, 然后对起点到终止点之间的数据使用脉冲识别算法, 判断是否符合按压波形特征。
步骤4 若脉冲识别结果为“符合按压波形特征”, 则根据窗口A的结果, 切割滑动窗口B。
其中步骤3中只有当2个滑动窗口都出现突变才作为起点是为了防止将A窗口中的锤击异常现象作为脉冲起点。
步骤3中使用的脉冲识别算法如下:
1) 幅宽PW判断
脉冲幅宽应满足下式:
| $ \frac{t_{1}}{T_{s}} \leqslant \mathrm{PW} \leqslant \frac{t_{2}}{T_{s}} $ | (1) |
其中, PW表示脉冲的幅宽, Ts表示每次采样时间, 本文选择t1=150 ms, t2=420 ms。
2) 幅高PH的判断
各传感器使用的值不同, 主要是因为加速度感知的数据不同, 在加速度a上反映也不同, 导致计算有差异,逆推公式如下:
| $ {P_{{\rm{MIN}}}} \le \sum\limits_o^n a \times {t^2} \le {P_{{\rm{MAX}}}} $ | (2) |
其中, n表示采样数, a为采样值, t为采样周期, PMIN为按压最小值, PMAX为按压最大值, 本文选择PMIN=5 cm, PMAX=6 cm。
3) 梯度判断
规定一个脉冲中梯度变化为反向-正向-反向的变化, 表现为二阶导数存在2个极值点且极小值点min1在极大值点max2前面, 上述2个点与横坐标位于此两者之间的曲线的均值点stdval形成3个斜率, 由于本文采用的是ADXL345的5 ms采样, 因而需符合min1与stdval的斜率为[1.3, 3], stdval与max2的斜率为[1.5, 6], min1与max2的斜率为[1.5, 8]。
算法1 按压脉冲识别与波形分割
输入 一组胸外按压波形数据
输出 每次按压波形的起始点与终止点
//窗口A存放采样值, 窗口B存放滤波结果
winA←a, winB←a2, winA←winB
If sample_startp = 0
//对窗口进行突变阈值检测
For k ∈(1, Sample_checkpoint-1)
If |winB.data[k] -winB.data[k-1]|>sample_defaultstd*21%
寻找波形起始点
End if
End for
End if
Truncate PW of winB //截取winB的波形幅宽
For t ∈(0, n)
Calculate PH
If不符合式(1)、式(2)幅宽和幅高判断条件
Continue
Else
获得波形均值点stdval和2个极大值点
If不符合梯度判断条件
Continue
End if
End if
calculate the distance of A
calculate the distance of B
//根据winB的结果截取winA的波形
Truncate winA reference winB
End
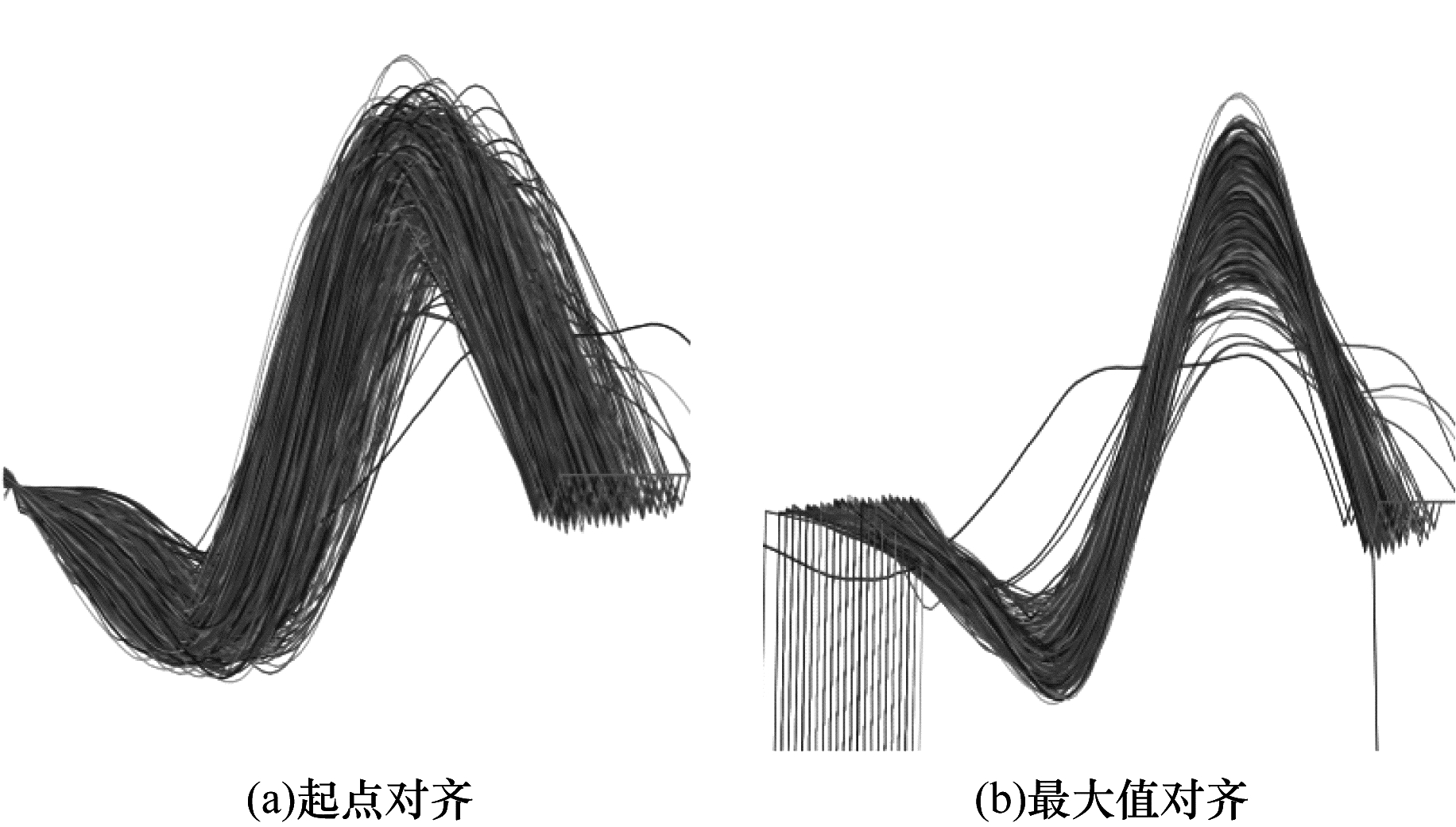
使用该算法处理全部18批次数据, 过滤并截取得到975个单次心脏胸外按压加速度波形, 将这些波形的起点对齐后整合在同一幅图中。
3 基于数据离散程度的标签修正方法胸外心脏按压救助是否规范有效一般通过按压深度来判定, 本文采用超声波测距的方法得到单次按压的深度, 然后根据按压深度是是否位于5 cm~6 cm之间判断本次按压是否正确规范, 从而建立数据集标签。而在实际按压实验中需要在短时间内连续多次按压, 难免存在测距遮挡、抖动等问题, 因此存在一定程度的标签数据缺失, 为了解决这一问题, 本文提出一种基于加权方差的弱监督学习策略, 从而对标签进行修正。
由图 4(a)可知, 由于截取后的波形长度并不一致, 起点对齐后的各个波形具有不同终点, 整体数据分布松散, 不能很好地提取关键特征和进行分类, 因此将所有按压曲线进行转换, 从原点对齐转换为最大值对齐, 以便后期的处理, 如图 4(b)所示。
|
Download:
|
| 图 4 波形对齐方式转换 Fig. 4 Waveform alignment conversion | |
将波形数据转换为最大值点对齐后, 可以发现数据分布情况大为改善, 并且可以忽略两侧端点的不一致性, 本文对每条曲线以最大值点为界, 左边取50个点, 右边取20个点构成数据集。汇总波形数据进行比对, 参考图 4(b)后得出3条规律, 基本内容已在概述中阐明, 若干特征补充如下:
特征1 规范的按压动作产生的加速度波形的极大值点和极小值点均位于整体波形的中部。
特征2 不规范的按压动作产生的加速度波形存在极值点过于平滑或突兀的现象。
根据上述特征, 本文设计一种基于数据离散程度的标签修正方法, 主要考虑极值点处的方差值, 为保证判别结果的全面性, 对非极值点进行主成分分析[10-11], 提取极值点以外的关键信息。
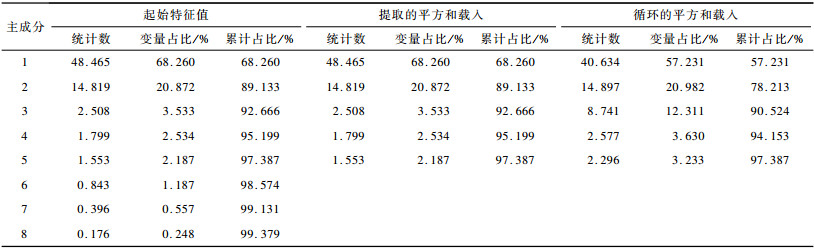
主成分分析结果如表 2所示, 以累计信息占比97%为界, 选取主成分1~5。综合2个极值点和5个非极值点主成分, 计算加权方差值, 构建数据离散程度的评估模型, 具体如下所示:
|
下载CSV 表 2 主成分分析结果 Table 2 Principal component analysis results |
| $ \begin{aligned} \text { weighted }_{-} \operatorname{var}_{i}=& \operatorname{var}_{i 1} \times w_{1}+\operatorname{var}_{i 2} \times w_{2}+\\ & \operatorname{var}_{i 3} \times w_{3}+\operatorname{var}_{i 4} \times w_{4}+\operatorname{var}_{i 5} \times w_{5}+\\ & \operatorname{var}_{i \min 1} \times 0.25+\operatorname{var}_{i \max 2} \times 0.25 \end{aligned} $ | (3) |
| $ {{\mathop{\rm var}} _{ij}} = \frac{{{X_{ij}} - u}}{N} $ | (4) |
| $ {w_j} = \frac{{50\% \times 主成分j的信息百分比}}{{97.387\% }} $ | (5) |
其中, 式(3)为波形数据的加权方差计算公式, 规定各极值点处方差的权重为常数0.25, 其余成分的方差的权重由式(5)计算得出, 式(4)中的N表示本批次数据中的波形总数, u表示特定成分在所有波形上的均值。波形i在主成分j中的取值为Xij, 其在主成分j上相对于其他波形的方差为varij。在本文模型中, 极值点方差在离散度信息中占主导地位, 其余成分的权重取决于该主成分的信息占比。
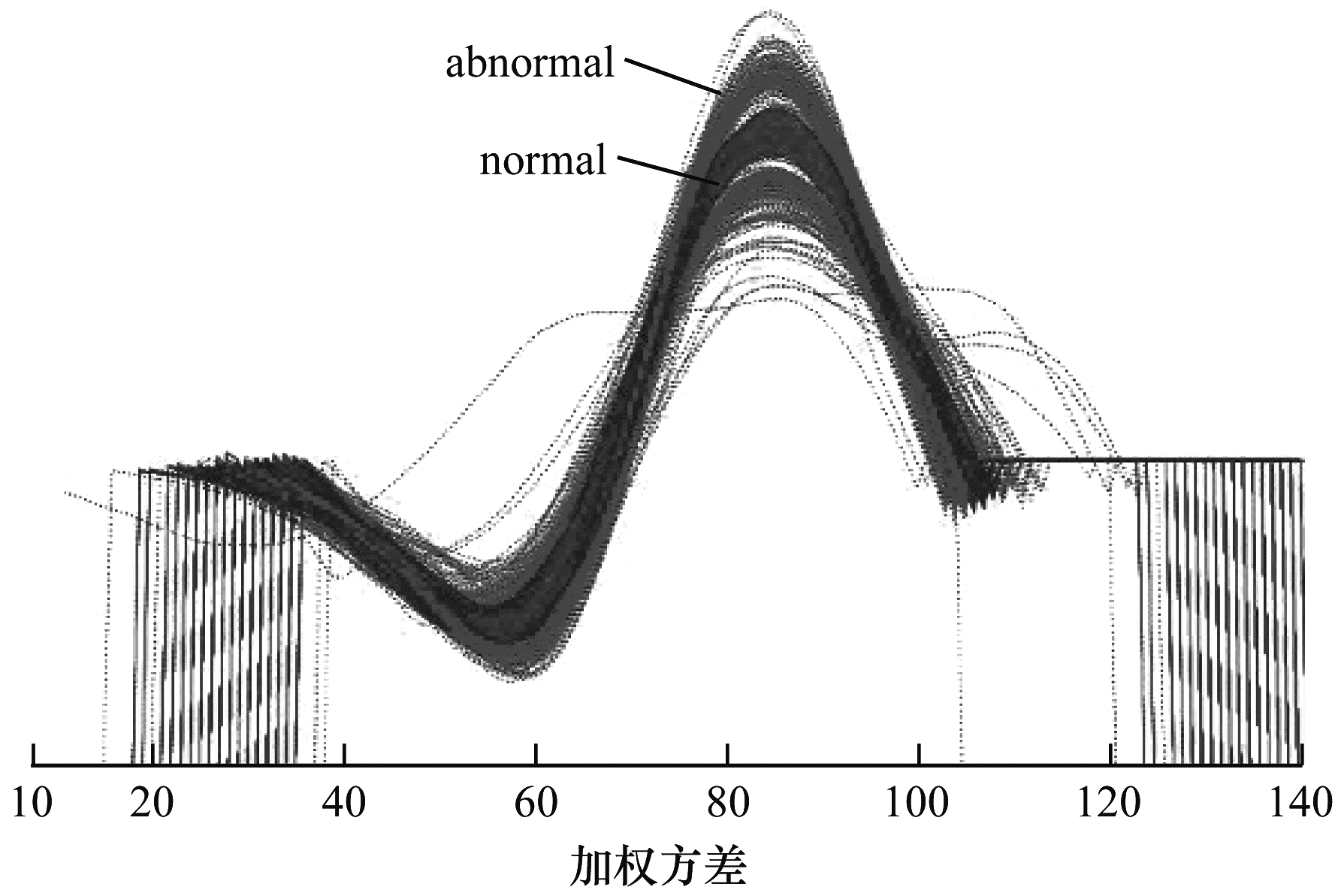
如图 5所示, 将已获得的波形数据代入离散度评估模型, 设置加权方差阈值为所有波形加权方差的中位数。
|
Download:
|
| 图 5 加权方差模型划分结果 Fig. 5 Partition results of weighted variance model | |
从图 5可以看出, 加权方差值大于阈值的波形视为偏离规范按压的情况, 标注为反例, 其余波形标注为正例。再结合实验中利用超声波测距得到的标签, 当超声波得到的按压深度因为遮挡而缺失或者因为抖动等因素而明显错误时, 使用上述加权方差模型对本次按压波形进行划分, 从而实现了对标签的修正。
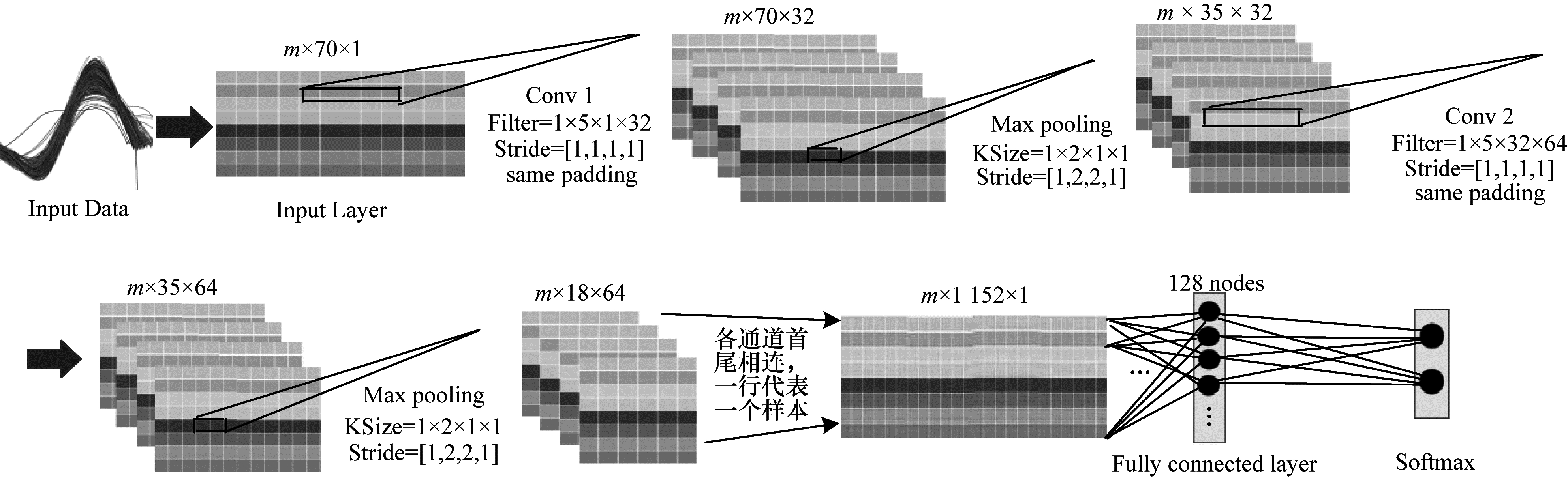
4 一维卷积神经网络设计卷积神经网络具备强大的特征提取能力和平移等变性质, 并在图像识别和目标检测领域得到了成功的应用。不同于二维图像数据, 本文研究的波形数据属于一维序列数据, 因而采用一维卷积核和一维池化方法。在一维网络中, 提取得到的特征向量可以直接首尾相接传入全连接层和Softmax层进行分类。图 6所示为本文提出的针对波形序列数据的卷积网络分类器的模型结构。实验验证结果表明, 初始网络模型存在训练速度缓慢、损失函数下降过程中发生震荡等问题, 需要采取优化措施对模型进行改进。
|
Download:
|
| 图 6 一维卷积神经网络的详细结构 Fig. 6 Detailed structure of a one-dimensional convolutional neural network | |
优化1 使用Mini-batch梯度下降策略[12-13]和滑动平均模型[14], 前者将数据分为大小相同的batch再输入网络, 用于加速梯度下降过程, 后者维护一个介于当前值和更新后的值的影子变量, 用以限制参数更新速度, 提高模型稳定性。影子变量的计算方法如下:
| $ \rm{shadow\_variable = shadow\_variable \times decay +\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1-\operatorname{decay}) \times variable} $ | (6) |
其中, variable为待更新参数, decay为衰减率。
在训练过程中动态调节衰减率有助于提高训练速度和模型稳定性, 可采用步数num_step控制衰减率, 计算公式如下:
| $ \min \left( {{\mathop{\rm decay}\nolimits} , \frac{{1 + {{{\mathop{\rm num}\nolimits} }_ - }{\mathop{\rm step}\nolimits} }}{{10 + {{{\mathop{\rm num}\nolimits} }_ - }{\mathop{\rm step}\nolimits} }}} \right) $ | (7) |
优化2 使用Adam优化算法代替随机梯度下降算法来最小化损失函数。随机梯度下降算法保持单一的学习率更新所有的权重, 学习率在网络训练过程中并不会改变。而Adam优化算法结合了momentum和RMSprop梯度下降算法, 通过计算梯度的一阶矩估计和二阶矩估计为不同的参数设计独立的自适应性学习率; 此外, Adam算法具有很高的计算效率和较低的内存需求, 对于除学习率外其他参数的调试要求较低, 使用较为方便。
优化3 理想的学习率在模型训练前期应尽量加快特征学习过程, 而在后期应减缓学习过程, 以免发生震荡, 即学习率应在训练过程中递减。经测试直接使用Adam算法损失函数的波动仍较大, 为了进一步优化模型, 因此本文在Adam优化算法的基础上采用指数下降的学习率衰减策略[15], 使得学习率随着训练步数逐渐减小。
| $ \alpha = {\alpha _0} \times {{\mathop{\rm decay}\nolimits} _ - }{{\mathop{\rm rate}\nolimits} ^{\frac{{{\rm{ globa}}{{\rm{l}}_ - }{\rm{steps}}}}{{{{{\mathop{\rm decag}\nolimits} }_ - }{\rm{steps}}}}}} $ | (8) |
| $ {{\mathop{\rm decay}\nolimits} _ - }{\mathop{\rm step}\nolimits} {\rm{s}} = \frac{N}{m} $ | (9) |
其中, α为学习率, α0为初始学习率, decay_rate为衰减因子, global_steps为当前训练步数, N为整个训练集样本个数, m为一个批处理中的样本数目。
优化4 影响机器学习方法泛化性能的主要因素是过拟合问题, 即模型会尝试学习数据中的噪声或人为特征, 因而本文在模型中引入正则化处理, 用以降低模型复杂度和不稳定程度, 从而避免过拟合的危险。常用的正则化方法有L1和L2正则化。
L1正则化为[16]:
| $ R(w) = {\left\| w \right\|_1} = \sum\limits_i {\left| {{w_i}} \right|} $ | (10) |
L2正则化为[17]:
| $ R(w) = \left\| w \right\|_2^2 = \sum\limits_i {\left| {w_i^2} \right|} $ | (11) |
相比于L1正则化, L2正则化具有处处可导、便于优化的特性, 适合应用于本文提出的模型。因此, 在更新卷积神经网络全连接层和Softmax层的权重时加入L2正则化。另外Inverted Dropout正则化方法[18]是通过修改神经网络本身来实现的, 即在进行反向传播时, 根据设定的保留概率使一部分神经元节点随机失活, 同时节点的输出需要除以保留概率达到缩放修正的目的。Dropout在实践中能很好地工作是因为其在训练阶段阻止神经元的共适应, 但Dropout不会阻止参数增长, 同时应用L2正则化可以起到作用[19], 故本文在全连接层中加入Inverted Dropout正则化技术。
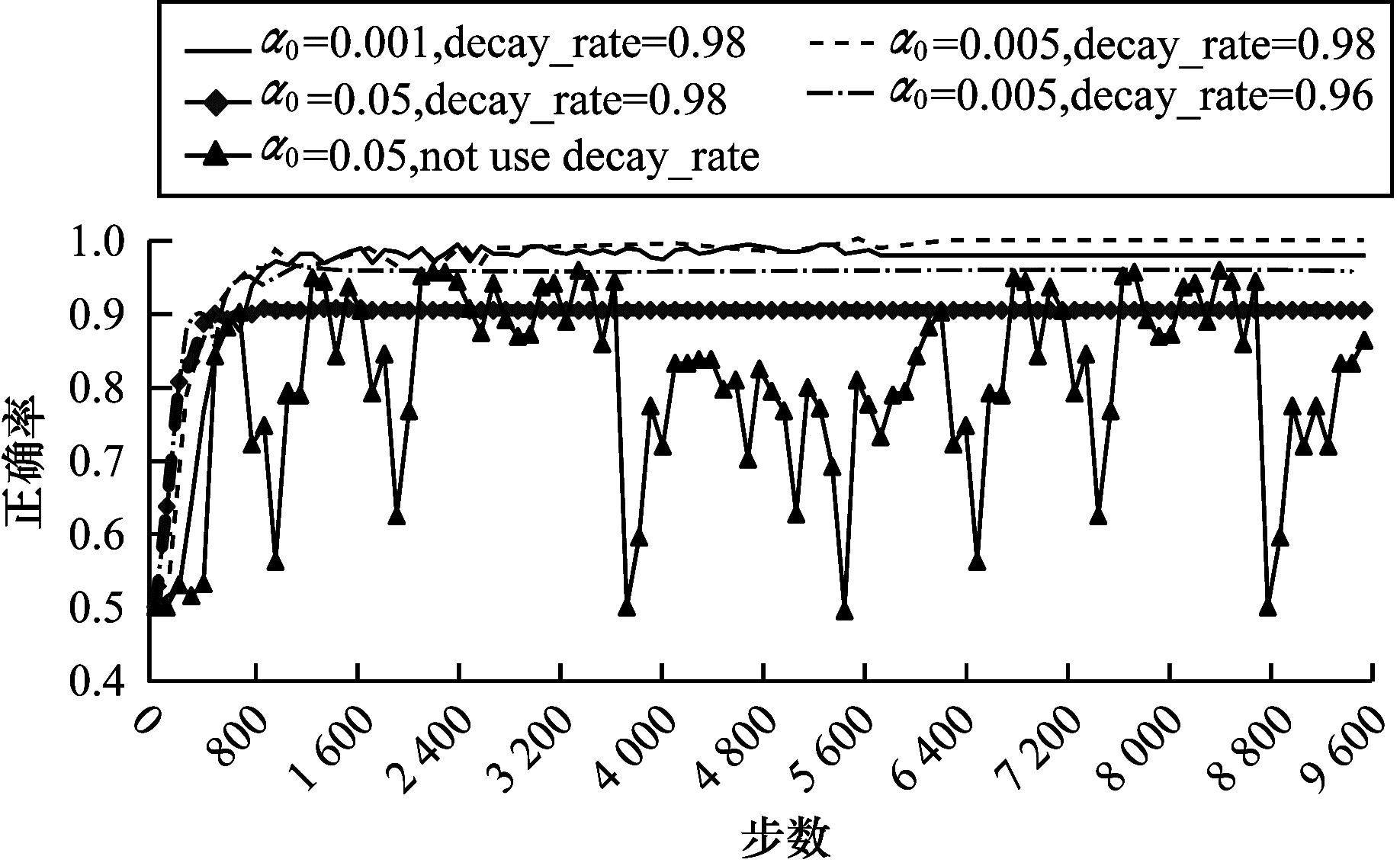
5 实验结果与分析 5.1 学习率调试图 7所示为采用不同的初始学习率和衰减率的训练正确率曲线, 引入学习率衰减策略后, 分类正确率表现出良好的稳定性。综合多次实验结果表明, 本文将初始学习率α0设置为0.005, 衰减率decay_rate设置为0.98, 在此条件下的分类正确率可以达到99.4%。
|
Download:
|
| 图 7 不同学习率和衰减率下的分类正确率 Fig. 7 Classification accuracy rate at different learning rates and decay rates | |
本文尝试了不使用正则化、使用L2正则化、Dropout以及将两者结合的正则化方法来防止过拟合, 实验结果如表 3所示。在相同数据集上, 同时使用L2正则化和Dropout技术能够获得最高的正确率。
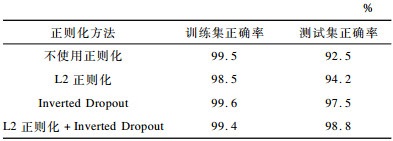
|
下载CSV 表 3 不同正则化对分类正确率的影响 Table 3 Effects of different regularizations on classification accuracy |
本文结合Mini-batch梯度下降、学习率衰减、L2正则化、Inverted Dropout等方法对模型进行了优化, 表 4显示了各种优化算法中参数的含义及其具体设置。

|
下载CSV 表 4 一维卷积神经网络参数设置 Table 4 One-dimensional convolutional neural network parameter settings |
为了评估本文提出的基于一维卷积神经网络的胸外心脏按压波形识别与传统识别方法相比的优势, 在相同数据集上进行多次实验, 结果如表 5所示。
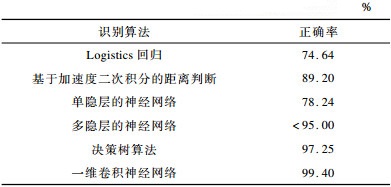
|
下载CSV 表 5 不同算法的正确率 Table 5 Accuracy of different algorithms |
测试结果表明, 传统的基于加速度二次积分的距离判断方法正确率只能达到89.20%左右, 而一般的机器学习算法, 如Logistics回归方法存在欠拟合问题, 而决策树算法得到的树形分类结构过于复杂, 存在过拟合风险。本文提出的基于一维卷积神经网络的分类模型正确率可以达到99.40%, 较大地提升了胸外心脏按压波形的识别正确率, 并且模型具有较好的鲁棒性和泛化能力。
6 结束语本文在波形分割和标签修正的基础上, 提出了一维卷积神经网络的心脏胸外按压波形识别算法。对实验采集的原始数据进行去噪滤波处理, 使用滑动窗口模型进行脉冲识别与波形分割, 得到起点对齐的单次按压波形。给出一种基于加权方差的弱监督学习策略解决部分数据标签缺失的问题, 并结合Softmax分类器构建一维卷积神经网络对按压波形进行分类, 使用Adam优化算法、Dropout和L2正则化、学习率衰减等方法对模型进行优化。实验结果表明, 与传统的基于加速度二次积分的距离判断方法相比, 卷积神经网络达到了99.4%的正确率, 具有更好的评估识别效果。在实际人工胸外按压时, 影响急救的成功率不仅只有单次按压, 还有按压频率, 如对溺水人员进行救助时, 常采用30次胸外按压辅以2次人工呼吸等方法, 因此下一步研究需要结合按压频率、救助类型等因素对胸外心脏按压是否规范有效做进一步的评估。
| [1] |
BOUSSEN S, IBOUANGA-KIPOUTOU H, FOURNIER N, et al. Using an inertial navigation algorithm and accelerometer to monitor chest compression depth during cardiopulmonary resuscitation[J]. Medical Engineering and Physics, 2016, 38(9): 1028-1034. DOI:10.1016/j.medengphy.2016.05.001 |
| [2] |
QIAN Shaowen, ZHENG Jiewen, ZHANG Guang, et al. The depth measurement of chest compression based on double integration of acceleration[J]. Beijing Biomedical Engineering, 2011, 30(5): 496-501. (in Chinese) 钱绍文, 郑捷文, 张广, 等. 基于加速度二次积分的胸外按压深度测量[J]. 北京生物医学工程, 2011, 30(5): 496-501. DOI:10.3969/j.issn.1002-3208.2011.05.12 |
| [3] |
WU Haojie, WU Shuicai, LIU Zhongying. Study on the detection of chest compressions based on acceleration waveform shape analysis[J]. China Medical Devices, 2018, 33(3): 6-10. (in Chinese) 吴豪杰, 吴水才, 刘忠英. 基于加速度波形形态分析的胸外按压深度检测研究[J]. 中国医疗设备, 2018, 33(3): 6-10. DOI:10.3969/j.issn.1674-1633.2018.03.002 |
| [4] |
RUSSELL J K, ZIVE D, DAYA M.Effect of chest compression leaning on accelerometry waveforms[C]//Proceedings of IEEE CinC'16.Vancouver, Canada: IEEE Computer Society, 2016: 11-14.
|
| [5] |
CHEN Runhang, HUANG Hanming, CHAI Huimin. Study on the discrimination of seismic waveform signals between earthquake and explosion events by convolutional neural network[J]. Progress in Geophysics, 2018, 33(4): 1331-1338. (in Chinese) 陈润航, 黄汉明, 柴慧敏. 地震和爆破事件源波形信号的卷积神经网络分类研究[J]. 地球物理学进展, 2018, 33(4): 1331-1338. |
| [6] |
KONG S, KIM M, HOANG L M, et al. Automatic LPI radar waveform recognition using CNN[J]. IEEE Access, 2017, 6: 4207-4219. |
| [7] |
LIU Jian, ZHANG Hui, LEI Long, et al. Acquisition and analysis of acceleration[J]. Information Technology, 2013(12): 110-112, 116. (in Chinese) 刘牮, 张辉, 雷龙, 等. 加速度数据的采集及分析[J]. 信息技术, 2013(12): 110-112, 116. DOI:10.3969/j.issn.1009-2552.2013.12.029 |
| [8] |
YU Zhennan, LIU Qian, GAO Xiuxiao, et al. Improvement and realization of digital-phase-sensitive-detection method based on low-pass filter[J]. Well Logging Technology, 2018, 42(5): 568-570, 576. (in Chinese) 于振南, 刘倩, 高秀晓, 等. 基于低通滤波的相敏检波算法改进与实现[J]. 测井技术, 2018, 42(5): 568-570, 576. |
| [9] |
ZHANG Jianming, LI Pei, LI Xudong, et al. Hybrid denoising algorithm combining median filtering with sparse representation[J]. Computer Engineering, 2016, 42(9): 240-245. (in Chinese) 张建明, 李沛, 李旭东, 等. 结合中值滤波与稀疏表示的混合去噪算法[J]. 计算机工程, 2016, 42(9): 240-245. DOI:10.3969/j.issn.1000-3428.2016.09.042 |
| [10] |
DUAN Sirui, CHEN Kan, YU Xiang, et al. Automatic multicarrier waveform classification via PCA and convolutional neural networks[J]. IEEE Access, 2018, 6: 51365-51375. DOI:10.1109/ACCESS.2018.2869901 |
| [11] |
YU Jinrui, SI Yujuan, LIU Xin, et al.ECG identification based on PCA-RPROP[C]//Proceedings of International Conference on Digital Human Modeling and Applications in Health, Safety, Ergonomics and Risk Management.Vancouver, Canada: [s.n.], 2017: 419-432.
|
| [12] |
REN J S, XU L.On vectorization of deep convolutional neural networks for vision tasks[C]//Proceedings of the 29th AAAI Conference on Artificial Intelligence.Austin, USA: [s.n.], 2015: 152-164. https://www.researchgate.net/publication/271531897_On_Vectorization_of_Deep_Convolutional_Neural_Networks_for_Vision_Tasks
|
| [13] |
KHIRIRAT S, FEYZMAHDAVIAN H R, JOHANSSON M.Mini-batch gradient descent: faster convergence under data sparsity[C]//Proceedings of the 56th IEEE Annual Conference on Decision and Control.Melbourne, Australia: IEEE Press, 2017: 128-136.
|
| [14] |
WANG Miaoyi, TONG Weiguo, LIU Shibo.Fault detection for power line based on convolution neural network[C]//Proceedings of 2017 International Conference on Deep Learning Technologies.Chengdu, China: [s.n.], 2017: 156-163.
|
| [15] |
ZHAO Jianmin, WANG Yumeng. The study of learning rate based on BP neural network[J]. Microcomputer Applications, 2018, 34(8): 89-92. (in Chinese) 赵建民, 王雨萌. 基于BP神经网络学习率优化的研究[J]. 微型电脑应用, 2018, 34(8): 89-92. DOI:10.3969/j.issn.1007-757X.2018.08.027 |
| [16] |
WEI Qingjie, WANG Benbin.Research on image retrieval using deep convolutional neural network combining L1 regularization and PRelu activation function[C]//Proceedings of the 3rd International Conference on Advances in Energy.Chengdu, China: [s.n.], 2017: 215-222.
|
| [17] |
SHI Guang, ZHANG Jiangshe, LI Huirong, et al. Enhance the performance of deep neural networks via L2 regularization on the input of activations[J]. Neural Processing Letters, 2019, 50: 57-75. DOI:10.1007/s11063-018-9883-8 |
| [18] |
SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout:a simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15: 1929-1958. |
| [19] |
ZHOU Anzhong, LUO Ke. Sparse Dropout regularization method for convolutional neural networks[J]. Journal of Chinese Computer Systems, 2018, 39(8): 1674-1679. (in Chinese) 周安众, 罗可. 一种卷积神经网络的稀疏性Dropout正则化方法[J]. 小型微型计算机系统, 2018, 39(8): 1674-1679. DOI:10.3969/j.issn.1000-1220.2018.08.008 |
 2020, Vol. 46
2020, Vol. 46
