2. 桂林电子科技大学 广西可信软件重点实验室, 广西 桂林 541004
2. Guangxi Key Laboratory of Trusted Software, Guilin University of Electronic Technology, Guilin, Guangxi 541004, China
随着信息技术的快速发展, 各行业的数据规模日益增加, 因此数据异常检测显得尤为重要, 其广泛应用于政务数据异常检测、商业欺诈检测、医疗记录异常分析等方面, 而针对网络社区的异常检测成为近年来研究的热点。传统无属性网络异常社区检测方法通常仅利用社区结构信息无法检测到内部属性不一致的社区[1-2], 可用于稠密子图的社区挖掘及仅考虑结构的异常社区检测, 但不适用于真实世界中的复杂网络。这是因为现实世界的网络多数由节点、边和与节点相关的属性向量组成, 且这些网络质量层次不齐、数量庞大, 如何量化属性网络中的社区质量显得尤为重要。近年来, 研究人员面向属性网络提出一些异常社区检测方法, 例如将所有可用属性视为同等重要[3-4], 或者采用无监督技术来确定属性的重要性权重构成属性子空间向量用于节点属性相似度计算[5-6]。社区子空间在结构上是内部紧密连接, 与网络其余部分分离, 并且在此类属性子空间下社区内部节点间具有相似性。在属性网络中, 高质量的社区更加模块化并且趋向于具有相似属性特征的社区[7], 即具有相同属性的节点结构也相似。
因此, 研究人员利用属性对异常社区检测的影响所提出的方法, 通过社区内部属性信息来衡量社区质量, 并对社区之间存在边界边的连通性进行量化, 用以衡量社区质量[8], 或用于寻找属性网络中的离群点及子图[9-10]。属性网络中社区质量的好坏可以通过综合社区结构和属性信息进行衡量, 例如社区内部节点连接稀疏程度、节点间子空间的属性相异度信息、社区内节点连向外部邻居节点的紧密程度和内部节点与社区邻居节点基于子空间的相似情况。AMEN[11]模型将模块度思想运用到社区检测中, 建立正规性模型量化社区质量, 用于检测属性网络中社区内部一致性较差但外部紧密连接的异常社区。然而, 基于AMEN模型的节点属性权重挖掘方法仅考虑节点结构相似度对异常社区检测的影响, 并未考虑到节点附着属性信息对异常社区检测所带来的影响。
鉴于节点属性信息相对于结构信息更能反映真实复杂网络的特性, 本文提出融合属性和结构的子空间异常社区检测方法(SBAM), 在高质量社区定义的基础上, 设计基于子空间的社区质量评估模型, 利用结构与属性同时量化社区质量, 挖掘较低分值的异常社区集合。
1 相关工作文献[12]研究真实网络中的社区统计特性、社区划分情况以及社区质量如何在不同社区规模下发生变化, 研究表明大型高质量社区存在, 并且这一发现已被GLEICH等人[13]的研究所证实。文献[14]分析社交网络结构并发现社交网络中在线和离线社交关系的相似性。文献[1]指出egonet特性在真实网络中形成类似幂律的模式, 其他有关大型真实图上结构和动态的研究均没有聚焦于社区[15-16]。上述研究主要关注无属性网络, 还有一些研究在无属性图上量化了社区结构, 例如文献[7]提出模块度; 文献[17]分析了一系列关于量化社区结构的研究并在基准社区上对这些方法的性能进行对比; 文献[18]研究了属性集与密集子图之间的结构相关模式。
社区挖掘算法旨在通过模块化实现社区检测[19-20], 还有一些应用于图划分的社区挖掘算法[21]以及基于种子集扩展[22-23]、非负矩阵分解[24]和标签传播[25]的重叠社区检测方法, 这些研究主要关注无属性图, 然而在属性图上的社区检测成为近年来的研究热点。此类研究的重点在于发现结构紧密且属性相似的子空间社区, 其侧重于社区内部密度, 却忽略了社区边界边。
文献[26]利用频繁子图挖掘和信息理论来识别具有单一属性的异常子图。文献[27]提出一个新的社区异常值识别方法, 但该方法识别出的异常值在完整属性空间和属于同一社区的其他属性空间中的数值不同。文献[10]侧重于提取从用户偏好推断出的预定义属性子集的社区, 同时该方法会输出在该子集中部分或完全偏离的社区异常值。
本文方法利用正态性, 从社区内部一致性和外部可分性上对社区质量进行评估。在结构上注重量化, 由于社区之间的边界边会影响社区质量的正态性分数, 因此本文方法融合社区内外部结构和属性子空间, 通过属性图的子空间与社区结构信息进行图异常检测。在真实数据集和人工数据集上验证了本文方法的鲁棒性和可扩展性, 并且其在精确度和性能上优于现有社区检测方法, 如OddBall[1]和AMEN等, 因此本文方法更适用于复杂网络。
2 属性子空间挖掘对于特定社区而言, 节点附加的属性对社区质量都有一定的影响, 然而不同属性的影响不同。因此, 本节针对不同的异常社区检测要求, 设计3种基于属性维度重要性量化的子空间求解策略, 即基于属性平均距离的子空间求解策略, 基于负熵加权的子空间推断策略和融合属性平均距离和基于负熵加权的子空间求解策略, 通过挖掘每个社区所对应的属性权重向量, 获得社区属性权重子空间。
2.1 问题定义与传统异常社区检测方法不同, 本文方法是在挖掘属性子空间下对社区质量进行评估, 将不同维度的重要程度属性权重共同作为衡量社区质量的因素, 消除异常社区检测过程中仅考虑社区结构的片面性, 使得挖掘到的异常社区更真实。
设G=(V, E, F)是属性图, 其中, V={v1, v2, …, vi, …, vn}是具有n个节点的节点集, E={e1, e2, …, ei, …, em}是由m条边组成的边集, F={f1, f2, …, fi, …, fr}是由r个属性或特征组成的集合。图G的邻接矩阵
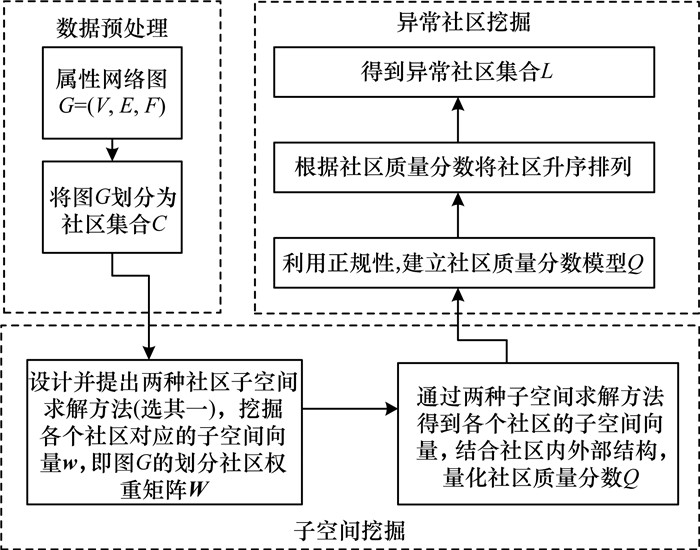
本文融合属性与结构的子空间异常社区检测框架如图 1所示, 其具体步骤如下:
|
Download:
|
| 图 1 融合属性与结构的子空间异常社区检测框架 Fig. 1 Framework of anomaly community detection via subspace combining attribute and structure | |
1) 给定:带节点属性的社区集合C。
2) 挖掘:各社区中的子空间向量wi, i∈(1, 2, …, k)。
3) 量化:依照定义的质量评估函数, 对社区内部紧密性和外部分离性定量计算质量分数Q。
4) 发现:将定量计算得到的社区质量分数升序排列, 输出质量分数较低的社区集合L。
2.2 基于属性平均距离的子空间求解策略在特定社区中挖掘子空间, 基于属性平均距离的子空间求解策略采用提取社区焦点属性维度的思想, 将对社区产生影响较大的属性维度赋予较大的权重值, 而忽略对社区影响较小的属性维度, 降低子空间的求解复杂度。另外, 该策略适用于提取焦点属性的异常社区检测, 并且量化了节点属性对社区生成的重要性影响。
设当前待检测社区为Ci=(Vi, Ei, Fi), Ci∈C, ∣Vi∣=ni, Sc={ < vi, vj>∣vi∈Vi, vj∈Vi}是社区Ci的节点对集合, ∣Sc∣=(ni2-ni)/2。设Se={ < vi, vj>vi∈V/Vi, vj∈V/Vi}是随机取自属性图G中去除社区Ci节点的节点对集合。为保证Se中包含足够多的节点对且各节点间距离较远, 设∣Se∣=r∣Sc∣, 隶属于同一社区中的节点对间距离较小, 即当前社区Ci中的节点对集合Sc节点间距离较小; 反之, 不属于同一社区的节点对间距离Se较大。
定义1(节点对属性平均距离) 给定节点对集合S, 节点vi和节点vj在第t维属性上的平均距离gt(S)定义为:
| $ {g_t}(S) = \frac{1}{{\left| S \right|}}\sum\limits_{({v_i},{v_j}) \in S} ( {f_{{v_{it}}}} - {f_{{v_{jt}}}}{)^2} $ | (1) |
其中, fvit表示节点vi的第t维属性, fvjt表示节点vj的第t维属性。社区Ci子空间向量wi应使得Sc中的节点对的平均距离, 即
| $ w_{it}' = \left\{ \begin{array}{l} \frac{{{g_t}({S_e})}}{{{g_t}({S_c}) + \frac{1}{{({S_c})}}}},{g_t}({S_c})<{g_t}({S_e}),t = 1,2, \cdots ,r\\ 0,{g_t}({S_c}) \ge {g_t}({S_e}),t = 1,2, \cdots ,r \end{array} \right. $ | (1) |
对子空间进行标准化处理得到:
| $ {w_{it}} = \frac{{w_{it}'}}{{\sum\limits_{t = 1}^r {w_{it}'} }},t = 1,2, \cdots ,r $ | (1) |
给定特定社区, 每个属性都对该社区产生影响, 但影响程度不同, 而其中影响程度大即为社区权重大, 影响程度小者即为社区权重小。然而, 部分权重小的影响因素也是社区中不可忽视的影响因素。高质量社区中的节点部分属性相似度较高, 其余属性影响较小。因此, 对于全局属性的子空间推断问题, 基于负熵加权的子空间推断策略考虑了所有属性对于社区的影响, 是一种精确求解子空间的方法。本文考虑属性间的相对重要性, 即对于特定社区Ci∈C, 均有
利用负熵加权法确定属性子空间, 对于每一个特定社区Ci都有特定属性权重向量wi, 求解目标函数如下:
| $ \mathop {\min }\limits_{{\mathit{\boldsymbol{w}}_i}} H({\mathit{\boldsymbol{w}}_i}) = \sum\limits_{i = 1}^{{n_i}} {\sum\limits_{j = i + 1}^{{n_i}} {\sum\limits_{t = 1}^r {{w_{it}}{{({f_{{v_{it}}}} - {f_{{v_{jt}}}})}^2} + \gamma \sum\limits_{t = 1}^r {{w_{it}}{\rm 1b}{w_{it}}} } } } $ | (4) |
其中, ni是社区Ci中的节点个数, fvit为节点vi第t维属性, γ是控制多维权重激励强度的一个正参数。式(4)中第一部分是衡量社区内部的紧密程度, 即社区内部节点间的距离, 第二部分是负熵值。
通过最小化目标函数求得社区Ci的属性子空间权重向量wi=(w1, w2, …, wr)T, wi在服从约束的条件下, 该社区属性子空间的少数维度权重较大, 其余维度的权重值较小。需要注意的是, 每一个社区中的权重列向量只与当前社区相关。
| $ {w_{it}} = \frac{{{{\rm e}^{\frac{{ - {D_t}}}{\gamma }}}}}{{\sum\limits_{t = 1}^r {{{\rm e}^{\frac{{ - {D_t}}}{\gamma }}}} }} $ | (5) |
其中,
为快速精确地求解社区子空间, 本文提出融合属性平均距离和负熵加权的子空间求解模型, 具体如下:
| $ {w_{it}} = \alpha w_{it}^g + (1 - \alpha )w_{it}^d $ | (6) |
其中, α∈[0, 1]为权重系数调节因子, 可由多次实验得出最佳值,
本节通过融合结构与属性挖掘子空间策略, 采用AMEN中的正规性分数设计思想[11]量化社区质量, 通过对社区质量分数进行排序, 找到分数较低的社区集合, 即为检测发现的异常社区集合。
在现实中大量社区互相重叠且不能直接简单分割, 即社区间有交叉边且边上权重不可忽略。在异常社区检测任务中, 很多社区并非是单独存在, 即某一社区与其他社区相互重叠并含有交叉边, 或在社区外部存在中心节点且对该社区内部产生影响。因此, 本文在挖掘各个社区的子空间后, 根据社区质量评估模型, 定义社区质量评估函数Q, 定量计算社区质量分数值, 并采集分数较低的异常社区集合。
社区质量评估函数与模块度概念相似, 用于量化社区质量。一个高质量的社区主要包含两个标准:1)社区内部节点连接紧密程度和节点之间在子空间上的相似度; 2)社区内节点连向外部邻居节点的稀疏程度和内部节点与社区邻居节点在子空间上的相异性。评估社区质量的优劣主要为:属性相似且结构相似的节点应隶属于同一社区, 而不相似的节点应分离并隶属于不同社区。
定义2(节点加权属性相似度) 社区Ci中两个节点vi、vj之间的加权属性相似度定义如下:
| $ s(\left. {{f_{{v_{i}}}},{f_{{v_{j}}}}} \right|{\mathit{\boldsymbol{w}}_i}) = \mathit{\boldsymbol{w}}_i^{\rm T} \times {{\rm e}^{ - {{\left\| {{f_{{v_i}}} - {f_{{v_j}}}} \right\|}_2}}} $ | (7) |
其中, ║fvi-fvj‖2表示节点vi、vj属性列向量差值二范式, 节点加权属性相似度为[0, 1], wi是属性子空间的权重行向量, 计算两个节点属性之间的相似度, 即节点属性的加权相似度。
设图G的两个社区Ci和Bj均为图G的子图, 则社区Ci的质量评估函数Q定义如下:
| $ \begin{array}{c} Q = \sum\limits_{i \in {C_i},j \in {C_i}} {({A_{ij}} - \frac{{{q_i}{q_j}}}{{2m}})s(\left. {{f_{{v_i}}},{f_{{v_j}}}} \right|{\mathit{\boldsymbol{w}}_i})} - \\ \ \ \ \ \sum {\left( {1 - {\rm \min} \left( {1,\frac{{{q_i}{q_b}}}{{2m}}} \right)} \right)} s(\left. {{f_{{v_i}}},{f_{{v_b}}}} \right|{\mathit{\boldsymbol{w}}_i}) \end{array} $ | (8) |
其中, Aij是社区Ci的邻接矩阵Ai中的元素, fvi为社区Ci中节点vi属性的列向量, fvb为社区Bj中节点vb属性的列向量, qi表示节点vi的度, qb表示节点vb的度。
对于具有最高质量分值的社区:1)存在所有可能的内部边缘且节点属性和结构对相似性高, 此时式(8)中的第一项最大化; 2)由于社区没有交叉边或社区与社区之间存在的重叠边相似性接近0, 因此式(8)中的第二项可忽略。属性图的社区质量分数为负表示异常或质量较差, 即异常社区。因此, 需要极大化社区质量评估模型(式(8)), 具体如下:
| $ \begin{align} & \underset{{{\mathrm{ \mathit{\boldsymbol{w}}}}_{i}}}{\mathop{{\rm max}}}\,\mathrm{{ \mathit{\boldsymbol{w}}}}_{i}^{{\rm T}}[\sum\limits_{i\in {{C}_{i}},j\in {{C}_{i}}}{({{A}_{ij}}-\frac{{{q}_{i}}{{q}_{j}}}{2m})s({{f}_{{{v}_{i}}}},{{f}_{{{v}_{j}}}})}- \\ & \sum\limits_{\begin{smallmatrix} {{v}_{i}}\in {{C}_{i}},{{v}_{b}}\in {{B}_{j}}, \\ ({{v}_{i}},{{v}_{b}})\in E \end{smallmatrix}}{\left( 1-\min \left( 1,\frac{{{q}_{i}}{{q}_{b}}}{2m} \right) \right)s({{f}_{{{v}_{i}}}},{{f}_{{{v}_{b}}}})}] \\ \end{align} $ | (9) |
其中, 相似性s(fvi, fvj)的计算可由定义2求得。
由于本文方法是一种启发式优化方法, 因此容易在社区划分中找到最佳解决方案以获得良好的图划分效果。因为图的划分会影响社区检测结果, 所以本文方法不是完全随机地将属性图初始化为若干子图, 而是使用重叠社区检测算法来初始化属性图进行社区划分。
4 实验结果与分析为全面评估本文SBAM方法的有效性和效率, 本节分别在人工数据集和真实数据集上设计两组实验。首先, 对实验所用的人工数据集和真实数据集进行描述; 其次, 观察不同参数值对实验结果的影响, 选择合适的参数; 最后, 选取两个典型的社区划分算法在人工网络中与本文方法进行比较, 并在真实网络中与AMEN方法[11]进行对比。由于本文方法涉及3种子空间求解策略, 因此为表示方便, 将基于属性平均距离的子空间求解策略记为SBAM-L1, 基于负熵加权的子空间推断策略记为SBAM-L2, 融合属性平均距离与负熵加权的子空间求解策略记为SBAM-L3。
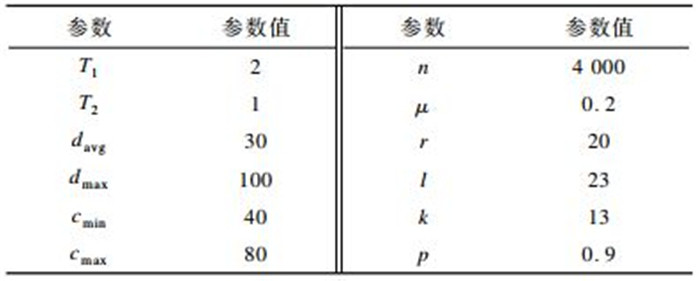
4.1 实验设置 4.1.1 数据集由于LFR基准网络[28]具有与真实网络类似的特征, 因此可基于LFR基准网络生成人工属性网络。社区的度和社区大小规模的分布是分别由指数T1和T2支配的幂律分布。基准网络的参数设置如下:节点个数n, 平均节点度davg, 最大节点度dmax, 最小社区成员个数cmin, 最大社区成员个数cmax、混合参数μ, 边数m、属性数d、社区数|C|、社区平均大小|S|。混合参数控制网络的失真程度, μ值越大, 基准网络越失真。为获得带属性的基准网络, 附加3种类型的属性向量到所有节点, 即数值、二进制和分类。附加的属性向量由4个参数控制, 即属性总个数r、属性子空间个数k、异常社区数量l和相似概率p。此外, 为选择合适的基准精确评估各对比方法的有效性和效率。在设定实验最佳参数时, 分别对n、μ、cmin、r、k和p进行600组基准测试, 实验结果中的最佳参数设置如表 1所示。
|
下载CSV 表 1 人工网络数据集参数设置 Table 1 Parameter setting of datasets in the artificial network |
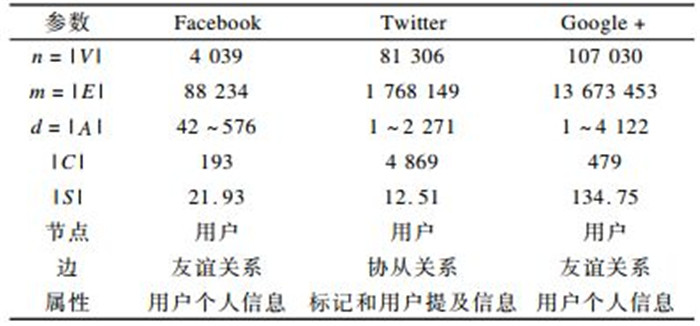
为验证本文方法在真实网络上的效果, 本节选取Facebook、Twitter和Google+ 3个具有真实社区的属性网络参数设置进行验证, 具体数据集如表 2所示。其中, 节点、边、属性是表述数据集中网络的构建方式, 节点代表网络中的用户, 依据用户与用户之间的友谊关系、协从关系构建节点之间的边, 节点上附着的属性是用户个人信息等特征。
|
下载CSV 表 2 真实网络数据集参数设置 Table 2 Parameter setting of datasets in the real network |
本文实验中人工网络部分采用LFR基准网络在混合参数μ=0时的网络形态, 真实网络的对比方法为AMEN[11]、OddBall[1]和SODA[29], 其中, OddBall方法通过无属性图上社区内部一致性评估社区质量, SODA方法根据属性图上社区内部一致性和外部可分性量化社区质量。实验评价指标为归一化互信息NMI[30]和AUC, 其中, NMI基于混淆矩阵N的定义, 矩阵中的行表示真实社区、列表示检测到的社区, 具体计算如下:
| $ {\rm NMI} = \frac{{ - 2\sum\limits_{i = 1}^{{C_A}} {\sum\limits_{j = 1}^{{C_B}} {{N_{ij}}{{\log }_a}({N_{ij}}\mathit{\boldsymbol{N}}/{N_{i.}}{N_{.j}})} } }}{{\sum\limits_{i = 1}^{{C_A}} {{N_{i.}}{{\log }_a}({N_{i.}}/\mathit{\boldsymbol{N}}) + \sum\limits_{j = 1}^{{C_B}} {{N_{.j}}{{\log }_a}({N_{.j}}/\mathit{\boldsymbol{N}})} } }} $ | (10) |
其中, Nij是属于真实社区i和检测到的社区j的节点数量, Ni.是矩阵N中第i行元素的总和, N.j是矩阵N中第j列元素的总和, A表示网络的真实划分, B表示基于算法得到的划分, CA是真实社区数量, CB是检测到的社区数量。
4.2 结果分析本节主要在人工网络上对LFR基准网络生成过程进行参数设置, 设计在LFR基准网络下各参数对SBAM方法的性能影响实验, 并对实验结果进行分析。在真实网络中, 采用AMEN方法对真实网络进行异常扰动并设计性能对比实验。
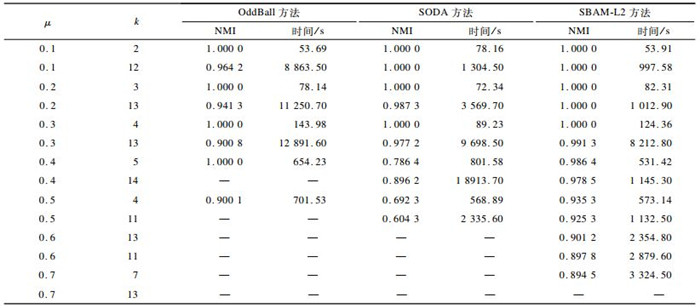
4.2.1 人工网络分析通过实验测试随着参数k、μ的变化, OddBall、SODA和SBAM方法的NMI及运行时间变化规律。表 3给出在人工网络上算法50次运行结果中最佳NMI和运行时间的平均值, 采用SBAM-L2方法进行性能对比, 其中“—”表示实验时间超过24 h, 其NMI和时间消耗不再列出。由表 3可以看出, 总体上, 随着参数k、μ的变化, 本文方法的有效性和效率均优于OddBall和SODA方法。在混合参数μ小于0.3时, 3种方法的NMI值均为1, 可见3种方法在没有异常扰动的情况下均能较好地完成异常社区检测任务, 而随着混合参数μ的增大, OddBall和SODA方法性能不同程度地降低; 在混合参数μ<0.3且挖掘子空间个数较少时, SODA方法时间消耗少于本文方法所需时间, 其原因在于本文方法适用于复杂网络中的属性网络, 其在挖掘多个属性子空间上具有优势, 而当需要挖掘较少的属性子空间时, SODA方法则更适用。
|
下载CSV 表 3 异常社区检测方法在人工网络数据集上的性能对比 Table 3 Performance comparison of anomaly community detection methods on artificial network datasets |
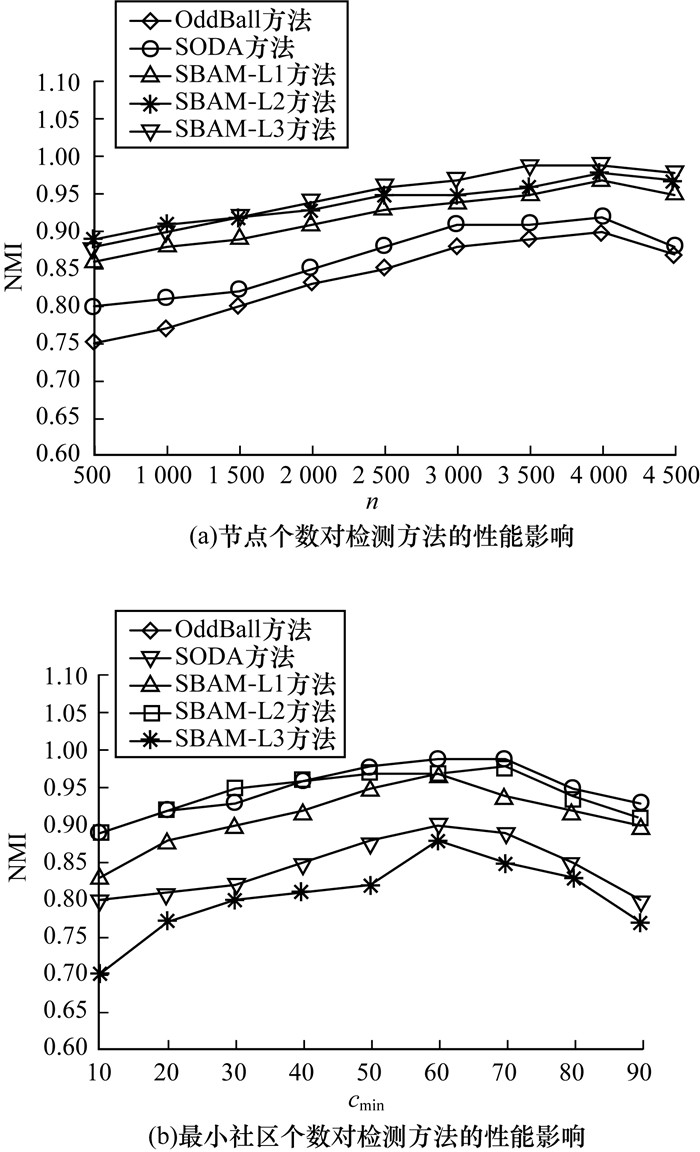
图 2表示随着网络中n和cmin的增加, 本文方法和对比方法的NMI值变化情况。实验中α的初始值设置为0.5, 结合多次实验结果表明:当α=0.42时实验效果最佳。
|
Download:
|
| 图 2 节点个数和最小社区个数对异常社区检测方法的性能影响 Fig. 2 Performance impact of the number of nodes and minimum communitys on anomaly community detection methods | |
由图 2可以看出, SBAM方法在LFR基准人工网络中, 节点个数和最小社区个数不断增加, NMI值也呈现上升趋势, 而OddBall和SODA方法的NMI值均低于SBAM方法, 即便在图 2(b)中SBAM方法的NMI值有所下降, 但也仍接近于1, 可见SBAM方法适合大型网络中的异常社区检测, 得到该实验结果的原因在于SBAM方法提供了3种节点属性子空间求解策略, 当网络中的节点个数逐渐增加时, 节点与节点之间的结构和属性信息均增加, 此时更容易实现子空间向量的求解, 所以SBAM方法更适合检测大型网络中的异常社区。
4.2.2 真实网络分析本节将SBAM方法在3个真实数据集Facebook、Twitter和Google+上与AMEN方法进行对比。首先, 为产生真实异常值, 采用AMEN中对真实网络进行不同程度异常扰动来获取异常社区的方法; 然后, 根据OddBall和SODA方法分别从结构、属性、属性融合结构的角度出发, 利用NMI均值和AUC值对实验结果进行综合评估, 本次实验采用SBAM-L2方法进行性能对比。
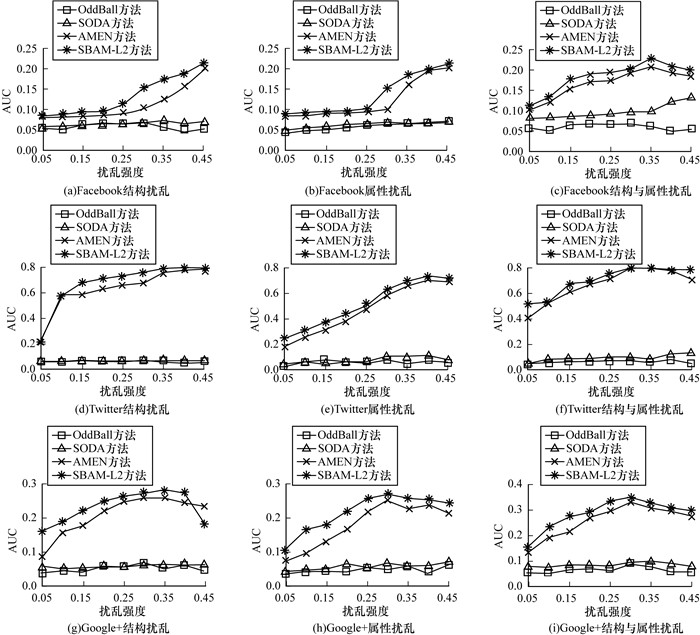
图 3表示随着真实网络异常扰动强度的增加, 在不同数据集上, SBAM-L2方法能够准确检测异常社区, AMEN方法次之, 但图 3不论是从属性或者结构角度, 还是从属性融合结构的角度评估方法性能, SBAM-L2方法均为最优, 其原因为SBAM-L2方法的特点是依据融合属性和结构的信息, 挖掘网络中的子空间, 实现异常社区检测。实验选取的真实网络数据集Facebook、Twitter和Google+中节点与边之间存在友谊关系或者协从关系, 通过计算子空间求出社区质量分数值, 而SBAM方法就是利用社区子空间结合社区结构信息得出异常社区质量分数值。
|
Download:
|
| 图 3 异常社区检测方法在真实网络数据集上扰动强度的变化情况 Fig. 3 Perturbation intensity changes of anomaly community detection methods on real network datasets | |
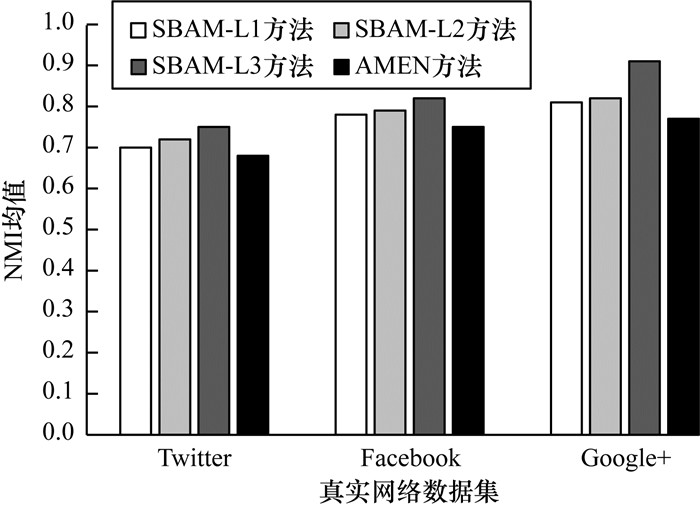
本文提出的3种子空间求解策略对异常社区检测性能产生了不同程度的影响, 因此分别采用SBAM-L1、SBAM-L2以及SBAM-L3 3种方法进行100次实验, 权重系数因子α设置为实验最佳值0.42, 求解SBAM方法和AMEN方法的NMI均值, 具体实验结果如图 4所示。
|
Download:
|
| 图 4 基于3种子空间求解策略的SBAM与AMEN方法性能对比 Fig. 4 Performance comparison of SBAM and AMEN methods based on three subspace solving strategies | |
由图 4可知, SBAM方法与AMEN方法在3种子空间求解策略的性能比较上, 本文方法的NMI均值略微高于AMEN方法, 且对于两种子空间求解策略而言, 在3个真实数据集上, SBAM-L2方法的性能略优于SBAM-L1方法。SBAM-L2方法性能更优的原因在于该方法考虑了每一维度的重要性, 仅维度权重不同, 而SBAM-L1方法是对属性进行权重重要性的提取, 不重要的属性维度权重赋值为0, 在某种程度上无法揭示出真实网络的属性子空间。然而, SBAM-L3方法融合了两种子空间求解策略, 既考虑求解子空间的计算速度也权衡属性每一维度的重要性, 采用权重系数调节因子α来量化两种策略对挖掘社区子空间的影响, 但SBAM-L2方法对模型影响更大, 在快速精准求解子空间的应用场景下, 可采用融合模型挖掘子空间。因此, 对于需要严格保留社区完整形态的异常社区检测, 负熵加权策略更实用; 而若仅选取局部的焦点属性来快速求解子空间, 则属性平均距离策略更适合。针对不同的异常社区检测任务, 可采用不同的子空间求解策略。由图 4可看出, 本文方法可在真实网络中较准确地发现异常社区。
5 结束语本文针对属性图中的异常社区检测问题, 提出融合属性与结构的子空间异常社区检测方法, 设计3种子空间求解策略, 并利用社区质量评估模型检测异常社区。实验结果表明, 该方法既能检测高质量社区, 又能发现异常社区。在人工网络数据集和真实网络数据集上的实验结果验证了本文方法的鲁棒性和可扩展性, 在真实属性图上的实验结果表明该方法更符合现实复杂网络特性, 但在网络节点结构信息上, 其未考虑社区重叠对社区检测结果的影响, 这将是下一步研究的重点。
| [1] |
AKOGLU L, MCGLOHON M, FALOUTSOS C.OddBall: spotting anomalies in weighted graphs[C]//Proceedings of Pacific-Asia Conference on Knowledge Discovery and Data Mining.Berlin, Germany: Springer, 2010: 410-421. 10.1007/978-3-642-13672-6_40
|
| [2] |
TSOURAKAKIS C E, BONCHI F, GIONIS A, et al.Denser than the densest subgraph: extracting optimal quasi-cliques with quality guarantees[C]//Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2013: 104-112. 10.1145/2487575.2487645
|
| [3] |
HE Chaobo, TANG Yong, LIU Hai, et al. Method for community mining integrating link and attribute information[J]. Chinese Journal of Computers, 2017, 40(3): 601-616. 贺超波, 汤庸, 刘海, 等. 一种集成链接和属性信息的社区挖掘方法[J]. 计算机学报, 2017, 40(3): 601-616. |
| [4] |
ZHOU Y, CHENG H, YU J X. Graph clustering based on structural/attribute similarities[J]. Proceedings of the VLDB Endowment, 2009, 2(1): 718-729. DOI:10.14778/1687627.1687709 |
| [5] |
HUANGX, CHENG H, YU J X. Dense community detection in multi-valued attributed networks[J]. Information Sciences, 2015, 314: 77-99. DOI:10.1016/j.ins.2015.03.075 |
| [6] |
XU Sen, LU Zhimao, GU Guochang. Two spectral algorithms for ensembling document clusters[J]. Acta Automatica Sinica, 2009, 35(7): 997-1002. 徐森, 卢志茂, 顾国昌. 解决文本聚类集成问题的两个谱算法[J]. 自动化学报, 2009, 35(7): 997-1002. |
| [7] |
NEWMAN M E. Modularity and community structure in networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(23): 8577-8582. DOI:10.1073/pnas.0601602103 |
| [8] |
LEMAN A, TONG H H, BRENDAN M, et al.PICS: parameter-free identification of cohesive subgroups in large attributed graphs[C]//Proceedings of 2012 SIAM International Conference on Data Mining.[S.l.]: SIAM, 2012: 439-450. 10.1137/1.9781611972825.38
|
| [9] |
MA Huifang, CHEN Haibo, ZHAO Weizhong, et al. Leveraging tag mean partition distance and social structure for overlapping microblog user community detection[J]. Acta Electronica Sinica, 2018, 46(11): 2612-2618. 马慧芳, 陈海波, 赵卫中, 等. 融合标签平均划分距离和结构关系的微博用户可重叠社区发现[J]. 电子学报, 2018, 46(11): 2612-2618. DOI:10.3969/j.issn.0372-2112.2018.11.007 |
| [10] |
PEROZZI B, AKOGLU L, SÁNCHEZ P I.Focused clustering and outlier detection in large attributed graphs[C]//Proceedings of ACM International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2014: 1346-1355. 10.1145/2623330.2623682
|
| [11] |
BRYAN P, LEMAN A.Scalable anomaly ranking of attributed neighborhoods[C]//Proceedings of 2016 SIAM International Conference on Data Mining.[S.l.]: SIAM, 2016: 1-10.
|
| [12] |
LESKOVEC J, LANG K J, DASGUPTA A, et al.Statistical properties of community structure in large social and information networks[C]//Proceedings of the 17th International Conference on World Wide Web.New York, USA: ACM Press, 2008: 695-704. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=WFHYXW320185&f=datatang
|
| [13] |
GLEICH D F, SESHADHRI C.Vertex neighborhoods, low conductance cuts, and good seeds for local community methods[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2012: 597-605.
|
| [14] |
ARNABOLDI V, CONTI M, PASSARELLA A, et al.Analysis of ego network structure in online social networks[C]//Proceedings of ASE/IEEE International Conference on Social Computing and ASE/IEEE International Conference on Privacy.Washington D.C., USA: IEEE Press, 2012: 31-40. 10.1109/SocialCom-PASSAT.2012.41
|
| [15] |
LESKOVEC J, KLEINBERG J, FALOUTSOS C.Graphs over time: densification laws, shrinking diameters and possible explanations[C]//Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining.New York, USA: ACM Press, 2005: 177-187. 10.1145/1081870.1081893
|
| [16] |
MCGLOHON M, AKOGLU L, FALOUTSOS C.Weighted graphs and disconnected components: patterns and a generator[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2008: 524-532. 10.1145/1401890.1401955
|
| [17] |
YANG J, LESKOVEC J.Defining and evaluating network communities based on ground-truth[C]//Proceedings of ICDM'12.Washington D.C., USA: IEEE Press, 2012: 745-754. 10.1007/s10115-013-0693-z
|
| [18] |
SILVA A, ZAKI M J. Mining attribute-structure correlated patterns in large attributed graphs[J]. Proceedings of the VLDB Endowment, 2012, 5(5): 466-477. DOI:10.14778/2140436.2140443 |
| [19] |
JIANG Shengyi, YANG Bohong, WANG Lianxi. An adaptive dynamic community detection algorithm based on incremental spectral clustering[J]. Acta Automatica Sinica, 2015, 41(12): 2017-2025. 蒋盛益, 杨博泓, 王连喜. 一种基于增量式谱聚类的动态社区自适应发现算法[J]. 自动化学报, 2015, 41(12): 2017-2025. |
| [20] |
CLAUSET A, NEWMAN M E J, MOORE C. Finding community structure in very large networks[J]. Physical Review E, 2004, 70(6): 66-111. |
| [21] |
KARPIS G, KUMAR V. A fast and high quality multilevel scheme for partitioning irregular graphs[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 359-392. |
| [22] |
YANG J, LESKOVEC J.Community-affiliation graph model for overlapping network community detection[C]//Proceedings of the 12th International Conference on Data Mining.Washington D.C., USA: IEEE Press, 2012: 1170-1175. 10.1109/ICDM.2012.139
|
| [23] |
ANDERSEN R, LANG K J.Communities from seed sets[C]//Proceedings of WWW'06.New York, USA: ACM Press, 2006: 223-232.
|
| [24] |
PAN Jianfei, DONG Yihong, CHEN Huahui, et al. The overlapping community discovery algorithm based on compact structure[J]. Acta Electronica Sinica, 2019, 47(1): 145-152. 潘剑飞, 董一鸿, 陈华辉, 等. 基于结构紧密性的重叠社区发现算法[J]. 电子学报, 2019, 47(1): 147-154. |
| [25] |
COSCIA M, ROSSETTI G, GIANNOTTI F, et al.DEMON: a local-first discovery method for overlapping communities[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2012: 615-623. 10.1145/2339530.2339630
|
| [26] |
NOBLE C C, VCOOK D J.Graph-based anomaly detection[C]//Proceedings of ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2003: 631-636. 10.1145/956750.956831
|
| [27] |
GAO J, LIANG F, FAN W, et al.On community outliers and their efficient detection in information networks[C]//Proceedings of KDD'10.New York, USA: ACM Press, 2010: 813-822.
|
| [28] |
WU P, PAN L.Mining target attribute subspace and set of target communities in large attributed networks[EB/OL].[2019-02-04].https: //arxiv.org/abs/1705.03590.
|
| [29] |
BROWN J N, BREWER H M, NICORA C D, at al. Protein and microRNA biomarkers from lavage, urine, and serum in military personnel evaluated for dyspnea[J]. BMC Medical Genomics, 2014, 7(1): 1-18. DOI:10.1186/1755-8794-7-1 |
| [30] |
DANON L, DUCH J, ARENAS A, et al. Community structure identification[M]. [S.l.]: Mendeley, 2005.
|
 2020, Vol. 46
2020, Vol. 46

 ,
,