2. 甘肃安信信息安全技术有限公司, 兰州 730000
2. Gansu Anxin Information Security Technology Co., Ltd., Lanzhou 730000, China
随着大数据和云计算的迅速发展, 越来越多的组织和个人倾向于将数据迁移到云服务器, 以便节省本地资源[1-2]。然而数据拥有者一旦将敏感数据上传到云服务器, 将会失去对数据的完全控制, 从而导致未授权用户和云服务器提供商访问或恶意窃取用户的敏感数据。因此, 数据的安全性是云计算亟待解决的关键问题之一[3-4]。为实现数据的机密性, 数据拥有者通常在数据外包之前对其进行加密, 但面临加密数据有效检索的问题[5-6]。可搜索加密技术具有密文的关键字搜索等功能, 能保障加密数据的安全性和隐私性, 已成为近年来云计算安全领域的一个研究热点[7]。
自可搜索加密思想[8]被提出后, 一些具有特殊性质的可搜索加密方案相继出现[9-10]。2004年, 文献[11]提出了公钥可搜索加密方案, 但需要在安全信道中传输关键字陷门。此后, 文献[12]提出了无安全信道的公钥可搜索加密方案, 但加密数据文件时需要访问用户和服务器的公钥。文献[13]提出了基于证书的可搜索加密方案, 但只满足选择明文安全性。文献[14]提出了另一个基于证书加密方案, 通过引入第三方经理减轻了云计算的负担。然而, 文献[13-14]提出的可搜索加密方案都面临复杂的证书管理开销问题。对此, 文献[15-16]分别提出了基于身份的可搜索加密方案, 但依然只满足选择明文攻击下的不可区分性, 并且需要一个可信的密钥生成中心(Key Generation Center, KGC)生成用户的私钥。文献[17-18]提出的基于无证书密码体制的密文检索方案, 有效解决了密钥托管问题, 但都只适用于单用户的密文数据检索, 在实际应用中具有一定的局限性。
针对有可搜索加密方案计算开销大和安全性现低[19-20]的问题, 本文提出一种多用户密文检索方案。该方案采用无证书密码体制生成关键字陷门, 避免使用公钥证书, 支持多用户的密文检索, 并可通过访问用户授权列表实现访问用户的加入与撤销等功能。同时, 在关键字加密阶段, 数据拥有者无须指定访问用户的身份, 由此提高计算性能, 使方案适用于云存储环境。
1 预备知识 1.1 双线性映射给定相同素数阶p的2个循环群G1和G2, 双线性映射e:G1×G1→G2满足以下性质:
1) 双线性:对于∀u, v∈G1, a, b∈
2) 非退化性:e(g, g)≠1, 其中, g是G1的一个生成元。
3) 可计算性:对于∀u, v∈G1, e(u, v)是有效可计算的。
1.2 困难问题假设给定一个四元组(g, ga, gb, gc), 其中, a, b, c∈
定义1 (BDH假设) 如果没有一个多项式时间算法能以不可忽略的概率解决BDH问题, 则称BDH问题是困难的。
给定一个五元组(g, gα, gβ, g1/α, R), 其中, α, β∈
定义2 (mDDH假设) 如果没有一个多项式时间算法能以不可忽略的概率解决mDDH问题, 则称mDDH问题是困难的。
1.3 可搜索加密方案一个公钥可搜索加密方案由以下9个多项式时间算法组成:
1) Setup(1λ):输入安全参数λ, KGC生成主密钥msk和系统公共参数param。
2) PatialKeyGen(param, msk, id):输入param、msk以及某个实体的身份id, KGC生成相应的部分私钥psk。
3) KeyGen(param, psk):输入param以及psk, 该算法输出对应的公钥pk以及完整私钥sk。
4) Enc(param, pk, W, F):输入param、服务器公钥pk、关键字集W和数据文件F, 输出数据文件密文CT以及密文索引CF。
5) Auth(param, pkidi, k):输入param、访问用户公钥pkidi以及文档密钥k, 输出授权用户授权列表LF。
6) Trapdoor(param, pkids, skidi, w′):输入param、服务器公钥pkids、数据拥有者私钥skidi以及查询关键字w′, 输出搜索陷门Tw′。
7) Search(param, skids, Tw′, I):输入param、服务器私钥skids、Tw′以及Ci, 输出相关数据文件密文。
8) Add(param, k, LF, pkidi):输入k、授权列表LF以及待授权访问用户公钥pkidi, 将新用户添加到授权列表中, 输出更新成功。
9) Revoke(LF, Ui):输入授权列表LF以及待撤销授权用户Ui, 将用户从授权列表中删除, 输出撤销成功。
一个公钥可搜索加密方案的安全模型[7]主要从密文索引不可区分性和陷门不可区分性两方面进行安全性定义, 但在定义陷门不可区分性时, 关键字攻击只考虑外部敌手而不考虑服务器猜测攻击。
2 本文方案 2.1 系统模型本文方案的系统模型如图 1所示, 其中包括KGC、数据拥有者(Data Owner, DO)、n个访问用户{U1, U2, …, Un}以及云服务提供商(Cloud Server Provider, CSP)。其中:KGC主要负责生成系统参数和每个实体的部分私钥; DO主要负责生成数据文件密文、关键字密文索引和访问用户的授权列表; 访问用户Ui生成关键字陷门, 并解密CSP返回的数据文件密文; CSP主要负责存储数据文件密文、关键字索引和访问用户的授权列表, 并响应访问用户的搜索请求。

|
Download:
|
| 图 1 本文方案的系统模型 Fig. 1 System model of the proposed model | |
本文方案中各算法的描述如下:
1) Setup算法。KGC选择2个阶为素数p的乘法循环群G1和G2, 1个群G1的生成元g, 1个双线性映射e:G1×G1→G2, 3个防碰撞哈希函数H:{0, 1}*→G1, H1:{0, 1}*→G1和H2:G2→{0, 1}logap; 随机选取x∈
2) PatialKeyGen算法。KGC为收到的每个访问用户身份idi计算生成部分私钥pskidi=H(idi)x, 并将部分私钥pskidi通过安全信道发送给访问用户; 类似地, 身份为ids的CSP获得部分私钥pskids=H(ids)x。
3) KeyGen算法。每个访问用户Ui随机选取si∈
4) Enc算法。DO首先从数据文件F中提取关键字wi∈ψ(1≤i≤m), 此处ψ是所有关键字集合, 然后随机选取文档密钥k∈
5) Auth算法。DO初始化数据文件F的访问用户授权列表LF=Ø。对于每个访问用户, 首先利用其公钥pkidi和文档密钥k计算授权信息ΔF→Ui=(pkidi)k=gsik, 然后在LF中添加(pkidi, ΔF→Ui), 最后将更新后的访问用户授权列表LF发送至CSP。
6) Trapdoor算法。访问用户Ui首先选取搜索关键字w′∈ψ, 然后随机选取r′∈
7) Search算法。当收到访问用户Ui的搜索请求后, CSP首先计算σ1=e(T2t/T1, ΔF→Ui)e(H(ids)x, gsi), σ2=e(T3, gx)·e(H(idi), Ci2t)和σ3=σ1/σ2, 然后利用每个关键字wi(1≤i≤m)的密文Ci=(Ci1, Ci2, Ci3)来验证等式H2(σCi33)=Ci1是否成立, 若该等式成立, 则说明关键字匹配成功, 并将匹配成功的所有文档返回给Ui; 否则将匹配失败的信息发送给Ui。
8) Add算法。当收到访问用户Uj对数据文件F的授权请求后, DO利用其公钥pkidj和文档密钥k计算ΔF→Ui=(pkidi)k=gsik, 将(pkidj, ΔF→uj)提交给CSP, 并请求更新文档F的授权列表, 同时将授权成功的信息发送给访问用户Uj。
9) Revoke算法。若DO想撤销访问用户Ui对数据文件F的访问授权, 则将Ui的公钥pkidi发送给CSP。收到DO的撤销请求后, CSP在LF中查找对应条目(pkidi, ΔF→Ui), 并将其从LF中删除。
对本文方案进行正确性分析:
CSP收到正确的关键字密文Ci=(Ci1, Ci2, Ci3)=(H2(e(H1(wi)k·ri, pkids)), gx·k, ri)和搜索陷门Tw′=(T1, T2, T3)=(gtr′, (H1(w′)·H(idi)x)1/si·gr′, H(ids)si)后, 计算:
| $ \begin{aligned} \sigma_{1}=& e\left(T_{2}^{t} / T_{1}, \Delta_{F \rightarrow u_{i}}\right) e\left(H\left(i d_{s}\right)^{x}, g^{s_{i}}\right)=\\ & e\left(H_{1}\left(w^{\prime}\right), g\right)^{t k} e\left(H\left(i d_{i}\right), g\right)^{t x k} e\left(H\left(i d_{s}\right), g\right)^{s_{i} x} \\ \sigma_{2}=& e\left(T_{3}, g^{x}\right) \cdot e\left(H\left(i d_{i}\right), C_{i 2}^{t}\right)=\\ & e\left(H\left(i d_{s}\right), g\right)^{s_{i} x} \cdot e\left(H\left(i d_{i}\right), g\right)^{t x k} \\ \sigma_{3}=& \sigma_{1} / \sigma_{2}=e\left(H_{1}\left(w^{\prime}\right), g\right)^{t k} \end{aligned} $ |
由于H2(σCi33)=H2(e(H1(w′), g)t·k·ri)=H2(e(H1(w′)k·ri, pkids))=Ci1, 因此当关键字w′=wi时, H2(σCi33)=Ci1成立, 即CSP能成功匹配到访问用户请求的数据文件。
3 安全性证明定理1 在BDH假设下, 本文方案在随机预言机模型下满足密文索引不可区分性。
证明:假设多项式时间攻击者
1) 密钥生成。
2) 哈希询问。
3) H1询问。
4) H2询问。
若H2-list中已有t的对应项(t, V),
5) 陷门询问1。当收到
对wi进行H1询问, 以获取对应项(wi, hi, ai, ci)。判断ci取值, 若ci=0, 游戏终止并返回失败信息; 否则返回hi, 随机选取r′i∈
6) 挑战。当收到
7) 陷门询问2。
8) 输出。
下面分析
在陷门询问阶段,
假设
通过上述分析可知, 因为游戏不终止概率为1/eqT, 所以
定理2 在mDDH假设下, 本文方案在随机预言机模型下对外部敌手满足陷门不可区分性。
证明:假设多项式时间攻击者
1) 密钥生成。
2) 哈希询问。此过程与定理1的H1询问基本相同, 只要求若ci=0, 计算hi=u1ai∈G1; 若ci=1, 计算hi=gai∈G1。
3) 陷门询问1。其过程与定理1的陷门询问1相同。
4) 挑战。此过程与定理1的挑战阶段基本相同, 只要求rb=α/β, 计算T1*=gβs′·α/β=gαs′=u1s′, T2*=(hi·H(idi)x)1/sα·gr′i=H(idi)x/sα·gab/s·gα/β, T3*=H(idu)x/sα·H(ids)1/sα, 定义T2*=H(idu)x/sα·gab/s·R, 将挑战陷门Twb=(T1*, T2*, T3*)发送给
5) 陷门询问2。此过程与定理1的陷门询问2相同。
6) 输出。
分析
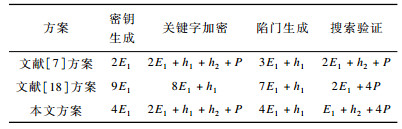
将本文方案与文献[7, 18]提出可搜索加密方案进行计算开销的比较, 如表 1所示。为便于表述, 用E1表示G1上的一次指数运算, h1和h2分别表示哈希函数H1和H2的一次运算, P表示一次双线性配对运算。可以看出:在密钥生成阶段, 本文方案较文献[18]方案减少了5次指数运算, 但较文献[7]增加了2次指数运算; 在关键字加密阶段, 本文方案较文献[18]减少了6次指数运算, 但增加了1次H2运算以及1次配对运算; 在陷门生成阶段, 本文方案较文献[18]减少了3次指数运算, 但较文献[7]增加了1次指数运算; 在搜索验证阶段, 本文方案较文献[18]减少了1次指数运算, 增加了1次H2运算, 较文献[7]减少了1次指数运算, 增加了3次配对运算。由于文献[7]方案面临证书的管理开销问题, 而文献[18]方案仅支持单用户的密文检索, 因此本文方案具有较高的计算效率和安全性能。
|
下载CSV 表 1 3种方案各阶段的计算开销 Table 1 Computational overhead of three schemes in each stage |
利用PBC库对3种方案进行仿真实验, 如图 2和图 3所示。硬件环境为:3.1 GHz英特尔酷睿i5-2400处理器, 4 GB内存, 512 GB硬盘空间。软件环境为:64位Windows 10操作系统, 密码库PBC-0.4.7 -VC。
|
Download:
|
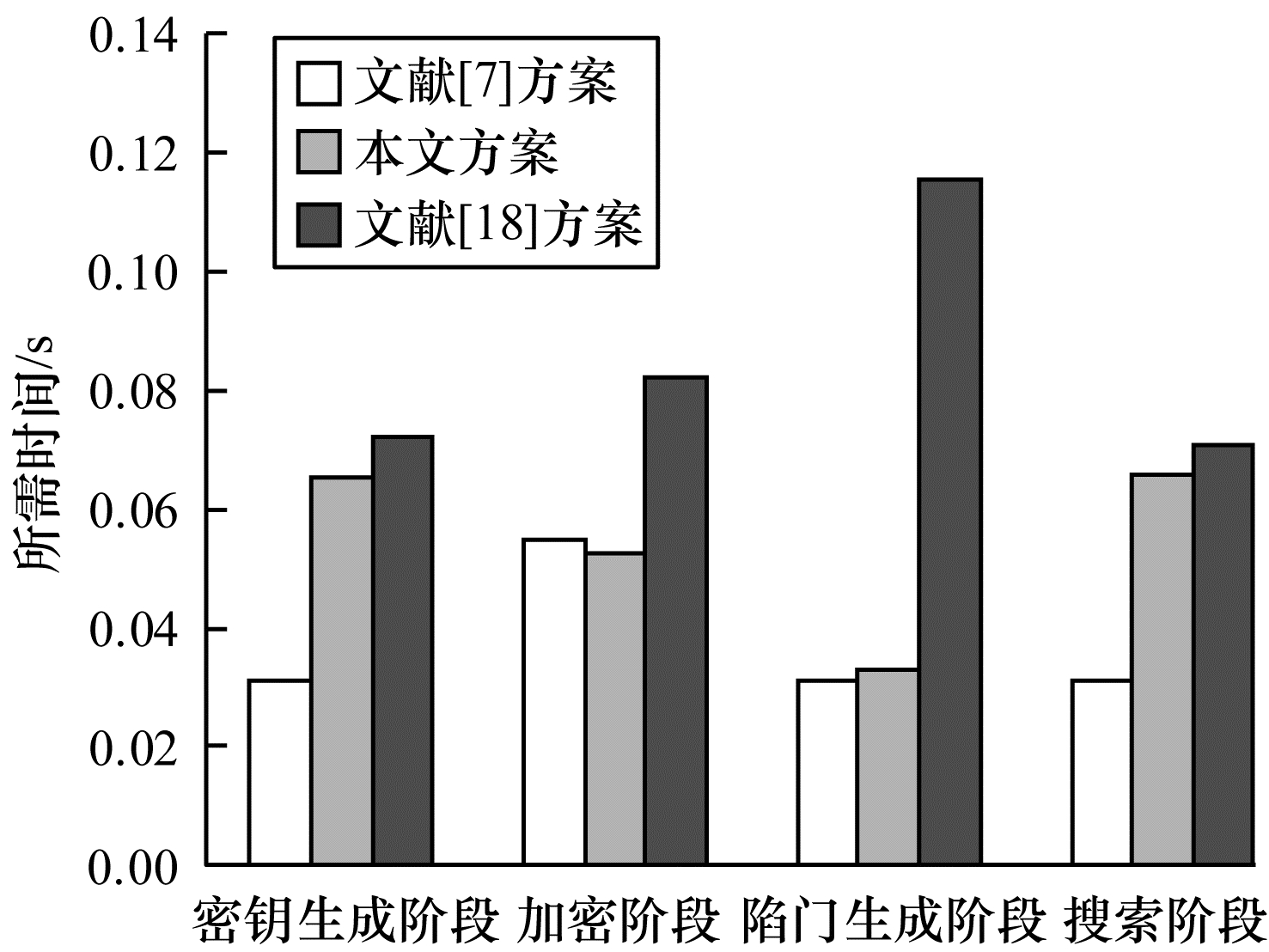
| 图 2 单个关键字情况下3种方案的计算性能 Fig. 2 Computational performance of three schemes in the case of a single keyword | |

|
Download:
|
| 图 3 多个关键字情况下3种方案的计算性能 Fig. 3 Computational performance of three schemes in the case of multiple keywords | |
图 2所示为单个关键字情况下3种方案密钥生成、关键字加密、关键字陷门生成以及搜索阶段的计算开销。同时, 从数据集中分别选取10个、20个、50个、100个关键字对3种方案的关键字加密算法、陷门生成算法以及搜索算法进行计算开销分析, 如图 3所示。其中, 图 3(a)反映了关键字加密时间随关键字数量的变化, 图 3(b)反映了陷门生成时间随关键字数量的变化, 图 3(c)反映了搜索时间随关键字个数的变化。由图 2和图 3可知, 本文方案在密钥生成、关键字加密、关键字陷门生成以及搜索阶段具有一定的计算优越性。
5 结束语本文基于无证书密码体制提出一种新的公钥可搜索加密方案, 其安全性依赖于BDH假设和mDDH假设, 并且在关键字加密阶段无需指定用户访问权限, 支持多用户密文检索, 可通过授权列表实现了用户的加入与撤销等功能。分析结果表明, 与文献[7, 18]提出的可搜索加密方案相比, 该方案具有较高的计算性能, 适用于多用户的云端密文检索环境。本文方案在随机预言模型下是可证明安全的, 下一步将在本文标准模型下设计基于无证书的多用户密文检索方案。
| [1] |
KHAN N A, PANCHAL V K, TANWEER S. Comprehensive analysis of data storage security in cloud[J]. Global Sci-Tech, 2019, 11(2): 82-92. DOI:10.5958/2455-7110.2019.00012.0 |
| [2] |
LIU S, GUO L, WEBB H, et al. Internet of things monitoring system of modern eco-agriculture based on cloud computing[J]. IEEE Access, 2019, 7: 37050-37058. DOI:10.1109/ACCESS.2019.2903720 |
| [3] |
ZHANG Jiale, ZHAO Yanchao, CHEN Bing, et al. Survey on data security and privacy-preserving for the research of edge computing[J]. Journal on Communications, 2018, 39(3): 1-21. (in Chinese) 张佳乐, 赵彦超, 陈兵, 等. 边缘计算数据安全与隐私保护研究综述[J]. 通信学报, 2018, 39(3): 1-21. |
| [4] |
FAN Yongkai, LIN Xiaodong, TAN Gang, et al. One secure data integrity verification scheme for cloud storage[J]. Future Generation Computer Systems, 2019, 96: 376-385. DOI:10.1016/j.future.2019.01.054 |
| [5] |
DONG Xiaolei, ZHOU Jun, CAO Zhenfu. Research advances on secure searchable encryption[J]. Journal of Computer Research and Development, 2017, 54(10): 2107-2120. (in Chinese) 董晓蕾, 周俊, 曹珍富. 可搜索加密研究进展[J]. 计算机研究与发展, 2017, 54(10): 2107-2120. |
| [6] |
LI Ying, MA Chunguang. Overview of searchable encryption research[J]. Chinese Journal of Network and Information Security, 2018, 4(7): 13-21. (in Chinese) 李颖, 马春光. 可搜索加密研究进展综述[J]. 网络与信息安全学报, 2018, 4(7): 13-21. |
| [7] |
ZUO Xinxin.Research on multi-user searchable encryption scheme in cloud environment[D].Chengdu: University of Electronic Science and Technology, 2018.(in Chinese) 左欣欣.云环境下多用户可搜索加密方案研究[D].成都: 电子科技大学, 2018. |
| [8] |
SONG D X, WAGNER D, PERRIG A.Practical techniques for searches on encrypted data[C]//Proceedings of 2000 IEEE Symposium on Security and Privacy.Washington D.C., USA: IEEE Press, 2000: 44-55.
|
| [9] |
CUI Jie, ZHOU Han, XU Yan, et al. OOABKS:online/offline attribute-based encryption for keyword search in mobile cloud[J]. Information Sciences, 2019, 489: 63-77. DOI:10.1016/j.ins.2019.03.043 |
| [10] |
LI Jingwei, JIA Chunfu, LIU Zheli, et al. Survey on the searchable encryption[J]. Journal of Software, 2015, 26(1): 109-128. (in Chinese) 李经纬, 贾春福, 刘哲理, 等. 可搜索加密技术研究综述[J]. 软件学报, 2015, 26(1): 109-128. |
| [11] |
BONEH D, DI CRESCENZO G, OSTROVSKY R, et al.Public key encryption with keyword search[C]//Proceedings of International Conference on the Theory and Applications of Cryptographic Techniques.Berlin, Germany: Springer, 2004: 506-522.
|
| [12] |
BEAK J, SAFAVI-NAINI R, SUSILO W.Public key encryption with keyword search revisited[C]//Proceedings of 2008 International Conference on Computational Science and Its Applications.Berlin, Germany: Springer, 2008: 1249-1259.
|
| [13] |
GUO Yuyan, JIANG Mingming, SONG Wangan. Provably secure certificate-based encryption with leakage resilience[J]. Journal of Huaibei Normal University(Natural Science), 2019, 40(1): 19-25. (in Chinese) 郭宇燕, 江明明, 宋万干. 可证明安全的弹性泄漏基于证书加密方案[J]. 淮北师范大学学报(自然科学版), 2019, 40(1): 19-25. |
| [14] |
VERMA S.A new lightweight approach for multiuser searchable encryption in the cloud[C]//Proceedings of International Conference on Communication, Networks and Computing.New York, USA: ACM Press, 2019: 49-63.
|
| [15] |
NI Lülin, XU Chungen. Dynamic searchable encryption scheme based on identity[J]. Computer Engineering, 2019, 45(1): 136-140. (in Chinese) 倪绿林, 许春根. 基于身份的动态可搜索加密方案[J]. 计算机工程, 2019, 45(1): 136-140. |
| [16] |
ZHU Minhui, CHEN Yanli, HU Yuanyuan. Identity-based searchable encryption scheme supporting proxy re-encryption[J]. Computer Engineering, 2019, 45(1): 129-135. (in Chinese) 朱敏惠, 陈燕俐, 胡媛媛. 支持代理重加密的基于身份可搜索加密方案[J]. 计算机工程, 2019, 45(1): 129-135. |
| [17] |
PENG Jiangtao, CUI Changgen, PENG Changgen, et al. Certificateless public key encryption with keyword search[J]. China Communications, 2014, 11(11): 100-113. DOI:10.1109/CC.2014.7004528 |
| [18] |
WU Qiying, MA Jianfeng, LI Hui, et al. Certificateless conjunctive keyword search over encrypted data[J]. Journal of Xidian University(Natural Science), 2017, 44(3): 55-60. (in Chinese) 伍祈应, 马建峰, 李辉, 等. 无证书连接关键字密文检索[J]. 西安电子科技大学学报(自然科学版), 2017, 44(3): 55-60. |
| [19] |
CAO Qiang, LI Yanping, LIU Qingqing, et al. Certificateless conjunctive keyword search on encrypted data in cloud storage[J]. Journal of Shaanxi Normal University(Natural Science Edition), 2019, 47(5): 115-124. (in Chinese) 曹强, 李艳平, 刘青青, 等. 云存储中无证书连接关键词密文检索[J]. 陕西师范大学学报(自然科学版), 2019, 47(5): 115-124. |
| [20] |
DENG Xiaoyan, CHENG Hao, SUN Bo, et al. ID-based deletion searchable encryption scheme[J]. IOP Conference Series:Earth and Environmental Science, 2019, 234(1): 12-52. |
 2020, Vol. 46
2020, Vol. 46
