开放科学(资源服务)标志码(OSID):
信息化浪潮正以前所未有的广度和深度影响着人们生活的方方面面。视频作为一种内容传播载体,逐渐成为人们生活中不可或缺的重要组成部分,而随着网络技术和电子技术的快速发展,超高清视频在远程教育、医疗检测、虚拟现实等任务得到广泛应用。人们能够通过终端设备便捷地获取到丰富的视频内容,但视频数据量的爆炸性增长给视频编码技术带来了新的挑战。
目前,高效视频编码标准H.265/HEVC[1]凭借其较高的编码效率逐步渗透到媒体产品中,然而由于版权问题限制了HEVC的进一步推广和使用。联合视频专家组JVET制定了新一代高效视频编码标准H.266/VVC[2],目标是提供比HEVC更优越的编码性能,并支持360°视频和HDR视频的编解码。H.266/VVC沿用H.265/HEVC中的混合编码框架,如帧内帧间预测、熵编码等,但同时引入多种新的编码技术,如基于四叉树加二叉树加三叉树的块分割结构、67种帧内预测模式、仿射运动补偿预测、自适应运动矢量精度、多核变换、自适应环路滤波等。在众多候选模式中,需要借助率失真优化(Rate Distortion Optimization,RDO)技术[3-4],通过获取率失真代价来确定最优的编码模式。这种模式判决方法在给定目标码率的条件下可以为用户提供最优的视频质量,但同时增加了编码复杂度。每一种候选帧内的预测模式均需经过预测、变换、量化、熵编码、反量化和反变换过程,占用大量的硬件资源,为实际应用带来了困难。
快速编码方法受到了业界的广泛关注。李跃等[5]提出一种提前Merge模式终止算法,该算法终止了多余候选模式的判决过程。JAMALI等[6]利用变换域残差来预测率失真代价,并通过排除不可能成为最优的预测模式来降低编码复杂度。TARIQ[7]根据相邻块率失真代价的动态变化预测当前块的率失真代价,并通过最小化率失真代价确定最优的预测模式。此外,TARIQ[8]借助智能优化算法,通过分析和研究帧内预测模式判决的特性,建立新的目标函数来选取最优预测模式。上述方法主要针对H.265/HEVC中35种帧内预测模式判决进行优化,并不适用于H.266/VVC。针对H.266/VVC的67种帧内预测模式判决,ZOUIDI等[9]利用相邻块的统计信息来缩小当前块在粗略模式判决模块中的候选模式集合,该方法从统计的角度选择候选模式集合,忽略了帧内模式判决原理和编码工具的影响,在降低编码复杂度的同时编码效率衰减较大。本文提出一种帧内预测模式快速判决方法,基于帧内预测编码原理,利用率失真优化理论建立适用于视频特性的码率预测模型,同时采用上下文信息预测编码失真,并根据率失真代价确定最优帧内预测模式。
1 H.266/VVC帧内预测模式判决为进一步利用空间相关性来去除视频帧内容的冗余,H.266/VVC引入67种帧内预测模式,包括多角度模式、Planar模式和DC模式[10-11]。图 1给出了67种帧内预测模式。依据视频的纹理特性,通过使用帧内预测模式判决,从众多模式中选择一种最优的模式来最大化H.266/VVC的帧内编码效率。图 2给出了量化参数(Quantization Parameter,QP)为22时视频Basket ballPass_416×240第1帧的最优帧内预测模式,其中不同灰度对应不同的预测角度,可以看出最优帧内预测模式可以较好地反映空域方向特性。

|
Download:
|
| 图 1 67种帧内预测模式 Fig. 1 The sixty-seven intra prediction modes | |

|
Download:
|
| 图 2 视频帧选用的最优帧内预测模式 Fig. 2 The optimal intra prediction mode selected for video frames | |
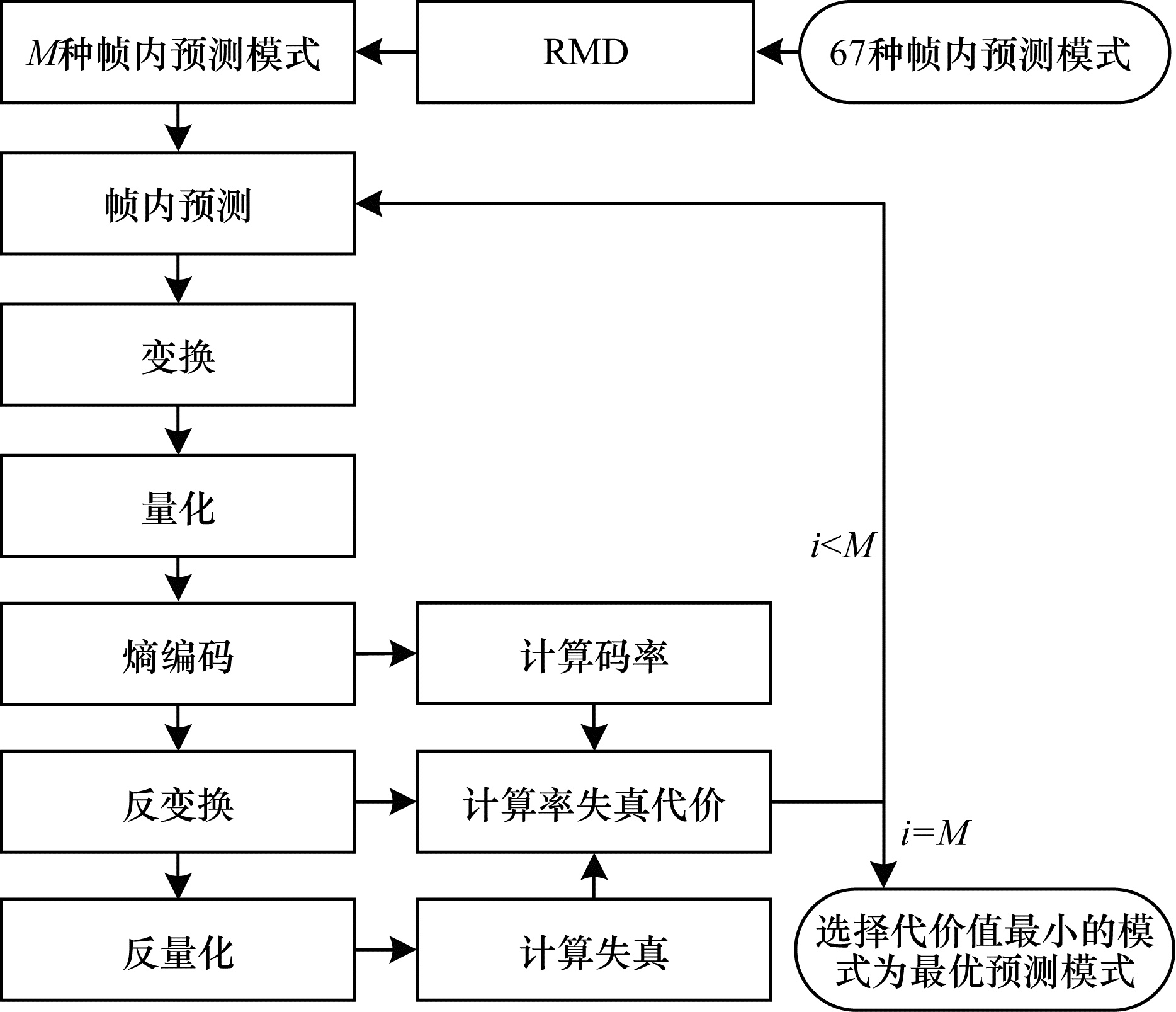
帧内预测模式判决主要借助于拉格朗日优化技术实现。每一种模式经过预测、变换、量化、熵编码、反量化、反变换、像素重构等步骤得到编码码率和编码失真,然后计算率失真代价,通过比较率失真代价来确定最优的预测模式。在H.266/VVC中,帧内预测模式判决方法分为粗略模式判决(Rough Mode Decision,RMD)和率失真优化两部分[12]。首先以哈达玛变换后的绝对误差和Ds为失真测度,计算帧内预测模式的率失真代价Js:
| $ {J}_{\mathrm{s}}={D}_{\mathrm{s}}+{\lambda }_{\mathrm{s}}\cdot {R}_{\mathrm{s}} $ | (1) |
其中:
| $ {J}_{\mathrm{e}}={D}_{\mathrm{e}}+{\lambda }_{\mathrm{e}}\cdot {R}_{\mathrm{e}} $ | (2) |
其中:
|
Download:
|
| 图 3 H.266/VVC帧内预测模式判决流程 Fig. 3 Decision procedure of H.266/VVC intra prediction mode | |
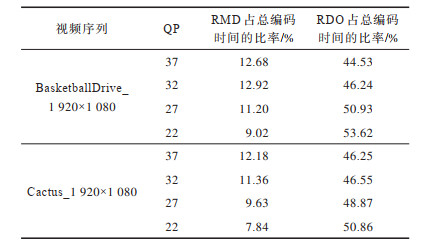
虽然多种模式可以很好地捕获帧中任意方向的视频信息,但给编码器带来了超负荷的运算量和超长的处理时延,这对基于H.266/VVC的多媒体业务拓展是极为不利的。表 1给出不同QP下序列采用帧内预测模式判决方法的耗时情况,其中RMD编码时间平均约占总编码时间的11.28%,RDO编码时间平均约占总编码时间的48.14%。可以看出,RDM耗时较小,RDO耗时较大,这是因为RDO模块需要运行一系列的编码工具,所以编码复杂度更高。此外,相同分辨率下内容复杂的视频比内容简单的视频耗时长。因此,本文方法一方面需考虑视频序列的特性,另一方面需考虑编码中应用的具体工具,通过借助RMD模块得到的编码信息来建立快速模式判决方法,在保证编码效率的同时尽量降低编码的复杂度。
|
下载CSV 表 1 RMD和RDO占总编码时间的比率 Table 1 Ratio of total coding time to that of RMD and RDO |
由于H.266/VVC帧内预测模式判决主要依据拉格朗日优化来确定最优模式,因此本文分别从码率和失真两个角度入手来建立预测模式快速判决方法。
2.1 码率预测通常变换域的残差可以被描述为零均值的高斯分布:
| $ f\left(x\right)={\left(2\mathrm{\pi }{\delta }_{\mathrm{h}}^{2}\right)}^{\frac{1}{2}}{\mathrm{e}}^{-\frac{{x}^{2}}{2{\delta }_{\mathrm{h}}^{2}}} $ | (3) |
其中:x表示残差;δh表示残差的标准差;e为自然常数。以均方误差和作为失真测度,残差经过量化后的理论率失真模型[13]如下:
| $ R\left(D\right)=\frac{1}{2}\mathrm{l}\mathrm{b}\frac{\mathrm{\pi }{\delta }_{\mathrm{h}}^{2}}{2\mathrm{e}D} $ | (4) |
在高比特率或低失真的情况下,残差的编码码率[14]如下:
| $ {R}_{\mathrm{r}}\approx \alpha \mathrm{l}\mathrm{b}{\delta }_{\mathrm{h}}^{2} $ | (5) |
其中:α=0.5。帧内预测模式主要采用基于上下文模型的熵编码,该编码码率可以通过RMD模块得到:
| $ {R}_{\mathrm{m}}={R}_{\mathrm{s}} $ | (6) |
总的编码码率Re为:
| $ {R}_{\mathrm{e}}\approx {R}_{\mathrm{m}}+{R}_{\mathrm{r}} $ | (7) |
上述码率预测方法不仅考虑了视频特性,还考虑了变换、量化和熵编码的影响,可在降低编码复杂度的同时最大化编码效率。
2.2码率预测过程需要使用变换域残差的标准差δ。假设变换前残差块大小为N×N,则残差系数c(x,y)经DCT变换[15]后得到的残差矩阵如下:
| $ \boldsymbol C(u,v) = \sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{N - 1} c } (x,y) \cdot \mathit{\boldsymbol{A}}(x,u) \cdot \mathit{\boldsymbol{A}}(y,v) $ | (8) |
| $ \boldsymbol{A}(m, n)=D\left(k\right)\mathrm{c}\mathrm{o}\mathrm{s}\frac{(2m+1)n\mathrm{\pi }}{8} $ | (9) |
若参数D(k)为已知量,则方差
| $ \begin{array}{*{20}{l}} {\delta _{\rm{h}}^2 \approx \frac{1}{{N \times N}}\sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{N - 1} {\delta _{\rm{h}}^2} } (u,v) = }\\ {\frac{1}{{N \times N}}\sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{N - 1} {\delta _{\rm{p}}^2} } \cdot \left[ {{\boldsymbol{AP}}{{\boldsymbol{A}}^{\rm{T}}}{]_{u,u}}} \right[{\boldsymbol{AP}}{{\boldsymbol{A}}^{\rm{T}}}{]_{v,v}} = }\\ {\frac{{\delta _{\rm{p}}^2}}{{N \times N}}\sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{N - 1} {\left[ {{\boldsymbol{AP}}{{\boldsymbol{A}}^{\rm{T}}}{]_{u,u}}} \right[} } {\boldsymbol{AP}}{{\boldsymbol{A}}^{\rm{T}}}{]_{v,v}}} \end{array} $ | (10) |
| $ \boldsymbol{P}=\left[\begin{array}{ccccc}1& \rho & {\rho }^{2}& \cdots & {\rho }^{N}\\ \rho & 1& \rho & \cdots & {\rho }^{N-1}\\ ⋮& ⋮& ⋮& & ⋮\\ {\rho }^{N}& {\rho }^{N-1}& {\rho }^{N-2}& \cdots & 1\end{array}\right] $ | (11) |
其中:ρ表示水平方向和垂直方向上像素值之间的相关性,本文中取0.6[16]。由于参数δp反映的是像素域的标准差,可通过平均绝对差值m近似[17]:
| $ {\delta }_{\mathrm{p}}\approx \sqrt{2}m $ | (12) |
通过结合式(10)和式(12)即可计算出DCT域标准差
由于H.266/VVC编码使用标量量化技术,导致像素经反编码后无法恢复到原始值而引起失真。根据帧内编码原理,位于(i,j)位置处的像素失真d可表示为原始像素值p与重构像素值p΄之差:
| $ \begin{array}{l}d(i, j)=p(i, j)-{p}_{}^{\text{'}}(i, j)=\\ \left[p\right(i, j)-{p}_{\mathrm{p}}(i, j\left)\right]+\left[{p}_{\mathrm{p}}\right(i, j)-{p}_{}^{\text{'}}(i, j\left)\right]=\\ {p}_{\mathrm{e}}(i, j)+\left[{p}_{\mathrm{p}}\right(i, j)-({p}_{\mathrm{p}}(i, j)+{p}_{\mathrm{e}}^{\text{'}}(i, j)\left)\right]=\\ {p}_{\mathrm{e}}(i, j)-{p}_{\mathrm{e}}^{\text{'}}(i, j)\end{array} $ | (13) |
其中:pp表示采用某种帧内预测模式后得到的像素预测值;pe表示原始像素值与预测像素值之差;pe΄表示重构像素值与预测像素值之差。考虑到当前像素与参考像素具有强相关性,且都使用相同的量化参数,因此当前像素的编码失真可以借助参考像素的编码失真d(ri,rj)进行预测:
| $ \begin{array}{l}d(i, j)={p}_{\mathrm{e}}(i, j)-{p}_{\mathrm{e}}^{\text{'}}(i, j)\approx \\ {p}_{\mathrm{e}}(i, j)-\frac{{p}_{\mathrm{e}}(i, j)}{{p}_{\mathrm{e}}({r}_{i}, {r}_{j})}\cdot \left({p}_{\mathrm{p}}\right({r}_{i}, {r}_{j})-d({r}_{i}, {r}_{j}\left)\right)=\\ {p}_{\mathrm{e}}(i, j)\cdot \left[1-\frac{{p}_{\mathrm{p}}({r}_{i}, {r}_{j})-d({r}_{i}, {r}_{j})}{{p}_{\mathrm{e}}({r}_{i}, {r}_{j})}\right]\end{array} $ | (14) |
最终编码块的总失真如下:
| $ {D_{\rm{e}}} \approx \sum\limits_{i,j} d {(i,j)^2} $ | (15) |
失真预测方法不仅考虑了当前块的预测误差,同时间接考虑了标量量化技术的影响,有助于设计准确的帧内预测模式判决方法。
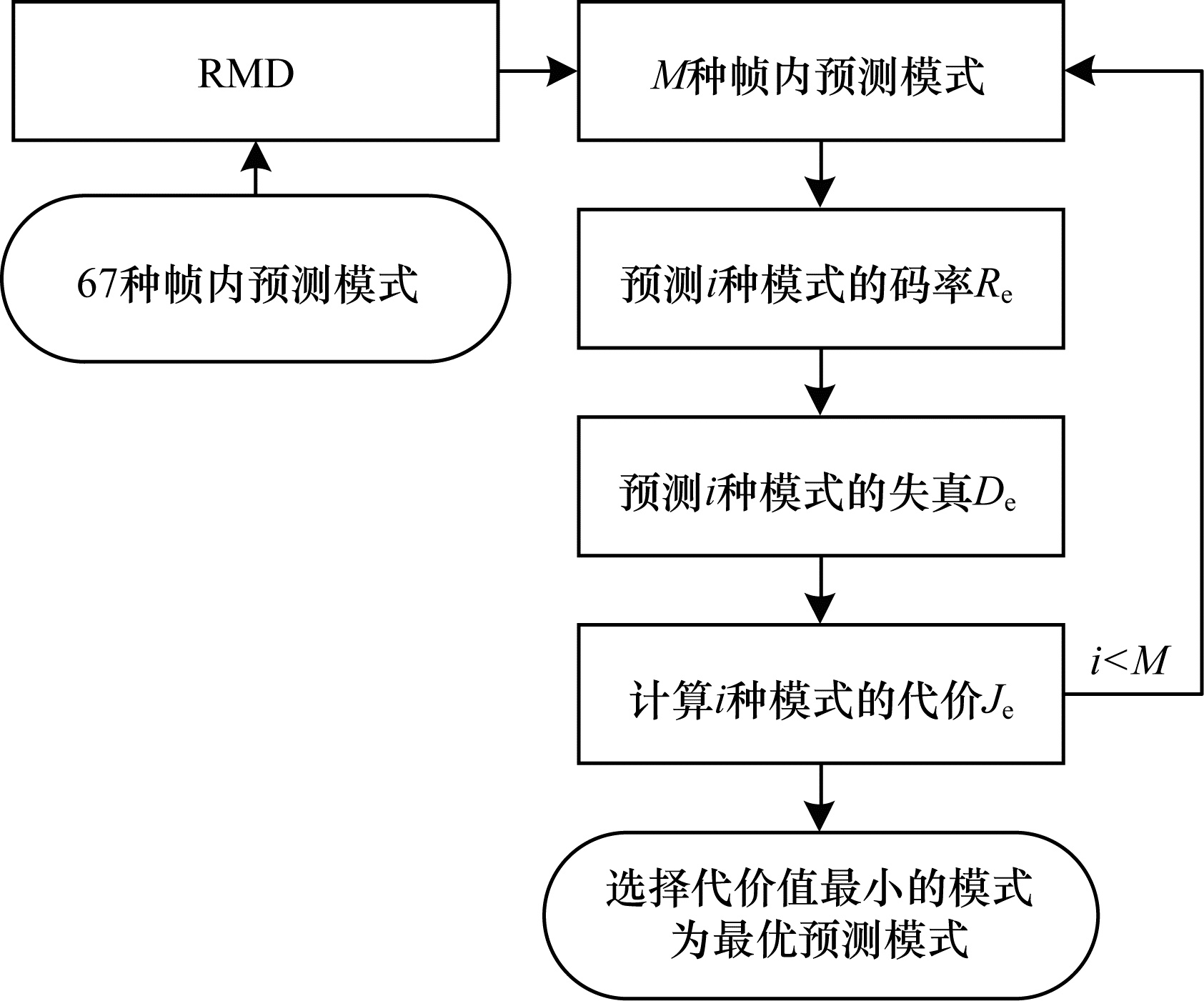
2.4 帧内预测模式判决首先,使用RMD方法从67种帧内预测模式中选择M种最有可能成为最优帧内预测模式的候选模式。然后,分别计算这M种候选模式的编码码率和编码失真,按照式(2)获取每种候选模式的总代价Je,从中选择总代价最小的预测模式作为编码块的最优帧内预测模式。帧内预测模式判决通过利用相邻块信息以及编码块特性,在RMD的基础上跳过H.266/VVC中原有的RDO编码,一方面有利于降低整个帧内预测模式选择的编码时间,另一方面可以最大化保留帧内编码性能。图 4给出了H.266/VVC帧内预测模式快速判决流程。
|
Download:
|
| 图 4 H.266/VVC帧内预测模式快速判决流程 Fig. 4 Fast decision procedure of H.266/VVC intra prediction mode | |
为验证本文方法的性能,将其加入到H.266/VVC原有算法中进行测试。实验硬件平台为Windows10,CPU为1.8 GHz,处理器为Intel Core i7-8550,内存为8.00 GB。在All_Intra配置[18]下使用测试软件平台VTM[19]对标准视频序列进行测试。序列选用JVET提供的不同场景下的Class B、Class C、Class D、Class E视频,其各自对应的分辨率分别为1 920像素×1 080像素、832像素×480像素、416像素×240像素、1 280像素×720像素。编码配置的量化参数分别为22、27、32和37,总编码帧数为200。本文从编码效率和编码复杂度两方面来验证并分析本文方法的编码性能。
3.1 编码效率本文使用相关系数Rc和相对误差Ra来分析码率预测与失真预测的准确性。Ra的计算公式如下:
| $ {R_{\rm{a}}} = \sum\limits_{i,j} {\frac{{|{V_{\rm{e}}}(i,j) - {V_{\rm{a}}}(i,j)|}}{{{V_{\rm{a}}}(i,j)}}} \times 100\% $ | (16) |
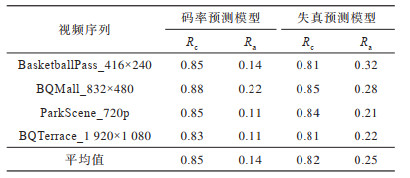
其中:Ra表示真实值Va相对于预测值Ve的偏离程度。表 2给出了码率预测模型和失真预测模型的平均相关系数和相对误差,其中,码率预测模型的平均相关系数和相对误差分别为0.85和0.14,失真预测模型的平均相关系数和相对误差分别为0.82和0.25。可以看出,码率预测模型和失真预测模型的准确度较高,预测值与实际值具有较好的一致性。
|
下载CSV 表 2 码率与失真预测模型的相关系数和相对误差 Table 2 The correlation coefficient and relative error relative to bit rate and distortion prediction model |
本文使用比特率差值ΔR作为评价指标[20]来评价H.266/VVC编码的率失真性能。表 3给出了不同类别序列下本文方法和文献[9]方法与H.266/VVC原始方法的编码性能对比结果。可以看出,本文方法的比特率平均增加了1.53%,文献[9]方法的比特率平均增加了1.71%,表明在保证一定视频质量的情况下,本文方法对编码效率的影响更小,这是因为其从视频序列特性本身以及H.266/VVC的编码原理两方面入手来构建帧内预测模式快速判决方法。

|
下载CSV 表 3 本文方法和文献[9]方法与H.266/VVC原始方法的编码性能对比 Table 3 Comparison of coding performance of the proposed method and Literature [9] method compared with H.266/VVC original method |
本文使用编码时间差ΔT来度量编码复杂度,ΔT的计算公式如下:
| $ \mathrm{\Delta }T=\frac{\left|{T}_{\mathrm{p}}-{T}_{\mathrm{o}}\right|}{{T}_{\mathrm{o}}}\times 100\mathrm{\%} $ | (17) |
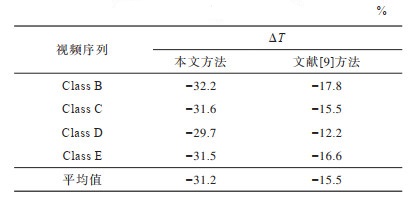
其中:Tp表示本文方法所消耗的编码时间;To表示原始方法所消耗的编码时间。表 4给出了本文方法和文献[9]方法与H.266/VVC原始方法的编码时间对比结果。可以看出,与H.266/VVC原始方法相比,本文方法的编码时间平均降低31.2%,文献[9]的编码时间平均降低15.5%。与文献[9]方法对比,本文对编码复杂度的贡献更大。综合上述结果可知,本文所提的帧内预测模式快速判决方法在最大化编码效率的同时,为H.266/VVC编码器减少了更多的编码时间。
|
下载CSV 表 4 本文方法和文献[9]与H.266/VVC原始方法的编码时间对比 Table 4 Comparison of coding time of the proposed method and Literature [9] method compared with H.266/VVC original method |
在视频编码中,帧内预测模式判决模块是重要的编码模块,也是编码耗时较长的模块。本文针对H.266/VVC帧内预测模式判决中的RDO子模块,提出一种考虑视频内容特性及帧内编码原理的快速帧内预测模式判决方法。利用残差概率分布建立码率预测模型,结合像素域中的上下文信息构建失真预测模型,根据总的率失真代价从候选模式集中确定帧内预测模式。实验结果表明,该方法在对编码效率影响较小的情况下有效降低了编码复杂度。下一步将研究不同特性视频的快速帧内编码方法,以期在降低编码时间的同时进一步提升编码效率。
| [1] |
SULLIVAN G J, OHM J R, HAN W J, et al. Overview of the High Efficiency Video Coding(HEVC) standard[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(12): 1649-1668. DOI:10.1109/TCSVT.2012.2221191 |
| [2] |
CHEN J, SULLIVAN G J, OHM J R. Algorithm description for Versatile Video Coding and Test Model 6(VTM6)[EB/OL]. [2020-06-14]. https://jvet-experts.org/doc_end_user/current_document.php?id=7826.
|
| [3] |
ORTEGA A, RAMCHANDRAN K. Rate-distortion methods for image and video compression[J]. IEEE Signal Processing Magazine, 1998, 15(6): 23-50. DOI:10.1109/79.733495 |
| [4] |
WIEGAND T, GIROD B. Lagrange multiplier selection in hybrid video coder control[C]//Proceedings of 2001 International Conference on Image Processing. Washington D.C., USA: IEEE Press, 2001: 542-545.
|
| [5] |
LI Y, YANG G B, DING X L, et al. Early Merge mode decision algorithm for 3D-HEVC based on learning model[J]. Journal on Communications, 2019, 40(7): 104-113. (in Chinese) 李跃, 杨高波, 丁湘陵, 等. 基于学习模型的3D-HEVC提前Merge模式终止算法[J]. 通信学报, 2019, 40(7): 104-113. |
| [6] |
JAMALI M, COULOMBE S. Fast HEVC intra mode decision based on RDO cost prediction[J]. IEEE Transactions on Broadcasting, 2019, 65(1): 109-122. DOI:10.1109/TBC.2018.2847464 |
| [7] |
TARIQ J. RD-cost as statistical inference for early intra mode decision in HEVC[J]. Multimedia Tools and Applications, 2019, 78(12): 16783-16801. DOI:10.1007/s11042-018-7111-1 |
| [8] |
TARIQ J, ARMGHAN A, IJAZ A, et al. Pure intra mode decision in HEVC using optimized firefly algorithm[J]. Journal of Visual Communication and Image Representation, 2020, 68: 102-166. |
| [9] |
ZOUIDI N, BELGHITH F, KESSENTINI A, et al. Fast intra prediction decision algorithm for the QTBT structure[C]//Proceedings of 2019 IEEE International Conference on Design & Test of Integrated Micro & Nano-Systems. Washington D.C., USA: IEEE Press, 2019: 1-6.
|
| [10] |
FILIPPOV A, RUFITSKIY V. Recent advances in intra prediction for the emerging H. 266/VVC video coding standard[C]//Proceedings of 2019 International Multi-Conference on Engineering, Computer and Information Sciences. Washington D.C., USA: IEEE Press, 2019: 525-530.
|
| [11] |
BROSS B, ANDERSSON K, BLÄSER M, et al. General video coding technology in responses to the joint call for proposals on video compression with capability beyond HEVC[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2019, 30(5): 1226-1240. |
| [12] |
ZHANG L, CHIEN W J, CHEN J L, et al. Multiple direct mode for intra coding[C]//Proceedings of 2017 IEEE Visual Communications and Image Processing. Washington D.C., USA: IEEE Press, 2017: 1-4.
|
| [13] |
BERGER T. Rate distortion theory[M]. [S. l. ]: Prentice Hall Inc., 1971.
|
| [14] |
SUN Y T, LIN Y Y. SATD-based intramode decision for H. 264/AVC video coding[C]//Proceedings of 2008 IEEE International Conference on Multimedia and Expo. Washington D.C., USA: IEEE Press, 2008: 61-64.
|
| [15] |
PARK S Y, MEHER P K. Flexible integer DCT architectures for HEVC[C]//Proceedings of 2013 IEEE International Symposium on Circuits and Systems. Washington D.C., USA: IEEE Press, 2013: 1376-1379.
|
| [16] |
PAO I, SUN M. Modeling DCT coefficients for fast video encoding[J]. IEEE Transactions on Circuits System Video Technology, 1999, 9(4): 608-616. DOI:10.1109/76.767126 |
| [17] |
LI W, ZHAO F, ZHANG E H, et al. Lagrange multiplier selection based on SATD for H.265/HEVC[J]. Journal on Communications, 2017, 38(6): 68-74. (in Chinese) 李维, 赵凡, 张二虎, 等. 基于SATD的H.265/HEVC拉格朗日因子选择算法[J]. 通信学报, 2017, 38(6): 68-74. |
| [18] |
BOSSEN F, BOYCE J, LI X. JVET common test conditions and software reference configurations for SDR video[EB/OL]. [2020-06-14]. https://jvet-experts.org/doc_end_user/current_document.php?id=6643.
|
| [19] |
JEM reference software[EB/OL]. [2020-06-14]. https://vcgit.hhi.fraunhofer.de/jvet/VVCSoftware_VTM.git.
|
| [20] |
HJONTEGAARD G. Calculation of average PSNR differences between RD-curves[EB/OL]. [2020-06-14]. https://www.itu.int/wftp3/av-arch/video-site/0104_Aus/VCEG-M33.doc.
|
 2021, Vol. 47
2021, Vol. 47
