2. 中国科学院自动化研究所 复杂系统管理与控制国家重点实验室, 北京 100190;
3. 澳门科技大学 资讯科技学院, 澳门 999078
2. State Key Laboratory for Management and Control of Complex Systems, Institute of Automation, Chinese Academy of Sciences, Beijing 100190, China;
3. Faculty of Information Technology, Macau University of Science and Technology, Macao 999078, China
开放科学(资源服务)标志码(OSID):
随着深度神经网络性能的提升,网络模型参数量和计算量也日益增长,AlexNet[1]、VGGNet[2]、GoogleNet[3]、ResNet[4]等经典神经网络模型深度不断增加,逐渐超过100层。深层大型模型的部署对计算量和存储资源提出了很高要求,使其难以应用到资源受限的移动和可穿戴设备上,应用受到了很大限制。同时,神经网络中存在很多冗余参数,文献[5]研究表明:神经网络模型中可能只要用5%的网络参数就能预测剩余的参数,甚至只要训练小部分参数就能达到和原网络相近的性能,这证明了神经网络的过度参数化。为降低计算成本,同时保证神经网络模型性能,研究人员提出模型剪枝方法,通过剪除网络模型中不重要的参数,压缩模型的体积和计算量,从而使得神经网络变得轻量化。模型剪枝的核心是对模型参数的重要性进行评价[6-7]。现有的模型剪枝方法多数依据参数自身的信息进行判别,忽略了其他网络层的信息。模型稀疏化是一种有效的模型压缩方法,通过在模型训练过程中对参数的优化过程增加限制条件,使模型的参数稀疏化以获得结构稀疏的网络模型,并且将模型剪枝和模型稀疏化相结合,可以进一步提升模型剪枝准确率和运算效率。
本文受此启发,提出一种基于稀疏正则化的卷积神经网络(Convolutional Neural Network,CNN)模型剪枝方法,利用L1正则化在模型训练中的稀疏化作用,对模型卷积层和BN层参数进行稀疏正则化训练,获得权值稀疏的神经网络模型,再根据滤波器的稀疏性和BN层的特征缩放系数对两者的重要性进行评估,最终利用结构化剪枝方法剪除稀疏滤波器及对应的连接。
1 相关工作模型剪枝是一种主流的模型压缩方法,通过对不重要的神经元、滤波器或者通道进行剪枝,能有效压缩模型的参数量和计算量。文献[8]通过对网络中神经元不断的迭代剪枝得到一个精简的网络模型。文献[9]提出由模型剪枝、参数量化和哈夫曼编码组成的一套完整模型压缩流程,极大减小了模型的体积,且对模型的准确率没造成太大损失。对于神经元的剪枝是非结构化剪枝,需要特殊的硬件设备和工具加以辅助才能有效部署,而针对滤波器与通道的结构化剪枝没有这方面的局限性,剪枝后的模型能直接部署到现有的硬件设备和深度学习架构中,但非结构化剪枝和结构化剪枝都需要对参数重要性进行评价。文献[6]根据模型参数的权重大小确定重要性,将低于设定阈值的参数剪除。文献[7]通过计算各滤波器的几何中位数,将数值相近的滤波器剪除。以上研究根据参数自身信息进行重要性判别,可能会造成偏差。
模型稀疏化是一种提升模型剪枝效果的有效方法。本文使用的稀疏性是指模型参数的部分子集的值为0这一属性,稀疏度是指稀疏参数占模型总参数的比例,较高的稀疏度意味着较低的存储要求。文献[10]通过对滤波器进行稀疏约束,得到权值稀疏的滤波器,加快了模型收敛速度。文献[11]提出一种结构化稀疏学习方法,对深度神经网络的滤波器、通道、滤波器形状和深度结构进行正则化处理,强制深度神经网络学习更加紧凑的结构,但不会降低准确率。文献[12]在深度神经网络中通过高稀疏性降低存储与推理成本,且能在资源受限的环境中部署模型。
研究人员还提出许多解决方案来稀疏化神经网络并保持原始网络准确率,例如在训练过程中使用稀疏表示[13-14]、稀疏性代价函数[15-16]和稀疏正则化[11, 17]。文献[18-20]利用贝叶斯统计和信息论对模型参数的Fisher信息进行估计,得到比已有研究成果更高的压缩率。从计算角度看,由于越来越多的神经网络模型采用ReLU激活函数,而函数在输入为0处的值同为0,值为0的权重在模型运算推理过程中反馈的信息量小,因此被认为重要性低于非0权重,可以将其剪除,文献[21]将神经元的激活值为0的平均比例作为评价神经元重要性的标准,可以精准地剪除冗余的神经元。在稀疏神经网络中包含大量权重为0的神经元,将稀疏神经网络与模型剪枝相结合可以很好地发挥两者的优势。基于权重幅度的剪枝方法具有较高的压缩率且准确率损失很小,而稀疏化的引入可使剪枝方法的准确率得到进一步提升,计算复杂度也大幅降低。
2 基于稀疏正则化的卷积神经网络模型剪枝针对深度神经网络压缩和过度参数化造成的过拟合问题,本文根据卷积层和BN层的权重参数,提出基于稀疏正则化的卷积神经网络模型剪枝方法。
2.1 稀疏正则化训练本文首先通过对模型进行稀疏正则化训练,使得网络部分参数在训练中趋向于0或者等于0,进而获得权重较为稀疏的深度神经网络模型;接着对模型进行剪枝,剪除稀疏的滤波器和通道;最后对模型进行微调,恢复模型准确率。
在神经网络中,卷积层和BN层被广泛使用。在卷积层中,减少滤波器数量能有效降低网络参数量和计算量,同时加速模型的推理速度。在BN层中,每个BN层的特征缩放系数对应每个通道,代表其对应通道的激活程度[22]。BN层的运算公式如式(1)所示:
| $ {Z}_{\mathrm{o}\mathrm{u}\mathrm{t}}=\alpha \frac{{Z}_{\mathrm{i}\mathrm{n}}-{\mu }_{\mathrm{c}}}{\sqrt[]{{\sigma }_{c}+\epsilon }}+\beta $ | (1) |
其中:
L1正则化对神经网络的稀疏作用已被证明并得到广泛使用[23-24]。本文在损失函数中添加惩罚因子,对卷积层的权重与BN层的缩放系数进行约束,并将模型稀疏化,正则化系数
| $ \delta =\lambda R\left(W\right) $ | (2) |
其中:
损失函数如式(3)所示:
| $ {L}^{\text{'}}=L+\lambda R\left(W\right) $ | (3) |
其中:L为原损失函数;
在训练过程中,求
| $ \frac{\partial R\left(W\right)}{\partial \left(W\right)}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(W\right) $ | (4) |
其中:
通过式(5)对权重
| $ {g}_{W}^{\text{'}}={g}_{W}+\lambda \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(W\right) $ | (5) |
其中:
目标函数
| $ \frac{\partial {L}^{\text{'}}}{\partial \left(W\right)}=\frac{\partial L}{\partial \left(W\right)}+\lambda \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(W\right) $ | (6) |
本文对卷积神经网络的滤波器和BN层进行稀疏正则化训练,并对稀疏通道和稀疏滤波器进行剪枝操作,这些通道和滤波器因为本身的稀疏性而不会对模型整体造成较大的损失,所以可以安全剪除。
2.2 剪枝和微调通过稀疏正则化训练后得到含有较多稀疏权重的模型,其中许多权重都接近于0,利用式(7)求滤波器权重绝对值的和,获得滤波器的整体权值信息,权值大小是体现重要性的一部分。
| $ {E}_{x}=\sum\limits _{j}^{k}R\left({W}_{j}\right) $ | (7) |
其中:
结合缩放系数
| $ {m}_{i}={\alpha }_{i}\times {E}_{i} $ | (8) |
其中:
通过式(8)获得网络整体的滤波器评分集
| $ \theta =\mathrm{s}\mathrm{o}\mathrm{r}{\mathrm{t}}_{P}\left(M\right) $ | (9) |
其中:
剪枝率P根据剪枝的模型不同进行选择,例如VGG-16模型设定的剪枝率为70%,通过式(9)获得评分在M集中70%处的值作为剪枝阈值
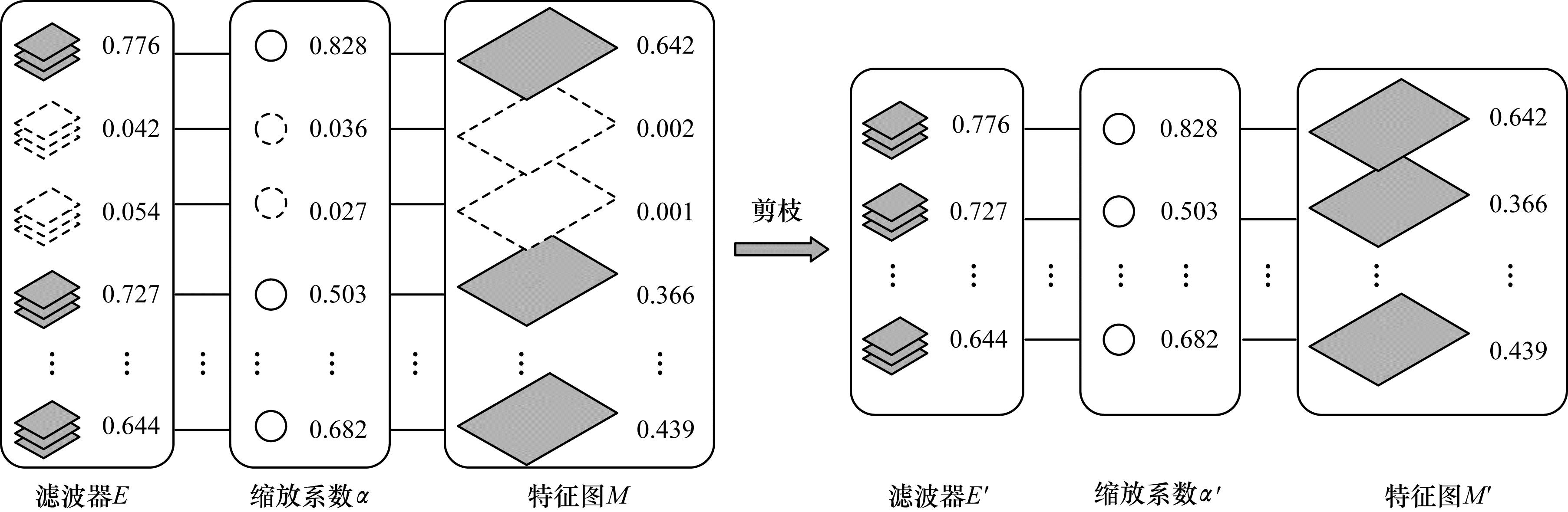
|
Download:
|
| 图 1 基于稀疏正则化的卷积神经网络模型剪枝流程 Fig. 1 Pruning procedure of convolutional neural network model based on sparse regularization | |
为验证模型剪枝方法的效果,基于Pytorch框架,在VGGNet[2]、ResNet[25]和DenseNet[26]模型上进行实验验证。
3.1 实验设定本文采用随机梯度下降(Stochastic Gradient Descent,SGD)方法进行模型训练,设置训练100个回合,学习率为0.1,并在进行到1/2至3/4的回合时学习率衰减为原来的1/10。在进行稀疏正则化训练时,正则化系数
稀疏化训练完成后对模型进行剪枝,分别根据式(7)和式(8)对模型的滤波器和BN层的权重进行综合判别,通过式(9)按预定的剪枝率将不重要的部分剪除,因为剪枝的是模型稀疏的部分,所以对模型的性能没有较大影响,且可以通过微调恢复模型的准确率,微调的步数为40或80步,微调的学习率为0.001。
3.2 不同数据集上的对比结果为对比模型剪枝前后的性能变化,本文在数据集上选用标准的CIFAR-10、CIFAR-100数据集和SVHN数据集。CIFAR-10是深度学习领域常用的图片数据集,该数据集分为10个类别,每个类别6 000张图像,共有60 000张彩色图像,图像大小为32×32,训练集包含50 000张图像,测试集包含10 000张图像。CIFAR-100是CIFAR-10数据集的一个衍生数据集,区别是CIFAR-100数据集包含100个类别,每个类别有600张图像,因此CIFAR-100数据集比CIFAR-10数据集对模型的分类性能要求更加严格。SVHN是街景门牌号数据集,由图像大小为32×32的彩色图片组成,每张图片包含一组阿拉伯数字,训练集包含73 257个数字,测试集包含26 032个数字。
在3个数据集上的测试结果如表 1~表 3所示,其中:准确率为Top-5准确率,表示模型输出的排名前5个种类中包含正确结果的准确率;FLOPs为浮点运算量,用来衡量模型的计算复杂度,FLOPs越低说明模型实际运算所需的计算量越少,模型加速效果越好;参数量是神经网络占用的内存大小量,参数量的变化可以直接体现模型压缩的效果。
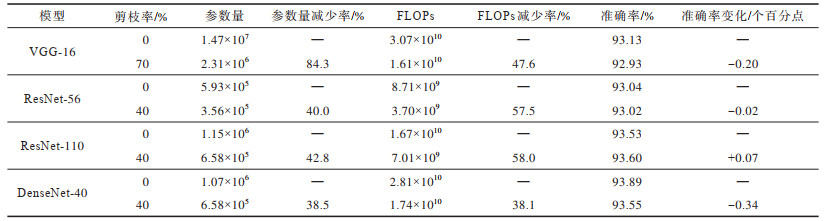
|
下载CSV 表 1 在数据集CIFAR-10上的Top5准确率测试结果 Table 1 The test results of Top5 accuracy on CIFAR-10 dataset |
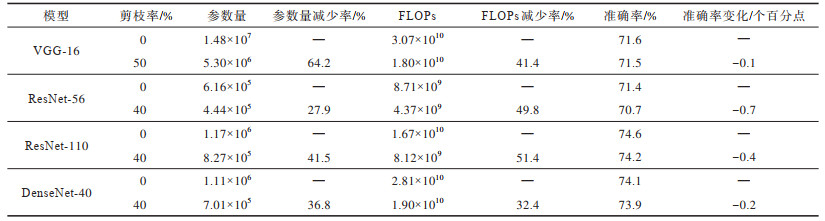
|
下载CSV 表 2 在数据集CIFAR-100上的Top5准确率测试结果 Table 2 The test results of Top5 accuracy on CIFAR-100 dataset |
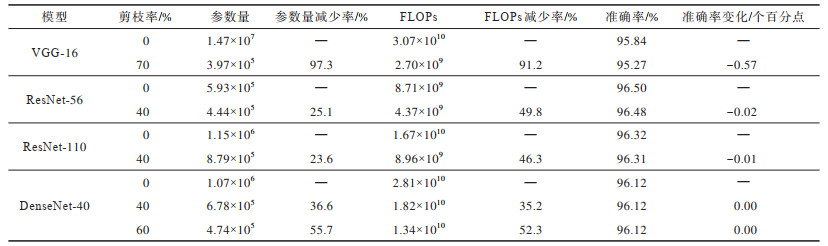
|
下载CSV 表 3 在数据集SVHN上的Top5准确率测试结果 Table 3 The test results of Top5 accuracy on SVHN dataset |
实验对VGG-16采用50%或70%的剪枝率,对ResNet-56、ResNet-110与DenseNet-40采用40%或60%的剪枝率,可以看出经过本文剪枝方法,网络的参数量和FLOPs都得到了压缩,但网络性能却没有受到影响。在进行大比率剪枝后,在SVHN数据集上,VGG-16和DenseNet-40的参数量分别压缩了97.3%和55.7%,而模型准确率没有大幅下降,进一步证明原有模型的过度参数化,并且验证了本文剪枝方法的有效性。
3.3 不同正则化系数对模型训练的影响在模型训练过程中,正则化系数
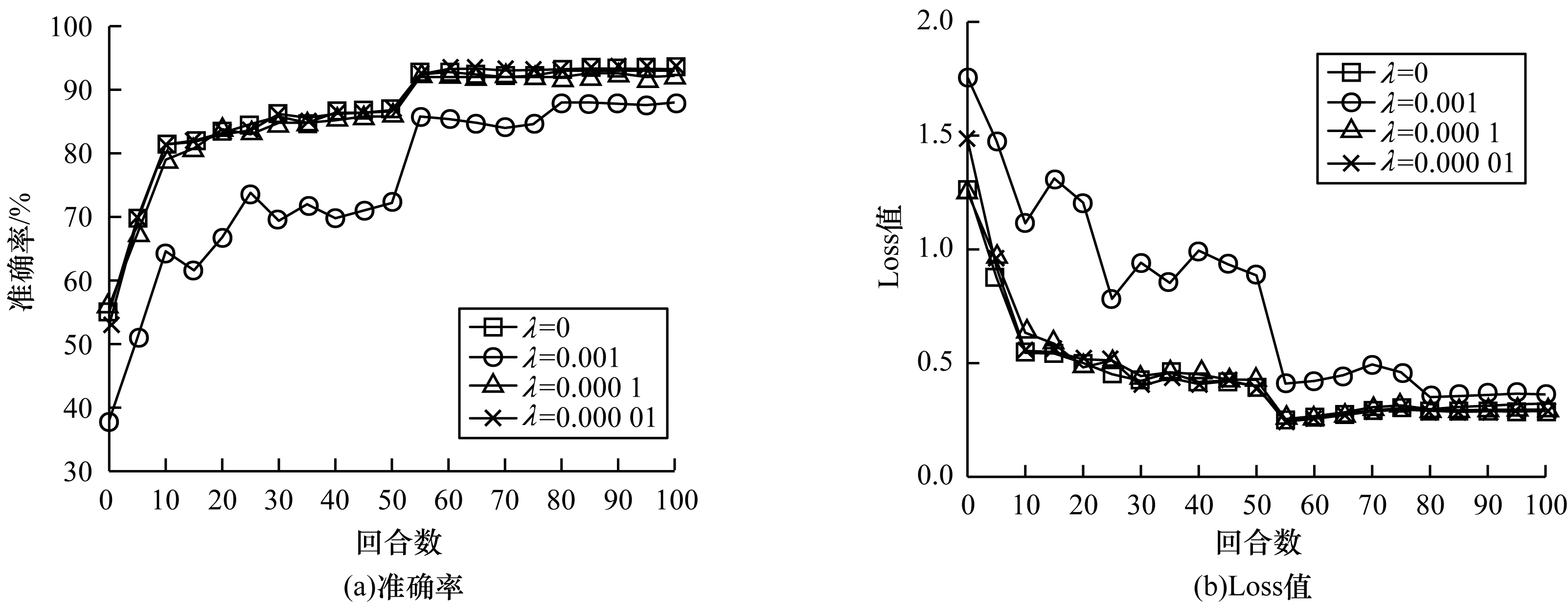
在不同正则化系数下,研究VGG-16网络准确率变化,设置的正则化系数分别为0、0.001、0.000 1、0.000 01,对模型的Loss值和准确率的变化情况进行统计,每个模型训练100个回合,学习率为0.1,并在进行到1/2至3/4的回合时,学习率下降为原来的1/10。Loss值是损失函数的输出值,Loss值越低,模型拟合情况越好。准确率是模型在数据集上的准确率,准确率越高,模型性能越好。实验结果如图 2所示,当正则化系数
|
Download:
|
| 图 2 不同正则化系数对模型训练效果的影响 Fig. 2 The influence of different regularization coefficients on model training effect | |
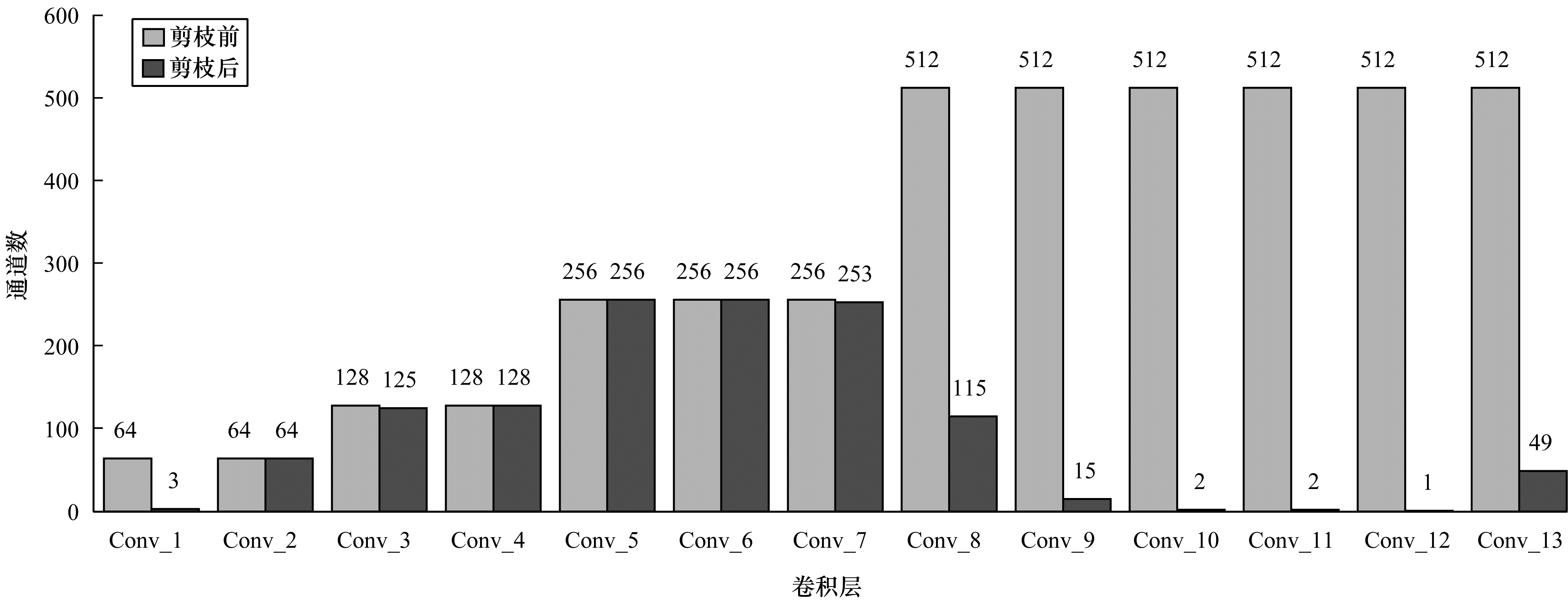
在CIFAR-10数据集上训练的VGG-16在剪枝前(准确率93.13%)和剪枝后(准确率92.93%)的各卷积层通道数对比如图 3所示,可以看出剪枝操作主要发生在网络的开始和最后几层,而中间层的参数在剪枝后会有所保留,模型参数量压缩了84.3%,而准确率仅降低了0.2个百分点,结果表明,模型大部分的冗余参数集中在深层网络中。通过图 3还可以看出,在模型剪枝后,模型结构呈现中间宽、两端窄的特点,表明依靠中间层的参数就能达到与剪枝前的模型相同的性能,同时可将本文剪枝方法看作网络结构搜索方法,通过去除冗余参数,发现有效的网络结构,这与文献[27]中提出的结论一致,并且能与其他网络结构搜索方法相结合,获得更有效的网络结构。
|
Download:
|
| 图 3 VGG-16在剪枝前后的卷积层通道数对比 Fig. 3 Comparison of the number of channels in the convolutional layer of VGG-16 before and after pruning | |
本文提出一种基于稀疏正则化的卷积神经网络模型剪枝方法,通过在训练过程中对卷积层和BN层的权重进行正则化约束,使得权重变得稀疏,再结合双层的稀疏信息对滤波器的重要性进行评估,选取冗余的滤波器进行剪枝。实验结果表明,该剪枝方法可有效压缩模型参数,且压缩后的网络模型仍能保持良好性能,尤其在SVHN数据集上,ResNet和DenseNet网络模型性能几乎没有影响,VGG网络模型参数量在压缩了97.3%的情况下,图像分类准确率仅降低0.57个百分点。同时,本文剪枝方法训练成本较小,无需特殊的硬件辅助即可完成模型部署。后续可将模型剪枝方法与网络结构量化、搜索等模型压缩方法相结合,进一步压缩和加速神经网络模型。
| [1] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [2] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1409.1556.
|
| [3] |
SZEGEDY C, LIU W, JIA Y Q, et al. Going deeper with convolutions[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2015: 1-9.
|
| [4] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2016: 770-778.
|
| [5] |
DENIL M, SHAKIBI B, DINH L, et al. Predicting parameters in deep learning[EB/OL]. [2020-07-14]. http://export.arxiv.org/pdf/1306.0543.
|
| [6] |
LI H, KADAV A, DURDANOVIC I, et al. Pruning filters for efficient ConvNets[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1608.08710.
|
| [7] |
HE Y, LIU P, WANG Z W, et al. Filter pruning via geometric Median for deep convolutional neural networks acceleration[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEEPress, 2019: 1-8.
|
| [8] |
HAN S, POOL J, TRAN J, et al. Learning both weights and connections for efficient neural network[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems. New York, USA: ACM Press, 2015: 1135-1143.
|
| [9] |
HAN S, MAO H, DALLY W J. Deep compression: compressing deep neural networks with pruning, trained quantization and Huffman coding[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1510.00149.
|
| [10] |
YE H J, LIU X Y. Research and application of convolutional neural network based on sparse convolution kernel[J]. Information Technology, 2017, 41(10): 5-9. (in Chinese) 叶会娟, 刘向阳. 基于稀疏卷积核的卷积神经网络研究及其应用[J]. 信息技术, 2017, 41(10): 5-9. |
| [11] |
WEN W, WU C P, WANG Y D, et al. Learning structured sparsity in deep neural networks[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1608.03665.
|
| [12] |
CHANGPINYO S, SANDLER M, ZHMOGINOV A. The power of sparsity in convolutional neural networks[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1702.06257.
|
| [13] |
RANZATO M A, POULTNEY C, CHOPRA S, et al. Efficient learning of sparse representations with an energy-based model[C]//Proceedings of NIPS'07. New York, USA: ACMPress, 2007: 1137-1144.
|
| [14] |
LEE H, EKANADHAM C, NG A Y. Sparse deep belief net model for visual area V2[C]//Proceedings of the 20th International Conference on Neural Information Processing Systems. NewYork, USA: ACM Press, 2008: 873-880.
|
| [15] |
RANZATO M A, BOUREAU Y L, LECUN Y. Sparse feature learning for deep belief networks[C]//Proceedings of NIPS'07. New York, USA: ACM Press, 2007: 1185-1192.
|
| [16] |
LEE H, BATTLE A, RAINA R, et al. Efficient sparse coding algorithms[C]//Proceedings of NIPS'07. New York, USA: ACM Press, 2007: 801-808.
|
| [17] |
MAO H Z, HAN S, POOL J, et al. Exploring the regularity of sparse structure in convolutional neural networks[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1705.08922.
|
| [18] |
DAI B, ZHU C, WIPF D. Compressing neural networks using the variational information bottleneck[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1802.10399.
|
| [19] |
LOUIZOS C, WELLING M, KINGMA D P. Learning sparse neural networks through L0 regularization[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1712.01312.
|
| [20] |
THEIS L, KORSHUNOVA I, TEJANI A, et al. Faster gaze prediction with dense networks and Fisher pruning[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1801.05787.
|
| [21] |
HU H Y, PENG R, TAI Y W, et al. Network trimming: a data-driven neuron pruning approach towards efficient deep architectures[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1607.03250v1.
|
| [22] |
LU H W, XIA H F, YUAN X T. Dynamic network pruning via filter attention mechanism and feature scaling factor[J]. Journal of Chinese Computer Systems, 2019, 40(9): 1832-1838. (in Chinese) 卢海伟, 夏海峰, 袁晓彤. 基于滤波器注意力机制与特征缩放系数的动态网络剪枝[J]. 小型微型计算机系统, 2019, 40(9): 1832-1838. DOI:10.3969/j.issn.1000-1220.2019.09.005 |
| [23] |
LIU Z, LI J G, SHEN Z Q, et al. Learning efficient convolutional networks through network slimming[C]//Proceedings of2017 IEEE International Conference on Computer Vision. Washington D.C., USA: IEEE Press, 2017: 2755-2763.
|
| [24] |
SCARDAPANE S, COMMINIELLO D, HUSSAIN A, et al. Group sparse regularization for deep neural networks[J]. Neurocomputing, 2017, 241: 81-89. DOI:10.1016/j.neucom.2017.02.029 |
| [25] |
HE K M, ZHANG X Y, REN S Q, et al. Identity mappings in deep residual networks[C]//Proceedings of European Conference on Computer Vision. Berlin, Germany: Springer, 2016: 630-645.
|
| [26] |
HUANG G, LIU Z, VAN DER MAATEN L, et al. Densely connected convolutional networks[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEEPress, 2017: 2261-2269.
|
| [27] |
LIU Z, SUN M J, ZHOU T H, et al. Rethinking the value of network pruning[EB/OL]. [2020-07-14]. https://arxiv.org/abs/1810.05270v2.
|
 2021, Vol. 47
2021, Vol. 47
