2. 中国人民解放军94162部队, 西安 710600;
3. 中国人民解放军78100部队, 成都 610031
2. 94162 Troops of PLA, Xi'an 710600, China;
3. 78100 Troops of PLA, Chengdu 610031, China
开放科学(资源服务)标志码(OSID):
近年来,深度学习(Deep Learning,DL)技术不断发展,凭借深度神经网络优异的特征表示能力,解决了许多学术界和工业界的难题并取得了重要的研究成果。强化学习(Reinforcement Learning,RL)作为解决序列决策的重要方法,赋予智能体自监督学习能力,能够自主与环境进行交互,通过获得的奖励不断修正策略。深度神经网络的引入,使得强化学习取得了很大的进步并衍生出深度强化学习(Deep Reinforcement Learning,DRL)。
深度强化学习近几年在各领域相继取得重大突破。在游戏领域:Atari系列视频游戏中的智能体使用DRL算法直接学习图像像素,表现超越了人类水平;DeepMind公司开发的AlphaGo[1]战胜了顶尖人类棋手,最终版的AlphaZero[2]更是经过自学习的方式,战胜了AlphaGo;腾讯AI Lab开发的绝悟AI在《王者荣耀》游戏中击败顶尖人类选手[3],又在Kaggle的足球AI比赛中获得冠军[4];Open AI的AlphaStar[5]在《星际争霸2》游戏中以5∶0战胜了职业选手,展现了AI在多智能体、复杂状态动作空间中的优秀表现。在商业领域:Facebook开源了Horizon强化学习平台,用于开发和部署基于DRL的推荐系统;阿里在双十一活动中,使用深度强化学习来提高用户点击率;Sliver提出使用深度强化学习构建针对客户交互的系统[6]。在控制领域,目前已经可以利用DRL方法实现从现实世界摄像机输入中学习机器人的控制策略[7-8],例如斯坦福大学使用DRL方法实现对直升机的控制完成特技飞行,达到了人类同等水平。
本文介绍深度强化学习的发展历程,结合当前深度强化学习的研究进展,按照研究目标将DRL方法分为解决高维状态动作空间任务上的算法收敛、复杂应用场景下的算法样本效率提高、奖励函数稀疏或难以定义情况下的算法探索以及多任务场景下的算法泛化能力增强问题4类,并对DRL方法的未来发展方向进行展望。
1 深度强化学习深度强化学习是深度学习和强化学习的结合,深度学习[9]使用表示学习对数据进行提炼,不需要选择特征、压缩维度、转换格式等数据处理方式,拥有比传统机器学习方法更强的特征表示能力,通过组合低层特征形成更加抽象的高层特征,实现数据的分布表示。强化学习[10]起源于控制论中的最优控制理论,主要用来解决时序决策问题,通过不断与环境的交互和试错,最终得到特定任务的最优策略并使得任务累计期望收益最大化。
传统强化学习的主流方法主要包含蒙特卡洛类方法和时序差分类方法[11-12],前者是无偏估计,方差较大,后者使用有限步数自举法,方差较小,但会引入偏差。实验验证表明,上述方法在高维状态动作空间任务上效果不理想,甚至算法难以收敛。原因在于上述方法需要先进行策略评估,得到状态价值函数或动作价值函数信息,再利用值函数信息改善当前的策略。算法使用表格型强化学习方法对值函数进行评估,建立一个表格,对于状态价值函数,索引是状态,对于动作价值函数,索引是状态行为对。值函数的迭代更新就是这个表中数据的更新。对于高维状态动作空间任务,表格法难以对所有状态动作对应的值函数进行评估处理。
为解决表格法在处理高维状态动作空间任务时产生的维度灾难问题,研究人员提出使用函数逼近的方法进行预测,利用参数化的方法对于值函数进行近似,近似的价值函数不再表示成一个表格,而是一个具有权值向量的参数化函数,通过调整权值可以得到不同的函数。根据逼近的方法不同,可以分为线性逼近方法和非线性逼近方法。线性逼近方法包括多项式基、傅里叶基[13]、粗编码、瓦片编码等方法,优点在于可以收敛到全局最优,缺点在于表示能力有限。由于基函数是固定的,对于复杂的函数,数量太少且形式固定的基函数无法得到较好的逼近效果。非线性逼近方法表现力较强,包括核函数逼近[14]、基于记忆的函数逼近[15]等方法,相比线性逼近方法有了很大进步,但是实验结果表明对于复杂任务的性能表现仍然不好。直到深度学习的出现,结合了深度神经网络的强化学习实现了算法效能的大幅提升。
深度强化学习结合了深度学习的结构和强化学习的思想,用于解决决策问题。借助深度神经网络强大的表征能力去拟合强化学习的任何组成部分,包括状态价值函数、动作价值函数、策略、模型等,将深度神经网络中的权重作为拟合参数。DRL主要用于解决高维状态动作空间任务,集成了深度学习在特征表示问题上强大的理解能力以及强化学习的决策能力,实现了端到端学习。深度强化学习的出现使得强化学习技术真正走向实用,得以解决现实场景中的复杂问题。最具代表的DQN算法[16]是在Atari系列视频游戏中被提出,通过端到端的方法直接从图像像素中进行学习,并取得了超过人类选手的成绩,至此深度强化学习开始蓬勃发展。
2 高维状态动作空间任务上的算法收敛问题传统的强化学习方法由于使用表格法进行价值函数评估,对于高维状态动作空间任务表现不佳。DRL方法利用深度神经网络优异的特征表示能力,可以对不同状态、动作下的价值函数进行拟合。根据优化过程中动作选取方式的不同,又可以分为值函数算法(基于价值的算法)和策略梯度(Policy Gradient,PG)算法(基于概率的算法)。策略梯度算法使策略参数化,将神经网络的权重参数作为价值函数的参数,能通过分析所处的状态,直接输出下一步要采取的各种动作的概率,然后根据概率采取行动,每种动作都有相应的概率被选中。值函数算法输出所有动作的价值,然后根据最高价值来选择动作,相比策略梯度算法,基于价值的决策更为准确,只选价值最高的决策,而基于概率的决策则会为每一个可能的动作分配一个对应的概率值。
2.1 值函数算法值函数算法利用神经网络拟合不同状态-动作组合的价值函数,深度神经网络强大的特征提取和泛化能力使得智能体在面对未遇到的状态、动作组合时,仍然可以较为准确地进行价值函数预测。但由于值函数算法架构设计原因,对于高维动作空间或连续动作空间任务学习效果不理想。
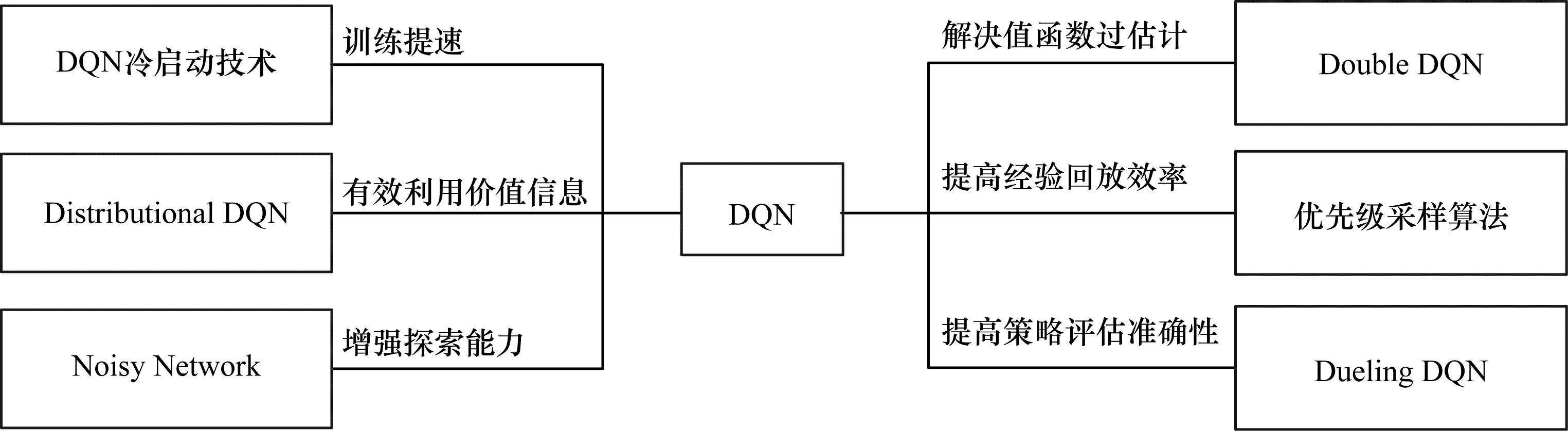
DQN[16]作为重要的值函数算法,使用深度学习模型直接从高维感官输入中学习控制策略,利用深度卷积神经网络逼近值函数,并结合经验回放及目标网络,极大地提高了价值函数的估计精度和稳定性,并打破了数据间的关联性。实验结果证明,在Atari系列游戏中,DQN算法在43项游戏中都取得了超过当时最佳强化学习方法的性能表现,同时在49项游戏中达到或超过了人类顶尖选手的水平,其中有29项游戏得分超过75%人类选手的得分。但是,在《蒙特祖玛的复仇》等奖励函数稀疏的游戏中表现不佳。DQN算法作为DRL中值函数算法的典型代表,后续基于其不断进行迭代改进,产生了许多重要算法,提升了DRL值函数算法的实用性,如图 1所示。
|
Download:
|
| 图 1 DQN算法的改进 Fig. 1 Improvement of DQN algorithm | |
过估计是DQN的一大缺陷,使得估计的值函数比真实值函数要大,并且这种过估计的影响会累积,导致所有价值函数估计不准确,从而影响最优策略的学习。为了解决DQN过估计的问题,Double DQN[17]将动作选择与值函数评估解耦,有效减少过估计,使得算法更加健壮,对于Atari系列游戏的得分相比DQN提高了接近1倍。但是,Double DQN容易受到噪声的干扰,从而影响收敛性能。优先级采样算法[18]创新地将TD偏差作为重要性考量,确保可以优先重放学习重要的经验,大幅提高了DQN学习效率,应用于Atari系列游戏后,使得其中49项游戏得分相比单纯使用DQN算法获得了48%到106%不等的性能提升。Dueling DQN算法[19]解耦价值函数和优势函数的学习网络,提高了对于动作价值函数的预测准确性,并且由于通用性强可以与其他算法相结合。为解决DQN算法前期值预测函数偏差较大,导致训练初期速度慢的问题,研究人员提出DQN冷启动技术[20],将RL与监督学习相结合,利用预先准备好的优质采样轨迹加快模型前期的训练速度,而该技术的局限性在于过度依赖用于监督学习的经验轨迹,如果轨迹存在噪声或样本过少将会导致算法无法收敛或产生过拟合。
鉴于DQN算法预测的目标值都是一个动作价值函数的期望值,所能提供的信息量过少,Distributional DQN算法C51[21]构建模型使得输出为一个价值的分布估计以获得相比期望值更多的信息,对于部分可观察马尔科夫过程(POMDP),避免了价值函数的混淆,最重要的是该算法保留了价值分布的多模态,使得学习更加稳定,缺点在于C51在理论上无法保证策略评估过程下,贝尔曼算子在多轮迭代后结果可以收敛,同时也无法保证当所表示的概率分布和样本集上距离最小时,与真实分布距离也最小。QR-DQN[22]不仅具有以上算法的优点,而且可确保多轮迭代后贝尔曼算子收敛,并减少了超参数的设置,但QR-DQN对于任务风险不敏感,在高风险任务中表现不佳。IQN[23]通过调节神经网络容量,调整拟合精度,设置超参数,决定风险偏好。为了增强DQN的探索能力,使得智能体可以有效探索未知状态动作对,评估其动作价值函数,研究人员设计Noisy Network[24],使用更加平滑的添加噪声的方式替代传统的ε-greedy方法,使智能体具有更强的探索能力,同时较好地平衡噪声效果和参数数量并保证目标函数无偏。Rainbow算法[25]集成了上述所有算法的优点,实验结果表明,Rainbow算法远超DQN算法,在Atari系列游戏中表现超过人类选手,相比DQN算法性能提升了3倍,相比double DQN算法提升了2倍。分析并研究这些改进算法对于DQN的优化程度,优先级采样算法是对于DQN改进效果最显著的算法。
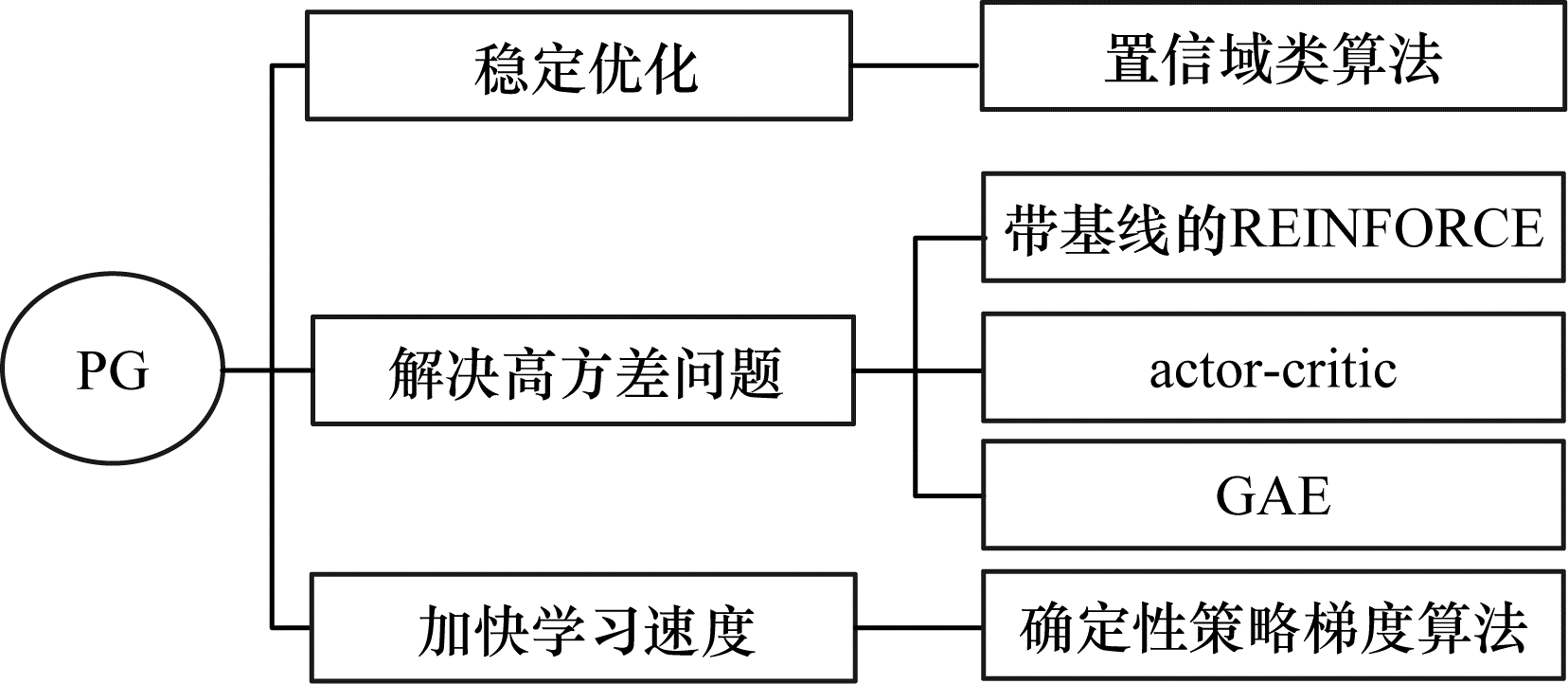
2.2 策略梯度算法对于离散型动作空间,神经网络拟合的是一个离散型分布,即执行每种动作的概率。对于连续型动作空间,神经网络拟合概率密度函数的参数,这就使得策略梯度算法可以很好地处理高维或者连续动作空间的任务,通过优化参数,直接对策略进行更新迭代,使得累积期望回报最大。相比值函数算法,策略梯度算法更简单、收敛性也更好,缺点在于算法方差较高、收敛速度较慢、学习步长不容易确定,针对以上不足,近年来研究人员提出多种改进思路,如图 2所示。
|
Download:
|
| 图 2 策略梯度算法的改进 Fig. 2 Improvement of policy gradient algorithm | |
原始的策略梯度算法将策略参数化,通过采样一系列轨迹之后,使用策略梯度定理求得参数增量,对参数进行更新。该算法虽然无偏但是方差很大,所以带有基线的REINFORCE算法[26]对此进行了改进,引入当前时刻的状态价值函数作为基线,减小方差,同时仍然可以保证无偏。但是,REINFORCE算法中状态价值函数仅作为基线函数,不具备判定器功能,所以方差依旧很大。为进一步减小方差,研究人员提出了使用自举法的actor-critic算法[27],使得状态价值函数不仅用作基线,而且可作为判定器,用于自举法进行价值预测,大幅降低了方差,并且是完全在线和增量式的,缺点在于引入了偏差。REINFORCE和actor-critic算法分别使用蒙特卡洛法和单步时序差分法估计误差,前者方差很大,但是没有偏差,后者偏差较大,但是方差很小。两者都过于极端,为了更好地调和方差和偏差,研究人员提出了GAE(Generalized Advantage Estimation)算法[28],该算法是一种新的奖励函数设计算法,通过调节超参数可以平衡收益的方差、偏差带来的影响,广泛应用于各种策略梯度法的奖励设计中,缺陷在于为了得到合适的奖励函数形式,需要对超参数进行精确调整。
为解决策略梯度算法难以确定学习步长的问题,需要找到使损失函数单调非增的最优步长,因此研究人员提出置信域类算法。TRPO算法[29]引入KL散度表示新旧策略之间的差距大小,最终可以求解得到一个置信区域内能够使策略单调提升的最大步长。TRPO减少了训练时的波动,使得策略单调稳步提升。为了解决TRPO存在的计算量较大、速度较慢、实现复杂问题,PPO算法[30]创新地使用Clipped替代函数,缩小新旧策略的差距,保证形式简洁。该算法有效降低了实现难度,提升了求解效率,同时依然保证策略单调稳步提升。ACKTR算法[31]优化置信域类算法并结合克罗内克曲率应用于RL,可大幅减少计算量,使该类算法能够用于大型模型,但是样本效率较低。
为加快策略梯度算法的学习速率,研究人员提出确定性策略梯度算法,相比随机策略梯度算法,一个状态只对应一个动作,在参数更新梯度计算时,可在最大限度上加快计算速度,减少数据空间和对于样本的依赖,同时使用离线学习(off-policy)方法弥补探索性差的问题。该类算法需要采样的数据少,算法效率高,无须在动作空间中进行数据采样。DPG[32]是最早的确定性策略梯度算法,但DPG中使用的仍是线性函数近似器,因此性能较差。DDPG[33]对DPG做了改进,使用actor-critic架构,通过神经网络代替线性函数进行值函数预测,同时引入DQN的相关优势方法大大提升了DPG算法的效能,解决了端到端的策略学习,并且拥有更高的采样效率。为解决DDPG对于Q值的高估,并且在超参数和其他参数调整方面存在脆弱性的问题,FUJIMOTO等[34]提出TD3算法,可缓解动作价值高估的影响,并消除方差累计问题,使得训练过程波动较小,同时避免了DDPG中可能发生的特性故障,但是TD3参数较多,使用者需要有较好的调参功底。
3 复杂应用场景下的算法样本效率提高问题样本效率低是DRL的主要缺陷,为解决该问题,具体思路为:对于无模型类方法使用off-policy学习;对于model-based方法进行策略学习,本节将对两种方法进行具体分析。
3.1 在线学习方法在线学习(on-policy)和off-policy的分类是依据产生数据的策略(行动策略)和正在通过训练来优化的策略(目标策略)是否一致。对于on-policy而言,行为策略和目标策略是一致的;对于off-policy而言,使用行动策略产生样本,存入经验池,然后使用重要性采样手段将样本作用于优化目标策略。智能体在面对一个陌生的环境时,希望学到的动作可以使随后的智能体行为是最优的,但是为了搜索所有动作,以保证找到最优动作,需要采取非最优的行动,因此在遵循试探策略采取行动的同时学习到最优策略中产生了矛盾。
on-policy方法不学习最优策略的动作值,而是学习一个接近最优而且仍能进行探索的策略的动作值。off-policy更加直接,使用多个策略,一个用来学习并最终成为最优策略,另外的策略更具试探性,用来产生智能体的行为样本。离线方法通过重放不同策略的采样经验来优化目标策略,不仅提高了样本效率,也降低了样本复杂度,这种思路已经广泛应用于各种算法,DQN算法以及确定性策略梯度算法都属于off-policy方法。
Retrace算法[35]定义了一种新的重要性采样算法,可避免方差爆炸问题,同时保证策略改进的安全性,并且有更强的收敛性。ACER算法[36]利用Retrace思想,融合对抗性网络结构和置信域优化方法,在对策略进行有效优化的同时,提高了样本效率。但在复杂任务中,ACER并没有表现出很好的效果,为进一步提高在复杂任务中的采样效率和训练效果,SAC算法[37]创新地引入了energy-based模型,将熵的概念融入到策略改进中。与其他离线方法相比,该算法更稳定,对于环境探索更积极,采样效率明显优于DDPG。实验结果表明,SAC在复杂任务上优于DDPG、PPO、TD3等算法,并且减少了超参数数量。同时,基于off-policy可建立并行架构,更高效地收集经验样本,提高学习速度。A3C算法[38]使用一个多核CPU实现快速的DRL训练,使多个智能体并行地在线程中收集经验样本,并异步地将参数更新到全局的模型参数中。该算法极大提升了样本多样性,使得学习得到的策略更加鲁棒,但是A3C使用异步方式进行更新,由于策略不同,可能会导致主网络累计更新效果不是最优。基于A3C算法,改进得到的同步版本A2C算法[39]与A3C差别在于各个环境中智能体仅负责收集经验数据,然后同步地将经验传到主网络统一进行计算,更新参数。A2C可使训练更加协调一致,从而加快收敛。实验结果证明,A2C相比A3C对于硬件利用率更高,对于相同任务的性能更好,但由于A2C在经验收集和策略学习步骤上仍然是串行的,因此效率仍然有提升的空间。IMPALA算法[40]是一种大规模强化学习训练算法,融合了A3C的结构和A2C的思想。IMPALA将经验收集和策略学习分开异步运行,并使用V-trace对off-policy偏差进行纠正,极大地提高了算法速率、数据效率和稳定性。凭借优化的模型,与传统agent相比,IMPALA可多处理一到两个数量级的经验,并且可推广至超大规模实验。APE-X算法[41]属于分布式架构,在DQN经验回放的基础上进行改进,结构没有变化,但分布式使用多个actor来生成数据,拥有更大的经验回放池,能容纳数百个actor采集的数据,大幅加快了训练速度。同时,通过不同的并行环境得到不同优先级的经验回放,提升样本多样性,防止过拟合。
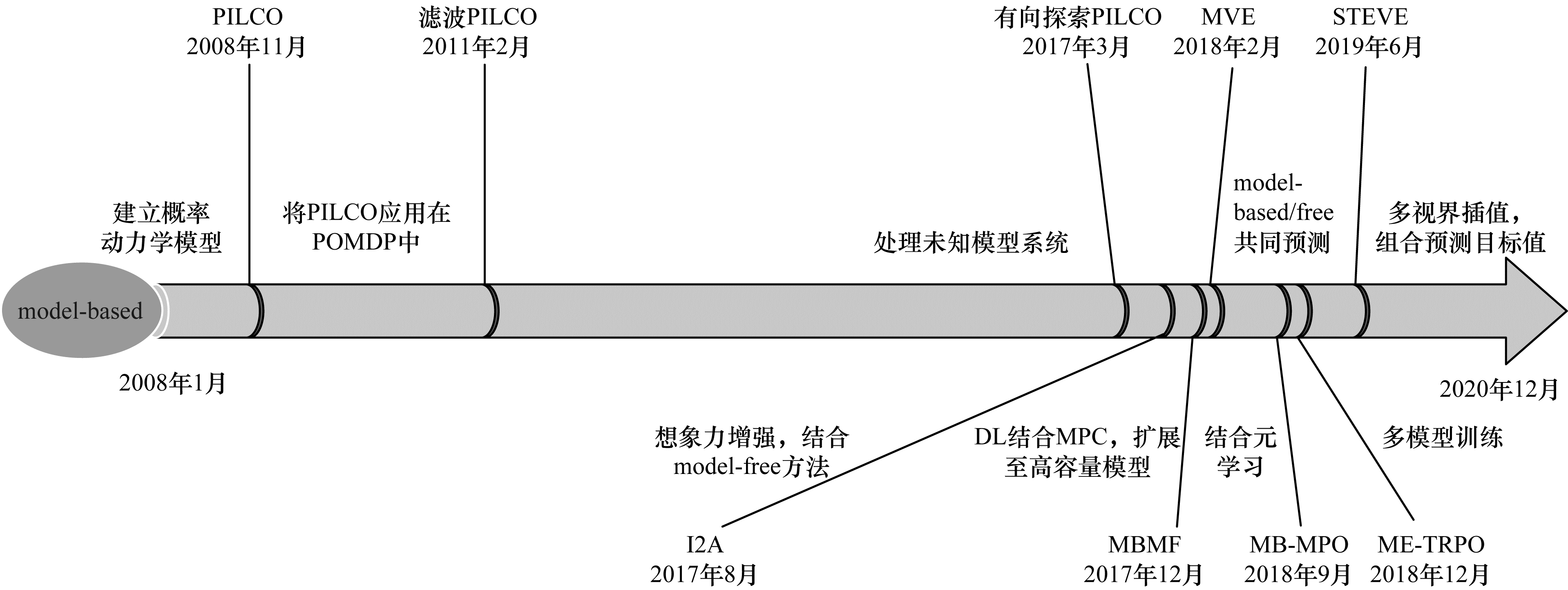
3.2 model-based方法off-policy方法与model-free结合,使得样本效率有了很大提高,但是由于不掌握状态转移函数和奖励函数的具体形式,因此所有经验数据依然依靠与环境交互来得到。为进一步提高样本效率,研究人员对model-based方法进行深入研究,从采样数据中对环境进行建模,之后在内部通过模拟仿真自动生成大量的样本数据,使用规划的手段快速进行策略学习。当前model-based方法最大的挑战就是模型误差,在数据量很少的情况下,学到得到的模型不准确,而使用不准确的模型预测就会产生更大的误差。针对此类问题,近年来研究人员提出了许多解决方案,如图 3所示。
|
Download:
|
| 图 3 model-based方法的发展历程 Fig. 3 Development course of model-based method | |
PILCO算法[42]将模型误差纳入考虑范围,建立了概率动力学模型,将不确定性集成到长期的规划和决策中,提高了算法的鲁棒性和样本效率。PILCO算法成立的前提是状态完全可观和可测。然而,在实际中状态并非完全可观,而且观测值存在噪声,因此研究人员将滤波器引入到PILCO算法的执行步和预测步,解决了PILCO算法中的POMDP问题[43]。由于PILCO优化过程仅考虑了当前最优,对于未知模型系统,智能体需要兼顾策略优化与环境探索两方面的问题,因此提出基于贝叶斯优化的有向探索方法[44]解决该问题。I2A算法[45]建立一种结合model-based和model-free的新型体系结构,提高了数据处理效率以及存在模型误差情况下的算法鲁棒性,可在几乎没有领域知识的低水平观测值上直接进行训练并得到了较好的结果,但仅限于较为简单的环境。MB-MPO算法[46]使用元学习的方法学习策略,使得算法可以不依赖于模型的精度,对任意一个模型都具有较好的学习效果,增强了算法鲁棒性。
PILCO、I2A等算法在对复杂的动力学模型建模时不能取得较好的效果,原因在于动力学模型规模较大,并且过长视界的动力学预测进一步加剧了模型的不准确性。MBMF算法[47]将model-based方法扩展到具有表达能力的高容量模型,实现了与模型预测控制(MPC)相结合,在复杂任务中实现稳定的动作控制,但由于MPC实时性较差,因此MBMF一般仅用于为无模型算法通过前期监督初始化,加快初期学习速率。MVE算法[48]致力于解决视界过长导致的模型不稳定问题,融合了model-based的短期稳定预估以及model-free的长期预估,提高预测值准确率,有效抑制模型预测不准确问题。STEVE算法[49]改进自MVE算法,目的是解决MVE算法手动设置展开步数不准确导致的精度下降问题。算法在不同的视界长度之间进行插值,得到不同视界的加权组合目标值,相比MVE可以更准确地预测目标值。ME-TRPO算法[50]通过使用多个不同的环境模型进行规划,减少过拟合现象,使得学习更加稳定。STEVE与ME-TRPO算法的共同缺陷在于模型规划时间较长,速度较慢。
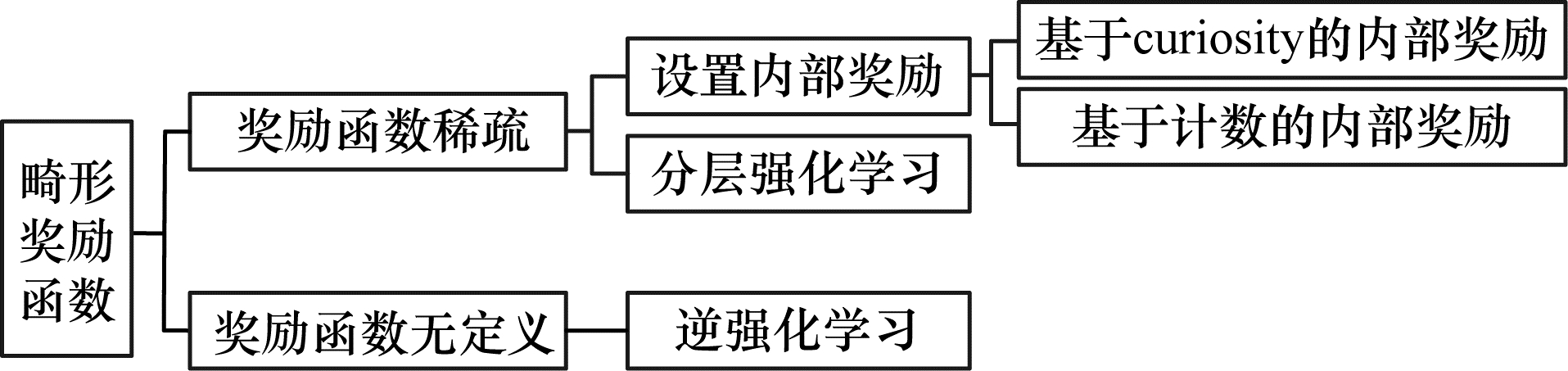
4 奖励函数稀疏或无明确定义情况下的算法探索问题很多任务的反馈是稀疏的,比如走迷宫的任务,只有在走出迷宫时才能得到一个正反馈,其余的动作不会获得任何正反馈,可见只有在成功完成任务时才会获得奖励。如果使智能体随机进行探索,则将很难得到任何正反馈,并且无法进行有效的策略评估,进而造成无法学到有用的经验。此外,奖励函数难以准确定义,即使使用人工方法也很难确定其形式。奖励函数的定义与总结如图 4所示。
|
Download:
|
| 图 4 奖励函数的定义与总结 Fig. 4 Definition and summary of reward function | |
为解决奖励函数稀疏的问题,可通过设置内部奖励及使用分层强化学习方法来增强算法探索能力。
设置内部奖励的方法将智能体的奖励分为内部奖励和外部奖励,当外部奖励很稀疏时,就需要使用内部奖励来激励指引智能体进行探索。内部奖励又分为基于curiosity和基于计数,基于curiosity的内部奖励倾向于探索未知,对预测误差比较大或是不确定程度比较大的状态动作对赋予一个较大的内部奖励值。基于计数的内部奖励是使用状态的访问频率来衡量状态的不确定性,传统方式是定义表格,若遇到相关的状态,相应的计数就加上1,但如今为了解决高维状态动作空间任务,表格法已经难以满足要求。
在基于curiosity的内部奖励方面,VIME算法[51]使用信息增益作为内在奖励,成功将内部奖励方法推广至高维任务中,并通过实验证明,相比启发式探索方法,VIME算法探索能力更强。BURDA等[52]在仅使用基于curiosity的内在奖励的情况下完成了探索,并取得了很好的效果,但该算法和VIME一样存在缺陷,当环境出现与智能体无关的随机性时,智能体会因为始终不能预测下一步的状态,而在相应的状态中进行停滞。为了解决该问题,PATHAK等[53]提出ICM算法,定义正反两个模型,通过两个相反的操作提取图像中的有用信息,对于环境中无关的信息则能自动忽略,解决了环境噪音对内部奖励设置的影响。RND算法[54]通过内部奖励和外部奖励灵活结合的方法和网络结构,对于复杂问题的探索能力显著提高。ICM和RND算法的缺陷在于面对复杂任务时,仅使用探索的手段很难提升效能。
在基于计数的内部奖励方面,CTS-based Pseudo Counts算法[55]将虚拟技术引入DRL,使用CTS模型作为概率模型来估计状态计数,以此作为衡量不确定性的指标,进而得到内在奖励。实验结果表明,该算法可以直接作用在像素游戏中显著改善探索能力,但稳定性较差。基于上述成果,研究人员将概率模型改为PixelCNN,得到基于PixelCNN的伪计数方法[56],该方法重新构建了内在激励形式,使得算法效果更加稳定。由于PixelCNN模型只能用于图像,在连续控制中无法使用,并且显式的概率模型计算复杂,因此TANG等[57]提出Hash-based Counts算法,使用自编码器代表哈希函数,将状态映射到低维特征空间中,在特征空间中进行计数,加快了算法速度,并且可以应用在连续动作空间中。
分层强化学习(Hierarchy Reinforcement Learning,HRL)方法将一个任务分解设定为一系列小目标,在完成这些小目标的过程中,智能体将不再关注环境本身的反馈。整个架构分为两部分,顶层负责制定小目标,底层负责完成小目标。顶层被称为元控制器,负责接收环境的状态和反馈,并根据这些信息产生小目标。底层被称为执行器,接收环境状态和小目标,并根据这些信息产生行动。通过使用HRL方法使得智能体更容易找到探索方向,加快解决问题的速度,解决稀疏奖励问题。
H-DQN算法[58]建立双层网络结构,两层都采用DQN网络,在Atari系列游戏和《蒙特祖玛的复仇》中取得了远超DQN算法的成绩,但对于《蒙特祖玛的复仇》做了太多条件设定,使得该算法对于其他任务可能并不普遍适用。RAFATI等[59]使用增量无监督学习方法和H-DQN架构开发新的无模型HRL方法,进一步在稀疏奖励问题上提高了算法效能。SUKHBAATAR等[60]使用分层自学习算法增强探索能力,同时使得策略能够不断自我改进优化。Fun算法[61]利用上下两层的架构,定义一个端到端模型,可以很好地解决奖励函数稀疏问题,但并未较好地解决控制权转移问题,顶层每步都会发出同步信号,使得子目标容易快速变换,影响底层策略执行。HIRO算法[62]使用off-policy的分层强化学习算法,算法思路和Fun相近,区别在于直接使用状态观测值作为目标,并将状态观测值的改变量作为高级策略的动作空间,相比Fun算法提高了下级策略效率和样本效率,但实验环境与Fun算法的实验环境并不相同,Fun算法使用视频作为输入,而HIRO算法使用低维输入,所以并不能证明其在性能上的优势。option-critic架构[63]将顶层策略和底层策略的控制权移交问题转换为函数学习问题,通过学习跨度不同的子策略,增大模型容量。
4.2 奖励函数无明确定义情况下的算法探索问题奖励函数是影响学习速率的一个重要因素,如果奖励函数形式不明确或者奖励函数设置不合理,难以进行高效学习。但在实际任务中,多数情况的奖励难以准确定义,没有准确的奖励函数,智能体就难以通过迭代手段正确修正自身策略。逆向强化学习(Inverse Reinforcement Learning,IRL)的思路和RL相反,RL通常在回报已知的情况下求出值函数和策略,IRL通过策略求回报,将专家经验看作最优策略与环境交互得到的结果,智能体做出符合专家经验的动作获得高回报,反之获得低回报,是一种类似监督学习的方式。通过不断迭代使智能体的策略逼近专家经验策略,专家经验一般根据人类处理相关任务记录得到[63-64]。对于IRL而言,机制是通过示范策略来反推回报函数,基于设计良好的奖励函数,智能体便可学习到泛化的策略。
对于一条专家经验轨迹可以找到许多奖励函数进行解释,这就会使得到的奖励函数不确定,导致学习的策略较差,因此需要对环境反馈信号进行建模。FIRL算法[64]使用基于逻辑联结的合成特征,实现非线性反馈信号的建模,之后结合深度信念网络设计DGP-IRL算法[65],极大增强了反馈信号的表示能力。
随着DL的发展,使用神经网络对反馈信号进行建模的方法成为主流方法。基于神经网络的最大熵逆强化学习方法解决了数据噪声问题。GCL算法[66]基于最大熵模型,使用神经网络表示奖励函数,解决了需要已知动力学模型进行奖励函数提取的问题,并将逆强化学习方法推广至高维动作空间任务,解决了现实场景中复杂系统的相关问题。但是,GCL需要先学习奖励函数后,再利用奖励函数进行策略优化,实现复杂且效率低下。为解决上述问题,GAIL算法[67]使用对抗生成网络来完成逆强化学习,与GCL算法不同,GAIL算法可以直接从专家数据中学到策略。目前,GAIL算法已经广泛用于各种复杂机械控制任务,但由于对抗性模型不稳定,因此研究人员提出VAIL算法[68],通过对内部表示之间的互信息进行约束保持训练稳定性。
5 多任务场景下的算法泛化性能增强问题当前的强化学习方法都是通过与环境交互,根据奖励函数动态优化策略。这就造成了策略是与环境紧密相关的,是用来处理单个任务的。然而现实世界问题本质是多模态的,生物大脑的数据处理也是遵循多任务处理策略的。当前算法在环境或目标发生变动后,算法的泛化性较差,制约RL在实际物理空间任务中的应用。近年来为了解决这个问题,学术界也提出了新的思路。
5.1 多任务强化学习多任务强化学习本质上是利用前期辅助任务训练得到的先验知识,提高面对新任务时的模型效果,核心思想是在不同但相关的源任务和目标任务之间迁移知识,以提高用于学习目标任务的机器学习算法的性能。
多任务强化学习的一种思路是使用多个辅助任务对网络架构进行训练,优化任务间共享的网络结构和参数。之前的学习经验迁移类似于参数微调,实质上是一种破坏性的过程,会使得原本学习到的策略被遗忘。RUSU等[69]提出渐进神经网络,并开发一个能够在学习过程中将特征层次的每一层纳入先验知识的系统,使得经验迁移的同时不会遗忘先验知识,但是缺点在于参数数量、网络复杂度会随着任务数量的增加而增加,并且通过辅助任务添加的网络结构是固定的。PathNet[70]是基于渐进神经网络开发的一种新型学习网络,在学习期间使用遗传算法通过神经网络进行复制和突变选择路径,可以进行灵活连接,同时可以避免灾难性遗忘,得到比渐进神经网络更好的泛化性能,但劣势在于遗传算法样本效率较低,并且收敛速度慢。Policy Distillation方法[71]将复杂模型学习到的特征压缩为比例更小、速度更快并保持性能不变的简化模型,可以使用该方法提取智能体策略,用于训练一个在专家级别上具有较小规模和较高效率的新网络。Actor-Mimic方法[72]使智能体能够学习如何同时执行多个任务,将积累的知识推广到新领域,可被视为通过使用一组相关源任务来训练单个深度策略网络的方法。使用Actor-Mimic训练的模型可在许多游戏中达到专家级的性能,并可推广到未训练过的新任务中。
多任务强化学习的另一种思路是使用基于目标的价值函数。UVFA算法[73]使用基于目标的价值函数,该价值函数是通用的,可以根据不同的任务目标对当前的状态进行评价,综合了状态和目标的价值函数,有助于泛化到相似但未见过的状态目标对。这类算法不仅针对状态进行概括,而且针对目标进行概括,并且可对没有见过的状态和目标进行预测,这使得UVFA可以作用于状态动作空间大的多任务模型中,使智能体进行多任务学习,但实验结果表明UVFA在多类型、高维度状态动作空间任务中的性能有待提升。UNREAL算法[74]可看作UVFA的并行版本,使用并行架构,加入若干无监督辅助任务,任务之间共享一些网络参数,用于学习更好的表示方式。通过训练多个面向同一个最终目标的任务来提升行动网络的表达能力和水平。HER算法[75]使用基于目标的价值函数建立经验池,并构建目标空间和状态空间的映射,高效利用了采样得到的样本经验,不但在多目标任务中完成泛化,而且在一定程度上缓解了稀疏奖励问题,但该方法的主要限制在于规定了目标和状态之间的对应关系,状态维度很低并且有明确的语义。如果状态维度高或者语义不明确,则不便于基于状态来制定有语义的目标,这一点可能限制了HER算法在多任务上的应用拓展。
5.2 元强化学习元学习(Meta-Learning)是近几年的研究热点,目的是基于少量无标签数据实现快速有效的学习模型,使其推广到在训练期间从未遇到过的新任务和新环境中。元学习首先通过学习与相似任务匹配的内部表示,为机器提供一种使用少量样本快速适应新任务的方法。学习这种表示的方法主要有基于模型的元学习(Model-Based Meta-Learning,MBML)和模型不可知的元学习(Model-Agnostic Meta-Learning,MAML)两类。基于模型的元学习方法利用少量样本的任务标记来调整模型参数,使用模型完成新任务,该方法最大的问题是设计适用于未知任务的元学习策略非常困难。模型不可知的元学习方法通过初始化模型参数,执行少量的梯度更新步骤就能成功完成新的任务。
元强化学习过程大致可以分为两步:1)构建inner loop的快速学习过程;2)设计out loop的元学习器,使得能够利用inner loop的样本来优化目标。RL2算法[76]的inner loop部分采用RNN网络的隐藏状态来代表记忆和经验,核心是使用之前经验的奖励,通过训练神经网络使得智能体能够自动学习判断任务层面的信息,从而加快新任务的训练过程。RL2无论是在小规模还是大规模实验中都有优异的表现,缺点在于有时会忘记优化目标,进而无法重用先前先验信息,因此需要设计更好的outer-loop算法。为避免在元强化学习中使用手工设计特征,SNAIL算法[77]基于通用的元学习器架构,将时间卷积和软注意力相组合。前者从过去的经验中收集信息;后者用于确定特定的信息,在因果关系上聚集过去经验中的有用信息,使得学习的泛化性更强。MQL算法[78]有效回收并利用训练任务中采集的数据,最大化智能体在当前所有任务上的表现,但算法实现过于复杂,待调参数也很多。与MQL算法思路不同,MAML算法[79]的目标不是使智能体在当前所有任务上表现最佳,而是学习一个初始化参数规则,该初始化的参数规则在参数空间中具有对每个任务最优参数解的高度敏感性,使其能够在一步梯度下降中沿着梯度方向快速达到最优点。MAML算法优化参数在各个任务上的梯度方向矢量和,并且由于学习的是对于多个任务最敏感的初始化参数位置,可以用于解决各种类型的任务,是一个适应性很强的通用算法,但当前MAML算法主要集中于解决较为简单的任务,对于复杂任务的性能表现并不理想。PEARL算法[80]使用任务编码方式从前期学习的任务中针对新的任务获取有效信息,并对新任务的不确定性做出更准确的判断,提高元强化学习中样本的利用率。
根据不同的研究目标,本文对DRL分类情况、算法优缺点和适用范围进行分析总结,如表 1所示,对于其他不常见的DRL研究分类,本文不再论述。
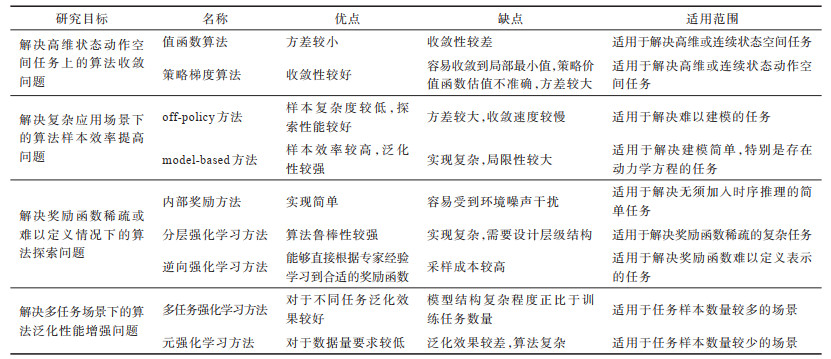
|
下载CSV 表 1 深度强化学习方法分类 Table 1 Classification of DRL method |
近几年,关于强化学习研究的论文在人工智能领域顶级会议中的录用数量逐年增加,在2021年ICLR会议中论文占比仅次于深度学习,位列第二。斯坦福大学AI实验室负责人Christopher D.MANNING等专家都对强化学习的崛起表示认同,也十分看好这一领域的发展前景。笔者认为深度强化学习未来将成为智能决策方向的主流技术,在机器人、自动驾驶、兵棋推演、金融投资等领域都会产生深远影响。
当前,DRL算法仍存在诸多挑战有待解决,例如:在高维状态动作空间任务中的收敛性能和速度无法保障,难以应用在实时性要求较高的场景中;样本效率较低,难以应用在采样成本较高的任务中;高度依赖奖励函数,如果奖励函数设计不合理或者难以定义,会使智能体学到不符合要求的策略;泛化性能较低,限制了在复杂任务场景中的应用。针对以上挑战,笔者认为DRL未来的研究方向主要包括:
1)提升算法收敛性。off-policy方法将行动策略和目标策略分开,很好地解决了探索利用困境,并且较高的样本效率加强了算法收敛性。如何进行有效的重要性采样是off-policy方法未来的研究热点,为保证目标策略可以有效利用行动策略采样得到样本,同时要对轨迹进行安全裁剪,避免模型发生较大波动影响收敛,可以考虑将重要性采样方法结合偏差纠正方法来平衡经验偏差和方差,保证模型不会发生较大波动。
2)提高算法样本效率。model-based方法通过建模可有效提高样本效率,但是模型误差导致学习到次优策略的问题依然存在,虽然很多DRL算法致力于解决该问题,但是仍然不能完全避免模型缺陷,并且当前model-based方法对于复杂环境应用效果不佳。未来可以考虑研究off-policy与on-policy相结合的方法,例如Q-Prop[81]、PCL[82]、trust-pcl[83]等方法通过结合两种学习方式,兼顾了稳定性和样本效率。
3)分层强化学习。在奖励函数稀疏或难以定义的任务中,内在奖励会受到环境中内在随机性的影响,逆强化学习使用人类经验作为样本,不一定能学到最优的策略,并且泛化性较差,所以逆强化学习发展前景不明朗。未来可以针对分层强化学习进行重点研究,主要集中在3个方面:(1)自动分层能力,不再受限于由人工进行层次划分的设定;(2)结合大规模并行架构,使用强大的算力提升学习效率;(3)融合多目标学习和元学习,提高策略的通用性。
4)增强算法适应性。多任务下的策略迁移和元学习可以考虑结合并行架构下不同的模拟环境进行样本收集和训练,提高样本多样性和训练速度,例如Distral框架[84]、Impala框架[40]和PopArt框架[85],借鉴迁移学习中神经网络复用架构,以及基于目标的强化学习算法中提取包含任务目标的价值函数的方法,同时关注神经科学、认知心理学等交叉领域,融合多领域知识优化强化学习算法。
7 结束语本文对近年来深度强化学习的研究进展进行概述,回顾深度强化学习的发展历程,依据研究目标对当前主流方法进行分类。在处理高维状态动作空间任务时,利用值函数算法,通过深度神经网络近似相应的动作价值函数,并使用策略梯度法,将动作选择的概率参数化,通过优化参数直接对策略进行更新迭代。在提高算法样本效率方面,使用off-policy方法,分离行动策略和目标策略,平衡智能体探索和利用之间的矛盾,并利用model-based方法,通过学习任务模型来提升算法效率。在面对奖励函数稀疏或难以表示的任务时,使用基于计数或curiosity的内部奖励,引导智能体优化策略,并利用分层强化学习,将任务分解成为一系列小任务,使得智能体更容易找到探索方向,加快学习速度,同时采用逆强化学习方法,以人类经验为模板进行学习。在提高算法泛化能力方面,多任务强化学习和元强化学习都取得了较好的学习效果。当前深度强化学习技术受到越来越多的关注,并在电子游戏、机械控制、推荐系统、金融投资等诸多领域得到了广泛应用并取得了大量研究成果,后续将针对深度强化学习算法的学习效率、运行速度、泛化性能等方面做进一步研究。
| [1] |
SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 |
| [2] |
SILVER D, HUBERT T, SCHRITTWIESER J, et al. A general reinforcement learning algorithm that masters chess, shogi, and go through self-play[J]. Science, 2018, 362(6419): 1140-1144. DOI:10.1126/science.aar6404 |
| [3] |
YE D H, CHEN G B, ZHAO P L, et al. Supervised learning achieves human-level performance in MOBA games: a case study of Honor of Kings[EB/OL]. [2021-02-25]. https://arxiv.org/abs/2011.12582.pdf.
|
| [4] |
YE D H, LIU Z, SUN M F, et al. Mastering complex control in MOBA games with deep reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1912.09729.pdf.
|
| [5] |
VINYALS O, BABUSCHKIN I, CZARNECKI W M, et al. Grandmaster level in StarCraft Ⅱ using multi-agent reinforcement learning[J]. Nature, 2019, 575(7782): 350-354. DOI:10.1038/s41586-019-1724-z |
| [6] |
SILVER D, NEWNHAM L, BARKER D, et al. Concurrent reinforcement learning from customer interactions[C]//Proceedings of 2013 International Conference on Machine Learning. New York, USA: ACM Press, 2013: 924-932.
|
| [7] |
LEVINE S, PASTOR P, KRIZHEVSKY A, et al. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1504.00702.pdf.
|
| [8] |
崔丽群, 郭相卓, 郭军, 等. 适用于偶发实时系统的过载控制策略[J]. 计算机工程, 2019, 45(6): 108-114. CUI L Q, GUO X Z, GUO J, et al. Overload control strategy for sporadic real-time system[J]. Computer Engineering, 2019, 45(6): 108-114. (in Chinese) |
| [9] |
GOODFELLOW I, BENGIO Y. Deep learning[M]. Cambridge, USA: MIT Press, 2017.
|
| [10] |
SUTTON R, BARTO A. Reinforcement learning[M]. Cambridge, USA: MIT Press, 2018.
|
| [11] |
GAVIN A R, NIRANJAN M. On-line Q-learning using connectionist systems[D]. Cambridge, UK: University of Cambridge, 1994.
|
| [12] |
WATKINS C J C H, DAYAN P. Technical note: Q-learning[J]. Machine Learning, 1992, 8(3): 279-292. |
| [13] |
KONIDARIS G, OSENTOSKI S, THOMAS P. Value function approximation in reinforcement learning using the Fourier basis[C]//Proceedings of 2011 AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2011: 1-17.
|
| [14] |
CONNELL M E, CONNELL E, UTGOFF P E. Learning to control a dynamic physical system[J]. Computational Intelligence, 1987, 3(1): 330-337. DOI:10.1111/j.1467-8640.1987.tb00219.x |
| [15] |
ATKESON C G, MOORE A W, SCHAAL S. Locally weighted learning for control[M]. Berlin, Germany: Springer, 1997.
|
| [16] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533. DOI:10.1038/nature14236 |
| [17] |
VAN HASSELT H, GUEZ A, SILVER D. Deep reinforcement learning with double Q-learning[C]//Proceedings of 2016 AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2016: 2094-2100.
|
| [18] |
HORGAN D, QUAN J, BUDDEN D, et al. Distributed prioritized experience replay[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1511.05952.pdf.
|
| [19] |
WANG Z, SCHAUL T, HESSEL M, et al. Dueling network architectures for deep reinforcement learning[C]//Proceedings of 2016 International Conference on Machine Learning. New York, USA: ACM Press, 2016: 1995-2003.
|
| [20] |
HESTER T, VECERIK M, PIETQUIN O, et al. Deep Q-learning from demonstrations[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1704.03732.pdf.
|
| [21] |
BELLEMARE M G, DABNEY W, REMI M. A distributional perspective on reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1707.06887.pdf.
|
| [22] |
DABNEY W, ROWLAND M, BELLEMARE M G, et al. Distributional reinforcement learning with quantile regression[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1504.00702.pdf.
|
| [23] |
DABNEY W, OSTROVSKI G, SILVER D, et al. Implicit quantile networks for distributional reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1806.06923.pdf.
|
| [24] |
FORTUNATO M, AZAR M G, PIOT B, et al. Noisy networks for exploration[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1706.10295.pdf.
|
| [25] |
HESSEL M, MODAYIL J, VAN HASSELT H, et al. Rainbow: combining improvements in deep reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1710.02298.pdf.
|
| [26] |
WILLIAMS R J. Simple statistical gradient-following algorithms for connectionist reinforcement learning[J]. Machine Learning, 1992, 8(3/4): 229-256. DOI:10.1023/A:1022672621406 |
| [27] |
DEGRIS T, MARTHA W, SUTTON R S. Off-policy actor-critic[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1205.4839.pdf.
|
| [28] |
SCHULMAN J, MORITZ P, LEVINE S, et al. High-dimensional continuous control using generalized advantage estimation[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1506.02438.pdf.
|
| [29] |
SCHULMAN J, LEVINE S, ABBEEL P, et al. Trust region policy optimization[C]//Proceedings of 2015 International Conference on Machine Learning. New York, USA: ACM Press, 2015: 1889-1897.
|
| [30] |
SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1707.06347.pdf.
|
| [31] |
WU Y, MANSIMOV E, LIAO S, et al. Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1708.05144.pdf.
|
| [32] |
SILVER D, LEVER G, HEESS N, et al. Deterministic policy gradient algorithms[C]//Proceedings of ICML'14. New York, USA: ACM Press, 2014: 387-395.
|
| [33] |
LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1509.02971.pdf.
|
| [34] |
FUJIMOTO S, VAN HOOF H, MEGER D. Addressing function approximation error in actor-critic methods[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1802.09477.pdf.
|
| [35] |
MUNOS R, STEPLETON T, HARUTYUNYAN A, et al. Safe and efficient off-policy reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1606.02647.pdf.
|
| [36] |
WANG Z, BAPST V, HEESS N, et al. Sample efficient actor-critic with experience replay[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1611.01224.pdf.
|
| [37] |
HAARNOJA T, ZHOU A, ABBEEL P, et al. Soft actor-critic off-policy maximum entropy deep reinforcement learning with a stochastic actor[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1801.01290.pdf.
|
| [38] |
MNIH V, BADIA A P, MIRZA M, et al. Asynchronous methods for deep reinforcement learning[C]//Proceedings of International Conference on Machine Learning. New York, USA: ACM Press, 2016: 1928-1937.
|
| [39] |
MNIH V, BADIA A P, MIRZA M, et al. Asynchronous methods for deep reinforcement learning[EB/OL]. [2021-02-25]. https://openai.com/blog/baselines-acktr-a2c/.
|
| [40] |
ESPEHOLT L, SOYER H, MUNOS R, et al. IMPALA: scalable distributed deep-RL with importance weighted actor-learner architectures[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1802.01561.pdf.
|
| [41] |
HORGAN D, QUAN J, BUDDEN D, et al. Distributed prioritized experience replay[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1803.00933.pdf.
|
| [42] |
RASMUSSEN C E, DEISENROTH M P. Probabilistic inference for fast learning in control[C]//Proceedings of 2008 European Workshop on Reinforcement Learning. Berlin, Germany: Springer, 2008: 229-242.
|
| [43] |
DEISENROTH M, PILCO R C E. A model-based and data-efficient approach to policy search[C]//Proceedings of the 28th International Conference on Machine Learning. Washington D.C., USA: IEEE Press, 2011: 465-472.
|
| [44] |
MCALLISTER R. Bayesian learning for data-efficient control[D]. Cambridge, UK: University of Cambridge, 2017.
|
| [45] |
ANTHONY T, TIAN Z, BARBER D. Imagination-augmented agents for deep reinforcement learning[C]//Proceedings of 2017 International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 5360-5370.
|
| [46] |
CLAVERA I, ROTHFUSS J, SCHULMAN J, et al. Model-based reinforcement learning via meta-policy optimization[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1809.05214.pdf.
|
| [47] |
NAGABANDI A, KAHN G, FEARING R S, et al. Neural network dynamics for model-based deep reinforcement learning with model-free fine-tuning[C]//Proceedings of 2018 IEEE International Conference on Robotics and Automation. Washington D.C., USA: IEEE Press, 2018: 7559-7566.
|
| [48] |
FEINBERG V, WAN A, STOICA I, et al. Model-based value estimation for efficient model-free reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1803.00101.pdf.
|
| [49] |
BUCKMAN J, HAFNER D, TUCKER G, et al. Sample-efficient reinforcement learning with stochastic ensemble value expansion[C]//Proceedings of 2019 International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2019: 8224-8234.
|
| [50] |
KURUTACH T, CLAVERA I, DUAN Y, et al. Model-ensemble trust-region policy optimization[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1802.10592.pdf.
|
| [51] |
HOUTHOOFT R, CHEN X, DUAN Y, et al. VIME: variational information maximizing exploration[C]//Proceedings of 2016 International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2016: 65-74.
|
| [52] |
BURDA Y, EDWARDS H, PATHAK D, et al. Large-scale study of curiosity-driven learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1808.04355.pdf.
|
| [53] |
PATHAK D, AGRAWAL P, EFROS A A, et al. Curiosity-driven exploration by self-supervised prediction[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Washington D.C., USA: IEEE Press, 2017: 488-489.
|
| [54] |
BURDA Y, EDWARDS H, STORKEY A, et al. Exploration by random network distillation[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1810.12894.pdf.
|
| [55] |
BELLEMARE M, SRINIVASAN S, OSTROVSKI G, et al. Unifying count-based exploration and intrinsic motivation[C]//Proceedings of 2016 International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2016: 1471-1479.
|
| [56] |
OSTROVSKI G, BELLEMARE M G, OORD A, et al. Count-based exploration with neural density models[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1703.01310.pdf.
|
| [57] |
TANG H, HOUTHOOFT R, FOOTE D, et al. #Exploration: a study of count-based exploration for deep reinforcement learning[C]//Proceedings of 2017 International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 2753-2762.
|
| [58] |
KRISHNAMURTHY R, LAKSHMINARAYANAN A S, KUMAR P, et al. Hierarchical reinforcement learning using spatio-temporal abstractions and deep neural networks[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1604.06057.pdf.
|
| [59] |
RAFATI J, NOELLE D C. Learning representations in model-free hierarchical reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1810.10096.pdf.
|
| [60] |
SUKHBAATAR S, LIN Z M, KOSTRIKOV I, et al. Intrinsic motivation and automatic curricula via asymmetric self-play[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1703.05407.pdf.
|
| [61] |
VEZHNEVETS A S, OSINDERO S, SCHAUL T, et al. FeUdal Networks for hierarchical reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1703.01161.pdf.
|
| [62] |
NACHUM O, GU S X, LEE H, et al. Data-efficient hierarchical reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1805.08296.pdf.
|
| [63] |
BACON P L, HARB J, PRECUP D. The option-critic architecture[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1609.05140.pdf.
|
| [64] |
LEVINE S, POPOVIC Z, KOLTUN V, et al. Feature construction for inverse reinforcement learning[C]//Proceedings of 2010 International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2010: 1-10.
|
| [65] |
JIN M, DAMIANOU A, ABBEEL P, et al. Inverse reinforcement learning via deep Gaussian process[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1512.08065.pdf.
|
| [66] |
FINN C, LEVINE S, ABBEEL P. Guided cost learning: deep inverse optimal control via policy optimization[C]//Proceedings of 2016 International Conference on Machine Learning. New York, USA: ACM Press, 2016: 49-58.
|
| [67] |
HO J, ERMON S. Generative adversarial imitation learning[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. New York, USA: ACM Press, 2016: 4572-4580.
|
| [68] |
PENG X B, KANAZAWA A, TOYER S, et al. Variational discriminator bottleneck: improving imitation learning, inverse RL, and GANs by constraining information flow[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1810.00821.pdf.
|
| [69] |
RUSU A A, RABINOWITZ N C, DESJARDINS G, et al. Progressive neural networks[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1606.04671.pdf.
|
| [70] |
FERNANDO C, BANARSE D, BLUNDELL C, et al. PathNet: evolution channels gradient descent in super neural networks[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1701.08734.pdf.
|
| [71] |
RUSU A A, COLMENAREJO S G, GULCEHRE C, et al. Policy Distillation[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1511.06295.pdf.
|
| [72] |
PARISOTTO E, BA J L, SALAKHUTDINOV R. Actor-Mimic: deep multitask and transfer reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1511.06342.pdf.
|
| [73] |
SCHAUL T, HORGAN D, GREGOR K, et al. Universal value function approximators[C]//Proceedings of 2015 International Conference on Machine Learning. New York, USA: ACM Press, 2015: 1312-1320.
|
| [74] |
JADERBERG M, MNIH V, CZARNECKI W M, et al. Reinforcement learning with unsupervised auxiliary tasks[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1611.05397.pdf.
|
| [75] |
ANDRYCHOWICZ M, WOLSKI F, RAY A, et al. Hindsight experience replay[C]//Proceedings of 2017 International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 5048-5058.
|
| [76] |
DUAN Y, SCHULMAN J, CHEN X, et al. RL2: fast reinforcement learning via slow reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1611.02779.pdf.
|
| [77] |
MISHRA N, ROHANINEJAD M, CHEN X, et al. A simple neural attentive meta-learner[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1707.03141.pdf.
|
| [78] |
FAKOOR R, CHAUDHARI P, SOATTO S, et al. Meta-Q-learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1910.00125.pdf.
|
| [79] |
FINN C, ABBEEL P, LEVINE S. Model-agnostic meta-learning for fast adaptation of deep networks[C]//Proceedings of the 34th International Conference on Machine Learning. New York, USA: ACM Press, 2017: 1126-1135.
|
| [80] |
RAKELLY K, ZHOU A, QUILLEN D, et al. Efficient off-policy meta-reinforcement learning via probabilistic context variables[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1903.08254.pdf.
|
| [81] |
GU S X, LILLICRAP T, GHAHRAMANI Z, et al. Q-Prop: sample-efficient policy gradient with an off-policy critic[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1611.02247.pdf.
|
| [82] |
NACHUM O, NOROUZI M, XU K, et al. Bridging the gap between value and policy based reinforcement learning[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1702.08892.pdf.
|
| [83] |
NACHUM O, NOROUZI M, XU K, et al. Trust-PCL: an off-policy trust region method for continuous control[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1707.01891.pdf.
|
| [84] |
TEH Y W, BAPST V, CZARNECKI W M, et al. Distral: robust multitask reinforcement learning[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York, USA: ACM Press, 2017: 4499-4509.
|
| [85] |
VAN HASSELT H, GUEZ A, HESSEL M, et al. Learning values across many orders of magnitude[EB/OL]. [2021-02-25]. https://arxiv.org/abs/1602.07714.pdf.
|
 2021, Vol. 47
2021, Vol. 47
