安全多方计算(Secure Multi-Party Computation,SMC)是指两个及两个以上的参与者在不泄露各自隐私数据的情况下,利用隐私数据进行保密计算并共同完成某项计算任务。SMC可满足人们利用隐私数据进行保密计算的需求,同时兼顾数据的保密性与共享性,因此被广泛应用于机器学习[1]、数据分析[2]、社交网络[3]以及医疗信息等领域。
百万富翁问题(Millionaires’ Problem,MP)是安全多方计算中的基本问题,其在1982年由YAO提出[4]后引起多方关注。近年来,研究人员相继提出多种解决该问题的方法。文献[5]将安全多方计算规约到智力游戏中,利用混淆电路解决百万富翁问题。文献[6]采用不经意传输工具对两方输入进行双重加密,设计一种解决百万富翁问题的安全双方计算协议。文献[7]使用不经意传输工具并通过简单异或运算解决百万富翁问题。文献[8-9]借助茫然第三方提出一种安全的百万富翁比较协议,解决第三方合谋问题。文献[10]利用零知识证明构造一种百万富翁问题协议。文献[11-13]通过私有置换操作提出基于卡片的密码协议,解决了百万富翁问题。文献[14-15]利用对称密码解决恶意模型下的百万富翁问题。
利用编码是解决百万富翁问题的有效措施之一。文献[16]采用0-1编码将双方待比较的数据转化为0/1集合,结合具有乘法同态性的加密算法解决百万富翁问题,但其计算复杂度较高且无法精确区分两数相等的情况。文献[17]利用基于二次剩余困难问题的GM加密算法,通过构造0-1编码将数据编码转换为向量,提出一种基于几何方法的有理数比较协议,但GM算法在解密过程中的时间开销随二次非剩余集合增大呈线性增长。文献[18]使用文献[16]中编码方式提出一种基于DDH假设的方案,但该方案仅适用于输入较小数据,当两个待比较数据较大时计算开销较高。文献[19]结合1-r编码方式和ELGamal同态加密算法解决数据比较问题,提出一种数据比较协议并将其应用于保密数据排序。文献[20-21]提出0-1-2编码方法,同时利用Paillier同态加密算法将百万富翁问题转化为向量问题求解。虽然文献[19-21]提出的方法能有效解决百万富翁问题中的两数相等问题,但计算效率均较低。
本文提出一种采用0-1编码的百万富翁问题协议。通过改进保密数据编码规则,利用ElGamal同态加密变体算法解决安全两数比较问题,在半诚实模型下证明协议的正确性和安全性,并从理论和实验两个角度对协议的计算复杂度与效率进行分析。
1 基础知识 1.1 安全多方计算的安全模型在安全多方计算协议的执行过程中,半诚实参与者在忠实履行协议的同时会保留协议执行过程中的有效信息,并尝试推导出其他参与方的隐私信息。若安全多方计算协议中参与者均为半诚实参与者,则称该协议使用的计算模型为半诚实模型。由于本文协议的计算模型均为半诚实模型,因此以下文给出半诚实模型下两方计算模型的安全性定义。
设Alice和Bob分别拥有隐私数据
定义1(半诚实参与者的保密性) 对于函数
| $ \begin{array}{l}{\left\{{S}_{1}\left(x, {f}_{1}\left(x, y\mathrm{ }\right)\right), {f}_{2}\left(x, y\mathrm{ }\right)\right\}}_{x, y}\stackrel{\mathrm{c}}{\equiv }\\ {\left\{\mathrm{v}\mathrm{i}\mathrm{e}{\mathrm{w}}_{1}^{\pi }\left(x, y\mathrm{ }\right), \mathrm{o}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}{\mathrm{t}}_{2}^{\pi }\left(x, y\mathrm{ }\right)\right\}}_{x, y}\end{array} $ | (1) |
| $ \begin{array}{l}{\left\{{f}_{1}\left(x, y\mathrm{ }\right), {S}_{2}\left(x, {f}_{2}\left(x, y\mathrm{ }\right)\right)\right\}}_{x, y}\stackrel{\mathrm{c}}{\equiv }\\ {\left\{\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}{\mathrm{t}}_{1}^{\pi }\left(x, y\mathrm{ }\right), \mathrm{v}\mathrm{i}\mathrm{e}{\mathrm{w}}_{2}^{\pi }\left(x, y\mathrm{ }\right)\right\}}_{x, y}\end{array} $ | (2) |
其中,
ELGamal同态加密[22]变体算法如下:
1)密钥生成(KeyGen)。给定安全参数
2)加密阶段(Enc)。给定消息
3)解密阶段(Dec)。将密文
| $ E\left({m}_{1}\right)=\left({c}_{1}, {c}_{2}\right)=\left({g}^{r}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{m}_{1}}{h}^{r}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right) $ | (3) |
| $ E\left({m}_{2}\right)=\left({c}_{1}, {c}_{2}\right)=\left({g}^{r}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{m}_{2}}{h}^{r}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right) $ | (4) |
由于存在以下关系式:
| $ \begin{array}{l}E\left({M}_{1}\right)\times E\left({M}_{2}\right)=\left({g}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{1}}{h}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)\times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({g}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{2}}{h}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({g}^{{r}_{1}+{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{1}+{M}_{2}}{h}^{{r}_{1}+{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;E\left({M}_{1}+{M}_{2}\right)\end{array} $ | (5) |
| $ \begin{array}{l}E{\left({M}_{1}\right)}^{b}=\left({\left({g}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{b}, {\left({g}^{{M}_{1}}{h}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{b}\right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({g}^{{r}_{1}b}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{1}b}{h}^{{r}_{1}b}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=E\left(b{M}_{1}\right)\end{array} $ | (6) |
因此,ELGamal同态加密变体算法满足如下性质:
| $ E\left({m}_{1}\right)E\left({m}_{2}\right)=E\left({m}_{1}+{m}_{2}\right) $ | (7) |
| $ E{\left({m}_{1}\right)}^{b}=E\left(b{m}_{1}\right) $ | (8) |
百万富翁问题的实质是在保密情况下比较两数大小,即Alice有1个隐私数据
0-1编码规则如下:
设
| $ {\alpha }_{i}=\left\{\begin{array}{c}0, {v}_{i}\le {v}_{k},i=\mathrm{1, 2}, \cdots , n\\ 1, {v}_{i}>{v}_{k},i=\mathrm{1, 2}, \cdots , n\end{array}\right. $ | (9) |
根据
本文利用0-1编码规则提出一种解决百万富翁问题的协议,以下介绍MP协议的具体设计方案,并对其正确性与安全性进行分析。
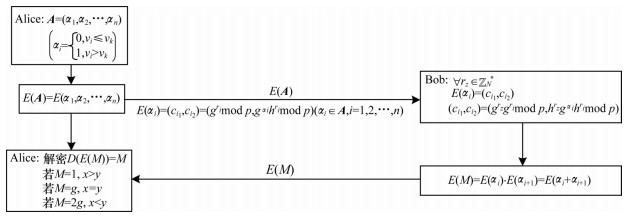
2.2.1 设计方案MP协议利用0-1编码规则将判断隐私数据
|
Download:
|
| 图 1 基于0-1编码规则的MP协议框架 Fig. 1 MP protocol framework based on 0-1 coding rule | |
基于0-1编码规则的MP协议实现流程如下:
协议1 基于0-1编码的MP协议
输入
输出
1.Alice:
2.
3.
//
//
4.
5.
该协议具体内容如下:
1)Alice按照式(9)中的规则利用自身隐私数据
2)Alice根据ELGamal同态加密算法生成公私钥对
3)Bob根据
(1)选取随机数
(2)计算
4)Bob将
5)Alice利用私钥
本文对基于0-1编码规则的MP协议正确性与安全性进行分析。
定理1 在半诚实模型下,协议1是正确的,同时也是安全的。
正确性证明:
1)Alice拥有密文信息
2)基于ELGamal的同态加密变体算法具有加法同态性,计算公式如下:
| $ \begin{array}{l}E\left({M}_{1}\right)\times E\left({M}_{2}\right)=\left({g}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{1}}{h}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)\times \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{2}}{h}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{1}+{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{1}+{M}_{2}}{h}^{{r}_{1}+{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;E\left({M}_{1}+{M}_{2}\right)\end{array} $ | (10) |
3)Bob利用公钥对
| $ \begin{array}{l} E\left({\alpha }_{l}\right)E\left({\alpha }_{l+1}\right)=\left({g}^{{r}_{z}}{g}^{{r}_{l}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {h}^{{r}_{z}}{g}^{{\alpha }_{l}}{h}^{{r}_{l}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)\times \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{l+1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{\alpha }_{l+1}}{h}^{{r}_{l+1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{z}+{r}_{l}+{r}_{l+1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left.{g}^{{\alpha }_{l}+{\alpha }_{l+1}}{h}^{{r}_{z}+{r}_{l}+{r}_{l+1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;E\left({\alpha }_{l}+{\alpha }_{l+1}\right)=E\left(M\right)\end{array} $ | (11) |
4)Bob对
| $ \begin{array}{l}D\left(E\left(M\mathrm{ }\right)\right)=\frac{{g}^{{\alpha }_{l}+{\alpha }_{l+1}}{h}^{{r}_{z}+{r}_{l}+{r}_{l+1}}}{{\left({g}^{{r}_{z}+{r}_{l}+{r}_{l+1}}\right)}^{x}}\mathrm{m}\mathrm{o}\mathrm{d}\;p=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{g}^{{\alpha }_{l}+{\alpha }_{l+1}}{\left({g}^{x}\right)}^{{r}_{z}+{r}_{l}+{r}_{l+1}}}{{\left({g}^{{r}_{z}+{r}_{l}+{r}_{l+1}}\right)}^{x}}\mathrm{m}\mathrm{o}\mathrm{d}\;p=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{g}^{{\alpha }_{l}+{\alpha }_{l+1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\end{array} $ | (12) |
5)由于选取的安全参数
安全性证明:
Alice根据自身隐私数据
1)构造模拟器
具体步骤如下:
(1)模拟器
(2)利用ELGamal同态加密算法选取不同
| $ \begin{array}{l}\boldsymbol{E}\left(\boldsymbol{A}\mathrm{ }\right)=\left(E\left({\alpha }_{1}\right), E\left({\alpha }_{2}\right), \cdots , E\left({\alpha }_{n}\right)\right)=\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left(\left({g}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{\alpha }_{1}}{h}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right), \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({g}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{\alpha }_{2}}{h}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right), \cdots ,\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{n}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{\alpha }_{n}}{h}^{{r}_{n}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)\right)\end{array} $ | (13) |
(3)根据
(4)对数据
在协议1中,
2)构造模拟器
具体步骤如下:
(1)模拟器
(2)利用ELGamal同态加密算法选取不同
| $ \begin{array}{l}E\left({\boldsymbol{A}}^{'}\mathrm{ }\right)=\left(E\left({\alpha }_{1}^{'}\mathrm{ }\right), E\left({\alpha }_{2}^{'}\mathrm{ }\right), \cdots , E\left({\alpha }_{n}^{'}\mathrm{ }\right)\right)=\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left(\left({g}^{{r}_{1}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{\alpha }_{1}^{'}}{h}^{{r}_{1}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right), \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{2}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{\alpha }_{2}^{'}}{h}^{{r}_{2}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right), \cdots , \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{n}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{\alpha }_{n}^{'}}{h}^{{r}_{n}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)\right)\end{array} $ | (14) |
(3)根据
(4)对数据
在协议1中,
对协议1和文献[16, 19, 21]协议的计算复杂度、通信轮数以及适用范围进行对比。由于文献[16, 19]协议基于ElGamal同态加密算法,文献[21]协议基于Paillier同态加密算法,本文协议基于ELGamal同态加密变体算法,因此为便于对比分析,令Paillier同态加密算法模为N,数据长度为n,ElGamal同态算法及其变体算法的模为P,比较结果如表 1所示。

|
下载CSV 表 1 3种协议的不同性能对比 Table 1 Performance comparison of three protocols |
从上述3种协议的计算复杂性来看,协议1、文献[16, 19]协议都是基于ElGamal同态加密,而采用ElGamal同态加密算法进行1次加密需
从通信轮数来看,协议1中Alice将密文
由上述分析可知,虽然协议1的通信轮数与其他协议相同,但是其计算复杂度较其他协议更低。此外,与文献[16]协议相比,协议1可更好地比较两数据相等的问题。因此,协议1整体计算效率优于其他协议。
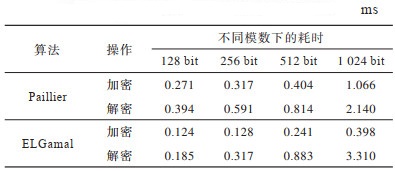
3.2 计算耗时分析将协议1和文献[16, 19, 21]协议加密和解密的计算耗时进行对比。实验采用Windows10 64位操作系统,Inter® CoreTM i7-4720HQ 2.60 GHz CPU,8 GB内存以及MyEclipse 2017CI编译环境。假设上述协议中双方商定向量元素个数n=100,令Paillier同态加密算法与ELGamal同态加密算法中模数相同,则在模数为128 bit、256 bit、512 bit和1 024 bit时分别计算这2种同态加密算法加密和解密的耗时,结果如表 2所示。
|
下载CSV 表 2 2种算法在不同模数下加密和解密的耗时 Table 2 Encryption and decryption time consumption of two algorithms under different modulus |
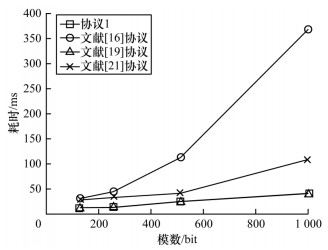
由表 2可计算得到这2种算法加密和解密的平均耗时,结合3.1节中对4种协议的效率分析可得到各协议在不同模数下的时间开销,结果如图 2所示(文献[21]协议中
|
Download:
|
| 图 2 4种协议在不同模数下的时间开销 Fig. 2 Time cost of four protocols under different modulus | |
|
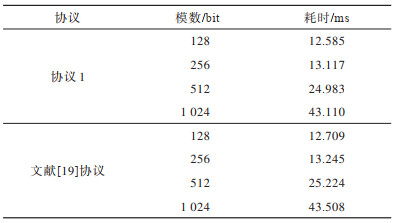
下载CSV 表 3 协议1与文献[19]协议在不同模数下的时间开销 Table 3 Time cost of the protocol 1 and the protocol in reference [19] under different modulus |
当前社交网络已深入人们的日常生活,为扩大用户交友范围,云服务器会向每个用户推荐可能认识的好友,其推荐时判断依据为用户之间相同好友数量。然而在服务器与用户交互过程中,服务器在精准计算不同用户之间相同好友数量的同时,还要保证用户隐私不被泄露。如果将计算相同好友数量的过程视为安全两方的计算问题,则该问题可转化为求解安全两方集合交集个数的问题,即:Alice拥有隐私数据集合
本文结合协议1,设计出求解保密集合交集势的协议,其具体内容如下:
1)Alice和Bob利用自身隐私数据集合与共有隐私数据集合
| $ {a}_{i}=\left\{\begin{array}{c}1, {v}_{i}\in U\\ 0, {v}_{i}\notin U\end{array}\right., i=\mathrm{1, 2}, \cdots , z $ | (15) |
| $ {b}_{i}=\left\{\begin{array}{c}1, {v}_{i}\in U\\ 0, {v}_{i}\notin U\end{array}\right., i=\mathrm{1, 2}, \cdots , z $ | (16) |
2)
3)Bob计算
4)Alice通过私钥
求解保密隐私数据集合交集势的协议实现流程如下:
协议2 求解保密隐私数据集合交集势的协议
输入 Alice:
输出
1.
2.
3.
4.
定理2 在半诚实模型下,协议2是正确的,同时也是安全的。
正确性证明:
1)Alice拥有密文信息:
2)基于ELGamal加密变体算法具有加法同态性,计算公式如下:
| $ \begin{array}{l}E{\left({M}_{1}\right)}^{b}=\left({\left({g}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{b}, {\left({g}^{{M}_{1}}{h}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{b}\right)=\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{1}b}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{1}b}{h}^{{r}_{1}b}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;E\left(b{M}_{1}\right)\end{array} $ | (17) |
| $ \begin{array}{l}E\left({M}_{1}\right)\times E\left({M}_{2}\right)=\left({g}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{1}}{h}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)\times \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{2}}{h}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left({g}^{{r}_{1}+{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{M}_{1}+{M}_{2}}{h}^{{r}_{1}+{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;E\left({M}_{1}+{M}_{2}\right)\end{array} $ | (18) |
3)Bob利用编码后的隐私数据集合
| $ \begin{array}{l}\prod\limits_{i = 1}^z E{\left({a}_{i}\right)}^{{b}_{i}}=\prod\limits_{i = 1}^z \left({\left({g}^{{r}_{i}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{{b}_{i}}, {\left({g}^{{a}_{i}}{h}^{{r}_{i}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{{b}_{i}}\right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\prod\limits_{i = 1}^z \left({g}^{{r}_{i}{b}_{i}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{i}{b}_{i}}{h}^{{r}_{i}{b}_{i}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)=\\\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \prod\limits_{i = 1}^z E\left({a}_{i}{b}_{i}\right)=E\left(\sum _{i=1}^{z}{a}_{i}{b}_{i}\right)=E\left(M\mathrm{ }\right)\end{array} $ | (19) |
4)Bob对
| $ D\left(E\left(M\right)\right)=\frac{{g}^{M}{h}^{r}}{{\left({g}^{r}\right)}^{x}}\mathrm{m}\mathrm{o}\mathrm{d}\;p=\frac{{g}^{M}{\left({g}^{x}\right)}^{r}}{{\left({g}^{r}\right)}^{x}}\mathrm{m}\mathrm{o}\mathrm{d}\;p=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{g}^{M}\mathrm{m}\mathrm{o}\mathrm{d}\;p=\omega $ | (20) |
5)由于选取的安全参数
安全性证明:
采用模拟器
1)模拟器
2)利用ELGamal同态加密算法选取不同的
| $ \begin{array}{l}E\left(\boldsymbol{A}\right)=\left(E\left({a}_{1}\right), E\left({a}_{2}\right), \cdots , E\left({a}_{z}\right)\right)=\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left(\left({g}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{1}}{h}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right), \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({g}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{2}}{h}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right), \cdots , \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({g}^{{r}_{z}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{z}}{h}^{{r}_{z}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)\right)\end{array} $ | (21) |
3)根据
| $ \begin{array}{l}E\left(M'\right)=\left(E{\left({a}_{1}\right)}^{{b}_{1}^{'}}, E{\left({a}_{2}\right)}^{{b}_{2}^{'}}, \cdots , E{\left({a}_{z}\right)}^{{b}_{z}^{'}}\right)=\\\;\;\;\;\;\;\;\;\;\left({\left({g}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{1}}{h}^{{r}_{1}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{{b}_{1}^{'}}, \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left({g}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{2}}{h}^{{r}_{2}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{{b}_{2}^{'}}, \cdots , \\\;\;\;\;\;\;\; {\left({g}^{{r}_{z}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{z}}{h}^{{r}_{z}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)}^{{b}_{z}^{'}}\right)=\\\;\;\;\;\;\;\; \left(\left({g}^{{r}_{1}{b}_{1}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{1}{b}_{1}^{'}}{h}^{{r}_{1}{b}_{1}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right), \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({g}^{{r}_{2}{b}_{2}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{2}{b}_{2}^{'}}{h}^{{r}_{2}{b}_{2}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right), \cdots ,\\\;\;\;\;\;\;\; \left({g}^{{r}_{z}{b}_{z}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p, {g}^{{a}_{z}{b}_{z}^{'}}{h}^{{r}_{z}{b}_{z}^{'}}\mathrm{m}\mathrm{o}\mathrm{d}\;p\right)\right)=\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left(E\left({a}_{1}{b}_{1}^{'}\right), E\left({a}_{2}{b}_{2}^{'}\right), \cdots , E\left({a}_{z}{b}_{z}^{'}\right)\right)\end{array} $ | (22) |
4)对数据
在协议2中,
采用与上述类似的方法构造模拟器
在协议2中,Alice需执行
在协议2中,Alice将编码后的隐私数据集合元素
百万富翁问题作为安全多方计算的基本模块,常见于数据挖掘、数据查询和计算几何等方面,而现有解决方案计算效率与安全性较低。本文提出一种基于0-1编码的百万富翁问题协议,利用ELGamal同态加密的性质解决百万富翁问题,在半诚实模型下证明其安全性,并用协议求解安全两方集合交集个数。实验结果表明,与采用ElGamal和Paillier同态加密算法的协议相比,该协议计算效率更高。后续将在两数比较的基础上进行多数比较,以解决带隐私保护的多集合交集问题。
| [1] |
FRITCHMAN K, SAMINATHAN K, DOWSLEY R, et al.Privacy-preserving scoring of tree ensembles: a novel framework for AI in healthcare[C]//Proceedings of 2018 IEEE International Conference on Big Data.Washington D.C., USA: IEEE Press, 2018: 2413-2422.
|
| [2] |
SUNDARI S, ANANTHI M.Secure multi-party computation in differential private data with data integrity protection[C]//Proceedings of 2015 International Conference on Computing and Communications Technologies.Washington D.C., USA: IEEE Press, 2015: 180-184.
|
| [3] |
CUI Weirong, DU Chenglie, CHEN Jinchao. PSP:proximity-based secure pairing of mobile devices using WIFI signals[J]. Wireless Networks, 2019, 25(2): 733-751. DOI:10.1007/s11276-017-1588-9 |
| [4] |
YAO A C.Protocols for secure computations[C]//Proceedings of the 23rd IEEE Sympsoium on Foundations of Computer Science.Washington D.C., USA: IEEE Press, 1982: 160-164.
|
| [5] |
GOLDREICH O, MICALI S, WIGDERSON A.How to play any mental game[C]//Proceedings of the 19th Annual ACM Symposium on Theory of Computing.New York, USA: ACM Press, 1987: 218-229.
|
| [6] |
YAO A C.How to generate and exchange secrets[C]//Proceedings of the 27th Annual Symposium on Foundations of Computer Science.Washington D.C., USA: IEEE Press, 1986: 162-167.
|
| [7] |
IOANNIDIS I, GRAMA A.An efficient protocol for Yao's millionaires' problem[C]//Proceedings of the 36th Annual Hawaii International Conference on System Sciences.Washington D.C., USA: IEEE Press, 2003: 6-9.
|
| [8] |
QIN Jing, ZHANG Zhenfeng, FENG Dengguo, et al. A protocol of comparing information without leaking[J]. Journal of Software, 2004, 15(3): 421-427. (in Chinese) 秦静, 张振峰, 冯登国, 等. 无信息泄露的比较协议[J]. 软件学报, 2004, 15(3): 421-427. |
| [9] |
JIA Hengyue, WEN Qiaoyan, SONG Tingting, et al. Quantum protocol for millionaire problem[J]. Optics Communications, 2011, 284(1): 545-549. DOI:10.1016/j.optcom.2010.09.005 |
| [10] |
JAWUREK M, KERSCHBAUM F, ORLANDI C.Zero-knowledge using garbled circuits: how to prove non-algebraic statements efficiently[C]//Proceedings of 2013 ACM SIGSAC Conference on Computer and Communications Security.New York, USA: ACM Press, 2013: 955-966.
|
| [11] |
NAKAI T, TOKUSHIGE Y, MISAWA Y, et al.Efficient card-based cryptographic protocols for millionaires' problem utilizing private permutations[C]//Proceedings of 2016 International Conference on Cryptology and Network Security.Berlin, Germany: Springer, 2016: 500-517.
|
| [12] |
MIYAHARA D, HAYASHI Y, MIZUKI T, et al.Practical and easy-to-understand card-based implementation of Yao's millionaire protocol[C]//Proceedings of 2018 International Conference on Combinatorial Optimization and Applications.Berlin, Germany: Springer, 2018: 246-261.
|
| [13] |
ONO H, MANABE Y.Efficient card-based cryptographic protocols for the millionaires' problem using private input operations[C]//Proceedings of 2018 Asia Joint Conference on Information Security.Washington D.C., USA: IEEE Press, 2018: 23-28.
|
| [14] |
MOHASSEL P, ROSULEK M, ZHANG Y.Fast and secure three-party computation: the garbled circuit approach[C]//Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security.New York, USA: ACM Press, 2015: 591-602.
|
| [15] |
ZHAO Chuan, ZHAO Shengnan, ZHANG Bo, et al. Secure comparison under ideal/real simulation paradigm[J]. IEEE Access, 2018, 6(5): 31236-31248. |
| [16] |
LIN H Y, TZENG W G.An efficient solution to the millionaires' problem based on homomorphic encryption[C]//Proceedings of 2005 International Conference on Applied Cryptology and Network Security.Berlin, Germany: Springer, 2005: 456-466.
|
| [17] |
LIU Xin, LI Shundong, LIU Jian, et al. Secure multiparty computation of a comparison problem[J]. SpringerPlus, 2016, 5(1): 1489-1497. DOI:10.1186/s40064-016-3061-0 |
| [18] |
LIU M, NANDA P, ZHANG X, et al.Asymmetric commutative encryption scheme based efficient solution to the millionaires problem[C]//Proceedings of 2018 IEEE International Conference on Big Data Science and Engineering.Washington D.C., USA: IEEE Press, 2018: 990-995.
|
| [19] |
LI Zhanli, CHEN Lichao, CHEN Zhenhua, et al. Design and applications of efficient protocol of millionaires' problem based on 1-r encoding[J]. Journal of Cryptologic Research, 2019, 6(1): 50-60. (in Chinese) 李占利, 陈立朝, 陈振华, 等. 基1-r编码的高效百万富翁问题协议及应用[J]. 密码学报, 2019, 6(1): 50-60. |
| [20] |
LI Shundong, ZUO Xiangjian, YANG Xiaoli, et al. Secure vector dominance protocol and its applications[J]. Acta Electronica Sinica, 2017, 45(5): 1117-1123. (in Chinese) 李顺东, 左祥建, 杨晓莉, 等. 安全向量优势协议及其应用[J]. 电子学报, 2017, 45(5): 1117-1123. DOI:10.3969/j.issn.0372-2112.2017.05.014 |
| [21] |
ZUO Xiangjian, LI Shundong, YANG Xiaoli. An efficient homomorphic encryption based solution to millionaires' problem[J]. Journal of Chinese Computer Systems, 2017, 38(3): 455-459. (in Chinese) 左祥建, 李顺东, 杨晓莉. 同态加密的百万富翁问题高效解决方案[J]. 小型微型计算机系统, 2017, 38(3): 455-459. |
| [22] |
FREEDMAN M J, HAZAY C, NISSIM K, et al. Efficient set intersection with simulation-based security[J]. Journal of Cryptology, 2016, 29(1): 115-155. DOI:10.1007/s00145-014-9190-0 |
 2021, Vol. 47
2021, Vol. 47
