2. 重庆邮电大学 通信与信息工程学院, 重庆 400065;
3. 重庆邮电大学 自动化学院, 重庆 400065;
4. 重庆第二师范学院 数学与信息工程学院, 重庆 400065
2. School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China;
3. School of Automation, Chongqing University of Posts and Telecommunications, Chongqing 400065, China;
4. School of Mathematics and Information Engineering, Chongqing University of Education, Chongqing 400065, China
为解决由于车辆增多造成的交通拥堵和事故等问题,提高出行效率并确保交通安全,智能交通系统(Intelligent Transport System,ITS)应运而生。蜂窝车联网(Cellular Vehicle-to-everything,C-V2X)作为智能交通系统的重要支撑[1],受到研究人员的广泛关注。C-V2X因其良好的远距离数据传输可达性和较高的非视距传输可靠性等优势,克服了传统Ad-Hoc网络的缺点,使其在高移动性情况下也能适用于高数据速率场景[2]。
针对V2X业务的低时延与高可靠特性[3],D2D通信被认为是最有可能实现C-V2X侧链通信的技术[4],且其具有重用、跳跃和邻近增益的优势[5]。在underlay模式下,车载用户(Vehicle Users,V-UEs)与蜂窝用户(Cellular Users,C-UEs)共享蜂窝上行频谱[6],这是因为上行子帧通常比下行链路占用频谱更少[7]。该方案的频谱利用率较高,但在非正交分配的情况下会产生复杂的同频干扰问题。此外,基于3GPP标准,每个V2X消息在将其传递到较低层时应通过应用层安排的近场通信数据包优先级(ProSe Per-Packet Priority,PPPP)排列[8],这意味着用户之间都应该发送符合优先级队列的数据。不考虑PPPP的无线资源管理(Radio Resource Management,RRM)可能会危害道路安全。由此可见,RRM对C-V2X的性能产生至关重要作用的同时也面临着诸多挑战[9]。为解决同频干扰问题与确定不同PPPP值用户的传输优先级,本文提出一种基于PPPP的RRM算法。该算法以最大化小区用户信息值之和为目标,通过将PPPP引入RRM算法,使得高PPPP值用户获得传输机会的几率增加,并将V-UEs通信可靠性作为优化问题的约束条件以抑制同频干扰。
1 相关工作目前,C-V2X的研究多数以优化网络吞吐量和提升用户速率为目标。文献[10]设计一种基于群集的资源管理方案(CROWN),以最大化C-UEs的总速率为目标,保证V-UEs的可靠性。该方案研究了V-UEs和C-UEs之间的资源共享,并将V-UEs分为不同的集群,在同一群集中,V-UEs使用正交的资源块(Resource Block,RB),而在不同的群集中,允许V-UEs共享相同的RB。文献[11]在保障C-UEs与安全V-UEs可靠性的前提下,以最大化非安全V-UEs与速率为目标,提出一种用于V2X通信的3D匹配资源分配算法。该算法在RB不能被同类型用户共享的前提下复用RB。文献[12]研究一种用于Overlay模式的群体智能资源分配算法,以在提高网络总速率的同时满足C-UEs和V-UEs的服务质量(Quality of Service,QoS)要求。该算法在C-UEs和V-UEs之间自适应地分配RB,采用蚁群优化机制来降低复杂度并获得令人满意的性能。文献[13]开发一种车联网通信测试系统,以测量车联网丢包率和抖动时延作为关键指标。文献[14]提出一种SCMF算法,该算法能够有效降低车联网开销与传输时延,提高网络资源利用率。文献[15]研究一种基于残差的模糊自适应算法,以提高算法准确性。文献[16]提出一种基于车辆位置的V2V通信资源分配方案,该方案根据车辆位置的不同提出高速公路案例和城市案例这两种资源分配策略。其中,针对城市情况,根据交通密度在交叉路口区域分配一组资源,而针对高速公路情况则根据车辆方向和位置来分配资源。高速公路的每个区域都有特定的资源池,它为进入一个区域内的车辆分配资源。文献[17-18]则讨论了如何在满足V2V用户可靠性和时延的同时,最大化V2I用户的速率。
然而,以上研究均没有考虑V-UEs的PPPP,若不考虑PPPP优化系统的吞吐量,基站将倾向于为CSI较好的用户优先分配资源,这将会导致PPPP较高的关键安全信息无法及时得到传输,从而对道路安全造成危害。文献[19-20]虽然考虑了PPPP在V2X通信中的影响,但文献[19]仅考虑了V-UEs,忽略了C-UEs的QoS,文献[20]只在频率分配阶段考虑了PPPP,其在功率分配阶段仅以最大化吞吐量为目标而忽略了PPPP,且其只允许C-UEs与V-UEs间的RB复用,而忽视了不同V2V对间的RB复用,同时每个用户在每个传输时间间隔(Transmission Time Interval,TTI)内只需求一个RB的假设也过于理想化。
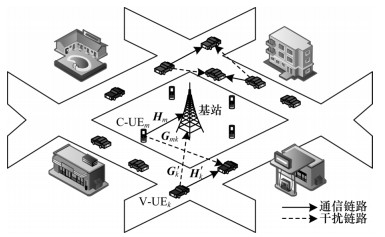
2 系统模型 2.1 系统模型的构建本文提出的系统模型仅考虑了单小区场景,具体如图 1所示。其中,
|
Download:
|
| 图 1 系统模型 Fig. 1 System model | |
假设C-UEm与V-UEk使用相同的RB进行通信,则会产生同频干扰。
为保障V2X业务的高可靠与低时延特性,需要考虑更加适合V2X场景的约束条件。本文使用文献[21]中的中断概率,即任何编码方案都不能无差错地传输N比特的概率,其更符和V2X业务的需求,这是因为V2X业务通常要求在一定时间内传输定量的数据。V-UEk的中断概率表示为:
| $ {p}_{k}^{\mathrm{o}\mathrm{u}\mathrm{t}}=\mathrm{P}\mathrm{r}\left\{\sum\limits_{i=1}^{{E}_{k}}\mathrm{l}\mathrm{b}(1+{\lambda }_{i})<{N}_{k}\right\} $ | (1) |
其中,
| $ {p}_{k}^{\mathrm{o}\mathrm{u}\mathrm{t}}\le {p}_{0} $ | (2) |
相对于V2X业务,传统蜂窝网业务更关注实时速率与网络吞吐量,因此对传统蜂窝网用户C-UEm设立约束条件如下:
| $ {\lambda }_{m}\ge {\lambda }_{0} $ | (3) |
其中,
本文在进行RRM时,需要同时考虑PPPP与信息速率以确保在一定的时间内传输更多高PPPP的数据。使用信息值作为能效函数来确定不同用户之间的传输优先级。对于第
| $ {f}_{i}={\rho }_{i}{r}_{i} $ | (4) |
其中,
RRM问题的目标是考虑小区内V-UEs和C-UEs约束的同时最大化整体信息值。为了应对一个用户需求多个RB的情况,文献[10]引入了子用户的概念。对于一个需求E个RB的用户,可将其分解为E个子用户,每个子用户需求一个RB,子用户的传输信道功率增益与干扰信道功率增益与其父用户相同。为防止2个父用户相同的子用户复用同一个RB,考虑将同一父用户的子用户间的干扰信道功率增益定义为
| $ (\mathit{\boldsymbol{X}}_{}^{C\mathrm{*}}, \mathit{\boldsymbol{X}}^{V\mathrm{*}}, \mathit{\boldsymbol{P}}^{C\mathrm{*}}, \mathit{\boldsymbol{P}}^{V\mathrm{*}})=\\ \underset{{\mathit{\boldsymbol{X}}}^{C}, {\mathit{\boldsymbol{X}} }^{V}, {\mathit{\boldsymbol{P}}}^{C}, {\mathit{\boldsymbol{P}}}^{V}}{\mathrm{a}\mathrm{r}\mathrm{g}\;\mathrm{m}\mathrm{a}\mathrm{x}}\left\{\sum\limits _{i=1}^{L}\sum\limits _{j=1}^{M\text{'}}{x}_{i, j}^{C}{\rho }_{j}^{C}{r}_{j}^{C}+\sum\limits _{i=1}^{L}\sum _{j=1}^{M\text{'}}{x}_{i, j}^{V}{\rho }_{j}^{V}{r}_{j}^{V}\right\} $ | (5) |
式(5)的约束条件为:
| $ {p}_{j}^{\mathrm{o}\mathrm{u}\mathrm{t}}<{p}_{0}, \forall j $ | (6) |
| $ {\lambda }_{j}>{\lambda }_{0}, \forall j $ | (7) |
| $ \sum\limits _{j=1}^{{M}^{\mathrm{\text{'}}}}{x}_{i, j}^{C}\le 1, \forall i $ | (8) |
| $ \sum\limits _{j=1}^{{K}^{\mathrm{\text{'}}}}{x}_{i, j}^{V}+\sum\limits _{i=1}^{{M}^{\mathrm{\text{'}}}}{x}_{i, j}^{C}\le 2, \mathrm{ }\forall i $ | (9) |
| $ {p}_{m\text{'}}^{C}\le {P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\text{'}} $ | (10) |
| $ {p}_{k\text{'}}^{V}\le {P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{V\mathrm{\text{'}}} $ | (11) |
其中,式(6)与式(7)是V-UEs的中断概率约束与C-UEs的SINR约束,式(8)表示C-UEs间正交使用RB,式(9)为假设的在一个TTI内,单个RB至多被两条通信链路复用的条件,式(10)与式(11)为C-UEs子用户与V-UEs子用户的最大功率约束。为简化问题,本文定义子用户的的最大功率为
式(5)的优化问题为一个混合整数非线性规划问题,为降低该问题求解复杂度,本文提出分组优先求解算法。该算法包括最大化单个RB内信息值的功率控制阶段以及最大化整体信息值的频率资源选择阶段。
4.1 功率控制阶段式(5)中的最大信息值可被视为
如果RB内只存在一个子用户,由于不会发生同频干扰,为了最大化信息值,该子用户将以最大功率进行发送。其中,V-UEs子用户为
如果RB被子用户
| $ \begin{array}{l}({p}_{m}^{C\mathrm{*}}, {p}_{k}^{V\mathrm{*}})=\underset{{p}_{m}^{C}, {p}_{k}^{V}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}\left({\rho }_{m}^{C}\mathrm{l}\mathrm{b}\left(1+\frac{{p}_{m}^{C}{\mathit{\boldsymbol{H}}}_{m}}{{\sigma }_{N}^{2}+{p}_{k}^{V}{\mathit{\boldsymbol{G}}}_{k}^{\mathrm{\text{'}}}}\right)+\right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left.{\rho }_{k}^{V}\mathrm{l}\mathrm{b}\left(1+\frac{{p}_{k}^{V}{\mathit{\boldsymbol{H}}}_{k}^{\mathrm{\text{'}}}}{{\sigma }_{N}^{2}+{p}_{m}^{C}{\mathit{\boldsymbol{G}}}_{mk}}\right)\right)\end{array} $ | (12) |
约束于:
| $ {p}_{k}^{\mathrm{o}\mathrm{u}\mathrm{t}}\le {p}_{0} $ | (13) |
| $ {\lambda }_{c}\ge {\lambda }_{0} $ | (14) |
| $ {p}_{m}^{C}\le {P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\mathrm{\text{'}}} $ | (15) |
| $ {p}_{k}^{V}\le {P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{V\mathrm{\text{'}}} $ | (16) |
其中,
| $ \frac{\partial R({P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\text{'}}, {p}_{k}^{V})}{\partial {p}_{k}^{V}}=\frac{A({p}_{k}^{V}{)}^{2}+B{p}_{k}^{V}+C}{D} $ | (17) |
其中:
| $ A={\rho }_{k}^{V}{\mathit{\boldsymbol{H}}}_{k}^{\mathrm{\text{'}}}{\mathit{\boldsymbol{G}}}_{k}^{2} $ | (18) |
| $ B={\rho }_{k}^{V}{\mathit{\boldsymbol{H}}}_{k}^{\mathrm{\text{'}}}(2{\mathit{\boldsymbol{G}}}_{k}{\sigma }_{N}^{2}+{\mathit{\boldsymbol{H}}}_{m}{\mathit{\boldsymbol{G}}}_{k}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\text{'}})-{\rho }_{m}^{C}{\mathit{\boldsymbol{H}}}_{m}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\text{'}}{G}_{k}{\mathit{\boldsymbol{H}}}_{k}^{\mathrm{\text{'}}} $ | (19) |
| $ C={\rho }_{k}^{V}{\mathit{\boldsymbol{H}}}_{k}^{\mathrm{\text{'}}}({\sigma }_{N}^{4}+{\mathit{\boldsymbol{H}}}_{m}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\mathrm{\text{'}}}{\sigma }_{N}^{2})-{\rho }_{m}^{c}{\mathit{\boldsymbol{H}}}_{m}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\text{'}}{\mathit{\boldsymbol{G}}}_{k}({\sigma }_{N}^{2}+{\mathit{\boldsymbol{G}}}_{mk}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\text{'}}) $ | (20) |
| $ D=({\sigma }_{N}^{2}+{\mathit{\boldsymbol{G}}}_{mk}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\text{'}}+{\mathit{\boldsymbol{H}}}_{k}^{\mathrm{\text{'}}})({\sigma }_{N}^{2}+{\mathit{\boldsymbol{G}}}_{k}{p}_{k}^{V}+{\mathit{\boldsymbol{H}}}_{m}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{C\text{'}})({\sigma }_{N}^{2}+{\mathit{\boldsymbol{G}}}_{k}{p}_{k}^{V}) $ | (21) |
由式(21)可以得出,当
求解
| $ {f}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{i}={\rho }_{i}\mathrm{l}\mathrm{b}\left(\frac{{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{i}{\mathit{\boldsymbol{H}}}_{i}}{{\sigma }_{N}^{2}}\right) $ | (22) |
其中,
算法1 功率控制算法
输入 Hm,
输出
1.根据式(22)求出两位子用户的最大信息值
2.将
3.根据式(7)得出极大值点
4.若
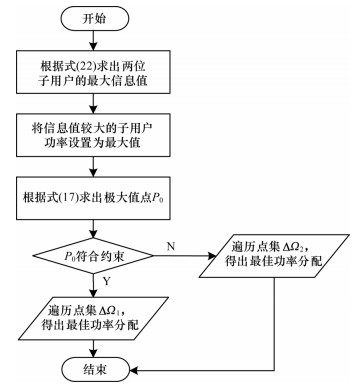
功率控制算法流程如图 2所示。类似地,当两条V2V链路复用一个RB时,只需要替换约束条件式(14)作为中断概率约束,其最佳发射功率也可由以上步骤得出。
|
Download:
|
| 图 2 功率分配算法流程 Fig. 2 Procedure of power allocation algorithm | |
利用功率控制的结果可以得出任意两个子用户配对形成的最大信息值。由于SSF在可分配的RB内是相同的,因此可将频率资源选择问题转换成子用户的配对问题,即组合子用户形成子用户对,并让其复用一个RB。只要不同的子用户对正交使用RB,具体使用哪一个RB对结果没有影响。
为了在配对问题中考虑单个子用户独享RB的情况,本文将
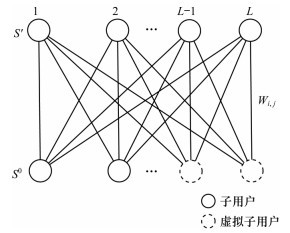
为降低求解复杂度,本文提出利用启发式算法来解决频率资源选择问题。首先,根据式(22)求出
|
Download:
|
| 图 3 带权二部图 Fig. 3 Weighted bipartite graph | |
对于
| $ \begin{array}{l}{W}_{i, j}=\\ \left\{\begin{array}{l}\mathrm{ }{\rho }_{i}\mathrm{l}\mathrm{b}\left(1+\frac{{\mathit{\boldsymbol{H}}}_{i}{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{i}}{{\sigma }_{N}^{2}}\right), \mathrm{ }{s}_{j}\mathrm{为}\mathrm{虚}\mathrm{拟}\mathrm{子}\mathrm{用}\mathrm{户}\\ \mathrm{ }0, \mathrm{ }{p}_{i}\mathrm{与}{p}_{j}\mathrm{无}\mathrm{法}\mathrm{同}\mathrm{时}\mathrm{满}\mathrm{足}\mathrm{约}\mathrm{束}\\ {\rho }_{i}\mathrm{l}\mathrm{b}\left(1+\frac{{\mathit{\boldsymbol{H}}}_{i}{p}_{i}^{\mathrm{*}}}{{\sigma }_{N}^{2}+{\mathit{\boldsymbol{G}}}_{ji}{p}_{j}^{\mathrm{*}}}\right)+{\rho }_{j}\mathrm{l}\mathrm{b}\left(1+\frac{{\mathit{\boldsymbol{H}}}_{i}{p}_{j}^{\mathrm{*}}}{{\sigma }_{N}^{2}+{\mathit{\boldsymbol{G}}}_{ij}{p}_{i}^{\mathrm{*}}}\right),\mathrm{ }\mathrm{其}\mathrm{他}\end{array}\right.\end{array} $ | (23) |
其中:当
值得注意的是,随着小区内用户的增加,一个TTI内所需求的RB总量也随之增加,由于可分配的RB有限,此时可能会出现一个用户的调度无法全部得到满足的情况。如功率控制小结中所讨论的子用户的最大功率为其父用户的最大功率除以申请的RB数,当一个用户只得到部分RB时,其子用户的最大功率约束需要得到更新,并再次进行功率分配。频率资源选择算法描述如算法2所示。
算法2 频率资源选择算法
输入
输出 XC,
1.分解用户形成子用户集,加入
2.根据式(22)求出
3.将
4.为
5.利用集合
6.利用匈牙利算法求解图
7.根据频率资源选择结果更新子用户的最大功率约束。
8.使用功率控制算法得到最终的发射功率
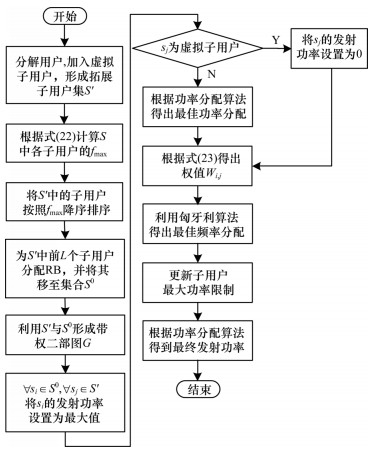
频率资源选择算法流程如图 4所示。
|
Download:
|
| 图 4 频率资源选择算法流程 Fig. 4 Procedure of frequency resource selection algorithm | |
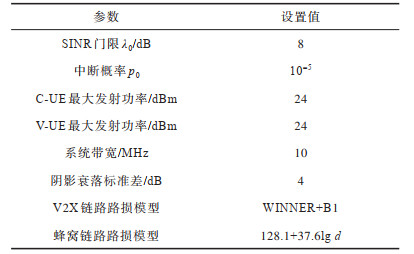
为简化系统,本文仅考虑单小区环境下的RRM。假设小区的载波为800 MHz,单个RB的带宽为180 kHz,小区的布局选用曼哈顿网格布局,在该环境下,小区为道路围成的440 m
|
下载CSV 表 1 仿真参数设置 Table 1 Setting of simulation parameters |
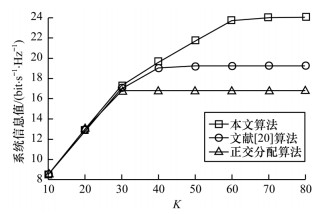
图 5是在
|
Download:
|
| 图 5 V-UEs数量对3种算法系统信息值的影响 Fig. 5 Effect of the number of V-UEs on the system information value of three algorithms | |
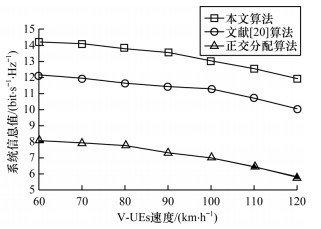
图 6是在
|
Download:
|
| 图 6 V-UEs速度对3种算法系统信息值的影响 Fig. 6 Effect of speed of V-UEs on the system information value of three algorithms | |
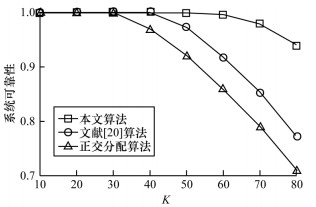
图 7是在
|
Download:
|
| 图 7 V-UEs数量对3种算法系统可靠性的影响 Fig. 7 Effect of the number of V-UEs on the system reliability of three algorithms | |
本文在保障V-UEs与C-UEs通信可靠性的前提下,以最大化小区用户信息值之和为优化目标,提出一种新的RRM算法。该算法通过引入子用户的概念将RRM问题分解成2个子问题:最大化单个资源块内信息值的功率控制与最大化全体用户信息值的频率资源分配。利用功率控制的结果将频率资源分配问题转换成无向图最大权匹配问题,并利用启发式算法实现低复杂度的频率资源选择。仿真结果表明,该算法不仅可提升整个系统的信息值,同时还可有效保障系统可靠性。后续将在本文研究基础上增加同一RB内的用户数量,以进一步提高频谱利用率。
| [1] |
3GPP. TR 22.861 V14.1.0 Feasibility study on new services and markets technology enablers for massive Internet of Things (Release 14)[S].[S.l.]: 3GPP Organizational Partners, 2016.
|
| [2] |
CHEN Shanzhi, HU Jinling, SHI Yan, et al. Technologies, standards and applications of LTE-V2X for vehicular networks[J]. Telecommunications Science, 2018, 34(4): 1-11. (in Chinese) 陈山枝, 胡金玲, 时岩, 等. LTE-V2X车联网技术, 标准与应用[J]. 电信科学, 2018, 34(4): 1-11. |
| [3] |
3GPP. TS 22.185 version 15.0.0 LTE Service require-ments for V2X services (Release 15)[S].[S.l.]: 3GPP Organizational Partners, 2018.
|
| [4] |
3GPP. TR 36.885 V14.0.0 Study on LTE-based V2X services (Release14)[S].[S.l.]: 3GPP Organizational Partners, 2016.
|
| [5] |
AHMAD M, AZAM M, NAEEM M, et al. Resource management in D2D communication:an optimization perspective[J]. Journal of Network and Computer Applica-tions, 2017, 93: 51-75. DOI:10.1016/j.jnca.2017.03.017 |
| [6] |
MACH P, BECVAR Z, VANEK T. In-band device-to-device communication in OFDMA cellular networks:a survey and challenges[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 1885-1922. DOI:10.1109/COMST.2015.2447036 |
| [7] |
GALLO L, HAERRI J. Unsupervised long-term evolution device-to-device:a case study for safety-critical V2X communications[J]. IEEE Vehicular Technology Magazine, 2017, 12(2): 69-77. DOI:10.1109/MVT.2017.2669346 |
| [8] |
3GPP. TS 23.303 V15.1.0 Generation partnership project; technical specification group services and system aspects; proximity-based services[S].[S.l.]: 3GPP Organizational Partners, 2018.
|
| [9] |
3GPP. TS 36.133 V14.3.0 Requirements for support of radio resource management (Release 14)[S].[S.l.]: 3GPP Organizational Partners, 2017.
|
| [10] |
SUN W L, YUAN D, STROM E G, et al. Cluster-based radio resource management for D2D-supported safety-critical V2X communications[J]. IEEE Transactions on Wireless Communications, 2016, 15(4): 2756-2769. DOI:10.1109/TWC.2015.2509978 |
| [11] |
WEI Q, SUN W L, BAI B, et al.Resource allocation for V2X communications: a local search based 3D matching approach[C]//Proceedings of 2017 IEEE International Conference on Communications.Washington D.C., USA: IEEE Press, 2017: 1-6.
|
| [12] |
FEKI S, MASMOUDI A, BELGHITH A, et al. Swarm intelligence-based radio resource management for V2V-based D2D communication[J]. International Journal of Communication Systems, 2019, 32(17): 3817-3826. DOI:10.1002/dac.3817 |
| [13] |
ZHANG Jiabo, LI Zhe, WANG Chaofan. Performance test and analysis of LTE network for car network[J]. Computer Engineering, 2018, 44(7): 303-307,315. (in Chinese) 张家波, 李哲, 王超凡. 面向车联网的LTE网络性能测试与分析[J]. 计算机工程, 2018, 44(7): 303-307,315. |
| [14] |
TAN Dayu, LI Jingzhao, YANG Dayu, et al. Optimization strategy of information interaction maximum flow transmission in vehicle ad hoc network[J]. Computer Engineering, 2017, 43(5): 8-15,22. (in Chinese) 谭大禹, 李敬兆, 杨大禹, 等. 车载自组网信息交互最大流传输优化策略[J]. 计算机工程, 2017, 43(5): 8-15,22. DOI:10.3969/j.issn.1000-3428.2017.05.002 |
| [15] |
TENG Honglei, WANG Yuegang, YANG Bo, et al. An improved algorithm for nonlinear target tracking based on residual fuzzy matching[J]. Piezoelectrics & Acoustooptics, 2019, 41(2): 311-317. |
| [16] |
BOTSOV M, KLUGEL M, KELLERER W, et al.Location dependent resource allocation for mobile device-to-device communications[C]//Proceedings of 2014 IEEE Wireless Communications and Networking Conference.Washington D.C., USA: IEEE Press, 2014: 1679-1684.
|
| [17] |
MASMOUDI A, FEKI S, MNIF K, et al.Efficient radio resource management for D2D-based LTE-V2X communica-tions[C]//Proceedings of the 15th International Conference on Computer Systems and Applications.Washington D.C., USA: IEEE Press, 2018: 1-6.
|
| [18] |
MASMOUDI A, FEKI S, MNIF K, et al.Efficient scheduling and resource allocation for D2D-based LTE-V2X communications[C]//Proceedings of the 15th International Wireless Communications & Mobile Computing Conference.Washington D.C., USA: IEEE Press, 2019: 496-501.
|
| [19] |
GU Yunan, CAI Lin, PAN Miao, et al.Exploiting the stable fixture matching game for content sharing in D2D-based LTE-V2X communications[C]//Proceedings of 2016 IEEE Global Communications Conference.Washington D.C., USA: IEEE Press, 2016: 1-6.
|
| [20] |
LI X S, SHANKARAN R, ORGUN M, et al.Joint autonomous resource selection and scheduled resource allocation for D2D-based V2X communication[C]//Proceedings of the 87th Vehicular Technology Conference.Washington D.C., USA: IEEE Press, 2018: 1-5.
|
| [21] |
CAIRE G, TARICCO G, BIGLIERI E. Optimum power control over fading channels[J]. IEEE Transactions on Information Theory, 1999, 45(5): 1468-1489. DOI:10.1109/18.771147 |
| [22] |
GJENDEMSJO A, GESBERT D, OIEN G E, et al.Optimal power allocation and scheduling for two-cell capacity maximization[C]//Proceedings of the 4th International Symposium on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks.Washington D.C., USA: IEEE Press, 2006: 1-6.
|
 2021, Vol. 47
2021, Vol. 47
