随着网络和信息技术的不断发展,现实社会中网络信息的数据量呈指数级增长。面对种类繁多的信息,如何获取个性化服务已成为人们的迫切需求。个性化推荐[1]通过各种推荐算法分析用户的行为喜好,能够有效过滤用户不需要的信息,主动为用户提供个性化的产品或服务。目前,个性化推荐已被广泛应用于社交[2]、新闻、音乐、图书和电影网站等应用[3],如网易云音乐[4]、淘宝商品推荐[5]、Netflix和MovieLens电影推荐等。
协同过滤(Collaborative Filtering,CF)技术[6]可用于推荐算法,其主要包括基于内存和基于模型两类算法。其中:基于内存的协同过滤推荐算法通过分析“用户-项目”评分矩阵计算相似度,并根据相似度进行预测推荐;基于模型的协同过滤推荐算法通过用户的历史购买记录、网络操作等数据训练一个预测模型,进而利用此模型对项目进行预测评分。许多研究通过改进协同过滤算法优化了推荐效果,如限制性玻尔兹曼机、K近邻算法[7]、奇异值分解[8](Singular Value Decomposition,SVD)算法及其改进模型(Singular Value Decomposition Plus Plus,SVDPP)。SVD不仅是一个数学问题,其在很多工程中也得到了成功应用。在推荐系统方面,利用SVD可以很容易地得到任意矩阵的满秩分解,进而实现对数据的压缩降维。SVDPP在SVD基础上进一步融入了隐式反馈信息,采用隐式偏好对SVD模型进行优化,因此性能更优。但是SVDPP与SVD都没有考虑时间戳对推荐性能的影响,而实际推荐效果与时间戳仍然有一定的关联性,如十年前的用户对某一部电影的评分与当前用户的评分是有一定差异的,因此有必要对其进行改进,优化预测效果。
本文考虑时间戳对推荐性能的影响,通过马尔科夫决策过程(Markov Decision Process,MDP)对用户、评分、电影和时间进行建模,并利用强化学习Q-learning算法优化推荐算法,从而提升推荐效果,实现更准确的预测。
1 问题描述在使用基于模型的推荐算法进行预测时,SVD和SVDPP模型都没有考虑时间戳对于推荐准确性的影响,而用户之前看过的电影会对他之后选择观看的电影类型及其对电影的评分产生影响。因此,本文利用马尔科夫决策过程对这种时序决策问题建模,反映时间戳数据与评分的关系,并通过强化学习对推荐算法进行优化。
Q-learning算法是一种基于反馈和智能体的无模型的强化学习方法,本文提出一种基于Q-learning算法优化的SVDPP推荐算法RL-SVDPP,以解决SVDPP在电影推荐预测中未考虑时间戳影响的问题。
强化学习[9-10]作为一种机器学习方法,主要原理是智能体以试错的方式进行学习,通过自身与环境交互获得奖励。目前,强化学习已经被成功应用到神经网络和文本处理等领域,但将该方法直接应用于推荐算法的研究较少,现有研究主要通过结合深度神经网络进行模型训练并推荐预测[11]。笔者受启发于Netflix Prize比赛中竞赛选手将时间戳应用到矩阵分解模型[12],以及文献[13]将强化学习用于协同过滤的思路,考虑到用户对一部未看过电影的评分可以通过他之前看过的电影评分来预测,即时间戳会影响用户对未知电影的评分,将SVDPP推荐算法得到的预测评分进一步采用马尔科夫决策过程中的奖惩函数进行优化,建立推荐预测评分与马尔科夫决策过程之间的映射关系,并利用强化学习Q-learning算法[14]进行模型训练,以优化预测过程。
2 建模过程 2.1 奇异值分解现实生活中的“用户-项目”矩阵规模很大,但是由于用户的兴趣和消费能力有限,单个用户消费产生评分的物品是少量的,SVD的核心思想是将高维稀疏的矩阵分解为2个低维矩阵,相对于特征值分解只能用于对称矩阵,SVD能对任意M×N矩阵进行满秩分解,以实现数据压缩。但是在采用SVD对矩阵进行分解之前,需要对矩阵中的空白项进行填充,以得到一个稠密矩阵。假设填充前的矩阵为R,填充后为R',则计算公式为:
| $ {\mathit{\boldsymbol{R}}^\prime } = \mathit{\boldsymbol{PR}}{\mathit{\boldsymbol{Q}}^{\rm{T}}} $ | (1) |
利用SVD算法获取预测评分的计算公式如下:
| $ {\hat r_{ui}} = \mu + {b_u} + {b_i} + \mathit{\boldsymbol{q}}_i^{\rm{T}}{\mathit{\boldsymbol{p}}_u} $ | (2) |
其中:μ代表评分的平均值;bu、bi分别代表用户u和电影i的偏置量;qi、pu分别对应电影和用户在各个隐藏特质上的特征向量,上标T代表转置。
如果用户对某个电影进行了评分,则说明他看过这部电影,这样的行为蕴含了一定的信息,从而可以推理出评分这种行为从侧面反映了用户的喜好,据此可将这种喜好通过隐式参数的形式体现在模型中,得到一个更为精准的模型SVDPP[15]。
利用SVDPP模型获取预测评分的计算公式如下:
| $ {\hat r_{ui}} = \mu + {b_u} + {b_i} + \mathit{\boldsymbol{q}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{p}}_u} + \frac{1}{{\sqrt {|\mathit{\boldsymbol{N}}(u)|} }}\sum\limits_{j \in \mathit{\boldsymbol{N}}(u)} {{y_j}} } \right) $ | (3) |
其中:N(u)为用户u浏览和评价过的所有电影的集合;yj为隐藏的评价了电影j的个人喜好偏置;用户u的偏好程度由显式反馈pu和隐式反馈
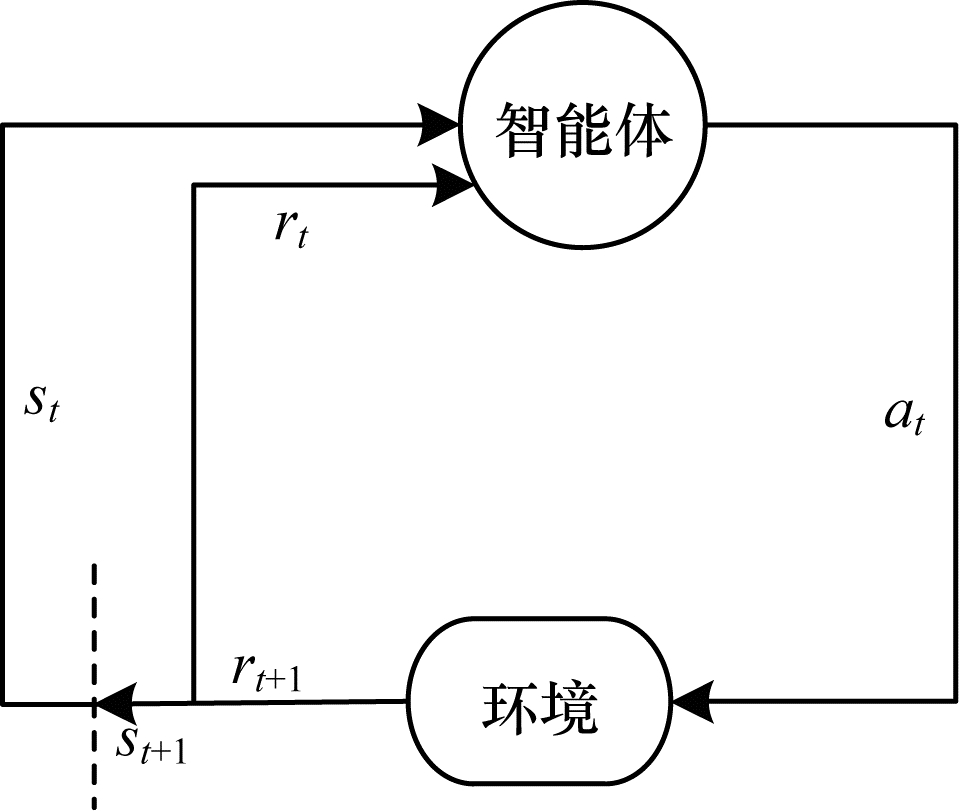
马尔科夫决策过程是决策理论规划、强化学习及随机域中其他学习问题的一种直观和基本的构造模型[16]。在这个模型中,环境通过一组状态和动作进行建模,可用于执行控制系统的状态。通过这种方式来控制系统的目的是最大化一个模型的性能标准。目前,很多问题(如多智能体问题[17]、机器人学习控制[18]和玩游戏的问题[19-20])成功通过马尔科夫决策过程进行建模,因此,马尔科夫决策过程已成为解决时序决策问题的标准方法[21]。
一般的马尔科夫决策过程由五元组
|
Download:
|
| 图 1 马尔科夫决策过程 Fig. 1 Markov decision process | |
采用强化学习方法对SVDPP推荐模型进行优化,首先需要建立推荐预测模型与马尔科夫决策过程的映射关系。由于本文采用MovieLens 1M数据集作为研究对象,因此需要将用户在不同时间戳下对电影的评分转换成五元组以构造马尔科夫决策过程。下面给出本文设计的电影评分到马尔科夫决策过程的映射关系。
1)状态空间S。本文将用户u在时间t下对电影的评分记为状态st(u),因为数据集中用户对电影的评分是[1, 5]区间内的5个整数,所以st(u)的范围为[1, 5],所有时间戳下的状态st(u)构成了状态空间S。
2)动作空间A。考虑到用户u在时间t下看了电影并给出了评分st(u),该评分会影响其(t+1)时间对电影的评分st+1(u),所以将at(u)记为从st(u)到st+1(u)的动作,如式(4)所示,所有时刻的动作at(u)构成了动作空间A。
| $ s_t^{(u)}\mathop \to \limits^{a_t^{(u)}} s_{t + 1}^{(u)} $ | (4) |
3)状态转移概率P。用户u在状态st(u)下采取的动作at(u)是由时间戳决定的,动作at(u)一旦确定,则下一个状态st(u)也同时确定,由此认为状态之间的转移概率也是确定的,即at(u)=st+1(u),P=1,动作at(u)的取值范围为[1, 5]。
4)折扣因子γ。在模型中,每次动作会产生对应的奖励,但是同一用户观看电影的时间远近对选择下一步将观看电影的影响也会不同,γ就是反映该影响的一个因子。越是后期的奖励折扣越大,同时得到的回报总是有限的,因此,设置0≤γ < 1。
5)奖惩函数Rew。奖惩函数值表征了一个状态中完成某个动作所获得的奖励,本文定义奖惩函数值Rew如下:
| $ {R_{{\rm{ew}}}}\left( {s_t^{(u)}, a_t^{(u)}} \right) = s_{t + 2}^{(u)} - {\hat r_{ui}} $ | (5) |
其中:st+2(u)为(t+2)时用户u对电影的评分;
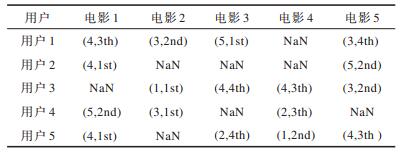
由上述马尔科夫决策过程可知,一个状态转移到下一个状态的动作对应下一个时间电影的评分,虽然这样在表面上忽略了电影名及电影类型,但用户对电影的喜好被隐式地反映在时间戳里,通过这个过程可将MovieLens 1M数据集处理为表 1所示的形式。其中,括号中的第1个数字反映了对应行用户给对应列电影的评分,第2个数字反映了对应行用户观看对应列电影的时间戳信息或者时间顺序,如第1行第1列(4,3th)表示用户1观看电影1的时间顺序是第3个,因此,时间戳t=3且用户1对电影1打了4分,NaN表示对应用户未观看这部电影。
|
下载CSV 表 1 MovieLens 1M数据集部分数据 Table 1 Partial data of MovieLens 1M data set |
将表 1的数据按照时间戳排序,生成的状态转移路径如下:
| $ \begin{array}{l} 5 \rightarrow 3 \rightarrow 4 \rightarrow 3 \\ 4 \rightarrow 5 \\ 1 \rightarrow 3 \rightarrow 4 \rightarrow 4 \\ 3 \rightarrow 5 \rightarrow 2 \\ 4 \rightarrow 1 \rightarrow 4 \rightarrow 2 \end{array} $ |
根据表 1得到该状态转移路径的规则,以第1行为例进行说明。第1行状态转移路径
此状态转移路径表示马尔科夫决策过程中状态的转移,指引了Q表更新的方向。
3 RL-SVDPP算法本文提出的RL-SVDPP算法包括训练与预测两部分。训练时,首先采用SVDPP算法对训练集进行模型训练,得到SVDPP推荐模型,如式(3)所示,然后对强化学习模型进行训练,利用式(5)所示的奖惩函数计算状态转移的奖惩值Rew,完成强化学习Q表的更新,用于SVDPP推荐评分的优化模型。预测时,首先根据SVDPP推荐模型得到预测评分值,再用本文设计的优化模型对预测评分进行优化,得到最终的预测评分。本文设计的优化模型表示如下:
| $ \hat r_{ui}^\prime = {\hat r_{ui}} + Q\left( {s_{t - 2}^{(u)}, a_{t - 2}^{(u)}} \right) $ | (6) |
其中:
首先通过式(3)对训练集进行训练,得到SVDPP推荐模型;然后对强化学习模型进行训练,利用式(5)计算奖惩值Rew,进而将Rew用于Q-learning算法中Q值的更新过程。Q表更新公式如下:
| $ \begin{array}{*{20}{l}} {Q\left( {s_{t + 1}^{(u)}, a_t^{(u)}} \right) = Q\left( {s_t^{(u)}, a_t^{(u)}} \right) + \alpha \left[ {{R_{{\rm{ew}}}}\left( {s_t^{(u)}, a_t^{(u)}} \right) + } \right.}\\ {\left. {\gamma \mathop {\max }\limits_{a_t^{u\prime }} Q\left( {\delta \left( {s_t^{(u)}, a_t^{(u)}} \right), a{{_t^{(u)}}^\prime }} \right) - Q\left( {s_t^{(u)}, a_t^{(u)}} \right)} \right]} \end{array} $ | (7) |
其中:
RL-SVDPP算法训练过程的伪代码如下:
算法 RL-SVDPP算法训练过程
输入 用户数量N,用户已评分的电影M,学习率α,折扣因子γ
输出 预测回报Q(s,a)
初始化Q(s,a)=0,对任意s∈S,a∈A:
训练SVDPP模型,由式(3)计算
从数据中获取初始状态s和动作a;
for each episode i=1:N do
for k=1:Mi do
根据式(5)计算奖惩函数;
将计算出的奖惩函数用于式(7),更新Q表;
end for
end for
3.2 预测过程预测过程根据SVDPP推荐模型得到的预测评分,结合训练的Q表来预测用户u对电影i的评分,同时可预测用户u未观看但是其他用户观看过的电影。
此外,在式(6)所示的预测评分优化模型中不用
本文所采用的MovieLens 1M数据集存在缺省值,即存在没有评分的电影信息。根据本文优化模型的构建思路,后续优化过程中需要利用未评分电影评分信息,这将导致
此外,当t=1,2时,边界的
本文实验采用MovieLens 1M数据集,其中包含6 040个用户对3 952个影片的近1亿条评分,评分范围为1分~5分。本文将数据的80%作为训练集来训练RL-SVDPP模型,其他的20%作为测试集,通过均方根误差(Root-Mean-Square Error,RMSE)来评价推荐算法的准确性。
4.2 评价指标评分预测的准确度一般通过均方根误差来决定,定义如下:
| $ {\rm{RMSE}} = \frac{{\sqrt {\sum\limits_{u, i \in T} {{{\left( {{r_{ui}} - \hat r_{ui}^\prime } \right)}^2}} } }}{N} $ | (8) |
其中:rui表示测试集中用户u对电影i的真实评分;
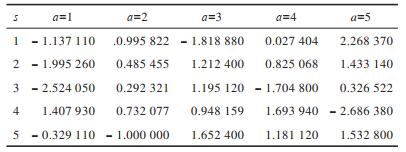
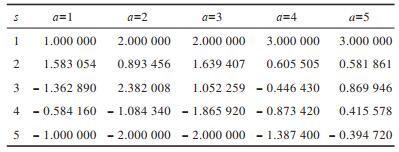
为验证本文算法的有效性,除了对SVDPP模型进行优化得到RL-SVDPP模型外,同时也对SVD模型进行训练,建立优化模型RL-SVD。实验分别建立SVD及SVDPP模型,并求出预测评分,以得到奖惩函数Rew,根据奖惩函数可得到对应的奖惩表,如表 2和表 3所示。奖惩函数作为马尔科夫决策过程中最重要的部分,能够隐式地反映学习目标,指出马尔科夫决策过程的前进方向。在表 2和表 3中,行表示状态,列表示动作,如-1.137 11表示在状态1时,进行动作1得到的奖励值为-1.137 11,其他以此类推,其中奖励值为正表明对正确行为给予奖励,奖励值为负表明对错误动作给予惩罚。
|
下载CSV 表 2 由SVD预测评分得到的奖惩表 Table 2 Reward and punishment table by SVD prediction scores |
|
下载CSV 表 3 由SVDPP预测评分得到的奖惩表 Table 3 Reward and punishment table based by SVDPP prediction scores |
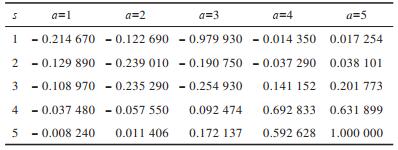
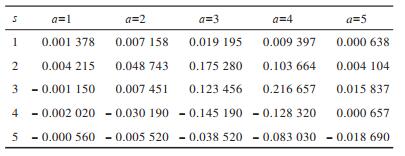
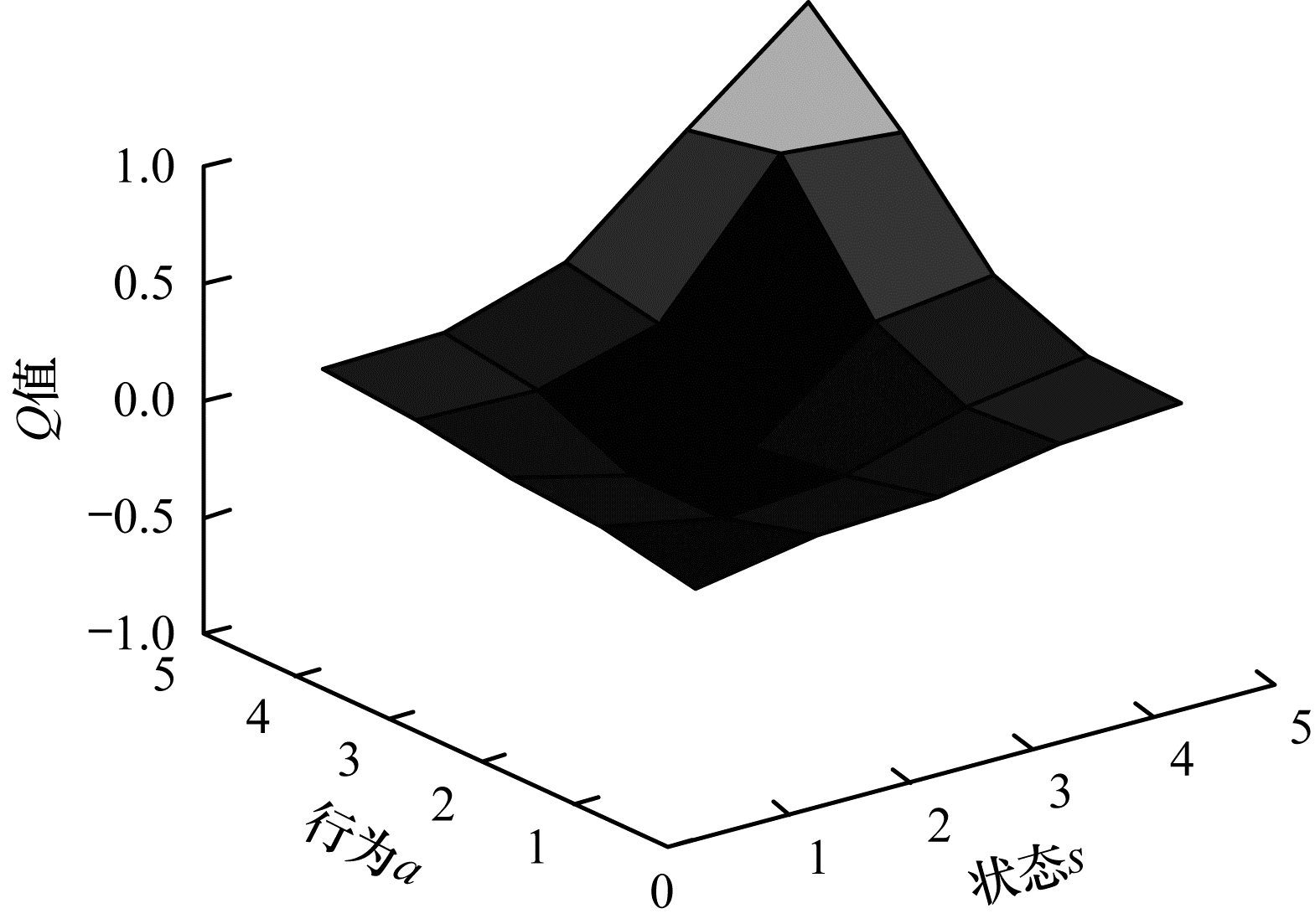
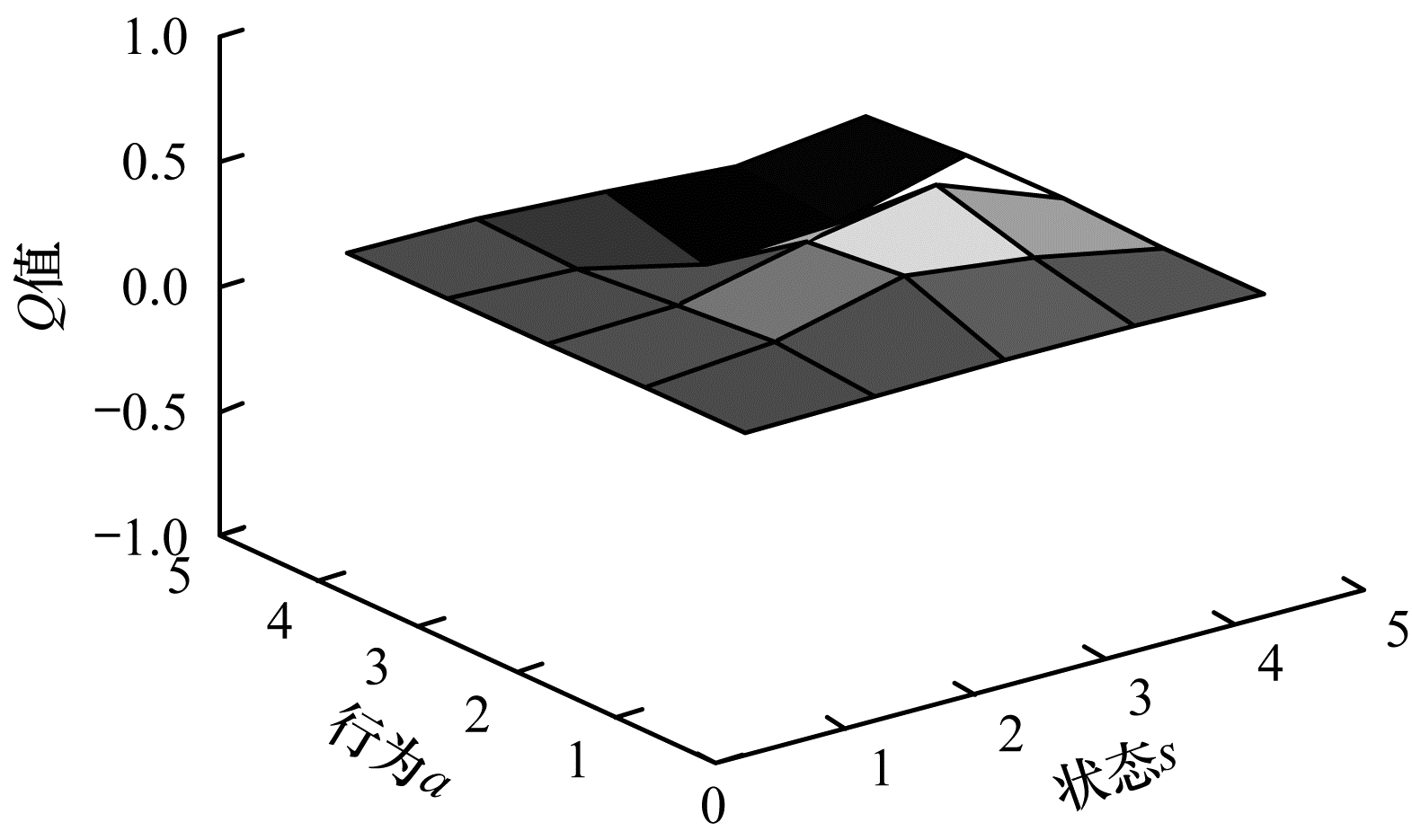
将奖惩函数Rew用于Q表更新过程,更新后的Q表如表 4和表 5所示。可以看出,通过Q-learning算法训练生成的Q表中的值有正有负。为更形象地进行描述,将表中数据绘制成三维空间图,如图 2和图 3所示,其中,凸起和凹陷部分表示在某状态下采取动作获得的期望收益有好有坏。可以看出:RL-SVD算法Q表三维图中Q值动态变化范围较大,变化范围为-0.979 930~1.000 000,25个Q值中有14个为负值;RL-SVDPP算法得到的Q表三维图中Q值动态变化范围较小,变化范围为-0.145 190~0.175 280,25个Q值中有10个为负值。这表明RL-SVDPP选择正确动作得到奖励的情况多于选择错误动作进行惩罚的情况,因此,其优化性能优于RL-SVD。下文将通过RMSE性能对比进一步验证该结论。
|
下载CSV 表 4 由SVD预测评分得到的Q表 Table 4 Q table by SVD prediction scores |
|
下载CSV 表 5 由SVDPP预测评分得到的Q表 Table 5 Q table by SVDPP prediction scores |
|
Download:
|
| 图 2 RL-SVD算法Q表三维图 Fig. 2 3D diagram of Q table for RL-SVD algorithm | |
|
Download:
|
| 图 3 RL-SVDPP算法Q表三维图 Fig. 3 3D diagram of Q table for RL-SVDPP algorithm | |
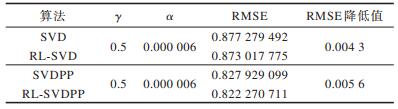
对20%的测试集采用本文提出的优化模型RL-SVD和RL-SVDPP计算预测评分,并通过式(8)求解其与实际评分的均方根误差,验证本文优化方法的有效性。RMSE比较结果如表 6所示。
|
下载CSV 表 6 本文算法与已有SVD/SVDPP的RMSE对比 Table 6 Comparison of RMSE by the proposed algorithm and the existing SVD/SVDPP |
可以看出:相对SVD算法,采用RL-SVD算法得到的预测结果比优化前SVD算法预测结果的RMSE降低了0.004 3;相对SVDPP算法,采用本文提出的RL-SVDPP算法得到的预测结果比优化前SVDPP的RMSE降低了0.005 6,验证了本文融合时间戳信息建立的强化学习优化的推荐模型的有效性,也说明用户对电影的评分与时间戳确实有一定的关系。
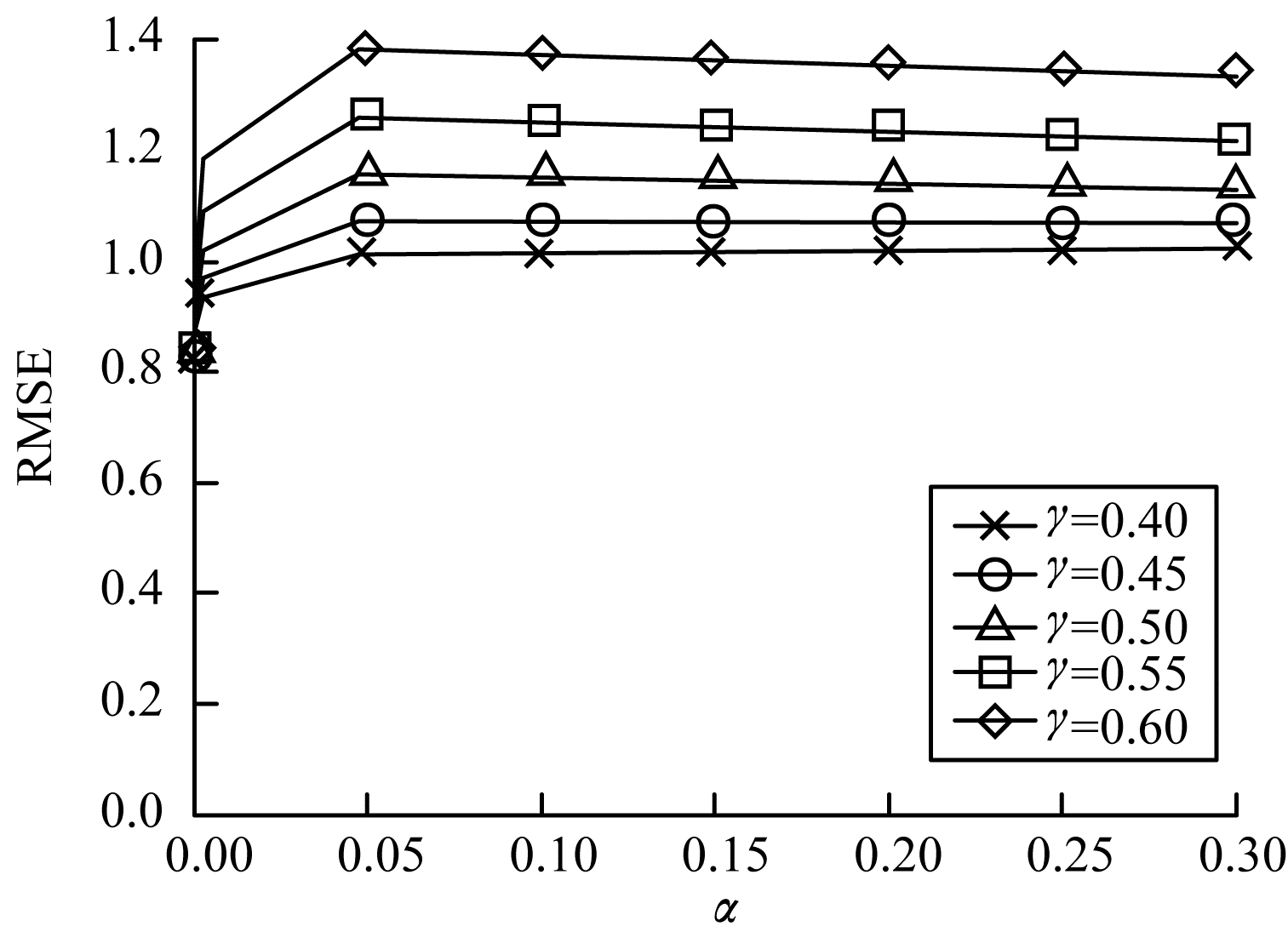
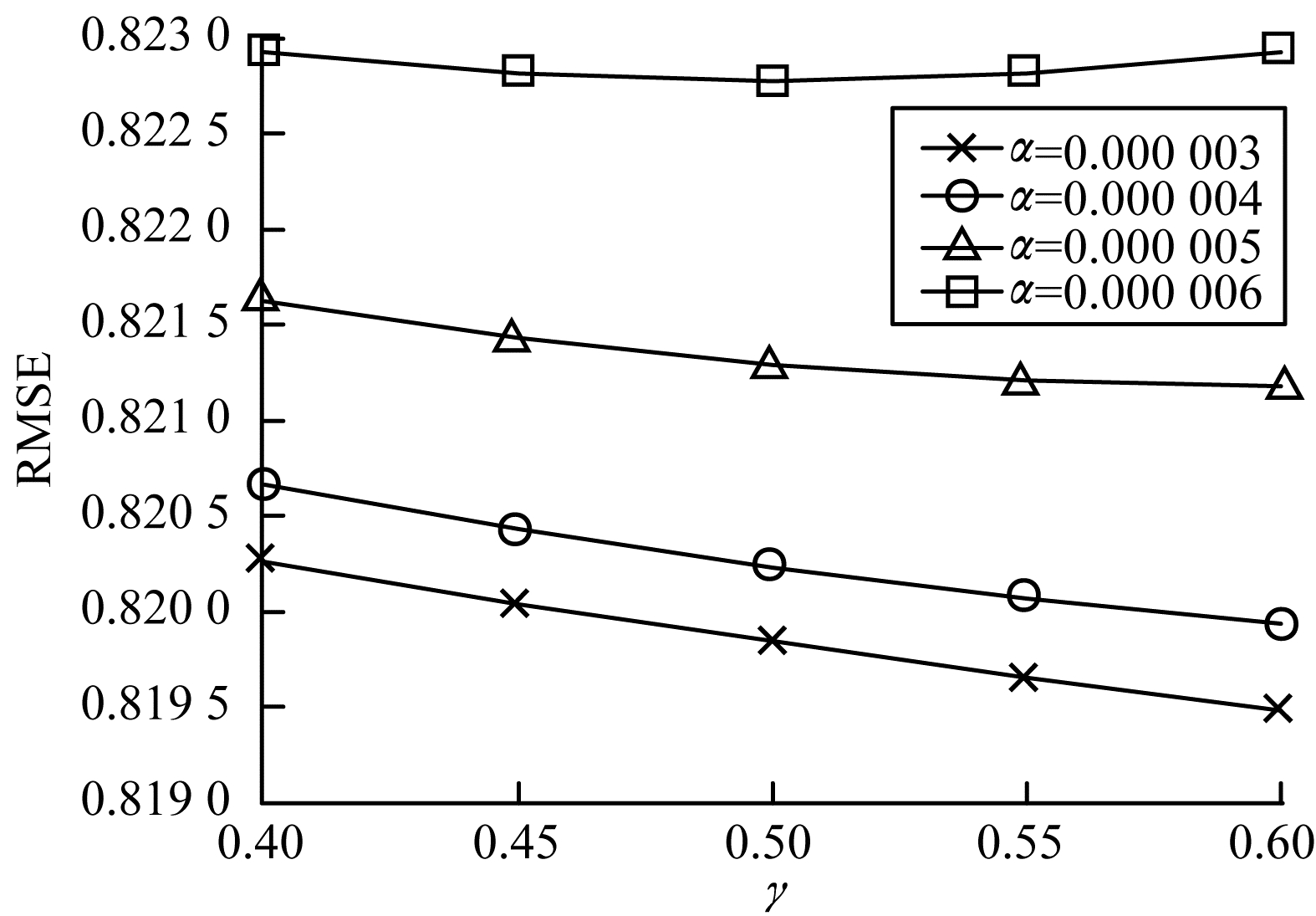
由于学习率α和折扣因子γ是可以动态调整的,因此进一步研究RL-SVDPP算法中α和γ的变化对预测性能的影响,实验结果如图 4和图 5所示。由图 4可知,当γ一定时,α从0.000 003增大到0.3,10倍递增,RMSE的值会增大,并且当α比较大时,RMSE变化很小,因此,α应尽可能取较小的值。由图 5可知,当α一定时,γ从0.4增大到0.6,RL-SVDPP算法的RMSE不断减小,实验中最好的效果是当α=0.000 003和γ=0.6时,此时RMSE能达到0.819 48,相比之前降低了0.008 6,由此证明了RL-SVDPP算法的可行性。
|
Download:
|
| 图 4 γ一定时α变化对RMSE的影响 Fig. 4 Effect of α change on RMSE with constant γ | |
|
Download:
|
| 图 5 α一定时γ变化对RMSE的影响 Fig. 5 Effect of γ change on RMSE with constant α | |
本文提出一种强化学习Q-learning算法优化的SVDPP推荐算法RL-SVDPP。将用户在不同时间戳下对电影的评分动作转化为马尔科夫决策过程,结合协同过滤算法与强化学习奖惩过程进行建模,对SVDPP推荐预测评分进行优化,并通过调整影响因子来改善预测效果。实验结果表明,用户过去的评分数据对当前的评分有显著影响,将用户对电影的喜好隐式地反映在时间戳中,有助于得到更精确的结果。本文仅采用强化学习方法中的Q-Learning对SVDPP进行优化,如何能通过融入时间戳对算法直接进行优化,或者将强化学习与其他推荐方法(如深度学习网络)相结合进行优化,将是下一步的研究方向。
| [1] |
WANG Guoxia, LIU Heping. Overview of personalized recommendation system[J]. Computer Engineering and Applications, 2012, 48(7): 66-76. (in Chinese) 王国霞, 刘贺平. 个性化推荐系统综述[J]. 计算机工程与应用, 2012, 48(7): 66-76. DOI:10.3778/j.issn.1002-8331.2012.07.018 |
| [2] |
GUO Jingjing, MA Jianfeng. Trust recommendation algorithm for Internet of things in virtual community[J]. Journal of Xi'an Dianzi University, 2015, 42(2): 52-57. (in Chinese) 郭晶晶, 马建峰. 面向虚拟社区物联网的信任推荐算法[J]. 西安电子科技大学学报, 2015, 42(2): 52-57. DOI:10.3969/j.issn.1001-2400.2015.02.009 |
| [3] |
XIANG Liang. Practice of recommendation system[M]. Beijing: People's Posts and Telecommunications Press, 2012. (in Chinese) 项亮. 推荐系统实践[M]. 北京: 人民邮电出版社, 2012. |
| [4] |
LI Zhuoyuan, ZENG Dan, ZHANG Zhijiang. Research on music recommendation system based on collaborative filtering and music emotion[J]. Industrial Control Computer, 2018, 31(7): 127-128, 131. (in Chinese) 李卓远, 曾丹, 张之江. 基于协同过滤和音乐情绪的音乐推荐系统研究[J]. 工业控制计算机, 2018, 31(7): 127-128, 131. DOI:10.3969/j.issn.1001-182X.2018.07.055 |
| [5] |
WANG Xiaohao, SUN Yanwu, HU Haoming, et al. Commodity recommendation modeling and simulation analysis based on reputation[J]. Computer Knowledge and Technology, 2019, 15(13): 294-296. (in Chinese) 王小豪, 孙彦武, 胡浩明, 等. 基于信誉度的商品推荐建模与仿真分析[J]. 电脑知识与技术, 2019, 15(13): 294-296. |
| [6] |
HERLOCKER J L, KONSTAN J A, TERVEEN L G, et al. Evaluating collaborative filtering recommender systems[J]. ACM Transactions on Information Systems, 2004, 22(1): 1-47. DOI:10.1145/963770.963771 |
| [7] |
YIN Hang, CHANG Guiran, WANG Xingwei. K-nearest neighbor collaborative filtering algorithm optimized by clustering algorithm[J]. Journal of Chinese Computer Systems, 2013, 34(4): 806-809. (in Chinese) 尹航, 常桂然, 王兴伟. 采用聚类算法优化的K近邻协同过滤算法[J]. 小型微型计算机系统, 2013, 34(4): 806-809. DOI:10.3969/j.issn.1000-1220.2013.04.023 |
| [8] |
WANG Yan, LI Fenglian, ZHANG Xueying, et al. An efficient SVD++ algorithm for improving learning rate[J]. Modern Electronics Technology, 2018(3): 35. (in Chinese) 王燕, 李凤莲, 张雪英, 等. 改进学习率的一种高效SVD++算法[J]. 现代电子技术, 2018(3): 35. |
| [9] |
SUTTON R S, BARTO A G. Reinforcement learning[J]. A Bradford Book, 1998, 15(7): 665-685. |
| [10] |
KAELBLING L P, LITTMAN M L, MOORE A W. An introduction to reinforcement learning[J]. IEEE Transactions on Neural Networks, 2005, 16(1): 285-286. DOI:10.1109/TNN.2004.842673 |
| [11] |
YEHUDA K. Collaborative filtering with temporal dynamics[J]. Communications of the ACM, 2010, 53(4): 1-5. |
| [12] |
CHEN Xu, XU Hongteng, ZHANG Yongfeng, et al.Sequential recommendation with user memory networks[C]//Proceedings of the 11th ACM International Conference on Web Search and Data Mining.New York, USA: ACM Press, 2018: 108-116. https://www.researchgate.net/publication/322965264_Sequential_Recommendation_with_User_Memory_Networks
|
| [13] |
LEE J, OH B, YANG J, et al. RLCF:a collaborative filtering approach based on reinforcement learning with sequential ratings[J]. Intelligent Automation and Soft Computing, 2017, 23(3): 439-444. DOI:10.1080/10798587.2016.1231510 |
| [14] |
WANG Xiaolei, CHEN Yunjie, WANG Chen, et al. Virtual network function scheduling method based on Q-learning[J]. Computer Engineering, 2019, 45(2): 64-69. (in Chinese) 王晓雷, 陈云杰, 王琛, 等. 基于Q-learning的虚拟网络功能调度方法[J]. 计算机工程, 2019, 45(2): 64-69. |
| [15] |
KOREN Y, BELL R. Advances in collaborative filtering[M]. .
|
| [16] |
WHITE D J. Markov decision processes[J]. European Journal of Operational Research, 2010, 39(1): 1-16. |
| [17] |
ZHANG Wenxu, MA Lei, HE Huilin, et al. Cover study on the ground-space heterogeneous multi-agent cooperation of reinforcement learning[J]. Journal of Intelligent Systems, 2018, 13(2): 202-207. (in Chinese) 张文旭, 马磊, 贺荟霖, 等. 强化学习的地-空异构多智能体协作覆盖研究[J]. 智能系统学报, 2018, 13(2): 202-207. |
| [18] |
ZHOU Yi, CHEN Bo. Method for robot obstacle avoidance based on improved dueling network[J]. Journal of Xi'an Dianzi University, 2019, 46(1): 46-50. (in Chinese) 周翼, 陈渤. 一种改进dueling网络的机器人避障方法[J]. 西安电子科技大学学报, 2019, 46(1): 46-50. |
| [19] |
CHEN Xingguo, YU Yang. Reinforcement learning and its application in computer Go[J]. Acta Automatica Sinica, 2016, 42(5): 685-695. (in Chinese) 陈兴国, 俞扬. 强化学习及其在电脑围棋中的应用[J]. 自动化学报, 2016, 42(5): 685-695. |
| [20] |
XU Yan, XIA Junjuan, WU Huijun, et al. Q-learning based physical-layer secure game against multiagent attacks[J]. IEEE Access, 2019, 7: 49212-49222. DOI:10.1109/ACCESS.2019.2910272 |
| [21] |
WIERING M, OTTERLO M.Reinforcement learning[G]//Adaptation, learning, and optimization.Berlin, Germany: Springer, 2012, 12: 3.
|
 2021, Vol. 47
2021, Vol. 47

 ,
,