0 概述

随着人工智能技术的快速发展，智能体规划被广泛应用于组合调度、游戏博弈等任务^[1-2]中，然而现实世界中的动态系统多数面向部分可观测环境，针对部分可观测环境下的智能体规划问题，部分可观测马尔科夫决策过程(Partially Observable Markov Decision Process，POMDP)模型应用而生^[3-5]。POMDP模型的核心思想是将动态系统中的不确定性规划问题转化为最优化问题进行求解，但由于其基于系统隐含状态空间进行建立，因此人为建立模型需要大量先验知识并且存在容易陷入局部极小值的问题^[6-7]。深度神经网络作为一种多层次特征学习网络，能够自动从训练数据中学习抽象特征^[8]。KARKUS等人在深度神经网络与QMDP模型的基础上，提出基于卷积神经网络(Convolutional Neural Network，CNN)的POMDP值迭代算法QMDP-net^[9]，其是QMDP模型的网络化表示，能使POMDP模型所需的参数以网络中权值的形式通过训练数据进行自动学习，无需提供大量的先验知识或假设POMDP模型已知。此外，QMDP-net已被证明在未预先给定环境模型的情况下可有效解决2D网格地图上的导航规划问题^[10-12]。

由于QMDP-net中的值迭代模块是通过卷积层与最大池化层相结合的网络结构进行表示，然而该网络结构使得QMDP-net存在训练结果不稳定、随机种子及超参数敏感等问题^[13-14]。为解决上述问题，本文提出一种基于循环卷积神经网络(Recurrent Convolutional Neural Network，RCNN)的POMDP值迭代算法RQMDP-net，使用门控循环单元(Gated Recurrent Unit，GRU)网络实现值迭代过程，并以经典游戏《格子世界》网格地图上的导航规划任务为例对RQMDP-net算法的有效性进行验证。

1 基于CNN的POMDP值迭代算法 1.1 POMDP模型

POMDP是一种对部分可观测环境规划问题进行系统建模的常用模型。POMDP模型由一个七元组构成：M=(S，A，O，T，Z，R，b₀)^[15]，其中：S、A、O分别表示动态系统的所有状态集合、动作集合和观测集合；$\mathit{\boldsymbol{T}}\left({s, a, {s^\prime }} \right) = \Pr \left({{s^\prime }\mid s, a} \right)$表示状态转移概率，即在状态s下执行动作a后，转移到其他状态s'的概率分布；$\mathit{\boldsymbol{Z}}(s, a, o) = \Pr (o\mid s, a)$表示观测概率，即在状态s下执行动作a后，获得观测值o的概率分布；R(s，a)表示在状态s下执行动作a所获得的奖励；b₀表示初始状态分布，即在初始时刻智能体在状态集合S上的分布。

在部分可观测环境下，智能体仅通过当前观测无法准确感知当前所处的状态，因此需要根据过去的历史序列$\left\{a_{1}, o_{1}, a_{2}, o_{2}, \cdots, a_{t}, o_{t}\right\}$对当前状态进行估计。POMDP引入信念状态b来表示智能体的当前状态，其中b是对过去所有历史信息的总体统计量，代表当前所有隐含状态的概率分布^[16]。在已知当前信念状态b、执行动作a和获得观测值o的情况下，通过贝叶斯公式的更新来获得下一时刻的信念状态^[17]可表示为：

$\begin{array}{*{20}{l}} {\mathit{\boldsymbol{b}}{\rm{'}}\left( {s{\rm{'}}} \right) = {\rm{Pr}}(s{\rm{'}}|o, a, \mathit{\boldsymbol{b}}) = \frac{{{\rm{Pr}}(o|s{\rm{'}}, a, \mathit{\boldsymbol{b}}){\rm{Pr}}(s{\rm{'}}|a, \mathit{\boldsymbol{b}})}}{{{\rm{Pr}}(o|a, \mathit{\boldsymbol{b}})}} = }\\ {\quad \quad \quad {\rm{}}\frac{{\mathit{\boldsymbol{Z}}\left( {s{\rm{'}}, a, o} \right)\mathop \sum\limits_{s \in S} \mathit{\boldsymbol{T}}\left( {s, a, s{\rm{'}}} \right)\mathit{\boldsymbol{b}}\left( s \right)}}{{{\rm{Pr}}(o|a, \mathit{\boldsymbol{b}})}}} \end{array}$

(1)

1.2 值迭代对POMDP的求解

值迭代对POMDP的求解是在建立准确POMDP模型的基础上，使用值迭代算法进行动作选择以达到回报最大化的目的。值迭代作为求解马尔科夫决策过程(Markov Decision Process，MDP)的一种经典动态规划算法，其从任意初始状态值开始，使用贝尔曼方程组迭代求解状态的值函数。令${\mathit{\boldsymbol{V}}_k}\left(s \right)$表示状态s在第k次迭代中的评估值，值迭代过程可表示为^[9]：

${\mathit{\boldsymbol{Q}}_{k + 1}}\left( {s, a} \right) = \mathop \sum \limits_{s{\rm{'}}} {\rm{Pr}}(s{\rm{'}}|s, a)\left( {\mathit{\boldsymbol{R}}\left( {s, a, s{\rm{'}}} \right) + \gamma {\mathit{\boldsymbol{V}}_k}\left( {s{\rm{'}}} \right)} \right)$

(2)

${\mathit{\boldsymbol{V}}_{k + 1}}\left( s \right) = \mathop {{\rm{max}}}\limits_a {\mathit{\boldsymbol{Q}}_{k + 1}}\left( {s, a} \right)$

(3)

POMDP模型使用信念状态b表示智能体当前所处状态，其向量中元素b(s)表示智能体当前处于状态s的概率。当k趋于无穷大时，值函数V(s)会收敛于最优值函数V^*(s)，此时在b状态下执行动作a所得的最大回报$\boldsymbol{Q}(\boldsymbol{b}, a)=\sum\limits_{s \in S} \boldsymbol{b}(s) \boldsymbol{Q}_{\infty}(s, a)$，其对应的最优策略可表示为：

${\pi ^{\rm{*}}}\left( \mathit{\boldsymbol{b}} \right) = \mathop {{\rm{argmax}}}\limits_a \mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{b}}, a} \right)$

(4)

1.3 QMDP-net算法

由于使用值迭代算法对POMDP问题进行求解的前提是建立准确的POMDP模型，然而学习动态系统的POMDP模型通常很困难，因此模型建立需要大量的先验知识。QMDP-net是一种用于解决部分可观测环境下动态规划问题的网络化值迭代算法。QMDP-net使用深度神经网络对POMDP算法的求解过程进行表示，使得所需POMDP模型的参数可以以网络中权值的形式通过训练数据进行自动学习^[9]。因此，QMDP-net可以在无先验知识的情况下对POMDP问题进行求解。

QMDP-net共分为POMDP模型和值迭代过程两部分。QMDP-net将POMDP模型中的状态转移概率、观测概率和奖励函数参数化为：

$ \mathit{\boldsymbol{T}}\left( {s, a, s{\rm{'}}} \right) = {f_\mathit{\boldsymbol{T}}}(s, a, s{\rm{'}}|{W_\mathit{\boldsymbol{T}}}) $

(5)

$\mathit{\boldsymbol{Z}}\left( {s, a, o} \right) = {f_\mathit{\boldsymbol{Z}}}(s, a, o|{W_\mathit{\boldsymbol{Z}}})$

(6)

$\mathit{\boldsymbol{R}}\left( {s, a} \right) = {f_\mathit{\boldsymbol{R}}}(s, a|{W_\mathit{\boldsymbol{R}}})$

(7)

其中，函数f_T、f_Z和f_R分别使用卷积神经网络进行表示，其对应的内核权重W_T、W_Z和W_R通过端到端的训练方式从训练数据中获得。

在使用卷积层来参数化规划所需模型的基础上，利用卷积层和最大池化层构造值更新过程，并通过循环更新操作达到价值迭代的目的。第k次状态值的更新过程可表示为：

${\mathit{\boldsymbol{Q}}_{k + 1}}\left( {s, \bar a} \right) = W_\mathit{\boldsymbol{R}}^{\bar a}\mathit{\boldsymbol{R}}\left( {s, a} \right) + W_\mathit{\boldsymbol{V}}^{\bar a}{\mathit{\boldsymbol{V}}_k}\left( s \right)$

(8)

${\mathit{\boldsymbol{V}}_{k + 1}}\left( s \right) = \mathop {{\rm{max}}}\limits_a {\mathit{\boldsymbol{Q}}_k}\left( {s, a} \right)$

(9)

其中，$\bar a \in A$表示系统中可执行的动作，Q、V、R分别表示动作-状态值函数、状态值函数和奖励函数，$W_\mathit{\boldsymbol{R}}^{\bar a}、W_\mathit{\boldsymbol{V}}^{\bar a}$是用于构造奖励函数和状态值函数的卷积网络中a对应的卷积核。

2 基于RCNN的POMDP值迭代算法 2.1 算法思想

虽然QMDP-net在无先验知识的情况下具有较好的性能表现，但其存在训练效果不稳定、参数敏感等优化难题。QMDP-net使用卷积层与最大池化层相结合的网络结构表示状态值的更新过程，由于卷积神经网络不具备记忆功能，因此需要通过不断循环运行该网络模块来达到值迭代的效果。循环神经网络(Recurrent Neural Network，RNN)具有记忆功能，更适合于循环处理时序问题^[18]，因此，将值迭代过程编码为循环神经网络可有效缓解QMDP-net的优化难题。

由于RNN无法解决长期依赖问题，当循环次数较多时容易出现梯度消失现象^[19]，因此本文使用门控循环单元网络来模拟值迭代过程，提出基于循环卷积神经网络的POMDP值迭代算法RQMDP-net。GRU通过门控机制有效缓解了RNN的梯度消失问题，而且相比LSTM具有更简单的网络结构^[20]。将值迭代过程使用由GRU和CNN结合构造的循环卷积神经网络进行表示，具体为：

$ {\mathit{\boldsymbol{V}}_k}\left( s \right) = {\rm{GRU}}\left( {W_\mathit{\boldsymbol{R}}^a\mathit{\boldsymbol{R}}\left( {s, a} \right) + W_\mathit{\boldsymbol{V}}^a{\mathit{\boldsymbol{V}}_{k - 1}}\left( s \right)} \right) $

(10)

其中：$W_\mathit{\boldsymbol{R}}^a$和$W_\mathit{\boldsymbol{V}}^a$表示转移函数的卷积神经网络中的卷积核，卷积核数量为|A|；GRU的隐含状态${\mathit{\boldsymbol{V}}_{k - 1}}\left(s \right)$和奖励$\mathit{\boldsymbol{R}}\left({s, a} \right)$在进行CNN状态转移计算后作为输入GRU进行新一轮迭代，在实现循环计算的同时保留QMDP-net的输入和递归权重矩阵的卷积特性。

2.2 RQMDP-net算法

RQMDP-net在经典游戏《格子世界》网格地图上的导航规划任务中，系统状态空间为N×N(其中N为网格数量)，对应信念状态b可由N×N矩阵表示，该模型已知包含地图和任务目标信息的环境参数X。

对于POMDP模型的建立，本文使用双卷积神经网络结构。对实现状态更新的贝叶斯公式进行分解并将其表示为神经网络，其模型网络结构表达式为：

$\mathit{\boldsymbol{b}}_t^{\rm{'}}\left( {s{\rm{'}}, a} \right) = {\rm{CNN}}({\mathit{\boldsymbol{b}}_t}\left( s \right){\rm{}}|{W_\mathit{\boldsymbol{T}}})$

(11)

$\mathit{\boldsymbol{b}}_t^{\rm{'}}\left( {s{\rm{'}}} \right) = {\mathit{\boldsymbol{\omega }}_{{a_t}}}\mathit{\boldsymbol{b}}_t^{\rm{'}}\left( {s{\rm{'}}, a} \right)$

(12)

$\mathit{\boldsymbol{b}}_t^{\rm{'}}\left( {s{\rm{'}}, o} \right) = {\rm{CNN}}(\mathit{\boldsymbol{b}}_t^{\rm{'}}\left( {s{\rm{'}}} \right){\rm{}}|{W_\mathit{\boldsymbol{Z}}})$

(13)

${\mathit{\boldsymbol{b}}_{t + 1}}\left( {s{\rm{'}}} \right) = {\mathit{\boldsymbol{\omega }}_{{o_t}}}\mathit{\boldsymbol{b}}_t^{\rm{'}}\left( {s{\rm{'}}, o} \right)$

(14)

其中：${\mathit{\boldsymbol{\omega }}_{{a_t}}}$表示输入动作a_t经过one-hot编码形成的权重向量；${\mathit{\boldsymbol{\omega }}_{{o_t}}}$表示当前观测o_t经过全连接层后输出的权重向量；$\mathit{\boldsymbol{b}}_t^{\rm{'}}\left({s{\rm{'}}, a} \right)$、$\mathit{\boldsymbol{b}}_t^{\rm{'}}\left({s{\rm{'}}, o} \right)$分别为具有|A|个卷积核和|O|个卷积核的卷积网络的输出，其大小为N×N×|A|和N×N×|O|。

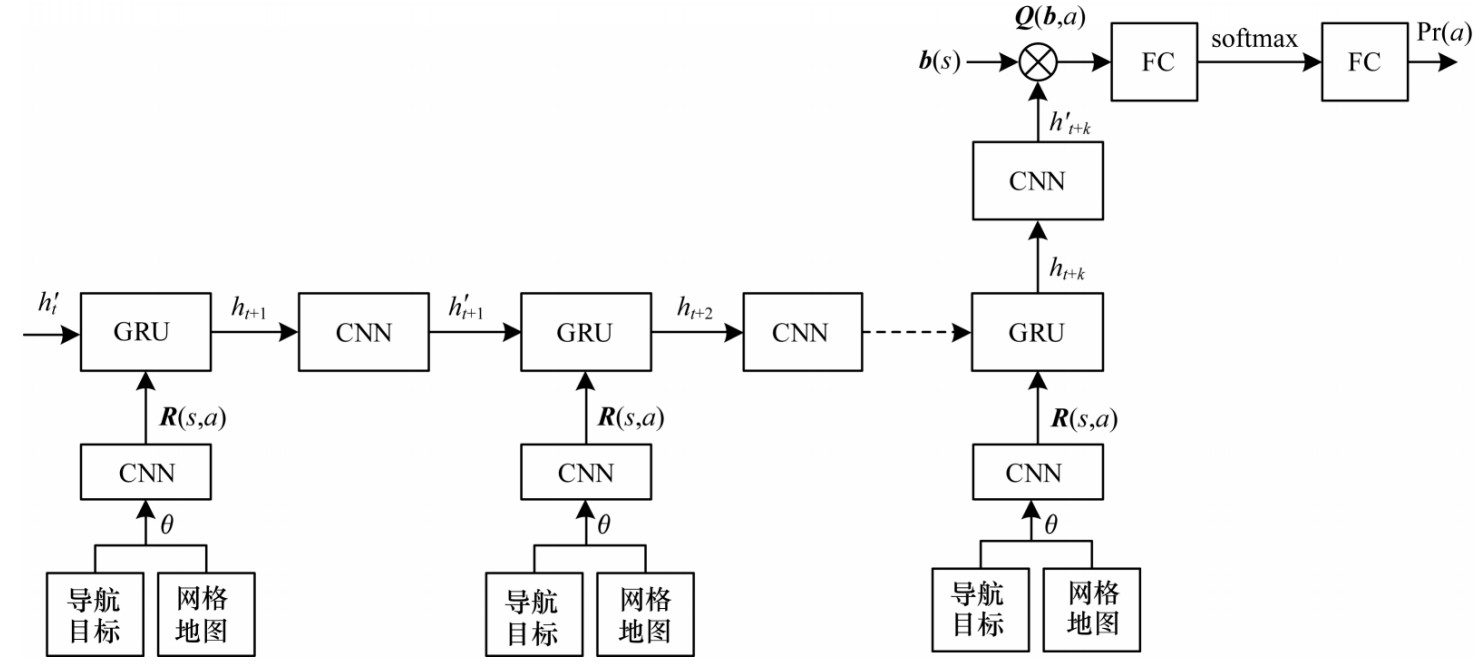
本文使用循环卷积神经网络实现值迭代过程，RQMDP-net网络结构如图 1所示。可以看出，表示网格地图和任务目标的图像信息θ通过表示奖励函数f_R的网络转换为大小为N×N×|A|的奖励信息R(s, a)，此网络是由两个卷积层组成的卷积神经网络：第一层卷积包含150个大小为3×3的卷积核，并使用线性整流函数(Relu)作为激活函数，其作用是对输入图像信息进行特征提取；第二层卷积包含|A|个1×1的卷积，其作用是将前一层输出的特征转换为用于价值迭代计算的R(s，a)。在奖励信息计算完成后，通过GRU实现价值迭代的计算过程，此处循环神经网络的神经元个数设置为150。在每次迭代时，作为状态价值V(s)的GRU隐含状态h_t经过表示转移函数f_T的网络后转换为表示Q(s, a)的h'_t，其网络由一个包含|A|个大小为3×3卷积核的卷积层组成，之后h'_t与R(s, a)分别作为GRU的隐含状态和输入参与下一次迭代的值计算。经过K次迭代后的h'_t+K与当前信念状态b(s)相乘并加和得到Q(b, a)，即在当前信念状态b下，执行动作可获得Q值。最终经过全连接(Fully Connected，FC)层和softmax层计算得到表示关于所有可执行动作的概率分布Pr(a)，并选择对应Pr(a)最大的a作为最优动作。

本文采用反向传播算法^[21]最小化交叉熵损失函数来优化深度神经网络模型，并将表示动作选择错误程度的损失函数定义为：

$ L=-\frac{1}{T} \sum\limits_{t=1}^{|T|} \sum\limits_{i=1}^{|A|} y_{t, i}^{\prime} \log _{a} y_{t, i} $

(15)

其中，y'_{t, i}为训练样本中t时刻标签动作经过one-hot编码后对应向量中第i个元素的值，y_{t, i}为t时刻网络输出的动作概率分布中第i个元素的值。

3 实验与结果分析

为验证基于循环卷积神经网络的值迭代算法RQMDP-net的有效性，实验在经典游戏《格子世界》网格地图上的导航规划任务中对RQMDP-net与QMDP-net的执行情况进行对比，并基于TensorFlow实现算法网络框架的搭建，同时使用NVIDIA 1060 GPU加速图像处理。

3.1 实验环境

实验任务是使智能体在N×N网格地图中进行导航。智能体已知的环境参数为标明障碍物和导航目标的N×N网格地图，其能观测四周是否有障碍物信息，而不同的位置周围障碍物的分布情况可能相同，因此智能体无法仅根据当前观测信息来获知自身在网格中的准确位置，即智能体状态。智能体可执行的动作包括向四周走动和原地不动5个。

3.2 实验设置与结果分析

在实验中，将来自1 300种随机环境下的65 000条专家轨迹(每个环境对应50条专家轨迹)作为数据集，其中，1 000种随机环境的50 000条轨迹作为训练集，300种环境的15 000条轨迹作为测试集。在网络训练过程中使用ADAM优化器更新网络参数，其初始学习率为0.000 1。

本文实验将导航准确率和交叉熵损失值作为算法性能评价指标，其中，导航准确率为智能体导航至目标位置的概率，交叉熵损失值为当前网络动作选择错误的概率。实验中有网格数量N和值迭代次数K 2个控制变量，其中，N取值为10、18、24、36，K取值为3、5、10、15。本文通过两组实验验证算法有效性及控制变量变化对算法性能的影响。

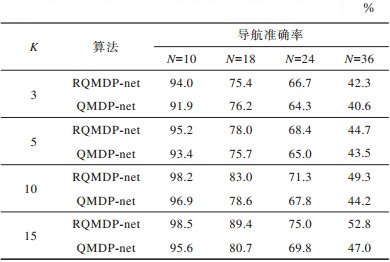
第1组实验通过设置不同的网格数量和值迭代次数来对比RQMDP-net和QMDP-net的导航准确率。由表 1可以看出，在不同的网格数量下，RQMDP-net的导航准确率高于QMDP-net。在相同的网格数量下，随着值迭代次数的增加，RQMDP-net的导航准确率在多数情况下相比QMDP-net增长更快。可见，RQMDP-net在10×10网格地图中的导航准确率高达98.5%，并且在36×36网格地图中相比QMDP-net最多提升5.8个百分点。

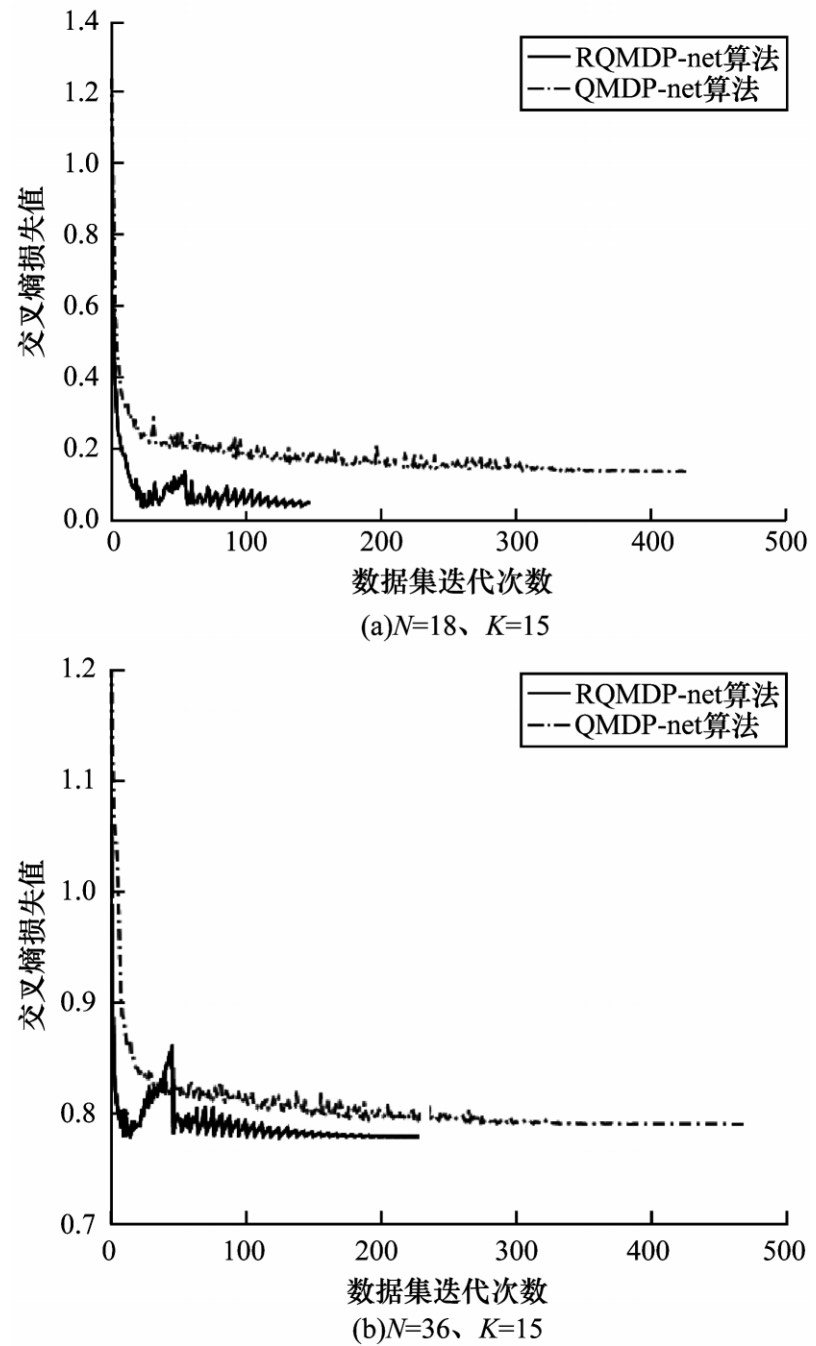
第2组实验通过设置不同的网格数量和值迭代次数来对比RQMDP-net和QMDP-net的交叉熵损失值下降情况。由图 2可以看出，与QMDP-net相比，RQMDP-net的交叉熵损失值下降更快，可经过更少的数据集迭代次数达到最低值，主要原因为RQMDP-net利用GRU网络使其时序处理能力更强，最终交叉熵损失值也更小，即相同条件下的RQMDP-net动作选择错误的概率小于QMDP-net。

4 结束语

本文提出一种基于循环卷积神经网络的POMDP值迭代算法RQMDP-net。利用GRU网络与CNN实现值迭代过程，解决了仅由卷积层和最大池化层构成的QMDP-net训练不稳定、超参数设置敏感等问题，并且通过GRU网络的强时序处理能力，提升了RQMDP-net的算法运行速度。实验结果表明，与QMDP-net相比，RQMDP-net在训练过程中网络收敛速度更快，任务规划能力更强。后续可将RQMDP-net扩展至具有更复杂状态空间的导航规划任务中，进一步提高其适用性与通用性。