开放科学(资源服务)标志码(OSID):
人员应急疏散安全是公共安全的一个重要环节,在人群密集的地方,如商场、医院大厅、地铁隧道等公共场所发生突发事件时,极易造成严重的拥堵,甚至是踩踏和伤亡事件。因此,高效安全地疏散人群成为保障社会安全问题的关键。
近年来,人群疏散问题得到了科研工作者的关注和重视。现有的疏散模型主要有两大类[1],一类是以人群整体为考察对象的宏观模型,如流体力学模型[2],另一类是以行人个体为考察对象的微观模型,如元胞自动机模型[3]和社会力模型[4-5]。流体力学模型将行人视为连续的流体,不考虑行人之间的作用力,忽视个体差异,因而该模型不适用于突发情形下的人群疏散。尽管元胞自动机因算法难度低而得到广泛运用,但其离散的状态和时空不连续导致模拟结果不准确,难以反映紧急情况下人群逃生时的真实状况。社会力模型考虑了行人的主观心理、行人之间的安全距离以及行人回避障碍物的行为等真实现象,有效地体现了行人在紧急情况下的运动状况。
计算机软硬件技术的快速发展使得研究人员能够利用智能设备、计算机技术等研究人群疏散问题。文献[6]提出利用智能移动终端内的传感器采集行人数据,能较为准确地疏散行人并引导至出口。文献[7]提出了利用机器人的自身运动来影响行人运动状态的方法,虽然人群疏散的效率得到有效提升,但是机器人单一的直线运动使其无法应用于其他复杂的疏散场景,灵活性较低。因此,更多研究者将机器学习的方法[8]应用到机器人运动规划领域,其中一种重要的模型就是深度Q网络(Deep Q-Network,DQN)[9]。DQN仅通过图像输入就能实现从感知到动作的端到端学习,并在基于视频感知的控制任务领域[10]以及无人机[11]、多智能体[12]领域取得了较高的成就。而机器人疏散人群时需要借助人群疏散场景图中的人群位置、机器人位置等空间特征进一步分析从而采取相应的疏散措施,因而将深度强化学习应用于机器人疏散人群范畴是一个有效手段。文献[13]利用DQN使机器人根据特定的场景学习获得疏散人群的运动策略,该方法对相似场景的移植性强,但网络模型较简单,难以提取复杂场景的空间特征。
长短期记忆网络[14](Long Short-Term Memory,LSTM)的提出较好地解决了时序数据表达的问题,LSTM吸引了大量研究者的关注并得到优化和发展,且在文本分类[15]和位置预测[16]领域也有很好的应用。而人群疏散是一个不间断的、前后时间有关联性的过程,如果只考虑每个独立帧的人群状态而忽视前后帧之间的时间特征,则在一定程度上会影响机器人疏散人群的效率。
针对目前人群疏散方法中存在机器人单一的运动规则、机器人灵活性差、场景适用性有限的问题,本文利用人机社会力模型,通过机器人的运动来“控制”周围人群的运动状态,设计一种基于深度时空Q网络(Deep Spatial-Temporal Q-Network,DSTQN)的机器人疏散人群的算法,通过加深CNN的网络层数提取复杂场景的空间特征,并在深度Q网络的基础上融入LSTM,研究人群疏散场景的时间关联性。
1 人机社会力模型机器人疏散人群的前提是机器人能够与人群进行交互,利用机器人的运动来影响和“控制”人群的运动。本文采用的人机社会力模型是建立在文献[4]提出的社会力模型基础上,实现机器人与行人的交互。社会力模型的理论基础是牛顿第二定律,通过将行人看作具有自驱动力的粒子,并计算粒子的自驱动力、粒子间的相互作用力以及粒子与障碍物的相互作用力之和来分析行人运动状态,综合考虑行人的主观心理和外界干扰因素而设计的行人运动力学模型,达到真实模拟行人在紧急情况下逃生状况的目的。人机社会力模型利用机器人和行人的相互作用力,即人机作用力来影响行人运动的方向和速度[7],进而达到人群疏散的目的,基本公式如式(1)所示:
| $ {m}_{i}\frac{\mathrm{d}{v}_{i}\left(t\right)}{\mathrm{d}t}={f}_{s}+\sum\limits_{j(\ne i)}{f}_{ij}+{f}_{iw}+{f}_{ir} $ | (1) |
式(1)定量地描述了行人i的受力情况,其中,mi是质量,vi(t)是当前速度,fs是自驱动力,fij是其与行人j的相互作用力,fiw是障碍物与行人i之间的相互作用力,人机作用力的计算如式(2)所示:
| $ \begin{array}{l}{f}_{ir}=\left[{A}_{r}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{{r}_{ir}-{d}_{ir}}{{B}_{r}}\right)+{K}_{r}\mathrm{g}({r}_{ir}-{d}_{ir})\right]{\boldsymbol{n}}_{ir}+\\ \;\;\;\;\;\;\;\;\;\;{}_{}{\kappa }_{r}\mathrm{g}({r}_{ir}-{d}_{ir})\mathrm{\Delta }{V}_{ir}\left(t\right){\boldsymbol{t}}_{ir}\end{array} $ | (2) |
其中,Ar和Br分别代表人机作用力的强度和范围,rir是机器人与人的几何中心距离,Kr、κr是系数,nir是机器人指向行人i的单位向量,tir是其正交单位向量,Δvir(t)是机器人与行人i的速度差。
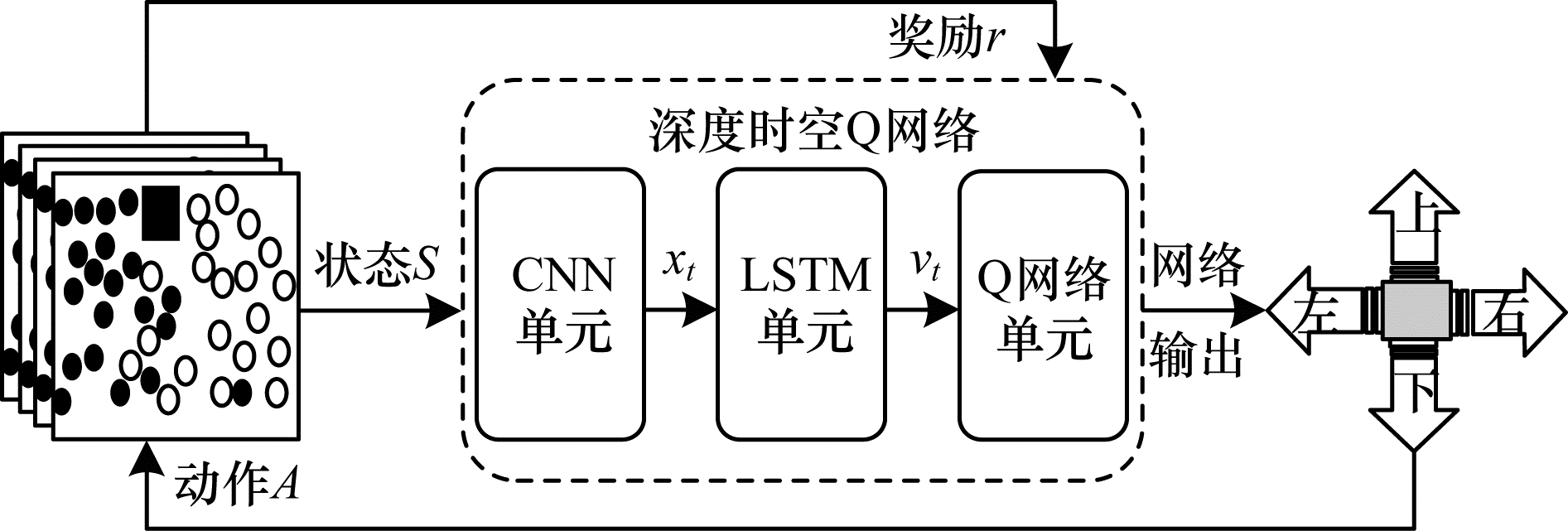
2 基于深度时空Q网络的人群疏散算法本文设计的基于深度时空Q网络的人群疏散算法流程如图 1所示,将人群疏散的场景图作为状态S输入DSTQN,通过CNN提取复杂的人机交互场景图像的空间特征xt,再送入LSTM提取时间特征vt,经过维度处理后输出一维的带有时空特征的特征序列,最后经过Q网络单元计算Q值得到当前疏散人群的动作A,并根据与环境交互得到的奖励r来判断此时动作的优劣。如此循环迭代,机器人再根据下一个状态和奖励不断学习,优化疏散人群的动作并输出得到更高的奖励。
|
Download:
|
| 图 1 基于深度时空Q网络的人群疏散算法流程 Fig. 1 Procedure of crowd evacuation algorithm based on deep spatio-temporal Q-network | |
DQN是一种结合卷积神经网络(Convolutional Neural Network,CNN)[17]和强化学习的Q学习[18]经典强化学习算法,用深度神经网络取代强化学习的Q表,使机器人在新环境中探索学习。状态、动作和奖励构成了DQN的核心三要素,DQN模型的建立依据Q学习和马尔科夫决策。本文采用的Q网络模型基于文献[19],由两层输出节点数量分别为512和4的全连接层构成,模型将机器人与环境交互的状态输入到主Q网络,机器人则根据Q值计算得到该值最大时的动作。目标Q网络的参数通过定期复制主Q网络的参数得到,并最小化当前Q值和目标Q值的均方误差更新网络参数以降低两者之间的相关性。DQN利用经验回放机制将机器人与环境交互的转移样本存储在记忆池,随机抽取小批量的样本通过随机梯度下降算法反向更新网络参数θ,不断重复直至损失函数收敛,使机器人找到最优的策略疏散人群。损失函数如式(3)所示,当前动作的Q值如式(4)所示,目标Q值如式(5)所示。
| $ L\left(\theta \right)=\mathrm{E}\left[{\left({T}_{\mathrm{T}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}Q-Q\left(s, a;\theta \right)\right)}^{2}\right] $ | (3) |
| $ {Q}^{*}(s, a)=Q(s, a)+\alpha (r+\gamma \mathrm{m}\mathrm{a}{\mathrm{x}}_{{a}^{\mathrm{'}}}Q(s', a')-Q(s, a\left)\right) $ | (4) |
| $ {T}_{\mathrm{T}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}Q=r+\gamma \mathrm{m}\mathrm{a}{\mathrm{x}}_{{a}^{\mathrm{'}}}Q(s', a';\theta ) $ | (5) |
其中,s为是机器人的当前状态,
本文将LSTM融入到DQN中来提取人群疏散场景图像前后帧之间的时间特征,并将包含时空特征的序列送入到Q网络中得到机器人的运动指令。因此,本文设计的DSTQN模型由CNN层网络、LSTM层网络和Q网络组成,如图 1所示。
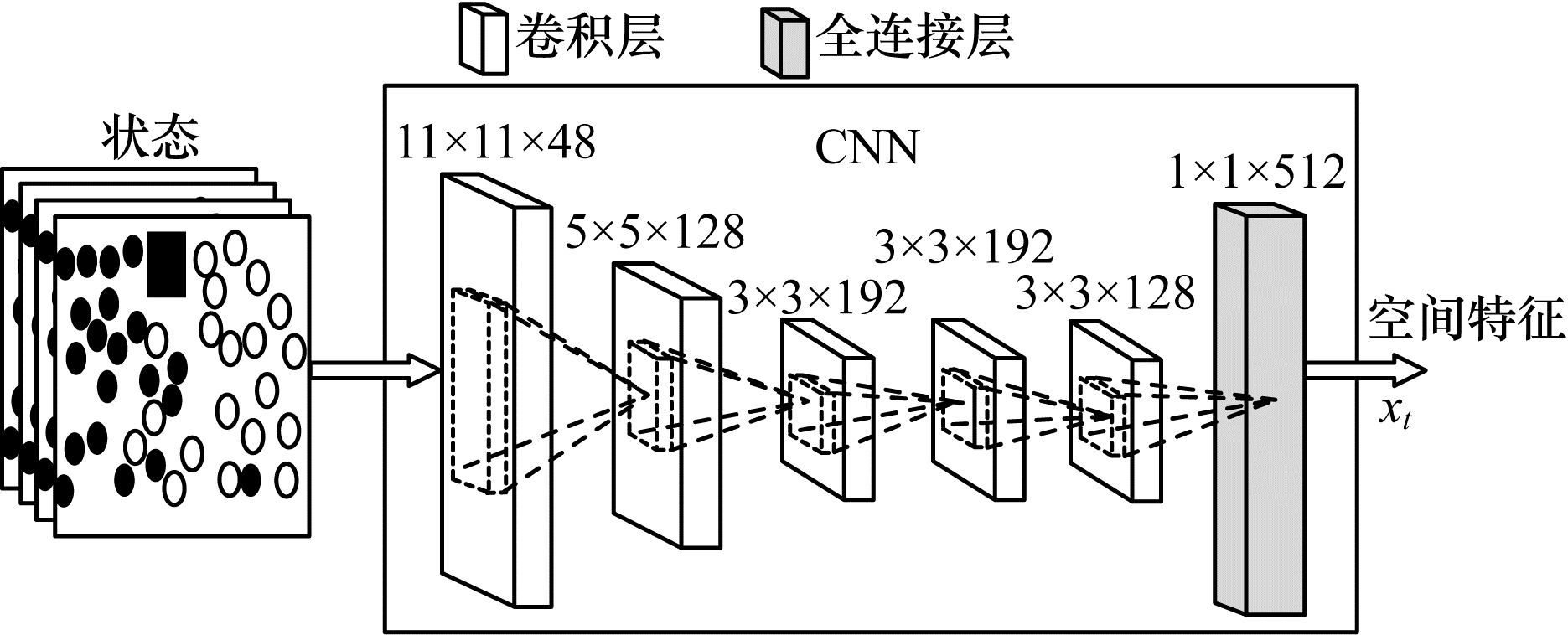
因为DQN算法的输入是原始的图像,所以本文将人群疏散场景的仿真图作为环境来提取状态信息。与原始DQN类似,本文DSTQN算法运用CNN拟合Q函数以减少算法复杂度,提取人群疏散场景图像的特征。在提取环境信息时,太浅的卷积网络只能提取简单的人群疏散场景的特征[13],无法提取复杂的人机交互的状态特征;过于深的卷积网络虽然能提取复杂的特征,但需要耗费大量的计算资源,难以收敛且有过拟合的风险。AlexNet是一种经典的CNN模型[19],在大规模视觉识别和图像分类等领域取得了很好的成效。如图 2所示,本文参照AlexNet,设计的CNN包含5个卷积层与1个全连接层。5个卷积层的卷积核大小依次为11×11、5×5、3×3、3×3、3×3,通道数依次是48、128、192、192、128,最终全连接层输出带有1×1×512个节点的映射集合。
|
Download:
|
| 图 2 CNN层网络结构 Fig. 2 Network structure of CNN layer | |
原始DQN只能表达静态人群疏散场景图像的空间特征,无法表达视频前后帧之间的时间信息。而动态人群疏散场景图像既有空间特征,又有前后帧对应位置的像素点,即时间特征,因此关联时间特征有利于机器人长期疏散人群,从而提高人群疏散的效率。LSTM是一种经典的时序特征提取模型,可以对视频进行时序性建模达到机器人长期记忆的目的,并在视频识别动作任务[20]中取得了较好的成果。因此,本文提出的DSTQN算法通过将CNN提取的空间特征送入LSTM层来实现时间关联。
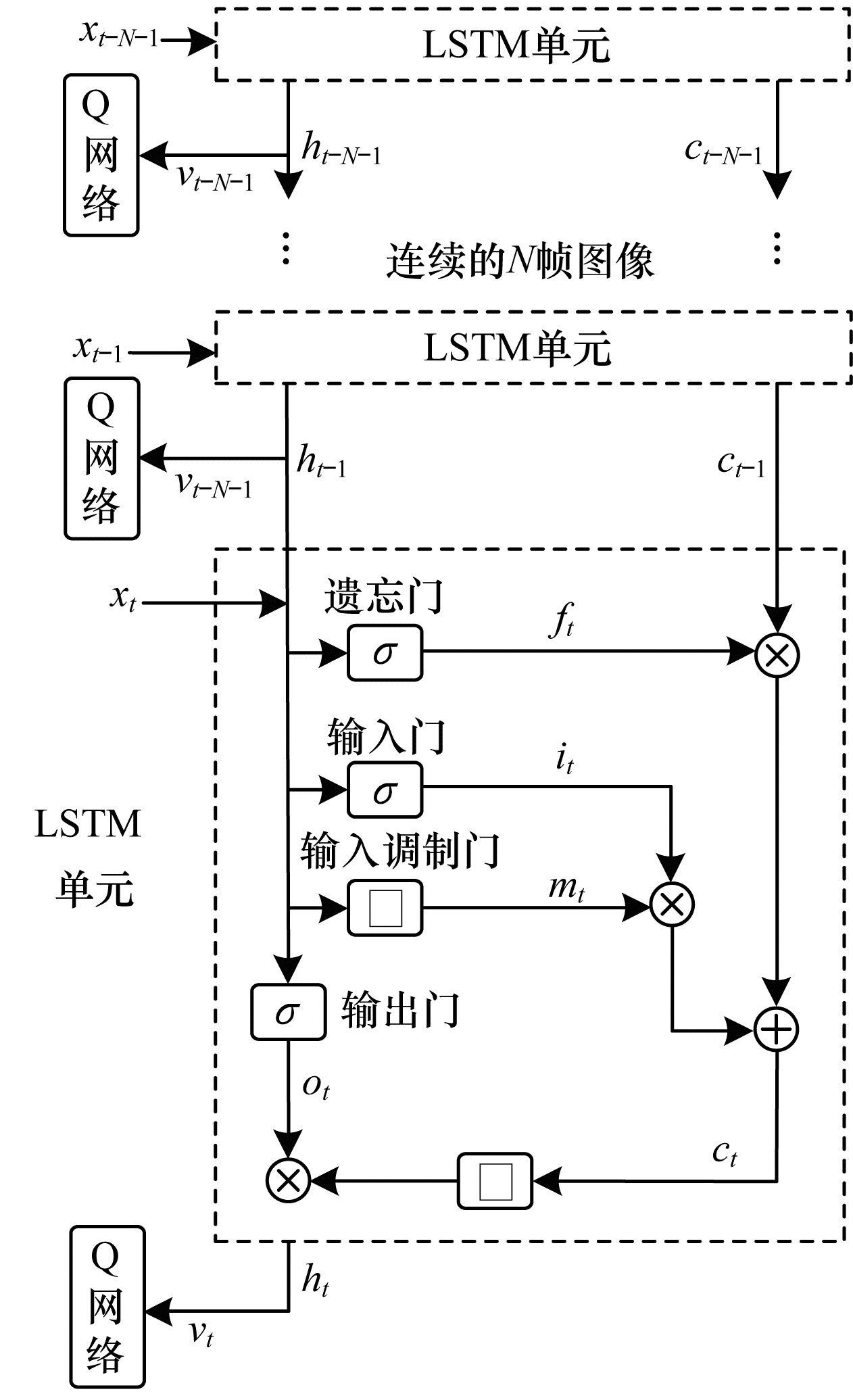
本文LSTM层结构如图 3所示,其中,虚线矩形框描述了LSTM单元内部结构,
|
Download:
|
| 图 3 LSTM层结构 Fig. 3 Structure of LSTM layer | |
LSTM利用4个“门”来决定信息在细胞状态的去留,从细胞状态中丢弃的信息由遗忘门确定,首先读取上一个LSTM单元的输出ht-1和当前LSTM单元的输入xt,然后通过sigmoid激活函数丢弃的信息输出到ƒt。ƒt取值范围为[0, 1],1表示“完全保留”,0表示“完全舍弃”。输入门决定存放哪些新信息,通过sigmoid函数输出需要更新的信息it;输出调制门利用tanh激活函数输出新的候选值向量mt;新信息it×mt加上旧状态细胞ct-1×ft完成细胞更新。输出门确定输出值,利用sigmoid函数输出[0, 1]区间的ot,并与通过tanh函数处理的新的细胞状态ct相乘,得到最终输出ht。LSTM各单元门的工作原理如式(6)~式(11)所示:
| $ {f}_{t}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}({W}_{xf}{x}_{t}+{W}_{hf}{h}_{t-1}+{b}_{f}) $ | (6) |
| $ {i}_{t}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}({W}_{xi}{x}_{t}+{W}_{hi}{h}_{t-1}+{b}_{i}) $ | (7) |
| $ {o}_{t}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}({W}_{xo}{x}_{t}+{W}_{ho}{h}_{t-1}+{b}_{o}) $ | (8) |
| $ {c}_{t}={f}_{t}\cdot {c}_{t-1}+{i}_{t}\cdot {m}_{t} $ | (9) |
| $ {m}_{t}=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}({W}_{xm}{x}_{t}+{W}_{hm}{h}_{t-1}+{b}_{m}) $ | (10) |
| $ {h}_{t}={o}_{t}\cdot \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left({c}_{t}\right) $ | (11) |
其中,Wx与b分别表示对应门控单元的权值与偏差,“
本文在提取人群疏散场景前后帧的时间特征时,首先把处理后的人群场景图像输入CNN提取空间特征xt,然后将距离当前时刻最近的N(N=10)帧图像的空间特征xt送入LSTM网络关联时间信息,输出带有时间和空间信息的特征vt,最后将vt送入Q网络中学习和优化机器人选择运动指令的策略。
2.3 机器人疏散人群算法在人群疏散算法中,机器人依据当前从CNN和LSTM提取的人群疏散场景状态st中,选择最好的疏散动作at,利用奖励函数得到当前奖励rt,再进入下一个状态st+1。机器人依据奖励辩别当前奖励的优劣,且更新目标Q网络的参数。不断重复以上过程,最终得到优化的目标Q网络。因此,状态、动作和奖励的设计是机器人疏散人群算法的重要内容。
1)状态空间S
状态集合S是机器人感知到的环境信息,也是对环境信息的数学表达。由于原始图像尺寸过大且包含了许多无效的信息,为了优化计算,降低网络的训练难度,本文设定输入DSTQN的状态是机器人附近的区域。首先通过缩放和灰度化处理距离当前时刻最近的4(经验值)帧场景图像使其尺寸为84×84×4,然后输入到CNN层中,状态集合如式(12)所示:
| $ S=\{{s}_{t-3}, {s}_{t-2}, {s}_{t-1}, {s}_{t}\} $ | (12) |
其中,st是输入的当前时刻状态图像,t为当前时刻。
2)动作空间A
动作空间A集合了机器人依据此时环境而选择的动作。机器人在疏散人群时,如果选取两个方向的运动,则动作局限性大且难以有效疏散人群;而选取八向运动则导致强化学习搜索空间过大,模型训练时难以收敛。为保证在一定的训练难度下有较好的疏散效果,本文设计的机器人可向上、下、左、右运动,动作集合如式(13)所示:
| $ A=\{{a}^{u}, {a}^{d}, {a}^{l}, {a}^{r}\} $ | (13) |
其中,A为机器人动作空间集合,au、ad al、ar分别表示机器人上、下、左、右4个方向运动指令。
3)奖励函数r
机器人通过奖励函数r判别当前动作的优劣,同时奖励函数引导机器人学习,强化学习的每一个动作都有相应的奖励。本文中机器人目的是更快地降低疏散场景中人群拥挤度,所以对机器人而言最直接的奖励是当前时刻疏散的人数。如果机器人当前动作使得后续有较多的人数逃生而当前很少甚至是没有人逃生,亦不可认定本次动作无效。因此,本文将智能体采取一个动作后的k(k=5为经验值)次迭代的疏散总人数作为环境反馈给机器人的奖励,奖励函数如式(14)所示:
| $ {r}_{t}=\sum\limits_{i=t}^{t+k}{M}_{i} $ | (14) |
其中,t表示当前时刻,Mi是时刻i的疏散人数值,rt是当前时刻t的奖励值。
4)其他参数和模型训练策略
参数的合理设计与适当调整对训练深度强化学习算法起着重要的作用。基于DSTQN的人群疏散算法的参数设置如表 1所示。

|
下载CSV 表 1 DSTQN算法参数 Table 1 Parameters of DSTQN algorithm |
在表 1中,学习率是更新策略时更新网络权重的幅度大小,折扣因子体现时间对奖励的影响,记忆池用来存储样本数据,训练批次大小等同于每次训练神经网络送入模型的样本数,周期性地更新目标Q网络可以提高算法稳定性。采用贪婪算法[21]训练策略,按照设定的探索因子的大小来确定动作模式,不同的探索因子对应不同阶段选取动作的概率。在训练初始阶段,机器人在初始探索因子ε的概率下进行探索,随机选择动作,ε随着训练次数增加而减小,最终机器人以稳定的终止探索因子,ε'概率选择当前最优的动作。
3 实验结果与分析本文使用Python语言实现人群疏散仿真环境和人群疏散算法,DSTQN算法基于Keras平台实现。硬件平台CPU为Intel i7-7700K,GPU为NVIDIA GTX 1080Ti,内存为32 GB。在实验场景方面,本文设计单出口室内人群疏散与走廊两群行人交错2种场景进行实验。
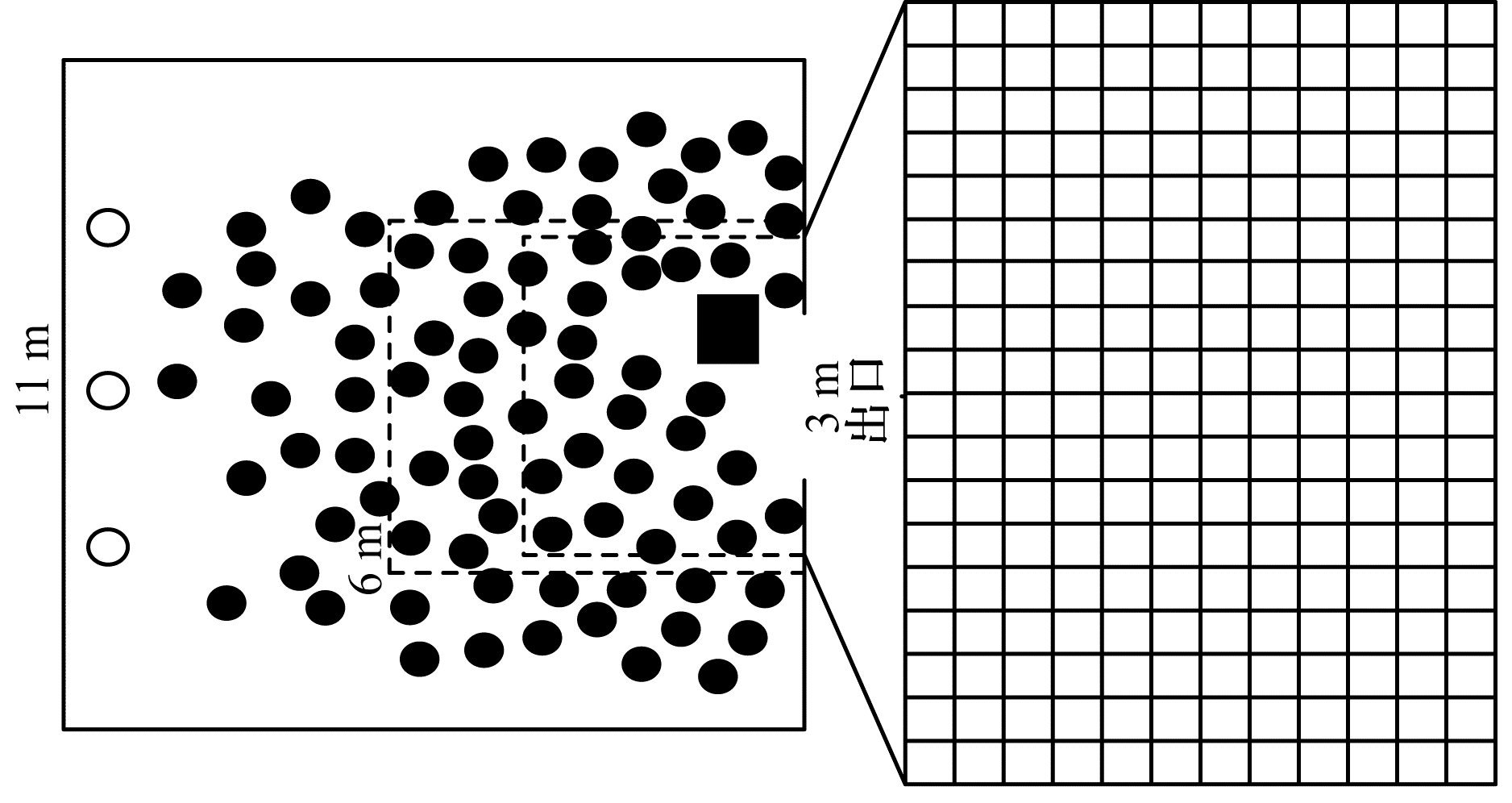
3.1 单出口室内人群疏散场景带有一个疏散口的室内场景是一个典型的人群疏散场景。图 4为本文建立的大小为11 m×11 m并带有一个3 m宽出口的室内实验场景,其中,实心圆表示行人,空心圆表示新增行人,方形表示机器人。当紧急事件发生时,行人出于恐慌心理在自驱动力的作用下快速向出口逃离。不同方向的行人逐渐聚集到出口附近,导致人群疏散效率降低。
|
Download:
|
| 图 4 单出口室内人群疏散场景和机器运动范围 Fig. 4 Single exit indoor crowd evacuation scene and machine movement range | |
为有效疏散人群,在室内场景中加入一个机器人进行仿真实验。图 4左侧6 m×6 m的外侧虚线框代表室内场景中人群主要聚集的区域,观察该区域并通过均匀采样得到84像素×84像素的图像后送入DSTQN网络来计算机器人的环境状态。此外,将机器人的运动范围划定在出口附近处行人逃生的矩形区域,如图 4左侧3.6 m×5.4 m内侧虚线框所示。综合考虑噪声和有限的计算资源,行人期望速度定为6 m/s[22],每秒迭代10次;机器人运动速度是0.6 m/s,每秒迭代2次,每次移动0.3 m。图 4右侧12 m×18 m的矩形网格是机器人在场景中的运动位置。在每轮实验中,人群初始人数是100人,疏散的时间是100 s,人群初始位置随机分布在场景中。在图 4中左侧每秒产生3个行人(用空心圆表示),他们的水平速度是6 m/s,纵向速度是0,目的是为了让行人源源不断地进入场景,避免状态空间太大。
本文的评判标准是单位时间(100 s)内疏散的人数,从而检验本文算法的有效性。文献[7, 13]与本文算法都是基于人机社会力模型研究单出口的室内场景的人群疏散工作。为检验时空Q网络在人群疏散应用的效果,本文将未加入LSTM的原始DQN与加入了LSTM的DSTQN进行对比。
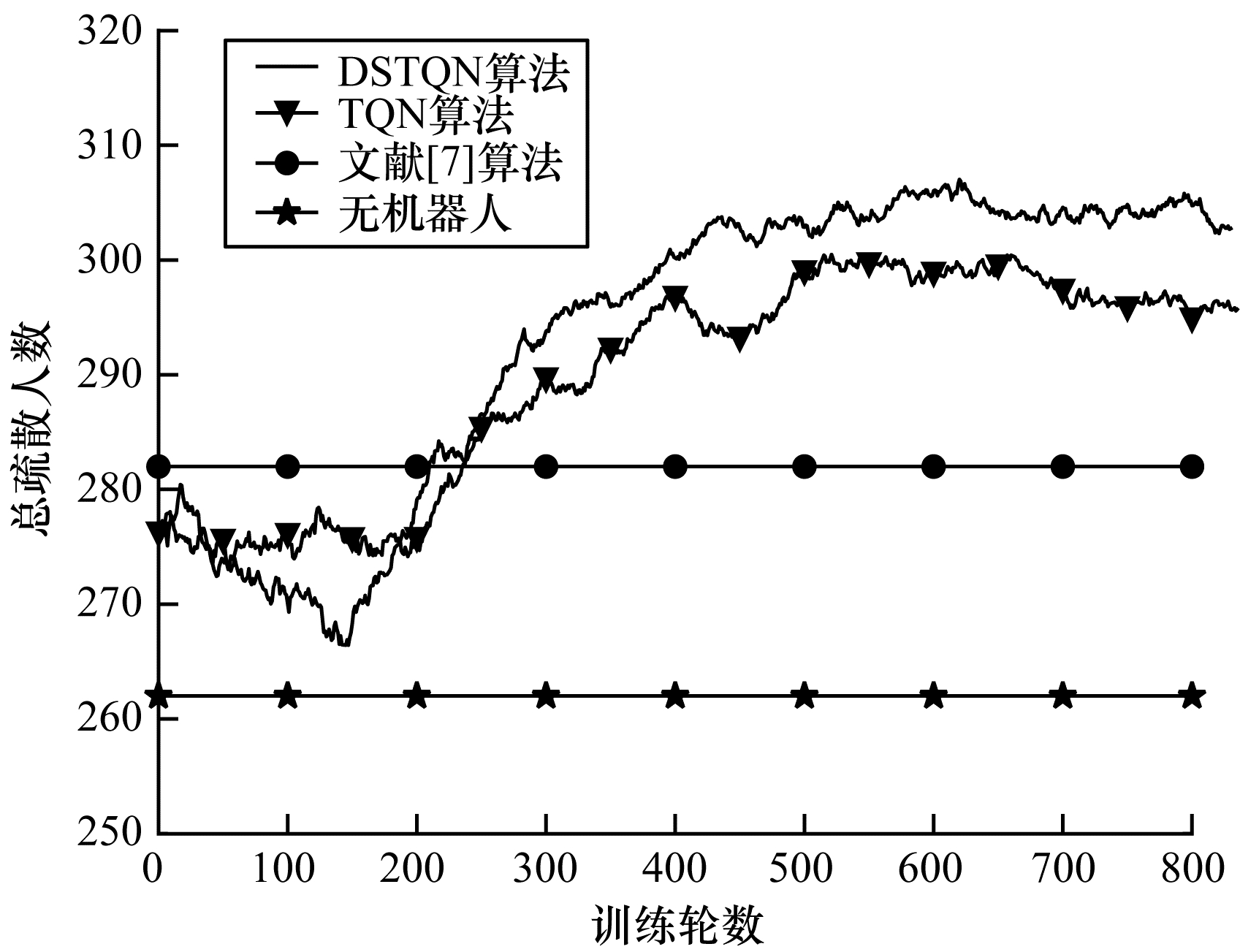
图 5为不同算法在室内场景的训练过程中疏散总人数变化曲线。在训练的前200轮时,DSTQN处于的观察前期,机器人随机选择疏散人群的动作;在200轮~400轮时处于探索中期,机器人将从经验池采集的样本优化机器人疏散人群的动作序列;在400轮之后训练收敛时,机器人根据学到的人群疏散策略来选择最合适的疏散人群动作,此时DSTQN算法在每轮实验中疏散人群的数量最多。
|
Download:
|
| 图 5 单出口室内场景训练过程中疏散人数曲线 Fig. 5 Curves of evacuee number in training process of indoor scene with a single exit | |
从图 5可以看出,本文提出的DSTQN算法疏散人群效果优于DQN和文献[7]算法。3种算法都是利用机器人自身运动状态来“控制”人群的运动状态,在文献[7]的算法中,机器人只是简单地在出口上下往复运动,尽管一定程度上提高了人群疏散效率,但这种单一的疏散路径不能根据场景内拥挤程度调整疏散策略;DSTQN、DQN算法中机器人则是在场景内学习高效的疏散人群策略来引导人群逃生,相比文献[7]的算法,这两种算法大幅提升了人群的疏散效率。同DQN算法相比,本文提出的DSTQN算法重新设计了CNN的结构来提取人群疏散场景图像复杂的空间特征,并且通过引入LSTM构成深度时空Q网络,关联人群疏散场景前后帧之间的时间信息,故机器人能够长期记忆之前学习到的信息,进一步提升了人群疏散的效率。
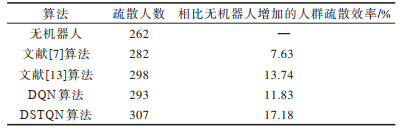
表 2为室内单出口场景不同算法的人群疏散结果对比,其中DQN和DSTQN都是训练800轮之后的测试结果。从表 2可知,与无机器人相比,文献[7, 13]、DQN、DSTQN等算法在每轮实验中人群的疏散效率分别增加7.63、13.74、11.83、17.18个百分点。本文DQN与文献[13]算法主要区别在于CNN的网络结构。本文重新设计了CNN的网络结构,目的是提取更复杂的空间特征。从疏散的效果来看,本文设计的CNN网络结构好于文献[13]算法。若仅使用DQN,机器人在提取人群图像的特征上只能获得每一个单独帧的人群位置、机器人的位置等空间信息,忽略了前后之间的时间信息。加入LSTM的网络有利于机器人根据前后帧之间的时间相关性,更快、更好地学习到某一时刻在何位置疏散人群效率高,同时机器人可以根据之前学习到的经验,如前后时刻人群场景中拥挤度的对比、前后时刻疏散人群效率对比等进一步提高人群的疏散效率。因此,在现有的算法中,本文DSTQN算法疏散人群的效果最好,效率最高。
|
下载CSV 表 2 室内单出口场景的不同算法人群疏散结果对比结果 Table 2 Comparative results of different crowd evacuation algorithm in indoor scene with a single exit |
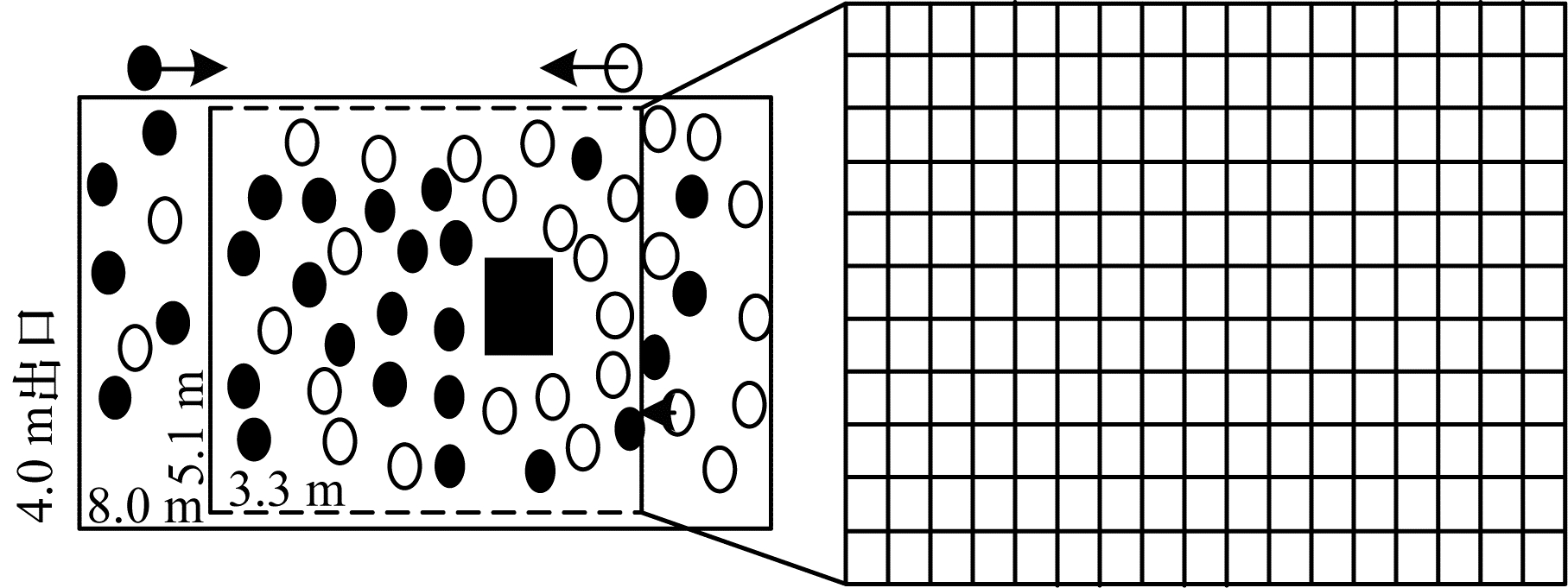
走廊通道如地铁隧道、商场通道等场景也人群疏散研究的典型场所。本文建立的走廊场景长8 m、宽4 m,墙壁用上下实线代替,行人的进出口用左右两边虚线表示,如图 6所示。为到达各自的期望地点,两群行人对向而行,在走廊相遇的位置发生严重的拥堵。
|
Download:
|
| 图 6 走廊两群行人交错场景和机器运动范围 Fig. 6 Corridor two groups of pedestrians interlaced scenes and machine motion range | |
由于文献[7]的算法没有涉及该类型场景,因此在实验过程中只将本文算法与DQN以及无机器人疏散的结果进行对比。实验中走廊左右两边的初始人数各设置30人,每轮训练中设定人群疏散的时间是100 s,在走廊左右两侧分别产生1个行人,其水平速度是6 m/s,纵向速度为0。本文选择走廊中部附近人群主要聚集的区域作为状态观测和机器人运动的范围,见图 6中5.1 m×3.3 m矩形虚线框。
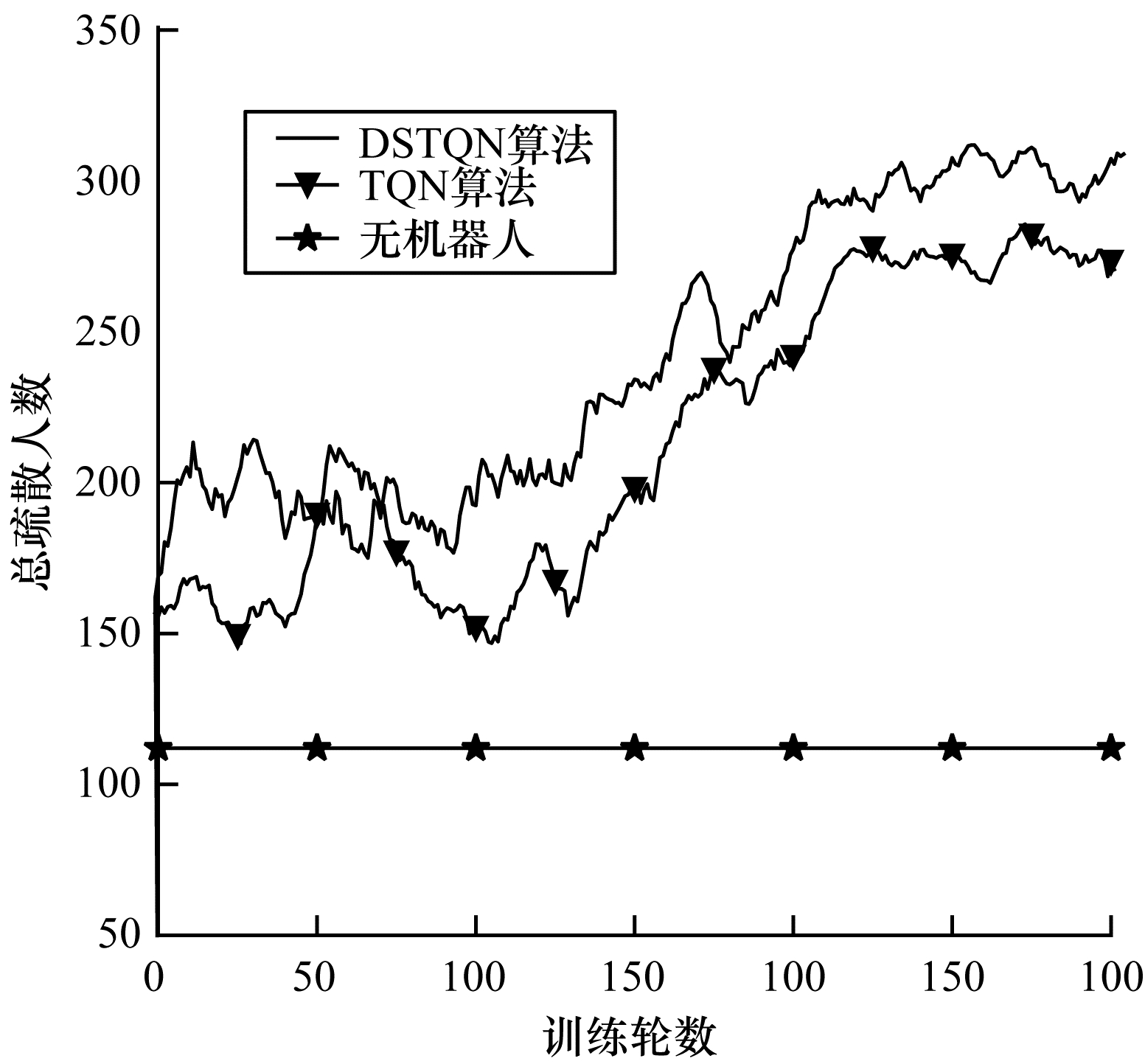
与室内单出口人群疏散场景相比,走廊两群行人交错的场景更为复杂。图 7为走廊场景的训练过程中疏散人数变化曲线。
|
Download:
|
| 图 7 走廊场景训练过程中疏散人数变化曲线 Fig. 7 Change curve of the number of people evacuated during the corridor scene training process | |
从实验结果可以看出,DSTQN的疏散效果优于DQN。虽然在50轮~100轮时DQN疏散的人数数量领先于其他算法,但在训练前100轮训练时,无论是DSTQN还是DQN都处于训练前期的观察状态,此时机器人随机选择疏散人群的动作。在训练中期以及训练后期,DSTQN算法疏散效果一直处于最优的地位,机器人利用回放池中的样本学习到越来越好的疏散人群的动作。模型收敛后,机器人依赖学习到的策略选择最优的疏散人群的动作,因此,DSTQN的人群疏散效率最高。
表 3为训练330轮之后的实验结果,从表 3可以看出,相比无机器人,DQN在每轮实验中人群的疏散效率增加了135.71%,而DSTQN在每轮实验中人群疏散效率增加了182.14%。DSTQN算法利用机器人自身的运动来“控制”行人的运动,在不同的场景下也能极大程度地提升人群疏散的效率,由此说明本文提出的DSTQN方法具有良好的场景移植性,能够迁移至不同的人群疏散场景,并且与现有的算法相比,DSTQN的疏散效果最优。

|
下载CSV 表 3 走廊两群行人交错场景的人群疏散结果统计 Table 3 Statistical results of crowd evacuation experiments in the scene with two groups of crowds crossing a corridor |
为观察机器人疏散人群的过程,在训练收敛时(330轮之后)进行实验,保存人群场景图像,如图 8所示。
|
Download:
|
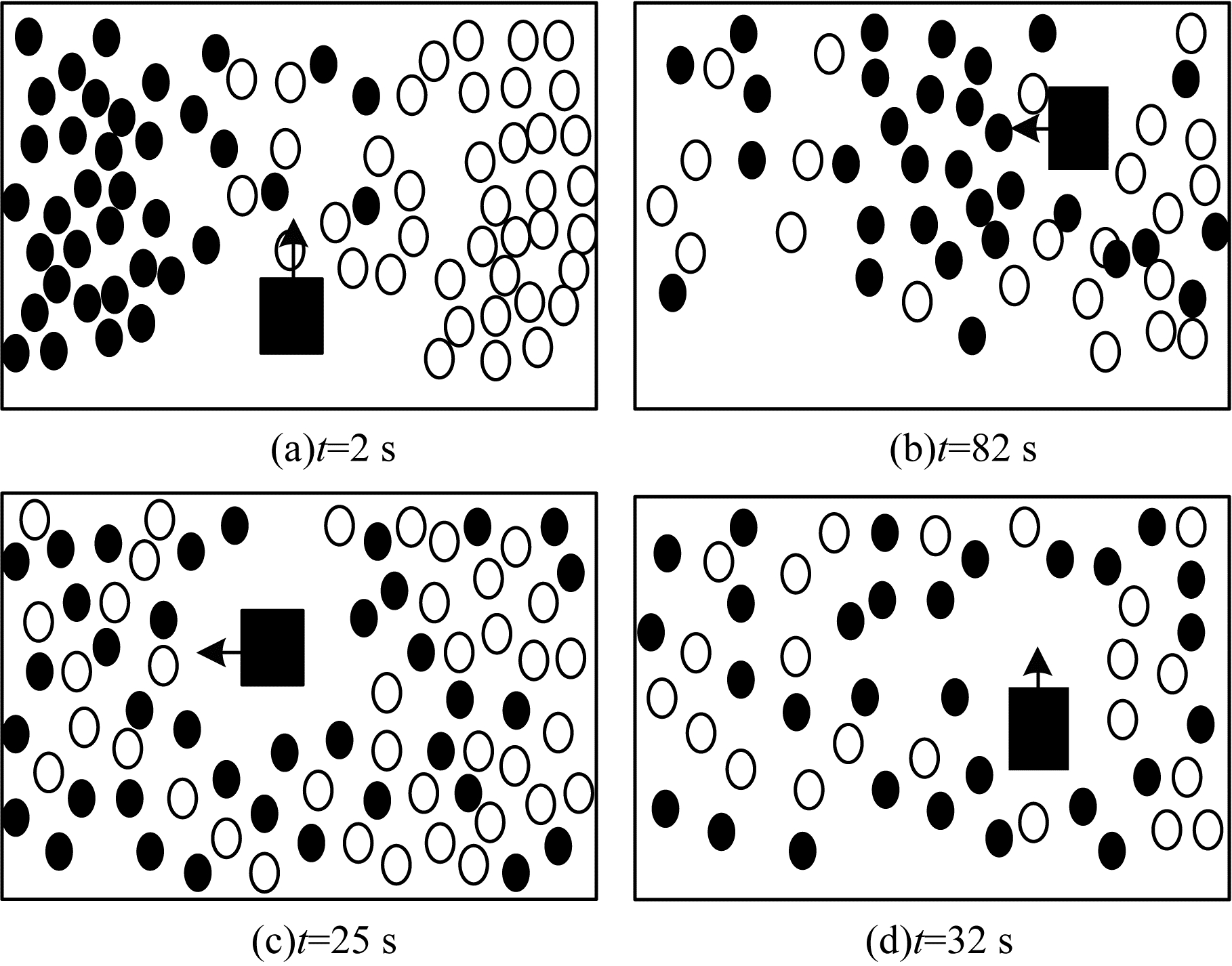
| 图 8 基于DSTQN的人群疏散过程示意图 Fig. 8 Schematic diagram of crowd evacuation process based on DSTQN | |
从图 8(a)可以看出,在t=2 s时,人群在走廊中部相遇并形成严重的拥堵,此时机器人利用学习到的策略做出疏散人群的动作向上方运动;在t=8 s时,该位置的人群被“冲散”,如图 8(b)所示。在t=25 s和t=32 s时可看出,机器人会通过自身运动来影响行人运动,降低人群的拥堵程度,进而疏散行人,如图 8(c)、图 8(d)所示。
4 结束语本文提出一种基于深度时空Q网络的机器人疏散人群算法,在原始DQN中引入LSTM网络以关联人机交互场景图像的时间特征,通过改进CNN网络提取更复杂的空间特征,并设计一种机器人疏散人群的学习策略。在单出口室内场景和走廊两群行人交错场景上的实验结果表明,该算法与DQN算法相比,明显提高了人群疏散效率。下一步将改善机器人动作设计,采用360°的连续动作取代上下左右4个离散动作来解决机器人疏散人群的问题。
| [1] |
ZHAN Yongsong, LU Zhaoming. Computer aided large-scale crowd evacuation platform[J]. Computer Engineering, 2008, 34(20): 77-79. (in Chinese) 湛永松, 卢兆明. 计算机辅助大规模人群疏散平台[J]. 计算机工程, 2008, 34(20): 77-79. |
| [2] |
NIEMI H, ESKOLA K J, PAATELAINEN R. Event-by-event fluctuations in a perturbative QCD + saturation + hydrodynamics model: determining QCD matter shear viscosity in ultrarelativistic heavy-ion collisions[J]. Physics, 2016, 93: 161-164. DOI:10.1103/PhysRevC.93.024907 |
| [3] |
BURSTEDDE C, KLAUCK K, SCAHDSHNEIDER A, et al. Simulation of pedestrian dynamics using a two-dimensional cellular automaton[J]. Physica A: Statistical Mechanics & Its Applications, 2001, 295(3/4): 507-525. DOI:10.1016/S0378-4371(01)00141-8 |
| [4] |
HELBING D, MOLNÁR P. Social force model for pedestrian dynamics[J]. Physical Review E: Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1995, 51(5): 4282-4286. |
| [5] |
XU Bo, MIN Huaqing. Solving minimum constraint removal problem using a social-force-model-based ant colony algorithm[J]. Applied Soft Computing, 2016, 43(1): 553-560. |
| [6] |
ZHANG Aihua, LIU Qingfang, CHEN Xiaolei. Mobile intelligent terminal-oriented trample prevention system[J]. Journal of Lanzhou University of Technology, 2017, 43(4): 81-86. (in Chinese) 张爱华, 刘庆芳, 陈晓雷. 面向移动智能终端的踩踏预防系统[J]. 兰州理工大学学报, 2017, 43(4): 81-86. |
| [7] |
HU Xuenin, XU Shanshan, KANG Meiyu, et al. Crowd evacuation algorithm based on human-robot social force model[J]. Journal of Computer Applications, 2018, 38(8): 2164-2169. (in Chinese) 胡学敏, 徐珊珊, 康美玉, 等. 基于人机社会力模型的人群疏散算法[J]. 计算机应用, 2018, 38(8): 2164-2169. |
| [8] |
POLYDOROS A S, NALPANTIDIS L. Survey of model-based reinforcement learning: applications on robotics[J]. Journal of Intelligent & Robotic Systems, 2017, 86(2): 153-173. |
| [9] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Play atari with deep reinforcement learning[C]//Proceedings of the 26th Workshop on Neural Information Processing Systems. Lake Tahoe, USA: [s. n. ], 2013: 201-220.
|
| [10] |
GAO Yang, CHEN Shifu, LLU Xin. Research on reinforcement learning technology: a review[J]. Acta Automatica Sinica, 2004, 30(1): 86-100. (in Chinese) 高阳, 陈世福, 陆鑫. 强化学习研究综述[J]. 自动化学报, 2004, 30(1): 86-100. |
| [11] |
HWANG K, JIANG W, CHEN Y. Pheromone-based planning strategies in dyna-Q learning[J]. IEEE Transactions on Industrial Informatics, 2017, 13(2): 424-435. DOI:10.1109/TII.2016.2602180 |
| [12] |
IMANBERDIYEV N, FU C, KAYACAN E, et al. Autonomous navigation of UAV by using real-time model-based reinforcement learning[C]//Proceedings of the 14th International Conference on Control, Automation, Robotics and Vision. Piscataway, USA: [s. n. ], 2016: 1-6.
|
| [13] |
ZHOU Wan, HU Xuemin, SHI Chenyin, et al. Motion planning algorithm of robot for crowd evacuation based on deep Q-network[J]. Journal of Computer Applications, 2019, 39(10): 2876-2882. (in Chinese) 周婉, 胡学敏, 史晨寅, 等. 基于深度Q网络的人群疏散机器人运动规划算法[J]. 计算机应用, 2019, 39(10): 2876-2882. |
| [14] |
HOCHREFFITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [15] |
PENG Yuqing, SONG Chubai, YAN Qian, et al. Research on Chinese text classification based on hybrid model of VDCNN and LSTM[J]. Computer Engineering, 2018, 44(11): 190-196. (in Chinese) 彭玉青, 宋初柏, 闫倩, 等. 基于VDCNN与LSTM混合模型的中文文本分类研究[J]. 计算机工程, 2018, 44(11): 190-196. |
| [16] |
XU Fangfang, YANG Junjie, LIU Hongzhi. Location prediction model based on ST-LSTM network[J]. Computer Engineering, 2019, 45(9): 1-7. (in Chinese) 许芳芳, 杨俊杰, 刘宏志. 基于ST-LSTM网络的位置预测模型[J]. 计算机工程, 2019, 45(9): 1-7. |
| [17] |
LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[EB/OL]. [2020-02-10]. https://arxiv.org/abs/1509.02971.
|
| [18] |
WATKINS C J C H, DAYAN P. Technical note: Q-learning[J]. Machine Learning, 1992, 8(3/4): 279-292. DOI:10.1023/A:1022676722315 |
| [19] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of NIPSʼ12. Cambridge, USA: MIT Press, 2012: 1097-1105.
|
| [20] |
DONAHUE J, HENDRICKS L A, ROHRBACH M, et al. Long-term recurrent convolutional networks for visual recognition and description[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(4): 677-691. DOI:10.1109/TPAMI.2016.2599174 |
| [21] |
CHEN D, VARSHNEY P K. A survey of void handling techniques or geographic routing in wireless network[J]. IEEE of Communications Surveys and Tutorials, 2007, 9(1): 50-67. DOI:10.1109/COMST.2007.358971 |
| [22] |
HELBING D, FARKAS I, VICSEK T. Simulating dynamic features of escape panic[J]. Nature, 2000, 407(6803): 487-490. |
 2021, Vol. 47
2021, Vol. 47
