开放科学（资源服务）标志码（OSID）：

0 概述

手势识别能摆脱触屏束缚，使设备的体积更小巧、佩戴方式更灵活，是一种更自然的人机交互方式。利用电磁波雷达^[1-2]或超声波^[3-5]作为手势识别的感知器，能够实现对光照条件不敏感、数据量小以及降低算法复杂度。一些轻量级可穿戴设备的控制系统是手势识别中一个重要的应用场景，但是它们普遍采用嵌入式系统，对实时性和功耗要求较高，因此，实用化的识别算法必须考虑在嵌入式系统中能否实现。

识别算法是手势识别的关键部分，随机森林^[6]为一种泛化能力强且灵活的机器学习算法，其预测过程简单，只涉及待预测数据与训练模型的多轮数值比较运算，可以满足系统实时性的要求，且能量消耗较低，因此，以谷歌的Soli项目^[2]为代表的多个基于雷达的手势识别系统选择将随机森林作为手势识别的分类器。然而，一方面，手势识别也可以采用其他识别算法，如支持向量机（SVM）、K近邻（KNN）和卷积神经网络（CNN）等^[7-9]；另一方面，算法的特征、具体参数和分类数需要因不同应用场景、手势种类而调整，因此，为了保证系统的灵活性，需要研究高效的识别算法嵌入式软件实现技术。由于识别模型可以进行离线训练，只有推理（预测）过程需要在嵌入式平台上实时运行，因此首要的问题是如何优化推理算法的程序。本文以随机森林的预测过程嵌入式实现方法为研究对象，针对文献[10]中提出的“一对其余”（One-vs.-Rest，OvR）多类别随机森林分类器，提出一种低开销手势识别实现算法，以期缩短程序的平均运行时间并降低预测过程的平均能量消耗。另外，本文基于FPGA的可编程片上系统（System on a Programmable Chip，SOPC）研究基于超声波的识别算法嵌入式实现技术，结合前端信号处理功能的FPGA实现，使整个系统在FPGA上独立运行并脱离PC机，从而实现装置的可移动性。

1 国内外研究现状

现有多数随机森林和手势识别算法的实现是基于PC平台，较少在嵌入式系统中实现上述算法。如谷歌的Soli系统，其采用的也都是高性能的嵌入式处理器^{[2, 11-12]}，只能在手机、移动电脑等高性能的设备平台上使用，系统的成本和功耗与智能手表、智能耳机等可穿戴应用的需求存在一定差距。

随机森林是由众多决策树组成的一种集成学习方法，预测过程依赖训练时生成的全部决策树参数。针对大量决策树的存储和访问，文献[13]提出的方案中每一棵决策树的选择路径映射一个地址，该地址中存放预测的类别，特征与选择路径的各个阈值可以同时比较，从而提高随机森林的预测速度，但是这种以空间换时间的方法会造成大量的存储资源浪费。文献[14]对每棵决策树赋予不同的权重，引入以分类错误率为参数的评价指标，舍弃部分决策树，该方案可以在一定程度上减少存储空间，但是舍弃决策树可能对识别率产生不利影响。文献[15-16]提出基于专用硬件的随机森林实现方案，研究寄存器传输级（RTL）的优化，但是，针对手势识别的具体应用缺少灵活性，导致RTL级的优化并不适用。

上述研究都是关于随机森林的实现方法，分别从减少树的数量和提高单棵树的识别速度等方面进行优化。但是在一些多分类应用中，一个分类器可能由多个随机森林组合而成，在整个分类器层次上的优化方案非常少。本文针对由多个二进制随机森林按照OvR方式构成的多类别分类器进行实现与优化。

2 手势识别系统介绍

本文针对文献[10]所设计的基于超声波雷达的手势识别嵌入式系统实现问题进行研究，在该系统原型的基础上将信号处理和识别算法的部分功能移植到FPGA平台上，以减小系统的体积并增强设备的移动性。

2.1 手势识别系统工作原理

图 1所示为本文手势识别系统采用的实验装置，通过一个超声波发射器主动发射超声波以进行目标探测，发射波经手反射产生回波信号，系统中有3个超声波接收器，手势的3路回波信号经过数字信号处理后得到一系列RDM图（能量在距离和速度维的联合分布）^[17]。系统从RDM图序列中提取特征，特征经过分类器后完成手势识别的训练和预测。

文献[10]中提取的系列特征包括从3路信号的RDM图中提取最大速度、最大距离、平均速度和平均距离等，共45维特征。1 s的回波信号采用滑窗的方式切分为19帧^[10]，对45维特征中某一维特征，计算其在19帧数据中的均值、标准差、均方根、最大值和最小值，总的特征数目为$ 45\times 19+45\times 5=1\mathrm{ }\mathrm{ }080 $。

2.2 OvR随机森林多分类算法 2.2.1 随机森林分类器

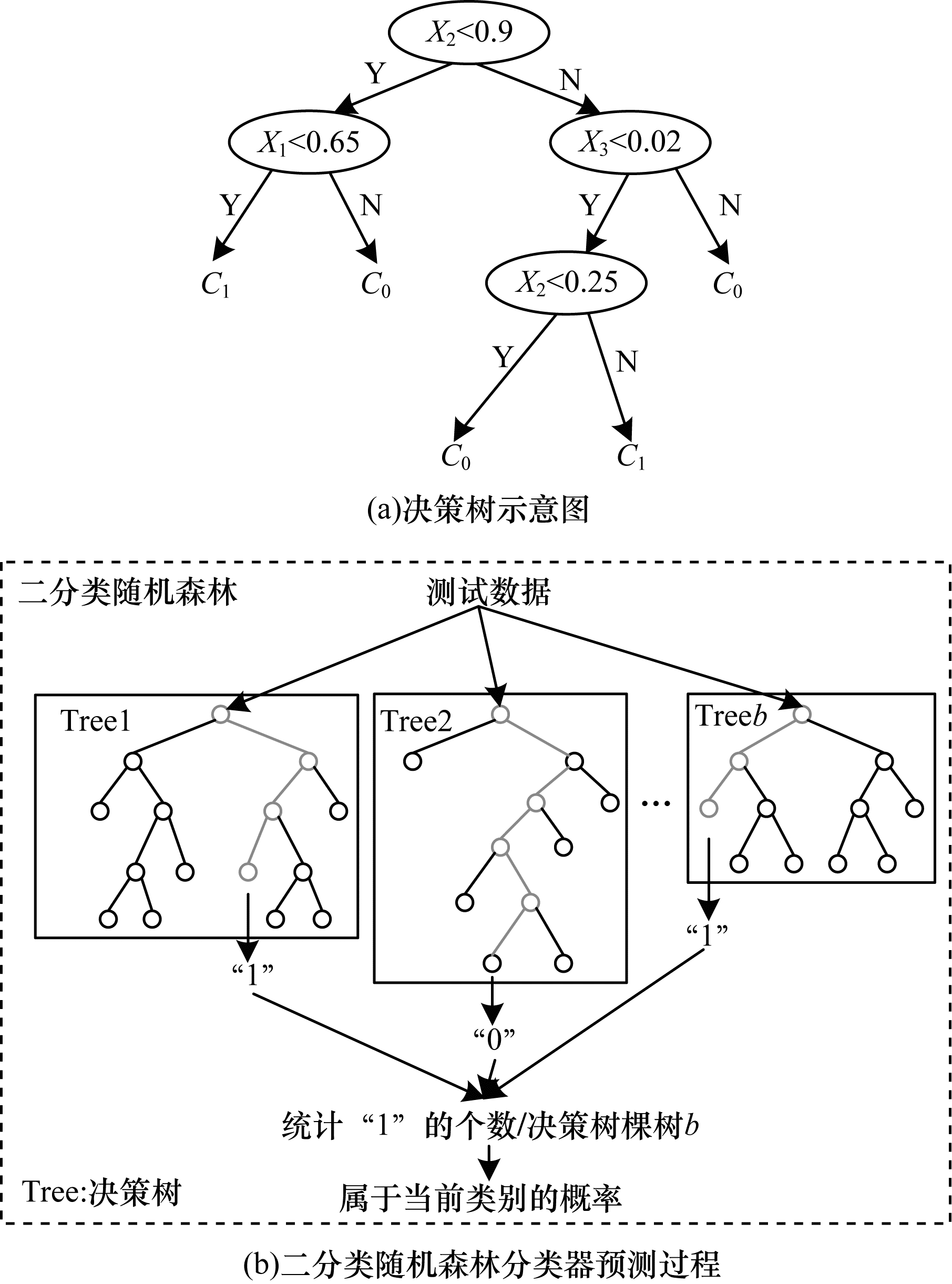
随机森林由多个决策树组成，一棵训练好的二叉决策树的结构示意图如图 2（a）所示，树的每个节点存储一个特征和对应的阈值，测试样本对应的特征（图 2（a）中的$ {X}_{1} $、$ {X}_{2} $、$ {X}_{3} $）与阈值比较，根据比较结果进行分支跳转，直至到达叶子节点，则叶子节点对应的类别为样本的预测类别。对于一棵决策树，其中包含的有用信息为选择的特征编号、比较阈值、内部节点的左右节点和叶子节点的输出类别。图 2（b）所示为二分类随机森林分类器的预测过程，对于测试数据，每棵决策树经过层层比较（比较路径为图中灰线部分）给出一个判定结果（测试样本是否属于当前类，“1”表示属于，“0”表示不属于）。随机森林会统计所有决策树输出“1”的比例，该比例即为测试样本属于该类别的概率。

2.2.2 特征对齐的随机森林算法

本文采用文献[10]中提出的用于多种手势识别的识别算法——特征对齐的随机森林算法。由于每个人的手势快慢不同，提取的时序特征在时间上存在错位，当测试样本的特征和训练样本之间存在错位时，直接采用随机森林进行分类，会出现样本和模型特征对应错位的问题，从而影响识别率。为了提高跨用户（训练集中不含有测试者的数据）的识别精度，特征在送入分类器之前需要经过一些处理从而解决特征序列扭曲的问题。在提取的众多特征中，平均速度特征能衡量手势的整体运动趋势，因此，本文运用所有训练样本的平均速度计算得到模板特征，然后通过动态时间规整（DTW）算法^[18]计算测试样本的平均速度以及与模板特征的距离，找到规整路径并进行帧对齐。特征集中所有时序特征根据规整路径进行缩放，将对应模板同一帧的一帧或几帧的特征求平均值以压缩成一帧的特征，或者将一帧的特征复制多份拓展到相邻帧。经过处理后的时序特征称为对齐后特征，对齐后特征加上统计特征再作为最终分类器的输入。实验结果表明，在其他实验条件不变的情况下，与传统的随机森林相比，特征对齐的随机森林算法中7个人交叉验证的平均识别率提高3.2%。最终分类器采用的是OvR^[19-20]的多分类器架构，总的多分类分类器由一组二分类随机森林组成，每个类别（手势）有一个二分类随机森林的子分类器。

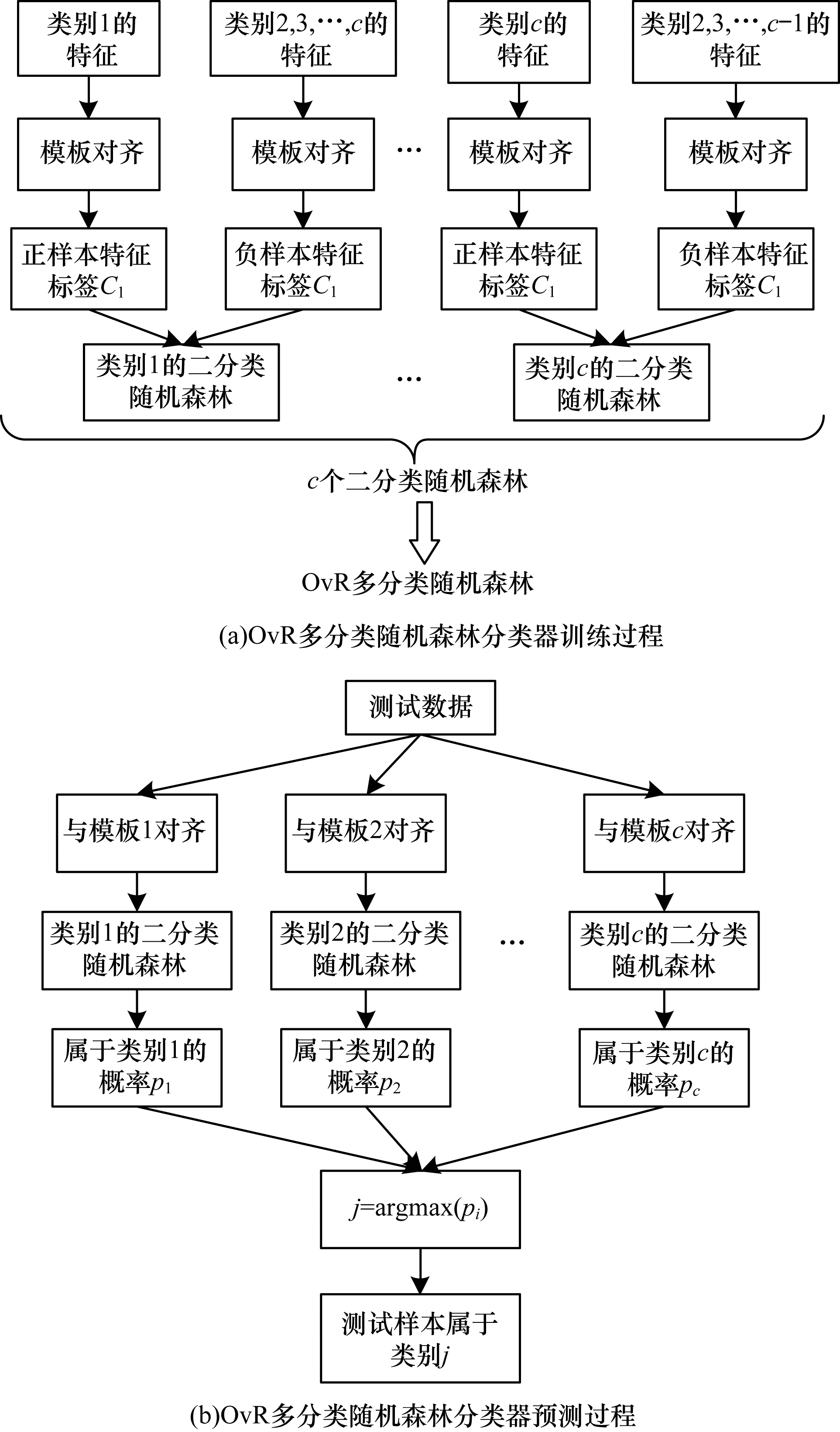
图 3（a）所示为OvR随机森林分类器的训练过程，当训练类别1的随机森林时，首先使用类别1的所有训练样本生成一个特征模板，然后将每个训练样本与该特征模板对齐，其对应的手势1的对齐特征为正样本，其他手势的对齐特征均为负样本，正样本定义为“1”类，负样本为“0”类，然后用正负样本训练一个二分类随机森林分类器。以此类推，有c种手势则共训练c个二分类随机森林，共同组成OvR多分类随机森林。图 3（b）所示为预测过程，对于进入的测试数据，经过特征对齐后，再用每个类别的子分类器按照图 2（b）进行判定，测试数据经过c组二分类随机森林判定后，可以得出属于各个类的概率，找出概率最大值对应的类别，即为测试数据的预测类别。随机森林决策树的数目和深度这两个可调的参数影响最终的识别率和模型大小。此外，为了方便存储和硬件读写，模型中的决策树均采用规则的二叉树。

为了衡量特征对齐的随机森林算法在实际系统中的应用可行性，本文评估该算法推理过程的计算复杂度。设一个模板所占的空间为A₁，一个二分类随机森林的空间复杂度为A₂，则本文算法的空间复杂度为$ c{A}_{1}+c{A}_{2} $（模板的数据量远小于二分类随机森林的数据量）。每个样本的识别要执行一次特征对齐，使用DTW算法对序列完成一次对齐的时间复杂度主要与序列长度L有关，为O（L²），采用加速算法可将时间复杂度降至O（L），二分类随机森林测试一个样本的时间复杂度为O（nD），其中，n和D分别为随机森林中决策树的棵数和最大深度，则手势识别算法完成一次手势预测的时间复杂度为$ O\left(c\right(L+nD\left)\right) $。特征对齐的随机森林算法推理的时间复杂度和空间复杂度都和手势类别数目c成正比。在实际应用中，手势的种类不会过多，一般不超过10，因此，该算法能够满足系统对实时性的要求。当L=19，n=50，D=10，c=8时，特征对齐的随机森林算法在PC机上的模型大小为700 KB，运算时间为37 ms^[10]。

3 基于FPGA平台的手势识别SOPC

文献[10]中仅在PC机上采用Python语言实现OvR多分类随机森林算法，核心算法调用的现有DTW和随机森林算法库无法直接移植到嵌入式平台上。本文手势识别系统在Xilinx的Artix7-100T FPGA的Nexys4开发板上实现，其为一个基于Xilinx FPGA的SOPC平台的嵌入式系统，采用Xilinx的软核微处理器Microblaze作为CPU。基于FPGA实现嵌入式系统的优势在于：1）可以在系统中添加硬件加速模块，提高系统的能量效率，效果优于基于单一嵌入式处理器的方案；2）开发周期短，设计灵活，易于修改。

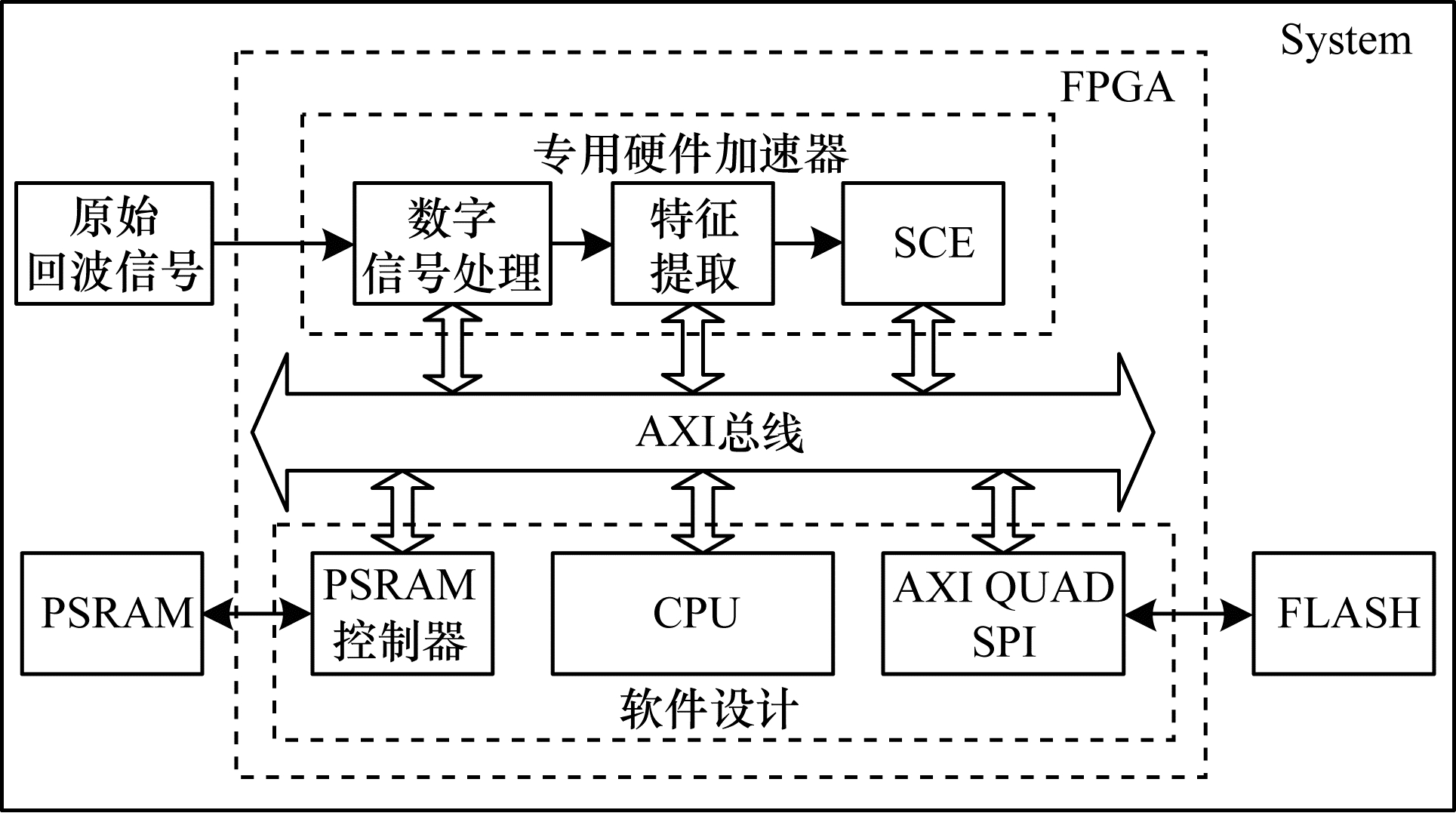
图 4所示为整个系统结构框图，包括信号处理、特征提取和分类识别等模块，其中，数字信号处理、特征提取由专门的硬件加速模块实现（硬件加速模块的设计不是本文的讨论范围），识别算法则采用软件实现，即由CPU运行。硬件部分输出的特征作为识别算法的输入，再根据加载的手势模型进行手势预测，输出的类别信息传递给具体应用。识别程序主要包括基于DTW算法的特征对齐和最终OvR随机森林分类器的推理计算两个部分，随机森林推理占其中主要的时间和功耗，因此，本文主要研究随机森林推理的程序设计问题。

系统的CPU主频设置为100 MHz，Artix7-100T FPGA电路板上有一个16 MB的伪静态存储器（PSRAM），用来存放SDK中的代码和支持代码运行的数据。手势识别模型的训练采用离线的方式，因此，本文系统中只需实现手势的预测运算，训练好的模型存处在开发板提供的FLASH芯片上，识别时加载到片内存储器使用。为了节省FPGA片内存储器和PSRAM的存储资源，采用动态加载模型的方式，即在识别算法运行过程中根据需要实时地从FLASH中读取所需的部分模型数据，而非一次性地将整个模型加载至片内。

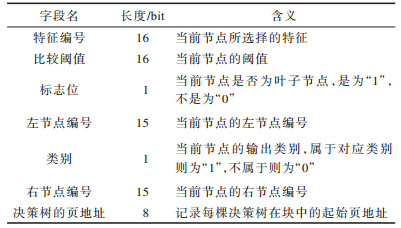
4 随机森林的嵌入式实现 4.1 模型数据结构

由PC程序训练生成的随机森林模型文件大小为5.4 MB，其中包含大量预测过程不需要的信息，如衡量特征之间相关性的基尼指数、随机抽样抽取的样本大小、参数含义的文字说明等。为了减少模型的存储空间，对该模型进行精简，只保留决策树的有用信息并对数据进行组合存储。为了方便硬件读取访问，决策树的数据存储设置为如图 5所示，每个节点的数据结构包含图 5（a）所示的6个域，每个节点分配一个编号，该编号是节点存储位置相对于整个树结构起始地址的偏移量；对于内部节点，如图 5（a）所示，数据结构中的叶子节点标志位为0；对于叶子节点，叶子节点标志位为1，左节点编号和右节点编号均为0。在硬件中，为了提高实现效率，一般采用定点数计算，系统中提取出的特征以定点数表示，考虑到定点数的不同位宽对识别率的影响，通过实验确定所有特征的最佳定点化位宽为16位，则决策树中的特征阈值位宽为16位。因为特征总数为1 080（$ {2}^{10}<1\mathrm{ }080<{2}^{11} $），特征编号至少需要11位的二进制数存储，所以一个节点数据结构占8个字节，节点数据的各个位宽说明如表 1所示。精简模型数据与原始模型相比，只有对特征阈值的处理这一操作会损失数据精度，影响最终的识别率。由于分类器本身的泛化功能，在训练随机森林模型时特征也会定点化，保留16位的位宽。实验测试结果表明，采用精简模型数据结构，识别率下降低于0.3%。

FLASH的读写操作以页为最小单位，写操作时，必须先擦除后写入，擦除的最小单位为1个块；读操作时，每次最少读取一页。本文系统中采用Spansion的一款型号为S25FL128的FLASH芯片，其一页的大小为256 B，一个块为256页，大小为64 KB。

模型在FLASH中存储时，考虑每棵决策树的大小约为1.8 KB，所以一棵决策树需要8页储存，一个块最少可存储32棵树。根据程序设计，每一棵树的数据在FLASH和内存中集中存储，图 5（b）显示了决策树在FLASH中的数据存储方式。每棵树各个节点的数据结构按照深度优先的规则顺序存储，对于每个块，先存储该块中每棵决策树所占的页数，然后存储决策树的数据，一棵决策树的数据大小如果不是页容量（256 KB）的整数倍，则用零补全，后一棵决策树紧接下一页开始，保证不会有两棵树的数据存储在同一页内，直到完成FLASH一个块的数据填充。按照这种方式存储模型的所有决策树。不同的块有不同的基地址，根据记录的每棵决策树的页首地址，可以任意访问不同的决策树。

本文定义8种手势，训练8个随机森林。在手势集选择时，主要考虑动作类型的代表性，其中包括：4种宏观手势（即手作为一个整体运动），分别对应于3维空间中整个手从左向右移动、从右向左移动、靠近目标和远离目标4种不同维度和方向的运动；4种微观手势（即手指运动，手被看作存在形变的目标），包括两种手指之间的滑动和多个手指的张开-聚合等。这些手势的典型性可以较完备地考察系统的识别能力。本文系统的算法与具体手势无关，在实际应用中用户可以根据实际需要定义适合的手势集合。当实际定义的手势种类变化时，只需更新训练的随机森林模型和模板数据。只要手势类型数量不变，改变手势集合对本文识别算法和程序的计算复杂度没有影响。每个随机森林有50棵树，总的决策树共有$ 50\times 8=400 $棵，400棵树之间相互独立，互不影响。按照上述方案精简后的模型数据文件大小仅为700 KB，较大程度地减轻了硬件的存储压力。

4.2 分支定界的最终分类器实现算法

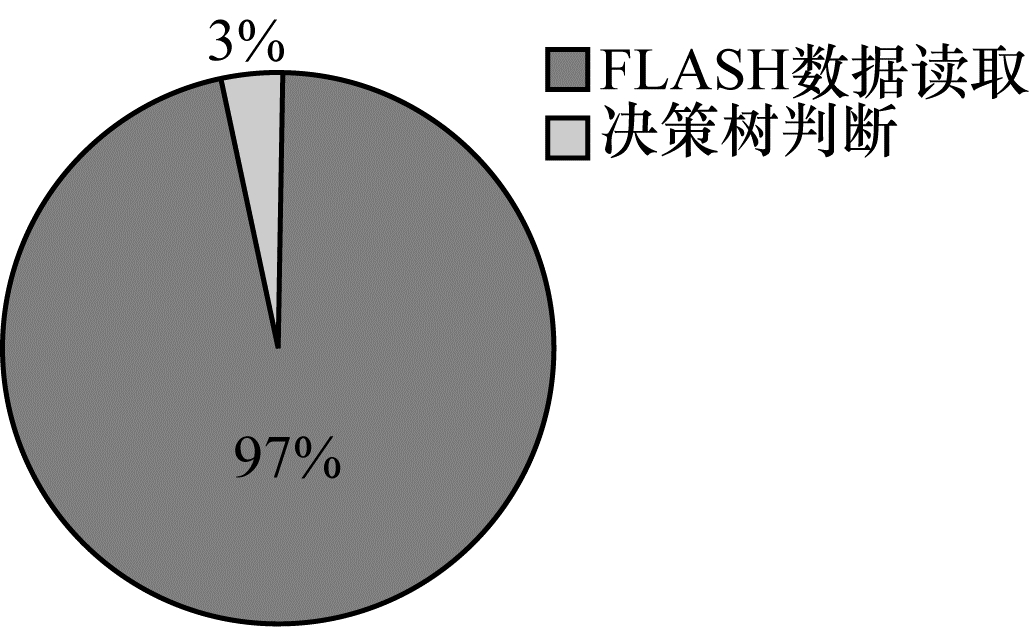
根据传统的随机森林预测算法，决策树按照预测时的读取顺序集中存储在FLASH中，测试数据经过每组随机森林的所有决策树的判定，才得出最终的结果。该方案需要从FLASH中顺序加载全部400棵树的数据，且进行400棵决策树的判定，如果一棵决策树的最大深度为$ D $，则一棵树的判定过程最多需要进行$ D $次比较和节点数据读取。由于决策树的数目很多，程序运行消耗大量时间，降低了系统的运行速度。图 6所示为在本文SOPC系统中实现传统OvR随机森林分类器测试程序时各部分操作的所用时间占比，从图 6可以看出，读FLASH数据占据了程序执行的绝大部分时间，因此，本文优化的重点是减少FLASH数据的读取时间，包括压缩模型的大小和减少对FLASH的访问两个方面。

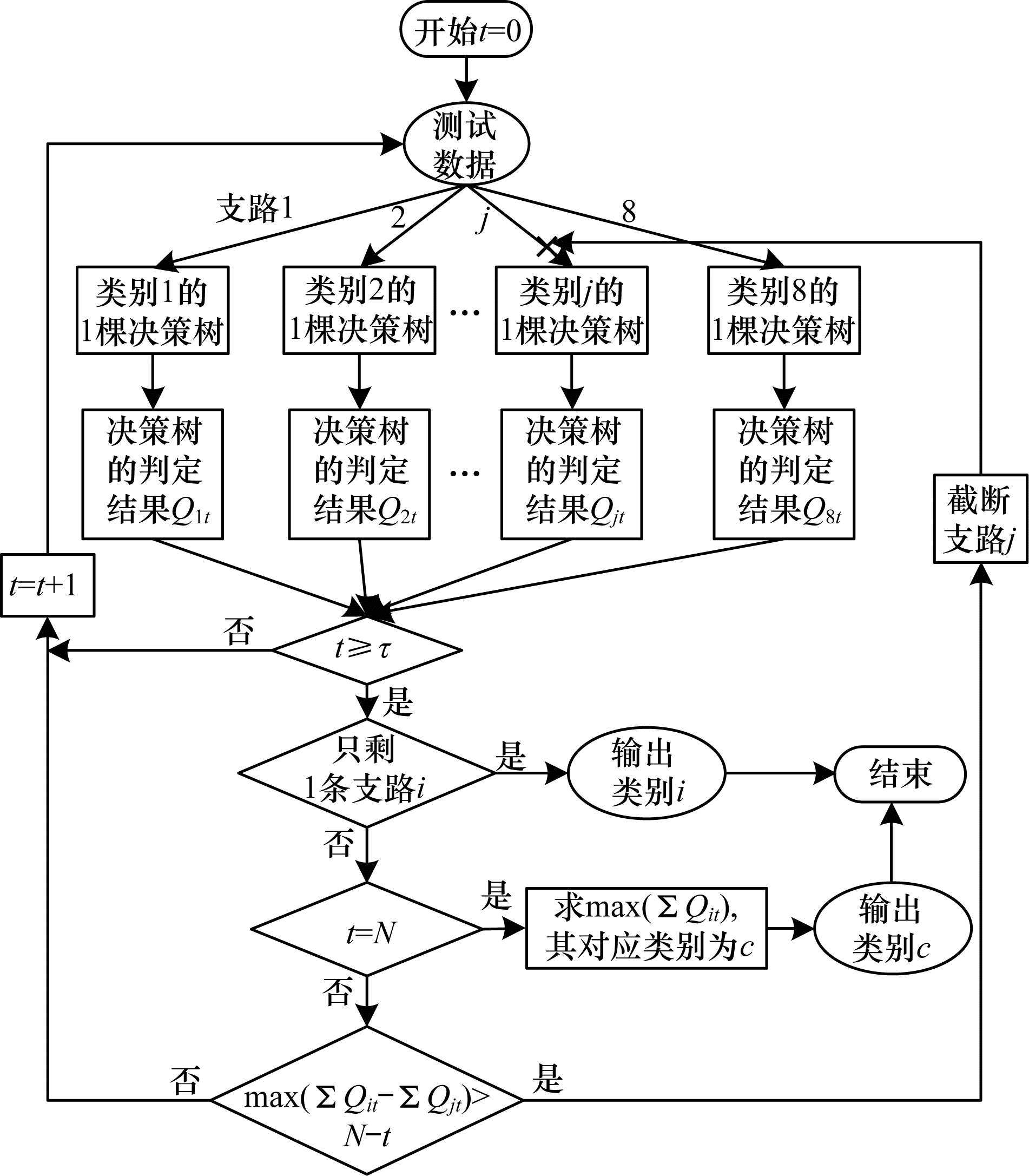
分支定界的思想就是在搜索过程中当发现某个分支所可能取得的最好结果也不会超过现有最优解时，则放弃对该分支的继续搜索，从而节省不必要的运算。将该思想用于本文随机森林分类器，并基于如下的事实：本文采用的OvR随机森林分类器，就是在寻找各个随机森林中的决策树给正结论（样本属于该类）“投票”的票数最大值，如果所有随机森林并行测试，即测试过程分成若干轮，每轮测试每个随机森林各自使用1棵决策树，当过程进行到第$ k $步，即所有随机森林都已经用$ k $棵决策树进行判定时，如果某一个类累计得到正结论的次数为$ M $，使得即使该随机森林内剩余的决策树（（$ 50-k $）棵）全部得出正结论，其总的得票数（$ M+50-k $）也不大于当前其他类的最高得票数（随机森林中给出正结论的决策树棵数），则测试样本必然不属于该类，对这个类就不再继续执行剩余的决策树判定，因此，可以对8个随机森林的测试过程进行如下优化：将$ c $个类别的随机森林测试过程称为$ c $个并行支路，每条支路对应随机森林中的所有决策树遍历判定过程。本文提出的随机森林预测算法结构框图如图 7所示，伪代码如算法1所示。

算法1   OvR多分类随机森林预测算法

参数

$ \tau $，开始执行分支定界检查的轮次

$ N $，每组随机森林决策树总数目

输入

s，被测样本的特征向量

决策函数：$ D{T}_{it}\left(\mathit{s}\right) $，第$ i $个随机森林的第$ t $棵决策树对样本s进行判定，输出为一个布尔值，正结论为“1”，否则为“0”

中间变量：$ {Q}_{it} $，第$ t $轮测试第$ i $组决策树的判定结果

$ \mathrm{F}\mathrm{l}\mathrm{a}{\mathrm{g}}_{i} $，第$ i $条支路是否进行决策树判定操作的标志位

S_i，第i个类别的累计得票数

M_q，当前所有分支的最高得票数

$ t $，测试轮次

输出

$ c $，类别

1.初始化$ \mathrm{F}\mathrm{l}\mathrm{a}{\mathrm{g}}_{\mathrm{i}}=1, {\mathrm{S}}_{\mathrm{i}}=0, \mathrm{i}=\mathrm{1, 2}, \cdots , 8 $

2.for $ \mathrm{t}\leftarrow \mathrm{ }1\;\mathrm{t}\mathrm{o}\;\mathrm{\tau } $

for $ \mathrm{i}\leftarrow \mathrm{ }1\;\mathrm{t}\mathrm{o}\;8 $

$ {\mathrm{Q}}_{\mathrm{i}\mathrm{t}}=\mathrm{D}{\mathrm{T}}_{\mathrm{i}\mathrm{t}}\left(\mathrm{s}\right), \mathrm{i}=\mathrm{1, 2}, \cdots , 8 $

$ {\mathrm{S}}_{\mathrm{i}}={\mathrm{S}}_{\mathrm{i}}+{\mathrm{Q}}_{\mathrm{i}\mathrm{t}} $//票数累加

end for i

$ {\mathrm{M}}_{\mathrm{q}}=\mathrm{m}\mathrm{a}{\mathrm{x}}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{i}}\right) $

$ {\mathrm{i}}_{\mathrm{m}}\ne \mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}{\mathrm{x}}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{i}}\right) $//得票最多的类序号

end for t

3.$ \exists {\mathrm{M}}_{\mathrm{q}} $-$ {\mathrm{S}}_{\mathrm{j}}>(\mathrm{N}-\mathrm{\tau }), \mathrm{j}\ne {\mathrm{i}}_{\mathrm{m}}, \mathrm{则}\mathrm{F}\mathrm{l}\mathrm{a}{\mathrm{g}}_{\mathrm{j}}=0 $//剪枝

4.for $ \mathrm{t}\leftarrow \mathrm{ }\mathrm{\tau }+1\;\mathrm{t}\mathrm{o}\;\mathrm{N} $

if $ \mathrm{F}\mathrm{l}\mathrm{a}\mathrm{g} $只有1个1（设为$ \mathrm{F}\mathrm{l}\mathrm{a}{\mathrm{g}}_{\mathrm{j}}=1 $），其他7个为0

输出最终的类别$ \mathrm{c}=\mathrm{j} $

程序结束；

else

for $ \mathrm{i}=\left\{\mathrm{1, 2}, \cdots , 8\left|\mathrm{F}\mathrm{l}\mathrm{a}{\mathrm{g}}_{\mathrm{i}}=1\right.\right\} $

$ {\mathrm{Q}}_{\mathrm{i}\mathrm{t}}=\mathrm{D}{\mathrm{T}}_{\mathrm{i}\mathrm{t}}\left(\mathrm{s}\right), \mathrm{i}=\mathrm{1, 2}, \cdots , 8$

$ {\mathrm{S}}_{\mathrm{i}}={\mathrm{S}}_{\mathrm{i}}+{\mathrm{Q}}_{\mathrm{i}\mathrm{t}} $//票数累加

end for i

$ {\mathrm{M}}_{\mathrm{q}}=\mathrm{m}\mathrm{a}{\mathrm{x}}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{i}}\right) $

$ {\mathrm{i}}_{\mathrm{m}}\ne \mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}{\mathrm{x}}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{i}}\right) $

$ \exists {\mathrm{M}}_{\mathrm{q}}-{\mathrm{S}}_{\mathrm{j}}>(\mathrm{N} $-$ \mathrm{t}), \mathrm{j}\ne {\mathrm{i}}_{\mathrm{m}}, \mathrm{则}\mathrm{F}\mathrm{l}\mathrm{a}{\mathrm{g}}_{\mathrm{j}}=0 $//剪枝

end if

end for t

输出最终的类别$ \mathrm{c}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}{\mathrm{x}}_{\mathrm{i}}\left({\mathrm{S}}_{\mathrm{i}}\right) $

程序结束

随机森林预测算法的基本思想是：

1）按照广度优先的原则，每轮测试每个随机森林各拿出1棵决策树进行判定，然后再取各个随机森林中的第2棵树进行判定，以此类推，使得各支路并行进行，根据前面的分析可得，只有当已经判定的轮次达到一定数量（设为$ \tau $轮）时，才可能出现某个支路能够判定为淘汰的情况，因此，在前$ \tau $轮，所有支路都进行判定，不用做分支定界条件的检查，当第$ \tau $轮测试结束，开始分别统计每个随机森林得出正结论的总票数。

2）在每一轮测试后（即各个支路每多执行一棵树的判定）就做如下检查：如果出现某一个类别j，其正结论的票数加上j类剩下的决策树数量之和小于此时其他类的得票数的最大值，则停止j类剩下的预测操作，即截断支路j；被截断的支路在接下来的测试中不再从中提取决策树进行判定，从而节省不必要的数据读入和阈值比较时间。上述过程不断进行，直到只剩下一条支路，则预测类别为该支路的类别，或者未截断支路剩余的决策树为0时，找出累计得票数最多的类别，即为预测类别，此时预测过程结束。

关于上述改进随机森林预测算法中的参数$ \tau $的取值，因为进行$ \tau $轮测试后，可能出现票数最大值不会超过$ \tau $，即存在限制不等式（1），又因为只有该最大值大于每组随机森林剩下的决策树数目时，才可能满足剪枝条件，所以$ \tau $应满足不等式（2）。

$ \mathrm{m}\mathrm{a}{\mathrm{x}}_{i}\left(\sum\limits _{t=1}^{\tau }{Q}_{it}\right)\le \tau $

(1)

$ \mathrm{m}\mathrm{a}{\mathrm{x}}_{i}\left(\sum \limits_{t=1}^{\tau }{Q}_{it}\right)>N-\tau $

(2)

由式（1）和式（2）得：

$ \tau >\frac{N}{2} $

(3)

当$ \tau $满足式（3）时，$ \tau $越大，进行剪枝条件检查的次数越少，但是决策树的平均判定次数越多，由于一棵决策树的判定过程的计算量远大于一次剪枝条件检查，因此应该选择尽量小的$ \tau $值。因为本文设定的模型中每个随机森林的决策树数目$ N=50 $，所以$ \tau $的最优值为26。每个随机森林分别进行26次决策树判定后，再开始运用分支定界决定是否可以截断某条支路。对于每个随机森林剩下的24棵决策树，每轮每个森林的一棵决策树参与判定后，进行一次分支定界。考虑到FLASH的一个块最少可以存储32棵决策树，为了便于分支定界预测方案的实现，8个类别各取4棵树一起组合成32棵树，存放入一个块中。模型的最终存储方案如下：

1）每个随机森林各拿出26棵决策树，分别按照图 5（b）的方式存入FLASH的8个块中，每个块存储26棵树。

2）每个随机森林将剩下的决策树分为6组，每组4棵树，每个块中存储8个类别的一组决策树，共$ 4\times 8=32 $棵树，一共占用6个块。

分类器预测过程中涉及的主要操作，或时间与功耗的主要来源是决策树的阈值比较和FLASH数据读取，前者的最坏情况和决策树深度成正比，后者则主要取决于所读取的FLASH页数。通过本文算法可以避免不必要的决策树判定，而且当一个分支被截断后，其数据也不用再读入片内存储器，还可以减少FLASH数据的读取，既节省了程序的执行时间又降低了数据读取的能耗。

5 实验结果分析

在FPGA的Microblaze上实现有/无采用精简数据存储结构、有/无采用分支定界思想的4组随机森林预测算法，系统的工作频率设置为100 MHz。在传统的随机森林预测算法中，每个样本需要$ 8\times 50=400 $次决策树判定。运用分支定界思想后，实际的判定次数和从FLASH实际读取的页数都与被测样本有关，不是确定的，因此，为了对改进算法的性能进行评估，选取800个随机样本（每种手势各100个样本）进行测试，统计各自的决策树判定次数和从FLASH实际读取的页数，实验结果表明，决策树平均判定次数为243。样本的决策树判定次数决定了一次推理所需参与的决策树数目，与CPU访问FLASH的时间成正相关关系，统计得到精简数据结构下的一个样本平均读取1 696页。

Xilinx的axi_timer IP核可以记录运行一段程序所需的时钟数，在每个操作对应代码的始末位置，调用计数函数得到完成该操作所消耗的时钟数与系统时钟频率的商值，即为实际运行时间。

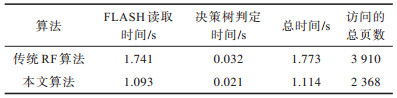
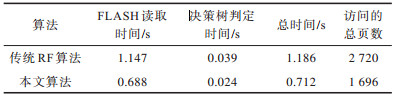
为了评估精简模型和分支定界算法对系统性能的影响，分别进行如下对比实验：原始树模型的有用信息未经组合压缩且比较阈值保留原来的整型数据类型，分别使用传统和分支定界的RF识别算法在实验平台上运行，得到的运行时间如表 2所示。采用精简的节点存储结构，不同算法的运行时间如表 3所示。表 2、表 3中的测试时间均为800个随机样本的平均值。对比表 2、表 3可以看出，采用精简的节点数据存储结构，传统RF算法访问FLASH的时间从1.741 s下降到1.147 s，减少0.594 s，说明模型压缩的重要性和数据结构设计的合理性。另外，在精简节点数据存储结构下，由于叶子节点标志位和类别信息需要经过与和移位运算得出，导致决策树的判定时间略有增加，从0.021 s上升到0.024 s，但是精简节点数据结构的使用减少了访问FLASH的平均次数。分支定界思想在随机森林算法中的运用缩短了模型的加载时间，同时减少了CPU执行决策树判定的运算时间，在未优化的模型存储结构下，改进RF算法总的运行时间（FLASH读取数据与决策树判定时间之和）从1.773 s下降到1.114 s，减少0.659 s。同时，采用模型存储结构精简和识别算法优化时得到的总运行时间为0.712 s。对比一般存储结构下的传统RF算法，最终整个程序的总执行时间缩短了约60%。

6 结束语

本文提出一种OvR多类别随机森林分类算法嵌入式软件实现方案，并将其用于手势识别SOPC系统，以缩短系统的识别时间，减少FLASH访问能耗以及内存空间。设计更紧凑的模型节点数据结构，针对模型存放在片外FLASH时FLASH读取数据以页为最小单位的情况，设计减少低速设备FLASH读取次数和决策树判定运算的分支定界多随机森林OvR分类器推理算法，根据算法设计相应的模型存储空间分配方案。实验结果表明，与传统的随机森林预测算法相比，本文算法在FPGA上的实测时间约缩短60%。下一步将采用神经网络算法作为手势识别的分类器，选择一种计算复杂度满足系统实时性和存储需求的网络结构，并研究其嵌入式实现方案。