开放科学(资源服务)标志码(OSID):
机器人学聚集了多种学科最先进的研究成果,一直以来都是科学技术领域的研究热点。路径规划算法作为移动机器人的重要组成部分,是移动机器人运行研究的重点问题[1]。
路径规划的基本任务是找到一条从起始位置到目标位置的无碰撞路径[2],并且使得这条路径能够具有距离短、用时少等优点。在传统路径规划方法中:A*算法[3-4]和D*算法[5]在实时规划或者局部规划中都有较好的性能,但两种算法需要的计算量较大,特别在三维空间中计算量剧增;人工势场法[6]易于实现的优点使其能被广泛应用,但容易陷入局部极小值;蚁群算法[7]可以获得全局最优解且有较强鲁棒性,但计算量大、收敛时间长。
快速扩展随机树(Rapidly exploring Random Tree,RRT)算法采用随机采样方法搜索[8],具有很强的搜索性,但是该算法的随机性也导致其搜索效率较低。为提高RRT算法的搜索效率,偏向RRT[9]、RRT-Connect[10]、双向RRT[11]等改进算法被相继提出,这些算法通过目标偏向、双树拓展等改进加快了收敛算法速度,但仍存在较大转折、绕远等问题。为得到最优路径,一些算法相继提出:RRT*[12-13]采用渐进优化思想改进了由基本RRT产生的并非概率最优解问题;Bi-RRT*[14]采用双树拓展同时结合RRT-Connect和启发式思想,在保证渐进最优的同时加快了收敛速度;Quick-RRT*[15]在重选父节点时扩大潜在父节点选择范围,以此减少路径不必要的拐弯来缩短路径长度;文献[16]通过重选父节点的方法改进RRT算法来缩短规划路径;文献[17]提出结合目标引力思想的变步长搜索方法提高搜索效率;文献[18]借鉴人工势场思想引导随机树更有效生长;文献[19]通过施加转角约束、两树连接处处理等一系列改进,提高规划路径质量。
虽然上述优化方法用于机器人路径规划时都取得了较好的效果,但RRT的强随机性仍然使所得路径存在曲折、绕远、连接不平滑等现象,这也将限制移动机器人的实际工作效率。本文针对RRT-Connect算法进行改进,通过设置多种约束优化新节点生成规则,进一步提高移动机器人规划路径的质量。
1 RRT-Connect算法1999年,LAVALLE提出RRT算法[8],基本思想是向随机的目标点拓展随机树上的最近点来探索搜索空间,通过不断迭代最终找到可行路径,但是RRT算法的拓展具有随机性,导致收敛速度慢。针对这一不足,2000年,LAVALLE和KUFFNER提出RRT-Connect算法,通过在起始点和目标点建立两棵随机树交替向彼此方向拓展,同时引入贪婪策略,进一步加快收敛速度。
RRT-Connect随机树生长过程如图 1所示,具体步骤如下:

|
Download:
|
| 图 1 RRT-Connect随机树生长过程 Fig. 1 Random tree growth process of RRT-Connect | |
1)初始化起始点、终点和障碍物,将起始点、终点坐标信息加入到随机树,并在机器人的C空间中生成一个随机点Xrand。
2)在Tree1上找到距Xrand欧氏距离最小的点,记为Xnearest1,方向指向Xrand,朝该方向生长一定步长Sstep得到Xnew1。如果Xnew1不满足C空间中的障碍物约束,则舍弃该点重新生成随机点;如果满足,则把生长后的树枝和端点注入到树上。
3)计算Tree2上距Xnew1欧氏距离最小的点,记为Xnearest2,方向指向Xnew1,朝该方向生长一定步长得到Xnew2。若通过碰撞检测,则将Xnew1注入Tree2中,同时启动贪婪策略子程序,继续往Xnew1方向生长,直到遇到障碍物或者两树最近距离小于阈值后停止;若遇到障碍物,则返回主程序交换两树并重复上述采样过程,若两树距离小于连接阈值,则返回连接点信息,路径搜索结束。
2 改进的RRT-Connect算法 2.1 考虑祖代点的重选父节点环节传统双向RRT算法在生成新节点后立即进入另一棵树生成新节点,这容易生成不必要的节点,并导致绕远现象的发生。为了使路径趋于渐进最优解,本文基于文献[14-15]的设计思想,在原RRT-Connect拓展的基础上增加重选父节点环节。
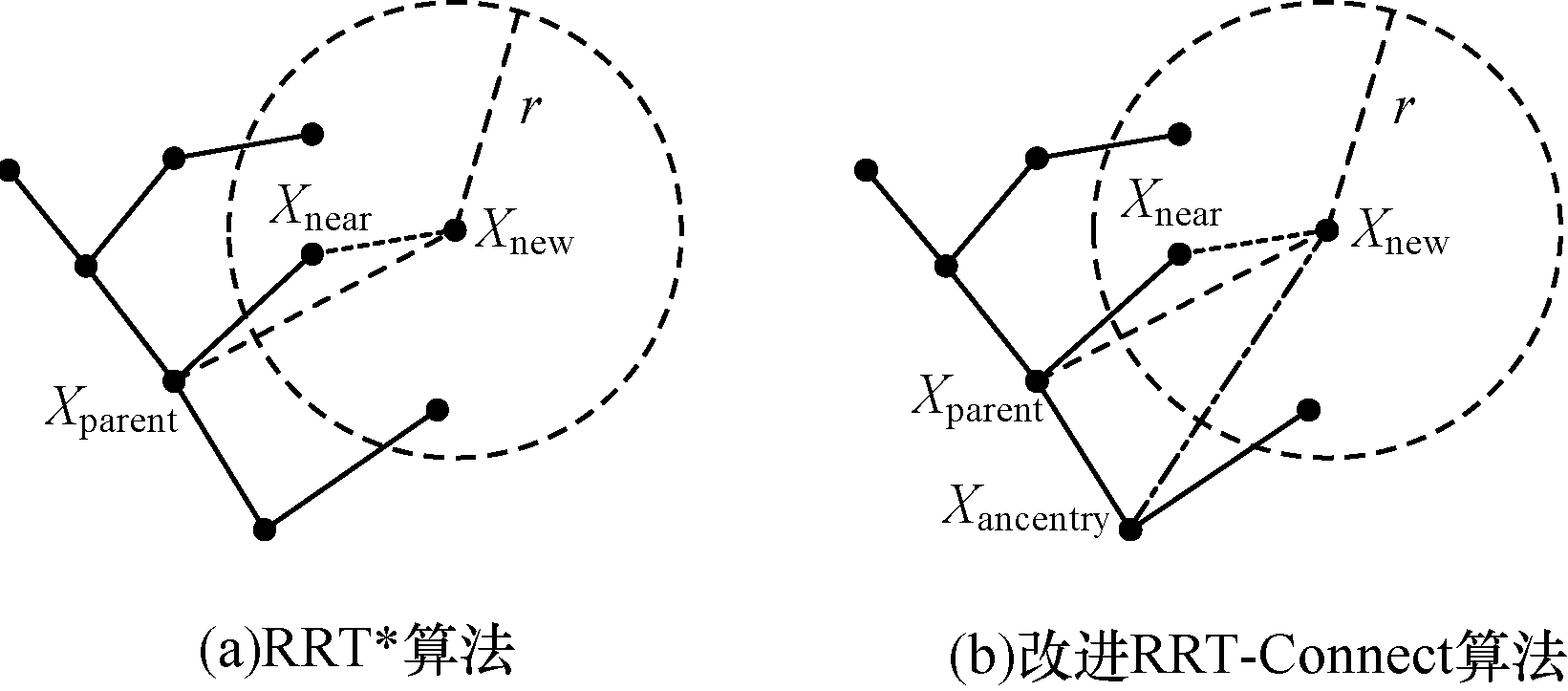
图 2(a)所示为RRT*的重选父节点环节,和传统的RRT算法一样生成Xnew点后,以特定的半径r搜索Xnew附近的顶点为父节点候选集,然后迭代计算Near圆内点到起始点距离成本,选取最小成本的点作为Xnew的父节点,以此达到渐进优化的效果,而如果要加快收敛速度,则需要增大搜索半径r,这会导致计算量呈指数级增加。相比于RRT*的增大搜索半径r,本文改进算法通过自定义父节点的深度范围来扩大新节点的潜在父节点候选集,使求得新节点到起始点更短距离路径的概率增加,而计算量却没有增加太多。改进RRT-Connect算法的重选父节点环节如图 2(b)所示。
|
Download:
|
| 图 2 2种算法树结构比较 Fig. 2 Tree structure comparison of two algorithms | |
上述改进主要得益于三角不等式原理和共享同一父节点。当生成Xnew并以特定的半径r搜索其附近的顶点时,同时求出圆内顶点的父节点和祖节点。由三角不等式原理可知,在考虑Near圆父节点后,只要新节点与圆外父节点碰撞检测通过,就可得到该新节点更低路径成本,由此求得新节点更短路径成本概率增加;而通过扩大父候选集的改进,Near圆内的点已倾向于共享同一父节点,因此,改进后Xnew扩大了父节点候选集,而候选集顶点总数却不会增加太多,另由于舍弃了RRT*中的Rewire过程,因此收敛时间相比于RRT*不会增加太多。上述过程考虑到深度为2的潜在父节点,因此,也称其为考虑祖代点的重选父节点环节。
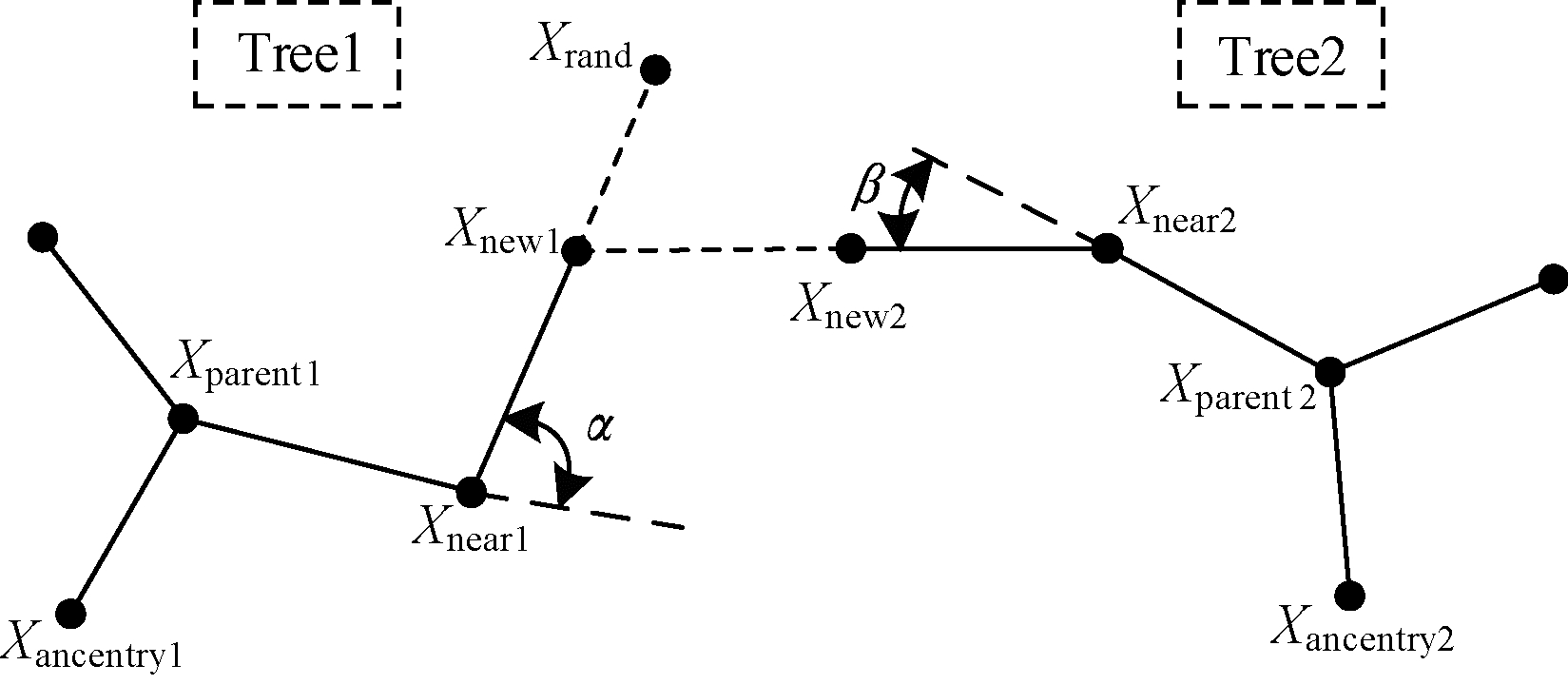
2.2 转角约束为使规划路径更平滑,对每一个拓展的新节点添加转角约束。图 3为Tree1、Tree2的转角约束示意图。
|
Download:
|
| 图 3 Tree1和Tree2转角约束 Fig. 3 Corner constraints of Tree1 and Tree2 | |
对于Tree1,新节点转角α由向量
| $\overrightarrow{{{X}_{\text{near1}}}{{X}_{\text{new1}}}}=[{{X}_{\text{new1}}}(x, y)-{{X}_{\begin{array}{*{35}{l}} \text{Near1} \\ \end{array}}}(x, y)] $ | (1) |
| $\overrightarrow {{X_{\begin{array}{*{20}{l}} {{\rm{parent1}}} \end{array}}}{X_{{\rm{near1}}}}} = [{X_{{\rm{near1}}}}(x, y) - {X_{\begin{array}{*{20}{l}} {{\rm{parent1}}} \end{array}}}(x, y)] $ | (2) |
| $\alpha = \begin{array}{*{20}{l}} {{\rm{arccos}}} \end{array}\left( {\frac{{\overrightarrow {{X_{{\rm{near1}}}}{X_{{\rm{new1}}}}} \cdot \overrightarrow {{X_{{\rm{parent1}}}}{X_{{\rm{near1}}}}} }}{{\left\| {\overrightarrow {{X_{{\rm{near1}}}}{X_{{\rm{new1}}}}} } \right\|\left\| {\overrightarrow {{X_{{\rm{parent1}}}}{X_{{\rm{near1}}}}} } \right\|}}} \right) $ | (3) |
| $\beta = \begin{array}{*{20}{l}} {{\rm{arccos}}} \end{array}\left( {\frac{{\overrightarrow {{X_{{\rm{near2}}}}{X_{{\rm{new2}}}}} \cdot \overrightarrow {{X_{{\rm{parent2}}}}{X_{{\rm{near2}}}}} }}{{\left\| {\overrightarrow {{X_{{\rm{near2}}}}{X_{{\rm{new2}}}}} } \right\|\left\| {\overrightarrow {{X_{{\rm{parent2}}}}{X_{{\rm{near2}}}}} } \right\|}}} \right) $ | (4) |
假设最大转角约束为θ。对于Tree1,当0 ≤ α ≤ θ时,转角约束通过,可将新节点注入Tree1中,接着进入Tree2的拓展,当θ < α ≤ 180°时则舍弃该新节点,并重新生成采样点;对于Tree2,当0 ≤ β ≤ θ时,转角约束通过,并将新节点注入Tree2中,接着进入贪婪拓展,当θ < α ≤180°时则舍弃该新节点,并退出拓展子程序进入交换两树环节。
2.3 动态步长优化在原RRT-Connect算法中,两树通过交换迭代拓展生成可行路径,如在图 3中:对于Tree1,生成随机点Xrand后计算最近邻节点Xnear1,然后以固定步长往Xrand方向拓展一步,计算表达式如式(5)所示;对于Tree2,生成Xnew1点后计算得到Xnew1距离Tree2最近的点Xnear2,然后以固定步长Sstep往Xnew1方向拓展一步或者多步,计算表达式如式(6)所示。
| ${X_{{\rm{new1}}}} = {X_{{\rm{near1}}}} + {S_{{\rm{step}}}} \cdot \frac{{{X_{{\rm{rand}}}} - {X_{{\rm{near1}}}}}}{{\left\| {{X_{{\rm{rand}}}} - {X_{{\rm{near1}}}}} \right\|}} $ | (5) |
| ${X_{{\rm{new2}}}} = {X_{{\rm{near2}}}} + {S_{{\rm{step}}}} \cdot \frac{{{X_{{\rm{new1}}}} - {X_{{\rm{near2}}}}}}{{\left\| {{X_{{\rm{new1}}}} - {X_{{\rm{near2}}}}} \right\|}} $ | (6) |
原RRT-Connect算法拓展步长固定, 收敛速度慢, 生成路径转折多, 特别经过改进即考虑祖代点的重选父节点环节后, 由于考虑到转角约束, 导致在连接处连接失败的概率增加, 进而增加了收敛时间。受文献[19-21]关于动态步长优化的启发, 本文结合改进算法的实际情况, 提出一种动态步长优化方法: 当两树距离Dtree小于设定阈值σ1时, 强制小步长, 以此增加两树连接成功率, 该步骤执行优先级为I级; 当两树距离大于设定阈值σ1时, 认为两树还未进入连接状态, 步长由机器人与障碍物距离决定; 当机器人与障碍物距离Dobs大于设定阈值σ2时, 认为机器人处于空旷环境, 采用最大步长; 相反, 当机器人与障碍物距离小于设定阈值σ2时, 认为机器人处于障碍物环境, 采用中步长, 也即默认步长, 当默认步长较小时, 小步长与默认步长可取等值, 该步骤执行优先级为II级。
动态步长表达式如式(7)所示。
| ${S_{{\rm{step}}}} = \left\{ \begin{array}{l} {S_{{\rm{step\_min}}}}, {D_{{\rm{tree}}}} < {\sigma _1}\\ {S_{{\rm{step\_middle}}}}, {D_{{\rm{tree}}}} > {\sigma _1}\& \& {D_{{\rm{obs}}}} < {\sigma _2}\\ {S_{{\rm{step\_max}}}}, {D_{{\rm{tree}}}} > {\sigma _1}\& \& {D_{{\rm{obs}}}} > {\sigma _2} \end{array} \right. $ | (7) |
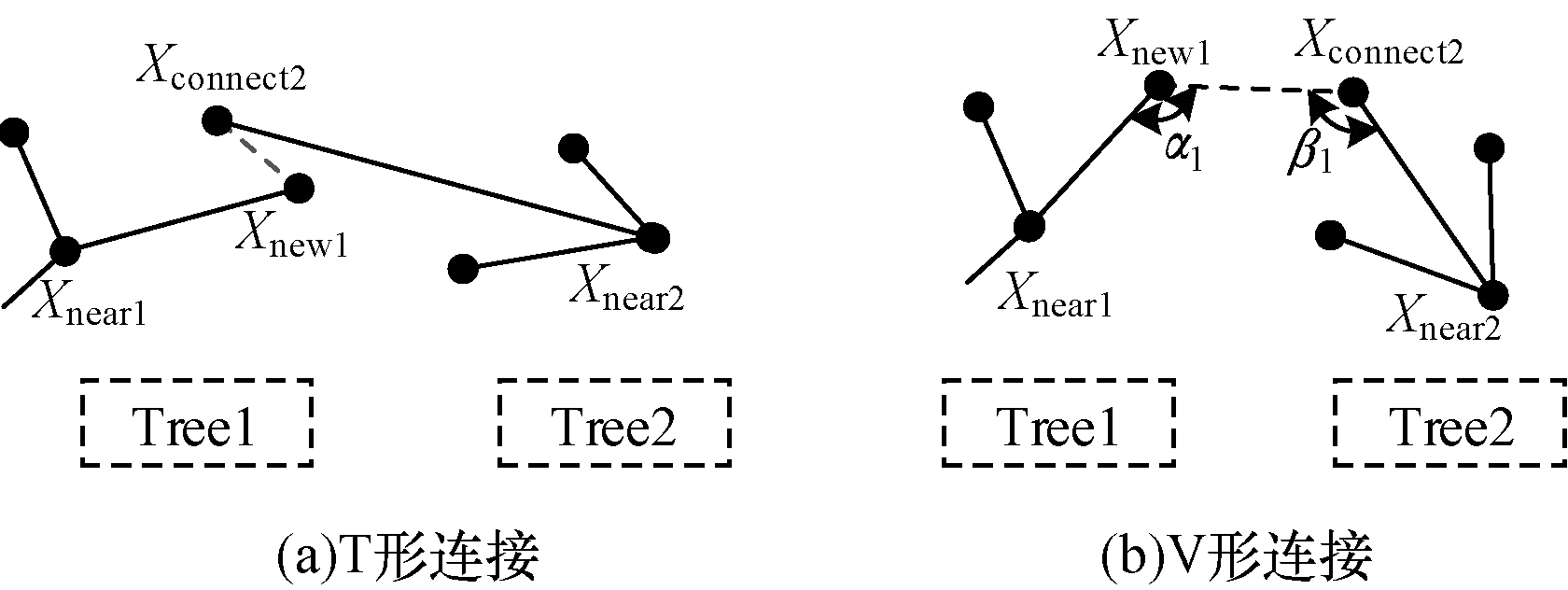
传统RRT-Connect算法在连接时,只要新节点与另一棵树的距离小于指定阈值,即将两点直接连接,这会导致连接处出现转角过大的问题,有时甚至出现180°转角,主要有图 4所示的T形连接和V形连接两种情况。
|
Download:
|
| 图 4 两种连接方式 Fig. 4 Two connection modes | |
为使生成路径更符合实际,在进入连接阶段作以下处理:
1)针对连接点的父节点、祖代点的处理
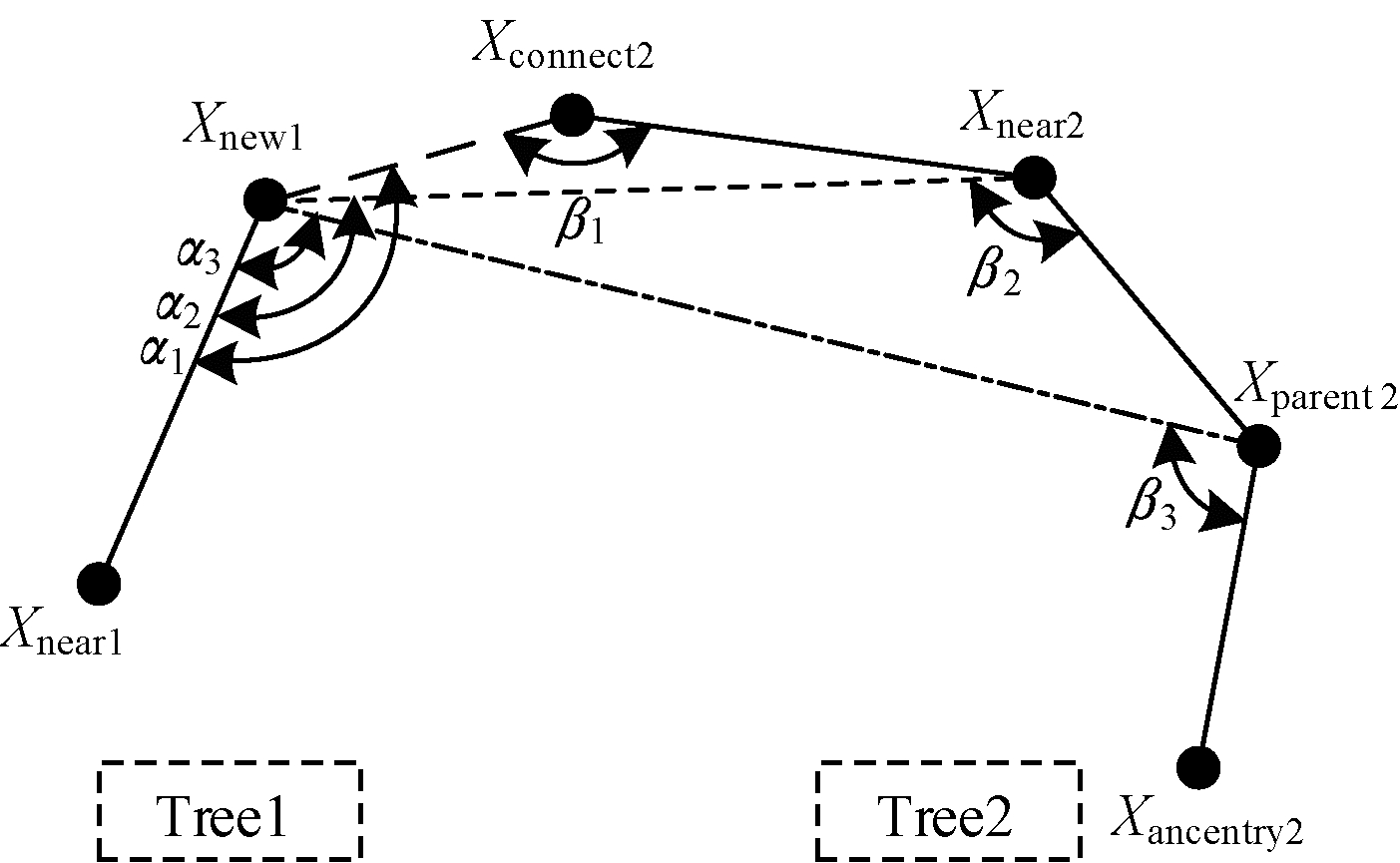
该过程依次对祖代点、父节点进行碰撞检测和角度检测,检测通过即可连接。如图 5所示,首先判断Xnew1到Xparent2、Xnear2的可连接性,即先计算α3、β3。若角度约束符合设定值,则对Xnew1到Xparent2进行碰撞检测,都通过则返回Xnew1坐标以及该点在两树的父节点Xnear1、Xparent2序号到主程序中;若上述约束不通过,则判断Xnear2的可连接性;若以上两种情况都不通过,则进行针对连接点Xconnect2的连接处理。
|
Download:
|
| 图 5 连接点连接结构 Fig. 5 Connection structure of connection points | |
2)针对连接点的处理
记
当φ > δ时,计算α1、β1。第1类相遇:α1 > δ且β1 > δ,只有V形连接存在此情况,判为有效相遇。第2类相遇:α1 < δ或β1 < δ,只有T形连接存在此情况,判为无效相遇,进入同父节点重连处理。
当φ < δ时,检测α1、β1。第3类相遇:α1 > δ且β1 > δ,只有V形连接存在此情况,引入安全距离处理。第4类相遇:α1 < δ或β1 < δ,只有T形连接存在此情况,判为无效相遇,舍弃。
下文简要阐述同父节点重连、安全距离这两个概念。
1)同父节点重连
在第2类相遇情况下,为减少搜索次数,增加连接成功率,提出同父节点重连概念,即考虑重新连接与连接点共享父节点的点。如图 6所示,Xconnect2为达到连接阈值的连接点,通过计算其父节点Xnear2共享该父节点的点信息,即Y1、Y2节点。若检测α1、β1都大于最小夹角约束,则判Y1为有效相遇点。
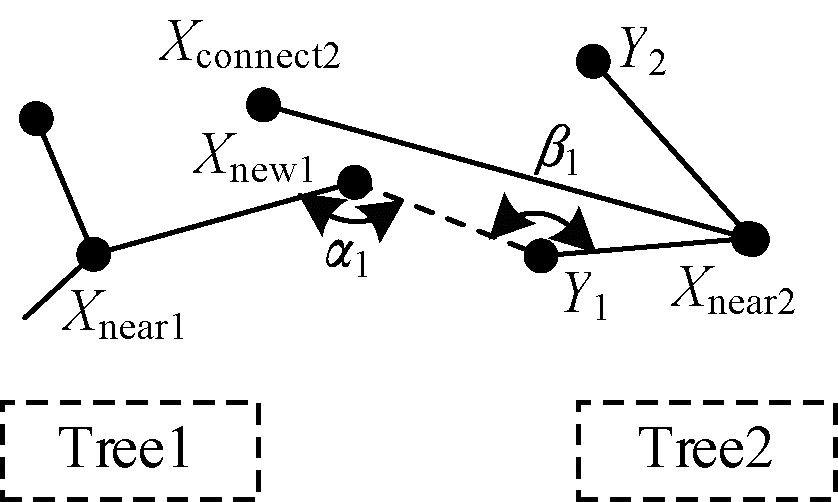
|
Download:
|
| 图 6 同父节点重连的情况 Fig. 6 Reconnection of parent node | |
2)安全距离
在第3类相遇情况下,V形连接,需要考虑机器人最小移动距离,即安全距离η。当Xnew1、Xconnect2两点距离小于连接阈值而大于η时,可判断为有效相遇,小于η则判为无效相遇,舍弃。
此外,判为有效相遇后,通过碰撞检测即可定为有效连接点。Tree2连接Tree1与Tree1连接Tree2类似。
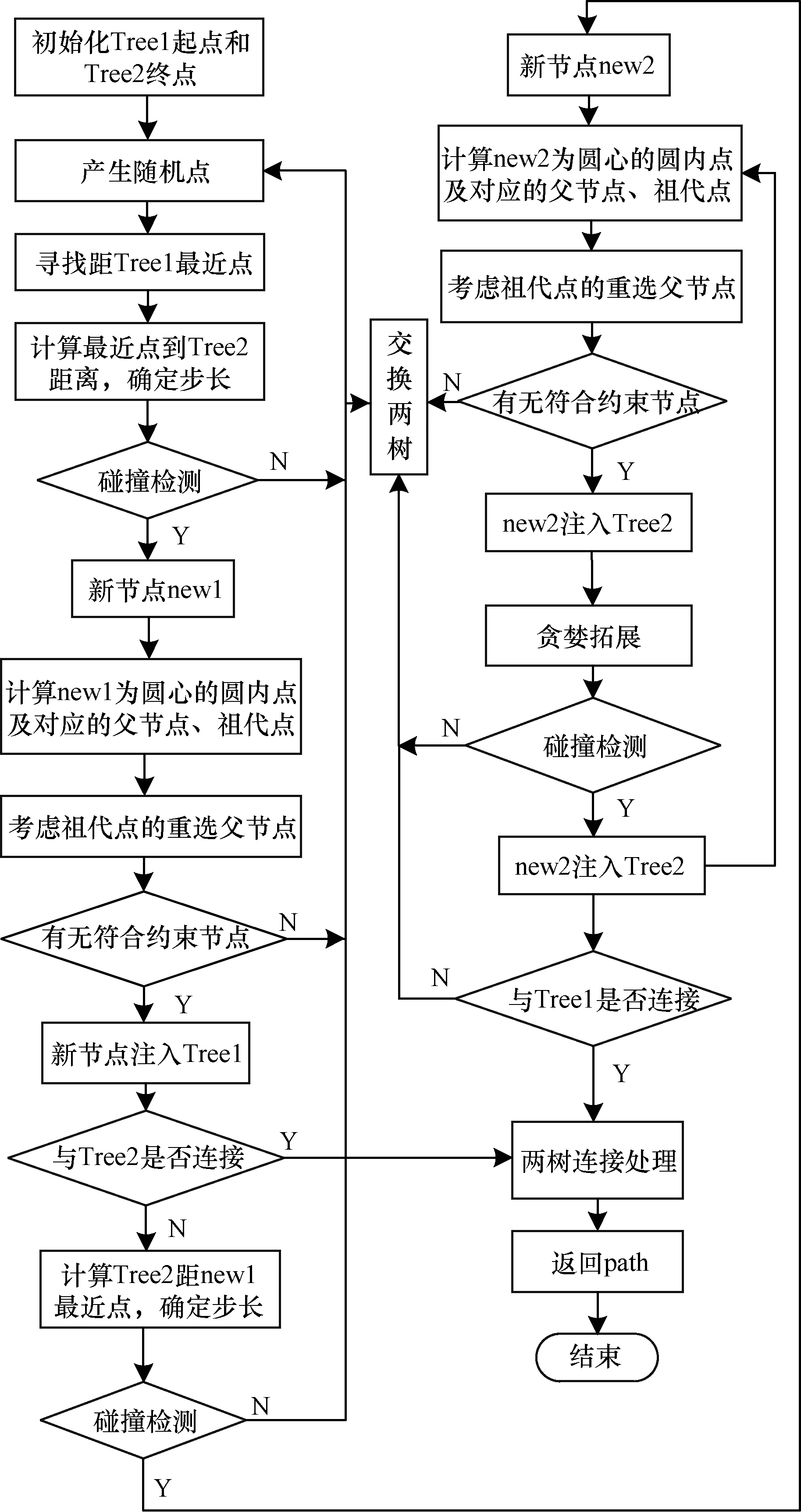
2.5 改进算法流程改进RRT-Connect算法流程如图 7所示,具体步骤如下:
|
Download:
|
| 图 7 改进RRT-Connect算法流程 Fig. 7 Procedure of improved RRT-Connect algorithm | |
步骤1 初始化地图,设置起止点、动态步长、安全距离等参数。
步骤2 生成随机点,确定离Tree1最近点,确定步长大小。
步骤3 生成Tree1新节点。若通过碰撞检测则判断是否与Tree2连接,若能连接则跳至步骤7,不能连接则进行步骤4,若不通过碰撞检测则重新采样。
步骤4 考虑祖代点的父节点重选,检测能否满足转角约束和碰撞检测,都满足则重连处理,不满足则返回重新采样。
步骤5 确定Tree2拓展步长,同时生成Tree2新节点,检测是否与Tree1连接,能连接则跳至步骤7,不能则考虑祖代点的父节点重选。
步骤6 贪婪拓展,同时连接检查,能连接则跳至Step7,不能则考虑祖代点的父节点重选,循环步骤6直至检测不通过,交换两树返回步骤2。
步骤7 若连接则进行连接处理程序,结束进程,返回路径信息path,不能连接则交换树,返回步骤2。
3 实验与结果分析实验仿真在Matlab2018a上进行,实验环境配置为:Window10,处理器Intel® CoreTM i5-3230M CPU@2.60 GHz,RAM 4 GB。
为验证改进算法的性能,采用简单环境和复杂环境两种地图,仿真地图大小为500 cm×500 cm,起点坐标(10,10),终点坐标(490,490),障碍物由多个圆形区域组成,分别对Bias-BiRRT、原始RRT-Connect、改进RRT-Connect这3种算法进行50次仿真,并将相应的平均搜索时间、平均采样点数、平均路径长度等进行对比分析,同时在复杂环境下,对改进前后算法进行平滑度分析实验。其中,Bias-BiRRT、原始RRT-Connect拓展步长10 cm,改进RRT-Connect拓展最大步长20 cm,默认步长10 cm,改进RRT-Connect最大转角设置为60°。
3.1 简单环境仿真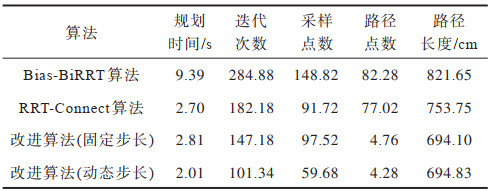
|
下载CSV 表 1 简单环境下3种算法的实验数据 Table 1 Experimental data of three algorithms in simple environment |
|
Download:
|
| 图 8 简单环境实验结果 Fig. 8 Experiment results in simple environment | |
1)在规划效率方面,由表 1可知,在简单环境中,改进算法固定步长时的平均迭代次数为147.18次,比Bias-BiRRT、RRT-Connect算法分别降低43%、19%,而平均规划时间为2.81 s,和RRT-Connect算法消耗的时间2.70 s相差不大。由这两项数据可得,引入改进重选父节点环节及设置多种约束后,改进算法的计算量和RRT-Connect算法相比没有增加很多,而迭代次数变少,规划效率更高。
2)在路径长度优化效果方面,由表 1可知,改进算法固定步长时的平均路径长度为694.10 cm,相比Bias-BiRRT和RRT-Connect算法分别减少127.55 cm、59.65 cm。可以看出,引入考虑祖代点的重选父节点环节能够起到减小路径长度的效果,提高规划路径质量。
3)在动态步长优化方面,由表 1可知,改进算法动态步长规划时间相比固定步长减小0.8 s,而路径长度几乎不变。由该数据可知,改进算法动态步长策略以较大步长通过空旷区域,而以较短步长规划障碍物区域、两树连接区域,总体上加快了改进算法收敛速度,减少了添加转角约束、父节点重连所消耗的时间。
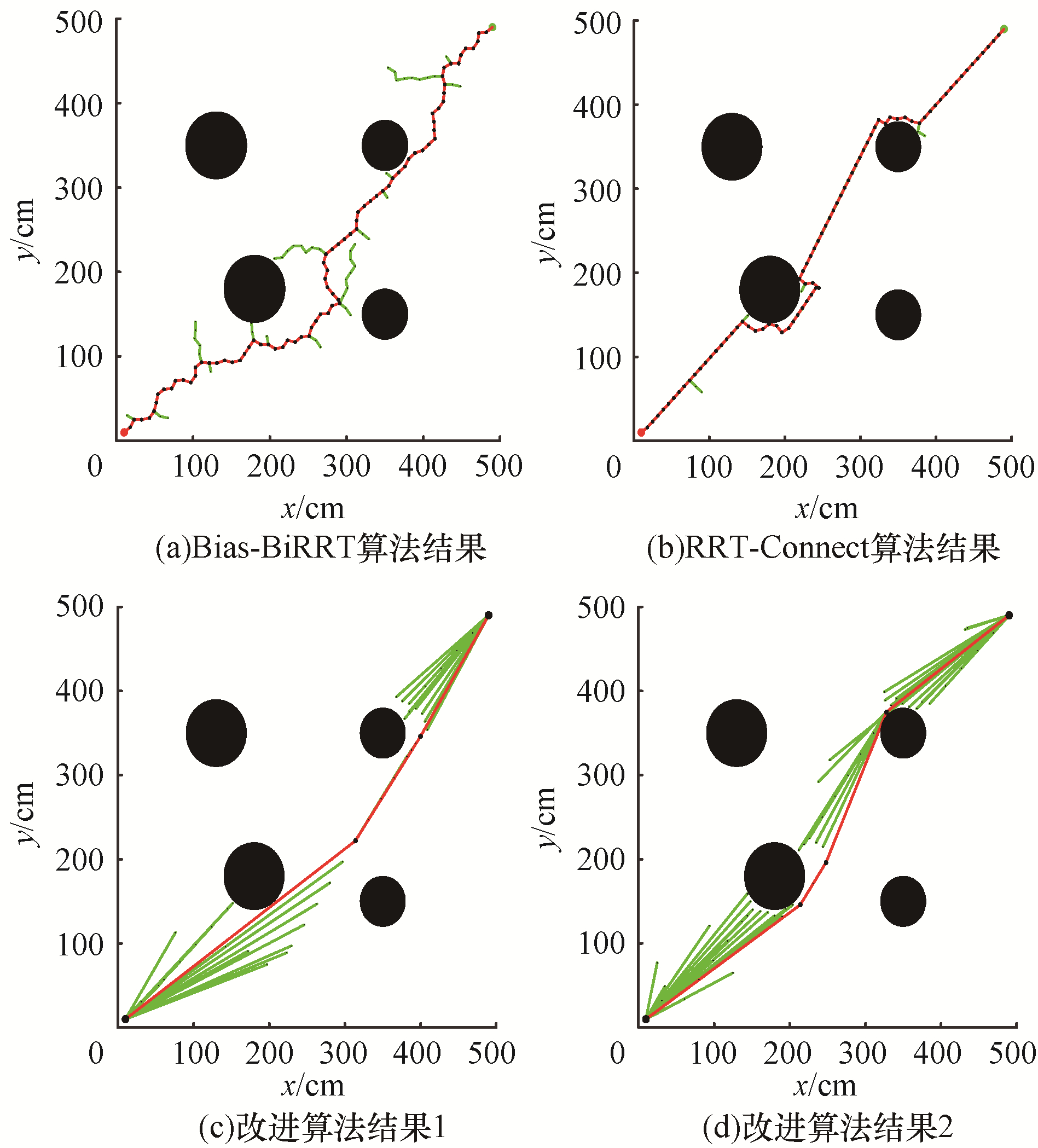
4)在图 8(a)~图 8(d)中,细线为拓展树树枝,粗线为规划路径,可以看出,在简单环境下,RRT-Connect算法的整条路径较Bias-BiRRT曲折变少,但也还存在一定的绕远情况,而改进算法规划路径更直、拐弯更少,两拓展树也能较好地连接,路径质量显著提高。
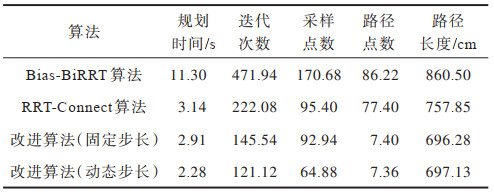
3.2 复杂环境仿真3种算法在复杂环境中的实验结果如表 2和图 9所示,可见其与在简单环境中实验结果整体趋势一致,主要有以下特点
|
下载CSV 表 2 复杂环境下3种算法实验数据 Table 2 Experimental data of three algorithms in complex environment |
|
Download:
|
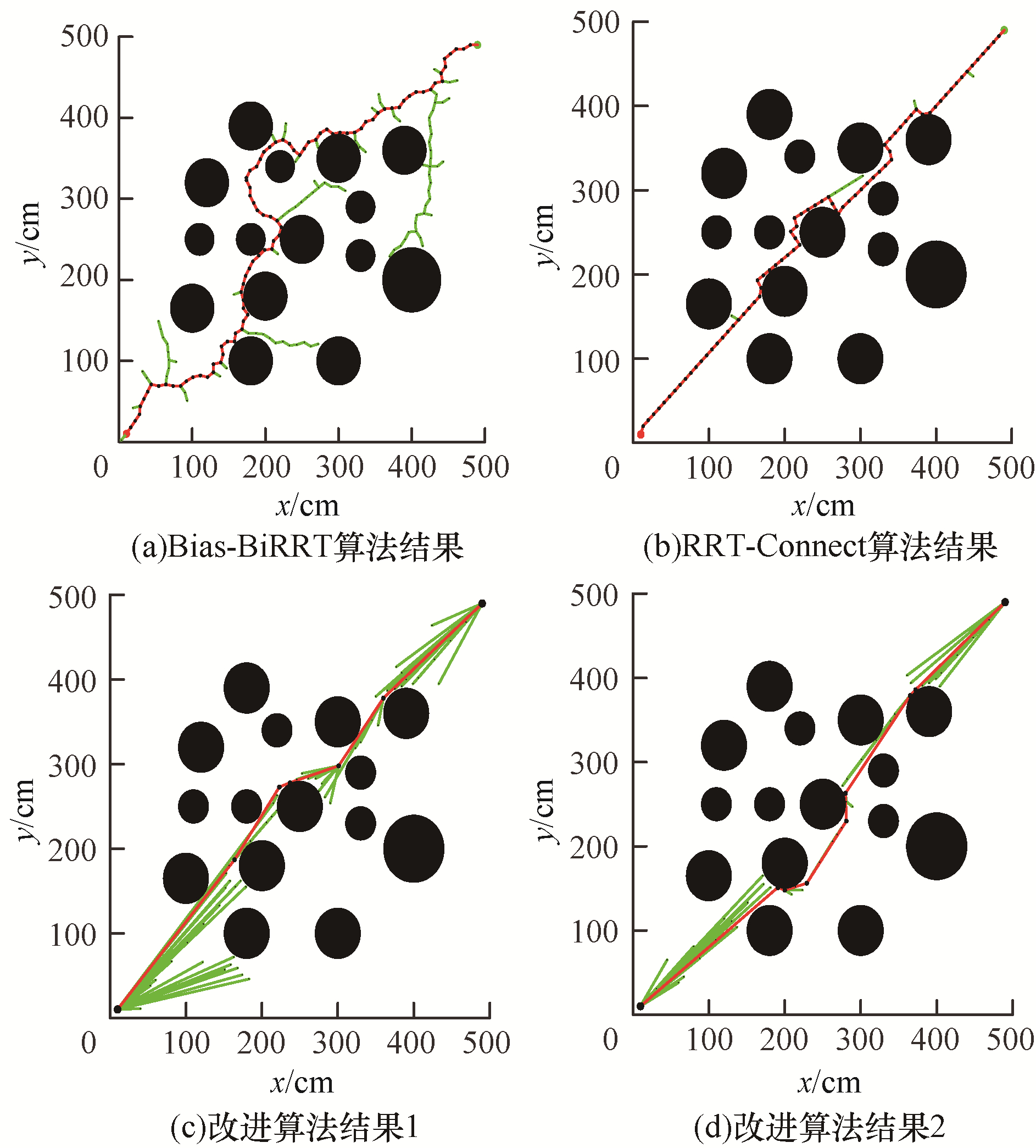
| 图 9 复杂环境实验结果 Fig. 9 Experimental results in complex environment | |
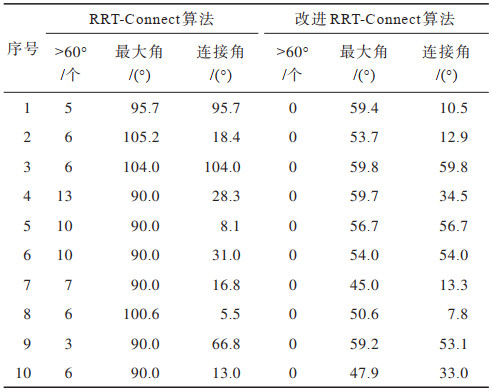
为进一步验证改进算法的平滑度情况,对原RRT-Connect和改进RRT-Connect两种算法分别在复杂环境中进行10次仿真,比较连接角度数、规划路径最大角度数、最大转角大于设定值60°的个数,对比数据如表 3所示。
|
下载CSV 表 3 算法改进前后平滑度仿真结果对比 Table 3 Comparison of smoothness simulation results before and after algorithm improvement |
1)在路径规划效率方面,由表 2可知,在复杂环境中,改进算法固定步长时平均规划时间相较于简单环境只增加了0.1 s,平均迭代次数也大致相等,而RRT-Connect算法平均规划时间增加了0.44 s,平均迭代次数增加39.9点,出现了绕远现象,这表明环境变复杂后改进算法规划效率仍然能保持较高水平。
2)在路径长度优化效果方面,由表 2可知,改进算法固定步长时的平均路径长度为696.28 cm,与简单环境相比,虽然路径点数多了2.64点,但规划路径长度基本一致,再次表明考虑祖代点的重选父节点能够使规划路径趋于最优。
3)在动态步长优化方面,改进算法动态步长相比于固定步长,路径总长变化不大,但是平均规划时间、迭代次数分别减少22%、17%,相比于简单环境的减小幅度变小,这是由环境的复杂程度决定的,但总体上仍加快了算法的收敛速度。
4)由图 9(a)~图 9(d)可知,在复杂环境中,改进算法相比Bias-BiRRT和RRT-Connect算法转折明显减少,绕远现象减小,RRT-Connect算法规划的路径存在多个超过90°转角,而改进算法更趋于平滑。
由表 3可知:RRT-Connect算法大于最大转角60°的平均个数为7.2个,并且出现3个超过100°的转角,而改进算法通过最大转角约束,将大于60°转角个数限制为0个:在连接角度方面,RRT-Connect算法出现3次转角过大的情况,而改进算法则全部维持在设定范围内。从以上数据可知,通过引入转角约束、连接处理等环节后,改进算法规划的路径在连接处能平滑连接,剔除急转拐角,规划路径质量更高,符合移动机器人的安全快速运行需求。
4 结束语本文提出一种改进的RRT-Connect算法,通过引入考虑祖代点的重选父节点环节,优化部分路径长度,并设计动态步长优化策略减小收敛时间。此外,还通过设置转角约束和添加连接处理单元,提高规划路径平滑度。实验结果表明,改进算法比原算法规划路径质量更高,收敛速度更快。由于本文研究只在静态障碍物场景下进行,未考虑到动态障碍物,因此下一步将融合局部路径规划算法组成混合算法,并在现有环境下随机加入动态障碍物,进一步提高路径规划环境的真实性和改进算法的适用性。
| [1] |
ZHANG Q F, GUO T L. Global path planning algorithm of robot based on multistage decision[J]. Computer Engineering, 2016, 42(10): 296-302. (in Chinese) 张启飞, 郭太良. 基于多阶段决策的机器人全局路径规划算法[J]. 计算机工程, 2016, 42(10): 296-302. DOI:10.3969/j.issn.1000-3428.2016.10.051 |
| [2] |
YU Z P, LI Y S, XIONG L. Overview of unmanned vehicle motion planning algorithms[J]. Journal of Tongji University (Natural Science Edition), 2017, 45(8): 1150-1159. (in Chinese) 余卓平, 李奕姗, 熊璐. 无人车运动规划算法综述[J]. 同济大学学报(自然科学版), 2017, 45(8): 1150-1159. DOI:10.11908/j.issn.0253-374x.2017.08.008 |
| [3] |
LI J Y. Path tracking algorithm for wheeled robots walking indoors[J]. Computer Engineering, 2010, 36(13): 178-179, 182. (in Chinese) 李积元. 轮式机器人室内行走路径的探索算法[J]. 计算机工程, 2010, 36(13): 178-179, 182. |
| [4] |
ZHOU T, ZHAO J, HU Q X, et al. Global path planning and tracking of mobile robots in complex environments[J]. Computer Engineering, 2018, 44(12): 208-214. (in Chinese) 周滔, 赵津, 胡秋霞, 等. 复杂环境下移动机器人全局路径规划与跟踪[J]. 计算机工程, 2018, 44(12): 208-214. |
| [5] |
WANG S J, HU L K, WANG Y F. Path planning of indoor mobile robot based on improved D* algorithm[J]. Computer Engineering and Design, 2020, 41(4): 1118-1124. (in Chinese) 王帅军, 胡立坤, 王一飞. 基于改进D*算法的室内移动机器人路径规划[J]. 计算机工程与设计, 2020, 41(4): 1118-1124. |
| [6] |
WEN S F, GUO G Y. Mobile robot path planning based on improved artificial potential field method[J]. Computer Engineering and Design, 2015, 36(10): 2818-2822. (in Chinese) 温素芳, 郭光耀. 基于改进人工势场法的移动机器人路径规划[J]. 计算机工程与设计, 2015, 36(10): 2818-2822. |
| [7] |
LIU J H, YANG J G, LIU H P, et al. Global path planning method of mobile robot based on potential field ant colony algorithm[J]. Transactions of the Chinese Society of Agricultural Machinery, 2015, 46(9): 18-27. (in Chinese) 刘建华, 杨建国, 刘华平, 等. 基于势场蚁群算法的移动机器人全局路径规划方法[J]. 农业机械学报, 2015, 46(9): 18-27. |
| [8] |
LAVALLE S. Rapidly-exploring random trees: a new tool for path planning: TR98-11[R]. Ames, USA: Iowa State University, 1998.
|
| [9] |
URMSON C, SIMMONS R. Approaches for heuristically biasing RRT growth[C]//Proceedings of 2003 IEEE/RSJ International Conference on Intelligent Robots & Systems. Washington D.C., USA: IEEE Press, 2003: 1178-1183.
|
| [10] |
KUFFNER J J, LAVALLE S M. RRT-Connect: an efficient approach to single-query path planning[C]//Proceedings of 2002 IEEE International Conference on Robotics and Automation. Washington D.C., USA: IEEE Press, 2002: 995-1001.
|
| [11] |
LAVALLE S M, KUFFNER J J. Randomized kinodynamic planning[C]//Proceedings of 1999 IEEE International Conference on Robotics and Automation. Washington D.C., USA: IEEE Press, 1999: 473-479.
|
| [12] |
KARAMAN S, FRAZZOLI E. Incremental sampling-based algorithms for optimal motion planning[J]. International Journal of Robotics Research, 2011, 30(7): 5326-5332. |
| [13] |
PEI Y J, YANG C J, YANG L L. Mobile robot path planning algorithm based on improved RRT*[J]. Computer Engineering, 2019, 45(5): 285-290. (in Chinese) 裴以建, 杨超杰, 杨亮亮. 基于改进RRT*的移动机器人路径规划算法[J]. 计算机工程, 2019, 45(5): 285-290. |
| [14] |
JORDAN M, PEREZ A. Optimal bidirectional rapily-exploring random trees: MIT-CSAIL-TR-2013-021[R]. Cambridge, USA: MIT Press, 2013.
|
| [15] |
JEONG I B, LEE S J, KIM J H. Quick-RRT*: triangular inequality-based implementation of RRT* with improved initial solution and convergence rate[J]. Expert Systems with Applications, 2019, 123: 82-90. |
| [16] |
CHENG Y, WANG Y, XIU C B. Application research of an improved RRT algorithm in path planning[J]. Control Engineering, 2020, 27(3): 567-571. (in Chinese) 成怡, 王赟, 修春波. 一种改进RRT算法在路径规划中的应用研究[J]. 控制工程, 2020, 27(3): 567-571. |
| [17] |
LIU C J, HAN J Q, AN K. RoboCup robot dynamic path planning based on improved RRT algorithm[J]. Robot, 2017, 39(1): 8-15. (in Chinese) 刘成菊, 韩俊强, 安康. 基于改进RRT算法的RoboCup机器人动态路径规划[J]. 机器人, 2017, 39(1): 8-15. |
| [18] |
LIU E H, GAO W B, KONG R P, et al. Improved RRT path planning algorithm[J]. Computer Engineering and Design, 2019, 40(8): 2253-2258. (in Chinese) 刘恩海, 高文斌, 孔瑞平, 等. 改进的RRT路径规划算法[J]. 计算机工程与设计, 2019, 40(8): 2253-2258. |
| [19] |
XIANG J L, WANG H D, OUYANG Z L, et al. Research on local path planning algorithm of unmanned boat based on improved two-way RRT[J]. China Shipbuilding, 2020, 61(1): 157-166. (in Chinese) 向金林, 王鸿东, 欧阳子路, 等. 基于改进双向RRT的无人艇局部路径规划算法研究[J]. 中国造船, 2020, 61(1): 157-166. |
| [20] |
CHEN M, LI X, WU J F. Differential robot path planning based on improved RRT algorithm[J]. Computer Applications and Software, 2019, 36(9): 276-280. (in Chinese) 陈敏, 李笑, 武交峰. 基于改进RRT算法的差动机器人路径规划[J]. 计算机应用与软件, 2019, 36(9): 276-280. |
| [21] |
DU M B, MEI T, CHEN J J, et al. Intelligent vehicle motion planning algorithm based on RRT in complex environment[J]. Robot, 2015, 37(4): 443-450. (in Chinese) 杜明博, 梅涛, 陈佳佳, 等. 复杂环境下基于RRT的智能车辆运动规划算法[J]. 机器人, 2015, 37(4): 443-450. |
 2021, Vol. 47
2021, Vol. 47

 ,
,