开放科学(资源服务)标志码(OSID):
随着互联网的高速发展和各种计算机技术的不断革新,网络的传输任务变得越来越重,如物联网技术让所有能行使独立功能的普通物体实现互联互通,这使得接入网络的设备增多,产生的网络流量更是呈指数级增长[1]。软件定义网络(Software Defined Network,SDN)作为一种新型网络架构,是优化网络资源管理的新范例,其不仅实现了转控分离和集中控制,而且开放了接口,这使得第三方应用只需要用编程的方式就可以定义一个新的网络功能[2]。SDN作为未来最有发展前景的网络技术之一,越来越多地被应用在网络性能更高的数据中心网络(Data Center Network,DCN)中。
目前,数据中心网络普遍采用基于Clos架构的网络拓扑,如Fat-Tree[3]、VL2[4]等多根拓扑结构。该类拓扑使一对主机间有多条等价路径可达,极大地缓解了数据传输时不同传输任务对带宽资源的竞争问题,一定程度上实现了负载均衡。但要解决数据中心网络的负载均衡问题仍面临一些挑战。有研究表明,在数据中心网络中,数据流可分为老鼠流和大象流两类,虽然大象流在数量上少于全部网络流的10%,但约80%的网络带宽资源却被大象流占据[5],且由于大象流的生存周期长,老鼠流经常被大象流阻塞,造成长时间的队列延迟[6]。因此,如何对大象流进行识别和处理,是解决数据中心网络中负载均衡问题的关键。
本文提出一种基于前馈神经网络(Feedforward Neural Network,FNN)的动态多路径负载均衡机制FNN-LB。利用SDN架构分层解耦的优势,使位于控制层的SDN控制器可以通过OpenFlow协议[7]与数据层的交换机进行信息交互,从而收集整个网络的实时状态信息。在以往的研究中,这些网络状态信息往往被当作独立变量使用,相关性很少被探究。本文基于前馈神经网络,将网络状态信息作为底层特征输入,将每段链路的负载作为输出,以此建立网络状态信息与链路负载之间的非线性映射模型,从而通过动态网络状态信息实时反映链路综合状况。为满足大象流传输时高吞吐量的需求,应将链路状况好的路径尽可能分配给大象流。因此,本文将预估的链路负载值与蚁群算法[8]中的启发信息相关联,利用蚁群算法的正反馈性和自适应性,使最优路径向预估低负载值路径收敛,从而实现路径的动态负载均衡。
1 相关工作数据中心网络中的负载均衡方案可分为静态负载均衡和动态负载均衡两类。
静态方案根据固定标准将数据流分配给可用路径。文献[9]提出的等价多路径(Equal-Cost Multi-Path,ECMP)算法是一种被广泛应用的负载均衡技术,其基于哈希散列,可通过多条等价路径传输数据流达到负载均衡的目的。文献[10]通过在主机端部署FlowBender程序进行路径拥塞检测,FlowBender会修改报文的生存时间(Time to Live,TTL)字段,并改进ECMP算法使哈希运算基于报文头部的更多字段,其中包括TTL字段,从而实现往返时延时间粒度的数据流动态调度。该方案利用主机端驱动路径规划,但最终的路径选择仍基于ECMP算法,不能确保因拥塞而重新选择的路径满足额外的传输需求,从而造成数据流的多次路由并发生网络动荡。
动态方案则根据各种当前网络指标自适应地选择路由路径。文献[11]提出了一种可扩展的动态流调度方案Hedera,在边缘交换机上识别出大象流后,系统根据其带宽需求,利用全局首次匹配(GFF)算法为大象流分配路径,自适应地调度多级交换结构以有效利用聚合网络资源。文献[12]提出了一种基于队列长度的定向自适应路由方案,根据交换机输出端口的队列长度对数据流进行路由。然而这两种方案都仅根据单一网络指标进行路由规划,不能综合反映链路状况,当网络负载严重时可能会导致网络拥塞。
此外,一些研究者试图从分割大象流的角度来优化数据中心网络的数据流传输问题。文献[13]旨在解决因大流与小流之间的差异导致的负载不均衡,因此Presto将数据流分割为相同大小的流单元,并结合循环调度算法寻找发送路径,但为了防止报文接收后乱序,需要修改通用接收卸载结构,这增加了流量管理的难度与成本。
为解决ECMP算法无法有效调度大象流的缺点,且在不增加流管理难度的前提下引入多种网络指标进行路由规划,本文提出一种基于前馈神经网络的动态多路径负载均衡机制FNN-LB。利用前馈神经网络预估链路负载,对大象流和老鼠流进行差异化路由,并通过仿真实验验证所提方案的有效性。
2 FNN-LB机制FNN-LB架构如图 1所示。根据数据流中传输字节的数据大小,大象流被主机终端中的流检测程序发现并标记。拓扑感知模块根据链路层发现协议(Link Layer Discovery Protocol,LLDP)获取网络的全局视图。FNN-LB机制是基于多种网络状态的负载均衡机制,因此在流量信息监控模块中,通过OpenFlow协议实现控制层和数据层的信息交互,从而对底层网络状况进行实时监控,获取每段链路的带宽利用率、时延、丢包率等流量信息。前馈神经网络模块则可将这些底层网络特征作为输入,预估每段链路对应的负载。最终,路由计算模块利用优化蚁群算法,使最优路径向预估负载值低的链路收敛,从而保证大象流传输时高吞吐量的需求,实现路径的动态负载均衡。
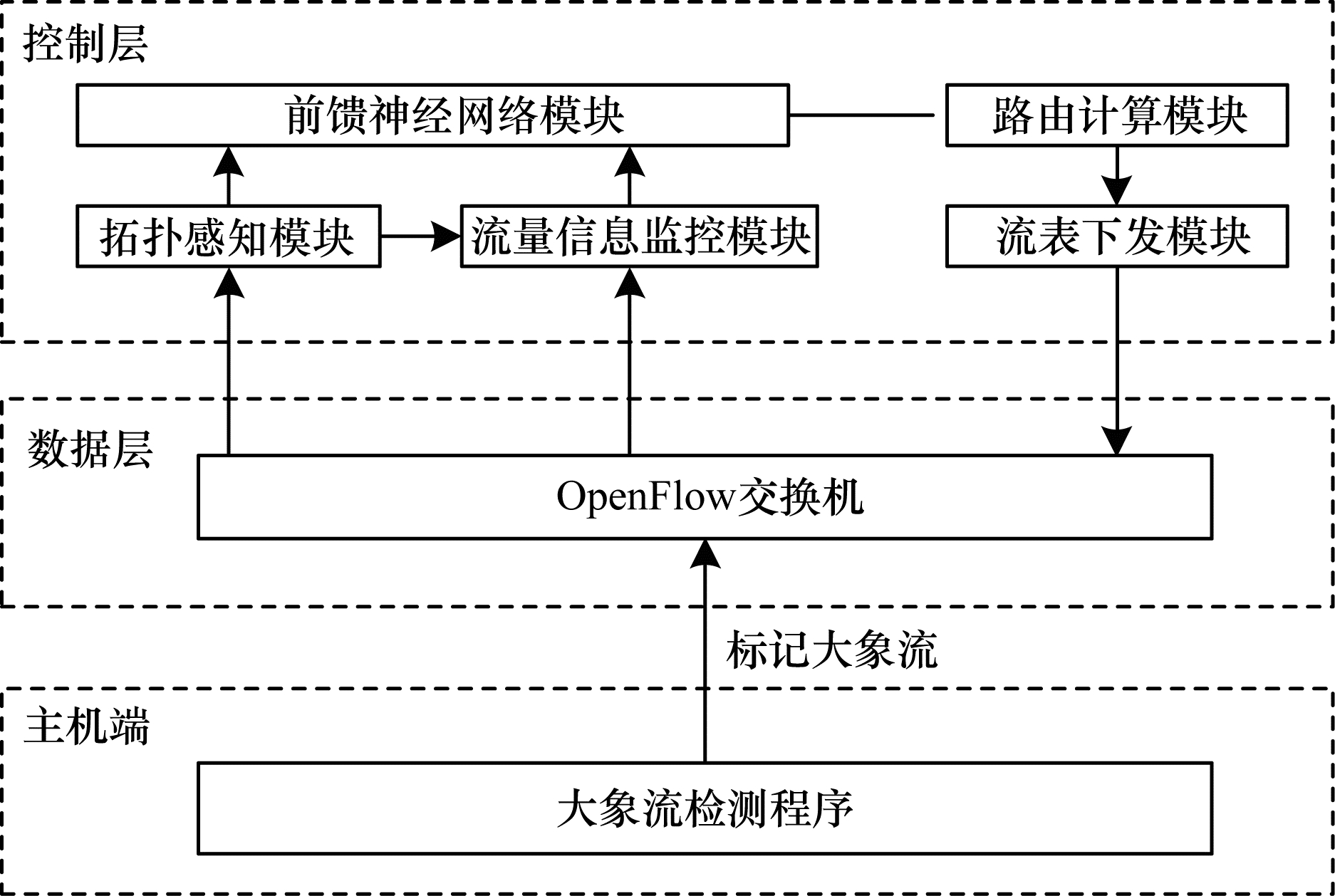
|
Download:
|
| 图 1 FNN-LB架构 Fig. 1 Architecture of FNN-LB | |
在数据中心网络中,由于大象流具有生存周期长的特点和高吞吐量的需求,因此对大象流的检测与标记一直是数据中心网络负载均衡研究工作中重要的一环。在以往研究中,对大象流的识别有多种方式。如在交换机处对每条数据流的流条目进行监控,定期提取统计信息用以标记大象流;或对交换机端口的数据包进行采样,并传至控制器分析样本以判断是否为大象流。虽然这些方法能完成检测任务,但消耗了大量交换机和控制器资源。本文采用Mahout[14]所提的大象流标记方法,在主机终端监视套接字缓冲区,判定传输字节数据超过100 KB的数据流为大象流,并修改数据包包头的区分服务字段以标记大象流。该方法将大象流的检测识别工作从交换机转移到了主机终端中,以期节约网络运行时对数据层的资源消耗。
2.2 网络拓扑感知在拓扑感知模块中,控制器通过LLDP协议进行链路发现,根据交换机反馈的信息构建网络拓扑结构。在软件定义网络中,控制器会通过Packet_out消息将LLDP报文封装进OpenFlow协议,并发送给所有与之相连的交换机。为减少对网络资源的消耗,本文将Packet_out消息由原来的每个端口下发一个改为每个交换机下发一个。当交换机收到从控制器端口发来的LLDP数据包后,会将其源MAC地址修改为端口MAC地址,然后从相应的端口转发出去。当下一个交换机收到从非控制器端口发来的LLDP数据包后,会再次将其封装进Packet_in消息,上传给控制器。控制器则可通过解析该数据包,获得目的交换机、目的端口、源MAC地址、源交换机等信息,并由它们的对应关系获取链路的逻辑连接情况[15]。此模块生成的网络拓扑图将提供给其他模块以辅助工作。
2.3 流量信息监控模块FNN-LB是一种基于当前网络流量信息状况的动态多路径负载均衡机制,因此,对流量信息进行实时准确的监控至关重要。本文采用周期性监控机制,根据OpenFlow协议,控制器可以预定周期T,向所有与之相连的交换机下发统计请求消息,获取端口、流表、流表项、组表等信息,在这些底层网络信息的基础上进行逻辑处理,可得到实时的网络状态信息,具体如下:
1) 带宽利用率:为一段时间内链路传输的总字节数与该链路的最大带宽的比值,如式(1)所示。
| $ {B}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}}^{\mathrm{u}\mathrm{v}}=\frac{{B}_{T}^{\mathrm{u}\mathrm{v}}-{B}_{T-1}^{\mathrm{u}\mathrm{v}}}{{B}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{u}\mathrm{v}}} $ | (1) |
其中:
2) 时延:本文通过对链路发现协议中的LLDP数据包和控制报文协议中的Echo数据包进行解析,获得两者的发送和接收时间戳,由此得到两者的正反向传输时延。根据式(2)可得该段链路的平均传输时延。
| $ {T}_{\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{y}}^{\mathrm{u}\mathrm{v}}=\frac{1}{2}\left[\right({t}_{\mathrm{l}\mathrm{l}\mathrm{d}\mathrm{p}}^{\mathrm{u}\mathrm{v}}+{t}_{\mathrm{l}\mathrm{l}\mathrm{d}\mathrm{p}}^{\mathrm{v}\mathrm{u}})-({t}_{\mathrm{e}\mathrm{c}\mathrm{h}\mathrm{o}}^{\mathrm{u}\mathrm{v}}+{t}_{\mathrm{e}\mathrm{c}\mathrm{h}\mathrm{o}}^{\mathrm{v}\mathrm{u}}\left)\right] $ | (2) |
其中:
3) 丢包率:为链路间丢失数据包数目与已发送数据包数目的比值,如式(3)所示。
| $ {P}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=\frac{{P}_{\mathrm{t}\mathrm{x}}^{\mathrm{u}\mathrm{v}}-{P}_{\mathrm{r}\mathrm{x}}^{\mathrm{u}\mathrm{v}}}{{P}_{\mathrm{t}\mathrm{x}}^{\mathrm{u}\mathrm{v}}} $ | (3) |
其中:
该模块接收流量信息监控模块收集的网络流量信息,并通过前馈神经网络预估每段链路的负载。前馈神经网络相较于其他概率统计类机器学习而言,其输入向量没有特定概率分布或变量之间独立性等需求限制,因此适用于处理复杂多变的网络流量数据。前馈神经网络一般包含一个输入层、一个或多个隐藏层和一个输出层。每一层都包含若干个神经元,各神经元从输入层开始,接收前一层的输入并输出给下一层,直到输出层,且位于同一层的神经元之间不能相互连接[16]。
本文采用三层前馈神经网络结构,如图 2所示。

|
Download:
|
| 图 2 前馈神经网络模块 Fig. 2 Feedforward neural network module | |
在输入层中,神经元数目一般等于所需处理数据的变量数,因此,本文将带宽利用率、时延、丢包率这3个网络特征作为3个输入单元。对于输出层仅设置一个神经元,用来输出链路负载。隐藏层的神经元个数的确定在以往的研究中通常都是一个难点,目前没有统一的解决方案[17]。因此,在下文实验中,通过设置5种不同隐藏层神经元个数的前馈神经网络结构,观察它们的均方误差,以此选取较合适的隐藏层神经元个数h。隐藏层神经元的输入输出关系可用式(4)和式(5)表示。最终输出的链路负载可用式(6)表示。
| $ {a}_{o}=\sum\limits _{i=1}^{n}{w}_{oi}{x}_{i}+{\theta }_{o}, i=\mathrm{1, 2}, \cdots , n, o=\mathrm{1, 2}, \cdots , h $ | (4) |
| $ {z}_{o}=f\left({a}_{o}\right), o=\mathrm{1, 2}, \cdots , h $ | (5) |
| $ L=f\left(\sum\limits _{j=1}^{h}{w}_{j}{z}_{o}+\theta \right), j, o=\mathrm{1, 2}, \cdots , h $ | (6) |
其中:
各个层次之间都采用全连接的方式进行连接,并采用反向传播算法不断训练整个神经网络以调整权值。
2.5 路由计算模块在路由计算模块中,控制器首先判断所要处理的流是大象流还是老鼠流。若是老鼠流,则采用ECMP算法。但对于大象流,ECMP算法可能会发生哈希碰撞,从而使多条大象流聚集在同一条链路上进行传输,造成网络拥塞。因此,对大象流的调度,本文采用优化蚁群算法进行路径计算。蚁群算法是由DORIGO等提出的一种启发式算法,该算法模拟了蚂蚁寻找食物的过程。蚂蚁在经过路径时会释放一种名为信息素的特殊激素,用于种群间的信息传递。蚁群内的其他蚂蚁会识别路径上留有的信息素,并选择信息素浓度最高的路径继续前进。与此同时,该蚂蚁在移动过程中同样也会释放自己的信息素,使整个过程形成正反馈。在单位时间内,越短的路径上信息素浓度越高,蚂蚁由此得到通往食物的最优路径。本文中应用蚁群算法的具体步骤如下:
1) 进行初始化设置。主要分为2个部分:首先是对蚁群算法涉及的主要参数进行设置,包括信息素和启发信息的加权因子、信息素蒸发率、信息素总量、蚂蚁数量、算法迭代次数以及对各路径的信息素浓度进行初始化;其次是网络信息获取。除了流量信息监控模块对底层网络状态的不断监控,还需要获取大象流的源地址和目的地址,以及大象流所需带宽大小,用于确定所需最优路径的数目。
2) 确定当前位置,计算转移概率。蚁群算法是一种寻找优化路径的概率型算法,当蚂蚁位于起始节点后,可根据式(7)计算转移概率。
| $ {P}_{\mathrm{u}\mathrm{v}}^{k}\left(t\right)=\left\{\begin{array}{l}\frac{{\left[{\tau }_{\mathrm{u}\mathrm{v}}\left(t\right)\right]}^{\alpha }\cdot {\left[{\eta }_{\mathrm{u}\mathrm{v}}\left(t\right)\right]}^{\beta }}{\sum _{s\in \mathrm{a}\mathrm{l}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}{\mathrm{d}}_{k}}{\left[{\tau }_{\mathrm{u}\mathrm{s}}\left(t\right)\right]}^{\alpha }\cdot {\left[{\eta }_{\mathrm{u}\mathrm{s}}\left(t\right)\right]}^{\beta }}, v\in \mathrm{a}\mathrm{l}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}{\mathrm{d}}_{k}\\ 0, v\notin \mathrm{a}\mathrm{l}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}{\mathrm{d}}_{k}\end{array}\right. $ | (7) |
其中:
3) 结合轮盘赌选择(Roulette Wheel Selection,RWS)算法[18],选择下一跳节点。由式(7)可得在当前节点处到下一跳所有可选节点的转移概率。为了保证算法的随机性,使具有较小转移概率的节点依然有被选择的可能性,不能直接选取转移概率最大的节点作为下一跳节点。本文结合轮盘赌选择算法选择下一跳节点。假设蚂蚁k在交换机u处时下一跳共有m个交换机可选。首先,由式(7)可计算这m个交换机的转移概率,再根据式(8)可计算这些交换机的累计概率
| $ {q}_{\mathrm{v}}=\sum \limits_{i=1}^{v}{P}_{ui}^{k} $ | (8) |
例如当前共有5个交换机可选,这5个交换机的转移概率

|
下载CSV 表 1 累计概率统计表 Table 1 Cumulative probability statistics table |
4) 判断蚂蚁是否到达目的节点。若蚂蚁没有到达目的节点则回到步骤2),继续寻找下一跳节点。若已到达目的节点,则转向步骤5),并使到达的蚂蚁数量加1。
5) 根据蚂蚁经过的节点记录,生成一条备选路径。根据到达的蚂蚁数量判断是否蚁群内所有蚂蚁均到达目的节点。若是,则转向步骤6),并使迭代次数加1;若否,则转回步骤2),对下一只蚂蚁进行操作。
6) 更新路径上的信息素浓度。当所有蚂蚁到达目的节点且生成备选路径后,根据式(9)和式(10)对路径上的信息素进行更新。
| $ {\tau }_{\mathrm{u}\mathrm{v}}(t+1)=(1-\rho )\cdot {\tau }_{\mathrm{u}\mathrm{v}}\left(t\right)+\sum _{k=1}^{N}\mathrm{\Delta }{\tau }_{\mathrm{u}\mathrm{v}}^{k}\left(t\right) $ | (9) |
| $ \mathrm{\Delta }{\tau }_{\mathrm{u}\mathrm{v}}^{k}\left(t\right)=\left|\begin{array}{l}\frac{Q}{{h}_{k}}, (\mathrm{u}, \mathrm{v})\in \mathrm{p}\mathrm{a}\mathrm{t}{\mathrm{h}}_{k}\\ 0,\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right. $ | (10) |
其中:
7) 判断算法是否达到最大迭代次数。若是,则停止迭代,获得所有的备选路径;若否,则返回步骤2)继续迭代。
8) 根据大象流的带宽需求,从备选路径中选择多条部署路径。一条路径中包含多段链路,每段链路的剩余带宽都不相同,将这些剩余带宽进行比较,最小值则为该条路径的可传输带宽量。考虑到当网络繁忙时,单条路径的可传输带宽量无法满足大象流的高带宽需求,最终选择多条路径作为大象流的传输路径。首先根据信息素浓度从大到小对备选路径进行排序,然后从已排序路径中依次选择一条路径作为部署路径,并判断该路径集合的可传输带宽总量是否满足大象流的传输需求。若不满足,则继续添加路径;若已满足,则输出最终的部署路径集合。
大象流的部署路径选择如算法1所示。
算法1 基于FNN的优化蚁群算法
输入 拓扑图G(V,E),源地址src,目的地址dst,大象流所需带宽BW_request
输出 路由部署路径R
Begin
set algorithm parameters
//M为迭代次数
Initialize pheromones for each link in set E
for i=1 to M do
for j=1 to N do
Node_curr = src
nodeset.add(Node_curr)
while Node_curr!= dst do
generate
calculate
use RWS to select Node_next with
nodeset.add(Node_next)
Node_curr = Node_next
end while
path = getPath(nodeset)
end for
update
end for
path_sort = sortPath(path)
//根据信息素浓度从大到小对备选路径path进行排序
R = addnext(path_sort)
//从path_sort中依次选取一条路径添加到R中
BW_path = calculateBW(R)
//计算R中所有路径的可传输带宽总量,记为BW_path
while BW_request > BW_path
R = addnext(path_sort)
BW_path = calculateBW(R)
end while
return R
end
3 仿真与分析 3.1 实验环境与相关参数本文采用开源控制器Ryu[19]和网络模拟平台Mininet[20]来仿真现实网络环境。Fat-Tree拓扑结构可分为接入层、汇聚层、核心层这3个层次,其中接入层交换机与汇聚层交换机可组合形成多个Pod。本文采用Pod数量为4的Fat-Tree拓扑结构进行仿真,如图 3所示。实验采用Iperf[21]工具产生数据流量,并服从泊松分布,其中大象流90%、老鼠流10%。网络流量信息监控模块的监听周期T设置为5 s。控制层与数据层之间采用OpenFlow1.3版本的协议进行交互。设置蚁群算法中的信息素和启发信息加权因子分别为

|
Download:
|
| 图 3 网络拓扑结构 Fig. 3 Network topology structure | |
由于网络安全与隐私问题,暂无公开的DCN负载数据集可用,因此本文在各主机随机通信的基础上,收集链路上的负载信息作为数据集,并分为训练集和测试集2个部分。再分别设置隐藏层神经元个数h为3、5、7、9、11的5种FNN结构,学习率均设置为0.01,通过实验比较这5种FNN的均方误差(Mean Square Error,MSE),以此确定较合适的隐藏层神经元个数。均方误差如式(11)所示。
| $ {M}_{\mathrm{M}\mathrm{S}\mathrm{E}}=\frac{1}{n}\sum \limits_{i=1}^{n}({X}_{i}-{Y}_{i}{)}^{2} $ | (11) |
其中:
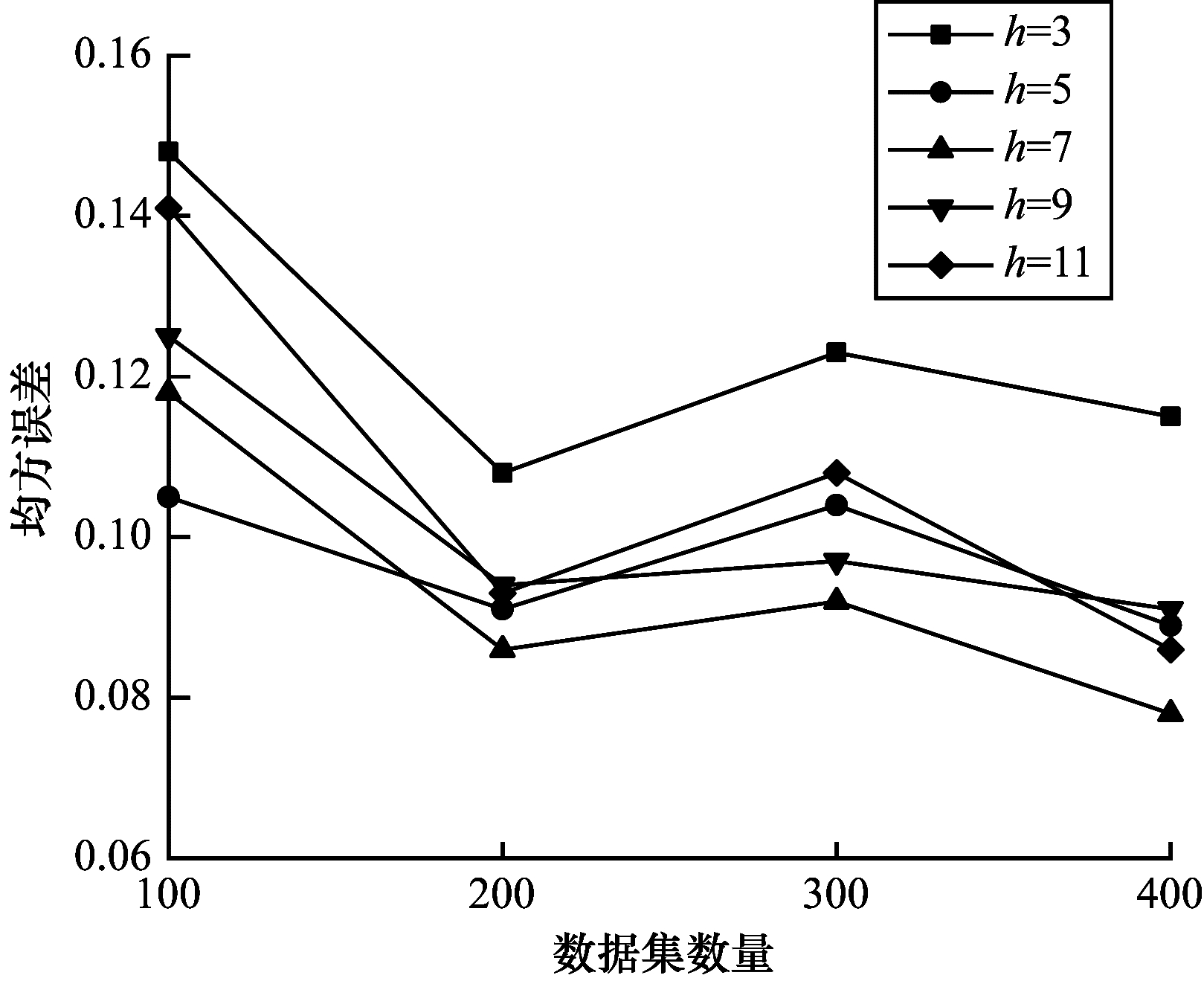
|
Download:
|
| 图 4 不同FNN结构下的均方误差 Fig. 4 Mean square error under different FNN structures | |
为验证FNN-LB算法的有效性,选取GFF算法和ECMP算法这2种负载均衡算法来进行实验对比,并观察上述算法在不同发包速率下传输时延、链路利用率和网络吞吐量这3种网络性能指标的变化情况。
由图 5可知,通过等价路径传输数据的ECMP算法,在各种发包速率下的传输时延都要高于另外2种算法。当发包速率低于600 Mb/s时,GFF算法与FNN-LB算法的传输时延相近。而当发包速率高于600 Mb/s时,由于FNN-LB算法将链路平均传输时延作为底层特征输入前馈神经网络以预估链路负载,故算法受此参数影响,最终部署的路由路径具有较小的传输时延。

|
Download:
|
| 图 5 不同发包速率下的传输时延 Fig. 5 Transmission delay under different packet sending rates | |
由图 6可知,当发包速率较低时,3种算法的链路利用率无明显差别。随着发包速率的增加,3种算法的链路利用率都有所增加,但ECMP算法会产生大象流阻塞,因此链路利用率最低。GFF算法在选取路径时考虑了路径是否满足当前大象流的带宽需求,因此链路利用率高于ECMP算法。而FNN-LB算法基于各种实时网络状态参数选择路径,相较于另外2种算法有动态调节的优势,因此当发包速率大于500 Mb/s时,其链路利用率在三者中最高。
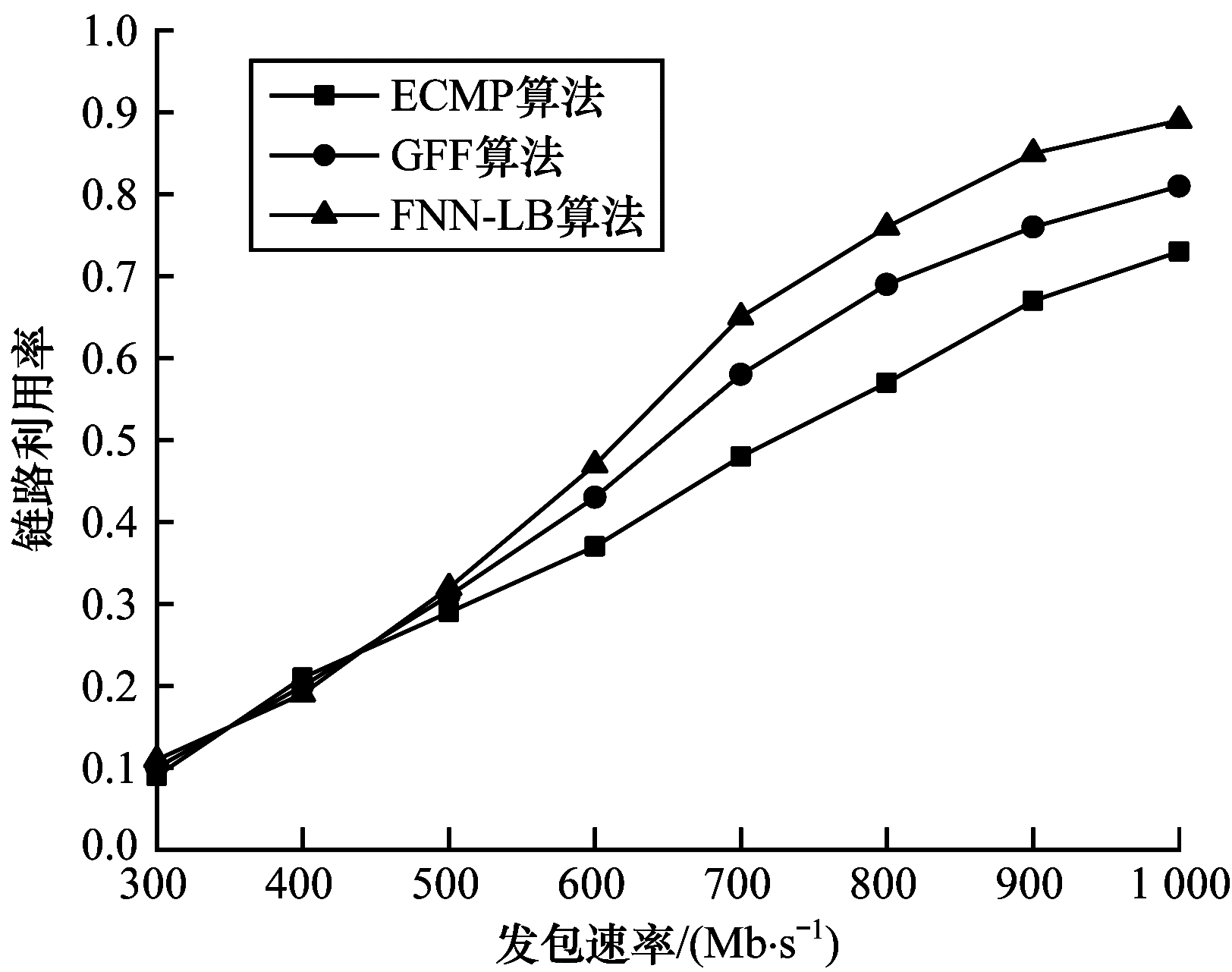
|
Download:
|
| 图 6 不同发包速率下的链路利用率 Fig. 6 Link utilization under different packet sending rates | |
图 7为不同发包速率下3种算法网络吞吐量的变化情况。可以看出:ECMP算法对大象流调度效果不佳,故网络吞吐量最先到达瓶颈且总体低于另外2种算法;FNN-LB算法基于预估链路负载选取路径,考虑了实时网络状况,因此当发包速率较高时,网络吞吐量仍高于另外2种算法。

|
Download:
|
| 图 7 不同发包速率下的网络吞吐量 Fig. 7 Network throughput under different packet sending rates | |
为解决数据中心网络中因大象流而引起的负载不均衡问题,本文提出一种基于前馈神经网络的动态多路径负载均衡方法。利用带宽利用率、时延、丢包率等多种网络状态参数,通过前馈神经网络预估链路负载,结合蚁群算法为大象流寻找满足高吞吐量需求的路径。仿真结果表明,该方法能够有效提高链路利用率和网络吞吐量,降低传输时延。下一步将考虑利用更多变的拓扑结构和差异性更大的数据集训练神经网络,以提高系统的可扩展性并评估链路负载的准确性。
| [1] |
AL-FUQAHA A, GUIZANI M, MOHAMMADI M, et al. Internet of things: a survey on enabling technologies, protocols, and applications[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 2347-2376. |
| [2] |
ZHANG C K, CUI Y, TANG H Y, et al. State-of-the-Art survey on Software-Defined Networking(SDN)[J]. Journal of Software, 2015, 26(1): 62-81. (in Chinese) 张朝昆, 崔勇, 唐翯祎, 等. 软件定义网络(SDN)研究进展[J]. 软件学报, 2015, 26(1): 62-81. |
| [3] |
AL-FARES M, LOUKISSAS A, VAHDAT A. A scalable, commodity data center network architecture[J]. ACM SIGCOMM Computer Communication Review, 2009, 38(4): 63-74. |
| [4] |
GREENBERG A, HAMILTON J R, JAIN N, et al. VL2:a scalable and flexible data center network[J]. Communications of the ACM, 2011, 54(3): 95-104. DOI:10.1145/1897852.1897877 |
| [5] |
LEE B, KANAGAVELU R, AUNG K M M. An efficient flow cache algorithm with improved fairness in software-defined data center networks[C]//Proceedings of 2013 IEEE International Conference on Cloud Networking. Washington D.C., USA: IEEE Press, 2013: 18-24.
|
| [6] |
LIU F, GUO J, HUANG X, et al. eBA: efficient bandwidth guarantee under traffic variability in datacenters[J]. IEEE ACM Transactions on Networking, 2017, 25(1): 506-519. DOI:10.1109/TNET.2016.2594295 |
| [7] |
MCKEOWN N, ANDERSON T, BALAKRISHNAN H, et al. OpenFlow: enabling innovation in campus networks[J]. ACM SIGCOMM Computer Communication Review, 2008, 38(2): 69-74. DOI:10.1145/1355734.1355746 |
| [8] |
DORIGO M, BIRATTARI M, STÜTZLE T. Ant colony optimization[J]. IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39. DOI:10.1109/MCI.2006.329691 |
| [9] |
HOPPS C. Analysis of an equal-cost multi-path algorithm: RFC2992[S]. [S.l.]: RFC Editor, 2000.
|
| [10] |
BALLANI H, COSTA P, GKANTSIDIS C, et al. Enabling end-host network functions[C]//Proceedings of 2015 ACM Conference on Special Interest Group on Data Communication. New York, USA: ACM Press, 2015: 493-507.
|
| [11] |
ALFARES M, RADHAKRISHNAN S, RAGHAVAN B, et al. Hedera: dynamic flow scheduling for data center networks[C]//Proceedings of the 7th USENIX Conference on Networked Systems Design and Implementation. Berkeley, USA: USENIX, 2010: 19.
|
| [12] |
MAHAPATRA S, YUAN X. Load balancing mechanisms in data center networks[C]//Proceedings of the 7th International Conference and Expo on Emerging Technologies for a Smarter World. Incheon, Korea: CEWIT, 2010: 1-5.
|
| [13] |
HE K, ROZNER E, AGARWAL K, et al. Presto: edge-based load balancing for fast datacenter networks[C]//Proceedings of 2015 ACM Conference on Special Interest Group on Data Communication. New York, USA: ACM Press, 2015: 465-478.
|
| [14] |
CURTIS A R, KIM W H, YALAGANDULA P. Mahout: low-overhead datacenter traffic management using end-host-based elephant detection[C]//Proceedings of IEEE International Conference on Computer Communications. Washington D.C., USA: IEEE Press, 2011: 1629-1637.
|
| [15] |
PAKZAD F, PORTMANN M, TAN W L, et al. Efficient topology discovery in OpenFlow-based software defined networks[J]. Computer Communications, 2016, 77: 52-61. DOI:10.1016/j.comcom.2015.09.013 |
| [16] |
BALDI P, VERSHYNIN R. The capacity of feedforward neural networks[J]. Neural Networks, 2019, 116: 288-311. DOI:10.1016/j.neunet.2019.04.009 |
| [17] |
CAI G W, FANG Z, CHEN Y F. Estimating the number of hidden nodes of the single-hidden-layer feedforward neural networks[C]//Proceedings of the 15th International Conference on Computational Intelligence and Security. Washington D.C., USA: IEEE Press, 2019: 172-176.
|
| [18] |
MA Z. Research on the improvement of ant colony algorithm and its application in TSP[D]. Qingdao: Qingdao University of Technology, 2016. (in Chinese) 马振. 改进蚁群算法及其在TSP中的应用研究[D]. 青岛: 青岛理工大学, 2016. |
| [19] |
Ryu OpenFlow controller[EB/OL]. (2017-09-05)[2020-06-12]. http://osrg.github.io/ryu/.
|
| [20] |
Mininet: an instant virtual network on your laptop(or other PC)[EB/OL]. (2018-08-28)[2020-06-12]. http://mininet.org/.
|
| [21] |
ZHANG B, SONG A J. Iperf-based network performance measurement[J]. Computer Knowledge and Technology, 2009, 36(5): 10227-10229. (in Chinese) 张白, 宋安军. 基于Iperf的网络性能测量研究[J]. 电脑知识与技术, 2009, 36(5): 10227-10229. |
 2021, Vol. 47
2021, Vol. 47
