开放科学(资源服务)标志码(OSID):
图像盲去模糊是在运动轨迹未知的情况下将模糊图像转变为清晰图像的过程,在生活和安防等领域有广泛的应用,例如修复拍摄时因手抖而模糊的照片,以及去除监控中物体的运动模糊,提升监控清晰度。图像模糊分为两种:均匀模糊和非均匀模糊。若图像的各个像素运动轨迹相同(例如相机抖动),则称为均匀模糊,反之若像素的运动轨迹不同(例如物体移动),则称为非均匀模糊。
传统的图像去模糊方法,例如基于零范数先验[1-2]、暗通道先验[3-4]和LMS自适应[5]的算法,通过交替估计清晰图像和模糊轨迹去模糊。其中,模糊轨迹通常使用一个二维的卷积核表示。这种方法去除大面积的均匀模糊有很好的效果。然而,真实世界中的模糊大部分是非均匀的,使用二维的卷积核表示非均匀的模糊轨迹会有较大的误差,因此传统算法在去除非均匀模糊时表现欠佳。
近年来,神经网络的方法在图像复原领域的应用取得了较大进展。文献[6]提出使用深度学习的方法提取特征图,再利用模糊图像和清晰图像的特征图估算模糊核。此后一些研究者开始探索不需要模糊核估计的端到端卷积神经网络。文献[7]提出了一个简单的全卷积网络用于去除文本图像的模糊。文献[8]提出了一个多层的神经网络并将其运用于自然图像处理。文献[9]提出了基于LSTM[10]的多层神经网络。文献[11]提出了DeblurGAN,一种基于对抗生成网络(GAN)[12]的去模糊神经网络。尽管这些研究取得了不错的实验结果,但神经网络的训练仍然是一个难题,研究人员必须通过海量实验选取最优的网络结构。为解决该问题,一些研究者开始探索通过神经网络架构搜索技术自动搜索出一个优质的去模糊神经网络。
Google公司最早提出基于强化学习的NASNet[13]用于神经网络架构搜索。NASNet使用LSTM作为控制器用于生成目标的网络结构,并用目标网络在验证集上的误差作为损失函数训练控制器。然而,NASNet每生成一个目标网络都必须通过完整训练并测试该目标网络来评价该网络的质量,这严重降低了NASNet的搜索速度。NASNet需要500块GPU训练28天才能在CIFAR10数据集上取得不错的实验结果。为了加快训练速度,文献[14]提出可微分神经网络架构搜索(DARTS)。DARTS将网络结构变为可微分的参数,使得网络的训练和架构的调优能够同时进行,能够一边训练一边评价直至收敛,因此DARTS可以在4小时内在CIFAR10上搜索出性能超过ResNet[15]的网络。
目前,DARTS多用于图像分类问题,如行为识别[16],图像识别[17-19]等,尚未应用于图像去模糊领域。这是因为分类问题输出的维度较少(仅为类别数),使用少于20个卷积层的神经网络(如VGG16[20])就可以取得不错的效果,使用过深的神经网络反而容易过拟合。而图像去模糊问题对图像细节要求高,浅层神经网络无法清晰地恢复模糊图像的细节,因此图像去模糊一般使用超深的神经网络,例如SRN-DeblurNet[9]和DeblurGAN[11]都拥有超过60个卷积层。因此,将可微分神经网络架构搜索技术应用于图像去模糊领域的难度显著大于应用于分类问题。此外,由于最初的DARTS只考虑了分类问题,其搜索空间是专门为分类问题而设计的,输出是维度等于类别数的向量而不是图像,因此,DARTS的搜索空间不能直接用于图像去模糊。
本文将DARTS应用于图像去模糊领域,提出U型残差搜索空间,并将搜索空间分割为9个不同分辨率的单元,通过多尺度结构有效地提取图像在不同分辨率上的特征,并通过残差结构加快训练和搜索的速度。最终将本文方法与UNet[21]、DeblurGAN等模型进行对比实验验证。
1 可微分神经网络架构搜索超边结构是可微分神经网络(DARTS)算法的核心,其基本结构如图 1所示。
|
Download:
|
| 图 1 超边结构的抽象图 Fig. 1 Illustration of the superedge structure | |
超边结构包括n种可能的操作和n个结构参数。假设x为张量,θ为神经网络的参数,简称“网络参数”(如卷积核张量或全连接层矩阵),f1(x,θ),f2(x,θ),…,fn(x,θ)为n种可微分的运算(如普通卷积,空洞卷积和恒同映射),DARTS的目标是在这n个运算中选取最优的操作。DARTS引入n个结构参数a1,a2,…,an并用Softmax函数归一化,如式(1)所示:
| $ {b}_{i}=\mathrm{e}\mathrm{x}\mathrm{p}\left({a}_{i}\right)/\sum \limits_{j=1}^{n}\mathrm{e}\mathrm{x}\mathrm{p}\left({a}_{j}\right)\text{,}\sum \limits_{i=1}^{n}{b}_{i}=1 $ | (1) |
定义输出y为f1(x,θ),f2(x,θ),…,fn(x,θ)的凸组合如式(2)所示:
| $ y=\sum \limits_{i=1}^{n}{b}_{i}{f}_{i}(x, \theta ) $ | (2) |
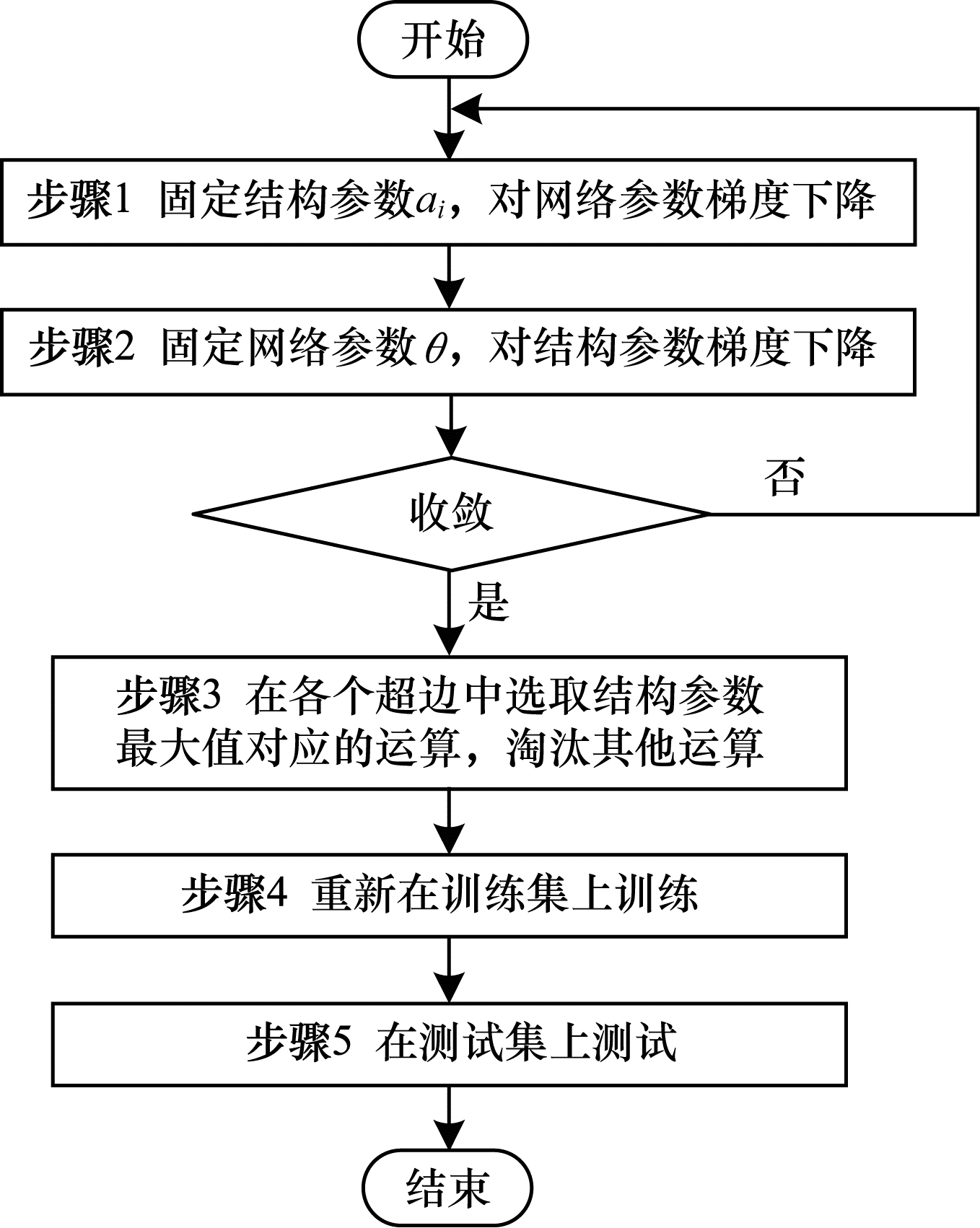
DARTS的搜索策略如图 2所示。
|
Download:
|
| 图 2 DARTS的搜索流程 Fig. 2 Overview of the searching process of DARTS | |
由图 2可以看出,DARTS算法的优点是可以一边训练网络参数,一边优化网络结构,而无需等到训练完成后再调优网络结构,这显著减少了优化时间。
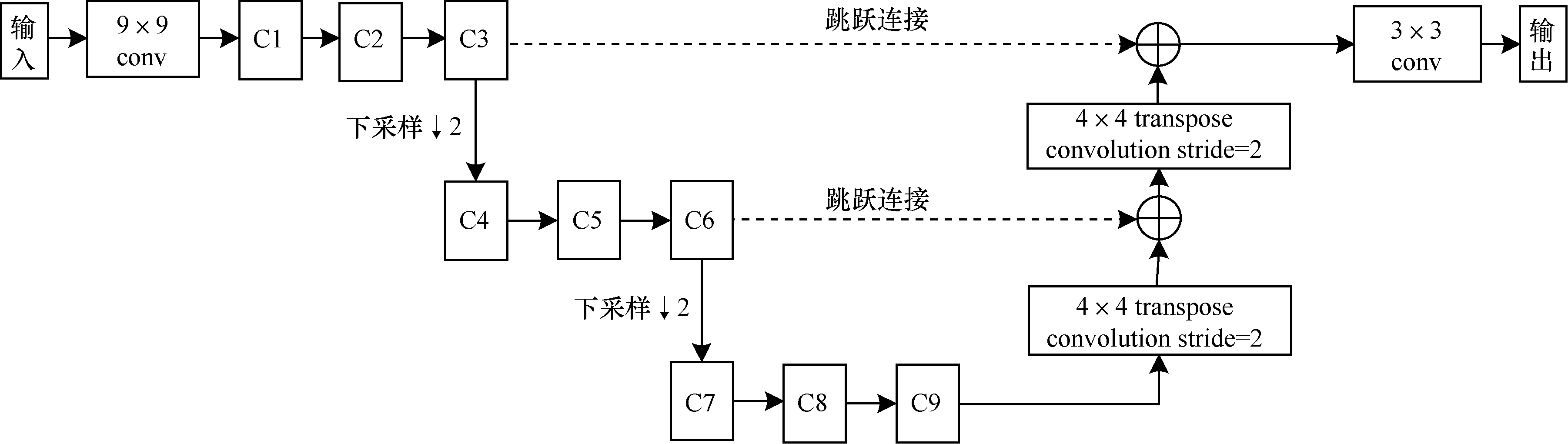
2 基于DARTS的图像盲去模糊方法 2.1 U型残差搜索空间结合式(1)与式(2)定义超边,再将这些超边组成一个神经网络,这个由超边组成的神经网络称为“搜索空间”。如图 3所示。
|
Download:
|
| 图 3 提出的U型残差搜索空间 Fig. 3 The proposed U-Shape search space | |
每条超边包括多种运算,因此,DARTS算法比较消耗内存。和图像分类不同的是,为了达到较好的实验效果,图像去模糊的神经网络一般比较大,因此无法做到神经网络的每两个数据节点都有超边连接,搜索一个图像去模糊的神经网络难度也远大于搜索一个分类网络。
基于分治的思路,本文将搜索空间分为9个单元3个分辨率尺度,每个分辨率尺度由3个单元组成,不同分辨率尺度之间使用图 3所示U型残差结构串联。单元内部使用自定义的搜索空间。这样设计充分考虑了各分辨率尺度的信息。最高分辨率尺度中的3个单元C1、C2、C3有64个特征图,中等分辨率尺度的3个单元C4、C5、C6有128个特征图,最低分辨率尺度中的三个单元有C7、C8、C9有256个特征图。较高分辨率的图像长宽均为较低分辨率图像的2倍。在相同分辨率的张量之间使用跳跃连接。每个单元后都使用ReLU激活函数。尽管9个单元的搜索空间是相似的,但训练完成后每条超边的结构参数可能互不相同,因此,训练结束后,即使在同一分辨率上,不同的单元可能搜索到不同的网络结构。
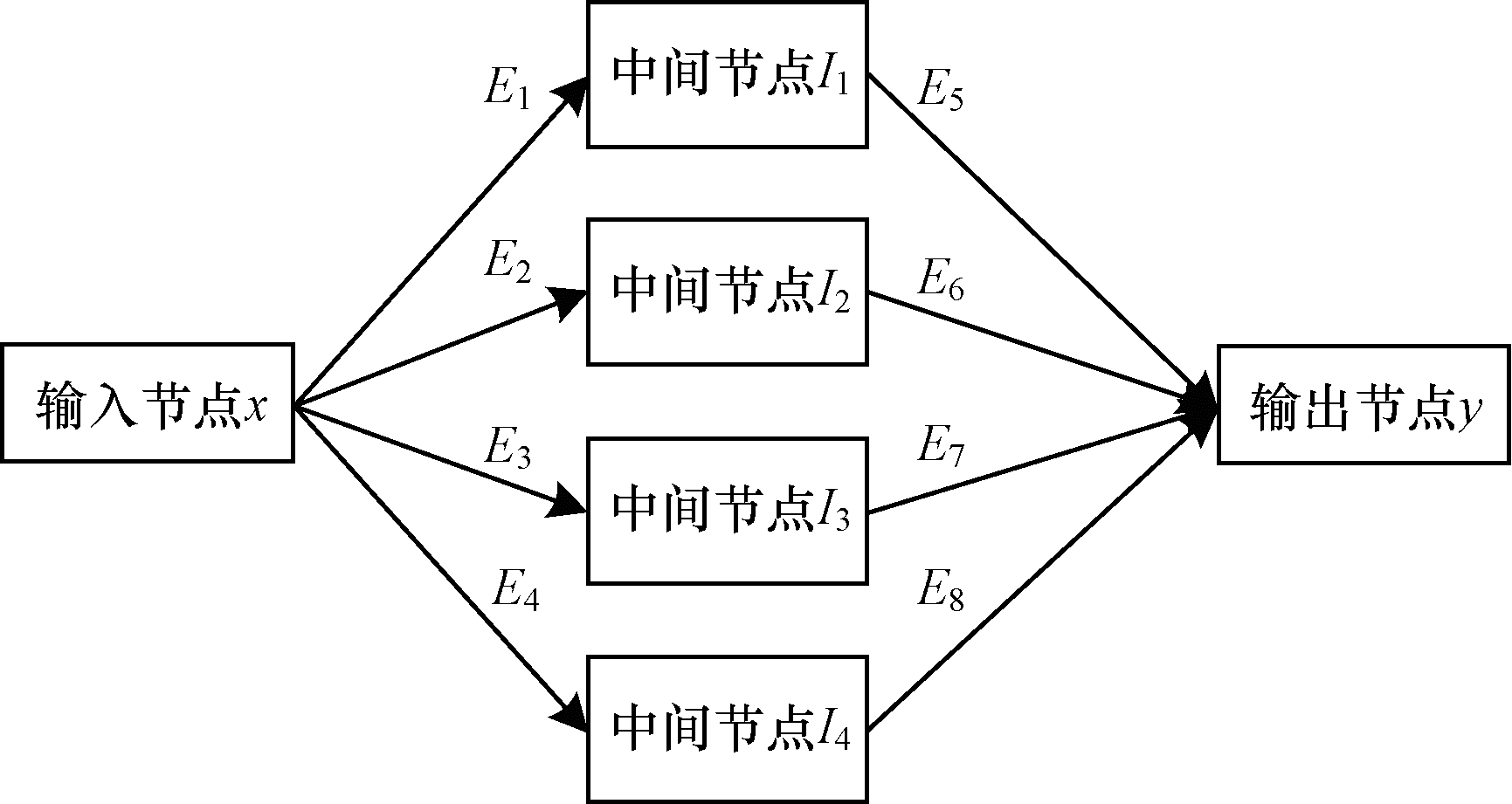
每个单元包括6个数据节点和8条超边。每条超边有5种可能的操作:1)恒同连接;2)普通卷积,卷积核尺寸3×3;3)普通卷积,卷积核尺寸5×5;4)空洞卷积,卷积核尺寸3×3,膨胀系数为1;5)普通卷积,卷积核尺寸1×1。由于内存限制,本文所选用的大多数为小卷积核。每个单元的设计如图 4所示。
|
Download:
|
| 图 4 搜索单元的定义 Fig. 4 Definition of our proposed search cell | |
x是单元的输入,E1~E8为该单元的8条超边,输出y如式(3)所示。
| $ y={E}_{5}\left({E}_{1}\right(x\left)\right)+{E}_{6}\left({E}_{2}\right(x\left)\right)+{E}_{7}\left({E}_{3}\right(x\left)\right)+{E}_{8}\left({E}_{4}\right(x) ) $ | (3) |
本文使用均方损失函数,即比较复原后图像和基准图像的均方误差。设模糊图像为B,结构参数为a,网络参数为θ,复原后图像为I,基准图像为Igt,神经网络为f,则损失函数Loss如式(4)所示:
| $ \mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}\mathrm{ }=\left|\right|f(B;a, \theta )-{I}_{\mathrm{g}\mathrm{t}}|{|}_{2}^{2}=||I-{I}_{\mathrm{g}\mathrm{t}}|{|}_{2}^{2} $ | (4) |
基于本文提出的U型残差搜索空间可以在显存仅8GB的NVIDIA GPU上训练,所选用的优化器为Adam[22]。结构参数和网络参数采用不同的学习率。结构参数的初始学习率为0.002 5,网络参数的初始学习率为0.000 1。训练总共进行50轮,每轮训练完毕后网络参数和结构参数的学习率均变为上一轮学习率的0.96,训练神经网络的框架是PyTorch 1.0。
由于图像去模糊的公开训练集较少(例如GOPRO数据集只包括2 103张训练图像),图 2所示的训练流程在GOPRO数据集上收敛到的结果较差,因此本文使用自己生成的模糊图像作为训练集和验证集。从MSCOCO[23]数据集中选取了56 000张图像,40 000张作为训练集,16 000张作为验证集。对每一张图像I,采用基于随机游走的算法(算法1)随机生成正方形模糊核k,k的边长从[7,75]中的奇数随机采样。算法1的思路是,定义一个游标(x,y),从模糊核中的任意一点出发,随机选取运动角度α并更新游标位置(算法1第4步)。在游标所在的位置处,使用双线性插值更新模糊核(算法1第5步)。最后更新运动角度α(算法1第6步)。生成模糊核后,使用式(5)生成模糊图像B:
| $ B=I\otimes k $ | (5) |
其中:
算法1 基于随机游走的模糊核生成算法
输入 模糊核边长N(N是奇数),步长S
输出 模糊核k(N×N二维矩阵)
//在本算法中,所有下标均从0开始
//初始化:
1. 初始化随机游走位置(x,y)为模糊核k中随机一点;0≤x≤N-1;0≤y≤N-1;
2. 对于卷积核k,将游走的初始位置初始化为1,其它位置初始化为0:
| $ \mathrm{k}(\mathrm{i}, \mathrm{j})=\left\{\begin{array}{l}1,i=\mathrm{x}, \mathrm{j}=\mathrm{y}\\ 0, \mathrm{其}\mathrm{他}\end{array}\right. $ |
3. 在[0,2π)区间内以均匀分布随机选取一个初始角度α。
//随机游走:
for(cnt = 1;cnt < = S;++cnt){ //循环
4.更新游走的位置
x += cos α;y += sin α
x=clip(x,0,N-1);y=clip(y,0,N-1)//超出边界则裁剪
5. 双线性插值,⎣x⎦表示向下取整,⎡x⎤表示向上取整。
| $ \begin{array}{l}k(\left\lfloor { x} \right\rfloor , \left\lfloor { y} \right\rfloor )+=(\left\lceil { x } \right\rceil -x)(\left\lceil { y } \right\rceil -y)\\ k(\left\lfloor { x} \right\rfloor , \left\lceil { y } \right\rceil )+=(\left\lceil { x } \right\rceil -x)(y-\left\lfloor { y} \right\rfloor )\\ k(\left\lceil { x } \right\rceil , \left\lfloor { y} \right\rfloor )+=(x-\left\lfloor { x} \right\rfloor )(\left\lceil { y } \right\rceil -y)\\ k(\left\lceil { x } \right\rceil , \left\lceil { y } \right\rceil )+=(x-\left\lfloor { x} \right\rfloor )(y-\left\lfloor { y} \right\rfloor )\end{array} $ |
或者最近邻插值:
| $ k(\left\lfloor { x} \right\rfloor , \left\lfloor { y} \right\rfloor )+=1 $ |
6.更新随机游走的角度
在均匀分布U(α
}
//后处理:
7. 使用文献[11]中的算法将模糊核中心化,并归一化模糊核:
| $ k=k/\sum \limits_{i}\sum \limits_{j}{k}_{ij} $ |
使得模糊核k中的元素和为1
由算法1生成的模糊核和得到的模糊图像如图 5所示。

|
Download:
|
| 图 5 由算法1生成的模糊核和模糊图像 Fig. 5 The blur kernel and the blurred image generated by algorithm1 | |
在算法1中,步长S是一个[300, 500]之间的随机整数。算法1采取双线性插值时在一台I7 CPU的PC机上生成一张256×256的图像平均耗时约0.50 s。通过实验发现,使用最近邻插值取代算法1步骤5中的双线性插值可以将生成时间从0.50 s降到约0.40 s,且两种插值之间的训练效果差别可以忽略不计。最近邻插值法在GOPRO数据集上PSNR为28.56/0.871,和双线性插值的28.55/0.873较为接近。
3 实验结果与分析 3.1 实验数据集为了客观评价本文的方法,使用两个公开的数据集Kohler[24]和GOPRO[8]作为测试集。Kohler是一个仿真数据集,数据集包括由4个原始图像和12个卷积核生成的48张分辨率为800像素×800像素的模糊图像,模糊类型均为均匀模糊。GOPRO数据集包括真实拍摄的1 111个分辨率为1 280像素×720像素的模糊图像,模糊类型为非均匀模糊。
本文采用两种客观的图像评价指标:峰值信噪比PSNR和结构相似度SSIM[25]。为充分体现搜索得到的网络的性能,本文选取了近年来在顶级会议/期刊上发表的论文中具有较高PSNR与SSIM的模型作为比较对象。此外,文献[26]指出,虽然这两个评价指标在绝大多数情况下非常重要,但有时具有较好视觉效果的图像未必在PSNR和SSIM指标上表现出色。因此,本文也和一些经典算法比较了去模糊的视觉效果。
3.2 实验结果在GOPRO数据集上的实验结果如表 1所示。在Kohler数据集上的实验结果如表 2所示。
|
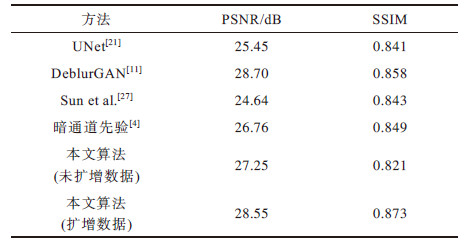
下载CSV 表 1 GOPRO数据集上的实验结果 Table 1 Experimental results on the GORPO dataset |
|
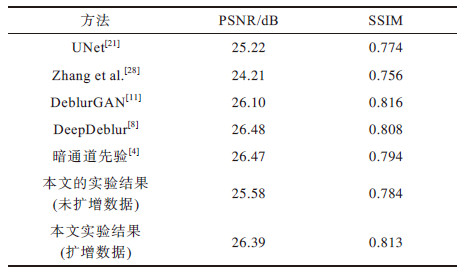
下载CSV 表 2 Kohler数据集上的实验结果 Table 2 Experimental results on the Kohler dataset |
在GOPRO数据集上,本文方法和UNet、暗通道先验的去模糊效果比较如图 6所示。在Kohler数据集上,本文方法和UNet、DeblurGAN的去模糊效果比较如图 7所示。为了增加实验效果的说服力,本文方法和当前最好的模型DeblurGAN的比较结果如图 8所示。使用算法1对数据集扩增前的视觉效果对比如图 9所示。本文方法相对于UNet,在性能与搜索过程的自动化程度方面有巨大提升,同时运行速度与LINet只相差0.02 s。本文方法与UNet方法的视觉效果对比如图 10所示。

|
Download:
|
| 图 6 GOPRO数据集上的视觉效果比较 Fig. 6 Visual quality comparisons on the GOPRO dataset | |

|
Download:
|
| 图 7 Kohler数据集上的视觉效果比较 Fig. 7 Visual quality comparisons on the Kohler dataset | |

|
Download:
|
| 图 8 本文方法与DeblurGAN的视觉效果对比 Fig. 8 Visual comparisons between the proposed method and DeblurGAN | |

|
Download:
|
| 图 9 使用算法1进行数据集扩增前后视觉效果对比 Fig. 9 Effectiveness of data augmentation using algorithm 1 | |

|
Download:
|
| 图 10 本文方法与UNet的视觉效果对比 Fig. 10 Visual comparisons between the proposed method and UNet | |
本文搜索得出的网络和开源模型的运行时间比较结果如表 3所示。
|
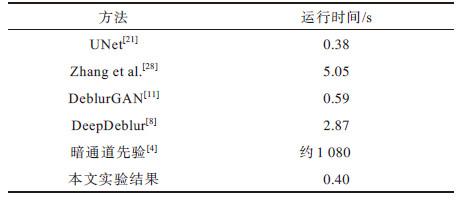
下载CSV 表 3 模型在分辨率为800像素×800像素的图像上的运行时间 Table 3 Running time on an image of resolution 800×800 pixel |
从表 1和表 2可以看出,基于可微分神经网络搜索技术(DARTS)搜索得到的神经网络,在去模糊领域两个知名公开数据集GOPRO和Kohler上的表现优于基于暗通道先验的经典方法,峰值信噪比相对于基线模型UNet分别提升3.10 dB和1.17 dB,与当前最先进的DeblurGAN性能基本相当。
从图 6和图 7看出,本文提出的方法有较好的视觉效果。如图 6的第1行所示,原始图像文字部分的模糊非常严重,使用UNet[21]和暗通道先验[4]算法,均无法看清图像中的文字,使用本文的算法,图像中的“ISTANBUL”和“SANAT”字样依稀可见。图 6的第2行展示了一个模糊的车辆,使用文献[21]和[4]算法均产生了明显的振铃伪影,而使用本文的算法可以较清晰地恢复出车辆的轮廓和车牌信息。从图 7可以看出,使用本文的算法可以更清晰地恢复教堂的细节。从图 8第2行可以看出,本文的算法可以从非常模糊的图像中部分恢复出人脸,而DeblurGAN完全无法恢复镜头前的人脸。
由表 3可知,本文搜索得到的网络测试一张分辨率为800像素×800像素的图像仅需要0.40 s,显著小于DeblurGAN[28]。这表明本文的结构不仅有不错的去模糊效果,而且具有较快的运行速度。
虽然DeepDeblur[8]和暗通道先验方法[4]在Kohler数据集上的PSNR超过了本文的算法,但它们的运算时间分别是本文算法的7.175倍和2 700倍,由于DeepDeblur使用了金字塔结构,其测试时间较长。文献[4]不仅使用了金字塔结构,而且还采用了迭代优化,因此很难在GPU上并行优化,只能在CPU上串行解决,这使得文献[4]的方法几乎不可能做到实时。此外,文献[4]的迭代算法是基于均匀模糊的数学模型,而在实际应用中模糊一般是非均匀的,因此文献[4]的实用性并不强。
采用本文方法,搜索得到神经网络后,重新训练这个神经网络大概需要一天时间。根据开发经验,传统设计神经网络很难一次成功,调试出一个既好又快的神经网络大约需要10-15次尝试,这需要花费研究人员大量的时间和计算资源。显然,本文方法对开发效率有显著的提升。此外,前人已经探索得到了大量的结构(如基于多尺度特征的DeepDeblur[8],基于对抗生成网络的DeblurGAN[11]),然而,通过引入当前最先进的可微分神经网络架构搜索技术(DARTS[14]),并结合本文设计的搜索空间,能够在不经过人为干预的情况下在两天内搜索得到性能和速度不逊于DeepDeblur和DeblurGAN的神经网络,这充分体现了可微分神经网络架构搜索技术的强大潜力:只要搜索空间的定义合理,可微分神经网络搜索技术就可以迁移到图像分类、分割以外的领域。
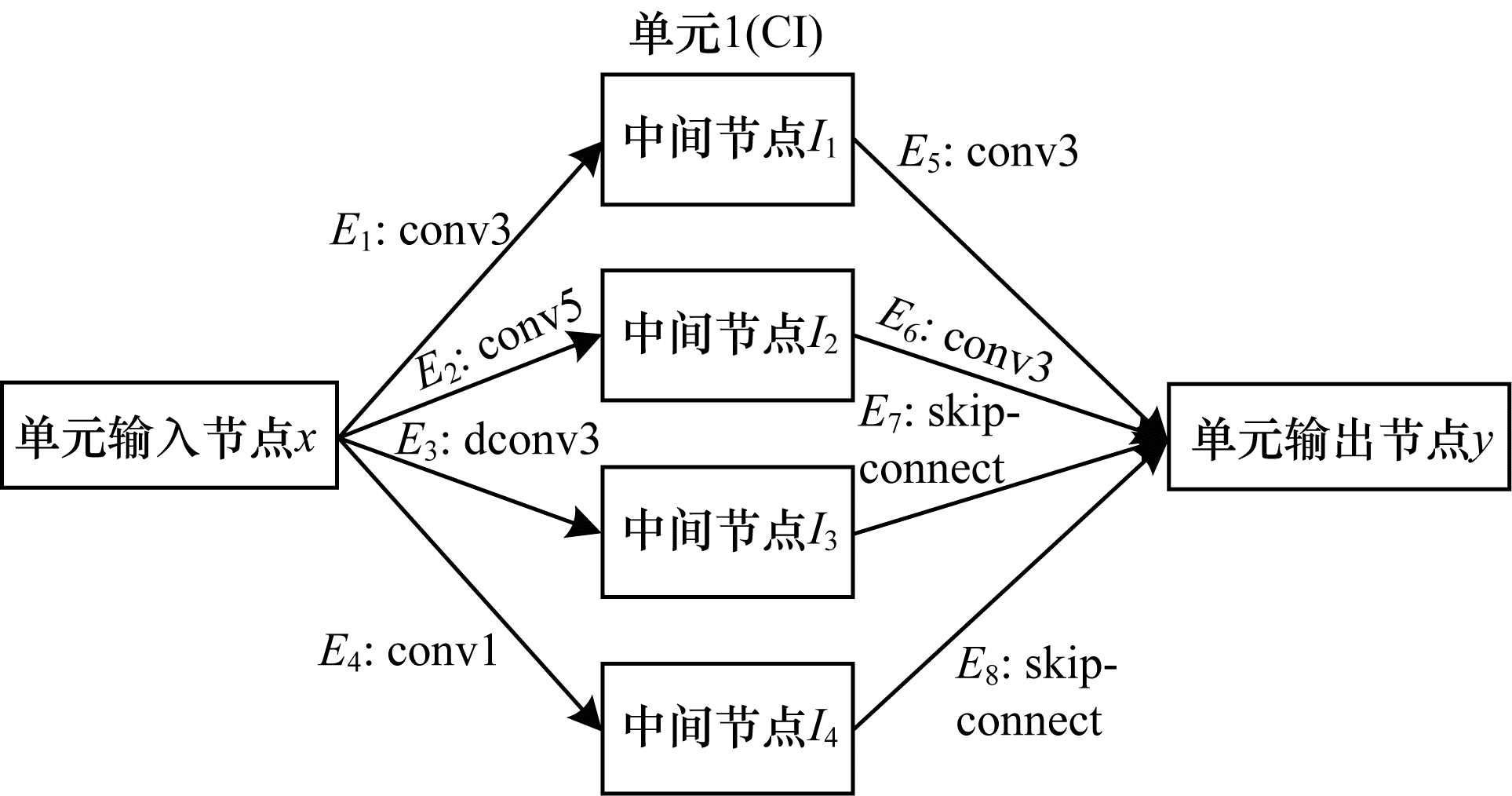
3.4 搜索结果以图 3中搜索单元C1为例,本文方法搜索得到的C1的结构如图 11所示。
|
Download:
|
| 图 11 搜索得出的单元C1的结构 Fig. 11 The structure of C1 searched by the proposed method | |
图 11中,超边E1、E5、E6为3×3卷积,超边E2为5×5卷积,超边E3为3×3空洞卷积,超边E4为1×1卷积,超边E7、E8均为恒同连接(skip-connect)。
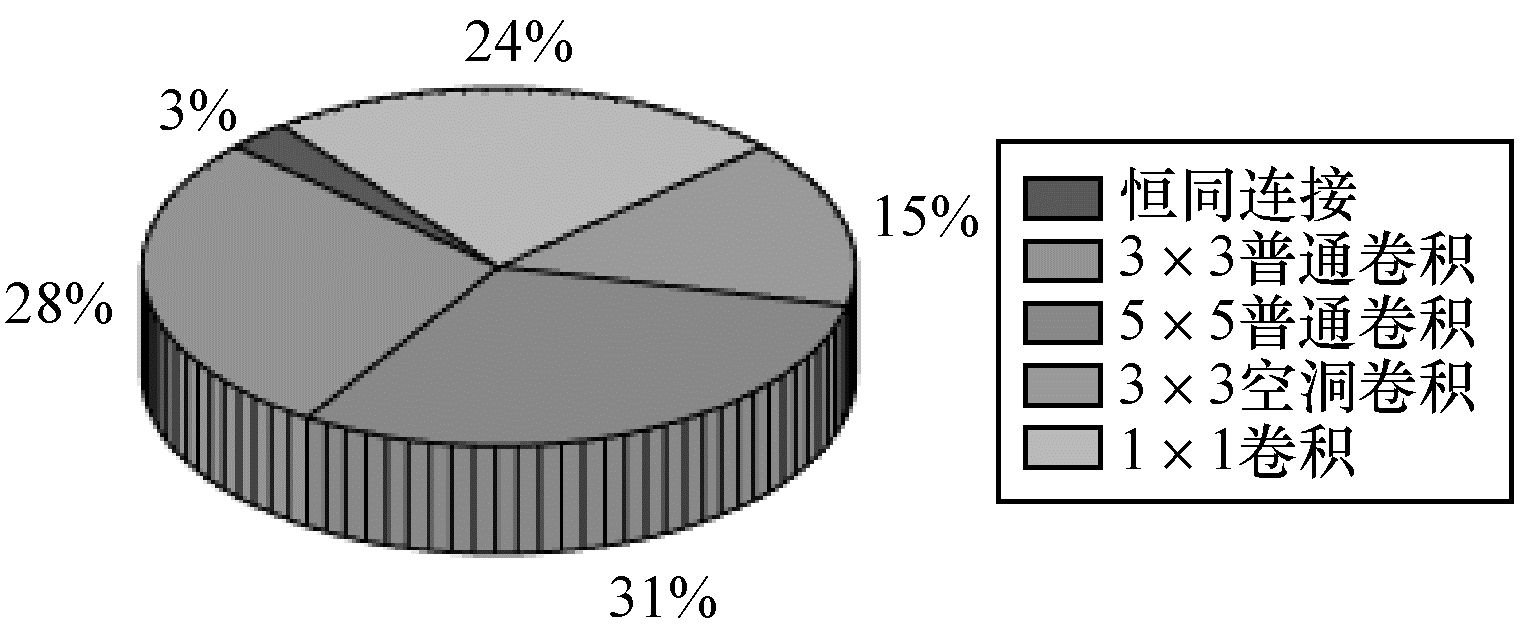
在单元C1~C9中,5种运算的分布如图 12所示。
|
Download:
|
| 图 12 5种候选操作的比重分布图 Fig. 12 Distribution of the five candidate operations | |
本文提出的搜索空间总共包括9个单元,每个单元8条超边共计72条超边。其中,有2条恒同连接,11个3×3空洞卷积,22个5×5卷积,20个3×3卷积和17个1×1卷积。从图 12可以看出,5×5普通卷积占了很大的比重,这是符合预期的。文献[29]表明,增大感受野对图像去模糊等复原问题有重要作用,而5×5卷积的感受野较大。恒同连接只有两个且全部出现在单元C1中,这也同样符合预期,因为恒同连接不能提取特征。
4 结束语本文将可微分神经网络架构搜索技术(DARTS)引入图像去模糊领域,提出了U型残差搜索空间,基于分治的思路,将搜索空间划分为9个搜索单元,显著降低了搜索的计算难度。在不需要人工调参的情况下搜索得出的网络,在GOPRO和Kohler数据集上,峰值信噪比相对于基准网络UNet分别提升3.10 dB和1.17 dB,与当前最先进的DeblurGAN性能基本相当。本文提出的搜索方法简化了繁重的调参工作,使得研究人员可以更加集中精力于算法和整体架构的设计。目前,搜索得到的神经网络较深,只能在性能强大的服务器上实验,难以在移动设备上测试。下一步将结合神经网络架构搜索与神经网络量化、剪枝等技术,同时引入低延迟模块,以搜索出一个可在移动端使用的轻量去模糊神经网络。
| [1] |
XU L, ZHENG S, JIA J. Unnatural l0 sparse representation for natural image deblurring[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2013: 1107-1114.
|
| [2] |
PAN J, SU Z. Fast l0-regularized kernel estimation for robust motion deblurring[J]. IEEE Signal Processing Letters, 2013, 20(9): 841-844. DOI:10.1109/LSP.2013.2261986 |
| [3] |
HE K, SUN J, TANG X. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 33(12): 2341-2353. |
| [4] |
PAN J, SUN D, PFISTER H, et al. Deblurring images via dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 40(10): 2315-2328. |
| [5] |
WANG J Z, YU Z M. Research on image debluring based on adaptive least mean square algorithm[J]. Computer Engineering, 2012, 38(17): 226-231. (in Chinese) 王俊芝, 玉振明. 基于LMS自适应算法的图像去模糊研究[J]. 计算机工程, 2012, 38(17): 226-231. |
| [6] |
SCHULER C J, HIRSCH M, HARMELING S, et al. Learning to deblur[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 38(7): 1439-1451. |
| [7] |
HRADIŠ M, KOTERA J, ZEMCIK P, et al. Convolutional neural networks for direct text deblurring[EB/OL]. [2020-05-11]. http://www.bmva.org/bmvc/2015/papers/paper006/paper006.pdf.
|
| [8] |
NAH S, HYUN K T, MU L K. Deep multi-scale convolutional neural network for dynamic scene deblurring[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2017: 3883-3891.
|
| [9] |
TAO X, GAO H, SHEN X, et al. Scale-recurrent network for deep image deblurring[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2018: 8174-8182.
|
| [10] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [11] |
KUPYN O, BUDZAN V, MYKHAILYCH M, et al. Deblurgan: blind motion deblurring using conditional adversarial networks[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2018: 8183-8192.
|
| [12] |
GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]//Proceedings of Advances in Neural Information Processing Systems. Montreal, Canada: MIT Press, 2014: 2672-2680.
|
| [13] |
ZOPH B, LE Q V. Neural architecture search with reinforcement learning[EB/OL]. [2020-05-10]. https://arxiv.org/pdf/1611.01578.pdf.
|
| [14] |
LIU H, SIMONYAN K, YANG Y. Darts: differentiable architecture search[EB/OL]. [2020-05-11]. https://arxiv.org/pdf/1806.09055.pdf.
|
| [15] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]//Proceedings of IEEE Cconference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2016: 770-778.
|
| [16] |
PENG W, HONG X, ZHAO G. Video action recognition via neural architecture searching[C]//Proceedings of IEEE International Conference on Image Processing. Washington D.C., USA: IEEE Press, 2019: 11-15.
|
| [17] |
WENG Y, ZHOU T, LIU L, et al. Automatic convolutional neural architecture search for image classification under different scenes[J]. IEEE Access, 2019, 7: 38495-38506. DOI:10.1109/ACCESS.2019.2906369 |
| [18] |
HUNDT A, JAIN V, HAGER G D. sharpDARTS: faster and more accurate differentiable architecture search[EB/OL]. [2020-05-15]. https://arxiv.org/pdf/1903.09900.pdf.
|
| [19] |
WU B, DAI X, ZHANG P, et al. Fbnet: hardware-aware efficient convnet design via differentiable neural architecture search[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2019: 10734-10742.
|
| [20] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. [2020-05-16]. https://arxiv.org/pdf/1409.1556.pdf.
|
| [21] |
RONNEBERGER O, FISCHER P, BROX T. U-net: convolutional networks for biomedical image segmentation[C]//Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention. Munich, Germany: Springer, 2015: 234-241.
|
| [22] |
KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. [2020-05-16]. https://arxiv.org/pdf/1412.6980.pdf.
|
| [23] |
CHEN X, FANG H, LIN T Y, et al. Microsoft coco captions: data collection and evaluation server[EB/OL]. [2020-05-17]. https://arxiv.org/pdf/1504.00325.pdf.
|
| [24] |
KÖHLER R, HIRSCH M, MOHLER B, et al. Recording and playback of camera shake: benchmarking blind deconvolution with a real-world database[C]//Proceedings of European Conference on Computer Vision. Florence, Italy: Springer, 2012: 27-40.
|
| [25] |
WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
| [26] |
LEDIG C, THEIS L, HUSZÁR F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]//Proceedings of IEEE Conference on Computer Vision And Pattern Recognition. Washington D.C., USA: IEEE Press, 2017: 4681-4690.
|
| [27] |
SUN J, CAO W, XU Z, et al. Learning a convolutional neural network for non-uniform motion blur removal[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2015: 769-777.
|
| [28] |
ZHANG H, DAI Y, LI H, et al. Deep stacked hierarchical multi-patch network for image deblurring[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2019: 5978-5986.
|
| [29] |
LIU S, PAN J, YANG M H. Learning recursive filters for low-level vision via a hybrid neural network[C]//European Conference on Computer Vision. Amsterdam, Netherlands: Springer, 2016: 560-576.
|
 2021, Vol. 47
2021, Vol. 47

