2. 云南财经大学 智能应用研究院, 昆明 650221
2. Intelligent Application Research Institute, Yunnan University of Finance and Economics, Kunming 650221, China
开放科学(资源服务)标志码(OSID):
随着区块链技术的不断普及,使用区块链在弱信任或无信任网络中进行数据共享已经非常普遍。但是由于区块链的“不可篡改”和“公开透明”的特点,使得区块链上的隐私数据保护成为一个挑战。近年来,研究人员针对区块链上的隐私保护和数据共享提出了新的解决方案[1-3]。其中,基于属性的加密算法由于其“一对多”加密和可以实现细粒度访问控制等优点,被广泛应用在数据溯源[4]、云存储[5]、医疗数据共享[6]、物联网[7]等区块链的各种方案中。
属性基加密(Attribute-Based Encryption,ABE)来源于SAHAI等[9]于2005年提出的基于模糊身份加密,后来演变为基于属性的加密。其中,在密钥策略属性基加密(Key Policy-Attribute Based Encryption,KP-ABE)中,密文与属性关联,密钥与访问策略关联;而在密文策略属性基加密[10](Ciphertext Policy Attribute Based Encryption,CP-ABE)中,密钥与属性关联,密文与访问策略关联,允许数据拥有者自由制定访问控制策略,适用于分布式存储和解密方不确定的环境[11]。近年来,关于ABE的研究主要集中于计算效率[12-13]、访问策略及属性隐藏[14]和身份管理[15]。2007年,BETHENCOURT等[16]描述了密文策略属性基加密算法,针对一个解密的对象群体,利用用户相关属性及其用户对象间的相互信任关系作为授权依据,设计访问控制结构,通过一个中心权威构建加解密原语,只有当属性满足访问结构时,用户才能成功解密密文,从而实现一对多加密以及细粒度的访问控制。2011年,WATERS[10]在标准模型下证明了CP-ABE的安全性,并提出一个采用线性秘密共享方案实现秘密共享的CP-ABE,在效率上有了明显提升。2012年,OKAMOTO等[17]提出一个无界内积属性基加密方案,解除了以往属性基加密方案对谓词和属性大小的限制。2013年,GORBUBOV[18]提出基于多项式逻辑电路的属性基加密方案,其公开参数和密文大小随着电路深度线性增长,实现了由基于布尔公式向基于电路的转变,可有效抵御合谋攻击。2014年,WATERS[19]受ROUSELAKIS等[20]提出的属性基加密方案启发,提出Online-Offline属性基加密方案,将所有配对操作进行离线处理,减少了在线阶段的计算开销。
随着量子计算的不断发展,基于数论问题的困难性将会极大降低,以数论为基础的传统公钥密码体系面临着被破解的风险。格密码采用格困难问题作为格密码构造的安全性基础,拥有最困难情况假设下无法求解的安全性,可以很好地抵抗量子攻击。目前,被证明安全的格困难问题主要由小整数解 [21](Small Integer Solution,SIS) 问题和容错学习问题[22](Learning With Errors,LWE) 问题。两种困难问题均从最坏情况理想格问题向一般变种问题归约,且计算效率高,易存储。目前,基于格的加密方案相继被提出,但主要集中于基于身份加密[23]、数字签名[24]和零知识证明[25]等。2021年5月,DATTA等[26]基于LWE困难问题,构造一种基于密文策略的属性基加密算法,实现了可抵抗量子攻击的CPABE方案。
本文通过改进CPABE方案,提出适用于区块链的抗量子攻击LWE-CPABE算法,并给出支持策略更新的密文策略属性基加密算法,以实现数据的动态访问控制。在此基础上,定义适用于LWE-CPABE算法的可公开验证数据的格式化交易结构,设计交易生成算法和交易验证合约。
1 预备知识 1.1 相关参数定义本文设
令PPT(Probability Polynomial-Time)为概率多项式时间,对于某一分布
对于整数
对于整数上的一组分布
| $ \mathrm{P}{\mathrm{r}}_{x\leftarrow {\mathcal{D}}_{\lambda }}\left[\mathrm{ }\right|x|\le B(\lambda \left)\right]=1 $ |
则认为
引理1 设
| $ {B}_{1}\left(\lambda \right)/{B}_{2}\left(\lambda \right)\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(\lambda \right) $ |
则认为分布族
定理1(剩余哈希定理) 令
| $ \begin{array}{l}{\mathcal{D}}_{1}\equiv \{(\boldsymbol{A}, \boldsymbol{A}\boldsymbol{R})|\boldsymbol{A}\leftarrow {\mathbb{Z}}_{q}^{n\times m}, \boldsymbol{R}\leftarrow {\{-\mathrm{1, 1}\}}^{m\times k}\}\\ {\mathcal{D}}_{2}\equiv \{(\boldsymbol{A}, \boldsymbol{S})|\boldsymbol{A}\leftarrow {\mathbb{Z}}_{q}^{n\times m}, \boldsymbol{S}\leftarrow {\mathbb{Z}}_{q}^{n\times k}\}\end{array} $ |
定义格
1) 离散高斯分布
令
| $ {\rho }_{\mathcal{L}, \sigma }\left(\boldsymbol{x}\right)={\rho }_{\sigma }\left(\boldsymbol{x}\right)\mathrm{ }/{\rho }_{\sigma }\left(\mathcal{L}\right) $ |
引理2 若离散高斯分布的参数
引理3 令
| $ \underset{\boldsymbol{x}\leftarrow {\mathcal{D}}_{\mathcal{L}, \sigma }}{\mathrm{P}\mathrm{r}}\left[‖\boldsymbol{x}‖ > \sqrt{m}\sigma \right]\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right) $ |
其中:
2) 截断离散高斯
3) 格中陷门
格陷门函数包括以下两个算法:
(1)
(2)
对于安全参数
| $ \mathrm{A}\mathrm{d}{\mathrm{v}}_{\mathcal{A}}^{\mathrm{L}\mathrm{W}{\mathrm{E}}_{n, q, \sigma }}\left(\lambda \right)\triangleq \left|\begin{array}{c}\mathrm{P}\mathrm{r}\left[\begin{array}{l}1\leftarrow {\mathcal{A}}^{{\mathcal{O}}_{1}^{s}(\mathrm{ }\cdot \mathrm{ })}\left({1}^{\lambda }\right)\\ \boldsymbol{s}\leftarrow {\mathbb{Z}}_{q}^{n}\end{array}\right]\\ -\mathrm{P}\mathrm{r}\left[1\leftarrow {\mathcal{A}}^{{\mathcal{O}}_{2}^{}(\mathrm{ }\cdot \mathrm{ })}\left({1}^{\lambda }\right)\right]\end{array}\right|\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(\lambda \right) $ |
谕言机
定义1 若存在一个PPT敌手可以解决LWE困难问题假设,那么存在一个PPT量子算法可以在最高困难下解决格困难问题。
鉴于目前有关格困难问题的技术方案,当所有
| $ 2\sqrt{n} < \sigma < q < {2}^{n} \text{,} n\cdot q/\sigma < {2}^{{n}^{ϵ}} \text{,} 0 < ϵ < 1/2 $ |
LWE困难问题假设对于任意多项式
如图 1所示,LWE-CPABE算法主要由系统初始化、用户属性私钥生成、明文加密、密文解密、密文策略生成以及密文策略更新6个部分组成。
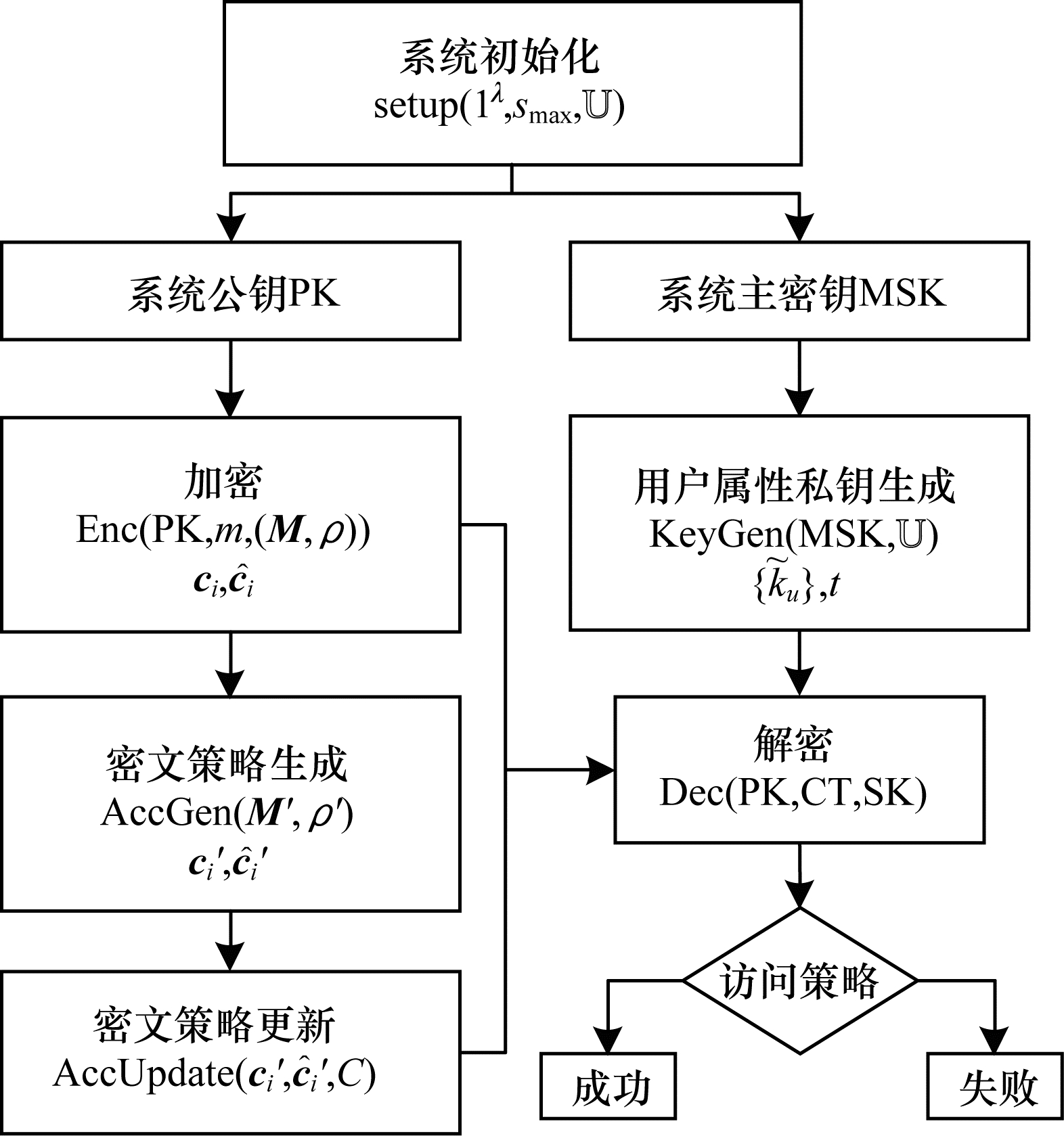
|
Download:
|
| 图 1 LWE-CPABE算法流程 Fig. 1 Procedure of LWE-CPABE algorithm | |
LWE-CPABE算法流程如下:
1)
对于系统中的每个属性
| $ \mathrm{P}\mathrm{K}=\left(\boldsymbol{y}\right\{{\boldsymbol{A}}_{\boldsymbol{u}}\}, \{{\boldsymbol{H}}_{\boldsymbol{u}}\left\}\right), \mathrm{M}\mathrm{S}\mathrm{K}=\left\{{\boldsymbol{T}}_{{\boldsymbol{A}}_{u}}\right\} $ |
2)
令
| $ \mathrm{S}\mathrm{K}=\left(\left\{{\tilde{\boldsymbol{k}}}_{u}\right\}, t\right) $ |
3)
设
| $ \begin{array}{l}{\boldsymbol{c}}_{i}=\boldsymbol{s}{\boldsymbol{A}}_{\rho \left(i\right)}+\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}\\ {\widehat{\boldsymbol{c}}}_{i}={M}_{i, 1}\left(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}, \stackrel{m-1}{\stackrel{⏞}{0, \cdots , 0}}\right)+\left[\sum\limits_{j\in \{\mathrm{2, 3}, \cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{M}_{i, j}{\boldsymbol{v}}_{j}\right]-\\ \boldsymbol{s}{\boldsymbol{H}}_{\rho \left(i\right)}+\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}\end{array} $ |
输出密文CT:
| $ \mathrm{C}\mathrm{T}=\left(\right\{{\boldsymbol{c}}_{i}{\}}_{i\in \left[\ell \right]}, \{{\widehat{\boldsymbol{c}}}_{i}{\}}_{i\in \left[\ell \right]}, C=\mathrm{M}\mathrm{S}\mathrm{B}(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}\left)\right) \oplus m) $ |
4)
设用户所拥有的属性满足访问控制策略。令
| $ K=\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}\left({\boldsymbol{c}}_{i}{\tilde{\boldsymbol{k}}}_{\rho \left(i\right)}^{\mathrm{T}}+{\widehat{\boldsymbol{c}}}_{i}{\boldsymbol{t}}_{}^{\mathrm{T}}\right) $ |
输出
5)
6)
LWE-CPABE安全游戏中包含一个挑战者和一个敌手,挑战者模拟系统运行并回答敌手询问。具体游戏如下:
1) 系统建立。敌手接收安全参数
2) 私钥询问。敌手对挑战者进行多项式时间的私钥询问,对于每次密钥查询,敌手发送一组属性
3) 挑战阶段。挑战者选择一个随机消息
4) 重复步骤2)。
5) 猜测阶段。敌手输出对
敌手
| $ \mathrm{A}\mathrm{d}{\mathrm{v}}_{\mathcal{A}}^{\mathrm{L}\mathrm{W}\mathrm{E}‐\mathrm{C}\mathrm{P}\mathrm{A}\mathrm{B}\mathrm{E}, \mathrm{S}\mathrm{E}\mathrm{L}‐\mathrm{C}\mathrm{P}\mathrm{A}}\left(\lambda \right)\triangleq \left|\mathrm{ }\mathrm{P}\mathrm{r}\right[b=b']-1/2\mathrm{ }| $ |
定义2 若对于任何PPT敌手
为实现区块链中的数据高效流转与策略更新,数据的上传、共享、修改及策略更新都通过交易的形式写入区块链中。用户可通过所持有的与自身属性相匹配的用户属性私钥访问链上的授权信息,完成安全可控的数据共享。LWE-CPABE区块链数据共享方案架构如图 2所示,其中,实线为交易过程,虚线为相关参数传递过程。
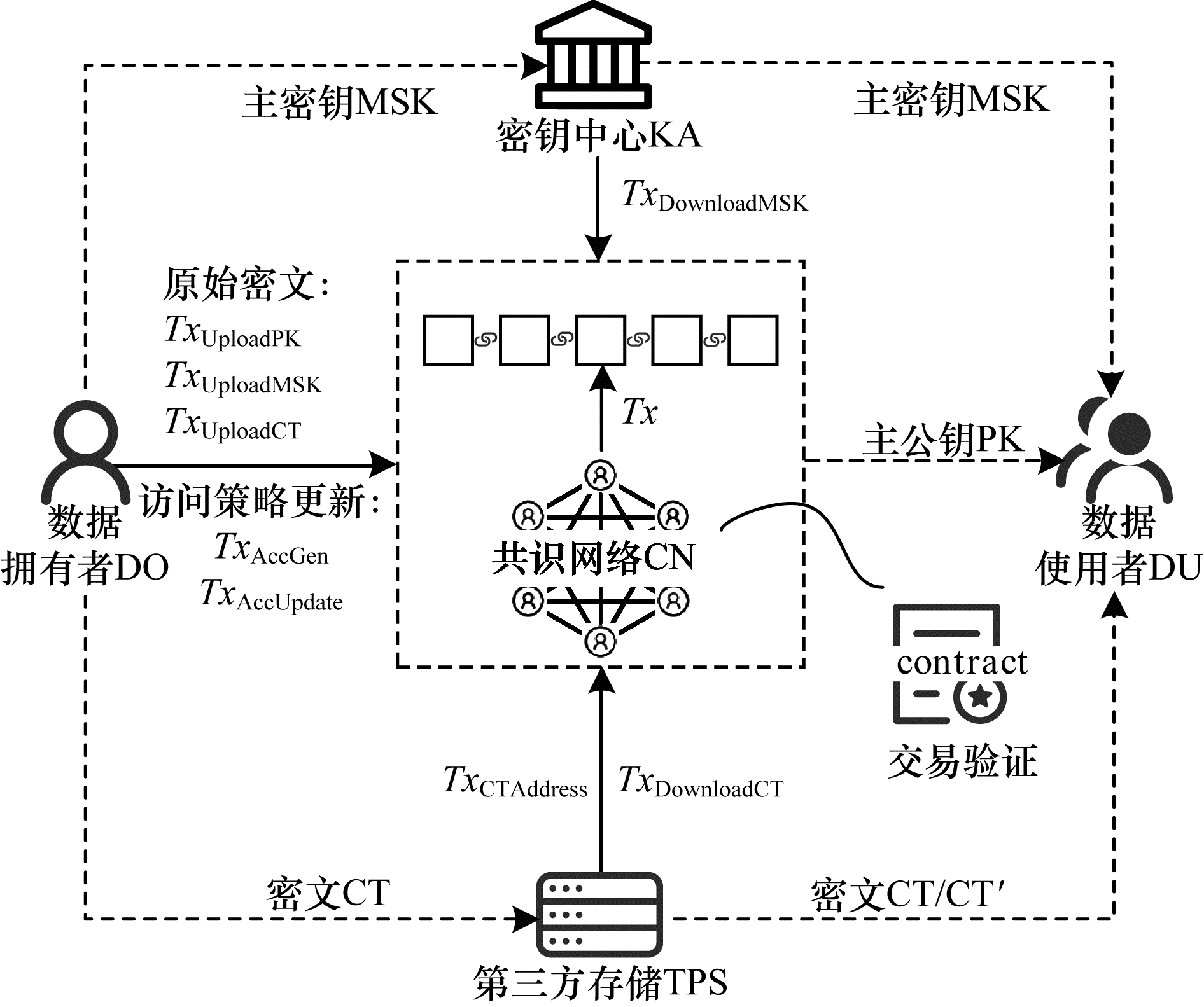
|
Download:
|
| 图 2 数据共享方案的架构 Fig. 2 Architecture of data sharing scheme | |
格式化交易结构如下:
1) 用户(DO、DU)。包括数据拥有者和数据使用者。数据拥有者DO制定访问控制策略,并生成相对应的密文,将密文上传至第三方存储并将地址上传至区块链,同时,将主密钥MSK委托密钥中心保管;数据使用者DU从密钥中心获取主密钥,之后利用自己的属性集合生成用户属性私钥SK,从区块链获取密文并解密。
2) 第三方存储(TPS)。提供加密数据的存储服务,并将加密数据地址存入区块链中。
3) 共识网络(CN)。由区块链中各记账节点组成,负责LWE-CPABE区块链加密协议中所涉及的交易的共识与记账更新。
4) 密钥中心(KA)。存储LWE-CPABE加密算法中的主密钥MSK,各用户通过密钥中心获取主密钥。
5) 智能合约(SC)。为协议各参与方提供交互接口。
LWE-CPABE区块链数据共享方案以区块链中的交易为载体实现数据的加密存储与细粒度访问控制。加密数据的访问控制权限由数据拥有者制定,数据被发布至链上后可以任意次数更新访问控制策略,直至加密数据被撤销,结束本次加密数据共享的生命周期。为使各参与方更高效地获取所需数据,便于审计和掌握访问控制动态,加密协议中定义了适用于该协议的交易格式:
Tx={From,To,TxType,OpType,Timestamp,Data,CheckText,Sign}
其中:From表示交易发起方;To表示交易接收方;TxType表示交易类型,A表示访问控制策略类消息,D表示数据类消息;OpType表示操作类型,P表示发布,U表示更新,R表示撤销;Timestamp表示交易发布的时间戳;Data表示交易包含的数据体;CheckText表示数据域Data的哈希值;Sign表示交易发起方的签名。
3.3 交易发布与验证合约在LWE-CPABE区块链数据共享方案中,各参与方通过交易的方式进行相关数据的流转。为保证交易的正确性、完整性和可追溯性,在交易生成后需共识网络中各节点进行共识验证。
参与数据共享的各参与方和全网节点通过智能合约的方式进行交易的生成与验证。交易生成合约如算法1所示。
算法1 交易生成算法
输入 格式化交易中各参数From、To、TxType、OpType、Timestamp、Data、CheckText、Sign;共识网络中交易发起方的区块链私钥BSK
输出 某特定交易Tx
1.CheckText=H(Data);/*计算数据中与相关数据的数字摘要*/
2.MD=H(From,To,TxType,OpType,Timestamp,Data,CheckText);/*计算交易数字摘要(除签名字段)*/
3.
4.Tx={From,To,TxType,OpType,Timestamp,Data,CheckText,Sign};/*生成交易*/
5.Return Tx;
交易生成后,将被广播至共识网络被其他节点验证。区块链中的节点可通过CheckText和签名Sign对该交易进行快速验证。
交易验证合约如算法2所示。
算法2 交易验证合约算法
输入 交易Tx,共识网络中交易发起方的区块链公钥BPK
输出 交易验证结果True或False
1.
2.MD=ComputeBPKSign;/*验证签名*/
3.if
4. Obtain Data From Tx;/*从交易中获取数据域数据Data*/
5. CheckTextʹ=H(Data);
6. if CheckTextʹ=CheckText then
7. Return True;
8.Return False;
当该交易获得节点验证成功并全网共识后,挖矿节点会打包交易、出块并全网广播,最终由本地节点接收并同步区块。
3.4 方案构造本节将详细阐述基于LWE-CPABE方案的区块链数据共享过程。
DO选择正确性证明所需的参数约束。对于任意
| $ \begin{array}{l}-n=\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{y}\left(\lambda \right), \sigma < q, n\cdot q/\sigma < {2}^{{n}^{ϵ}}, {\mathcal{X}}_{lwe}={\tilde{\mathcal{D}}}_{{\mathbb{Z}}^{m}, \sigma }\\ -m > 2{s}_{\mathrm{m}\mathrm{a}\mathrm{x}}n\mathrm{l}\mathrm{o}{\mathrm{g}}_{a}q+\omega \mathrm{l}\mathrm{o}{\mathrm{g}}_{a}n+2\lambda \\ -\sigma > \sqrt{{s}_{\mathrm{m}\mathrm{a}\mathrm{x}}n\mathrm{l}\mathrm{o}{\mathrm{g}}_{a}q\mathrm{l}\mathrm{o}{\mathrm{g}}_{a}m}-\lambda \\ -{\mathcal{X}}_{1}={\tilde{\mathcal{D}}}_{{\mathbb{Z}}^{m-1}, \sigma }, {\mathcal{X}}_{2}={\tilde{\mathcal{D}}}_{{\mathbb{Z}}^{m}, \sigma }\\ -{\mathcal{X}}_{big}={\mathcal{U}}_{\widehat{B}}, \widehat{B} > ({m}^{3/2}\sigma +1){2}^{\lambda }\\ - | \mathbb{U} | \cdot 3{m}^{3/2}\sigma \widehat{B} < q/4 \end{array} $ |
1) 系统初始化。数据拥有者DO选取安全参数
系统初始化算法如算法3所示。
算法3 系统初始化算法
输入 安全参数
输出 公钥PK,主密钥MSK
1. Choose an LWE modulus q,dimensions n,m and distributions
2. Choose a vector
3.
| $ \mathrm{P}\mathrm{K}=\left(\mathrm{n}, \mathrm{m}, \mathrm{q}, {\mathcal{X}}_{\mathrm{l}\mathrm{w}\mathrm{e}}, {\mathcal{X}}_{1}, {\mathcal{X}}_{2}, {\mathcal{X}}_{\mathrm{b}\mathrm{i}\mathrm{g}}, \mathrm{y}\{{\mathrm{A}}_{\mathrm{u}}{\}}_{\mathrm{u}\in \mathbb{U}}, \{{\mathrm{H}}_{\mathrm{u}}{\}}_{\mathrm{u}\in \mathbb{U}}\right) $ |
MSK
DO生成交易TxUploadPK={DO,BC,A,P,Timestamp,PK,CheckText,SigDO}将公钥上链。然后使用KA公钥对主密钥加密得到CTMSK,并生成交易TxUploadMSK={DO,KA,A,P,Timestamp,CTMSK,CheckText,SigDO},将主密钥MSK委托KA保管。
2) 数据加密。数据拥有者DO制定访问控制策略
数据加密算法如算法4所示。
算法4 数据加密算法
输入 公钥PK,明文m,访问控制策略
输出 密文CT
1.Generate Access Policy
2.Select a random vector
3.Sample a vector
4.for each
Select random noise
Compute
| $ \begin{array}{l}{\mathrm{c}}_{\mathrm{i}}=\mathrm{s}{\mathrm{A}}_{\mathrm{\rho }\left(\mathrm{i}\right)}+{\mathrm{e}}_{\mathrm{i}}\\ {\widehat{\mathrm{c}}}_{\mathrm{i}}={\mathrm{M}}_{\mathrm{i}, 1}\left(\mathrm{s}{\mathrm{y}}^{\mathrm{T}}, \stackrel{\mathrm{m}-1}{\stackrel{⏞}{0, \cdots , 0}}\right)+\left[\sum\limits_{\mathrm{j}\in \{\mathrm{2, 3}, \cdots , {\mathrm{s}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{\mathrm{M}}_{\mathrm{i}, \mathrm{j}}{\mathrm{v}}_{\mathrm{j}}\right]-\mathrm{s}{\mathrm{H}}_{\mathrm{\rho }\left(\mathrm{i}\right)}+{\widehat{\mathrm{e}}}_{\mathrm{i}}\end{array} $ |
| $ \mathrm{C}\mathrm{T}=\left(\right\{\mathrm{M}, \mathrm{\rho }\left\}\right\{{\mathrm{c}}_{\mathrm{i}}{\}}_{\mathrm{i}\in \left[\ell \right]}, \{{\widehat{\mathrm{c}}}_{\mathrm{i}}{\}}_{\mathrm{i}\in \left[\ell \right]}, \mathrm{C}=\mathrm{M}\mathrm{S}\mathrm{B}(\mathrm{s}{\mathrm{y}}^{⊺}\left)\right) \oplus \mathrm{m}) $ |
DO生成交易TxUploadCT={DO,TPS,A,P,Timestamp,CTMSK,CheckText,SigDO},将密文上传至第三方存储TPS,TPS生成交易TxCTAddress={TPS,BC,A,D,Timestamp,CTAddress,CheckText,SigTPS},将密文地址上链。
3) 用户属性私钥生成。各数据使用者DU从密钥中心KA处申请获得主密钥,KA使用各用户区块链公钥对MSK加密后生成交易TxDownloadMSK={KA,DU,A,P,Timestamp,CTMSK,CheckText,SigDO}。之后DU输入自身属性信息
用户属性私钥生成算法如算法5所示。
算法5 用户属性私钥生成算法
输入 主密钥MSK,自身属性信息
输出 用户属性私钥SK
1. Select a random vector
2. Let
3. for each
Select
Compute
then Compute
4) 密文解密。DU从区块链BC检索密文地址,通过密文地址CTAddress从TPS搜索到相对应密文CT并下载至本地,TPS生成交易TxDownloadCT={TPS,DU,D,P,Timestamp,CT,CheckText,SigTPS}进行密文下载记录。DU使用SK对密文CT进行解密,获取明文。
在密文解密过程中,SK对应于属性集合
解密算法如算法6所示。
算法6 解密算法
输入 密文CT,用户属性私钥SK
输出 明文数据m
1. Compute
2. Compute
5) 密文策略生成。当访问控制策略发生变更时,重新加密需要耗费更多密钥空间成本和密文加密时间成本。在LWE-CPABE区块链加密协议中,数据使用者可进行原始密文保留的访问控制策略更新。在进行策略更新时,DO生成新的访问控制策略
| $ \begin{array}{l}{\boldsymbol{c}}_{i}^{\mathrm{'}}=\boldsymbol{s}{\boldsymbol{A}}_{\rho '\left(i\right)}+{\boldsymbol{e}}_{i}\\ {\widehat{\boldsymbol{c}}}_{i}^{\mathrm{'}}={M}_{i, 1}^{\mathrm{'}}\left(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}, \stackrel{m-1}{\stackrel{⏞}{0, \cdots , 0}}\right)+\left[\sum\limits_{j\in \{\mathrm{2, 3}, \cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{M}_{i, j}^{\mathrm{'}}{\boldsymbol{v}}_{j}\right]-\boldsymbol{s}{\boldsymbol{H}}_{\rho \left(i\right)}+{\widehat{\boldsymbol{e}}}_{i}\end{array} $ |
随后生成策略更新交易TxAccGen={DO,TPS,A,U,Timestamp,UpdateCT,CheckText,SigDO}发送给第三方存储TPS。同时,生成原密文撤销交易发送至区块链以更新密文信息TxAccUpdate={DO,BC,A,R,Timestamp,CT,CheckText,SigDO}告知各数据使用者DU。
6) 密文策略更新。TPS获取更新后的策略密文后,从原CT中获取密文C,输入更新的访问控制策略密文
| $ \mathrm{C}\mathrm{T}'=\left((\boldsymbol{M}', \rho '), \{{\boldsymbol{c}}_{i}^{\mathrm{'}}{\}}_{i\in \left[\ell \right]}, \{{\widehat{\boldsymbol{c}}}_{i}^{\mathrm{'}}{\}}_{i\in \left[\ell \right]}, C=\mathrm{M}\mathrm{S}\mathrm{B}\left(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}\right)) \oplus m\right) $ |
更新后密文仍使用原密文地址,各数据使用者仍可通过上述步骤获取密文并进行解密。
在基于LWE-CPABE的区块链加密协议中,各用户利用格式化的交易结构可快速高效地检索到各自所需信息,同时,整个数据流转周期内实现了各节点行为全过程链上监管,可以更好地进行审计和掌握访问控制动态。
4 方案分析 4.1 正确性分析假设某数据使用者拥有的属性
| $ K=\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}\left({\boldsymbol{c}}_{i}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}+{\widehat{\boldsymbol{c}}}_{i}{\boldsymbol{t}}_{}^{\mathrm{T}}\right) $ |
展开
| $ \begin{array}{l}K=\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}\boldsymbol{s}{\boldsymbol{A}}_{\rho \left(i\right)}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{M}_{i, 1}(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}, 0, \cdots , 0){\boldsymbol{t}}^{\mathrm{T}}+\\ \sum\limits_{i\in \boldsymbol{I}, j\in \{\mathrm{2, 3}, \cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{\omega }_{i}{M}_{i, j}{\boldsymbol{v}}_{j}{\boldsymbol{t}}^{\mathrm{T}}-\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}\boldsymbol{s}{\boldsymbol{H}}_{\rho \left(i\right)}{\boldsymbol{t}}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\widehat{\boldsymbol{e}}}_{i}{\boldsymbol{t}}^{\mathrm{T}}\end{array} $ |
对于每个
| $ {\boldsymbol{A}}_{u}{\tilde{\boldsymbol{k}}}_{u}^{\mathrm{T}}={\boldsymbol{H}}_{u}{\boldsymbol{t}}^{\mathrm{T}}-{\boldsymbol{A}}_{u}{\widehat{\boldsymbol{k}}}_{u}^{\mathrm{T}} $ |
因此,对于每个
| $ {\boldsymbol{A}}_{\rho \left(i\right)}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}={\boldsymbol{A}}_{\rho \left(i\right)}{\widehat{\boldsymbol{k}}}_{\rho \left(i\right)}^{\mathrm{T}}+{\boldsymbol{A}}_{\rho \left(i\right)}{\tilde{\boldsymbol{k}}}_{\rho \left(i\right)}^{\mathrm{T}}={\boldsymbol{H}}_{\rho \left(i\right)}{\boldsymbol{t}}^{\mathrm{T}} $ |
可得:
| $ \begin{array}{l}K=\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}\boldsymbol{s}{\boldsymbol{H}}_{\rho \left(i\right)}{\boldsymbol{t}}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{M}_{i, 1}(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}, 0, \cdots , 0){\boldsymbol{t}}^{\mathrm{T}}+\\ \sum\limits_{i\in \boldsymbol{I}, j\in \{\mathrm{2, 3},\cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{\omega }_{i}{M}_{i, j}{\boldsymbol{v}}_{j}{\boldsymbol{t}}^{\mathrm{T}}-\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}\boldsymbol{s}{\boldsymbol{H}}_{\rho \left(i\right)}{\boldsymbol{t}}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\boldsymbol{e}}_{i}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}+\\ \sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\widehat{\boldsymbol{e}}}_{i}{\boldsymbol{t}}^{\mathrm{T}}=\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{M}_{i, 1}(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}, 0, \cdots , 0){\boldsymbol{t}}^{\mathrm{T}}+\\ \sum\limits_{i\in \boldsymbol{I}, j\in \{2,3, \cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{\omega }_{i}{M}_{i, j}{\boldsymbol{v}}_{j}{\boldsymbol{t}}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\boldsymbol{e}}_{i}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\widehat{\boldsymbol{e}}}_{i}{\boldsymbol{t}}^{\mathrm{T}}=\\ \left(\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{M}_{i, 1}\right)(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}, 0, \cdots , 0){\boldsymbol{t}}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}, j\in \{\mathrm{2, 3},\cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{\omega }_{i}{M}_{i, j}{\boldsymbol{v}}_{j}{\boldsymbol{t}}^{\mathrm{T}}+\\ \sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\boldsymbol{e}}_{i}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\widehat{\boldsymbol{e}}}_{i}{\boldsymbol{t}}^{\mathrm{T}}\end{array} $ |
当
| $ K=\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\boldsymbol{e}}_{i}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\widehat{\boldsymbol{e}}}_{i}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}} $ |
对于噪声部分
1) 由引理3可知,因为
2) 因为
3) 因为
4) 因为
因此可得:
| $ ‖\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\boldsymbol{e}}_{i}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}+\sum\limits_{i\in \boldsymbol{I}}{\omega }_{i}{\widehat{\boldsymbol{e}}}_{i}{\boldsymbol{k}}_{\rho \left(i\right)}^{\mathrm{T}}+‖ < $ |
| $ \left|\mathbb{U}\right|({m}^{3/2}{\sigma }^{2}+m\sigma \widehat{B}+{m}^{3/2}\sigma \widehat{B}) < $ |
| $ \left|\mathbb{U}\right|\cdot 3{m}^{3/2}\sigma \widehat{B} < q/4 $ |
因此,以
证毕。
4.2 安全性分析本文基于LSSS访问控制结构的LWE-CPABE,定义了更灵活的选择性安全,即“线性独立约束下的选择性安全”。因此,将游戏中的密钥询问阶段修改如下:
在密钥询问阶段,敌手向挑战者进行多项式的密钥询问,对于每次密钥询问,攻击者发送一系列不满足访问控制策略
敌手
| $ \mathrm{A}\mathrm{d}{\mathrm{v}}_{\mathcal{A}}^{\mathrm{L}\mathrm{W}\mathrm{E}‐\mathrm{C}\mathrm{P}\mathrm{A}\mathrm{B}\mathrm{E}, \mathrm{S}\mathrm{E}\mathrm{L}‐\mathrm{L}\mathrm{I}‐\mathrm{C}\mathrm{P}\mathrm{A}}\left(\lambda \right)\triangleq \left|\mathrm{ }\mathrm{P}\mathrm{r}\right[b=b']-1/2\mathrm{ }| $ |
定义3 若上述游戏中任意PPT敌手
定义4 若LWE困难问题假设成立,则本文所构造的LWE-CPABE满足选择性安全。
证明 为证明定义4,本文设置了一系列混合博弈游戏,该系列游戏在公共参数的生成、密文挑战和密钥询问阶段各不相同。系列游戏中的第一个游戏对应于所提出的LWE-CPABE方案在线性独立约束博弈下的选择性安全,最后一个游戏是证明敌手
证毕。
以下是混合游戏的构建与归约:
Hyb0:该混合游戏对应于ABE方案的真实弱安全选择性博弈。
Setup阶段:
1.
2.
3.
4.
Key query阶段:
1.
2.
3.
4.
5.
6.
Challenge阶段:
1.
2.
3.
4.
5.
6.
7.
Hyb1:该游戏与Hyb0类似,但是在Setup阶段增加了矩阵
1.将原来
2.将原来
| $ \begin{array}{l}\forall i\in \left[\ell \right]:{\widehat{\boldsymbol{c}}}_{i}^{}={M}_{i, 1}\left(\boldsymbol{s}{\boldsymbol{y}}^{\mathrm{T}}, \stackrel{m-1}{\stackrel{⏞}{0, \cdots , 0}}\right)+\\ \left[\sum\limits_{j\in \{\mathrm{2, 3}, \cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{M}_{i, j}^{}{\widehat{\boldsymbol{v}}}_{j}{\boldsymbol{B}}_{j}\right]-\boldsymbol{s}{\boldsymbol{H}}_{\rho \left(i\right)}+{\widehat{\boldsymbol{e}}}_{i}\end{array} $ |
Hyb1和Hyb0之间的变化仅仅是句法上的变化,因此这两个混合游戏是无法区分的。
Hyb2:该游戏与Hyb1类似,区别是在Setup阶段矩阵
1.
2.
| $ \sum\limits_{j\in \{\mathrm{2, 3}, \cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{M}_{{\rho }^{-1}\left(u\right)}^{}{\boldsymbol{B}}_{j}+{\boldsymbol{H}}_{u}^{\mathrm{'}} 。$ |
Hyb2和Hyb1之间的变化同样仅仅是句法上的变化,因此这两个混合游戏是无法区分的。
Hyb3:该游戏与Hyb2类似,区别是在Setup阶段矩阵
1.
2.
由定理1可知,Hyb3和Hyb2在选择上是不可区分的。
Hyb4:该游戏与Hyb3类似,区别在于Setup阶段矩阵
1.
2.
3.
Hyb4和Hyb3的不可区分性源于格陷门函数
Hyb5:该游戏与Hyb4类似,区别在于回答敌手
1.
| $ \left(\begin{array}{c}{\boldsymbol{A}}_{u}\text{,}{T}_{{\boldsymbol{A}}_{u}}, \sigma \\ \boldsymbol{t}{\left({M}_{{\rho }^{-1}\left(u\right), 1}\left[{\boldsymbol{y}}^{\mathrm{T}}, \stackrel{m-1}{\stackrel{⏞}{\left|{0}^{\mathrm{T}}\right|\cdots \left|{0}^{\mathrm{T}}\right|}}\right]\right)}^{\mathrm{T}}+\\ \sum\limits_{j\in \{\mathrm{2, 3}, \cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}\boldsymbol{t}({M}_{{\rho }^{-1}\left(u\right), j}^{}{\boldsymbol{B}}_{j}{)}^{\mathrm{T}}-{\widehat{\boldsymbol{k}}}_{u}{\boldsymbol{A}}_{u}^{\mathrm{T}}\end{array}\right) 。$ |
2.
Hyb5和Hyb4的不可区分性见引理1。
Hyb6:该游戏与Hyb5类似,区别在于回答敌手
1.
2.
Hyb6和Hyb5的不可区分性源于格陷门函数
Hyb7:该游戏与Hyb6类似,区别在于回答敌手
1.
2.
3.
| $ {\tilde{\boldsymbol{k}}}_{u}\leftarrow \mathrm{E}\mathrm{n}\mathrm{S}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{P}\mathrm{r}\mathrm{e}({\boldsymbol{A}}_{u}^{}, {T}_{{\boldsymbol{A}}_{u}}, \rho , {\boldsymbol{z}}_{u}) 。$ |
Hyb7和Hyb6之间的变化同样仅仅是句法上的变化,因此这两个混合游戏是无法区分的。
Hyb8:该游戏与Hyb7类似,区别在于回答敌手
1.
2.
Hyb8和Hyb7的不可区分性源于格陷门函数
Hyb9:该游戏与Hyb8类似,区别是在Setup阶段矩阵
| $ \{{\boldsymbol{A}}_{u}^{}{\}}_{u\in U\bigcap \rho \left(\right[\ell \left]\right)}\leftarrow {\mathbb{Z}}_{q}^{n\times m} $ |
Hyb9和Hyb8的不可区分性源于格陷门函数
Hyb10:该游戏与Hyb9类似,区别是在Challenge阶段挑战密文中向量
1.
2.
由定理1可知,Hyb10和Hyb9在选择上是不可区分的。
Hyb11:该游戏与Hyb10类似,区别是在Challenge阶段挑战密文的改变。
Challenge阶段:
1.
2.
3.
4.
5.
| $ {\widehat{\boldsymbol{c}}}_{i}=\left[\sum\limits_{j\in \{\mathrm{2, 3}\cdots , {s}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}}{M}_{i, j}^{}{\widehat{\boldsymbol{v}}}_{j}^{\mathrm{'}}{\boldsymbol{B}}_{j}\right]-{\boldsymbol{c}}_{i}{\boldsymbol{R}}_{\rho \left(i\right)}+{\boldsymbol{e}}_{i}^{\mathrm{'}} 。$ |
6.
由LWE困难问题假设可知,Hyb11和Hyb10在选择上是不可区分的。
证明 对于任意敌手
| $ \left|{p}_{\mathcal{A}, x-1}\left(\lambda \right)-1/2\right|=\mathrm{A}\mathrm{d}{\mathrm{v}}_{\mathcal{A}}^{\mathrm{L}\mathrm{W}\mathrm{E}‐\mathrm{C}\mathrm{P}\mathrm{A}\mathrm{B}\mathrm{E}, \mathrm{S}\mathrm{E}\mathrm{L}‐\mathrm{C}\mathrm{P}\mathrm{A}}\left(\lambda \right) $ |
另外,对于所有
| $ \mathrm{A}\mathrm{d}{\mathrm{v}}_{\mathcal{A}}^{\mathrm{L}\mathrm{W}\mathrm{E}‐\mathrm{C}\mathrm{P}\mathrm{A}\mathrm{B}\mathrm{E}}\left(\lambda \right)\le \sum\limits_{\boldsymbol{x}\in \left[11\right]}\left|{p}_{\mathcal{A}, x-1}\left(\lambda \right)-{p}_{\mathcal{A}, x}\left(\lambda \right)\right| $ |
在Hyb0与Hyb1中,由于向量
同理分析可知,在Hyb1与Hyb2中,
由于
又由于LWE困难问题假设成立,因此对于任意PPT敌手
由此可知,敌手
证毕。
4.3 链上安全性分析本节将介绍常见的区块链攻击模型及本文方案如何抵抗这些典型攻击。
合谋攻击:在分布式体系中,攻击者通过多个秘密集合反向计算出授权方的主密钥或其他用户的用户属性私钥。在本文方案中,每个用户属性私钥在生成时会生成一个均匀独立分布的随机向量
中间人攻击:中间人攻击是指攻击者在通信方两端分别建立独立联系,交换其所收到的数据,监听或篡改信息。在本文方案中,各节点间所有的通信均以交易的方式进行,交易由发起方利用其区块链私钥进行签名,返回的秘密数据通过对方公钥进行加密,中间人无法通过篡改地址或伪造签名来通过验证。因此,本文方案可以很好地防止中间人攻击。
链接攻击:链接攻击是指攻击者通过链接同一地址的多条交易查找用户的隐私数据。在本文方案中,用户属性相关授权过程可由用户自己决定,用户可以选择公开其身份属性,也可以隐藏身份信息以保护隐私。此外,相关数据在链上均为密文,安全性通过算法安全性得到保证,攻击者无法获取用户相关信息,做到抗链接攻击。
4.4 性能对比分析通过对比本文方案与文献[5]方案的功能特性,分析本文方案在数据共享上的优缺点,如表 1所示。

|
下载CSV 表 1 不同方案的性能对比分析 Table 1 Performance comparison and analysis of different schemes |
文献[5]由于采用q-PBDHE困难问题假设,即无法在多项式时间内破解私钥和对单向函数求逆,以可以忽略的概率被破解,但随着量子计算的不断发展,这些困难问题假设将会面临被破解的风险,因此基于此类困难问题所构造的密码学方案是非绝对安全的,但本文所构造的LWE-CPABE方案可以得到绝对的安全性证明。此外,本文的LWE-CPABE方案是基于最高困难的安全类型,其他代数结构中均为平均困难的安全类型。在该安全类型中,若破解密码算法,则需要解决最高情况的困难问题。最后,文献[5]所构造的CPABE方案在计算上需要乘法运算、模指数运算和双线性映射等开销较大的运算,而本文方案则只需进行开销较小的加法运算,极大地提高了运算效率。
另外,通过对比本文方案和文献[26]方案的功能特性,分析本文方案在数据共享上的优缺点,结果如表 2所示。

|
下载CSV 表 2 不同方案的功能对比分析 Table 2 Functional comparison and analysis of different schemes |
在文献[26]方案中,若数据使用者群体发生改变,则需要数据使用者重新生成访问控制矩阵并对明文数据进行重新加密。而在本文方案中,增加了策略撤销与更新算法,当数据使用者集合发生改变时,数据拥有者仅需生成新的访问控制矩阵即可实现对密文访问控制策略的变更。同时,通过策略撤销交易即可实现原有访问策略的撤销,有效地减少了计算代价和存储代价。另外,本文方案支持公共数据(如密文、公钥等)的共识验证,可有效保证公共数据的安全性、完整性与来源真实性。在基于密码学的数据共享方案中,其安全性依赖于密钥的安全性,而密钥盗版及滥用问题一直是属性基加密中难以解决的问题。因此,在本文方案中,利用格式化的交易结构、改进的密钥生成算法、严格的密钥申请交易和密钥传递交易,可实现密钥流转的全过程行为记录,实现快速、准确的密钥相关行为追溯。因此,对比文献[26]方案,本文方案更适用于区块链数据共享。
4.5 实验仿真分析本节主要针对方案的实现性能进行分析。实验采用一台主机(Intel Core i7-8750H CPU @2.20 GHz,8.0 GB RAM,Win10操作系统),并利用PBC密码库、PALISADE密码库和编程语言C++来构建实验框架。在对性能指标进行选择时,本文方案并未对区块链网络的交易流程进行改动,只是将网络中上链的数据采用LWE-CPABE进行加密,不会影响到区块链网络的运行效率。因此,本文首先对LWE-CPABE方案的性能指标进行评估。
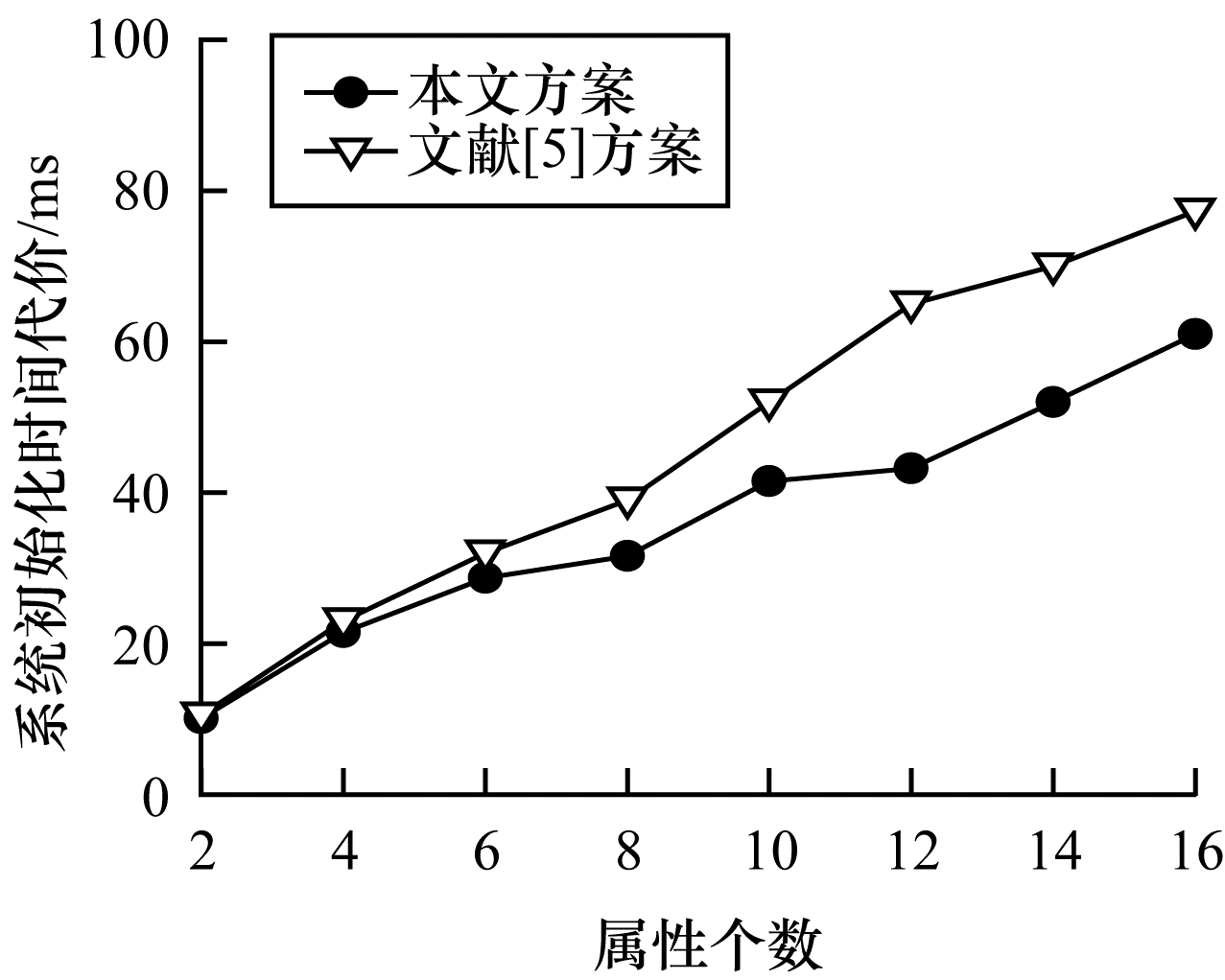
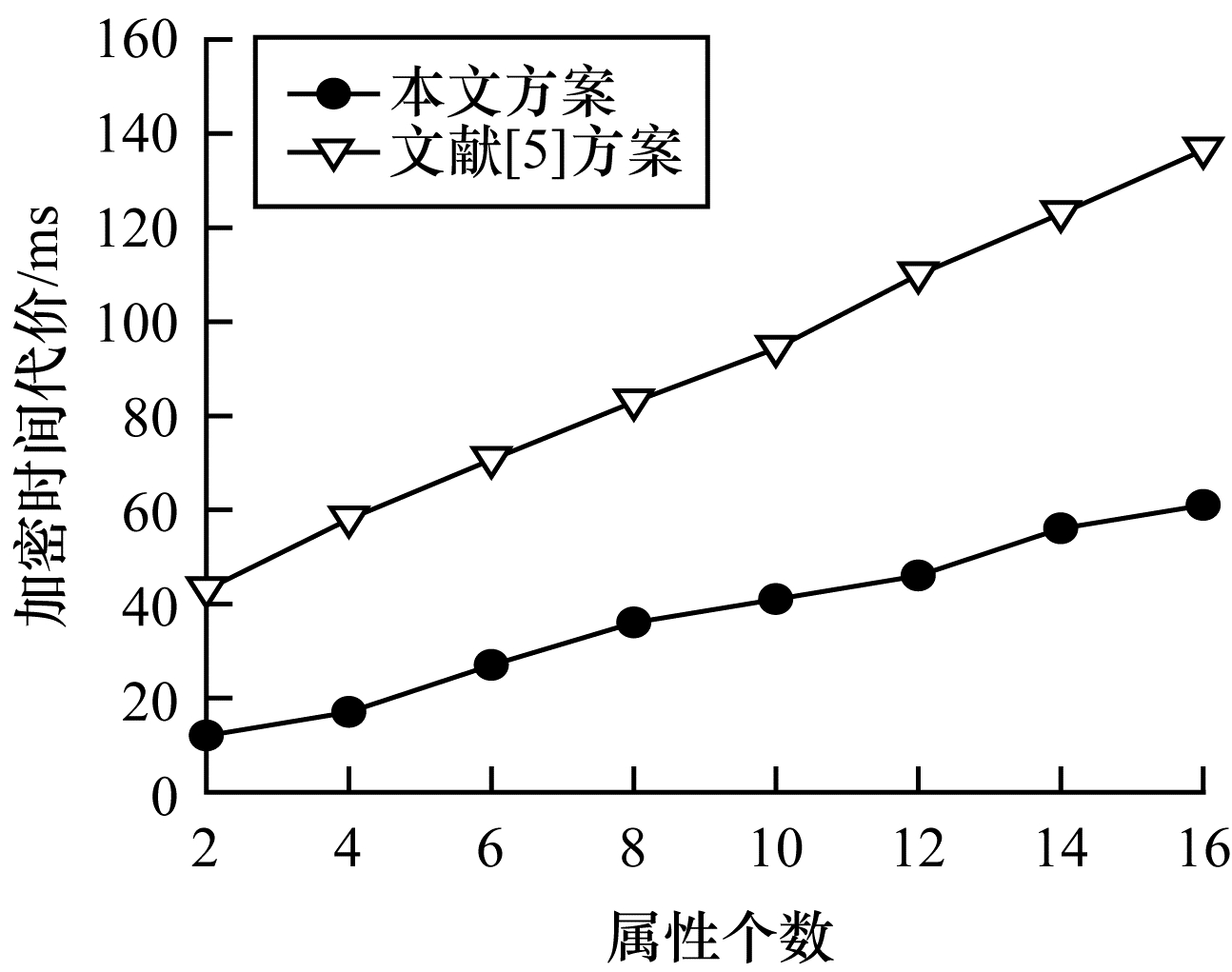
在实验中,明文数据设置为308 Byte。因为本文方案无需进行模指数、双线性映射等复杂运算,仅需要进行加法运算,所以在各阶段的时间代价均明显优于文献[5]方案。
如图 3所示,系统初始化时间与系统属性数量呈线性增长关系。该阶段文献[5]方案时间代价增长率明显大于本文方案,即随着属性数量的增加,本文方案在分布式数据共享和访问控制方面更具优势。
|
Download:
|
| 图 3 不同方案的系统初始化时间 Fig. 3 System initialization time of different schemes | |
如图 4所示,随着系统中属性的不断增加,本文方案中数据拥有者在链下加密所花费的时间明显少于文献[5]的方案,其原因是在以文献[5]方案为代表的传统属性基加密方案中需要复杂的双线性配对运算和指数运算,而本文方案仅需加法运算,因此,将本文LWE-CPABE方案应用于区块链数据共享,将对系统的整体效率有极大的提升。
|
Download:
|
| 图 4 不同方案的加密时间 Fig. 4 Encrypt time of different schemes | |
如图 5所示,在密钥生成阶段,随着属性的不断增加,本文方案明显优于文献[5]的方案,在进行多用户、多属性集合的密钥生成时,本文方案具有更强的实用性。
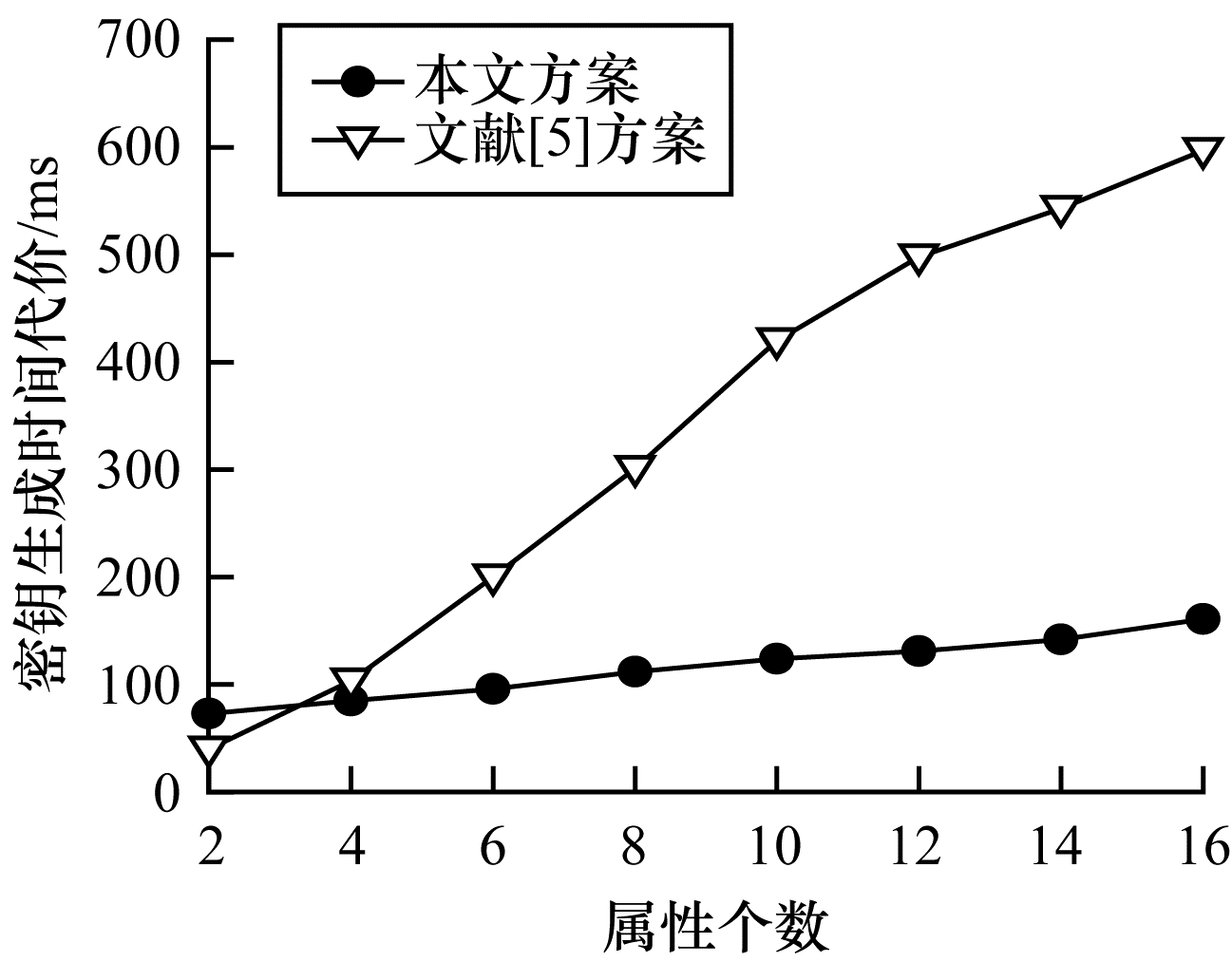
|
Download:
|
| 图 5 不同方案的密钥生成时间 Fig. 5 Key generation time of different schemes | |
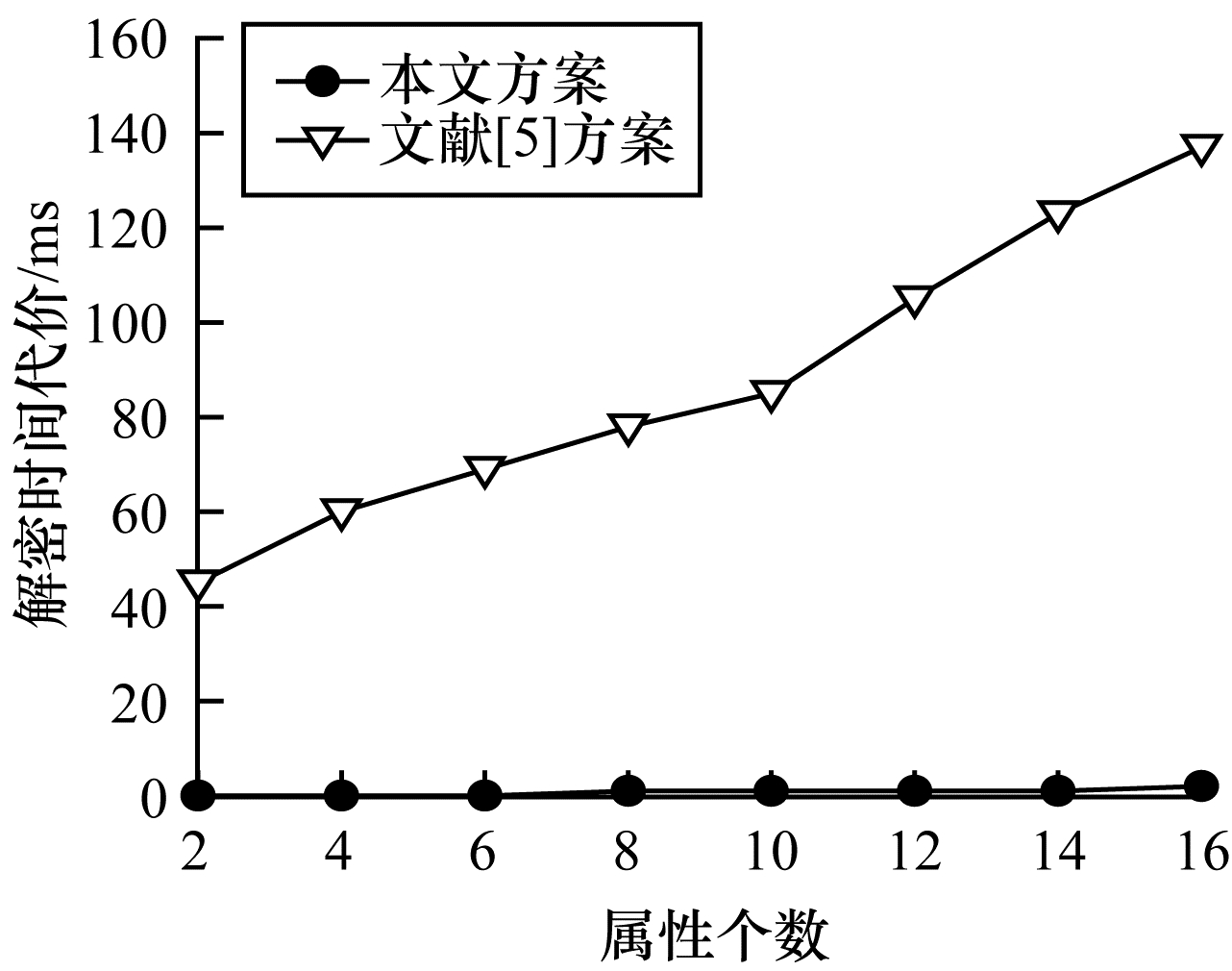
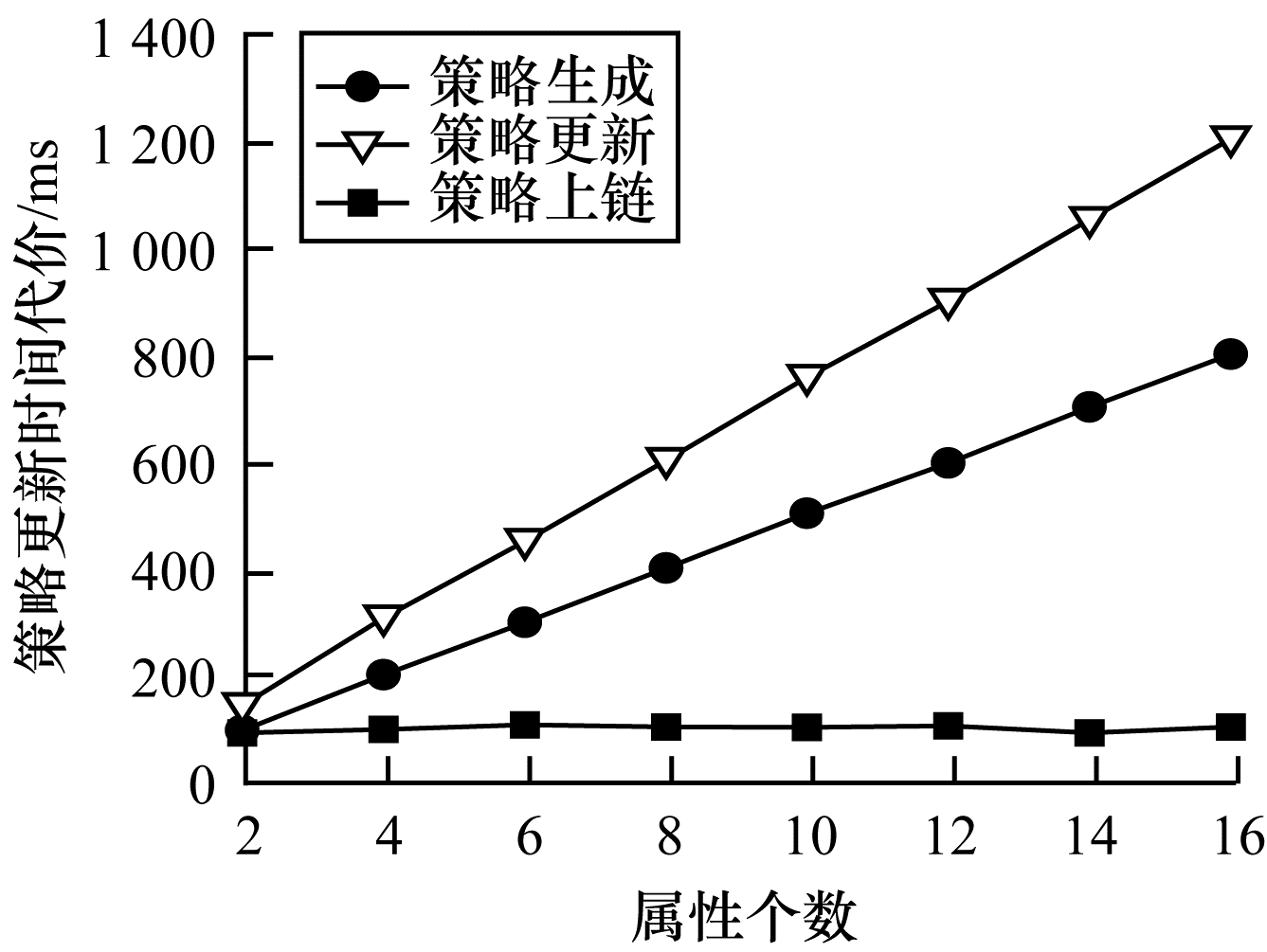
如图 6所示,在解密阶段,本文方案在0~2 ms左右远低于文献[5]方案,对于分布式系统的整体效率有非常大的提升,因此更适合区块链数据共享。为完整模拟整个策略更新过程,本文实验利用1台主机4个节点并采用C++编写的PBFT共识算法对数据流转操作进行模拟。访问控制策略更新过程可分解为策略生成、策略更新和策略上链3个步骤。通过模拟本文算法步骤得到各部分时间代价如图 7所示,当更新算法的属性个数依次为2、4、6、8、12、14和16时,策略生成、更新和上链时间代价总和维持在1 500 ms以内。
|
Download:
|
| 图 6 不同方案的解密时间 Fig. 6 Decrypt time of different schemes | |
|
Download:
|
| 图 7 策略更新时间 Fig. 7 Policy update time | |
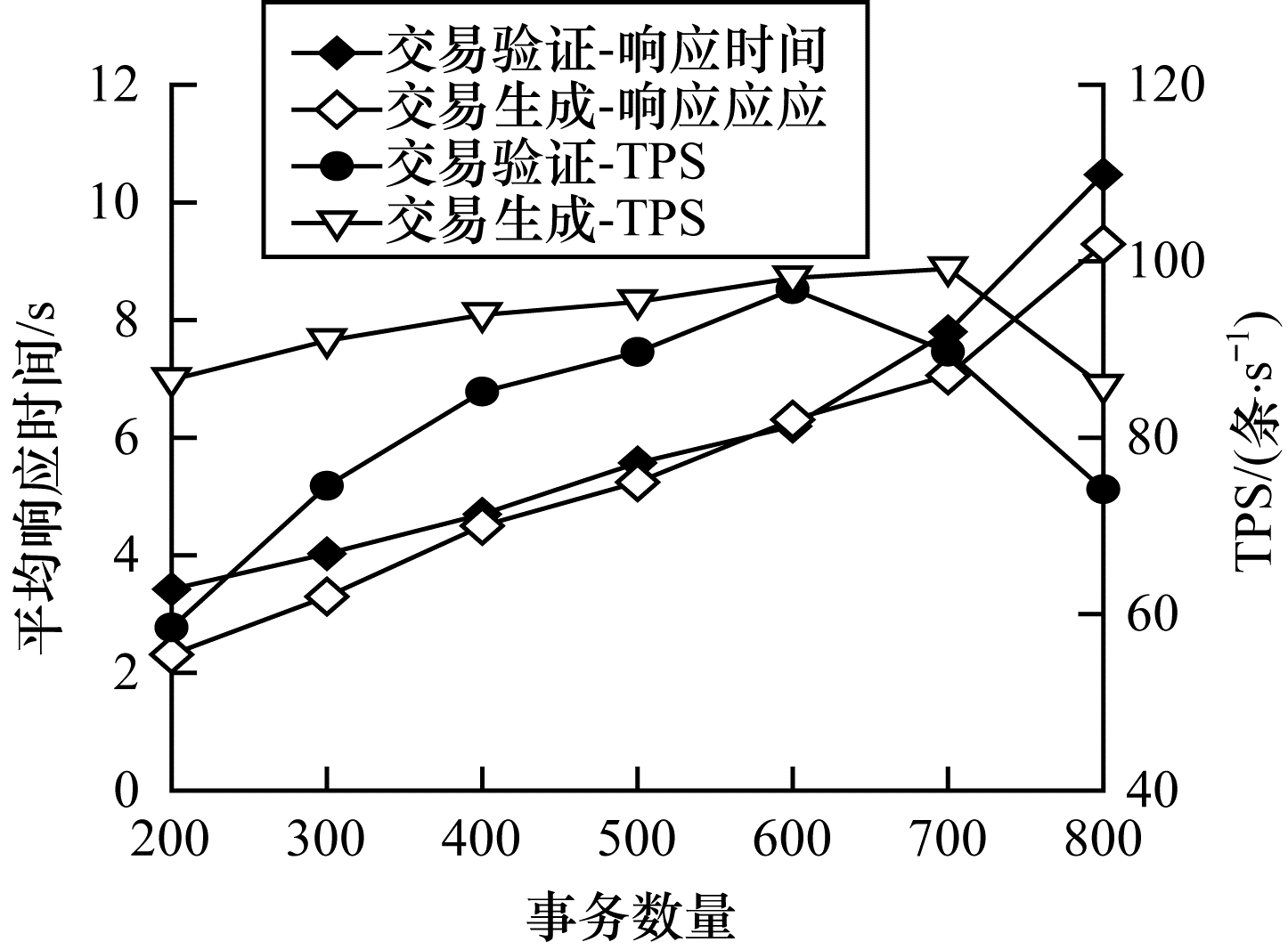
如图 8所示,在模拟交易数量与交易响应时间及TPS的关系时,测试对象为从区块链网络中随机挑选的一个节点,测试内容为调用CITA SDK生成交易与交易信息查询,并发数条件分别为200~800。在性能测试时,单节点保持较高的响应速度和TPS。在400~700并发数下,交易生成和验证时间保持在14 s内,TPS为每秒80条以上。因此,本文方案可以实现区块链上数据访问控制策略的快速更新,且拥有较快的交易生成及验证速度,可以提供高性能的服务。
|
Download:
|
| 图 8 交易平均响应时间与TPS Fig. 8 Average transaction response time and TPS | |
区块链上的隐私保护技术是数据安全共享的重要因素,随着量子计算的快速发展,传统的以数论为基础的公钥密码体系无法抵抗量子攻击。因此,本文将区块链技术与格属性基加密算法有效融合,提出一种基于LWE-CPABE的区块链数据共享方案。通过对CPABE方案进行改进,给出可更新策略的抗量子攻击属性基加密算法,以实现数据的动态保护。在此基础上,设计区块链格式化交易结构实现基于格的CPABE细粒度访问控制,在保证算法抗量子攻击特性的同时,确保过程的可追溯性。实验结果表明,与传统CPABE算法相比,基于格的算法可以明显提升计算速度。下一步将研究区块链上基于LWE-CPABE的分布式密钥生成方案及策略隐藏,以实现更加安全高效的基于属性基加密的分布式数据共享。
| [1] |
黄穗, 陈丽炜, 范冰冰. 基于CP-ABE和区块链的数据安全共享方法[J]. 计算机系统应用, 2019, 28(11): 79-86. HUANG S, CHEN L W, FAN B B. Data security sharing method based on CP-ABE and blockchain[J]. Computer Systems & Applications, 2019, 28(11): 79-86. (in Chinese) |
| [2] |
王秀利, 江晓舟, 李洋. 应用区块链的数据访问控制与共享模型[J]. 软件学报, 2019, 30(6): 1661-1669. WANG X L, JIANG X Z, LI Y. Model for data access control and sharing based on blockchain[J]. Journal of Software, 2019, 30(6): 1661-1669. (in Chinese) |
| [3] |
杨亚涛, 蔡居良, 张筱薇, 等. 基于SM9算法可证明安全的区块链隐私保护方案[J]. 软件学报, 2019, 30(6): 1692-1704. YANG Y T, CAI J L, ZHANG X W, et al. Privacy preserving scheme in block chain with provably secure based on SM9 algorithm[J]. Journal of Software, 2019, 30(6): 1692-1704. (in Chinese) |
| [4] |
田有亮, 杨科迪, 王缵, 等. 基于属性基加密的区块链数据溯源算法[J]. 通信学报, 2019, 40(11): 101-111. TIAN Y L, YANG K D, WANG Z, et al. Algorithm of blockchain data provenance based on ABE[J]. Journal on Communications, 2019, 40(11): 101-111. (in Chinese) DOI:10.11959/j.issn.1000-436x.2019222 |
| [5] |
FAN Y K, LIN X D, LIANG W, et al. TraceChain: a blockchain-based scheme to protect data confidentiality and traceability[J]. Software: Practice and Experience, 2022, 52(1): 115-129. DOI:10.1002/spe.2753 |
| [6] |
WANG H, SONG Y J. Secure cloud-based EHR system using attribute-based cryptosystem and blockchain[J]. Journal of Medical Systems, 2018, 42(8): 152. DOI:10.1007/s10916-018-0994-6 |
| [7] |
ZHANG Y R, HE D B, CHOO K K R. BaDS: blockchain-based architecture for data sharing with ABS and CP-ABE in IoT[J]. Wireless Communications and Mobile Computing, 2018, 18: 1-9. |
| [8] |
SAHAI A, WATERS B. Fuzzy identity-based encryption[C]//Proceedings of Annual International Conference on Theory and Applications of Cryptographic Techniques. Berlin, Germany: Springer, 2005: 457-473.
|
| [9] |
GOYAL V, PANDEY O, SAHAI A, et al. Attribute-based encryption for fine-grained access control of encrypted data[C]//Proceedings of the 13th ACM Conference on Computer and Communications Security. New York, USA: ACM Press, 2006: 89-98.
|
| [10] |
WATERS B. Ciphertext-policy attribute-based encryption: an expressive, efficient and provable secure realization[C]//Proceedings of the 14th International Conference on Practice and Theory in Public Key Cryptography. Washington D. C., USA: IEEE Press, 2011: 53-70.
|
| [11] |
王悦, 樊凯. 隐藏访问策略的高效CP-ABE方案[J]. 计算机研究与发展, 2019, 56(10): 2151-2159. WANG Y, FAN K. Effective CP-ABE with hidden access policy[J]. Journal of Computer Research and Development, 2019, 56(10): 2151-2159. (in Chinese) DOI:10.7544/issn1000-1239.2019.20190343 |
| [12] |
ZHOU Z, HUANG D, WANG Z. Efficient privacy-preserving ciphertext-policy attribute based-encryption and broadcast encryption[J]. IEEE Transactions on Computers, 2015, 64(1): 126-138. DOI:10.1109/TC.2013.200 |
| [13] |
YANGLI C, LINGLING S, GNEG Y. Attribute-based access control for multi-authority systems with constant size ciphertext in clouds[J]. China Communications, 2016, 13(2): 146-162. |
| [14] |
PHUONG T V X, YANG G M, SUSILO W. Hidden ciphertext policy attribute-based encryption under standard assumptions[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(1): 35-45. DOI:10.1109/TIFS.2015.2475723 |
| [15] |
RUJ S, STOJMENOVIC M, NAYAK A. Decentralized access control with anonymous authentication of data stored in clouds[J]. IEEE Transactions on Parallel and Distributed Systems, 2014, 25(2): 384-394. |
| [16] |
BETHENCOURT J, SAHAI A, WATERS B. Ciphertext-policy attribute-based encryption[C]//Proceedings of 2007 IEEE Symposium on Security and Privacy. Washington D. C., USA: IEEE Press, 2007: 321-334.
|
| [17] |
OKAMOTO T, TAKASHIMA K. Fully secure unbounded inner-product and attribute-based encryption[C]//Proceedings of Advances in Cryptology-ASIACRYPTʼ12. Washington D. C., USA: IEEE Press, 2012: 349-366.
|
| [18] |
GORBUNOV S, VAIKUNTANATHAN V, WEE H. Attribute-based encryption for circuits[C]//Proceedings of the 45th Annual ACM Symposium on Theory of Computing. New York, USA: ACM Press, 2013: 545-554.
|
| [19] |
HOHENBERGER S, WATERS B. Online/offline attribute-based encryption[C]//Proceedings of International Conference on Theory and Application of Cryptology. New York, USA: ACM Press, 2014: 293-310.
|
| [20] |
ROUSELAKIS Y, WATERS B. Practical constructions and new proof methods for large universe attribute-based encryption[C]//Proceedings of 2013 ACM SIGSAC Conference on Computer & Communications Security. New York, USA: ACM Press, 2013: 463-474.
|
| [21] |
AJTAI M. Generating hard instances of lattice problems [C]//Proceedings of STOCʼ96. Washington D. C., USA: IEEE Press, 1996: 99-108.
|
| [22] |
REGEV O. On lattices, learning with errors, random linear-codes, and cryptography[J]. Journal of the ACM, 2009, 48(5): 1-40. |
| [23] |
钱心缘, 吴文渊. 基于R-SIS和R-LWE构建的IBE加密方案[J]. 计算机科学, 2021, 48(6): 315-323. QIAN X Y, WU W Y. Identity-based encryption scheme based on R-SIS/R-LWE[J]. Computer Science, 2021, 48(6): 315-323. (in Chinese) |
| [24] |
周艺华, 董松寿, 杨宇光. 标准模型下基于格的身份代理部分盲签名方案[J]. 信息网络安全, 2021, 21(3): 37-43. ZHOU Y H, DONG S S, YANG Y G. A lattice-based identity-based proxy partially blind signature scheme in the standard model[J]. Netinfo Security, 2021, 21(3): 37-43. (in Chinese) |
| [25] |
张彦华, 胡予濮, 刘西蒙, 等. 格上本地验证者撤销属性基群签名的零知识证明[J]. 电子与信息学报, 2020, 42(2): 315-321. ZHANG Y H, HU Y P, LIU X M, et al. Zero-knowledge proofs for attribute-based group signatures with verifier-local revocation over lattices[J]. Journal of Electronics & Information Technology, 2020, 42(2): 315-321. (in Chinese) |
| [26] |
DATTA P, KOMARGODSKI I, WATERS B. Decentralized multi-authority abe for DNFs from LWE[C]//Proceedings of Advances in Cryptology-EUROCRYPTʼ21. Washington D. C., USA: IEEE Press, 2021: 145-158.
|
 2022, Vol. 48
2022, Vol. 48

 ,
,