开放科学(资源服务)标志码(OSID):
交通标志识别是智能交通系统(Intelligent Traffic System,ITS)的主要研究内容,也是计算机视觉道路应用的重要组成部分。交通标志识别算法通常包括特征提取和分类器。随着图像识别领域的快速发展,卷积神经网络(Convolutional Neural Network,CNN)被广泛应用于交通图像特征的提取,相比传统算法中的人工特征提取,具有较优的图像识别性能。
文献[1]提出基于图模型与CNN的交通标志识别算法,根据提取过程中的多级信息,实现对目标图像内部精细特征的学习。文献[2]通过对LeNet-5网络结构进行改进,减少冗余信息并添加多层融合结构,从而提高算法的实时性和特征表达能力。文献[3]提出一种基于局部背景的Faster R-CNN来识别交通标志图像中的小目标。为提高算法的实用性和识别精度,研究人员提出多种基于多尺度特征的方法。文献[4]提出基于Faster R-CNN模型改进的多路特征识别模型,通过图像预处理提高模型的适应能力。文献[5]训练适应于不同尺寸图像的CNN并构建融合模型,该方法能够有效提取多尺度特征。文献[6]融合网络不同层级的特征信息,以提高对低层特征的利用率,模型在德国交通标志识别(GTSRB)数据集上的识别率达到99.25%。
在上述算法中用于特征提取的网络都是基于专家经验改进的网络模型,需要复杂的模型调参过程。图像预处理是多尺度特征提取算法中的重要步骤,以获得更优的识别性能。然而,交通标志图像数据一旦出现任何更改,则导致整体训练过程重复,需要大量的处理时间。此外,在网络模型设计过程中网络深度对识别性能的影响并未引起研究人员的重视。受移动端平台硬件水平的限制,在保证分类性能的同时设计更加轻量化的网络模型成为研究热点。
进化神经架构是一种自动化设计网络模型的方法[7-8]。由于进化算法(Evolutionary Algorithms,EAs)不依赖于优化对象的梯度信息,因此可以解决复杂、非线性、不可微、多模态的优化问题,被广泛应用于优化神经网络的权值、架构和学习规则[9-10]。进化神经架构将网络的基本模块和参数嵌入到进化算法中,设计架构的生成方式,并使用变异、交叉和选择等遗传算子对网络模型进行优化搜索。文献[11]设计包括层、连接等简单的初始化条件,仅使用变异算子进化出用于解决大规模图像分类问题的CNN,具有与专家设计网络相近的分类性能。为实现架构的高效搜索,文献[12-13]设计基于块的初始化空间,能够自动设计用于图像分类的网络架构,同时极大减少了进化搜索所需的计算量。针对进化神经网络架构计算量较大的问题,文献[14-15]训练端到端代理机制进行适应度评估,以代替进化过程中对所有网络的训练和测试评估。文献[16]采用抽样训练和节点继承策略,种群中的个体共享一个网络的训练周期并将权值遗传给后代,大幅提高了进化搜索的效率。文献[17]设计进化稠密网络,在车辆图像数据集上具有较优的分类性能。
本文提出基于进化ResNet的交通标志识别算法。将提取ResNet的基础块嵌入到进化算法中,构建以残差块为单位的个体初始化空间,利用交叉、变异等遗传算子,确保进化搜索的有效性,同时将网络深度作为可变参数,搜索网络的最佳深度,在确保识别精度的前提下设计轻量化的网络。
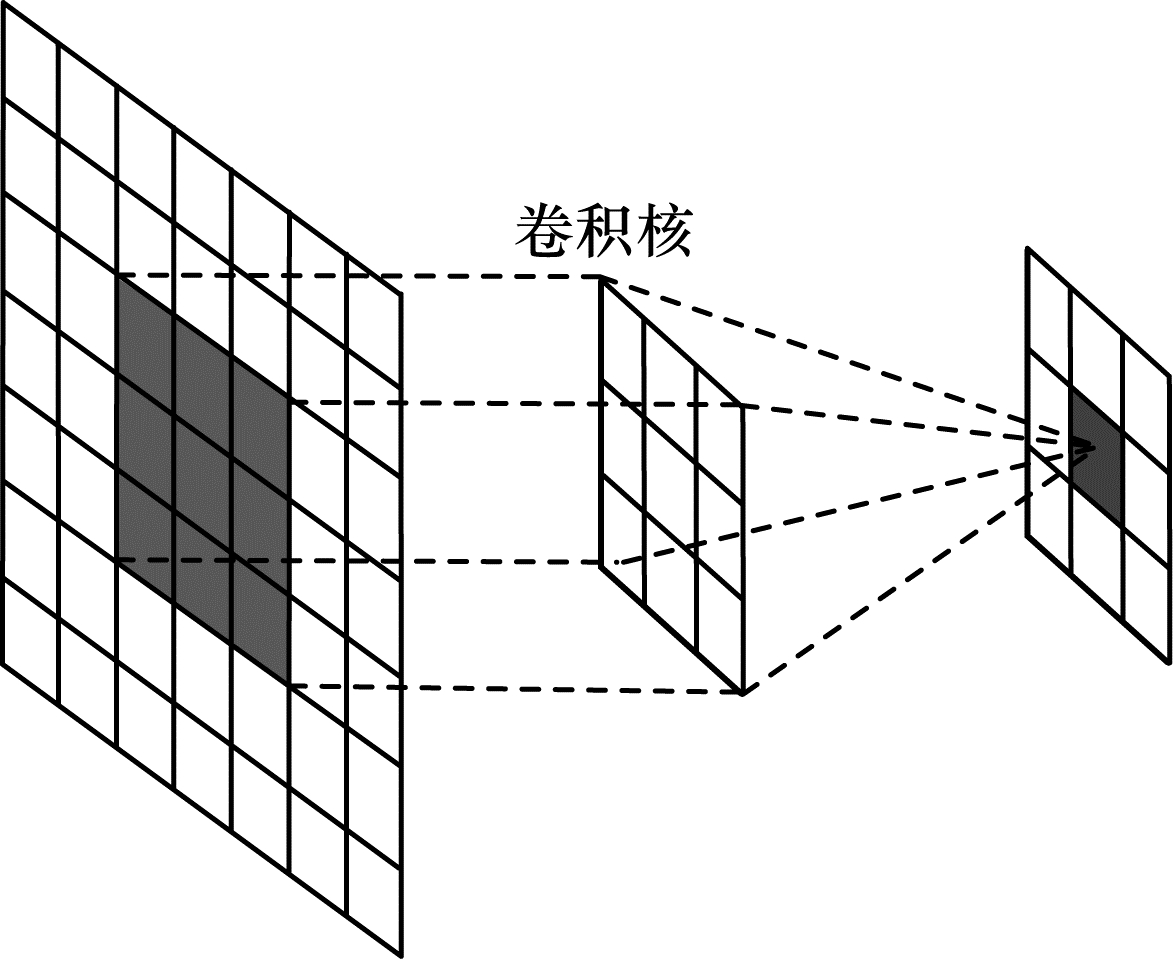
1 相关工作 1.1 卷积神经网络卷积神经网络主要由卷积层、池化层和全连接层构成。卷积操作过程如图 1所示,将卷积核滑动到二维图像上的所有位置,在每个位置上进行内积运算,从而提取图像特征。卷积层的主要参数包括卷积核尺寸、个数(特征图数)和滑动步长。在深层卷积神经网络中,不同的卷积核提取不同的图像特征,经过多次卷积操作提取复杂的底层特征。
|
Download:
|
| 图 1 卷积操作过程 Fig. 1 Convolution operation process | |
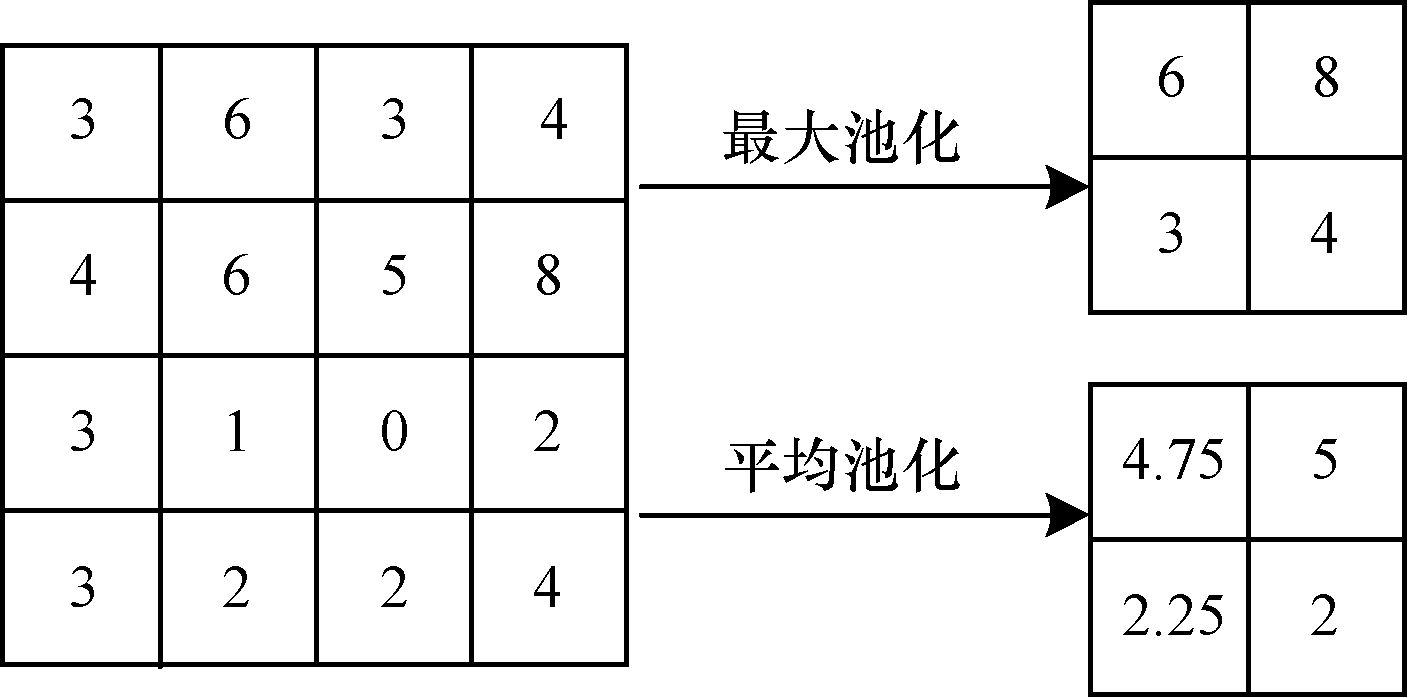
池化是一种非线性下采样方式,主要作用是减少网络参数,进而降低计算量,并在一定程度上避免过拟合现象的发生。池化层通常位于卷积层的后面,主要包括最大池化和平均池化,分别选取池化域内特征点的最大值或平均值,并将其作为该邻域的池化值。最大池化与平均池化操作过程如图 2所示(池化步长为2)。
|
Download:
|
| 图 2 最大池化与平均池化操作过程 Fig. 2 Operation process of maximum pooling and mean pooling | |
全连接层通过将前一层的输出连接到所有节点,用于把提取到的特征图线性展开,并输入到非线性变换Sigmoid函数中进行分类或回归操作,通常位于网络结构的末端。
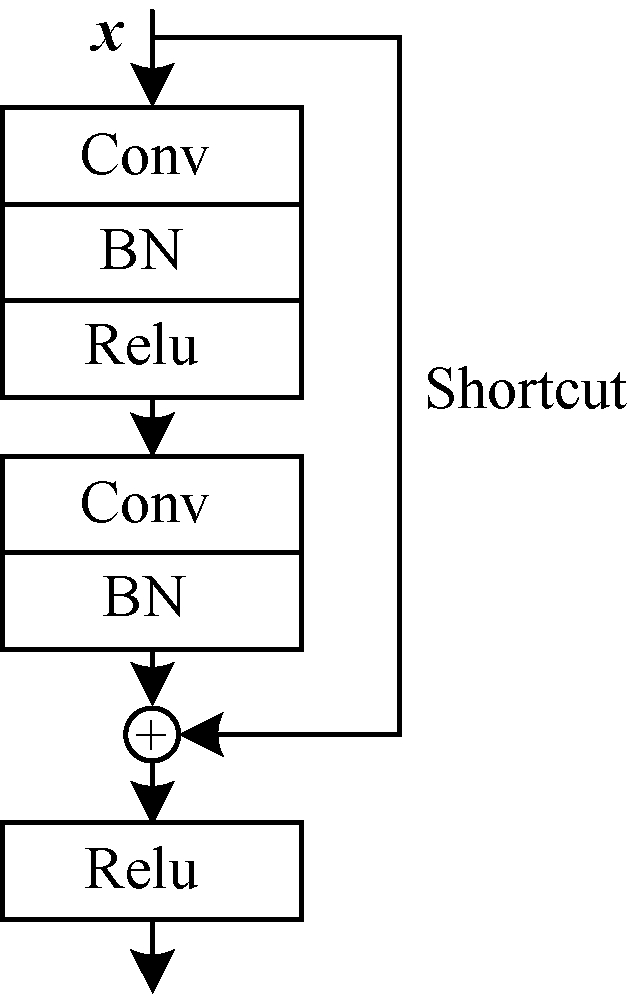
1.2 残差网络文献[18]提出残差网络(ResNet),通过残差块结构训练152层的神经网络,在top5上的错误率仅为3.57%,同时参数量较少。一个标准残差块结构如图 3所示。
|
Download:
|
| 图 3 残差块结构 Fig. 3 Residual block structure | |
卷积过程如式(1)所示:
| $ y^k=f\left(\sum \boldsymbol{w}^k \times \boldsymbol{x}^{k-1}+\boldsymbol{b}^k\right) $ | (1) |
其中:f(·)为激活函数;k为网络层数;w为权重;b为偏置项;y为输出特征。为解决在深度神经网络训练过程中性能不稳定和收敛困难的问题,批量归一化将输入特征转换为正态分布,并引入学习参数
| $ \mathrm{B}{\mathrm{N}}_{\gamma , \beta }\left({\widehat{\boldsymbol{x}}}_{i}\right)=\gamma {\widehat{\boldsymbol{x}}}_{i}+\beta $ | (2) |
| $ {\widehat{\boldsymbol{x}}}_{i}=\frac{{x}_{i}-\stackrel{-}{\boldsymbol{x}}}{\sqrt{{\sigma }_{x}^{2}-a}} $ | (3) |
其中:输入特征向量x = {x1,x2,…,xn};
残差块通过跳跃连接增加一个恒等映射,如式(4)所示:
| $ H(\boldsymbol{x})=F(\boldsymbol{x})+\boldsymbol{x} $ | (4) |
残差块将输入信息x加入到特征计算过程中,即在特征提取过程中结合上一层网络提取的特征信息。其中,跳跃连接将残差块的输入和输出进行一个简单的元素级叠加,在不增加额外参数和计算量的前提下,能够有效解决深层结构网络训练过程中的退化问题,加快模型的训练速度,提升训练效果。
1.3 进化算法进化算法是一种受自然进化启发的优化算法,不依赖于优化对象的梯度信息,具有智能性和并行性特点,可以解决复杂、非线性、不可微、多模态的优化问题。因此,EAs在神经网络的权值、架构和学习规则等优化问题中具有一定的研究范围。
进化算法包括参数编码、初始化种群、适应度评估、遗传算子和控制参数5个要素。进化算法用基因模式表示系统结构,参数编码将个体表示为长度为L的染色体I={I1,I2,⋯,IL},在第N位基因上存在一系列等位基因In={in1,in2,⋯,ink},n=1,2,⋯,L,k表示第n位等位基因的数量,所有等位基因的组合构成搜索空间,如式(5)所示:
| $ \mathit{\Phi} ={I}_{1}\times {I}_{2}\times \cdots \times {I}_{l}=\prod\limits _{i=1}^{l}{i}_{n} $ | (5) |
Φ是可能存在的个体最大空间,算法中种群空间一般为Φ的真子集。P(t)表示处于t阶段的种群,E(t)表示目标环境提供的信息,在适应计划τt作用下生成新的种群,如式(6)所示:
| $ P(t+1)={\tau }_{t}\left(P\right(t), E(t\left)\right) $ | (6) |
在进化算法的适应过程中,初始种群由一组随机生成基因编码的个体组成,根据适应度大小对个体进行排序选择,经过选择、交叉、变异等进化操作,适应度较差的个体被淘汰。变异算子搜索新的等位基因,而交叉算子将个体的不同基因以新的方式相结合。进化后的新一代群体质量得到提高,经过多次迭代,逐步提高种群中个体的整体性能。
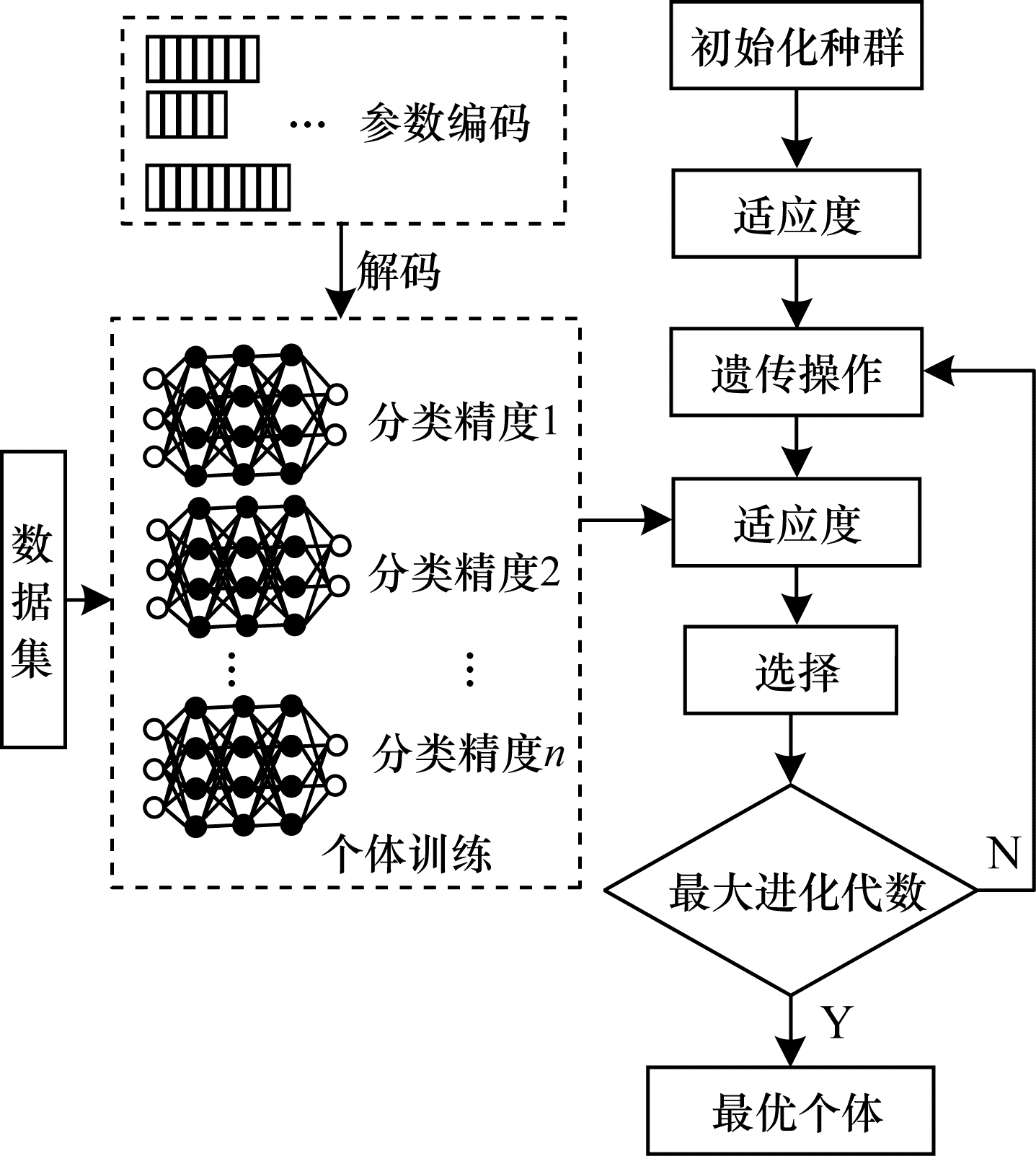
2 进化ResNet算法进化ResNet算法从初始化种群开始,采用初始化方式随机生成一系列代表不同架构的个体,将个体的代码解码成相应的网络后进行适应度评估,然后根据适应度选择父代个体进行交叉、变异等遗传操作后产生子代个体,再经过环境选择产生新一代种群。这个过程反复迭代直到满足预定的最大进化代数,最后在种群中选择适应度最高的个体作为优化架构。进化ResNet算法流程如图 4所示。在进化过程中,适应度评估只训练新生成的个体模型,包括初始种群和遗传操作后产生的新个体,对于已经训练过的模型,直接加载训练数据作为其适应度。
|
Download:
|
| 图 4 进化ResNet算法流程 Fig. 4 Procedure of evolutionary ResNet algorithm | |
初始化种群需要定义参数编码和初始化方式,其中,参数编码是指在架构搜索空间中可变参数的编码方式。本文提出的进化ResNet算法的网络模型主要由输入层、残差块、池化层和全连接层构成。进化ResNet算法的可变参数设置如表 1所示。

|
下载CSV 表 1 进化ResNet算法的可变参数设置 Table 1 Variable parameters setting of evolutionary ResNet algorithm |
可变模块包括残差块、最大池化层和平均池化层。残差块由特征图数量编码为c1_c2两个卷积层组成,范围为{64,128,256}。卷积层的滤波器和步长分别设置为3×3和1×1,将步长设置为1×1是为了保持输入数据的维数不变,并使架构搜索更加灵活。池化层由数字编码范围是[0, 1]的池化类型组成,其中,介于[0,0.5]之间的数字表示最大池化,[0.5,1]之间的数字表示平均池化。池化层的内核大小和步长设置为2×2。
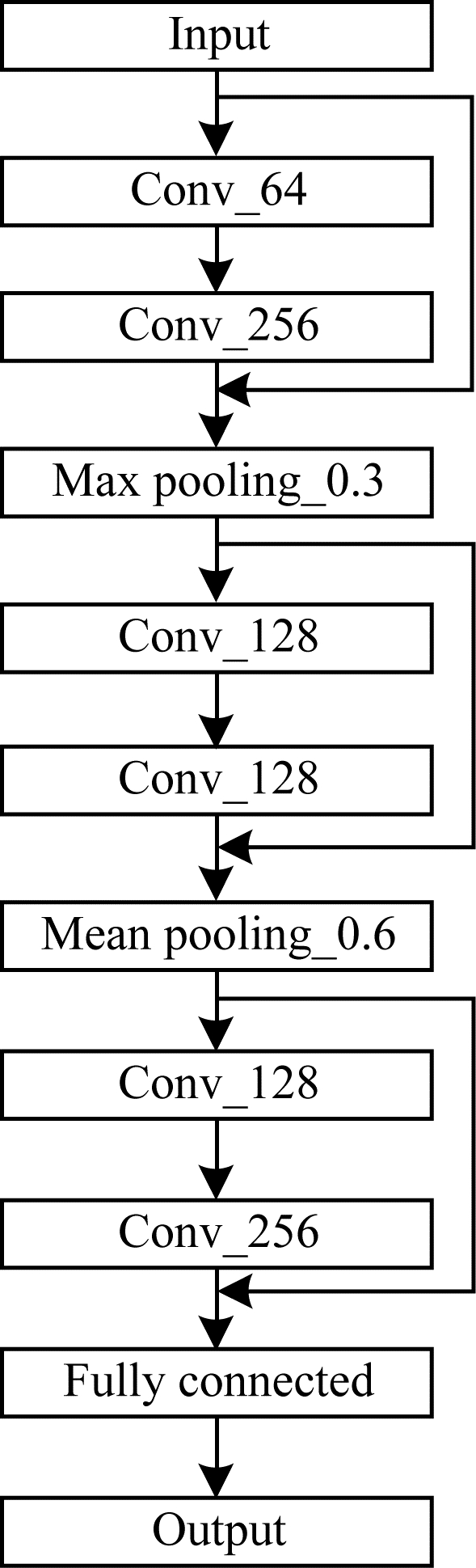
在初始化过程中,进化ResNet算法将网络深度作为可变参数,以搜索网络模型的最佳深度,在预定的长度范围内生成一个随机数作为架构的长度L,创建包含L个节点的列表,然后根据节点类型加载参数编码,最后搭建完整网络架构。在初始化种群中随机架构如图 5所示。该架构包含3个卷积块和2个池化块,全连接层固定在个体尾部,编码是“64-256-0.3-128-128-0.6-128-256”。
|
Download:
|
| 图 5 在初始化种群中随机架构示例 Fig. 5 Example of random architecture in initialized population | |
适应度是通过评估群体中个体的优劣,指导进化算子搜索重要参数。在适应度评估中,每个基因型被解码成相应的网络模型,在训练集上通过随机梯度下降(Stochastic Gradient Descent,SGD)算法进行训练,权值更新过程如式(7)和式(8)所示:
| $ {w}_{i}={{w}_{i}}_{{}_{\mathrm{o}\mathrm{l}\mathrm{d}}}-r\frac{\partial J(\boldsymbol{w}, \boldsymbol{b})}{\partial {w}_{t}} $ | (7) |
| $ \frac{\partial J(\boldsymbol{w}, \boldsymbol{b})}{\partial {w}_{t}}=\left[\frac{1}{m}\sum\limits _{m}\left(\frac{\partial J(\boldsymbol{w}, \boldsymbol{b};{x}_{m}, {y}_{m})}{\partial {w}_{t}}\right)\right]+\beta {w}_{t} $ | (8) |
其中:J(w,b;xm,ym)为单个样例计算得到的方差代价函数;w为权值矩阵;b为偏置矩阵;(xm,ym)为第m个样例的标记数据;r为学习速率;
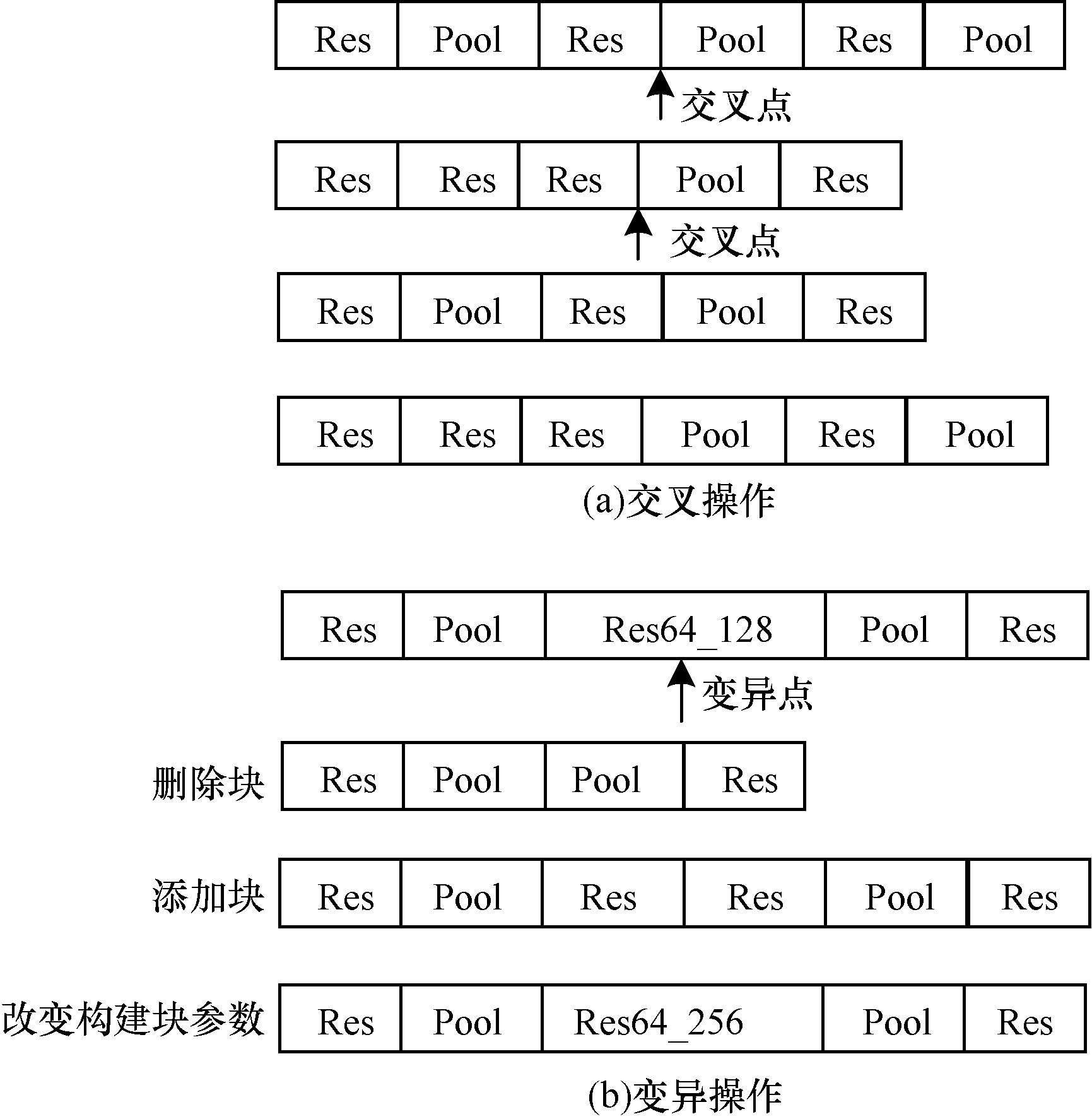
遗传算子包括交叉和变异,直接决定了后代的生成,即在进化过程中可以搜索到网络架构。遗传算子的操作过程如图 6所示。
|
Download:
|
| 图 6 遗传算子的操作过程 Fig. 6 Operation process of genetic operators | |
在交叉操作过程中,首先选择两个父代个体,根据预定义的交叉率决定是否执行交叉操作。在执行过程中,随机选择位于每个父代个体上的交叉点,然后在该点相互交换两个个体的部分基因。若不执行交叉操作,这两个父代个体将被直接放入到子代种群中。
在变异操作过程中,根据预定义的变异率选择部分个体,然后从个体的构建块中随机选择变异点执行变异操作。变异操作包括删除块、添加块和改变构建块参数。对于残差块,参数更改是指更改卷积层特征图的数量。池化层的参数更改即为改变池化类型。
2.4 环境选择本文在环境选择过程中,根据遗传算法中的锦标赛选择策略,使用二进制锦标赛法来选择下一代种群。该方法主要分为3个步骤:1)从父代和子代个体中随机选择两个个体,每个个体被选择的概率相等;2)根据个体的适应度,选择较优的个体进入下一代种群;3)重复该过程数次(重复次数为种群大小),直到新种群的大小等于原始种群的大小。
3 实验结果与分析 3.1 实验平台与参数设置本文实验所用的计算机配置是Intel core i9-9900kf处理器,使用2个NVIDIA GeForce RTXs显卡加速计算,操作系统为Ubuntu18.04,深度学习框架为Pytorch,软件编程环境为Python3.7。本文将识别准确率KAcc作为评价架构性能的主要指标,如式(9)所示:
| $ {K}_{\mathrm{A}\mathrm{c}\mathrm{c}}=\frac{\sum\limits _{i=1}^{N}{n}_{i}}{N}\times 100\mathrm{\%} $ | (9) |
其中:ni表示识别正确的样本;N表示测试的样本总量。本文实验参数设置如表 2所示。

|
下载CSV 表 2 本文实验参数设置 Table 2 Parameter settings of the proposed experiment |
本文在GTSRB数据集[20]上进行实验。该数据集是在IJCNN2011图像分类挑战赛上由INIRTCV组织建立。该数据集图像截取于在驾驶场景中车载高清摄像头拍摄的视频,共包含43类交通标志,如图 7所示。其中,训练集有39 209幅,测试集有12 630幅,总计51 839幅图像。样本图像包含10%的标记区域及其周围区域,大小为(15×15)~(250×250)像素。受自然场景光照、图片采集角度变化、人为涂抹污染等诸多条件的影响,图像质量参差不齐。该数据集可以检验交通标志图像识别算法的实时性与鲁棒性。

|
Download:
|
| 图 7 GTSRB数据集的43类交通标志 Fig. 7 43 types of traffic signs in the GTSRB dataset | |
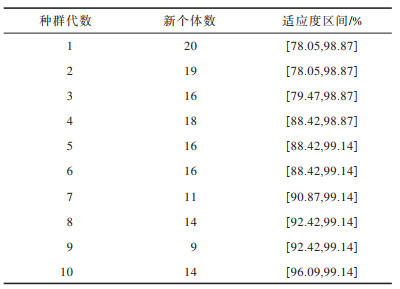
进化ResNet算法经过交叉、变异和选择等遗传操作,共消耗6 h 45 min,搜索到153种网络架构并对其进行性能评估。153种网络架构在种群中的分布及每一代种群的个体适应度区间如表 3所示。
|
下载CSV 表 3 种群个体分布 Table 3 Distribution of population individuals |
种群个体在第5代时的最高适应度由98.87%提升到99.14%,并一直持续到进化过程结束。种群个体的最低适应度由78.05%提升到96.09%,表明种群个体的整体适应度不断提升,而此时种群中产生的新个体数保持稳定,说明本文的进化ResNet算法搜索到更多性能较优的网络架构,同时验证了最优架构在进化过程中的稳定性。
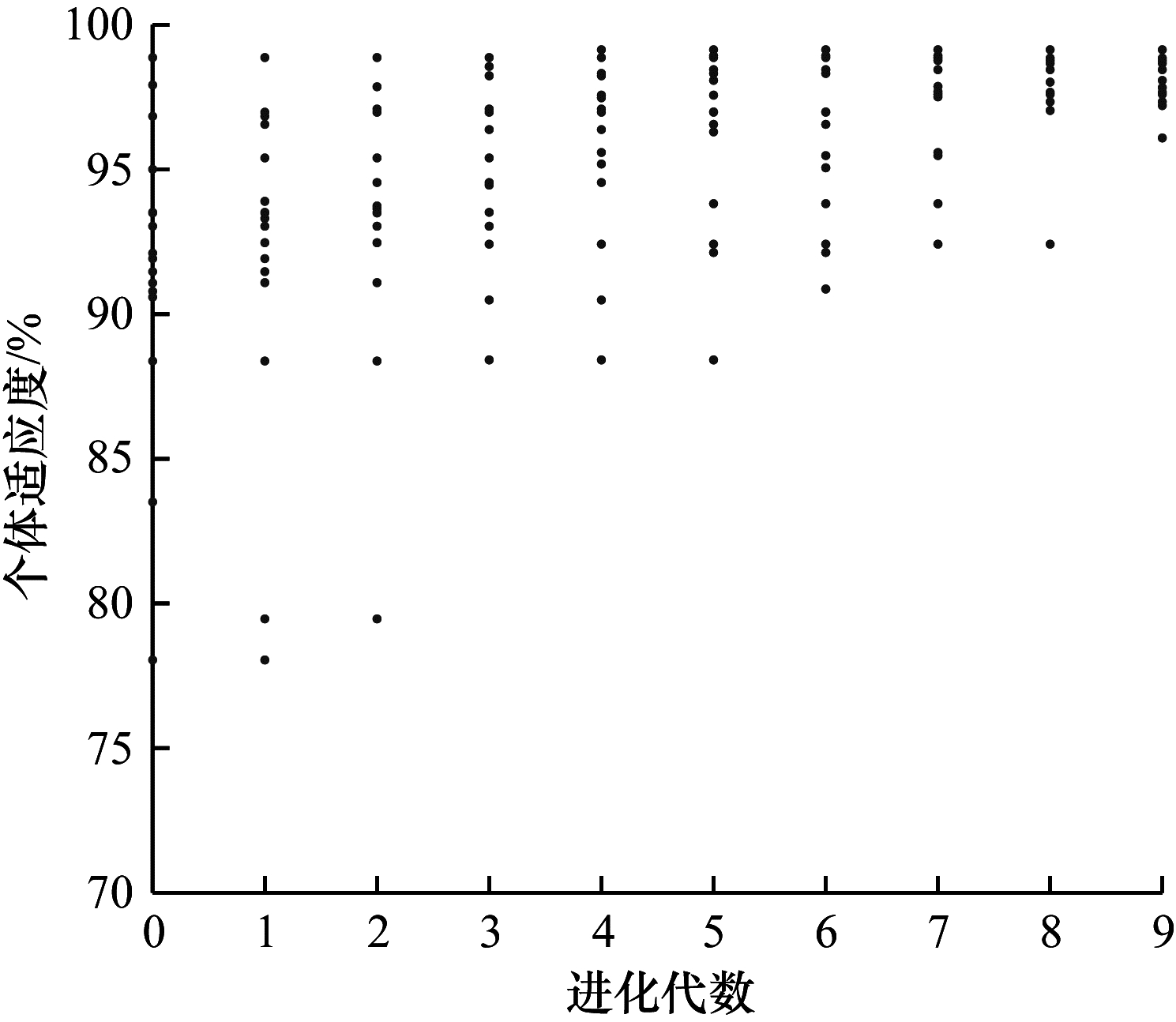
为了更好地理解进化过程中的细节,在GTSRB数据集上进化ResNet算法的进化轨迹如图 8所示。
|
Download:
|
| 图 8 进化ResNet算法的进化轨迹 Fig. 8 Evolutionary trajectory of evolutionary ResNet algorithm | |
从图 8可以看出,随着进化代数的增加,种群中个体的分类精度向高精度方向聚拢,验证了进化搜索中遗传算子的有效性。最佳分类精度随着进化轨迹的进行而增加,但相对平稳,这表明基于构建块的网络架构生成方式可以确保设计架构的有效性。进化的终止条件是进化代数,虽然进化算法搜索到了具有较优分类性能的个体,但是无法在适应度评估过程中确保搜索到的架构是全局最优。本文实验的最优个体在进化结束之前就已产生。
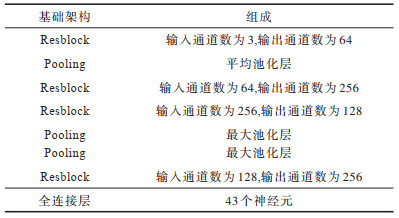
3.4 进化ResNet算法的识别效果分析本文选取最后一代种群中适应度最高的个体作为进化设计的最优架构。进化ResNet算法的基础架构组成如表 4所示。残差网络共包含7个基础块,其中4个残差块和3个池化层,最后连接全连接层进行分类操作。
|
下载CSV 表 4 进化ResNet算法的基础架构组成 Table 4 Infrastructure composition of evolutionary ResNet algorithm |
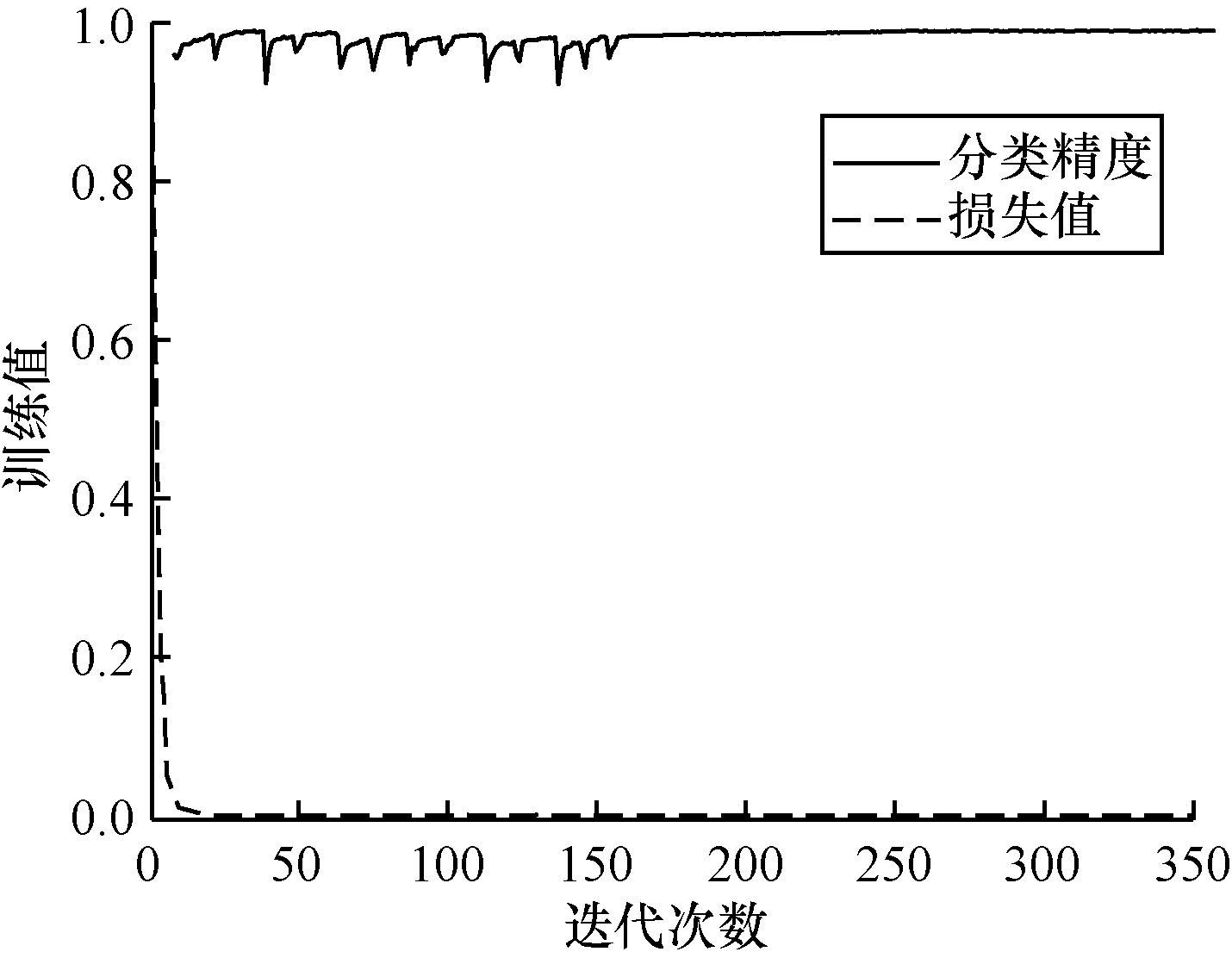
本文用GTSRB对进化ResNet算法生成的架构进行重新训练,使用随机梯度下降算法进行参数更新,调整3段学习率,初始学习率为0.1。当epoch次数大于148时,学习率设置为0.01;当epoch次数大于248时,学习率设置为0.001。进化ResNet算法生成架构模型的分类精度和测试损失值变化曲线如图 9所示。随着迭代次数的不断增加,模型的损失值在前几次迭代过程中快速降低后趋于平稳,表明模型的学习能力逐渐下降。分类精度在学习前期快速增长后不断波动,在迭代次数为148以后趋于平稳,达到了99.41%。
|
Download:
|
| 图 9 本文模型训练曲线 Fig. 9 Training curves of the proposed model | |
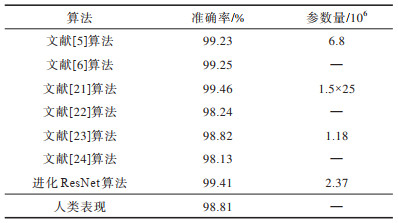
在GTSRB数据集上不同算法的准确率与参数量对比如表 5所示。对比算法的实验结果来自相关参考文献中提供的数据。表 5中文献[21]Multi-column DNN的算法是由25个CNN组成的多纵CNN模型。文献[22]使用基于优化卷积神经网络和支持向量机分类的模型(Conv + GLP + BN + SVM)。文献[5-6, 23-24]是4种基于多尺度特征改进的特征提取模型,其中,文献[6, 23]使用全连接层进行分类,文献[5, 24]使用极限学习机分类,以加快分类速度。在多尺度特征提取过程中,文献[6]MFC算法融合网络中不同层级所产生的单尺度特征,提高了对单尺度卷积神经网络中低层特征的利用率。文献[24]MFC+ELM算法通过在特征提取过程中增加多尺度池化操作,提高了特征提取的鲁棒性。文献[5]MFC+ELM算法训练3种适应于不同尺寸图像的网络模型,然后将3个训练网络的参数级联到融合模型的全连接层。同时,文献[23]MFC算法采用限制对比度自适应直方图均衡化方法优化图像质量。
|
下载CSV 表 5 不同算法的准确率和参数量对比 Table 5 Accuracy and parameter quantity comparison among different algorithms |
从表 5可以看出,本文进化ResNet算法的识别准确率优于人类表现,超过了其他5种基于CNN的改进算法,而略低于Multi-column DNN算法中99.46%的识别准确率。文献[22]基于CNN使用批量归一化,逐层贪婪预训练和支持向量机的改进算法,未达到人类表现的准确率。文献[23]MFC算法的准确率与人类表现相近。文献[5]中MFC+ELM算法是基于多尺度特征的方法取得了较大的性能提升,但本文进化ResNet算法在参数量上较该模型减少了4.43×106,网络模型更轻量化。虽然文献[21]Multi-column DNN算法中多纵卷积神经网络模型的识别准确率最高,但是该方法由25个网络组成,需要大量的预处理操作,在4个GPU同时计算下需要37 h才能完成模型的训练任务。因此,本文进化ResNet算法具有更优的整体性能。
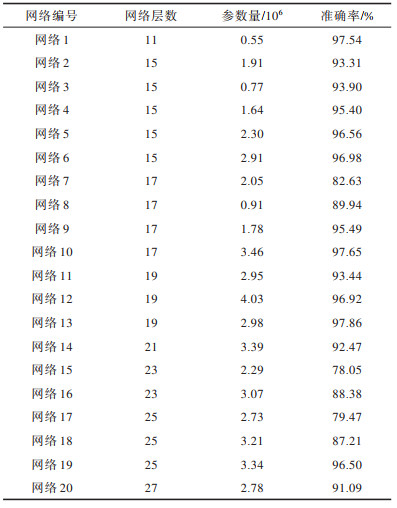
3.6 网络深度与性能对比本文将网络深度作为可变参数,在进化过程中自适应搜索最优的网络深度。为对比不同深度的网络参数和识别准确率,表 6所示为第一代种群中20个不同网络的层数(残差块计算为两层卷积)和分类性能,并按照网络层数递增顺序排序。
|
下载CSV 表 6 第一代种群中20个不同网络的参数量与准确率对比 Table 6 Parameter quantity and accuracy comparison among 20 different networks in the first generation population |
从表 6可以看出,随着网络层数的递增,识别准确率并不呈递增关系。准确率达到97%以上的网络层数为11、17和19(对应网络编号分别为网络1、网络10和网络13)的参数量分别为0.55×106、3.46×106和2.98×106。准确率低于80%的网络层数23和25(对应网络编号为网络15和网络17)的参数量分别为2.29×106和2.73×106。
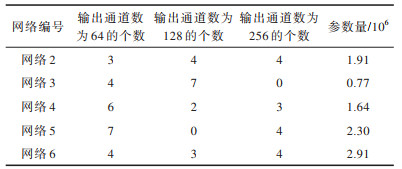
为进一步分析网络性能和架构与参数量的关系,本文分别统计网络层数为15的架构参数。网络2~网络6中15层网络的残差块输出通道数与网络参数量对比如表 7所示。
|
下载CSV 表 7 15层网络残差块的输出通道数与参数量对比 Table 7 Comparison of the number of output channel and parameter quantity of the 15 layers network residual block |
从表 7可以看出,在性能递增的情况下,网络3~网络6的参数量呈递增关系。网络的参数量主要取决于卷积层,其参数量计算如式(10)所示:
| $ \mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}={C}_{o}\times \left({k}_{w}\times {k}_{h}\times {C}_{i}+1\right) $ | (10) |
其中:Co表示输出通道数;Ci表示输入通道数;kw和kh表示卷积核宽和核高。
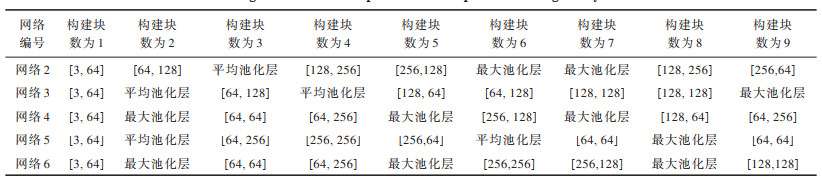
网络2的残差块具有4个256和128通道数,卷积核数量较多,因此,网络参数量较大。15层网络构建块的顺序与参数对比如表 8所示。
|
下载CSV 表 8 15层网络构建块的顺序与参数对比 Table 8 Building block order and parameter comparison among 15 layers networks |
从表 8可以看出,在网络4、网络5、网络6三组架构的结构组成相似的情况下,参数量较大的网络可以取得更高的识别准确率,说明网络可以提取到更多的有效特征信息。网络2虽然具有一定的模型复杂度,但是在该架构搭建方式下,网络并没有获得较优的识别准确率。因此,本文算法能够自适应地搜索构建块顺序、参数和架构深度,从而设计更高效的网络模型。
4 结束语本文设计基于进化ResNet的交通标志识别算法。通过将提取ResNet的基础块嵌入到进化算法中,自适应地设计适用于交通标志识别的网络模型。实验结果表明,本文进化ResNet算法在德国交通标志数据集上的识别精度和参数量分别为99.41%和2.37×106。该算法能够自适应搜索网络构建块的顺序、参数和架构深度,设计更高效的网络模型。下一步将在进化神经架构搜索算法中,设计一种数学机制分析问题域的复杂性,同时设置更高效的进化终止条件,并寻找关联网络架构性能的直接评价标准来代替基于分类准确度的适应度评估,以实现交通标志的实时检测与识别。
| [1] |
刘占文, 赵祥模, 李强, 等. 基于图模型与卷积神经网络的交通标志识别方法[J]. 交通运输工程学报, 2016, 16(5): 122-131. LIU Z W, ZHAO X M, LI Q, et al. Traffic sign recognition method based on graphical model and convolutional neural network[J]. Journal of Traffic and Transportation Engineering, 2016, 16(5): 122-131. (in Chinese) DOI:10.3969/j.issn.1671-1637.2016.05.014 |
| [2] |
LI L F, WANG Y R. Improved LeNet-5 convolutional neural network traffic sign recognition[J]. International Core Journal of Engineering, 2021, 7(4): 114-121. |
| [3] |
CHENG P, LIU W, ZHANG Y F, et al. LOCO: local context based Faster R-CNN for small traffic sign detection[C]//Proceedings of International Conference on Multimedia Modeling. Berlin, Germany: Springer, 2018: 329-341.
|
| [4] |
尉天成, 陈小锋, 殷元亮. 基于多尺度卷积神经网络的道路交通标志识别方法研究[J]. 西北工业大学学报, 2021, 39(4): 891-900. WEI T C, CHEN X F, YIN Y L. Research on traffic sign recognition method based on multi-scale convolution neural network[J]. Journal of Northwestern Polytechnical University, 2021, 39(4): 891-900. (in Chinese) |
| [5] |
马永杰, 程时升, 马芸婷, 等. 多尺度特征融合与极限学习机结合的交通标志识别[J]. 液晶与显示, 2020, 35(6): 572-582. MA Y J, CHENG S S, MA Y T, et al. Traffic sign recognition based on multi-scale feature fusion and extreme learning machine[J]. Chinese Journal of Liquid Crystals and Displays, 2020, 35(6): 572-582. (in Chinese) |
| [6] |
薛之昕, 郑英豪, 肖建, 等. 基于多尺度卷积神经网络的交通标志识别[J]. 计算机工程, 2020, 46(3): 261-266. XUE Z X, ZHENG Y H, XIAO J, et al. Traffic sign recognition based on multi-scale convolutional neural network[J]. Computer Engineering, 2020, 46(3): 261-266. (in Chinese) |
| [7] |
LIU Y Q, SUN Y N, XUE B, et al. A survey on evolutionary neural architecture search[EB/OL]. [2021-10-08]. https://arxiv.org/abs/2008.10937v1.
|
| [8] |
DARWISH A, HASSANIEN A E, DAS S. A survey of swarm and evolutionary computing approaches for deep learning[J]. Artificial Intelligence Review, 2020, 53(3): 1767-1812. DOI:10.1007/s10462-019-09719-2 |
| [9] |
STANLEY K O, CLUNE J, LEHMAN J, et al. Designing neural networks through neuroevolution[J]. Nature Machine Intelligence, 2019, 1(1): 24-35. DOI:10.1038/s42256-018-0006-z |
| [10] |
STANLEY K O, MIIKKULAINEN R. Evolving neural networks through augmenting topologies[J]. Evolutionary Computation, 2002, 10(2): 99-127. DOI:10.1162/106365602320169811 |
| [11] |
REAL E, AGGARWAL A, HUANG Y P, et al. Regularized evolution for image classifier architecture search[EB/OL]. [2021-10-08]. https://arxiv.org/pdf/1802.01548.pdf.
|
| [12] |
SUN Y N, XUE B, ZHANG M J, et al. Completely automated CNN architecture design based on blocks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(4): 1242-1254. DOI:10.1109/TNNLS.2019.2919608 |
| [13] |
SUN Y N, XUE B, ZHANG M J, et al. Automatically designing CNN architectures using the genetic algorithm for image classification[J]. IEEE Transactions on Cybernetics, 2020, 50(9): 3840-3854. DOI:10.1109/TCYB.2020.2983860 |
| [14] |
SUN Y N, WANG H D, XUE B, et al. Surrogate-assisted evolutionary deep learning using an end-to-end random forest-based performance predictor[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(2): 350-364. DOI:10.1109/TEVC.2019.2924461 |
| [15] |
SUN Y N, SUN X, FANG Y H, et al. A novel training protocol for performance predictors of evolutionary neural architecture search algorithms[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(3): 524-536. |
| [16] |
ZHANG H Y, JIN Y C, CHENG R, et al. Efficient evolutionary search of attention convolutional networks via sampled training and node inheritance[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(2): 371-385. |
| [17] |
马永杰, 刘培培. 基于DenseNet进化的卷积神经网络图像分类算法[J]. 激光与光电子学进展, 2020, 57(24): 50-57. MA Y J, LIU P P. Convolutional neural network based on DenseNet evolution for image classification algorithm[J]. Laser & Optoelectronics Progress, 2020, 57(24): 50-57. (in Chinese) |
| [18] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D. C., USA: IEEE Press, 2016: 770-778.
|
| [19] |
马永杰, 李雪燕, 宋晓凤. 基于改进深度卷积神经网络的交通标志识别[J]. 激光与光电子学进展, 2018, 55(12): 250-257. MA Y J, LI X Y, SONG X F. Traffic sign recognition based on improved deep convolution neural network[J]. Laser & Optoelectronics Progress, 2018, 55(12): 250-257. (in Chinese) |
| [20] |
STALLKAMP J, SCHLIPSING M, SALMEN J, et al. The German traffic sign recognition benchmark: a multi-class classification competition[C]//Proceedings of International Joint Conference on Neural Networks. Washington D. C., USA: IEEE Press, 2011: 1453-1460.
|
| [21] |
CIREŞAN D, MEIER U, MASCI J, et al. Multi-column deep neural network for traffic sign classification[J]. Neural Networks, 2012, 32: 333-338. |
| [22] |
王晓斌, 黄金杰, 刘文举. 基于优化卷积神经网络结构的交通标志识别[J]. 计算机应用, 2017, 37(2): 530-534. WANG X B, HUANG J J, LIU W J. Traffic sign recognition based on optimized convolutional neural network architecture[J]. Journal of Computer Applications, 2017, 37(2): 530-534. (in Chinese) |
| [23] |
宋青松, 张超, 田正鑫, 等. 基于多尺度卷积神经网络的交通标志识别[J]. 湖南大学学报(自然科学版), 2018, 45(8): 131-137. SONG Q S, ZHANG C, TIAN Z X, et al. Traffic sign recognition based on multi-scale convolutional neural network[J]. Journal of Hunan University (Natural Sciences), 2018, 45(8): 131-137. (in Chinese) |
| [24] |
孙伟, 杜宏吉, 张小瑞, 等. 基于CNN多层特征和ELM的交通标志识别[J]. 电子科技大学学报, 2018, 47(3): 343-349. SUN W, DU H J, ZHANG X R, et al. Traffic sign recognition method based on multi-layer feature CNN and extreme learning machine[J]. Journal of University of Electronic Science and Technology of China, 2018, 47(3): 343-349. (in Chinese) |
 2022, Vol. 48
2022, Vol. 48

