2. 中国人民解放军陆军参谋部, 北京 100000
2. Staff Department, PLA Army, Beijing 100000, China
开放科学(资源服务)标志码(OSID):
卷积神经网络(Convolutional Neural Network,CNN)已在图像识别和图像分类领域中得到广泛应用,并表现出良好的性能[1-3]。但是若在原始图像中加入人类无法察觉的扰动,由此形成的对抗样本将影响CNN的性能,从而导致模型分类错误[4]。该现象给许多实际应用系统带来了安全隐患[5],如人脸识别系统的识别错误可能会导致准入权限管理失效[6],自动驾驶车辆的识别错误可能会造成严重的交通事故[7]等。因此,研究人员提出多种对抗样本攻击和防御的方法,以提高模型的鲁棒性,从而促进应用系统的安全部署和稳定使用。
现有的攻击方法主要分为白盒攻击和黑盒攻击两类。在白盒条件下,对抗样本生成方法可以针对性地生成关于某个模型的对抗样本,现有技术已经具有较高的白盒攻击成功率。但是,白盒攻击需要攻击者掌握更多的模型信息,这在现实世界中难以实现。在黑盒条件下,攻击者只需要掌握较少模型信息便可实施攻击[8],因此,黑盒攻击具有更强的实用性。研究表明[9],对抗样本具有良好的迁移特性,即针对某一模型生成的对抗样本对其他模型也具有一定的攻击效果。根据该性质,文献[10]通过引入动量项、优化梯度损失函数更新方向和加快收敛速度,提高对抗样本的黑盒攻击成功率。黑盒攻击成功率低的主要原因是在对抗样本生成过程中产生“过拟合”现象[11],即针对已知模型生成的对抗样本仅对该模型具有较强的攻击成功率,但是攻击其他模型的成功率较低。
本文提出基于平移随机变换的对抗样本生成方法。从数据增强角度,利用平移随机变换方法优化对抗样本的生成过程。通过构建概率模型,并对原始图像进行随机变换操作,利用变换后的图像生成对抗扰动,同时逐步添加到原图像上迭代生成对抗样本,根据应用场景设计单模型攻击算法和集成模型攻击算法,提高黑盒攻击成功率。
1 相关研究对抗样本的攻击和防御在一定意义上可以相互促进。针对深度神经网络在对抗攻击情况下表现出的脆弱性,对抗样本既可以用于攻击已训练好的模型,将攻击成功率作为一种重要指标来评价模型的鲁棒性,同时可将对抗样本作为训练数据来进一步训练模型,提高模型对对抗样本的识别能力,从而提高其对恶意攻击的防御性能。现有对抗样本生成方法和防御方法相关研究的优点和不足如表 1所示。

|
下载CSV 表 1 对抗攻击和对抗防御相关研究成果对比 Table 1 Comparison of research results related to adversarial attack and adversarial defense |
从表 1可以看出,现有的对抗样本攻击方法改进主要从寻找优化算法角度提高攻击性能,如文献[12]提出迭代快速梯度符号方法(Iterative Fast Gradient Sign Method,I-FGSM),通过将单步生成调整为多步迭代,细化对抗样本生成过程中的损失函数更新过程。文献[10]提出向量迭代快速梯度符号方法(Momentum Iterative Fast Gradient Sign Method,MI-FGSM),通过引入动量项并稳定损失函数的更新方向,以避免陷入局部最大值,从而使损失函数更快达到真实最优解,进一步提高生成对抗样本的攻击成功率。优化算法可以更高效地生成对抗样本,但同时会加剧对抗样本与图像分类模型的过度拟合。因此,本文从数据增强的角度提高对抗样本的泛化攻击能力,提高黑盒攻击成功率。
2 背景知识FGSM是典型的对抗样本生成方法。本文研究也是基于FGSM。因此,本节介绍FGSM类中的几种基本方法,定义
快速梯度符号方法[15]是FGSM类中的初始版本。该方法中通过计算输入图像
| $ {x}^{\mathrm{a}\mathrm{d}\mathrm{v}}=x+\varepsilon \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left({\mathit{\triangledown}}_{x}L\right(x, {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}};\theta \left)\right) $ | (1) |
针对FGSM白盒攻击成功率低的问题,迭代快速梯度符号方法(I-FGSM)[12]将FGSM损失函数计算时的单步计算改为多步迭代计算。该方法的实现过程如式(2)所示:
| $ {x}_{n+1}^{\mathrm{a}\mathrm{d}\mathrm{v}}=\mathrm{C}\mathrm{l}\mathrm{i}{\mathrm{p}}_{x}^{\varepsilon }\left\{{x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}}+\alpha \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left({\mathit{\triangledown}}_{x}L\right({x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}}, {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}};\theta \left)\right)\right\} $ | (2) |
在初始状态时,令
实验结果表明,利用I-FGSM优化损失函数,损失函数容易陷入局部最优值,这也是导致黑盒攻击成功率降低的一个原因。针对该问题,动量迭代快速梯度符号方法(MI-FGSM)[10]将衰减因子引入到对抗样本生成过程中,使得损失函数在计算过程中保持前进的惯性,以稳定更新方向,从而突破损失函数的局部最大值,获得真实的最优解。MI-FGSM实现过程如式(3)和式(4)所示:
| $ {g}_{n+1}=\mu \cdot {g}_{t}+\frac{{\mathit{\triangledown}}_{x}L({x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}}, {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}};\theta )}{{‖{\mathit{\triangledown}}_{x}L({x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}}, {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}};\theta )‖}_{1}} $ | (3) |
| $ {x}_{n+1}^{\mathrm{a}\mathrm{d}\mathrm{v}}=\mathrm{C}\mathrm{l}\mathrm{i}{\mathrm{p}}_{x}^{\varepsilon }\left\{{x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}}+\alpha \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left({g}_{n+1}\right)\right\} $ | (4) |
其中:
FGSM类方法具有简洁易懂、生成效率高、可拓展性好等优点,但其黑盒攻击成功率较低。为此,本文利用数据增强技术,提出基于平移随机变换的对抗样本生成方法,通过将平移变换引入到对抗样本的生成过程中,并将其作为数据增强的一种典型应用,扩展了对抗样本生成过程中图像输入的多样化,有效缓解在对抗样本生成过程中存在的“过拟合”现象,从而提高攻击方法的黑盒攻击成功率。
对抗样本生成方法通常采用单模型攻击和集成模型攻击。单模型攻击是指将原始干净图像输入到单个图像分类模型中,以生成对抗样本。集成模型攻击是指将图像同时输入到多个图像分类模型中,以生成对抗样本。这两种不同的攻击方式具有不同的攻击效果。单模型攻击是针对某个单模型生成对抗样本,再攻击该模型和其他模型,攻击自身时为白盒攻击,攻击其他模型时为黑盒攻击,攻击成功率可作为对抗样本的评价指标。由于集成模型攻击采用多模型集成的方式,因此生成的对抗样本可以学习到更多的模型信息,以降低对抗样本对单模型的过拟合,从而提高对抗样本的迁移性,因此黑盒攻击成功率也更高。在实际应用中,单模型攻击只需要调用单个模型文件,占用的计算资源较少,以便对对抗样本生成方法的优劣进行比较。而集成模型攻击需要调用多个模型文件,消耗的时长和占用的计算资源较多,但是可以生成迁移性更强的对抗样本,因此,集成模型攻击常用于进一步提高对抗样本的黑盒攻击成功率。
3.1 目标优化问题从攻击角度分析,对抗样本的目的是使图像分类模型分类出错,即在不改变人眼可辨识类别的基础上,使图像分类模型无法正常实现分类的功能。为此,本文将该问题建模为目标优化问题,如式(5)所示:
| $ \underset{{x}^{\mathrm{a}\mathrm{d}\mathrm{v}}}{\mathrm{a}\mathrm{r}\mathrm{g}\ \mathrm{m}\mathrm{a}\mathrm{x}}\ L({x}^{\mathrm{a}\mathrm{d}\mathrm{v}}, {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}};\theta ) $ | (5) |
其中:
为提高攻击成功率,对抗样本需具有攻击性和隐蔽性的特点。为有效衡量对抗扰动的可感知性,本文对该优化问题的约束条件进行建模,如式(6)所示:
| $ {‖r‖}_{\mathrm{\infty }}={‖{x}^{\mathrm{a}\mathrm{d}\mathrm{v}}-x‖}_{\mathrm{\infty }}\le \varepsilon $ | (6) |
对抗样本与输入模型的原始图像的差值为添加的对抗扰动
在FGSM类生成方法中,黑盒攻击成功率低的主要原因是对抗样本与图像分类模型发生了过拟合。研究发现[10],对抗样本生成过程与神经网络模型的训练过程有相似性,对抗样本的迁移性可以与神经网络模型的泛化能力相对应。因此,本文将提高模型泛化能力的方法引入到对抗样本的生成过程中。在图像分类模型的训练过程中,数据增强常被用于提高模型的泛化能力,同样,可以将平移随机变换作为数据增强的手段,应用于对抗样本的生成过程中,以提高对抗样本的迁移性,从而有效提高对抗样本的黑盒攻击成功率。
本文将概率变换模型建模为平移随机变换过程,并设置超参数变换概率
| $ T({x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}};p, D)=\left\{\begin{array}{l}T({x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}}, D), \mathrm{概}\mathrm{率}\mathrm{为}p\\ {x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}}, \mathrm{概}\mathrm{率}\mathrm{为}1-p\end{array}\right. $ | (7) |
在平移随机变换函数
在对单模型攻击的过程中,基于此变换函数,本文优化目标函数式(5),新的目标函数如式(8)所示:
| $ \underset{{x}^{\mathrm{a}\mathrm{d}\mathrm{v}}}{\mathrm{a}\mathrm{r}\mathrm{g}\ \mathrm{m}\mathrm{a}\mathrm{x}}\ L\left(T\right({x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}};p, D), {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}};\theta ) $ | (8) |
本文提出将平移变换过程与MI-FGSM相结合的TT-MI-FGSM方法,其过程如式(9)和式(10)所示:
| $ {g}_{n+1}=\mu \cdot {g}_{t}+\frac{{\mathit{\triangledown}}_{x}L\left(T\right({x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}};p, D), {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}};\theta )}{{‖{\mathit{\triangledown}}_{x}L\left(T\right({x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}};p, D), {y}^{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}};\theta )‖}_{1}} $ | (9) |
| $ {x}_{n+1}^{\mathrm{a}\mathrm{d}\mathrm{v}}=\mathrm{C}\mathrm{l}\mathrm{i}{\mathrm{p}}_{x}^{\varepsilon }\left\{{x}_{n}^{\mathrm{a}\mathrm{d}\mathrm{v}}+\alpha \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left({g}_{n+1}\right)\right\} $ | (10) |
基于以上研究,本文设计针对单模型攻击的算法,具体过程如算法1所示。
算法1 单个分类模型攻击算法(TT-MI-FGSM)
输入 原始输入图像
输出 对抗样本图像
1.计算每轮添加的扰动大小:
2.初始化对抗样本生成系统:
3.for
4.通过
5.得到关于单模型的损失函数
6.通过式(4)更新
7.通过式(5)更新
8.返回对抗样本
在该算法中,平移变换概率
从单个分类模型攻击算法中可以看出,在对抗样本的生成过程中,本文设置
在对抗样本防御领域中,集成对抗训练的方法可以有效提高分类模型对对抗样本的防御能力[19]。从模型训练角度,集成模型解决了模型训练过程中的拟合问题,提高了模型的泛化能力,从而有助于提高对抗样本的防御能力。因此,在集成模型条件下的攻击算法流程如图 1所示,以进一步缓解对抗样本对分类模型的“依赖”,增加模型的多样性,从而提高对抗样本的泛化能力和黑盒攻击成功率。
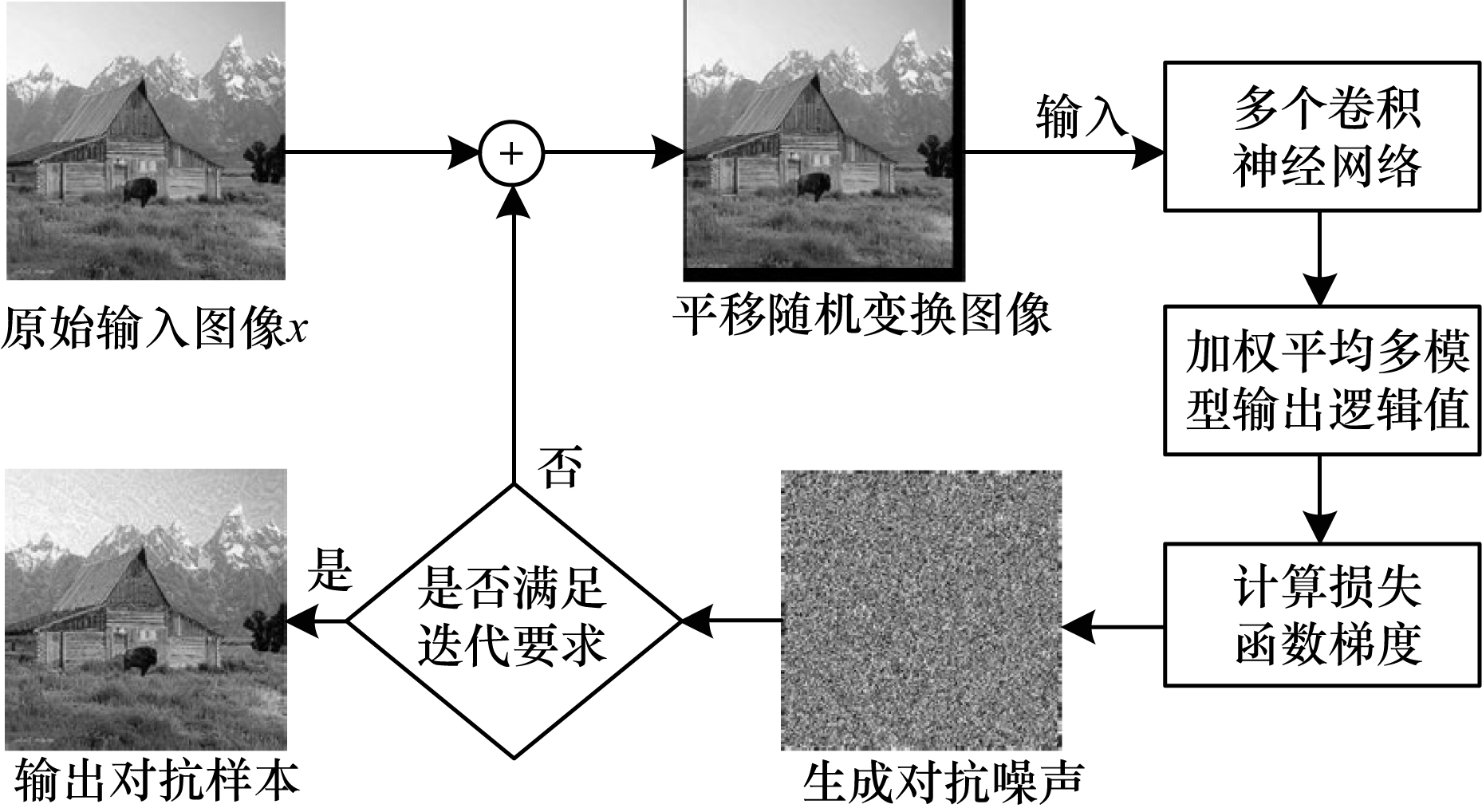
|
Download:
|
| 图 1 集成模型攻击算法流程 Fig. 1 Procedure of integrated model attack algorithm | |
从图 1可以看出,将原始干净图像输入到对抗样本生成系统后,首先根据概率模型进行平移随机变换,变换后出现的空白区域将采用补0的方式实现边界填充,得到299×299×3的变换后图像;将得到的图像输入到多个图像分类模型中,并得到各模型的输出逻辑值;根据加权平均后的逻辑值计算损失函数,并沿损失函数的梯度方向迭代更新,直到完成迭代,此时输出对抗样本图像。
在对抗样本生成过程中,本文在集成分类模型上利用TT-MI-FGSM生成对抗样本,如算法2所示。
算法2 集成分类模型攻击算法(TT-MI-FGSM)
输入 原始输入图像
输出 对抗样本图像
1.计算每轮添加的扰动大小:
2.初始化对抗样本生成系统:
3.for
4.通过
5.将
6.求集成逻辑值
7.得到关于集成模型的损失函数
8.通过式(4)更新
9.通过式(5)更新
10.返回对抗样本
在算法2中,超参数的意义及设置的取值范围与单模型攻击算法一致,而两个算法之间的区别在于生成对抗样本的同时将图像输入到多个图像分类模型,并通过多模型输出逻辑值并权重集成的方式,实现生成对抗样本的目的。该算法可大幅提高黑盒攻击成功率,但其生成的对抗样本白盒攻击成功率略有降低。
3.4 方法的可扩展性平移随机变换作为数据增强的一种手段,可用于改进FGSM类方法的性能,并通过与I-FGSM和MI-FGSM的结合,提高对抗样本的黑盒攻击成功率。通过调整方法中的衰减因子
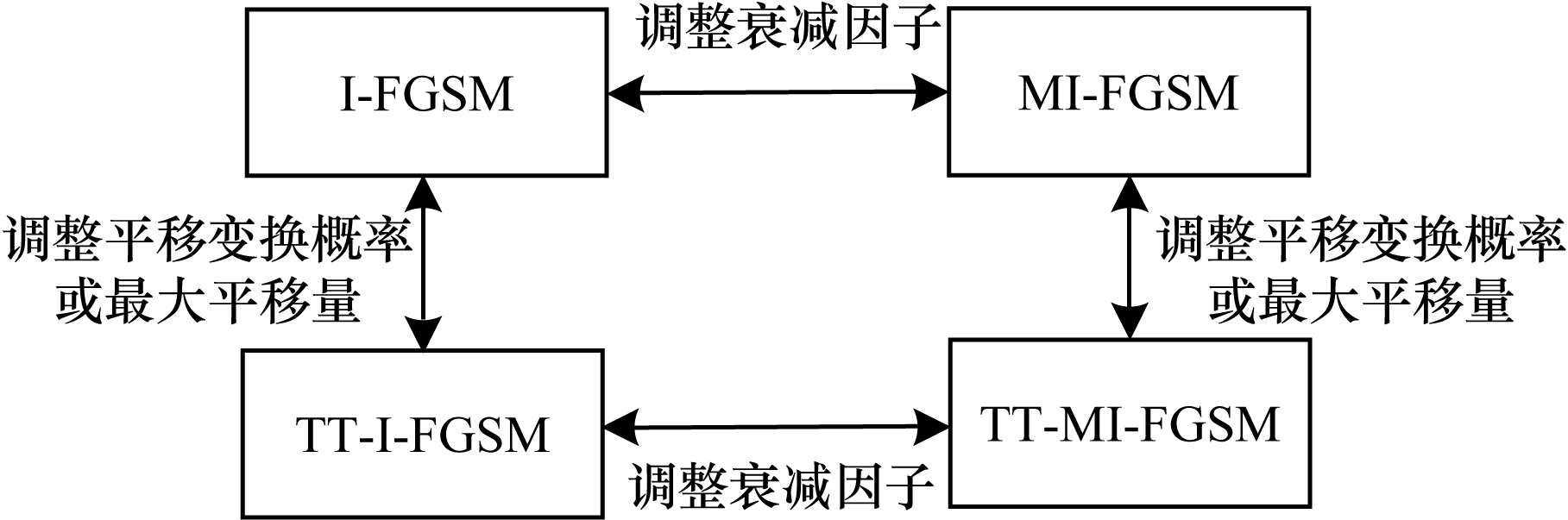
|
Download:
|
| 图 2 不同对抗样本生成方法之间的转化关系 Fig. 2 Conversion relationship among different adversarial examples generation methods | |
当衰减因子
本文在Intel Core i9-10900K上,利用python 3.8.5和Tensorflow 1.14.0深度学习框架对比本文提出方法TT-I-FGSM、TT-MI-FGSM与其他方法(I-FGSM[12]和MI-FGSM[10])的攻击成功率。目标平台的操作系统为Windows 10(专业版),内存为64 GB,主频为3.7 GHz。为提高对抗样本生成效率,实验使用NVIDIA GeForce RTX 2080Ti GPU加速完成计算过程。
4.1 实验设置 4.1.1 数据集ImageNet数据集[23]是由斯坦福大学李飞飞教授带领创建的计算机视觉数据集,是目前图像识别领域最大的数据库,也是评估图像分类算法性能的基准。该数据集中的每张图片都被手工标注类别,在对抗样本的生成过程中,本文利用其标签以生成对抗样本并进行攻击效果检测,并从ImageNet数据集验证集的每个类别中各随机选择图片,利用这1 000张分类正确的图片进行对抗样本的生成。
4.1.2 分类模型在实验中共使用7个分类模型,其中,4个正常训练分类模型分别是Inception-v3[24](Inc-v3)、Inception-v4[25](Inc-v4)、Inception-ResNet-v2[25](IncRes-v2)和ResNet-v2-101[26](Res-101);3个对抗训练分类模型[19]分别是ens3-adv-Inception-v3(Inc-v3ens3)、ens4-adv-Inception-v3(Inc-v3ens4)和ens-adv-Inception-ResNet-v2(IncRes-v2ens)。
4.1.3 基准方法为更好地评估本文方法的有效性,本文选择另外两种典型的对抗样本生成方法(I-FGSM[13]和MI-FGSM[10])作为对比基准,与本文提出的TT-I-FGSM和TT-MI-FGSM进行对比分析。
4.1.4 超参数设置为了方便攻击成功率对比,本文按照动量法[10]中的规范设置超参数,最大扰动值
本文在白盒和黑盒条件下对本文方法TT-I-FGSM和TT-MI-FGSM和基准方法进行单模型攻击测试。I-FGSM、TT-I-FGSM、MI-FGSM和TT-MI-FGSM方法分别在Inc-v3、Inc-v4、IncRes-v2和Res-101 4个正常训练模型上生成对抗样本,并在7个分类模型上(Inc-v3、Inc-v4、IncRes-v2、Res-101、Inc-v3ens3、Inc-v3ens4、IncRes-v2ens)进行测试。不同对抗样本生成方法的黑盒和白盒攻击成功率如表 2所示。表中攻击成功率为分类错误的图像数在图像总数中所占的比例,*表示白盒攻击。
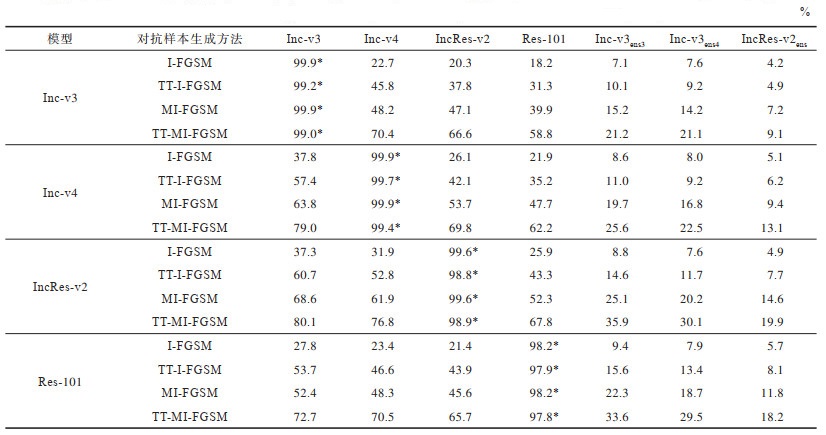
|
下载CSV 表 2 不同对抗样本生成方法攻击单个模型的成功率对比 Table 2 Success rate of attack on a single model comparison among different adversarial examples generation methods |
从表 2可以看出,在白盒条件下,本文提出的方法TT-I-FGSM和TT-MI-FGSM在各模型上攻击成功率保持在97.8%以上的水平。在黑盒条件下,TT-MI-FGSM在正常训练模型上提高了攻击成功率,例如,在Inc-v3模型上生成的对抗样本,攻击IncRes-v2模型时,TT-MI-FGSM攻击成功率比MI-FGSM提高19.5个百分点。此外,TT-MI-FGSM在针对防御模型的黑盒攻击中也表现出较高的攻击性能,例如,在Res-101模型上生成的对抗样本,当攻击Inc-v3ens3模型时,TT-MI-FGSM算法的攻击成功率为33.6%,比MI-FGSM提高11.3个百分点。因此,本文提出的TT-MI-FGSM方法可以有效提高对抗样本的迁移性。
4.3 集成模型攻击实验集成模型通常对对抗样本具有更好的防御能力。本文通过同时攻击多个分类模型组成的集成模型来评估对抗样本生成方法的性能。本文分别利用I-FGSM、TT-I-FGSM、MI-FGSM和TT-MI-FGSM同时攻击具有相同权重的4个正常训练模型(Inc-v3、Inc-v4、IncRes-v2和Res-101)构成的集成模型,并通过生成的对抗样本分别在7个图像分类模型中测试得到攻击成功率,实验结果如表 3所示。表中攻击成功率为分类错误的图像数在图像总数中所占的比例,*表示白盒攻击。

|
下载CSV 表 3 不同对抗样本生成方法攻击集成模型的成功率对比 Table 3 Success rate of attack on intergated model comparison among different adversarial examples generation methods |
从表 3可以看出,TT-MI-FGSM方法可在保持或提高白盒攻击成功率的基础上,较大幅度提高黑盒攻击的成功率。例如,在Inc-v3、Inc-v4、IncRes-v2和Res-101 4个正常训练模型的白盒攻击上,TT-I-FGSM的攻击成功率比I-FGSM提高了0.9个百分点。而在黑盒攻击中,TT-MI-FGSM比MI-FGSM的攻击成功率平均提高12.83个百分点。针对Inc-v3ens3模型的攻击,TT-MI-FGSM的攻击成功率为54.2%。
不同方法生成的对抗样本图片对比如图 3所示,与原图片相比,图片进行平移随机变换后生成的对抗样本,整体区域均添加了对抗扰动,在人眼视觉上未出现肉眼可见的辨识偏差。

|
Download:
|
| 图 3 不同方法生成的对抗样本图片对比 Fig. 3 Comparison of adversarial examples images generated by different methods | |
本节重点分析在攻击方法中各超参数对攻击成功率的影响。本文运用TT-I-FGSM和TT-MI-FGSM攻击相同权重的4个正常训练模型(Inc-v3、Inc-v4、IncRes-v2和Res-101)组成的集成模型,通过调整超参数设置,以消融实验的方式探究超参数对实验结果的影响。超参数主要有平移变换概率
其他超参数设置:最大扰动值
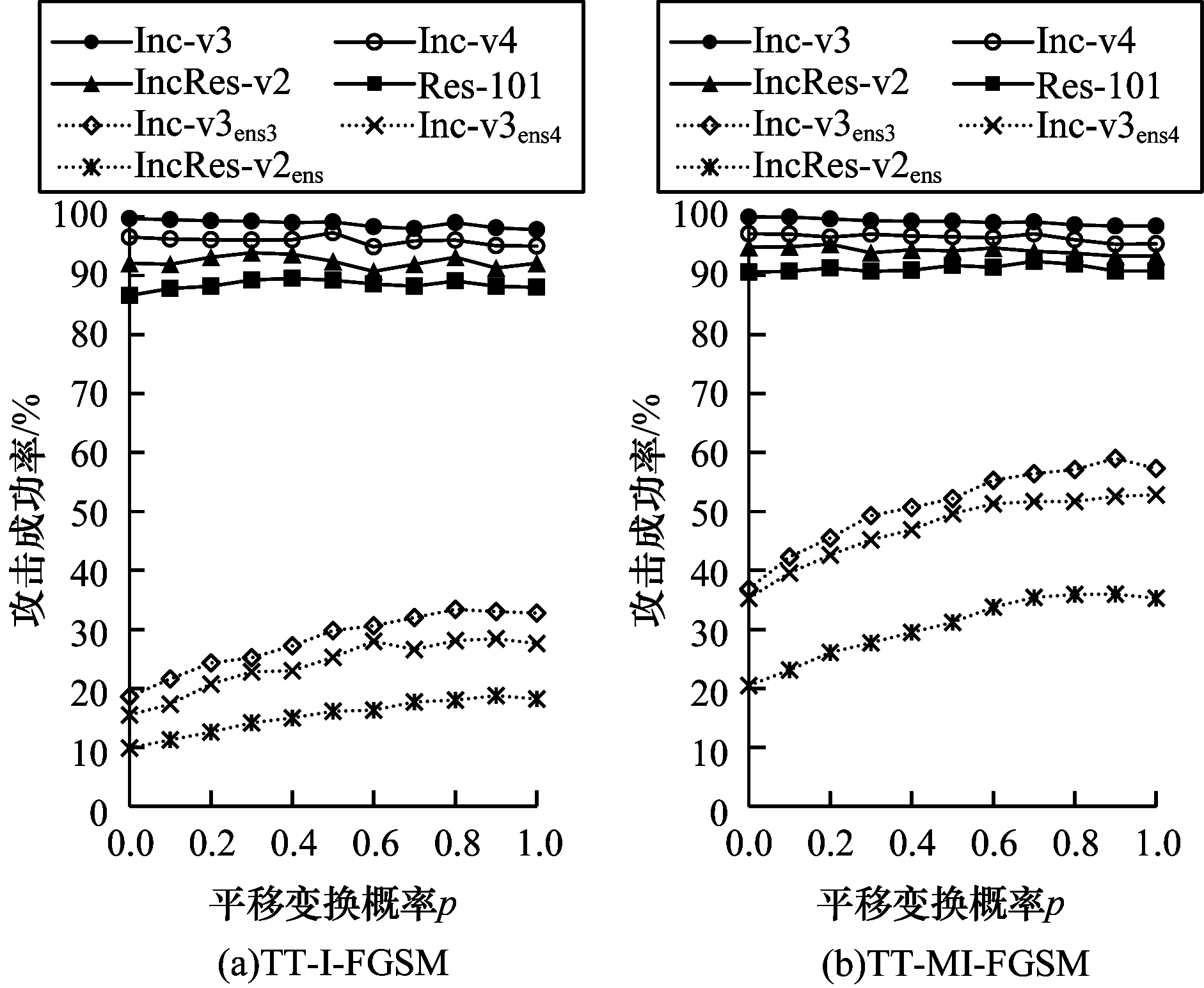
|
Download:
|
| 图 4 平移变换概率与攻击成功率关系 Fig. 4 Relationship between translation conversion probability and attack success rate | |
在白盒攻击中,将生成的对抗样本在4个正常分类模型上进行分类测试,TT-I-FGSM和TT-MI-FGSM白盒攻击成功率保持平稳态势,并可实现均值90%以上的攻击成功率。在黑盒攻击中,当攻击3个对抗训练模型时,随平移变换概率
最大平移距离
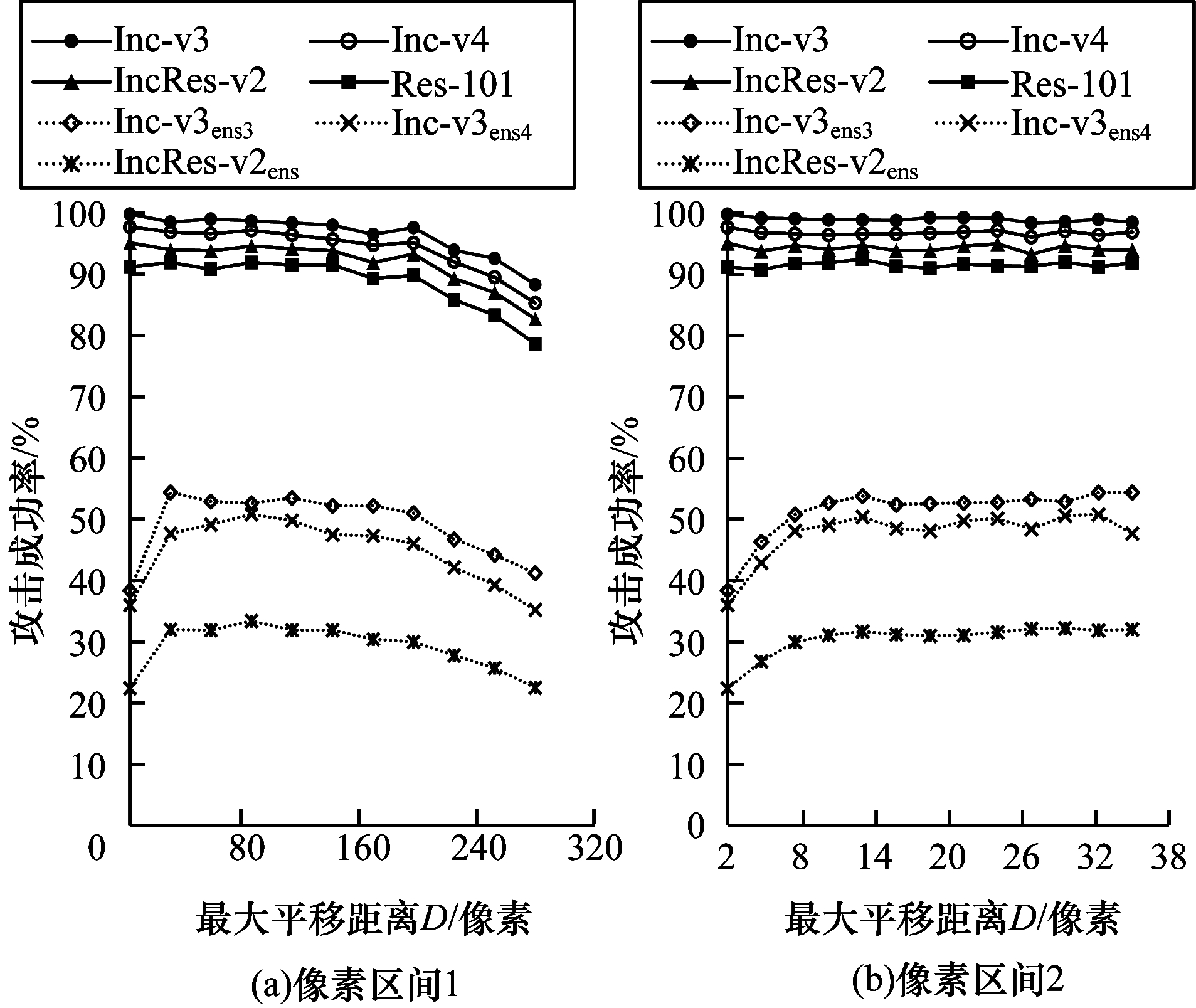
|
Download:
|
| 图 5 最大平移距离与攻击成功率关系 Fig. 5 Relationship between maximum translation distance and attack success rate | |
最大平移距离
本文分别使用TT-I-FGSM和TT-MI-FGSM进行白盒攻击和黑盒攻击。超参数设置:迭代轮数
|
Download:
|
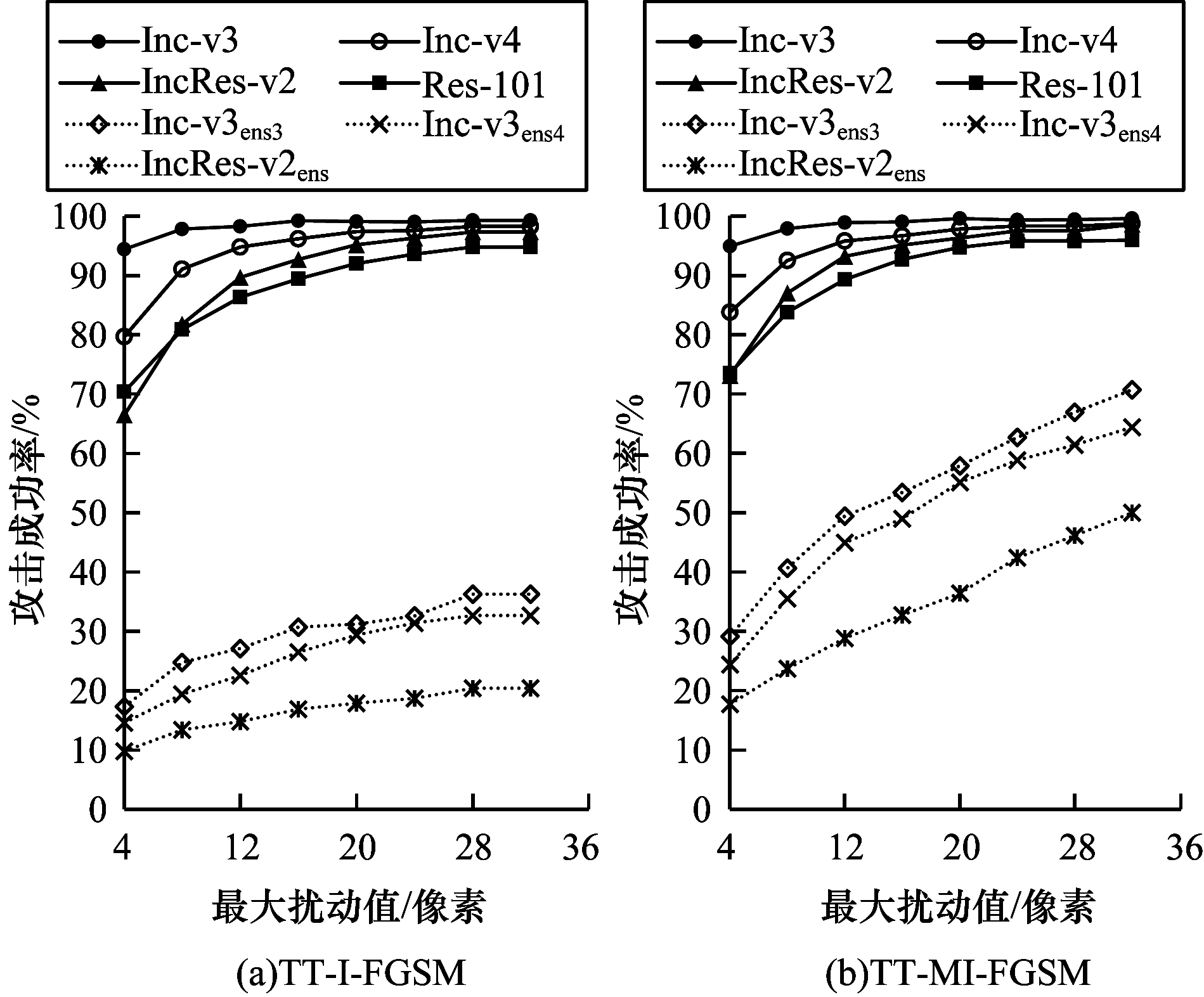
| 图 6 最大扰动值与攻击成功率关系 Fig. 6 Relationship between maximum disturbance values and attack success rate | |
最大扰动值

|
Download:
|
| 图 7 最大扰动值对对抗样本图像的影响 Fig. 7 Influence of maximum disturbance values on adversarial examples image | |
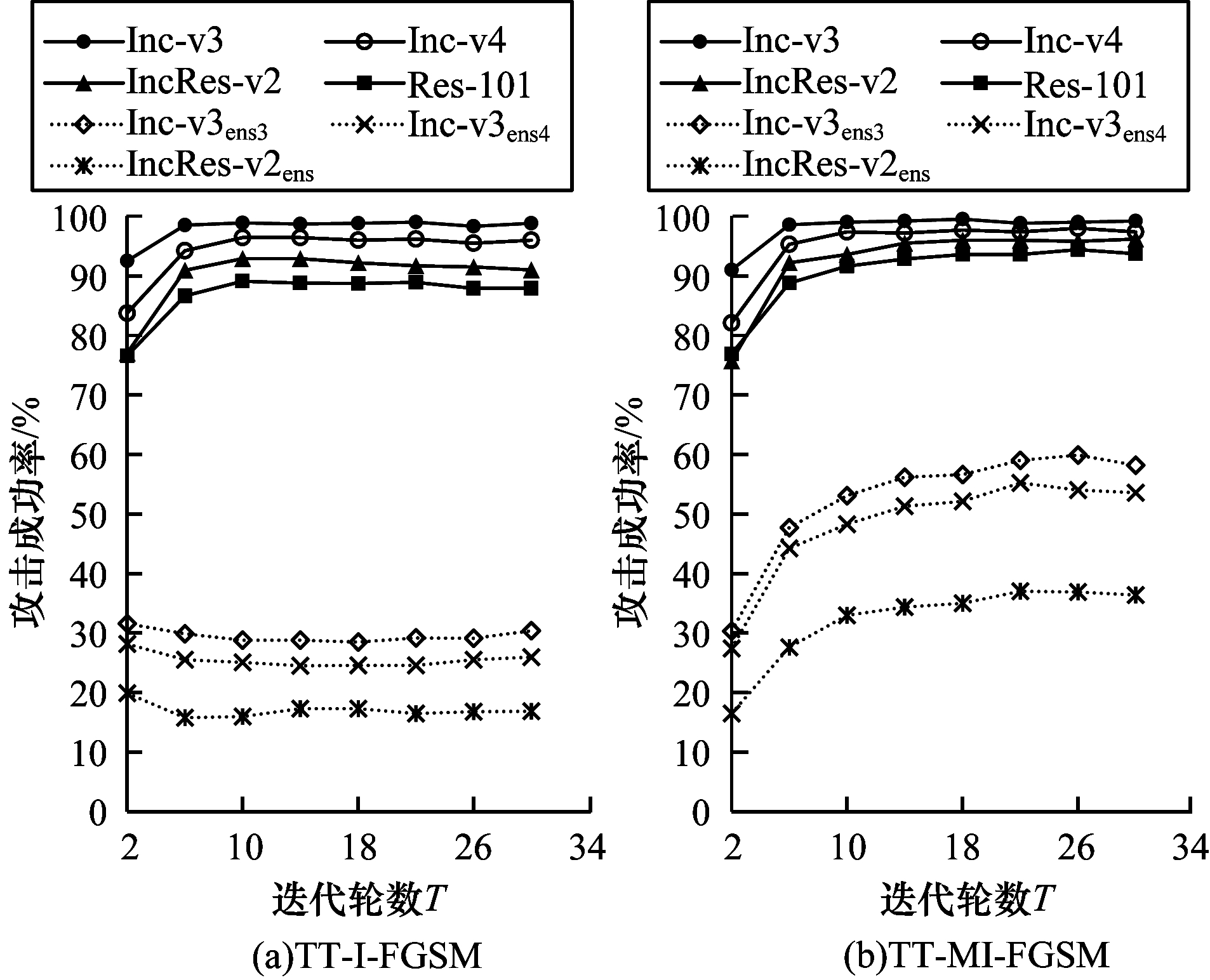
本文将迭代轮数从2开始以4为步长增大,最大值为30。其他的超参数设置:最大扰动值
|
Download:
|
| 图 8 迭代轮数与攻击成功率的关系 Fig. 8 Relationship between iteration number and attack success rate | |
在以上的超参数消融实验中,本文讨论了平移变换概率
本文提出一种基于平移随机变换的对抗样本生成方法TT-MI-FSGM。通过对原图像进行平移随机变换,扩展图像分类模型的输入多样性,缓解对抗样本生成过程中的过拟合现象,从而提高对抗样本的黑盒攻击成功率。此外,通过构建集成模型攻击算法,以生成迁移性更强的对抗样本。实验结果表明,与I-FGSM相比,该方法在集成模型上的黑盒攻击成功率平均提高了30.4个百分点。下一步将对物理世界中对抗样本的实际应用进行研究,从而为神经网络模型的实际部署提供更有效的鲁棒性测试方法。
| [1] |
SADAK F, SAADAT M, HAJIYAVAND A M. Real-time deep learning-based image recognition for applications in automated positioning and injection of biological cells[J]. Computers in Biology and Medicine, 2020, 125(10): 103976. |
| [2] |
GUO G D, ZHANG N. A survey on deep learning based face recognition[J]. Computer Vision and Image Understanding, 2019, 189: 102805. |
| [3] |
MOPURI K R, GANESHAN A, BABU R V. Generalizable data-free objective for crafting universal adversarial perturbations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(10): 2452-2465. DOI:10.1109/TPAMI.2018.2861800 |
| [4] |
陈晓楠, 胡建敏, 张本俊, 等. 基于模型间迁移性的黑盒对抗攻击起点提升方法[J]. 计算机工程, 2021, 47(8): 162-169. CHEN X N, HU J M, ZHANG B J, et al. Black box attack adversarial starting point promotion method based on mobility between models[J]. Computer Engineering, 2021, 47(8): 162-169. (in Chinese) |
| [5] |
PAPERNOT N, MCDANIEL P, GOODFELLOW I, et al. Practical black-box attacks against machine learning[C]//Proceedings of ACM on Asia Conference on Computer and Communications Security. New York, USA: ACM Press, 2017: 506-519.
|
| [6] |
SHARIF M, BHAGAVATULA S, BAUER L, et al. Accessorize to a crime: real and stealthy attacks on state-of-the-art face recognition[C]//Proceedings of ACM SIGSAC Conference on Computer and Communications Security. New York, USA: ACM Press, 2016: 1528-1540.
|
| [7] |
EYKHOLT K, EVTIMOV I, FERNANDES E, et al. Robust physical-world attacks on deep learning model[C]//Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D. C., USA: IEEE Press, 2018: 1-10.
|
| [8] |
姜妍, 张立国. 面向深度学习模型的对抗攻击与防御方法综述[J]. 计算机工程, 2021, 47(1): 1-11. JIANG Y, ZHANG L G. Survey of adversarial attacks and defense methods for deep learning model[J]. Computer Engineering, 2021, 47(1): 1-11. (in Chinese) |
| [9] |
LIU Y P, CHEN X Y, LIU C, et al. Delving into transferable adversarial examples and black-box attacks[EB/OL]. [2021-09-20]: https://arxiv.org/abs/1611.02770.
|
| [10] |
DONG Y P, LIAO F Z, PANG T Y, et al. Boosting adversarial attacks with momentum [EB/OL]. [2021-09-20]. https://arxiv.org/pdf/1710.06081v2.pdf.
|
| [11] |
WANG X S, HE X R, WANG J D, et al. Admix: enhancing the transferability of adversarial attacks[EB/OL]. [2021-09-20]. http://arxiv.org/abs/2102.00436V3.
|
| [12] |
KURAKIN A, GOODFELLOW I, BENGIO S. Adversarial examples in the physical world [EB/OL]. [2021-09-20]. https://arxiv.org/abs/1607.02533v4.
|
| [13] |
BIGGIO B, CORONA I, MAIORCA D, et al. Evasion attacks against machine learning at test time [C]//Proceedings of European Conference on Machine Learning and Knowledge Discovery in Databases. New York, USA: ACM Press, 2013: 387-402.
|
| [14] |
SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks [C]//Proceedings of International Conference on Learning Representations. Banff, Canada: [s. n. ], 2014: 1-10.
|
| [15] |
GOODFELLOW I J, SHLENS J, SZEGEDY C. Explaining and harnessing adversarial examples [EB/OL]. [2021-09-20]. https://arxiv.org/pdf/1412.6572.pdf.
|
| [16] |
EYKHOLT K, EVTIMOV I, FERNANDES E, et al. Robust physical-world attacks on deep learning visual classification [C]//Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D. C., USA: IEEE Press, 2018: 1625-1634.
|
| [17] |
DONG Y P, PANG T Y, SU H, et al. Evading defenses to transferable adversarial examples by translation-invariant attacks[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D. C., USA: IEEE Press, 2019: 4312-4321.
|
| [18] |
KURAKIN A, GOODFELLOW I J, SAMY B. Adversarial machine learning at scale [EB/OL]. [2021-09-20]. https://arxiv.org/pdf/1611.01236.pdf.
|
| [19] |
TRAMER F, KURAKIN A, PAPERNOT N, et al. Ensemble adversarial training: attacks and defenses [EB/OL]. [2021-09-20]. https://arxiv.org/abs/1705.07204v5.
|
| [20] |
LIU G X, KHALIL I, KHREISHAH A. Using single-step adversarial training to defend iterative adversarial examples[C]//Proceedings of the 7th ACM Conference on Data and Application Security and Privacy. New York, USA: ACM Press, 2021: 17-27.
|
| [21] |
XIE C H, WU Y X, MAATEN L V D, et al. Feature denoising for improving adversarial robustness[C]//Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D. C., USA: IEEE Press, 2019: 1-10.
|
| [22] |
METZEN J H, GENEWEIN T, FISCHER V, et al. On detecting adversarial perturbations[EB/OL]. [2021-09-20]. https://arxiv.org/abs/1702.04267v1.
|
| [23] |
RUSSAKOVSKY O, DENG J, SU H, et al. ImageNet large scale visual recognition challenge[J]. International Journal of Computer Vision, 2015, 115(3): 211-252. |
| [24] |
SZEGEDY C, SHNATHON J, IOFFE S, et al. Rethinking the inception architecture for computer vision[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D. C., USA: IEEE Press, 2016: 2818-2826.
|
| [25] |
SZEGEDY C, IOFFE S, VANHOUCKE V, et al. Inception-v4, inception-ResNet and the impact of residual connections on learning[C]//Proceedings of the 31st AAAI Conference on Artificial Intelligence. San Francisco, USA: AAAI Press, 2017: 4278-4284.
|
| [26] |
HE K M, ZHANG X Y, REN S Q, et al. Identity mappings in deep residual networks[C]//Proceedings of European Conference on Computer Vision. Berlin, Germany: Springer, 2016: 630-645.
|
 2022, Vol. 48
2022, Vol. 48

 ,
,