开放科学(资源服务)标志码(OSID):
随着互联网的快速发展,网络数据量呈指数级增长,用户面临信息过载问题[1]。由于面对海量信息用户很难快速获取感兴趣信息,信息生产者也很难将信息推荐给需要的用户,因此推荐系统应运而生。推荐系统是基于对用户和物品的分析,推荐给用户最有可能感兴趣的物品[2]。在推荐系统中协同过滤算法是使用较广泛的算法,其利用用户和项目的相似模式来提供个性化推荐[3]。但是协同过滤算法过多依赖用户对项目的显式反馈或隐式反馈,存在数据稀疏的问题。然而深度神经网络的应用在很大程度上缓解了数据稀疏问题,推荐系统的准确度也得到较大提升[4]。近些年,变分自动编码器(Variational Auto-Encoder,VAE)[5]受到研究人员的广泛关注,也产生了很多的变体模型。文献[6]将VAE应用在协同过滤算法中,构建多项变分自动编码器(Multinomial Variational Auto-Encoder,Multi-VAE)模型,使用多项似然函数替代高斯似然函数,同时在损失函数中加入正则化项以增强模型的解耦能力和提高模型的推荐效果。考虑模型限制条件,文献[7]设计基于条件的变分自动编码器(Conditioned Variational Auto-Encoder,C-VAE)模型,该模型将标签条件加入到VAE中,同时对损失函数做出了改进,增加了模型的可解释性。文献[8]提出宏观和微观双层结构变分自动编码器(Macro-Micro Disentangled Variational Auto-Encoder,Macrid-VAE)模型,该模型使用多层神经网络获取高层次概念,再与用户行为进行结合,然后通过VAE获取微观表现,提高了模型精确度,同样也增加了模型可解释性。
上述研究成果提高了模型的可解释性和精确度,但却忽略了VAE模型本身的局限性。传统的VAE模型除了会导致模型过度正则化外,还会造成只有少量隐向量被激活,该情况会随着网络深度的加深变得更加严重[7]。为此,本文提出融合复杂隐向量先验和注意力机制的变分自动编码器模型,简称为CCPAM-VAE。使用复杂隐向量先验分布替代标准正态分布,利用神经网络训练生成的伪输入作为假数据替代原数据,提高模型执行效率。通过添加辅助隐向量,增加隐向量的低维表现能力和解耦性。基于注意力机制强化具有较高权重值的重要信息,弱化具有较低权重值的不重要信息。
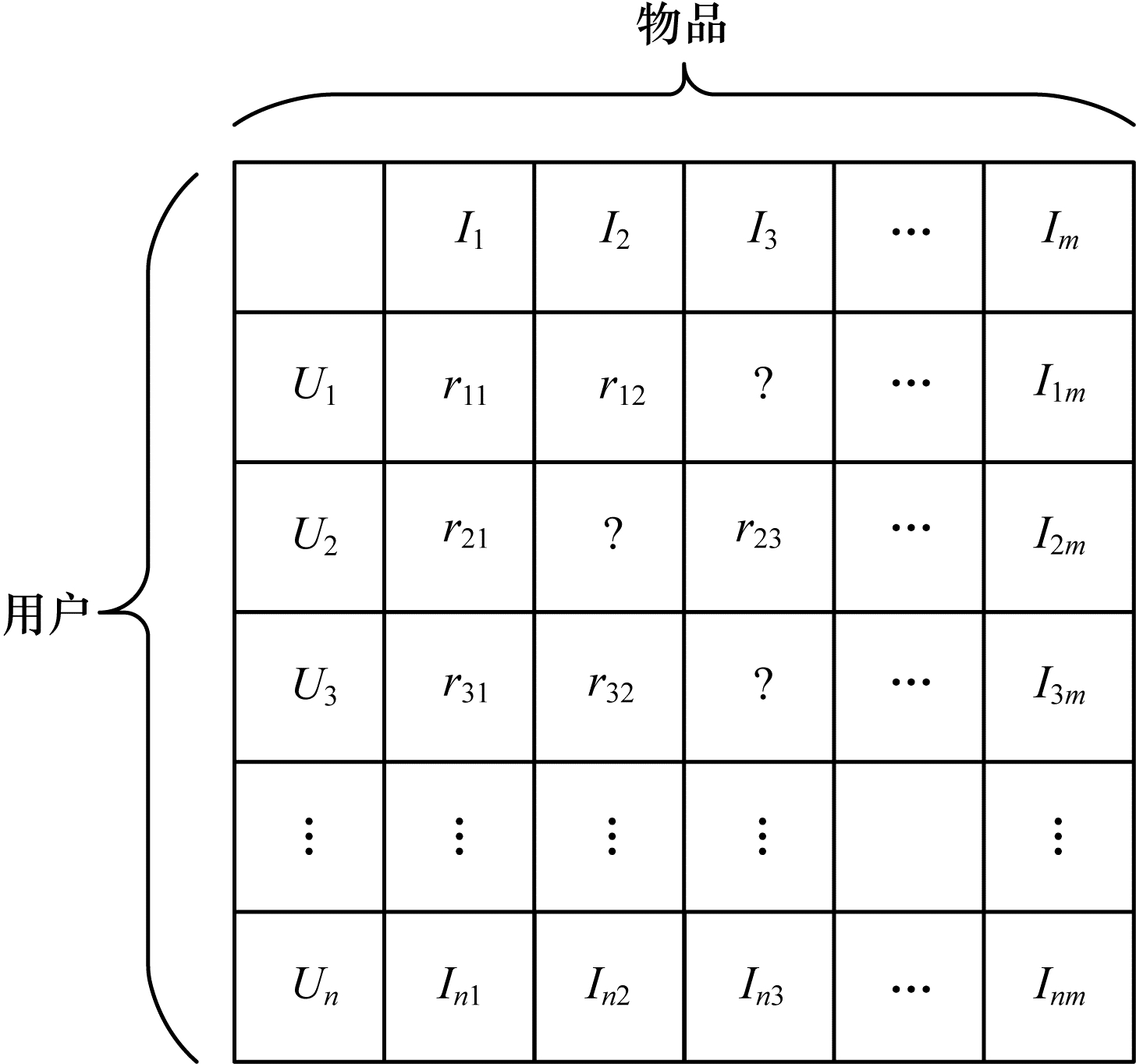
1 VAE模型变分自动编码器由KINGMA等[9]于2013年提出,是一个深度生成模型,结合了变分贝叶斯方法和神经网络,将求和问题转化为优化问题,大大增加了模型适用范围,广泛应用于自然语言处理、计算机视觉、推荐系统等领域[10-12]。变分自动编码器的整体框架由编码器和解码器组成,因为编码器和解码器具有很大的灵活性,所以可以选择不同的神经网络作为组成部分。用户-物品的评分矩阵(见图 1)作为输入数据输入模型,解码器最终输出得到重构后的数据,通过最小化与输入数据的误差来优化模型参数。同时,重构后的数据包含了之前评分矩阵的未评分数据[13-15]。VAE模型分为变分推理过程和生成过程,对于每个用户
| $ {\boldsymbol{z}}_{u}~{p}_{\theta }\left({\boldsymbol{z}}_{u}\right) $ | (1) |
| $ {x}_{u}|{\boldsymbol{z}}_{u}~p({x}_{u}\left|{\boldsymbol{z}}_{u}\right) $ | (2) |
| $ {p}_{\theta }\left({x}_{u}\right)=\int {p}_{\theta }\left({x}_{u}\right|{\boldsymbol{z}}_{u}\left){p}_{\theta }\right({\boldsymbol{z}}_{u})\mathrm{d}{\boldsymbol{z}}_{u} $ | (3) |
|
Download:
|
| 图 1 用户-物品评分矩阵 Fig. 1 User-item rating matrix | |
其中:
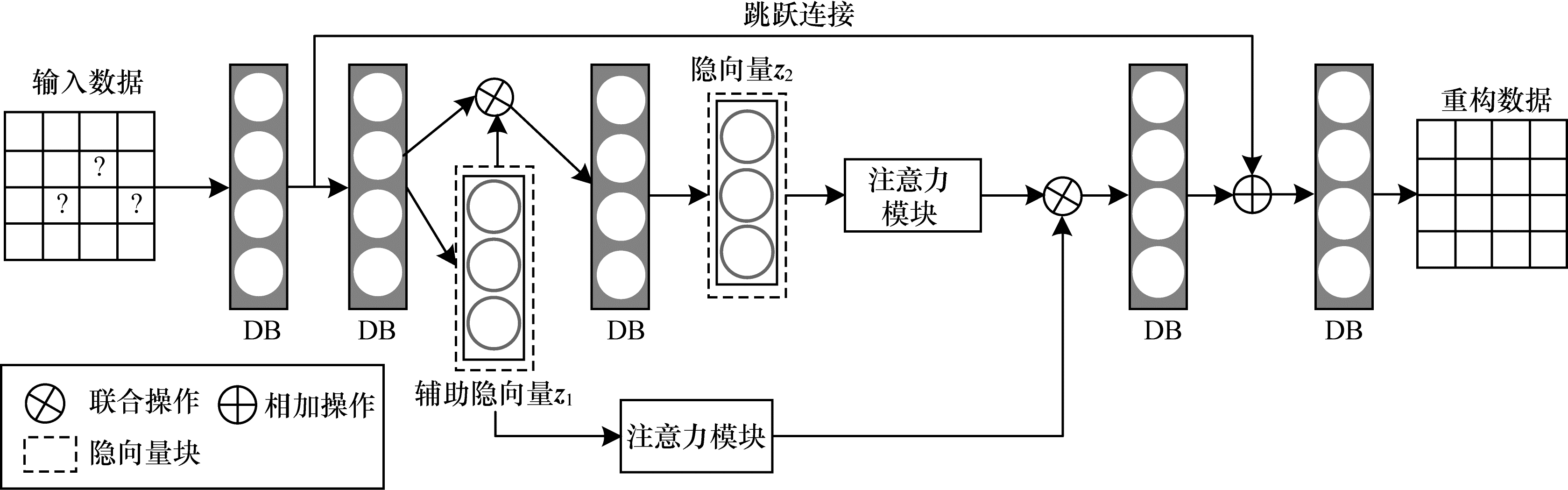
本文设计的CCPAM-VAE模型整体采用编码器-解码器结构,如图 2所示。在编码器阶段,输入数据经过密集块(Dense Block,DB)生成辅助隐向量
|
Download:
|
| 图 2 CCPAM-VAE模型结构 Fig. 2 CCPAM-VAE model structure | |
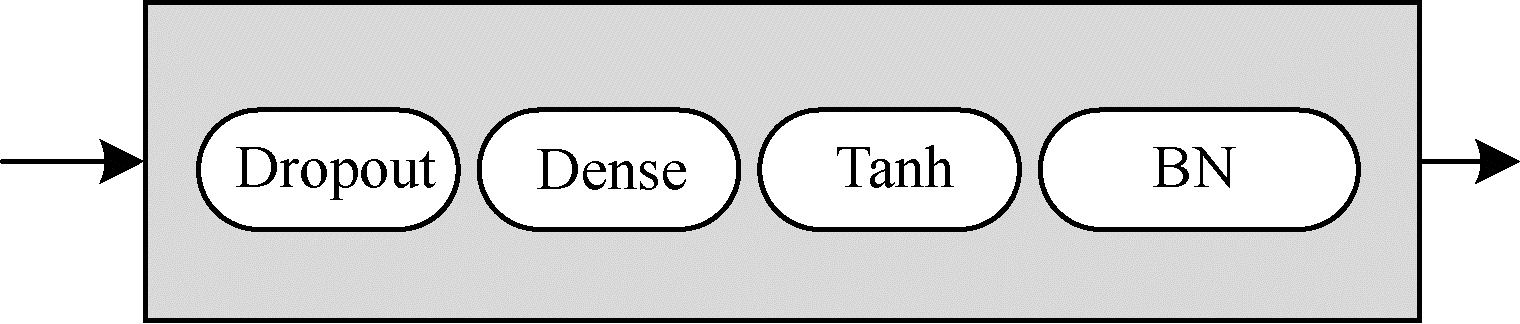
DB模块结构如图 3所示。首先对输入数据x进行Dropout[16]操作,可以暂时屏蔽部分神经元,由于每次训练所屏蔽的神经元不一定相同,因此在一定程度上增加了模型的泛化能力;然后经过一个带有Tanh激活函数的全连接层进行特征提取;最后使用批量标准化(Batch Normalization,BN)进行归一化处理,加快模型收敛速度。DB模块的表达式如式(4)所示:
| $ {\boldsymbol{x}}_{1}=\mathrm{B}\mathrm{N}\left(\mathrm{T}\mathrm{a}\mathrm{n}\mathrm{h}\right({w}_{0}\times \left(\mathrm{D}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}\right({\boldsymbol{x}}_{0})+{b}_{0})\left)\right) $ | (4) |
|
Download:
|
| 图 3 DB模块结构 Fig. 3 DB module structure | |
其中:
通过最大化下界
| $ \begin{array}{l}\mathrm{l}\mathrm{g}{p}_{\theta }\left({\boldsymbol{x}}_{u}\right)\ge {{\rm E}}_{{q}_{\varphi }\left({\boldsymbol{z}}_{u}|{\boldsymbol{x}}_{u}\right)}\left[\mathrm{l}\mathrm{g}{p}_{\theta }\right({\boldsymbol{x}}_{u}\left|{\boldsymbol{z}}_{u}\right)]-\\ \mathrm{K}\mathrm{L}\left({q}_{\varphi }\right({\boldsymbol{z}}_{u}\left|{\boldsymbol{x}}_{u}\right)\left|\right|{p}_{\lambda }\left({\boldsymbol{z}}_{u}\right))=L({\boldsymbol{x}}_{u};\theta , \varphi , \lambda )\end{array} $ | (5) |
式(5)也被称为证据下界(Evidence Lower Bound,ELBO),其中,
对KL散度部分进行分解可得到:
| $ L({\boldsymbol{x}}_{u};\theta , \varphi , \lambda )={{\rm E}}_{{q}_{\varphi }\left({\boldsymbol{z}}_{u}\right|{\boldsymbol{x}}_{u})}\left[\mathrm{l}\mathrm{g}{p}_{\theta }\left({\boldsymbol{x}}_{u}\right|{\boldsymbol{z}}_{u})\right]-{{\rm E}}_{{q}_{\varphi }\left({\boldsymbol{z}}_{u}\right|{\boldsymbol{x}}_{u})}\left[\mathrm{l}\mathrm{g}{q}_{\varphi }\left({\boldsymbol{z}}_{u}\right|{\boldsymbol{x}}_{u})\right]-{{\rm E}}_{{q}_{\varphi }\left({\boldsymbol{z}}_{u}\right|{\boldsymbol{x}}_{u})}\left[-\mathrm{l}\mathrm{g}{p}_{\lambda }\left({\boldsymbol{z}}_{u}\right)\right] $ | (6) |
其中,
式(6)右边的第一部分是重构误差,第二部分是变分后验分布的熵,第三部分是变分后验和先验的交叉熵。使用拉格朗日乘子对第三部分求最大值,如式(7)所示:
| $ \underset{{p}_{\lambda }\left({\boldsymbol{z}}_{u}\right)}{\mathrm{m}\mathrm{a}\mathrm{x}}-\left[{{\rm E}}_{{q}_{\varphi }\left({\boldsymbol{z}}_{u}\right|{\boldsymbol{x}}_{u})}\right[-\mathrm{l}\mathrm{g}{p}_{\lambda }\left({\boldsymbol{z}}_{u}\right)\left]\right]+\beta \left(\int {p}_{\lambda }\left({\boldsymbol{z}}_{u}\right)\mathrm{d}\boldsymbol{z}-1\right) $ | (7) |
后验分布如式(8)所示:
| $ {p}_{\lambda }\left({\boldsymbol{z}}_{u}\right)=\frac{1}{N}\sum\limits_{i=1}^{N}{q}_{\varphi }\left({\boldsymbol{z}}_{u}\right|{\boldsymbol{x}}_{i}) $ | (8) |
其中:N是数据集的大小。
由于求解先验分布需要使用整个数据集,这样做不仅浪费计算资源,还会导致模型过拟合,因此使用可学习数据替代原数据,可以很好地解决该问题,如式(9)所示:
| $ {p}_{\lambda }\left({\boldsymbol{z}}_{u}\right)=\frac{1}{M}\sum\limits_{i=1}^{M}{q}_{\varphi }\left({\boldsymbol{z}}_{u}\right|{\tilde{\boldsymbol{x}}}_{i}) $ | (9) |
其中:
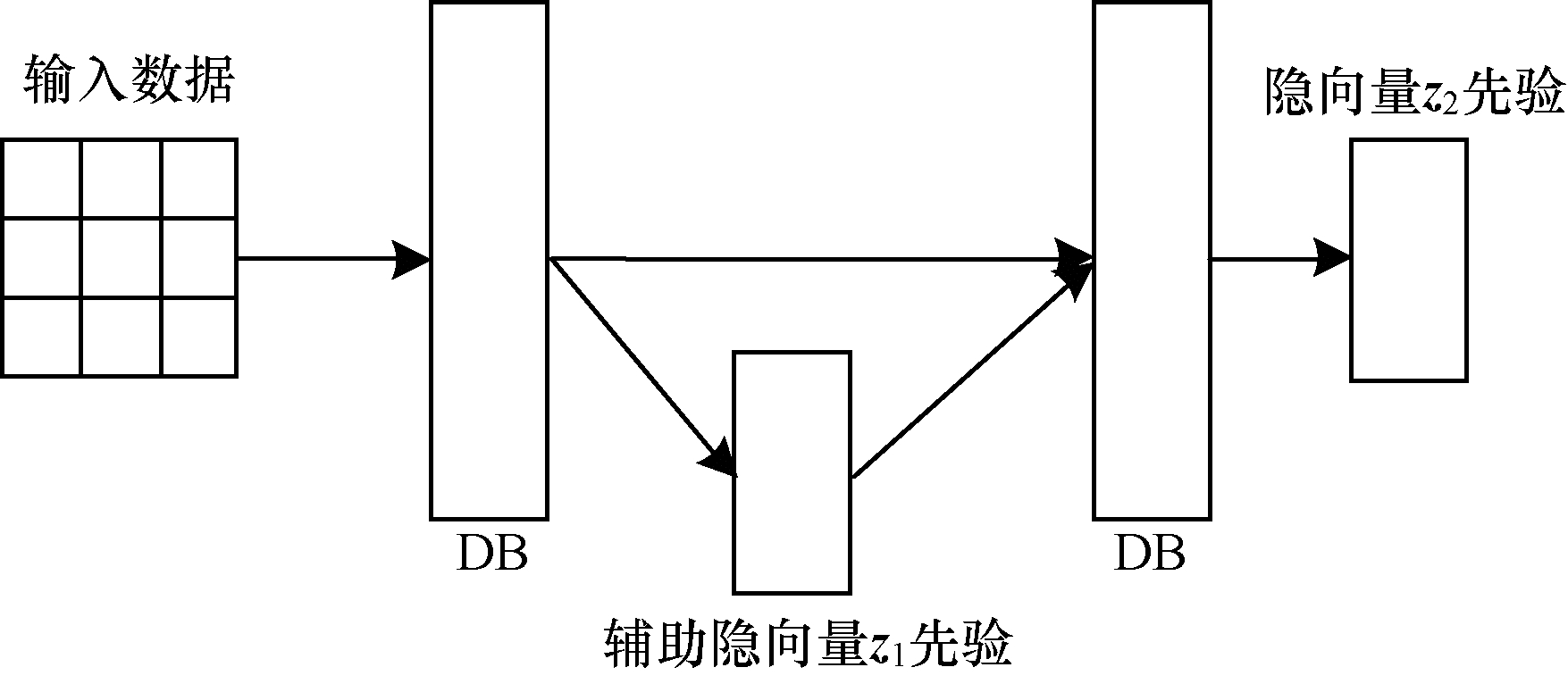
如图 4所示,在伪输入模块中,首先将输入数据
| $ {\mu }_{1}={\sigma }_{1}=\mathrm{D}{\mathrm{B}}_{2}\left(a\times \mathrm{D}{\mathrm{B}}_{1}\left(\tilde{\boldsymbol{x}}\right)\right) $ | (10) |
| $ {\boldsymbol{z}}_{1}={\mu }_{1}+{\sigma }_{1}\times \varepsilon , \varepsilon ~N(0, I) $ | (11) |
|
Download:
|
| 图 4 伪输入模块结构 Fig. 4 Pseudo input module structure | |
|
Download:
|
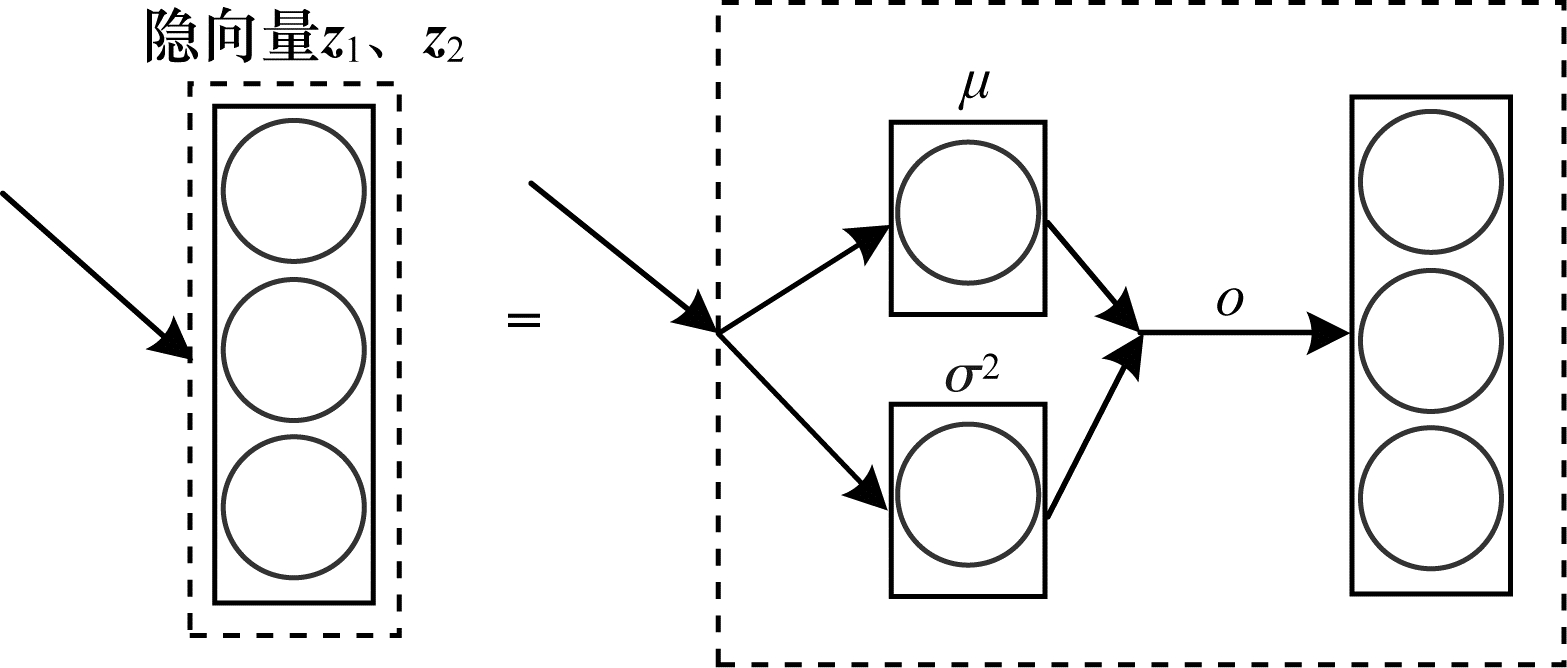
| 图 5 隐向量模块 Fig. 5 Hidden vector module | |
接着将
| $ {\mu }_{2}={\sigma }_{2}=\mathrm{D}{\mathrm{B}}_{2}\left(\left(a\times \mathrm{D}{\mathrm{B}}_{1}\left(\tilde{\boldsymbol{x}}\right)\right)\otimes {\boldsymbol{z}}_{1}\right) $ | (12) |
| $ {\boldsymbol{z}}_{2}={\mu }_{2}+{\sigma }_{2}\times \varepsilon $ | (13) |
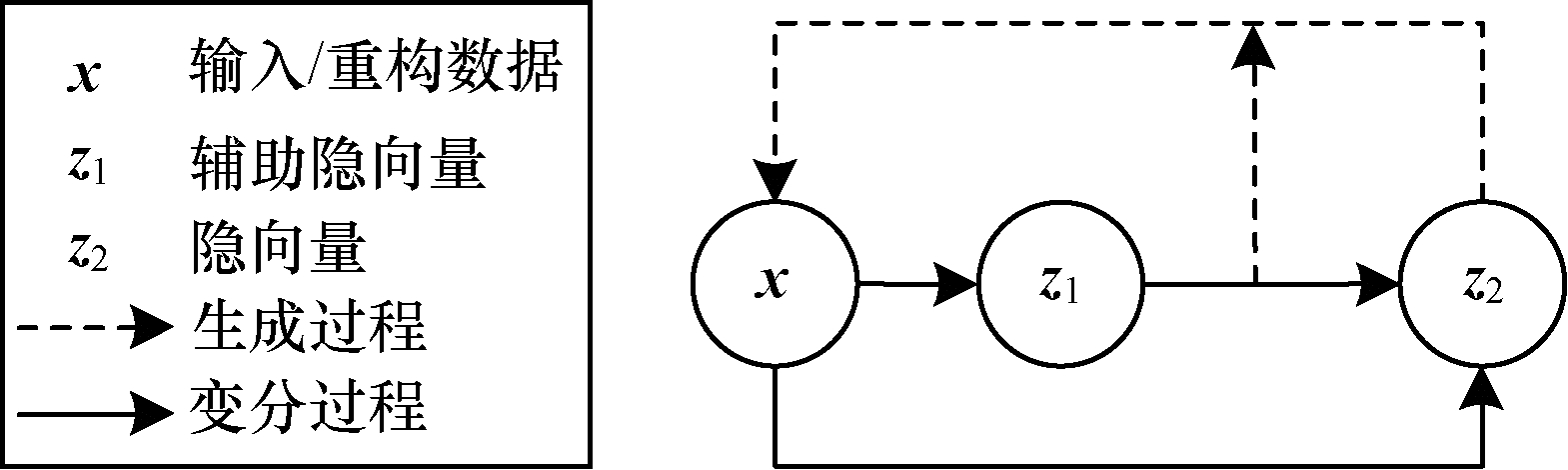
在训练过程中,传统的变分自动编码器模型经常出现隐向量非激活情况,这种情况会随着网络深度的加深变得更加严重。为解决该问题,在模型中添加辅助隐向量,双隐向量结构如图 6所示,包含x作为输入数据的变分过程和x作为生成数据的生成过程。
|
Download:
|
| 图 6 双隐向量结构 Fig. 6 Double implicit vector structure | |
变分过程如式(14)所示:
| $ {q}_{\varphi }\left({\boldsymbol{z}}_{u}^{2}\right|{\boldsymbol{x}}_{u}, {\boldsymbol{z}}_{u}^{1}\left){q}_{\delta }\right({\boldsymbol{z}}_{u}^{1}\left|{\boldsymbol{x}}_{u}\right) $ | (14) |
生成过程如式(15)所示:
| $ {p}_{\theta }\left({\boldsymbol{x}}_{u}\right|{\boldsymbol{z}}_{u}^{1}, {\boldsymbol{z}}_{u}^{2}) $ | (15) |
其中:
最终得到带有辅助隐向量的损失函数,如式(16)所示:
| $ \begin{array}{l}L({\boldsymbol{x}}_{u};\theta , \varphi , \lambda )={{\rm E}}_{{q}_{\varphi }\left({\boldsymbol{z}}_{u}^{2}\right|{\boldsymbol{x}}_{u}, {\boldsymbol{z}}_{u}^{1}\left){q}_{\delta }\right({\boldsymbol{z}}_{u}^{1}\left|{\boldsymbol{x}}_{u}\right)}\left[\mathrm{l}\mathrm{g}{p}_{\theta }({\boldsymbol{x}}_{u}|{\boldsymbol{z}}_{u}^{1}, {\boldsymbol{z}}_{u}^{2})\right]-\\ {{\rm E}}_{{q}_{\varphi }\left({\boldsymbol{z}}_{u}^{2}\right|{\boldsymbol{x}}_{u}, {\boldsymbol{z}}_{u}^{1}\left){q}_{\delta }\right({\boldsymbol{z}}_{u}^{1}\left|{\boldsymbol{x}}_{u}\right)}\left[\mathrm{l}\mathrm{g}({q}_{\varphi }({\boldsymbol{z}}_{u}^{2}|{\boldsymbol{x}}_{u}, {\boldsymbol{z}}_{u}^{1}){q}_{\delta }({\boldsymbol{z}}_{u}^{1}\left|{\boldsymbol{x}}_{u}\right))+\mathrm{l}\mathrm{g}{q}_{\delta }({\boldsymbol{z}}_{u}^{1}|{\boldsymbol{x}}_{u})\right]-\\ {{\rm E}}_{{q}_{\varphi }\left({\boldsymbol{z}}_{u}^{2}\right|{\boldsymbol{x}}_{u}, {\boldsymbol{z}}_{u}^{1}\left){q}_{\delta }\right({\boldsymbol{z}}_{u}^{1}\left|{\boldsymbol{x}}_{u}\right)}\left[-\mathrm{l}\mathrm{g}{p}_{\lambda }({\boldsymbol{z}}_{u}^{1})-\mathrm{l}\mathrm{g}p({\boldsymbol{z}}_{u}^{2})\right]\end{array} $ | (16) |
随着近些年深度学习的快速发展,注意力机制已成为计算机视觉、自然语言处理、语音识别等领域的重要技术[17-19]。Transformer[20]等神经网络模型与注意力机制相结合后,性能得到大幅提升。
隐向量作为用户-物品评分数据的高维表示,对于重构数据起着至关重要的作用。因为隐向量非激活问题也同样影响着重构数据的质量,所以本文通过融合注意力机制,对隐向量中含有重要信息的节点赋予更大的权重值,增强重要信息在重构数据中的作用;对于不重要的信息赋予更小的权重值,弱化其在重构数据中的影响,同时也减少了噪声。
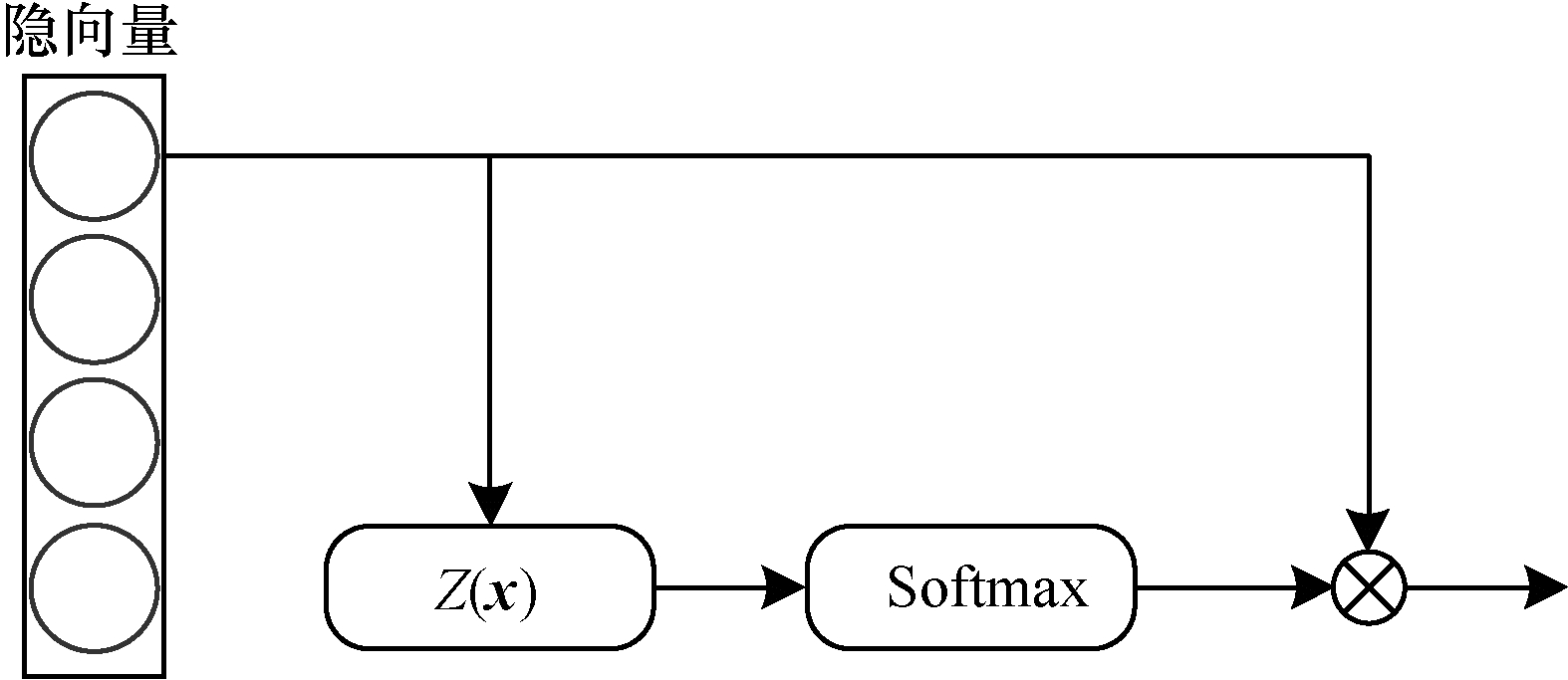
在注意力模块中,首先将隐向量输入函数Z生成注意力得分,然后经过Softmax函数,对注意力得分进行0-1范围映射,将其转化为和为1的概率值,最后将概率值与隐向量做乘积,如式(17)~式(19)所示,注意力模块结构如图 7所示。函数Z的选择很多,本文仅使用带有激活函数的全连接层作为函数Z。
| $ Z=\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left(w\boldsymbol{x}\right) $ | (17) |
| $ a=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(Z\right) $ | (18) |
| $ {o}_{\mathrm{o}\mathrm{u}\mathrm{t}}=a\times \boldsymbol{x} $ | (19) |
|
Download:
|
| 图 7 注意力模块 Fig. 7 Attention module | |
其中:w是全连接层权重;Z是注意力评分;a是经过0-1范围映射的评分值;
采用4个公开的数据集Movielens-1M(ML-1M)、Movielens-Latest-Small(ML-LS)、Movielens-20M(ML-20M)、Netflix测试模型性能,数据集包含用户对物品的评分,评分范围为[1, 5]。数据集介绍具体如下:
1) ML-1M数据集是Movielens数据集之一,包括6×103个用户、4×103部电影和1×108个电影评分。
2) ML-LS数据集来源于Movielens电影网站,能够进行自动采集更新,包含6×102个用户、9×103部电影和1×105个电影评分。
3) ML-20M数据集来源于Movielens电影网站2015年4月提供的数据,包括1.38×105个用户、2.7×104部电影和2×107个电影评分。
4) Netflix数据集来源于电影租赁网站Netflix 2005年公布的数据,包含4.8×105个用户、1.7×104部电影和1×108个电影评分。
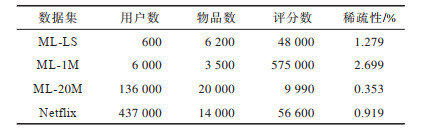
数据集详细信息如表 1所示。
|
下载CSV 表 1 数据集详细信息 Table 1 Dataset details |
为测试模型在强泛化下的性能,对数据集进行如下处理[20]:
1) 将数据集划分为训练集(80%)、验证集(10%)、测试集(10%)3个部分,使用训练集的用户历史点击记录训练模型。首先从验证集和测试集的用户中获取一部分历史点击记录了解模型性能表现,然后通过查看模型对其他未显示的历史点击记录的排名来计算性能指标。
2) 对数据集进行预处理。首先将用户-项目评分表转化为值为0或1的二值化矩阵,将其作为隐式反馈表,具体方式是将评分大于3.5的值设为1,评分小于或者等于3.5的值设为0;然后移除评分次数少于5的用户。
3.3 实验环境设置CCPAM-VAE模型算法由Python语言实现。实验硬件设备为Intel® CoreTM i7-8700 @3.2 GHz处理器,GeForce RTX 2080Ti 11 GB显卡,32 GB运行内存。为了使模型达到较好的效果,使用网格搜索法进行超参数搜索。超参数搜索范围如表 2所示。使用Adam优化器[21]训练模型,使用ReLU作为层与层之间的激活函数。采用Xavier随机初始化[22]对模型参数进行初始化,保证了每层输出的方差不受该层输入个数影响,且每层梯度的方差也不受该层输出个数影响。

|
下载CSV 表 2 超参数取值范围 Table 2 Super-parameter value ranges |
Multi-DAE[5]将DAE应用于协同过滤算法,并使用多项式逻辑似然函数替代经典高斯似然函数,实验结果证明其取得了不错的效果。
Multi-VAE[5]将VAE应用于协同过滤算法,并使用β-VAE[4]损失函数,其中超参数β作为重建损失和KL损失之间的权衡参数添加到损失函数中。
Macrid-VAE[7]在Multi-VAE的基础上,将神经网络拟合生成的类别向量矩阵与输入相乘,对输入数据高维度和低维度解耦,增强了模型的可解释性。
CDAE[7]将用户潜在因素作为额外输入,添加到标准去噪自动编码器模型中。与标准去噪自动编码器模型一样,使用Dropout方式对输入数据添加噪声。
NCF[23]构建用于协同过滤的神经网络特征学习框架,并将用户和物品潜在特征输入到该框架中。
3.5 评估指标在测试集上,CCPAM-VAE模型使用NDCG@K和Recall@K两个评估指标为每个用户预测项目排名,并将其与真实项目排名进行比较。
DCG@K为折损累计增益,是一种对排序结果的评价指标,用户u的DCG@K如式(20)所示,其中,
| $ \mathrm{D}\mathrm{C}\mathrm{G}@{K}_{u}=\sum\limits_{i=1}^{k}\frac{{2}^{{\rm I}\left[r\right(i)\in {T}_{u}]}-1}{\mathrm{l}\mathrm{g}\left(i+1\right)} $ | (20) |
Recall@K为召回率,是一种衡量推荐效果的指标,用户u的Recall@K如式(21)所示,其中分母是K和用户点击的物品数的最小值。
| $ \mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}@{K}_{u}=\frac{\sum\limits_{i=1}^{K}{\rm I}\left[r\right(i)\in {T}_{u}]}{\mathrm{m}\mathrm{i}\mathrm{n}(K, |{T}_{u}\left|\right)} $ | (21) |
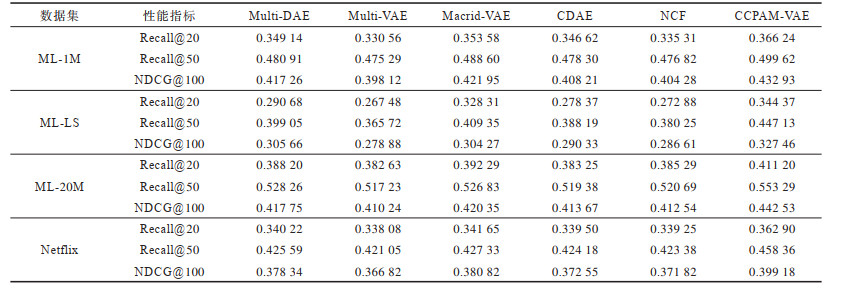
表 3从Recall@20、Recall@50、NDCG@100 3个指标对CCPAM-VAE模型进行评估,在数据集ML-1M上,指标平均提升了10.79%、5.12%、8.74%;在数据集ML-LS上,指标平均提升了26.20%、22.26%、17.42%;在数据集ML-20M上,指标平均提升了7.47%、6.97%、6.97%;在数据集Netflix上,指标平均提升了7.34%、8.86%、8.82%。上述结果表明,相较于基线模型,本文模型不仅在大数据集ML-1M、ML-20M、Netflix上有较好的表现,在小数据集ML-LS上也有不错的效果。这表明复杂先验能够帮助模型学习更加复杂的数据关系,减少模型出现过拟合的情况。同时,基线模型Macrid-VAE在这4个数据集上的表现要优于其他基线模型,这表明高维度解耦能够显著提升性能。
|
下载CSV 表 3 CCPAM-VAE模型与基线模型的性能对比 Table 3 Performance comparison among CCPAM-VAE model and baseline models |
图 8给出了当隐藏层维度d取100、200、300、400、500而其他参数不变的情况下,CCPAM-VAE模型在4个数据集上的NDCG@100值。从图 8可以看出,隐藏层维度的增加不一定能带来模型性能的提升,过高维度或者过低维度会导致模型过拟合或者欠拟合的现象,使模型表现不佳。对于数据集ML-LS,在隐藏层维度d=200时,模型性能达到最佳。对于数据集ML-1M、ML-20M、Netflix,隐藏层维度d=300时,模型性能达到最佳。这说明对于不同规模的数据集,模型达到最佳性能所需的隐藏层维度不一定是相同的。

|
Download:
|
| 图 8 隐藏层维度对NDCG@100的影响 Fig. 8 Impact of hidden layer dimensions on NDCG@100 | |
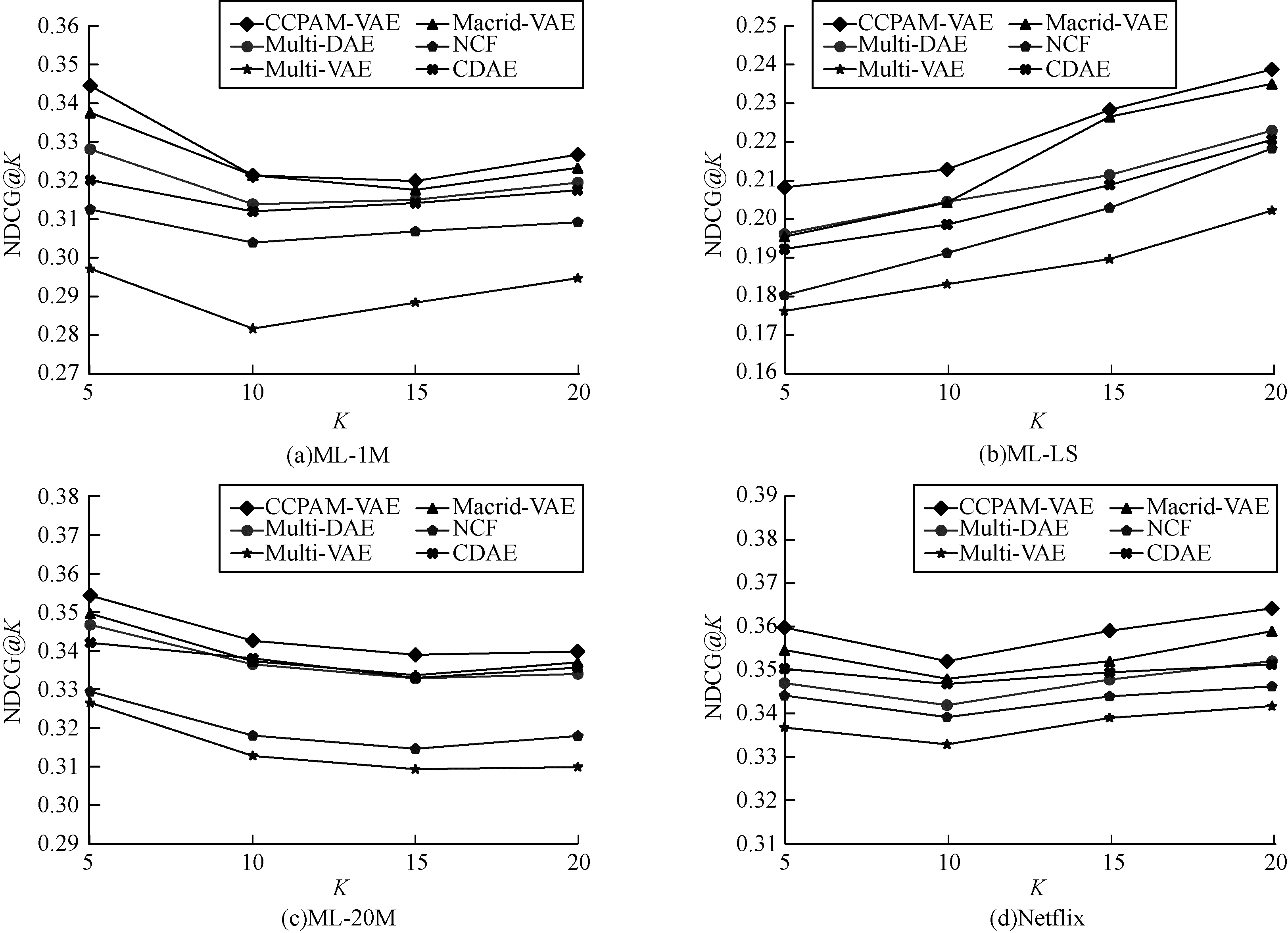
图 9给出了当K取5、10、15、20时,CCPAM-VAE模型和基线模型在4个数据集上的NDCG@K值。在数据集ML-20M、Netflix、ML-1M上,当K取5时,NDCG@K的值几乎最大,这表明在数据量比较大的情况下,CCPAM-VAE模型和基线模型不仅适合对物品进行Top-K推荐,而且适合应用于推荐数量有限的场景。在数据量较小的数据集ML-LS中,随着K值的增大,NDCG@K的值也不断增大,这表明在数据量比较小的情况下,CCPAM-VAE模型和基线模型不适合进行Top-K推荐。由此可见,CCPAM-VAE模型在4个数据集上的表现均优于基线模型。
|
Download:
|
| 图 9 CCPAM-VAE模型与基线模型在4个数据集上的NDCG@K对比 Fig. 9 NDCG@K comparison among CCPAM-VAE model and baseline models on four datasets | |
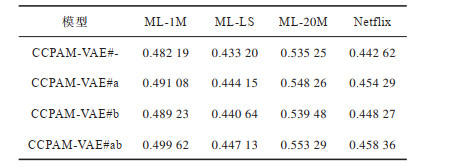
在数据集ML-1M、ML-LS、ML-20M和Netflix上对CCPAM-VAE模型的复杂先验和注意力模块进行有效性验证,结果如表 4所示。其中,#-表示不使用复杂先验和注意力模块,#a表示使用复杂先验,#b表示添加注意力模块,#ab表示使用复杂先验和注意力模块。从表 4可以看出,独立使用复杂先验和添加注意力模块均能提升模型精确度,将两者同时加入CCPAM-VAE模型,可使模型精确度达到最佳。
|
下载CSV 表 4 CCPAM-VAE模型消融实验的Recall@50对比 Table 4 Recall@50 comparison of ablation experiment of CCPAM-VAE model |
本文提出融合复杂隐向量先验与注意力机制的变分自动编码器模型,使用复杂隐向量先验分布使模型获得更多的潜在表征,通过添加辅助隐向量增加隐向量的低维表现能力和解耦性。在公开的数据集Movielens-1M、Movielens-Latest-Small、Movielens-20M和Netflix上,基于Recall@20、Recall@50和NDCG@100指标进行性能评估,验证了该模型相较于基线模型能够有效提高推荐精确度。但由于本文仅将评分矩阵作为模型输入,在后续研究中还将在变分自动编码器中融入知识图谱、图神经网络[24-25]等更复杂的数据形式和数据关系,进一步研究其对推荐效果的影响。
| [1] |
刘华玲, 马俊, 张国祥. 基于深度学习的内容推荐算法研究综述[J]. 计算机工程, 2021, 47(7): 1-12. LIU H L, MA J, ZHANG G X. Review of studies on deep learning-based content recommendation algorithms[J]. Computer Engineering, 2021, 47(7): 1-12. (in Chinese) |
| [2] |
FELFERNIG A, JERAN M, NINAUS G, et al. Toward the next generation of recommender systems: applications and research challenges[M]//TSIHRINTZIS G A, VIRVOU M, JAIN L C. Multimedia services in intelligent environments. Berlin, Germany: Springer, 2013: 81-98.
|
| [3] |
HU Y F, KOREN Y, VOLINSKY C. Collaborative filtering for implicit feedback datasets[C]//Proceedings of the 8th IEEE International Conference on Data Mining. Washington D. C., USA: IEEE Press, 2009: 263-272.
|
| [4] |
HE X N, LIAO L Z, ZHANG H W, et al. Neural collaborative filtering[C]//Proceedings of International World Wide Web Conferences Steering Committee. Washington D. C., USA: IEEE Press, 2017: 173-182.
|
| [5] |
BURGESS C P, HIGGINS I, PAL A, et al. Understanding disentangling in β-VAE[EB/OL]. [2021-10-07]. https://arxiv.org/abs/1804.03599.
|
| [6] |
LIANG D W, KRISHNAN R G, HOFFMAN M D, et al. Variational autoencoders for collaborative filtering[C]//Proceedings of 2018 World Wide Web Conference. New York, USA: ACM Press, 2018: 689-698.
|
| [7] |
POLATO M, CARRARO T, AIOLLI F. Conditioned variational autoencoder for top-N item recommendation[EB/OL]. [2021-10-07]. https://arxiv.org/abs/2004. 11141.
|
| [8] |
SIDDHARTH N, PAIGE B, DESMAISON A, et al. Learning disentangled representations for recommendation[EB/OL]. [2021-10-07]. http://stat.columbia.edu/~cunningham/teaching/GR8201/STAT_GR8201_2019_SPRG_slides.pdf.
|
| [9] |
KINGMA D P, WELLING M. Auto-encoding variational Bayes[EB/OL]. [2021-10-07]. https://arxiv.org/abs/1312. 6114v4.
|
| [10] |
MIAO Y S, YU L, BLUNSOM P. Neural variational inference for text processing[EB/OL]. [2021-10-07]. https://arxiv.org/abs/1511.06038.
|
| [11] |
LU Y, HUANG B. Structured output learning with conditional generative flows[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 5005-5012. |
| [12] |
TAHIR R, SARGANO A B, HABIB Z. Voxel-based 3D object reconstruction from single 2D image using variational autoencoders[J]. Mathematics, 2021, 9(18): 2288. |
| [13] |
SOHN K, YAN X C, LEE H, et al. Learning structured output representation using deep conditional generative models[C]//Proceedings of International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2015: 3483-3491
|
| [14] |
BOUCHACOURT D, TOMIOKA R, NOWOZIN S. Multi-level variational autoencoder: learning disentangled representations from grouped observations[C]//Proceedings of AAAI Conference on Artificial Intelligence. Palo Alto, USA: AAAI Press, 2018: 1-10.
|
| [15] |
OUYANG Y X, LIU W Q, RONG W G, et al. Autoencoder-based collaborative filtering[M]. Berlin, Germany: Springer, 2014.
|
| [16] |
HINTON G E, SRIVASTAVA N, KRIZHEVSKY A, et al. Improving neural networks by preventing co-adaptation of feature detectors[EB/OL]. [2021-10-07]. https://arxiv.org/abs/1207.0580.
|
| [17] |
LUONG M T, PHAM H, MANNING C D. Effective approaches to attention-based neural machine translation[EB/OL]. [2021-10-07]. https://arxiv.org/abs/1508. 04025.
|
| [18] |
SPERBER M, NIEHUES J, NEUBIG G, et al. Self-attentional acoustic models[EB/OL]. [2021-10-07]. https://arxiv.org/abs/1803.09519v1.
|
| [19] |
BRAUN S, NEIL D, ANUMULA J, et al. Multi-channel attention for end-to-end speech recognition[EB/OL]. [2021-10-07]. https://www.researchgate.net/publication/327388671_Multi-channel_Attention_for_End-to-End_ Speech_Recognition.
|
| [20] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[EB/OL]. [2021-10-07]. https://arxiv.org/abs/1706.03762.
|
| [21] |
KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. [2021-10-07]. https://arxiv.org/abs/1412.6980.
|
| [22] |
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of International Conference on Artificial Intelligence and Statistics. Washington D. C., USA: IEEE Press, 2010: 249-256.
|
| [23] |
HE X N, LIAO L Z, ZHANG H W, et al. Neural collaborative filtering[C]//Proceedings of the 26th International Conference on World Wide Web. Geneva, Switzerland: International World Wide Web Conferences Steering Committee, 2017: 1-8.
|
| [24] |
JI S, PAN S, CAMBRIA E, et al. A survey on knowledge graphs: representation, acquisition, and applications[EB/OL]. [2021-10-07]. https://blog.csdn.net/byn12345/article/details/106128275.
|
| [25] |
WANG X, HE X N, WANG M, et al. Neural graph collaborative filtering[C]//Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM Press, 2019: 165-174.
|
 2022, Vol. 48
2022, Vol. 48

 ,
,