开放科学(资源服务)标志码(OSID)：

0 概述

深度学习具有可直接从数据中提取和学习特征的优势，是计算机视觉领域中的重要方法，其中卷积神经网络（Convolutional Neural Network，CNN）^[1]在深度学习中扮演了重要角色。自LECUN等^[2]于1998年提出Le-Net后，CNN不断发展并取得了巨大成功。一系列优越CNN结构的提出是CNN取得成功的重要原因，如AlexNet^[3]、VGG^[4]、GoogLeNet^[5]、ResNet^[6]、DenseNet^[7]、MobileNet^[8]、SENet^[9]等。近年来，CNN的发展逐渐由特征参数的调整转向结构的创新，每个结构的性能都因结构的创新而不断提高。

上述手动设计的网络结构，有许多巧妙的结构仍旧影响着网络结构的设计，例如3×3卷积核、跳跃连接等。然而，创新设计CNN结构并非易事，需要大量的专业知识，这对需要使用CNN结构的其他职业人员并不友好，限制了CNN更好地应用于实际任务。近年来，为了获得更好的CNN结构，出现了神经网络结构搜索（Neural Architecture Search，NAS）算法。NAS算法由于具有高度的自动化和智能化特性，引起了广泛研究和讨论。

NAS算法最初可分为基于强化学习（Reinforcement Learning，RL）和基于进化算法（Evolutionary Algorithm，EA）两类，基于RL的NAS算法又分为Q-learning和策略梯度两种类型。Q-learning方法从有限的搜索空间中通过学习代理模型来选择CNN架构^[10]。相比之下，基于策略梯度的方法以递归神经控制器为特征来生成模型，其参数由一系列策略梯度算法更新^[11]。近端策略优化NASNet^[12]在RL算法的基础上，使用了一种新的基于单元的搜索空间和正则化技术，并重复堆叠相同单元^[13]。基于RL可以搜索出准确性较好的网络结构，但是在搜索中会耗费大量的计算资源，如NASNet^[12]需要2 000个GPU Days，MetaQNN^[14]需要100个GPU Days，Block-QNN-S^[15]需要32个GPU Days。

EA将NAS看作一个优化问题，通过进化过程来不断演化神经网络结构，近期的研究成果有AmeobaNet-A^[16]、AE-CNN^[17]、FAE-CNN^[18]、NASG-Net^[19]等。基于EA的NAS算法也需消耗大量计算资源，如Genetic CNN^[20]需要17个GPU Days，AmoebaNet需要3 150个GPU Days，AE-CNN和CNN-GA^[21]分别需要27个和35个GPU Days。FAE-CNN通过划分数据集方法将搜索时间缩短为3.5个GPU Days，但也因此增大了不稳定性。

最近，可微结构搜索（Differentiable Architecture Search，DARTS）^[22]作为一种新的NAS算法被提出，取得了比基于RL和EA的NAS算法更好的分类效果，并且仅需要4个GPU Days。但是DARTS为了减少时间和资源开销，在搜索阶段和评估阶段体系结构大小不同，存在深度鸿沟^[23]，这导致了搜索评估的不相关性。针对DARTS存在的深度鸿沟等问题，研究人员提出了相应的改进。P-DARTS^[23]使用了渐进式搜索方法，将搜索阶段分为结构逐步增大的三个阶段，一定程度上减少了深度鸿沟的影响。同样针对搜索评估不相关性，SGAS^[24]使用了一种贪心结构搜索算法，通过选边指标来提升搜索阶段评估的相关性，使得搜索过程中的验证准确度与评价过程中的测试准确度相关程度更高。虽然SGAS将CIFAR-10上的错误率降低到2.39%，但在10组实验中稳定性不高，错误率最高达到3.18%，存在平方差较大、不稳定的情况。

本文针对DARTS及其改进算法深度鸿沟和搜索稳定性不高的问题，提出一种快速渐进式NAS（Fast and Progressive NAS，FPNAS）算法，通过结合渐进性搜索和贪心搜索中的选边指标，增强搜索阶段和评估阶段的相关性，提高搜索稳定性。同时，在渐进式搜索中使用划分数据集方法，减少搜索的资源和时间开销。

1 快速渐进式卷积神经网络搜索 1.1 可微结构搜索算法

在连续域搜索方法^[25-26]的基础上，DARTS^[22]引入了一种连续松弛的体系结构表示方法，使体系结构搜索可微化。DARTS采用了NASNet^[12]中Cell和Block的设计方法，将搜索问题简化为寻找最优单元（Cell），并将该单元作为基础单元堆叠多次构成最终的卷积神经网络。基于单元的NAS方法可得到可伸缩和移植性强的结构。DARTS避免了挑选子网络的过程，其将单元中所有的可能性以参数化的形式表示，最核心的步骤是利用Softmax函数来选择连接，优化后再选取Softmax输出概率最大的连接方式^[27]。在训练时，单元中所有的可能性连接和操作都会进行前向计算和反向推理，所有操作的模型参数都会进行更新，可能性更大的参数有更多的梯度更新。在搜索过程中，一个单元被定义为一个由N个节点组成的有向无环图，其中每个节点是一个网络层。搜索空间被表示为$ \mathcal{O} $，其中每个元素表示一个候选函数o（$ \cdot $）。一个边（$ i $，$ j $）表示连接节点$ i $和节点$ j $的信息，由一组由体系结构参数$ {\alpha }^{(i, j)} $加权的操作组成。两个节点间的操作可以表示为：

$ {\stackrel{-}{o}}^{(i, j)}\left({x}^{\left(i\right)}\right)=\sum\limits _{o\in \mathcal{O}}\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\alpha }_{o}^{(i, j)}\right)}{\sum\limits _{{o}^{'}\in \mathcal{O}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\alpha }_{{o}^{'}}^{(i, j)}\right)}\cdot o\left({x}^{\left(i\right)}\right) $

(1)

式（1）表示两个节点之间的操作是它们之间所有操作的Softmax之和，其中$ i $ < $ j $，中间任意一个节点可以表示为：

$ {x}^{\left(j\right)}=\sum\limits _{i < j}{\stackrel{-}{o}}^{(i, j)}\left({x}^{\left(i\right)}\right) $

(2)

式（3）表示通过对所有中间节点进行归约运算得到一个单元的输出，其中concat（$ \cdot $）函数连接通道维度中的所有输入信号。

$ {x}_{N-1}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({x}_{2}, {x}_{3}, \cdots , {x}_{N-2}\right) $

(3)

DARTS结构训练是一个双重优化的过程，需要交替对网络的模型参数$ \mathcal{W} $和结构参数$ \mathcal{A} $进行优化，优化的两个目标函数如式（4）和式（5）所示，其中$ {\mathcal{L}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}} $和$ {\mathcal{L}}_{\mathrm{v}\mathrm{a}\mathrm{l}} $分别表示训练损失和验证损失。

$ \underset{\mathcal{A}}{\mathrm{m}\mathrm{i}\mathrm{n}}\;{\mathcal{L}}_{\mathrm{v}\mathrm{a}\mathrm{l}}\left({\mathcal{W}}^{\mathcal{*}}\left(\mathcal{A}\right), \mathcal{A}\right) $

(4)

$ \mathrm{s}.\mathrm{t}.{\mathcal{W}}^{\mathcal{*}}\left(\mathcal{A}\right)=\underset{\mathcal{W}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}{\mathcal{L}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}(\mathcal{W}, \mathcal{A}) $

(5)

1.2 快速渐进式卷积神经网络搜索算法

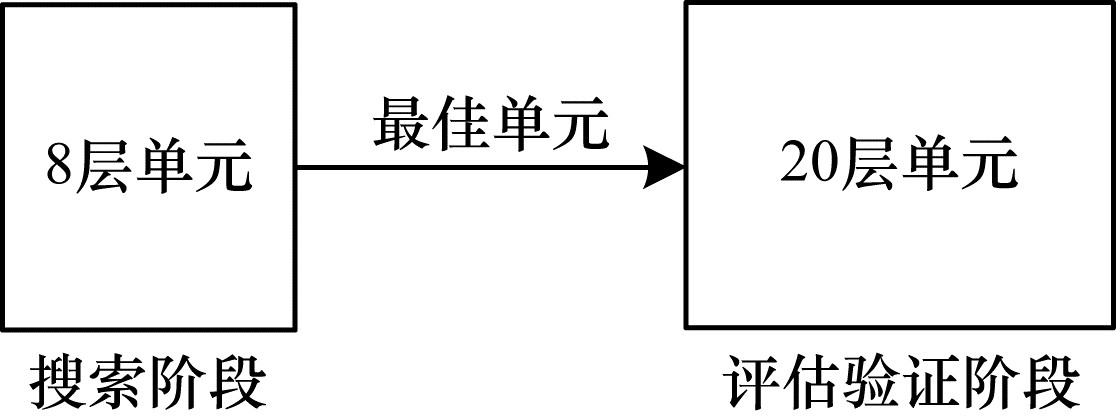
如图 1所示，出于对搜索时间的考虑，DARTS^[22]在搜索阶段中的网络结构包含8层单元，而在评估验证阶段，将搜索阶段搜索到的最佳单元扩充为20层，组成最终的网络结构。

这种搜索方式可以大幅减少搜索的时间以及计算资源消耗，但搜索和评估阶段层数不对等，导致搜索评估相关性低，会造成结构性能的波动。在搜索阶段准确度表现很好的单元，经过扩充之后，性能反而会下降，出现深度鸿沟现象^[23]。对此，本文提出结合渐进式搜索以及贪心指标的搜索算法FPNAS，其中包含两部分，一是通过结合贪心选边指标和渐进式搜索来提高搜索的稳定性，二是使用划分数据集方法来加速搜索并在一定程度上减轻过拟合。

1.2.1 渐进式搜索方法

SGAS^[24]针对DARTS搜索过程的不相关性，考虑了影响边选择的重要因素：边的重要性（Edge Importance，EI）和选择确定性（Selection Certainty，SC），并通过这两个因素提高搜索评估的相关性。

根据这两个影响边选择的因素，SGAS提出了选边指标$ {S}_{1}^{(i, j)} $，指标用于衡量选边的重要性和确定性^[24]，可用式（6）表示：

$ {S}_{1}^{(i, j)}=\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e}\left({S}_{\mathrm{E}\mathrm{I}}^{(i, j)}\right)\times \mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e}\left({S}_{\mathrm{S}\mathrm{C}}^{(i, j)}\right) $

(6)

$ {S}_{\mathrm{E}\mathrm{I}}^{(i, j)} $为边的重要性，如果某条边非零运算选择的可能性越高，则表明这条边越重要。$ {S}_{\mathrm{E}\mathrm{I}}^{(i, j)} $可通过式（7）计算：

$ {S}_{\mathrm{E}\mathrm{I}}^{(i, j)}=\sum\limits _{o\in \mathcal{O}, o\ne 0}\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\alpha }_{o}^{(i, j)}\right)}{\sum\limits _{{o}^{'}\in \mathcal{O}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\alpha }_{{o}^{'}}^{(i, j)}\right)} $

(7)

另一个选边因素$ {S}_{\mathrm{S}\mathrm{C}}^{(i, j)} $代表选择确定性，由于熵是概率分布中用来度量不确定性的量，因此SGAS将选择确定性定义为操作分布归一化熵的总和^[24]。$ {S}_{\mathrm{S}\mathrm{C}}^{(i, j)} $可通过式（8）计算：

$ {S}_{\mathrm{S}\mathrm{C}}^{(i, j)}=1-\frac{-\sum\limits _{o\in \mathcal{O}, o\ne 0}{p}_{o}^{(i, j)}\mathrm{l}\mathrm{n }{p}_{o}^{(i, j)}}{\mathrm{l}\mathrm{n}\left(\right|\mathcal{O}|-1)} $

(8)

式（8）中的$ {p}_{o}^{(i, j)} $是一种分布，代表着非零运算的归一化权重，可以用式（9）表示：

$ {p}_{o}^{(i, j)}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\alpha }_{o}^{(i, j)}\right)}{{S}_{\mathrm{E}\mathrm{I}}^{(i, j)}\sum\limits _{{o}^{'}\in \mathcal{O}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\alpha }_{{o}^{'}}^{(i, j)}\right)} $

(9)

虽然SGAS通过选择准则提高了搜索评估的相关性，但是搜索过程中仍然使用单元数为8的结构。由于深度鸿沟的影响，导致最终结果的上下限差别较大，准确率最高达到97.62%，而最低准确率却只有96.82%，并且10组数据的平方差达到了0.24，最终的结果波动较大。为了解决这一问题，本文使用渐进式搜索方法在搜索阶段逐步增加结构单元层数，三个渐进式阶段包含的单元数分别为5、11和17，与P-DARTS设置相同。为了减少因层数增加而增加的计算量，在每个阶段对搜索空间进行校正，减少候选操作数量^[23]。在渐进式搜索过程中加入贪心搜索SGAS中的选边指标$ {S}_{1}^{(i, j)} $，每次渐进式搜索迭代将$ {S}_{1}^{(i, j)} $作为评估标准进行选边，在高稳定性的基础上通过贪心指标来增强搜索评估之间的相关性。

1.2.2 渐进式划分数据集方法

为降低搜索成本，本文使用渐进式划分数据集方法，在渐进式搜索的三个阶段中按不同比例对数据集进行划分。划分数据集方法具有两个优点：一是划分数据集可以大幅减少搜索时间，在划分的数据集上，由于图片数量较少，种类和完备数据集一样，因此在搜索阶段所消耗的时间是远少于完备数据集的；二是在划分数据集上训练的指定代数，远小于模型达到稳定时所需要的训练代数，这在一定程度上可以减轻过拟合。

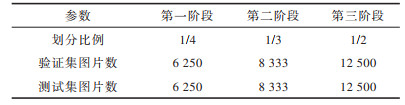
使用划分数据集方法可以减少计算资源和时间的消耗。但是，划分数据集方法只在一定比例的数据集上进行模型训练，这样得到的训练准确度往往不可靠。针对这一问题，本文对划分数据集过程进行了渐进式校正，具体参数如表 1所示。在渐进式方法中，将搜索阶段分为层数为5、11和17三个阶段，每个阶段分别以1/4、1/3和1/2的比例进行划分，比例逐渐增加。三个阶段训练集图片数量依次为6 250、8 333和12 500，因为搜索阶段对于数据集训练测试的比例为1︰1，所以测试集与训练集相同。渐进式的划分方法可以在一定程度上减少划分数据集带来的不可靠性，同时大幅缩短搜索时间。

1.2.3 FPNAS算法总体流程

FPNAS的算法流程如算法1所示，具体步骤如下：

1）初始化算法参数，输入搜索结构的通道数16，渐进式搜索阶段数3，每个阶段迭代次数25。

2）创建网络参数$ \mathcal{W} $和结构参数$ \mathcal{A} $，并对每个边创建混合操作集合$ {\stackrel{-}{o}}^{(i, j)} $。为了使搜索过程更稳定，搜索过程分3个搜索阶段依次进行，每个阶段的结构层数逐渐增加，每个阶段迭代25次，每次迭代更新网络参数和结构参数，并通过选择确定性的贪心指标$ {S}_{1}^{(i, j)} $进行最优选边。为了使搜索过程更快速，在三次搜索阶段分别以不同的比例对数据集进行划分，减少搜索成本。

3）通过迭代选边最终选择的操作集合搭建CNN结构。

算法1   FPNAS算法

输入  通道数c，阶段数s，迭代次数T，划分数据集

输出  通过选择的操作构造的最终CNN结构

1.创建结构参数$ \mathrm{A}=\left\{{\mathrm{\alpha }}^{(\mathrm{i}, \mathrm{j})}\right\} $和网络权重$ \mathrm{W} $；

2.对每个边（i，j）创建由$ {\mathrm{\alpha }}^{(\mathrm{i}, \mathrm{j})} $参数化的混合操作集合$ {\stackrel{-}{\mathrm{o}}}^{(\mathrm{i}, \mathrm{j})} $；

3.for s=1，2，3 do

4.while t < T do；

5.在划分数据集上通过梯度下降$ {\nabla }_{\mathrm{A}}{\mathrm{L}}_{\mathrm{v}\mathrm{a}\mathrm{l}}(\mathrm{W}, \mathrm{A}) $更新结构参数$ \mathrm{A} $；

6.在划分数据集上通过梯度下降$ {\nabla }_{\mathrm{W}}{\mathrm{L}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}(\mathrm{W}, \mathrm{A}) $更新权重$ \mathrm{W} $；

7.根据贪心指标$ {S}_{1}^{(\mathrm{i}, \mathrm{j})} $选择边edge$ \left({\mathrm{i}}^{†}, {\mathrm{j}}^{†}\right) $；

8.通过用$ {\mathrm{o}}^{(\mathrm{i}, \mathrm{j})}=\underset{\mathrm{o}\in \mathrm{O}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}{\mathrm{\alpha }}_{\mathrm{o}}^{\left({\mathrm{i}}^{†}, {\mathrm{j}}^{†}\right)} $替换$ {\stackrel{-}{\mathrm{o}}}^{\left({\mathrm{i}}^{†}, {\mathrm{j}}^{†}\right)} $来最终决定操作集合；

9.end while

10.s=s+1；

11.增加划分比例；

12.end for

2 实验结果与分析

本节将介绍所用的基准数据集以及具体的实验参数设置，并对所得实验结果进行分析，与一些经典的以及近期的NAS算法进行比较。

2.1 实验设置

为验证搜索到的CNN的结构性能，本文选用图像分类中比较常用的CIFAR-10数据集。CIFAR-10包含分辨率为32×32像素的50 000张训练图片和10 000张测试图片。与其他的DARTS系列算法类似，在搜索阶段，对于CIFAR-10的训练评估拆分比例为0.5，即一半的训练集和一半的测试集。

在搜索阶段，与P-DARTS^[23]设置的相同，将渐进式过程分为三个阶段，每个阶段分别包含5、11和17个单元，初始化通道数为16，训练的batch size为64。对于实验具体参数，与一系列对比算法相同，都以交叉熵函数作为损失函数，然后采用标准的随机梯度下降（Stochastic Gradient Descent，SGD）反向传播算法进行训练，SGD优化在CIFAR-10的重量衰减为0.000 3。此外，auxiliary towers的权重是0.4，学习率初始值为0.025，根据余弦定律衰减为0。

算法迭代结束后，将得到的最优CNN个体在50 000张图片的训练集上进行训练，在10 000张图片的验证集上进行评估，评估所得的精度即为模型最后的精度，评估时网络结构的初始化通道数为36，单元数为20。在搜索阶段，搜索的epoch为25次，分为三个阶段，共75次。在评估最优个体模型最终精度时，迭代结果需要达到稳定需要的epoch为600次。评估时随机梯度下降算法的参数同对比算法保持一致，一次训练batch size为64或96，根据模型大小和GPU的显存大小决定。在评估时，本文使用了数据预处理技术cutout^[28]，cutout的正则化长度为16。

2.2 消融实验

消融实验包含两个实验：一是FPNAS在完整数据集上进行稳定的渐进式搜索，表示为FPNAS-all；二是在FPNAS-all的基础上加入划分数据集快速渐进式搜索算法，表示为FPNAS-fast。本文首先验证结合贪心指标和渐进式搜索对于搜索稳定性的提升效果，然后对渐进式划分数据集方法的有效性进行验证，最后对消融实验结果进行分析总结。

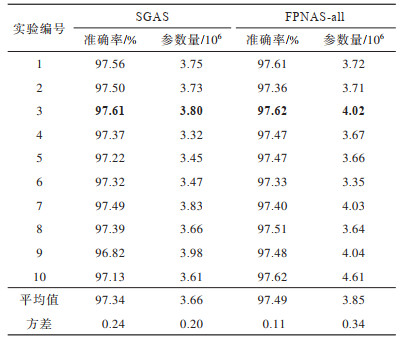
2.2.1 FPNAS-all消融实验

为验证FPNAS-all的有效性以及在提升搜索结构性能上的作用，本文针对该方法和贪心算法SGAS^[24]，在CIFAR-10数据集上进行了10次连续独立实验，实验结果如表 2所示，表中数据分别是SGAS和FPNAS-all的实验结果，包含10次连续实验所得的准确率和结构参数量，最优结果加粗标出。可见，在CIFAR-10上，FPNAS搜索到的CNN结构不仅在准确率上表现较好，平均达到97.49%，高于SGAS的97.34%，同时在稳定性上也优于SGAS，方差（数值）仅为0.11，相较于SGAS的0.24有所降低。

2.2.2 FPNAS-fast消融实验

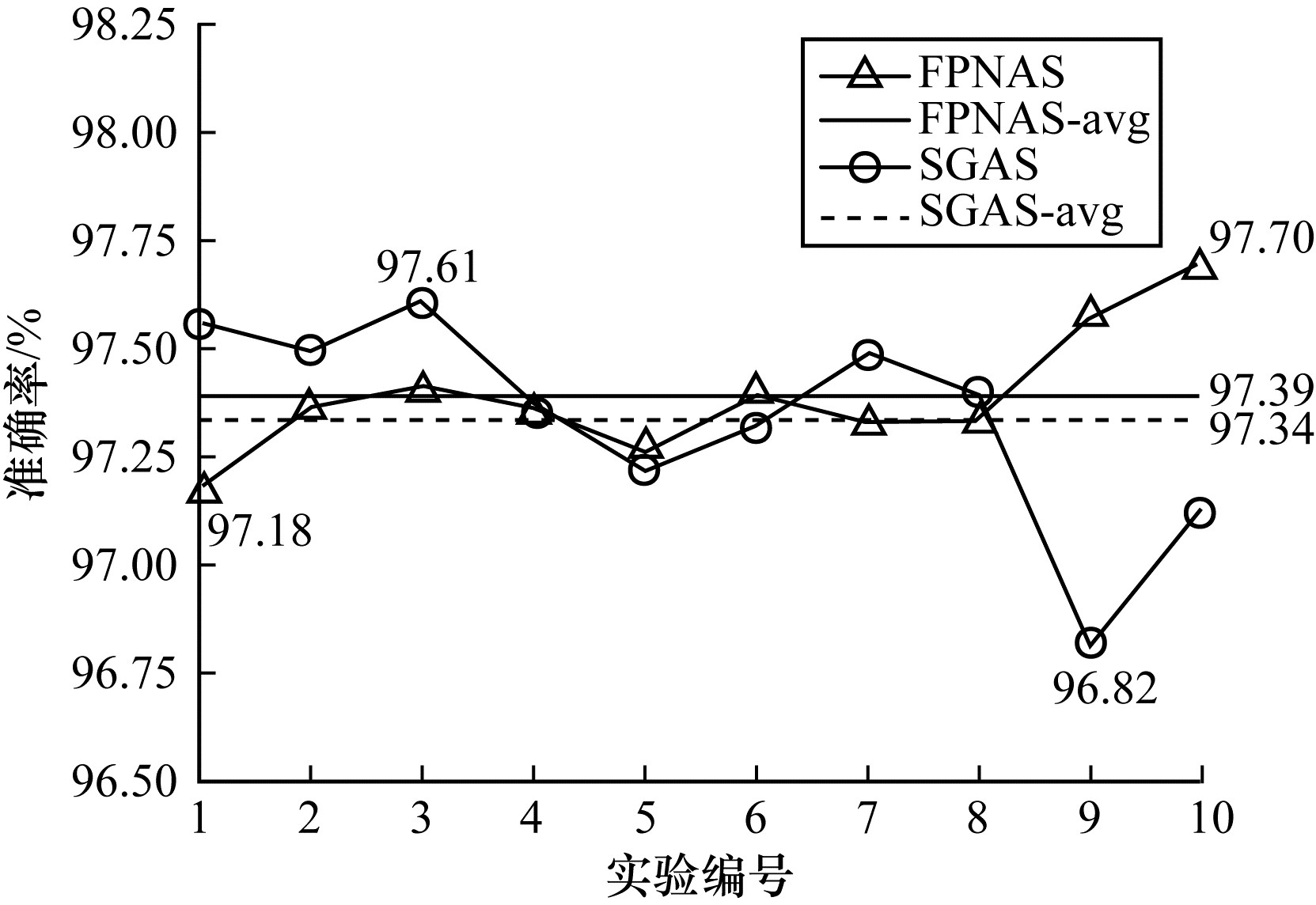
为验证FPNAS-fast的可靠性，在CIFAR-10数据集上，对渐进式划分数据集方法进行10次连续独立的实验，实验结果如图 2所示，图中FPNAS-avg和SGAS-avg代表 10次连续独立实验所得准确率的平均值。

由于划分数据集的不稳定性，虽然实验结果波动范围较大，最高可达到97.7%，最低为97.18%，但是搜索时间大幅减少，在1080Ti上的搜索时间是0.11个GPU Days，少于SGAS在1080Ti的0.25个GPU Days。同时，在平均值和方差（数值）的表现上，FPNAS-fast的平均值分别是97.39%和0.15，优于SGAS的97.34%和0.24，说明FPNAS不仅在最高准确率上优于SGAS，稳定性也优于SGAS。

2.3 算法性能对比

为验证FPNAS的优越性，本文使用人工设计的CNN结构、基于RL的NAS算法、基于EA的NAS算法和基于梯度可微的NAS算法进行对比。人工设计的CNN结构包含DenseNet^[7]、ResNet^[6]、VGG^[4]和DenseNet-BC（k = 40）^[7]。基于RL的NAS算法包括EAS^[29]、Block-QNN-S^[15]和MetaQNN^[13]。基于EA的NAS算法包括Genetic CNN^[20]、Hierarchical Evolution^[30]、Large-scale Evolution^[31]、AE-CNN^[17]、FAE-CNN^[18]、NSGA-Net^[19]和CNN-GA^[21]。基于梯度的NAS算法包括P-DARTS^[23]和SGAS^[24]。

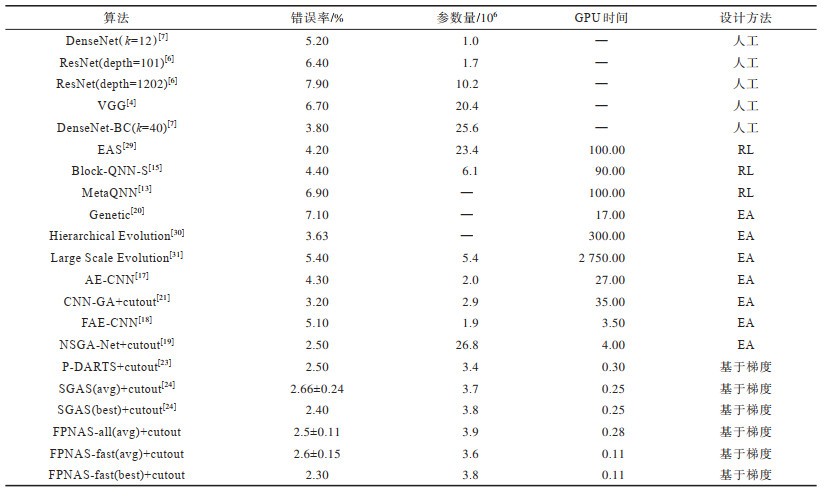
本文使用CNN结构在不同数据集分类的错误率、模型参数量以及算法执行所用GPU时间这三个指标，将FPNAS与上述算法进行比较。表 3给出了FPNAS与其他算法在CIFAR-10上的对比结果，avg代表 10次连续实验得到结果平均值，±后的数字代表方差，best代表 10次连续实验中的最优结果。

对于人工设计的CNN结构，如DenseNet（k=12）、ResNet和VGG等，由于提出较早，在CIFAR-10上表现都比较一般，DenseNet-BC（k=40）在错误率上有较大提升，但在参数量上不占优势，占用资源较多。在基于RL的NAS算法中，EAS结构参数量较大，Block-QNN-S和MetaQNN耗时较长。

在基于EA的NAS算法中，Genetic CNN作为经典的算法，在两个数据集上错误率都较高。Hierarchical Evolution在CIFAR-10数据集上表现良好，错误率只有3.63%，但是该算法需要300个GPU Days，耗时较多。Large Scale Evolution虽然在错误率方面表现良好，但是耗时巨大，需要2 750个GPU Days，需要大量计算资源。AE-CNN和CNN-GA在CIFAR-10上的错误率和参数量都表现优异，但在CIFAR-10分别需要耗时27个GPU Days和35个GPU Days。在AE-CNN基础上改进的FAE-CNN算法，搜索时间缩短为3.5个GPU Days，相对于AE-CNN取得了较大提升，但在错误率上没有优势。多目标NAS算法NSGA-Net在错误率和参数量上都表现优秀。基于梯度可微的NAS算法，如P-DARTS和SGAS等，均表现了优异的分类准确率，同时耗时很少。本文提出的算法FPNAS在CIFAR-10运行一次只需要0.11个GPU Days，进一步减少了搜索耗时，所需要的计算资源大幅减少，且错误率最低仅为2.30%。同时FPNAS大幅提高了搜索的稳定性，在完整数据集上得到10次连续独立结果，方差（数值）仅为0.11。

4 结束语

本文针对现有基于梯度可微的结构搜索算法存在的深度鸿沟、搜索稳定性不高等问题，提出FPNAS算法来自动搜索CNN结构。通过结合渐进式搜索和贪心选择指标使得搜索阶段的结构接近评估阶段，提高CNN结构的稳定性，弥补搜索评估深度鸿沟带来的不利影响，同时使用渐进式划分数据集方法缩短结构搜索时间。在CIFAR-10上的实验结果表明，FPNAS能够在短时间内搜索出分类错误率仅为2.30%的CNN结构。下一步将研究EA种群的特点和优势，结合可微结构搜索和种群并运用多目标方法优化CNN结构的参数量和浮点计算数，进一步减少算法的资源消耗。