2. 武汉大学 计算机学院, 武汉 430072
2. School of Computer Science, Wuhan University, Wuhan 430072, China
开放科学(资源服务)标志码(OSID):
基于面片的三维多视角立体视觉(Patch-based Multiple View Stereo,PMVS)算法将已知内外参数的多幅图像作为输入,重建出真实世界中物体/场景的三维模型。由于该算法原理以及图像分辨率和规模的增大,会导致计算时间过长,因此可将其并行化,使输入图像分别在CPU和GPU上处理来降低计算时间。目前,加快计算速度的并行编程方法主要有MPI[1-3]、OpenCL[4-5]、OpenMP[6-8]、OpenACC[9]和CUDA[10-12]。然而,手动或半自动翻译大量串行程序仍是一个巨大的挑战,一些已有的自动翻译工具的加速效率不理想,并且翻译效果甚至比人工翻译的结果差很多,因此亟须开发和改进从串行程序到并行程序的自动翻译方法[13-15]。
目前,研究人员已提出许多自动并行翻译工具与方法。BASKARAN等[16]提出一种基于Pluto[17]和ClooG[18]的C到CUDA的自动转换框架,以生成目标CUDA代码。PPCG[19]是一种基于多面体编译技术的源到源编译器,结合仿射变换以使用代码生成器提取数据并行性。Bones[20]是一种基于骨架的源到源的自动并行化方法,用于将C转换为5种类型的目标代码。此外,还包括Cetus[21-23]、Par4All[24]和ROSE[25-26]等工具。Cetus和ROSE支持CPU粗粒度并行化与OpenMP;Pluto和Par4All支持OpenMP和CUDA。刘松等[27]根据程序的控制流和数据依赖信息将源程序代码映射成可计算单元图,从中提取出可并行执行的非规则代码段。李雁冰等[28]基于开源编译器Open64,提出一种面向异构众核处理器的并行编译框架,将程序自动转换为异构并行程序。王鹏翔等[29]对Intel编译器、Open64编译器和GCC编译器3个典型编译器自动并行化的效果进行评估。丁丽丽等[30]提出一种能够处理分支嵌套循环的依赖测试方法,并通过检测距离向量判断循环是否存在依赖。高雨辰等[31]对循环并行方式进行分析。
这些自动并行翻译工具与方法一般遵循解析源代码、执行并行化分析、重构适合GPU并行化的循环结构和优化生成目标代码4个步骤。它们多数仅用GPU来执行计算密集型任务。然而,尽管GPU具有出色的加速能力,但CPU必须等待GPU完成其计算任务,这样就浪费了多核CPU的计算资源。针对这些问题,本文提出一种面向PMVS算法的自动两级并行翻译方法。基于ANTLR(Another Tool for Language Recognition)[32-33]的分析器自动识别图像处理算法源C程序中的可并行化循环结构,映射成多线程CPU代码和CUDA代码,对于高分辨率图像在CPU和GPU上进行分别处理,以降低图像处理算法的总计算时间。
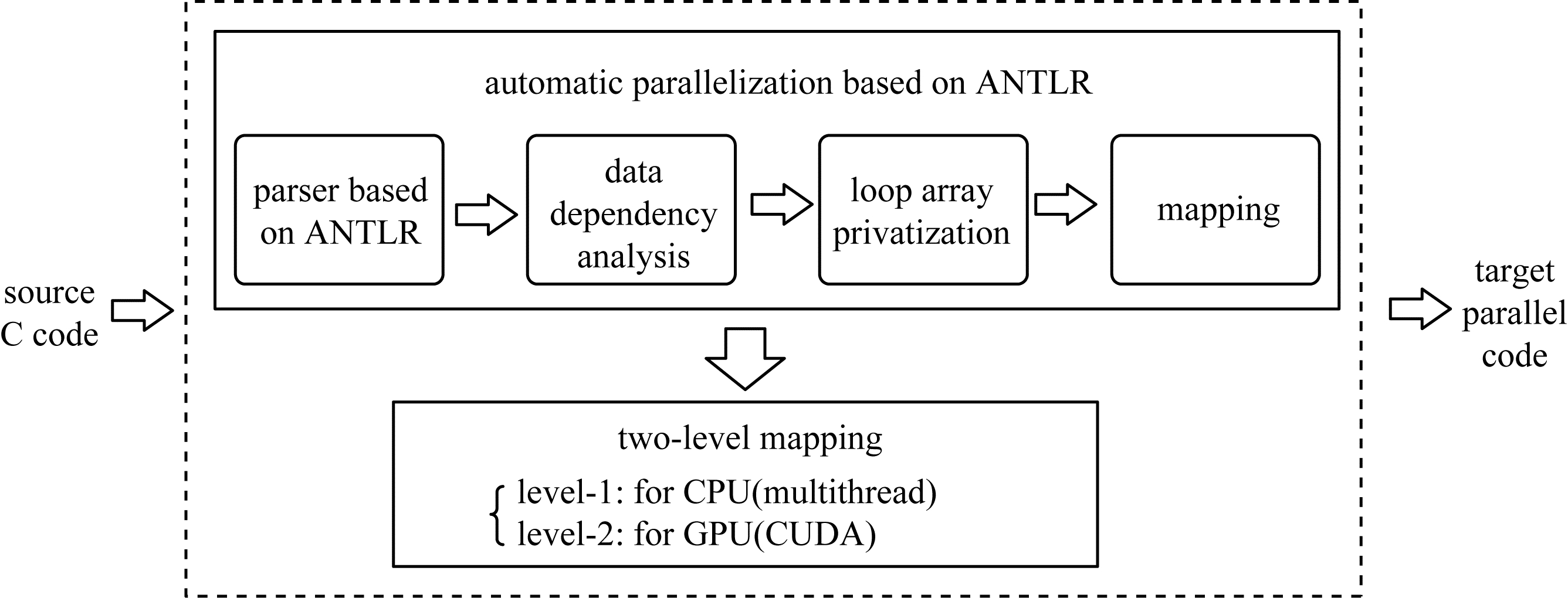
1 自动两级并行翻译方法 1.1 总体结构本文提出的一种用于PMVS算法的自动两级并行翻译模型如图 1所示,以源C程序为输入,经过基于ANTLR的解析、数据依赖性分析、循环数组私有化和映射阶段,把可并行化的程序分别映射到多核CPU和GPU架构上,最终输出生成多线程CPU和GPU两级代码。
|
Download:
|
| 图 1 自动两级并行翻译模型 Fig. 1 Automatic two-level parallel translation model | |
自动两级并行翻译方法的主要步骤如下:
1) 通过ANTLR解析源C代码。首先扫描源代码,然后可以自动生成扩展Backus-Naur范式(Extended Backus-Naur Form,EBNF)语法描述,最后根据EBNF描述,ANTLR为抽象语法树(Abstract Syntax Tree,AST)生成相应的词法分析器。
2) 分析数据依赖关系。分析从分析器中提取的循环信息。如果找到流依赖项,则包含这些依赖项的循环语句是不可并行的。如果发现数据之间的反依赖和输出依赖,则在第3步处理循环结构以消除依赖。如果没有数据依赖,这样的循环语句是可并行的。
3) 循环数组私有化。需要消除变量重用引起的反依赖和输出依赖。循环数组私有化技术将与循环迭代相关的存储单元本地化,使其与其他循环迭代的存储单元的交互分离。
4) 映射。首先,将可并行化的循环结构映射到CUDA架构和CPU多线程架构;然后,生成对应的CUDA代码和CPU多线程代码;最后,多核CPU创建相应数量的线程,一个线程负责GPU调度,其他线程执行分配给CPU的并行任务,同时GPU执行分配给它的任务。
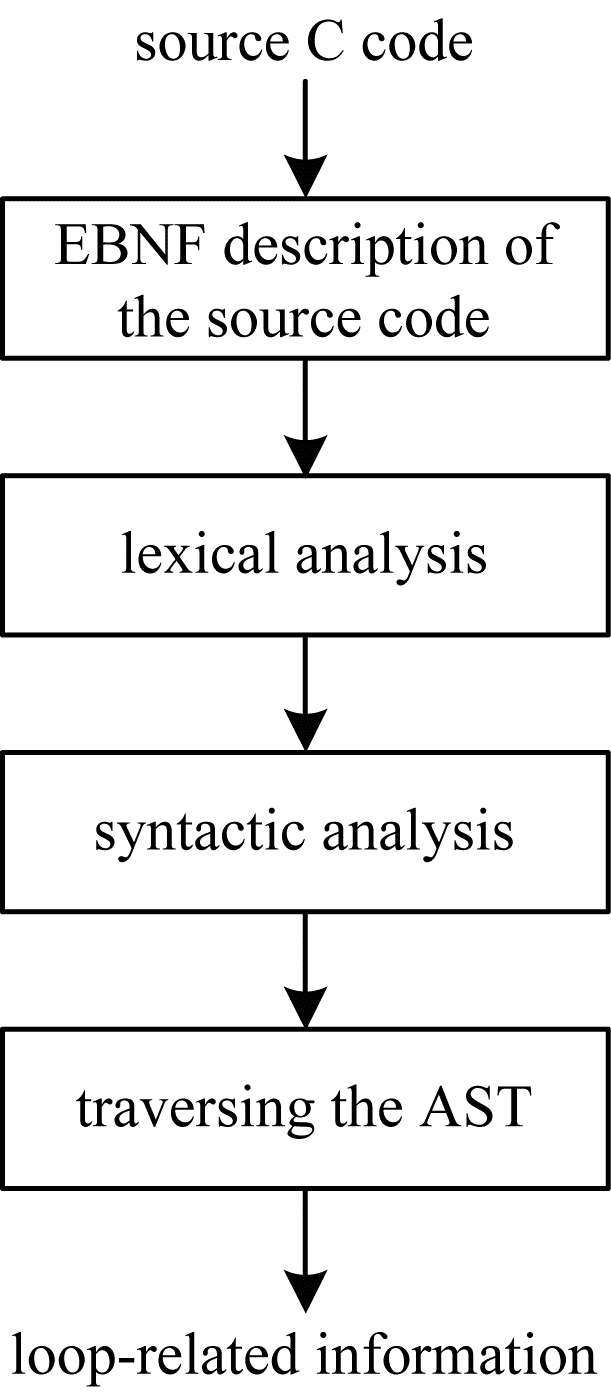
1.2 基于ANTLR的源C代码解析ANTLR是一种可根据输入自动生成语法树并可视化显示的开源语法分析器,其前身是PCCTS,它为包括Java、C++、C#在内的语言提供了一个通过语法描述来自动构造自定义语言的识别器、编译器和解释器的框架。ANTLR使用EBNF规则生成源C代码的语法描述,根据语法的属性,对源程序执行词法分析和句法分析,然后生成AST。ANTLR提供了一种遍历AST的机制,可以帮助提取循环相关信息。使用ANTLR解析C源代码以生成AST并提取循环相关信息的流程如图 2所示。
|
Download:
|
| 图 2 使用ANTLR解析C源代码的流程 Fig. 2 Procedure of parsing source C code using ANTLR | |
首先,利用ANTLR创建串行源代码的EBNF描述。EBNF描述的语法可以用四元组表示如下:
| $ G\left(Z\right)=({V}_{n}, {V}_{t}, S, P) $ | (1) |
其中,

|
下载CSV 表 1 EBNF语法符号 Table 1 EBNF syntax symbol |
然后,执行词法分析,匹配输入流中的字符,掩盖或过滤不相关的内容,并生成用于语法分析的标记。为了达到这个目的,ANTLR在词法分析的语法中增加了一系列过滤方法。在源代码中,空格、制表符、回车符和换行符等字符通常是无意义的冗余字符。ANTLR提供了skip()方法来跳过这些无意义的符号,例如,在使用WS:(''|'\ t'|'\ n'|'\ r')+{skip();}遍历这些字符时,将调用skip()方法以跳过相应的字符。在源代码中的注释在编译时毫无意义,在生成最终文档时需要重新使用。ANTLR提供了一种在编译时隐藏注释的渠道机制,例如,使用COMMENT:'/∗'.∗'∗/'{$channel = HIDDEN;}可以将匹配的注释块放入HIDDEN通道中,而不会出现在后续的语法分析中。
其次,分析上一步语法中的标记,ANTLR在默认情况下无上下文规则,可以添加规则参数以实现上下文信息的传递,以弥补上下文无关文法的不足。例如,使用规则参数的代码片段确定变量分配的类型是否满足要求:
1.declare:type idList[$type.text]';';
2.idList[String type]
3.:ID '='(con = INT | con = FLOAT)
4.{
5.if (type.equals("int") & & $con.text.indexOf(".")!= 1)
6.{
7.printf("error:value of float cannot assign to var of int.");
8.}
9.}
在变量声明语法中,定义规则参数idList[$type.text],因此在以下语法中,idList携带类型信息。为了提取与循环相关的变量信息,将返回值添加到循环语句声明的语法表达式中,以便可以直接从各种循环声明中提取与变量相关的信息。在while语句声明中添加返回值int的示例代码具体如下:
1.loop_example returns[int a]
2.:'while' '('expression')' statement
3.;
最后,AST是在语法分析后形成的,以树的形式存储句子的数据结构,树上的每个节点代表源代码中的结构。串行C代码抽象语法树的遍历主要用于遍历循环结构。本文使用ANTLR提供的Visitors方法来遍历AST,并重载visitForStatement()方法。该方法存储循环嵌套级别和与循环相关的变量信息source C代码,包括变量名称、变量类型和存储循环位置的行号,并将收集的变量信息移交给下一个阶段进行处理。
1.3 数据依赖分析数据依赖关系是指程序中语句的部分顺序关系,反映了维护程序语义所需的固有顺序。影响程序并行性的是对数据的读写访问,因此并行翻译中需要考虑数据依赖关系。
根据对同一内存区域的读写操作,数据依赖关系可以由流依赖关系、反依赖关系和输出依赖关系组成。在循环结构中:流依赖关系指的是一个存储单元在一次迭代中写入,然后在后续迭代中读取;反依赖关系指的是在一个迭代中读取一个存储单元,然后在随后的迭代中写入一个存储单元;输出依赖关系指的是一个存储单元是一次迭代写入,然后在后续迭代中再次写入。
假设在循环语句F(循环结构)中,I是迭代空间,i(i∈I)是I中一次迭代的循环控制变量。在迭代i下,
| $ \forall i\forall j({R}_{\mathrm{R}\mathrm{e}\mathrm{a}{\mathrm{d}}_{i}}\bigcap {W}_{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{e}}_{j}}=\mathrm{\varnothing })\wedge ({W}_{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{e}}_{i}}\bigcap {W}_{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{e}}_{j}}=\mathrm{\varnothing }) $ | (2) |
式(2)表示该循环结构不存在流依赖关系,并且不存在反依赖关系或者输出依赖关系,其中,i,j∈I并且i≠j。如果F中存在流依赖关系,则应满足以下条件:
| $ {R}_{\mathrm{R}\mathrm{e}\mathrm{a}{\mathrm{d}}_{i}}\bigcap {W}_{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{e}}_{j}}\ne \mathrm{\varnothing } $ | (3) |
其中:i,j∈I并且i > j。在相同的存储区域上进行写入操作,并且需在读取操作之前执行。这个写入操作和读取操作类似于生产者和消费者之间的关系,包含流依赖关系的循环结构不能在GPU上并行执行。
如果F中存在反依赖关系,则应满足以下条件:
| $ {R}_{\mathrm{R}\mathrm{e}\mathrm{a}{\mathrm{d}}_{k}}\bigcap {W}_{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{e}}_{l}}\ne \mathrm{\varnothing } $ | (4) |
其中:k,l∈I并且k < l。对同一存储区的读取操作发生在写入操作之前,这是由于重复引用同一存储区引起的。自动并行翻译可以通过创建一个临时存储区来实现。如果输出依赖项存在于F(循环结构F包含输出依赖关系)中,则应满足以下条件:
| $ {W}_{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{e}}_{m}}\bigcap {W}_{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{e}}_{n}}\ne \mathrm{\varnothing } $ | (5) |
其中:
在串行C代码中,重复使用相同的变量会给自动并行转换带来巨大困难。变量的使用使得存储地址具有数据依赖关系、反依赖关系和输出依赖关系。循环数组私有化可以消除这些依赖关系。循环语句中存储单元的显式表示形式是变量和数组。变量也可以看作是数组的一种特殊表示形式,表示只有一个元素数组。在串行C代码中,全局数组通常用于存储数据,从而减少了存储空间。全局数组将在循环语句中的每次迭代中使用。循环数组私有化在每次迭代中使用新的存储空间来私有化原始重用空间,因此不存在交叉迭代依赖项。
除了数组的初始化之外,循环语句中数组重新分配的位置可以分为3类:1)在当前迭代中为数组分配新值,然后在下一次迭代中使用;2)在循环外为数组分配一个值,并在迭代中重用;3)先分配数组,再在同一迭代中重复使用。
第1类的示例代码具体如下:
1.for (int i = 0;i < n;i++)
2.{
3.…
4.temp1 = A + 1;
5.A = temp2 + 2;
6.…
7.}
在此循环语句中:当i=0时,在第5行为数组A分配值“temp2+2”;当i=1时,在第4行的语句“temp1=A+1”中使用数组A。这是一个具有流依赖关系的循环,因此该循环不能通过循环数组私有化来翻译。
第2类的示例代码具体如下:
1.A = 1
2.for (int i = 0;i < n;i++)
3.{
4.…
5.temp1 = A + 1;
6.…
7.}
在此代码段中,除在循环第5行中使用的循环语句外,为数组A分配了值“1”。在这种情况下,数组A可以私有化,对第2类的数组私有化代码具体如下:
1.A = 1;
2.for (int i = 0;i < n;i++)
3.{
4.…
5.private Atemp;
6.Atemp = A;
7.temp1 = A + 1;
8.…
9.}
第3类的示例代码具体如下:
1.for (int i = 0;i < n;i++)
2.{
3.…
4.A = temp2 + 2;
5.temp1 = A + 1;
6.…
7.}
在此循环语句中,当i=0时,首先在第4行中为数组A赋值“temp2+2”,然后在第5行的语句“temp1=A+1”中对其进行调用。在同一迭代中分配并重用该数组。在这种情况下,可以将数组A私有化,对第3类的数组私有化代码具体如下:
1.for (int i = 0;i < n;i++)
2.{
3.…
4.private Atemp;
5.Atemp = temp2 + 2;
6.temp1 = Atemp + 1;
7.if (i == n ‒ 1)
8.{
9.A = Atemp;
10.}
11.…
12.}
循环语句私有化的第一个条件是迭代之间不存在流依赖关系,第二个条件是在循环外重新分配数组,或者在相同迭代中使用之前重新分配的数组。结合反依赖关系和输出依赖关系的条件,采用数组私有化的必要条件如式(6)所示:
| $ \begin{array}{l}\forall i\forall j\left({R}_{\mathrm{R}\mathrm{e}\mathrm{a}{\mathrm{d}}_{i}}\bigcap {W}_{\mathrm{W}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{e}}_{j}}=\mathrm{\varnothing }\right)\wedge \\ \left(\exists k\exists l\exists m\exists n({R}_{Rea{d}_{k}}\bigcap {W}_{Writ{e}_{l}}\ne \varnothing \right.)\vee \\ \left.({W}_{Writ{e}_{m}}\bigcap {W}_{Writ{e}_{n}}\ne \mathrm{\varnothing })\right)\end{array} $ | (6) |
其中:
为了不浪费任何计算资源,需要获得目标的两级并行化代码CPU多线程和GPU CUDA,RAHTP将可并行化的循环结构映射到C多线程代码和CUDA代码,具体如下:
1.#pragma parallel
2.void loop_func(*ctasks)
3.{
4.for (…) { … }
5.}
6.int t_count = kthread
7.for (i = 1;i < t_count;i++)
8.{ thread tid
9.thread_create( & tid,NULL,(void *)loop_func,NULL);
10.thread_join(tid,NULL)
11.}
12.thread tid
13.thread_create( & tid,NULL,(void *)sheduling,NULL);
14.thread_join(tid,NULL);
15.// sheduling GPU,CUDA kernel
16._global_ void kernel_func(unsigned *gtasks,paras)
17.{ int bid_in_grid = blockx.y * gridDim.x + blockIdx.x;
18.int tid_in_block = threadIdx.x;
19.for (…) { … }// parallel
20._syncthreads();
21.}
标记为“parallel”的是经过解析的可并行代码块。“kthread”表示应该在CPU上创建的线程数,“ctasks”和“gtasks”分别表示将在CPU和GPU上处理的任务。如第1行~第14行所示,循环函数包括可并行化的循环结构,CPU创建相应数量的线程,其中一个线程负责GPU调度,而其他线程则执行并行任务。如第15行~第21行所示,CUDA内核处于CPU线程的调度之下,并且包含相同的可并行循环来执行。映射的实现过程具体为:首先,将循环结构的串行代码映射为CUDA并行代码,创建CUDA核心kernel函数,在GPU上运行;其次,在CPU上创建线程来调度GPU和执行串行代码。
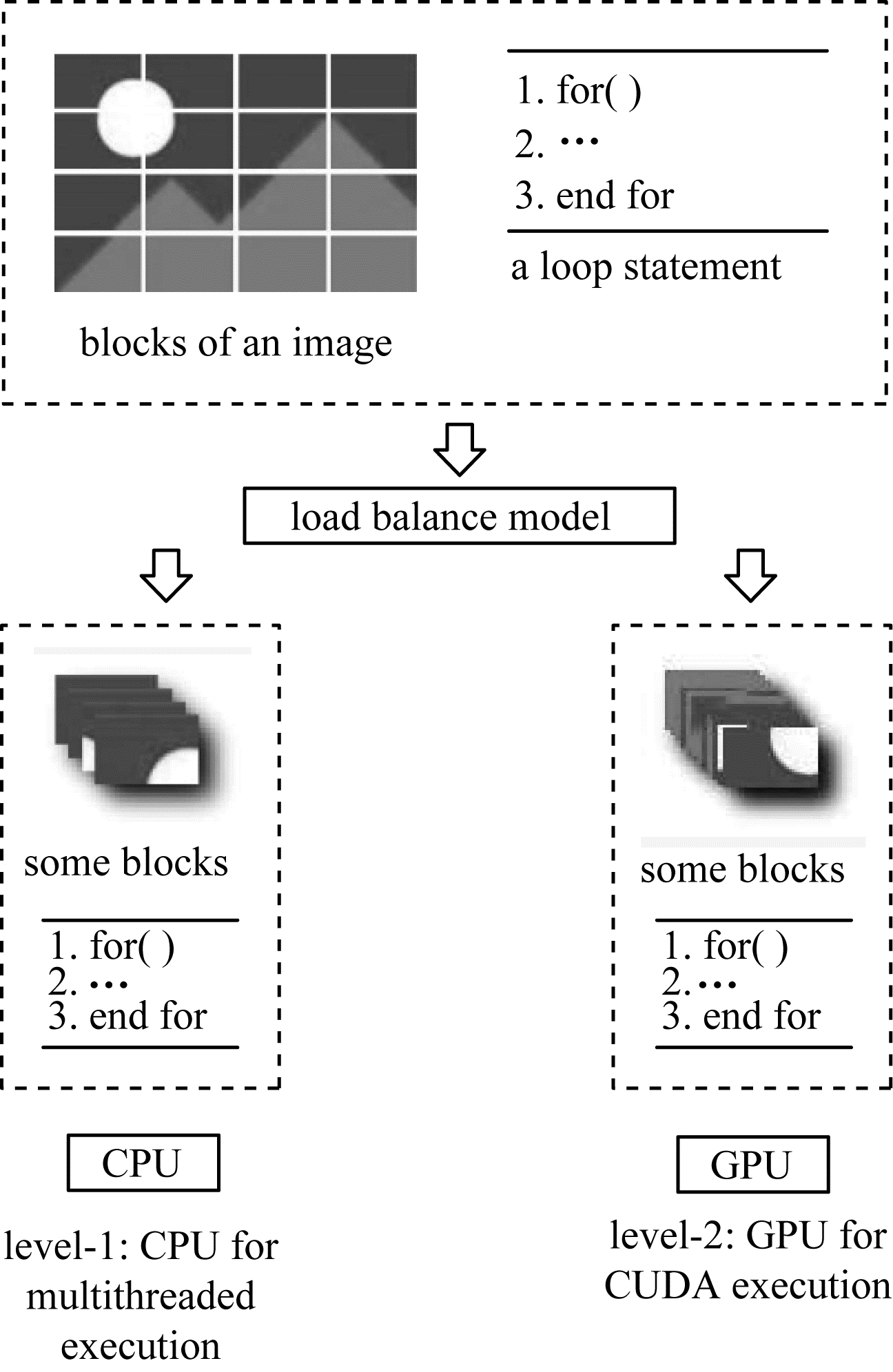
在图像处理算法中,把高分辨率输入图像分割成块。对于同一个可并行化循环语句,一部分图像块会在CPU上并行处理,而其他块会在GPU上处理,如图 3所示。
|
Download:
|
| 图 3 图像两级并行处理 Fig. 3 Two-level parallel processing for the images | |
使用8核Intel i7-9700 CPU和12 GB显存的Nvidia Tesla p4 GPU,编译器是NVCC 10.0。实验主要包括以下3个部分:1)将本文方法与其他自动并行翻译方法在Poly-Bench/C4.2.1的10个基准测试程序上进行有效性验证;2)选择PMVS算法进行图像处理,将本文方法与其他自动并行翻译方法进行性能比较;3)验证线程数目对本文方法的影响。
2.1 基准实验将本文方法与PPCG、OpenACC这两种自动并行翻译方法进行比较。PolyBench是俄亥俄州立大学创建的一组基准测试套件,包含30个带有静态控制流的数值计算,提取自线性代数计算、图像处理、物理模拟、动态编程、统计信息等应用领域。
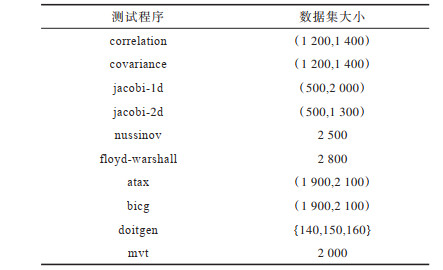
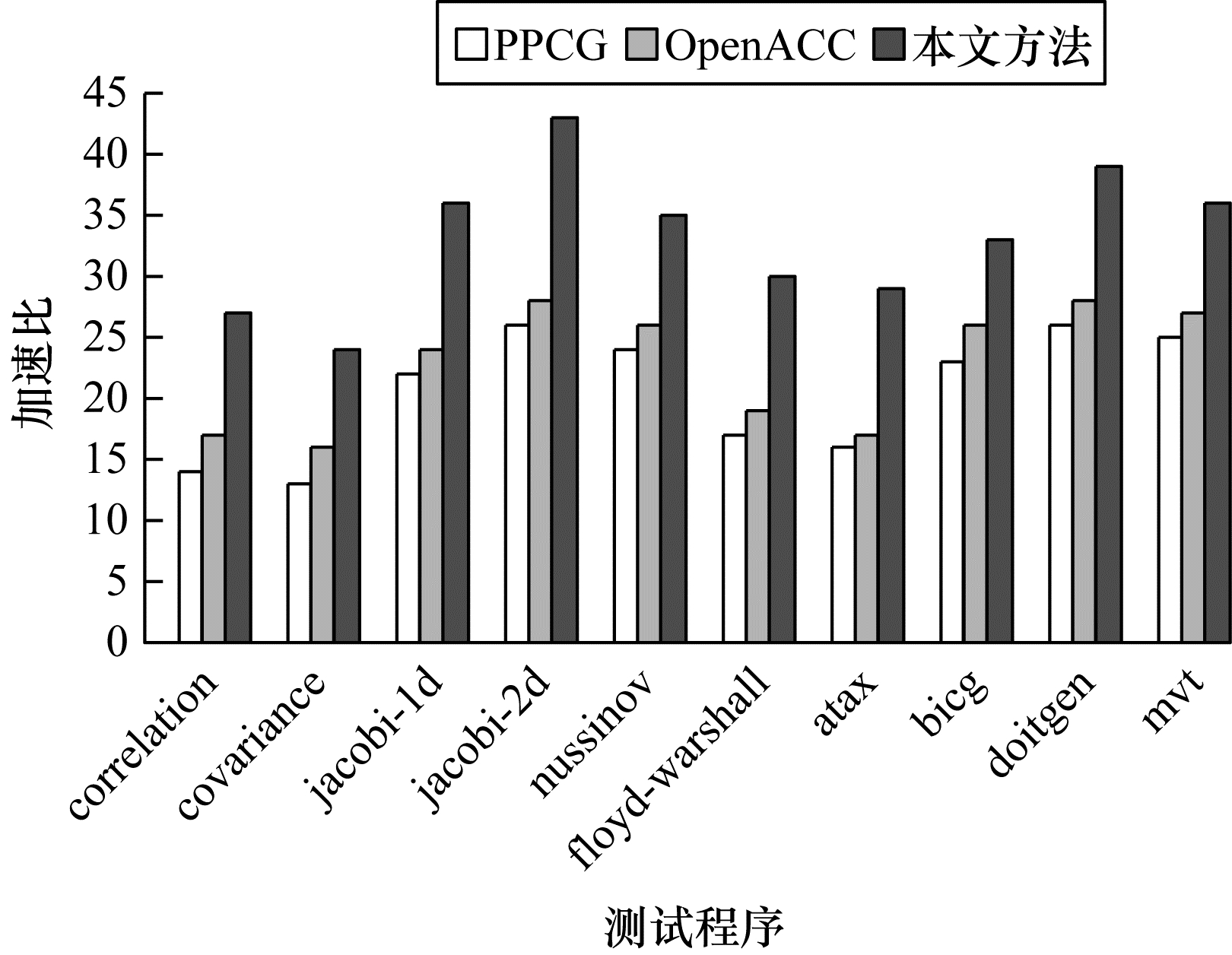
从PolyBench/C 4.2.1中选择10个程序作为基准测试,其中,correlation、covariance是数据挖掘领域的程序,jacobi-1d、jacobi-2d是stencils计算程序,nussinov、floyd-warshall是动态规划程序,atax、bicg、doitgen、mvt是线性代数核函数程序。这些测试程序包含可并行化的循环结构,具有良好的数据重用性,适合作为自动并行翻译方法的测试基准。输入数据集为LARGE_DATASET。每个算法设置的任务数量为1 000。测试程序信息如表 2所示。每种自动并行翻译方法对每种算法的执行时间与加速比如图 4所示。
|
下载CSV 表 2 测试程序信息 Table 2 Test program information |
|
Download:
|
| 图 4 基准实验结果 Fig. 4 Benchmark experimental results | |
在图 4中,加速比是指CPU串行和并行方法的执行时间之比,在10个测试程序的运行中,PPCG、OpenACC、本文方法分别平均获得了19.81、22.25、31.62的加速比,可以看出本文方法的加速比最高,PPCG和OpenACC的性能接近。本文方法有最高加速比的原因是使用了GPU以外的CPU多线程,在GPU上执行任务的同时,一部分任务会在CPU上执行,降低了所有任务的总执行时间,而PPCG和OpenACC只在GPU上执行任务。通过基准实验,证明了本文方法比其他自动并行翻译方法具有更优越的性能。
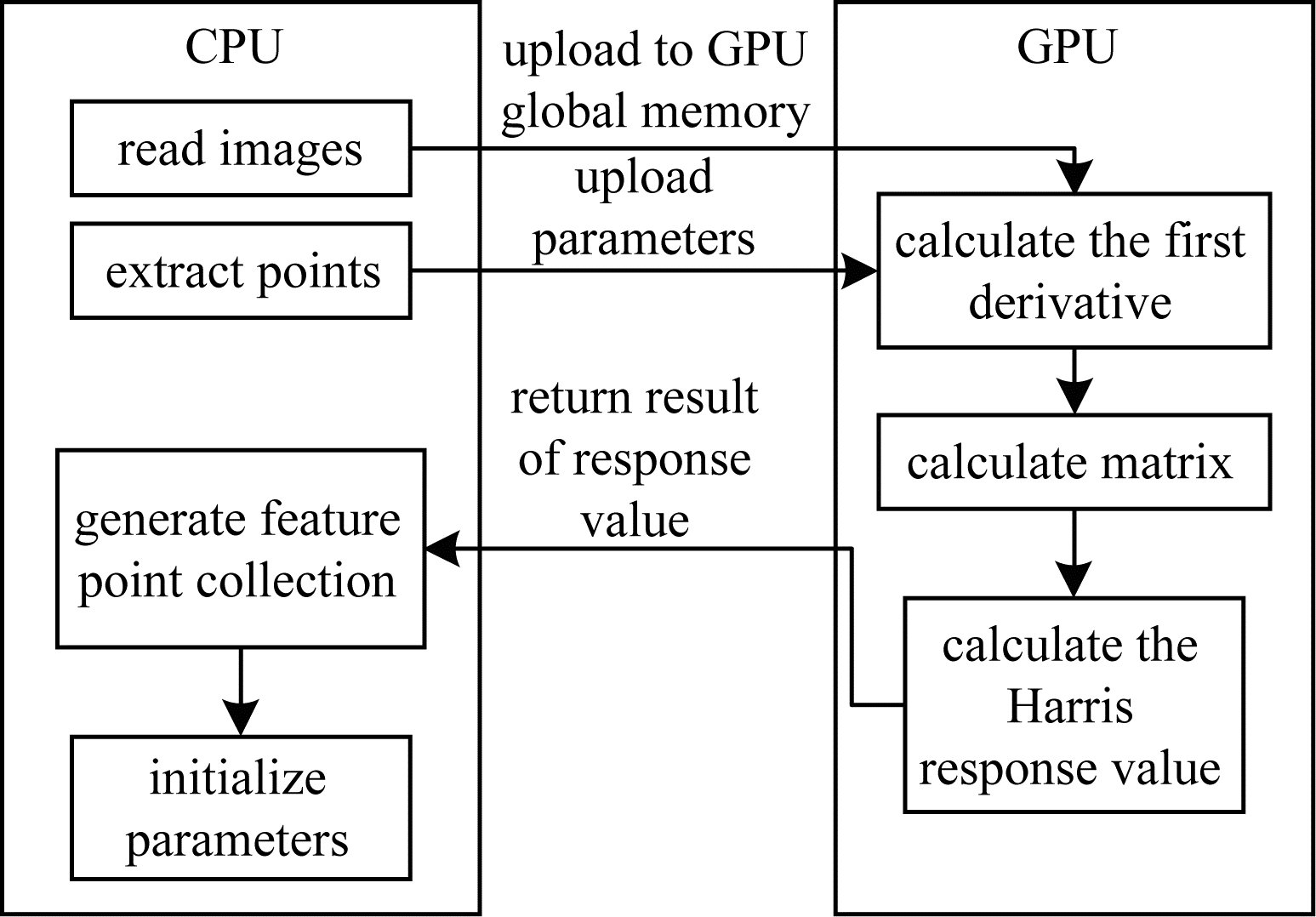
2.2 图像处理算法实验将PMVS算法作为图像处理示例算法进行分析与研究。PMVS是图像处理领域的使用2D图像重建3D场景的算法,从不同角度使用同一对象的多个2D图像进行3D建模,基于匹配点还原场景的立体信息。PMVS包括许多可并行处理的过程,包括高斯函数的Harris差分(Harris-DOG),可以从2D图像序列中提取特征点。PMVS算法流程如图 5所示。
|
Download:
|
| 图 5 PMVS算法流程 Fig. 5 Procedure of PMVS algorithm | |
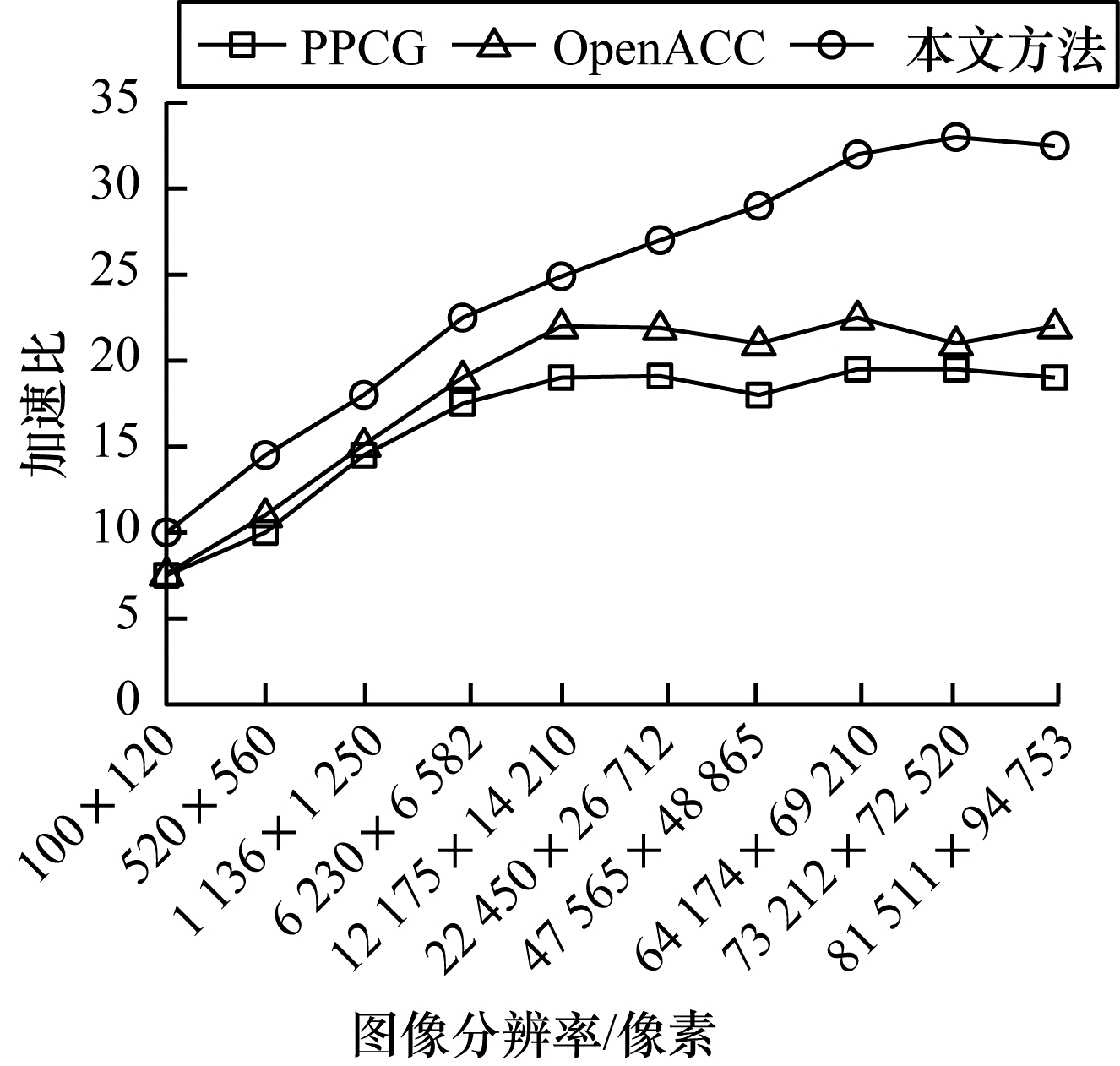
对于输入数据集,选用10张不同分辨率的图片进行实验,分别为100×120像素、520×560像素、1 136×1 250像素、6 230×6 582像素、12 175×14 210像素、22 450×26 712像素、47 565×48 865像素、64 174×69 210像素、73 212×72 520像素、81 511×94 753像素。基于PMVS算法,将本文方法与PPCG和OpenACC进行对比,实验结果如图 6所示。
|
Download:
|
| 图 6 PMVS实验结果 Fig. 6 PMVS experimental result | |
在图 6中,图像分辨率从100×120像素到81 511×94 753像素逐渐增加。PPCG和OpenACC的加速比先是增加,因为GPU并行效率随着输入数据的增大而提升,当图像分辨率达到12 175×14 210像素时,加速比达到最大,分别是19.47和21.76,此后图片再增大加速比也不再增加,在最大值附近波动。本文方法也呈现相同的趋势,但是在每一种图像分辨率上,加速比都大于PPCG和OpenACC,最高值在64 174×69 210像素附近,达到32.03,这是因为本文方法使用了两级并行策略,输入图像的一部分在CPU上处理,降低了整个图片的处理时间,并且随着图像分辨率的增加,分配在CPU上处理的任务也会增加,当图像分辨率达到64 174×69 210像素时,CPU发挥最大性能,当再增加图像分辨率时,任务会串行执行,总执行时间不会再缩短,最大加速比稳定在32.15左右。通过图像处理实验证明了在处理高分辨率图像时,本文方法比其他自动并行翻译方法的效率更高。从100×120像素开始,随着图像分辨率的增加,加速比的增幅不断提升,当图像分辨率达到64 174×69 210像素时性能最优。
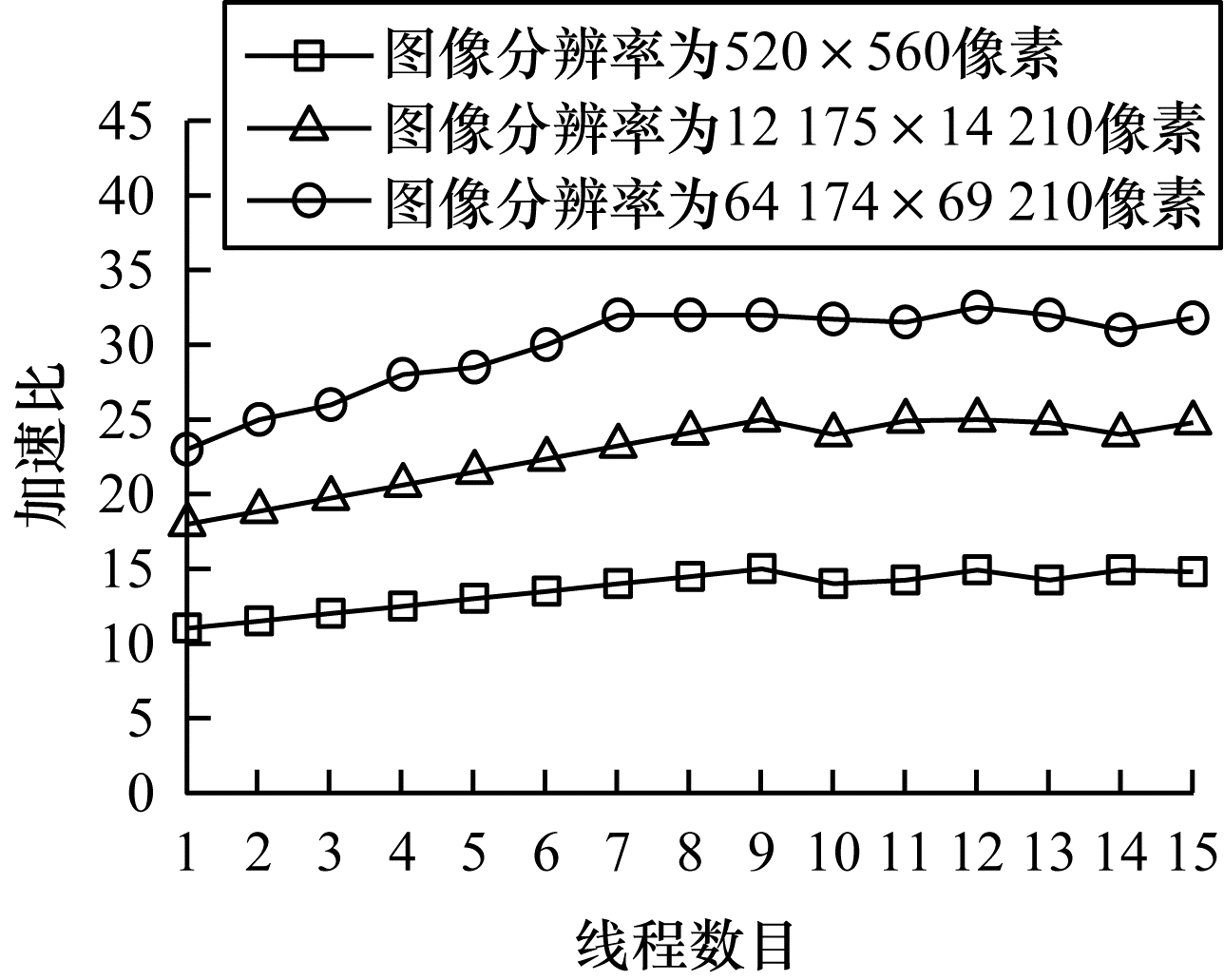
2.3 多线程实验为确定线程数目对本文方法的影响,通过改变CPU线程数目评估本文方法的性能,实验条件与设置同图像处理算法实验,输入图像分辨率分别为520×560像素、12 175×14 210像素和64 174×69 210像素,实验结果如图 7所示。
|
Download:
|
| 图 7 多线程实验结果 Fig. 7 Multi-thread experimental results | |
在图 7中,加速比是指CPU串行与本文方法执行时间之比。3种不同分辨率的图像呈现相同的变化,当线程数目从1增加到8时,三者的加速比都持续增加,图像分辨率为520×560像素的图像加速比从11.83增加到14.67,图像分辨率为12 175×14 210像素的图像加速比从19.13增加到24.61,图像分辨率为64 174×69 210像素的图像加速比从23.24增加到31.62,这是因为多线程并行执行任务,可以提高CPU的负载能力。当线程数目达到8时,因为CPU核心数目为8,所以此时CPU并行能力最强,加速比最高,之后随着线程数目增加,超过了CPU核心数目后,加速比不再增加。因此,当线程数目等于CPU核心数目时,本文方法达到最优性能。
3 结束语本文提出一种用于PMVS算法的自动两级并行翻译方法,可自动将串行C程序转换为CPU多线程和CUDA的两级并行程序。经过本文方法并行化后,PMVS算法可使高分辨率图像在CPU和GPU上分别进行处理,降低了算法计算时间。实验结果表明,与其他自动并行翻译方法相比,本文方法能更有效地提升图像处理算法的性能。后续将在任务分配过程中考虑CPU与GPU之间的任务负载量,使CPU与GPU达到负载均衡状态,进一步提升图像处理算法的性能。
| [1] |
GROUP W, LUCK E, SKJELLUM A. Using MPI: portable parallel programming with the message passing interface[M]. Cambridge, USA: MIT Press, 1994.
|
| [2] |
STELLNER G. CoCheck: check pointing and process migration for MPI[C]//Proceedings of International Conference on Parallel Processing. Washington D. C., USA: IEEE Press, 1996: 526-531.
|
| [3] |
GABRIEL E, FAGG G E, BOSILCA G, et al. Open MPI: goals, concept, and design of a next generation MPI implementation[C]//Proceedings of European Parallel Virtual Machine/Message Passing Interface Users' Group Meeting. Berlin, Germany: Springer, 2004: 97-104.
|
| [4] |
STONE J E, GOHARA D, SHI G C. OpenCL: a parallel programming standard for heterogeneous computing systems[J]. Computing in Science & Engineering, 2010, 12(3): 66-73. |
| [5] |
JÄÄSKELÄINEN P, LAMA C S, SCHNETTER E, et al. POCL: a performance-portable OpenCL implementation[J]. International Journal of Parallel Programming, 2015, 43(5): 752-785. DOI:10.1007/s10766-014-0320-y |
| [6] |
DAGUM L, MENON R. OpenMP: an industry standard API for shared-memory programming[J]. IEEE Computational Science and Engineering, 1998, 5(1): 46-55. DOI:10.1109/99.660313 |
| [7] |
CHAPMAN B, JOST G, VAN DER PAS R. Using OpenMP: portable shared memory parallel programming[M]. Cambridge, USA: MIT Press, 2008.
|
| [8] |
ATZENI S, GOPALAKRISHNAN G, RAKAMARIC Z, et al. ARCHER: effectively spotting data races in large OpenMP applications[C]//Proceedings of 2016 IEEE International Parallel and Distributed Processing Symposium(IPDPS). Washington D. C., USA: IEEE Press, 2016: 53-62.
|
| [9] |
WIENKE S, SPRINGER P, TERBOVEN C. OpenACC—first experiences with real-world applications[C]//Proceedings of European Conference on Parallel Processing. Berlin, Germany: Springer, 2012: 859-870.
|
| [10] |
KIRK D. Nvidia CUDA software and GPU parallel computing architecture[C]//Proceedings of the 6th International Symposium on Memory Management. New York, USA: ACM Press, 2007: 103-104.
|
| [11] |
YANG Z Y, ZHU Y T, PU Y. Parallel image processing based on CUDA[C]//Proceedings of International Conference on Computer Science and Software Engineering. Washington D. C., USA: IEEE Press, 2008: 198-201.
|
| [12] |
SANDERS J, KANDROT E. CUDA by example: an introduction to general-purpose GPU programming[M]. [S. l.]: Addison-Wesley Professional, 2010.
|
| [13] |
FONSECA A, CABRAL B, RAFAEL J, et al. Automatic parallelization: executing sequential programs on a task-based parallel runtime[J]. International Journal of Parallel Programming, 2016, 44(6): 1337-1358. DOI:10.1007/s10766-016-0426-5 |
| [14] |
ZHANG Y Q, CAO T, LI S G, et al. Parallel processing systems for big data: a survey[J]. Proceedings of the IEEE, 2016, 104(11): 2114-2136. DOI:10.1109/JPROC.2016.2591592 |
| [15] |
OH T, BEARD S R, JOHNSON N P, et al. A generalized framework for automatic scripting language parallelization[C]//Proceedings of the 26th International Conference on Parallel Architectures and Compilation Techniques(PACT). Washington D. C., USA: IEEE Press, 2017: 356-369.
|
| [16] |
BASKARAN M M, RAMANUJAM J, SADAYAPPAN P. Automatic C-to-CUDA code generation for affine programs[M]. Berlin, Germany: Springer, 2010.
|
| [17] |
BONDHUGULA U, RAMANUJAM J. Pluto: a practical and fully automatic polyhedral parallelizer and locality optimizer[EB/OL]. [2022-01-11]. https://www.xueshufan.com/publication/2034761517.
|
| [18] |
BASTOUL C. Efficient code generation for automatic parallelization and optimization[C]//Proceedings of the 2nd International Symposium on Parallel and Distributed Computing. Washington D. C., USA: IEEE Press, 2003: 23-30.
|
| [19] |
VERDOOLAEGE S, JUEGA J C, COHEN A, et al. Polyhedral parallel code generation for CUDA[J]. ACM Transactions on Architecture and Code Optimization, 2013, 9(4): 1-23. |
| [20] |
NUGTEREN C, CORPORAAL H. Bones: an automatic skeleton based C-to-CUDA compiler for GPUS[J]. ACM Transactions on Architecture and Code Optimization, 2015, 11(4): 1-35. |
| [21] |
LEE S I, T. A. JOHNSON T A, EIGENMANN R. Cetus—an extensible compiler infrastructure for source-to-source transformation[C]//Proceedings of International Workshop on Languages and Compilers for Parallel Computing. Berlin, Germany: Springer, 2003: 539-553.
|
| [22] |
DAVE C, BAE H, MIN S J, et al. Cetus: a source-to-source compiler infrastructure for multicores[J]. Computer, 2009, 42(12): 36-42. DOI:10.1109/MC.2009.385 |
| [23] |
BAE H S, MUSTAFA D, LEE J W, et al. The Cetus source-to-source compiler infrastructure: overview and evaluation[J]. International Journal of Parallel Programming, 2013, 41(6): 753-767. DOI:10.1007/s10766-012-0211-z |
| [24] |
AMINI M, CREUSILLET B, EVEN S, et al. Par4All: from convex array regions to heterogeneous computing[EB/OL]. [2022-01-11]. https://hal-mines-paristech.archives-ouvertes.fr/hal-00744733.
|
| [25] |
QUINLAN D. ROSE: compiler support for object-oriented frameworks[J]. Parallel Processing Letters, 2000, 10(2): 215-226. |
| [26] |
QUINLAN D, LIAO C H. ROSE source-to-source compiler infrastructure[EB/OL]. [2022-01-11]. https://engineering.purdue.edu/Cetus/cetusworkshop/papers/4-1.pdf.
|
| [27] |
刘松, 赵博, 蒋庆, 等. 一种面向循环优化和非规则代码段的粗粒度半自动并行化方法[J]. 计算机学报, 2017, 40(9): 2127-2147. LIU S, ZHAO B, JIANG Q, et al. A semi-automatic coarse-grained parallelization approach for loop optimization and irregular code sections[J]. Chinese Journal of Computers, 2017, 40(9): 2127-2147. (in Chinese) |
| [28] |
李雁冰, 赵荣彩, 韩林, 等. 一种面向异构众核处理器的并行编译框架[J]. 软件学报, 2019, 30(4): 981-1001. LI Y B, ZHAO R C, HAN L, et al. Parallelizing compilation framework for heterogeneous many-core processors[J]. Journal of Software, 2019, 30(4): 981-1001. (in Chinese) |
| [29] |
王鹏翔, 韩林, 丁丽丽, 等. 典型编译器自动并行化效果和评估[J]. 信息工程大学学报, 2018, 19(2): 186-190. WANG P X, HAN L, DING L L, et al. Effect and evaluation of automatic parallelization of typical compiler[J]. Journal of Information Engineering University, 2018, 19(2): 186-190. (in Chinese) |
| [30] |
丁丽丽, 李雁冰, 张素平, 等. 分支嵌套循环的自动并行化研究[J]. 计算机科学, 2017, 44(5): 14-19, 52. DING L L, LI Y B, ZHANG S P, et al. Auto-parallelization research based on branch nested loops[J]. Computer Science, 2017, 44(5): 14-19, 52. (in Chinese) |
| [31] |
高雨辰, 赵荣彩, 韩林, 等. 循环自动并行化技术研究[J]. 信息工程大学学报, 2019, 20(1): 82-89. GAO Y C, ZHAO R C, HAN L, et al. Research on automatic parallelization of loops[J]. Journal of Information Engineering University, 2019, 20(1): 82-89. (in Chinese) |
| [32] |
PARR T J, QUONG R W. ANTLR: a predicated-LL(k) parser generator[J]. Software: Practice and Experience, 1995, 25(7): 789-810. |
| [33] |
PARR T. The definitive ANTLR 4 reference[M]. [S. l.]: Pragmatic Bookshelf, 2013.
|
 2022, Vol. 48
2022, Vol. 48
