开放科学(资源服务)标志码(OSID)：

0 概述

在传统TCP/IP网络架构中，用户提出服务请求，网络将用户请求传送到服务器，服务器执行用户请求，并在完成所要求的操作后将结果返回用户。当用户请求在网络缓存区中找到对应内容时，即发生缓存命中，节点会将对应内容封装后发送给请求者。信息中心网络（Information-Centric Networking，ICN）是一种以内容为中心的新型网络架构，特点是网络拓扑中的所有节点都有缓存区。在ICN中用户仅关心内容本身，网络对内容进行统一标识并基于内容进行定位、路由和传输^[1]。缓存的存在使得热门的内容更接近于用户，选取合适的缓存策略能够有效减小用户访问延迟和服务器负载，并缓解网络链路负担^[2-3]。目前，ICN主要包括命名数据网络（Named Data Networking，NDN）、内容中心网络（Content Centric Networking，CCN）和发布/订阅互联网路由范式（Publish/Subscribe Internet Routing Paradigm，PSIRP）等^{[1, 4]}典型架构。

随着社会信息量的日益增加，网络内容更新速率越来越快。如果缓存存储过期内容，请求到达时则不会发生缓存命中，因此缓存一致性维护受到研究人员的广泛关注^[5-7]。目前，缓存一致性维护研究主要分为验证和失效^[6-7]两类策略。验证策略即缓存定期向服务器询问内容是否过期，是一类实现缓存弱一致性的策略，原因在于源服务器的内容可能在两次验证之间发生更新，但是一些实时性要求较高的应用期望获得最新的内容。失效策略是一类实现缓存强一致性的策略，主要分为被动查询、主动移除、主动更新和主动选择更新4种^[7]。在被动查询策略中，当缓存中发现请求对应副本时，缓存会首先询问服务器，若服务器告知这是最新的内容，则会发生缓存命中。在主动移除策略中，当服务器更新某个内容时，会推送消息到所有的缓存节点，过期的内容将被移除。在主动更新策略中，在服务器更新内容后，不但会将缓存中过期的内容移除，还会推送最新的副本到缓存中。主动选择更新策略是对主动更新策略的改进，通过只推送一些较为热门内容的副本而减轻服务器的负担。

目前，针对缓存强一致性研究的数学模型普遍基于最近最少使用（Least Recent Used，LRU）替换策略^[6-7]，但在实际环境中，根据应用场景和缓存节点能力的不同，需要采取q-LRU、先进先出（First In First Out，FIFO）、随机替换（Random Replacement，RANDOM）等不同的缓存替换策略。同时，建立准确的缓存分析模型对于构建资源消耗较小且性能更高的网络结构具有重要作用。本文提出一种缓存强一致性策略下的通用建模方法，在内容失效的时间间隔分布不同时，模型计算可达到较高的精确度。通过实验以验证模型精确度并探究不同缓存参数和应用场景下的缓存性能变化。

1 相关研究

针对缓存到达最大容量后在新的内容到达时的内容替换问题，研究人员提出了LRU、FIFO、RANDOM、LFU、q-LRU、gLRU^[8]、TinyLFU^[9]等一系列缓存替换算法。

1.1 缓存分析模型

建立准确的缓存分析模型有助于更好地分析缓存行为。因此，在进行缓存部署前，需要进行资源估算，选择合适的缓存替换策略，从而有效减少资源消耗。文献[10]证明了RANDOM和FIFO在独立引用模型（Independent Reference Model，IRM）下具有相同的分析效果。文献[11]给出LRU和FIFO缓存命中率的近似解法，提高了计算效率。文献[12]将极限定理应用于平均场相互作用模型，推导出RANDOM策略的缓存命中率公式。文献[13]使用连续时间Markov链对LRU和FIFO的瞬时命中率进行研究。文献[14]提出一种基于列表的缓存替换策略的缓存分析模型，具有很高的精确度。

文献[15]提出使用特征时间近似的方法描述缓存在LRU中的生存行为，称为Che近似。文献[16]证明了Che近似在计算缓存命中率时具有极高的准确度。至此基于特征时间近似的缓存分析方法受到研究人员的广泛关注^[17-18]并取得了一系列研究成果^[19-21]。文献[22]在Che近似的基础上，提出一类可以用特征时间近似的缓存替换策略的缓存命中率计算公式。

上述研究推进了缓存替换策略的数学分析模型向更简单精确的方向发展，但考虑的都是理想模型，并未考虑存在缓存一致性等问题的实际应用场景。

1.2 缓存一致性分析模型

缓存一致性维护对一些实时性要求较高的应用而言非常重要。缓存一致性策略主要分为验证和失效。基于生存时间（即特征时间）的缓存替换策略是一种较为常见的验证策略^[23]。内容在缓存中存活规定的时间，超时即被驱逐出缓存，在缓存时被认为是最新的内容，如果有对该内容的请求到来即发生缓存命中。验证策略是一种弱一致性策略，如果内容在缓存中存在的这段时间内服务器发生内容失效事件，用户请求到的即是过期的内容。时间戳也是一个维护缓存弱一致性的验证策略，通过在数据包前加上时间戳的字段。文献[24]设计了一种分布式缓存策略，根据内容剩余生存时间、流行度和对邻居节点相同内容的感知性，使缓存自主决定存储哪些内容。文献[25]采用时间戳匹配方式满足用户对请求响应时间的要求，有效提高了信息准确率。失效策略主要分为被动策略和主动策略^[6-7]，其中主动策略相较于被动策略会降低用户的请求响应时间，但是会带来服务器负载的增加。

文献[6-7]针对失效策略建立Detti模型和Zheng模型。在Detti模型中，对被动查询策略和主动移除策略进行建模，将失效事件定义为独立的更新过程。在Zheng模型中，将失效事件和存在事件相关联，使用条件概率的方法对于被动查询策略和3种主动策略建模，其中主动选择更新策略能够在有效降低服务器负载的同时使缓存取得相较于其他3种策略更高的命中率，模型具有很高的精确度。在被动查询策略下，Detti模型实际计算的是不考虑一致性的情况，此时Zheng模型具有更高的精确度。在主动移除策略下，两种模型均能很好地拟合仿真结果。但是这两种模型均仅对LRU缓存替换策略进行研究，并未对更多的缓存替换策略进行研究。

为扩展缓存强一致性分析模型的适用范围，使其适用于可以使用特征时间近似的缓存替换策略，并在不同失效策略下均具有很高的计算精确度，本文基于缓存建模基本假设，对q-LRU、FIFO和RANDOM这3种缓存替换策略进行缓存强一致性模型分析。

2 缓存强一致性通用分析模型 2.1 模型假设

在建立缓存强一致性通用分析模型前进行如下假设：

1）假设有$ M $个不同的内容，为了简化计算，这些内容块的大小均为1。在实际环境中的内容大小并不为1，但由于内容一般是可分块的^[16]，假设同一个内容分块后流行度均相同，且在本文模型中仅考虑特征时间，因此设置相同大小的内容不会影响建模分析结果^[15]。

2）假设每个内容的流行度分布满足Zipf分布^[26]。内容的流行度等级为$ {i}^{m} $，其中$ {i}^{m}=\mathrm{1, 2}, \cdots , M $，流行度等级越小，流行度越高。内容$ m $的请求概率计算公式如下：

$ {P}_{\mathrm{r}}^{m}=\frac{A}{{i}^{m}} $

(1)

其中：$ A=1/\sum \limits_{m=1}^{M}\frac{1}{{\left({i}^{m}\right)}^{\alpha }} $为Zipf归一化因子，$ \alpha $是Zipf参数，Zipf参数越大，流行内容越集中。本文假设内容流行度是固定不变的，但在实际环境中并非如此，因此针对内容流行度变化的情况，本文仅考虑一小段时间内的流行度，假设在这个时间片内的内容流行度是固定的。

3）假设每个到达过程满足泊松分布及IRM模型，即所有内容之间的到达过程是相互独立的且流行度分布不发生变化。假设所有内容的总到达速率为$ \lambda $，则内容$ m $的到达速率为$ {\lambda }_{m}={P}_{\mathrm{r}}^{m}\cdot \lambda $。

4）假设内容在缓存节点间的传输时延为0。服务器和缓存间用于通信的包的大小相较于携带数据的包要小得多，因此不考虑这部分信息对服务器负载的影响。

2.2 特征时间近似 2.2.1 缓存替换策略

一般缓存大小设定为内容总数的0.5%~1.5%。当缓存存满后，如果有新的内容到达，可能会触发缓存替换事件，则需要选择一个内容驱逐以存储最新的内容。

LRU策略内部相当于一个栈，栈顶为最新的内容，当栈满后会驱逐栈底的内容。若请求内容已存在栈中，则会将该内容移动至栈顶，并且LRU具有良好的时间相关性，若同一段时间内请求相同的内容较为密集时，则LRU会体现出其优越性。q-LRU是LRU的改进策略，内容访问策略和驱逐策略与LRU相同，但在内容缓存时会以q的概率缓存。

FIFO策略会维护一个定长的队列，先进来的内容在驱逐时会被最先驱逐。RANDOM策略在发生缓存替换时，会在缓存中随机选择一个内容驱逐。RANDOM和FIFO非常相似，从替换角度看它们的处理方式对于每个内容都是平等的，适用于请求流量较为均匀的场景。

2.2.2 分析模型

Che近似中用特征时间来描述内容从进入LRU到被驱逐的过程，这里的特征时间$ {T}_{\mathrm{c}} $也可以称为生存时间，即内容在缓存中存在的时间^[15]。如果在某个时刻$ t $到达一个对内容$ m $的请求，此时发生缓存命中，则说明缓存中已存在该内容。按照特征时间的概念，即在$ \left(t-{T}_{\mathrm{c}}, t\right] $时间内至少需要有一次相同的请求到达。由于内容的到达满足泊松过程，且到达速率为$ {\lambda }^{m} $，因此得到内容$ m $在缓存中存在的概率如式（2）所示。当缓存趋于稳态时，缓存稳定地进行内容替换，即缓存总是满的。由于内容大小单位为1，缓存的大小即可以用所有内容存在概率的期望表示，如式（3）所示，其中$ C $为缓存大小。这里$ {T}_{\mathrm{c}} $是一个常数，LRU认为对于所有内容的特征时间是相同的^{[6-7, 15]}。根据PASTA属性得到内容m的平均缓存命中率如式（4）所示。对于所有内容的平均缓存命中率如式（5）所示。对q-LRU而言，若缓存中存在内容$ m $则要求上一次请求以q的概率存储在缓存中或已经存在缓存中^[22]，如式（6）所示。根据式（3）、式（4）可求得内容$ m $的平均缓存命中率如式（7）所示，当q=1时，与LRU的缓存命中率公式相同。FIFO的缓存命中率推导可以使用排队论的方法，对于每个内容而言，计算如式（8）所示。在使用式（3）计算时，可将特征时间取均值。在IRM流量下，认为RANDOM的推导公式等同于FIFO^[10]。

$ {P}_{\mathrm{e}}^{m}=1-{\mathrm{e}}^{-{\lambda }^{m}{T}_{\mathrm{c}}} $

(2)

$ \sum \limits_{m=1}^{M}{P}_{\mathrm{e}}^{m}=C $

(3)

$ {P}_{\mathrm{h}}^{m}={P}_{\mathrm{e}}^{m} $

(4)

$ {P}_{\mathrm{h}}=\sum \limits_{m=1}^{M}{P}_{\mathrm{r}}^{m}{P}_{\mathrm{h}}^{m} $

(5)

$ {P}_{\mathrm{e}}^{m}=\left(1-{\mathrm{e}}^{-{\lambda }^{m}{T}_{\mathrm{c}}}\right)\left[{P}_{\mathrm{e}}^{m}+q\left(1-{P}_{\mathrm{e}}^{m}\right)\right] $

(6)

$ {P}_{\mathrm{h}}^{m}=\frac{q\left(1-{\mathrm{e}}^{-{\lambda }^{m}{T}_{\mathrm{c}}}\right)}{{\mathrm{e}}^{-{\lambda }^{m}{T}_{\mathrm{c}}}+q\left(1-{\mathrm{e}}^{-{\lambda }^{m}{T}_{\mathrm{c}}}\right)} $

(7)

$ {P}_{\mathrm{e}}^{m}=\frac{{\lambda }^{m}{T}_{\mathrm{c}}}{1+{\lambda }^{m}{T}_{\mathrm{c}}} $

(8)

2.3 强一致性分析模型

维护缓存强一致性的策略即失效策略，包含被动查询、主动移除、主动更新和主动选择更新4种，其中主动选择更新实际是主动更新策略的一种变体，因此只考虑前3种情况，即被动查询、主动移除和主动更新。在此失效事件的到达采用通用分布，当存在失效事件时内容存在概率和命中率不同。

设$ {P}_{\mathrm{R}}^{m}\left(t\right) $为内容$ m $在$ t $时间段内到达且缓存因此至少发生一次替换行为的概率。由于内容$ m $到达过程满足泊松过程，即要求在$ t $时间段内至少有一次相同的请求到达过，因此对于LRU、FIFO、RANDOM：

$ {P}_{\mathrm{R}}^{m}\left(t\right)=1-{\mathrm{e}}^{-{\lambda }^{m}t} $

(9)

由于q-LRU缓存中均以q的概率进行首次插入，因此缓存替换行为至少发生一次的概率如下：

$ {P}_{\mathrm{R}}^{m}\left(t\right)=1-\sum \limits_{n=0}^{\mathrm{\infty }}{\left(1-q\right)}^{n}{\mathrm{e}}^{-{\lambda }^{m}t}\frac{{\left({\lambda }^{m}t\right)}^{n}}{n!}=1-{\mathrm{e}}^{-q{\lambda }^{m}t} $

(10)

根据Zheng模型的计算公式，可推算出内容有效概率的期望值如下：

$ E\left({P}_{\mathrm{v}}^{m}\right)=\frac{1}{{\mu }_{\mathrm{s}}^{m}}\underset{0}{\overset{\mathrm{\infty }}{\int }}\underset{0}{\overset{{t}_{\mathrm{s}}^{m}}{\int }}{P}_{\mathrm{R}}^{m}\left(t\right)\mathrm{d}t\mathrm{d}F\left({t}_{\mathrm{s}}^{m}\right) $

(11)

其中：$ {P}_{\mathrm{v}}^{m} $为内容$ m $在缓存中有效的概率；$ {\mu }_{\mathrm{s}}^{m} $为内容$ m $发生失效事件时间间隔的期望；$ F\left({t}_{\mathrm{s}}^{m}\right) $为内容$ m $发生失效事件时间间隔的概率分布函数。

2.3.1 被动查询

由于被动查询是缓存在接收到用户对内容的请求后向服务器发出询问，因此内容在缓存中的生存时间仍按无一致性策略进行计算。将计算结果与失效时间间隔相比较，按照有效且存在或存在且有效的计算方法可以得到内容的平均命中率^[7]。内容$ m $的平均命中率如下：

$ \begin{array}{l}{P}_{\mathrm{h}}^{m}=\frac{1}{{\mu }_{\mathrm{s}}^{m}}\underset{0}{\overset{{T}_{\mathrm{c}}}{\int }}\underset{0}{\overset{{t}_{\mathrm{s}}^{m}}{\int }}{P}_{\mathrm{R}}^{m}\left(t\right)\mathrm{d}t\mathrm{d}F\left({t}_{\mathrm{s}}^{m}\right)+\\ \frac{1}{{\mu }_{\mathrm{s}}^{m}}\underset{{T}_{c}}{\overset{\mathrm{\infty }}{\int }}\left(\underset{0}{\overset{{T}_{\mathrm{c}}}{\int }}{P}_{\mathrm{R}}^{m}\left(t\right)\mathrm{d}t+\left({t}_{\mathrm{s}}^{m}-{\mathrm{T}}_{\mathrm{c}}\right){P}_{\mathrm{e}}^{m}\right)\mathrm{d}F\left({t}_{\mathrm{s}}^{m}\right)\end{array} $

(12)

2.3.2 主动移除

在主动移除策略中，由于服务器会主动移除已经失效的内容，因此缓存并不总是满的，缓存到达最大容量和内容过期均会将内容删除，且特征时间的计算不能直接使用非一致性公式。此时缓存中存在的内容总量可以表示为缓存大小和缓存中有效内容的最小值：

$ O\approx \mathrm{m}\mathrm{i}\mathrm{n}\left(C, \sum \limits_{m=1}^{M}1\cdot {P}_{\mathrm{v}}^{m}\right) $

(13)

$ \sum \limits_{m=1}^{M}{P}_{\mathrm{h}}^{m}=O $

(14)

联立式（12）、式（13）、式（14）可以求得特征时间，继而可以求出平均缓存命中率。

2.3.3 主动更新

当服务器发生更新事件，即缓存中的内容失效时，服务器会主动推送最新的内容到缓存节点，此时所有请求只要在缓存中发现内容，即是有效的，会发生缓存命中，实际的计算公式与非一致性公式相同。

上述q-LRU、FIFO和RANDOM缓存替换策略均可用特征时间来近似，对于其他策略，只要能给出特征时间近似的解法，本文缓存分析模型同样适用。

2.3.4 服务器负载

对于被动查询和主动移除策略而言，服务器负载仅和未命中的缓存内容相关，计算公式如下：

$ {S}_{\mathrm{L}}=\lambda \left(1-{P}_{\mathrm{h}}\right) $

(15)

对于主动策略而言，除了处理未命中内容，在失效事件发生时会主动推送新的内容，服务器负载计算如下：

$ {S}_{\mathrm{L}}=\lambda \left(1-{P}_{\mathrm{h}}\right)+\sum \limits_{m=1}^{M}\frac{1}{{\mu }_{\mathrm{s}}^{m}}{P}_{\mathrm{e}}^{m} $

(16)

由于服务器只会对缓存中存在的内容进行主动推送，因此式（16）等式右边的后半部分可以理解为需要更新内容大小的均值。

3 实验结果与分析

通过仿真实验验证缓存强一致性分析模型的准确性，同时探究选取不同缓存场景或缓存参数时缓存命中率和服务器负载的变化规律。

使用基于Python开发的实验环境进行仿真实验。实验环境设置为：操作系统为Windows10，CPU为Intel Core i7-8750H，内存为16 GB，Python版本为3.6。仿真拓扑中包括：1个用户模拟器，用于发出请求；1个缓存节点，用于放置不同的缓存替换策略，同时监测并统计缓存性能的变化；1个服务器，用于响应缓存的请求。

在实验中，设定内容总数为6 000，不失一般性，将这些内容编号，内容块的编号越大，流行度越低。内容流行度分布满足Zipf分布，Zipf参数在实验中设定为0.8。设定缓存默认大小为60，内容总的请求速率为80 req/s，失效时间间隔的期望值默认设定为20 s。对于失效事件的到达间隔，可以是常数及均匀分布、指数分布等分布描述，由于文章篇幅的限制，下文仅给出常数时间间隔和满足指数分布时间间隔的情况。

为验证模型的准确性，采用式（17）计算误差：

$ \delta =\frac{\left|{\left({P}_{\mathrm{h}}\right)}_{model}-{\left({P}_{\mathrm{h}}\right)}_{sim}\right|}{{\left({P}_{\mathrm{h}}\right)}_{\mathrm{s}\mathrm{i}\mathrm{m}}} $

(17)

其中：$ {\left({P}_{\mathrm{h}}\right)}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}} $为缓存分析模型计算得到的命中率；$ {\left({P}_{\mathrm{h}}\right)}_{\mathrm{s}\mathrm{i}\mathrm{m}} $为实际仿真实验得到的缓存命中率。

在所有实验中利用缓存分析模型计算出对应的数值结果，用线的形式进行表示，同时用点的形式表示仿真器在对应条件下生成的结果。首先进行模型的准确性验证，分别在q-LRU、FIFO和RANDOM策略下，依次使用3种不同的缓存强一致性策略进行实验。然后在缓存参数变化时，探究q-LRU中缓存概率q的大小、Zipf参数、平均失效时间间隔和缓存大小变化对缓存性能的影响。最后在缓存参数不同时，对不同缓存替换策略进行性能比较。通过缓存分析模型计算结果和仿真结果的比较，以验证模型准确性。

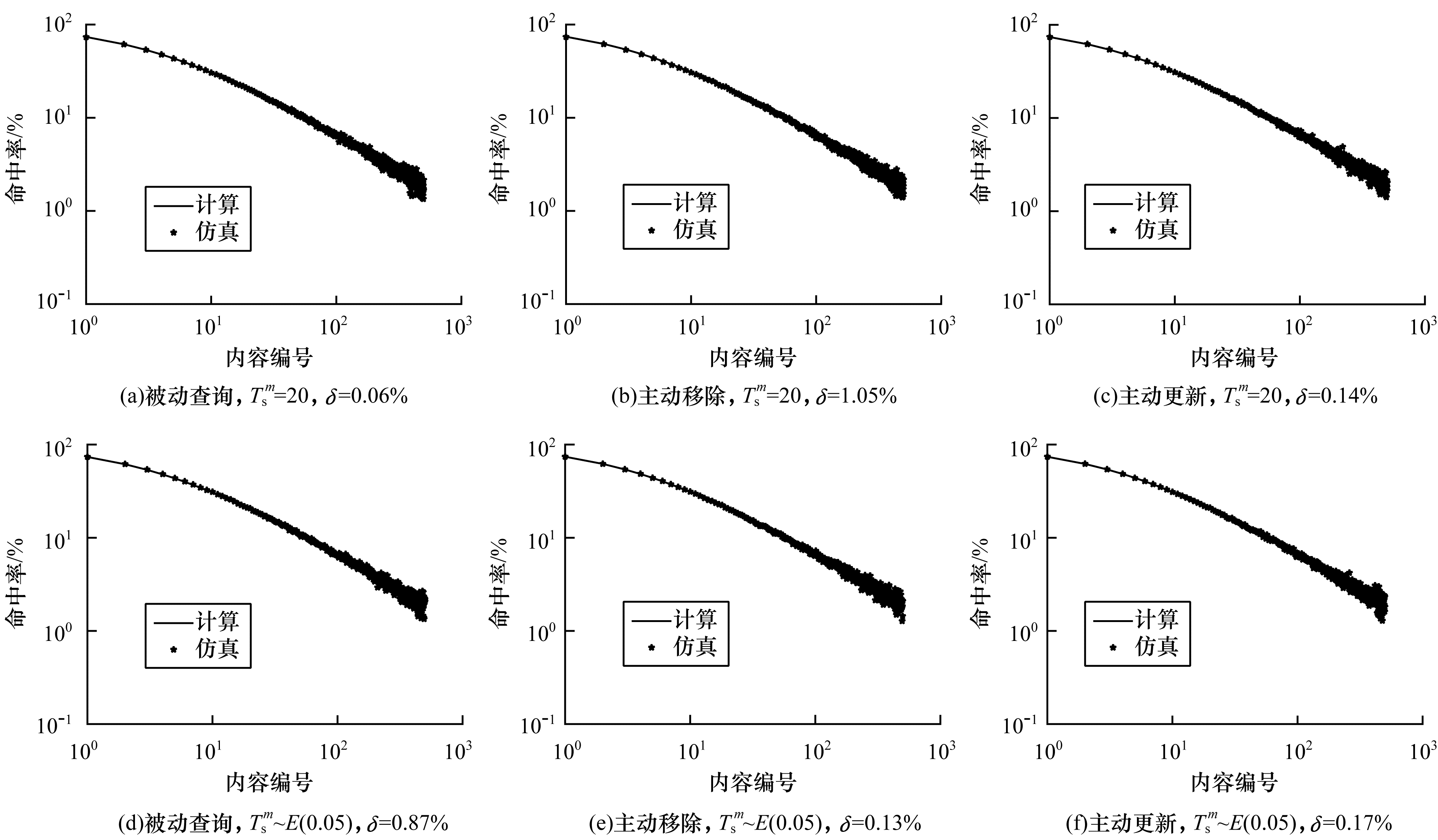
3.1 不同缓存替换策略的缓存强一致性实验

图 1~图 3验证了在内容$ m $发生失效事件的时间间隔为常数（$ {T}_{\mathrm{s}}^{m} $=20）和其时间间隔分布满足指数分布（$ {T}_{\mathrm{s}}^{m}\sim E\left(0.05\right) $，请求速率为20 req/s）时，不同失效策略下模型内容平均命中率计算结果与仿真结果的吻合程度。由于篇幅限制，所有实验在图片中仅展示内容编号前500的比较结果。由图 1~图 3可以看出，在不同缓存替换策略、不同失效策略下缓存强一致性分析模型均取得了较高的准确度，最大误差为2.18%。模型与仿真的误差来源既与模型有关，又与仿真器设计本身有关，若仿真时间足够大，事件产生足够准确，则仿真器的误差可忽略不计。另外，无一致性策略的模型本身可能也存在误差。由于主动更新模型计算公式等同于无一致性策略的模型，因此其误差即是无一致性策略的模型误差的计算公式。

3.2 参数变化对缓存性能的影响

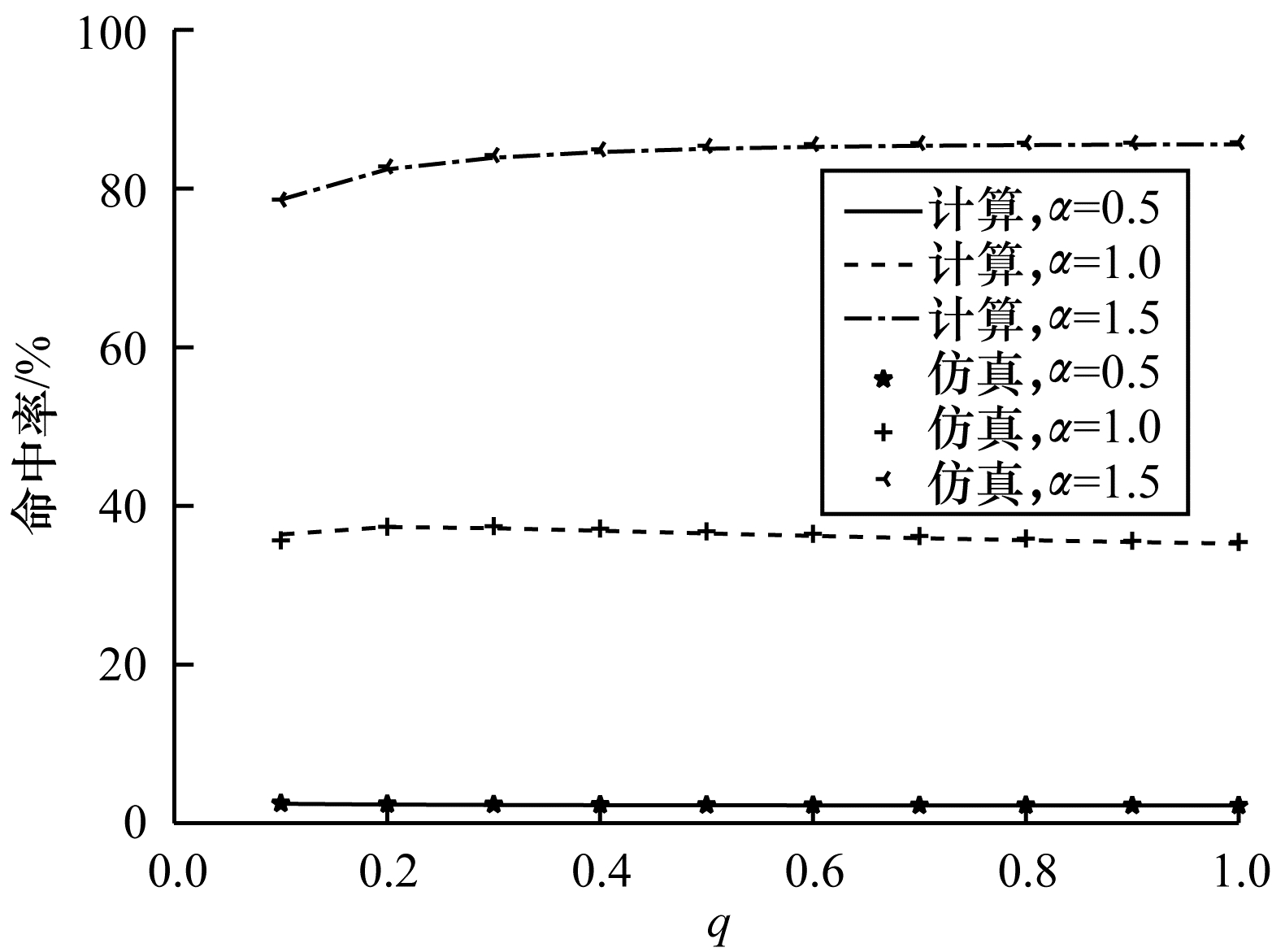
由于指数分布的失效间隔在实际环境中更为常见，考虑篇幅限制，因此分析参数变化对缓存性能的影响时，仅考虑指数分布。图 4给出了在不同Zipf参数下，当q=0.6且$ {T}_{s}^{m}\sim E\left(0.05\right) $时q-LRU随着q的变化缓存命中率的变化曲线，计算结果与仿真结果相比最大误差为2.81%。

不同的失效策略带来的趋势是相同的，因此此处仅研究被动查询情况下缓存性能的变化。不同的Zipf参数代表着不同的流量环境：当Zipf参数较大时（$ \alpha =1.5 $），流行内容非常集中，当q变大时缓存性能趋近于LRU，由于LRU具有良好的时间相关性，流行的内容在缓存中生存的时间会更久，因此会取得更大的命中率；当Zipf参数稍小一些时（$ \alpha =1.0 $），流行内容集中度降低，编号靠后的内容出现的概率增加，频繁进行内容替换容易产生缓存污染，q取值较小时缓存命中率会大一些，但是当q取值很小时，缓存的替换变得困难，缓存命中率反而会变得很小；当Zipf参数较小时（$ \alpha =0.5 $），流量相对均匀，在q大于0.1时，q的变化基本不会影响缓存命中率。

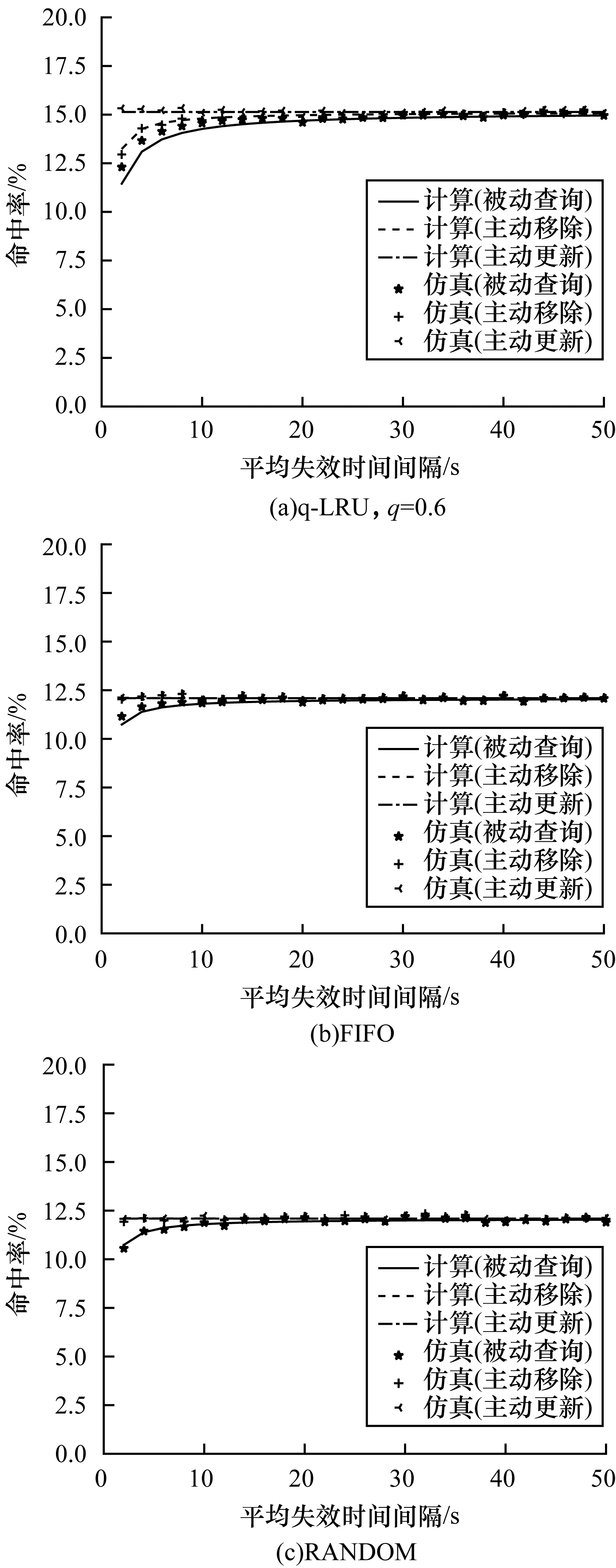
在图 5中，改变发生失效事件的速率，即失效平均时间间隔，在q-LRU策略处于被动查询策略下最大误差为6.92%，在FIFO策略处于被动查询策略下最大误差为3.73%，在其他策略下最大误差为2.17%，计算模型仍可以很好地拟合仿真结果。随着失效平均时间间隔的增加，失效行为发生的越来越少，存储在缓存中的内容更可能是最新的内容，因此缓存命中率增加。主动更新策略使缓存一直是最新的，具有最高的命中率，且与失效事件无关。对于q-LRU而言，主动移除策略会使缓存有更多空间存储新的内容，因此缓存命中率比被动查询策略稍大一些。对于FIFO和RANDOM而言，它们驱逐内容的方式对每个内容均是平等的，因此主动更新策略和主动移除策略的性能相似。

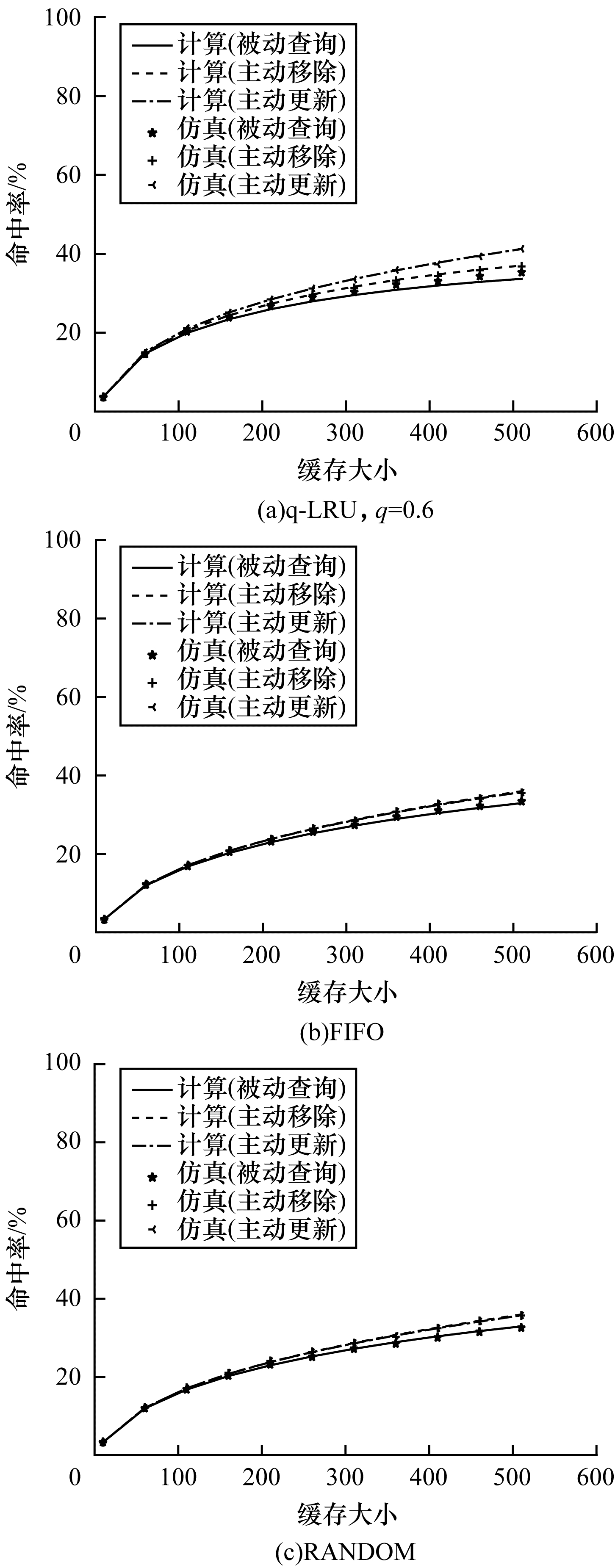
在图 6中，随着缓存大小的增加，缓存能够存储更多的内容，缓存命中率得到提高。在图 6（a）中最大误差为4.68%，在图 6（b）中最大误差为2.06%，在图 6（c）中最大误差为1.79%，本文模型依然具有较高的计算精确度。

3.3 缓存替换策略比较

在Zipf参数、平均失效时间间隔、缓存大小等影响缓存性能的变量已知的情况下，选择合适的缓存替换策略能有效提升缓存命中率，减小服务器负载。

基于式（15）和式（16）可知，在被动查询策略和主动移除策略下，服务器负载取决于缓存的未命中率，即当服务器负载较小的时候，也是缓存命中率最高的时候，所选的策略也是最优的。在同样场景下，应用主动更新策略，虽然缓存命中率最高，但服务器负载也是最大的。在图 7中，改变Zipf参数，观察4种缓存替换策略随着Zipf参数变化服务器负载的变化情况。在图 7（a）中最大误差为2.49%，在图 7（b）中最大误差为0.88%，在图 7（c）中最大误差为0.69%。可以看出，当Zipf参数变大时，选择FIFO或RANDOM策略的服务器负载要更大，缓存命中率更低，此时选择LRU或q-LRU更优。在Zipf参数较大时，LRU与q-LRU的选择可以参考图 4及其解析。从图 7可以看出：当Zipf参数较大时q-LRU对应的服务器负载略低于LRU，此时缓存替换策略选取q-LRU最优；当Zipf参数较小时，这些策略都可以选择，从实现难度来看，FIFO和RANDOM要更为简单。从这些缓存替换策略的本身分析也可以看出，FIFO和RANDOM策略适合流行度比较均匀的内容，而LRU具有良好的时间相关性，在热门内容更多时具有更好的性能。

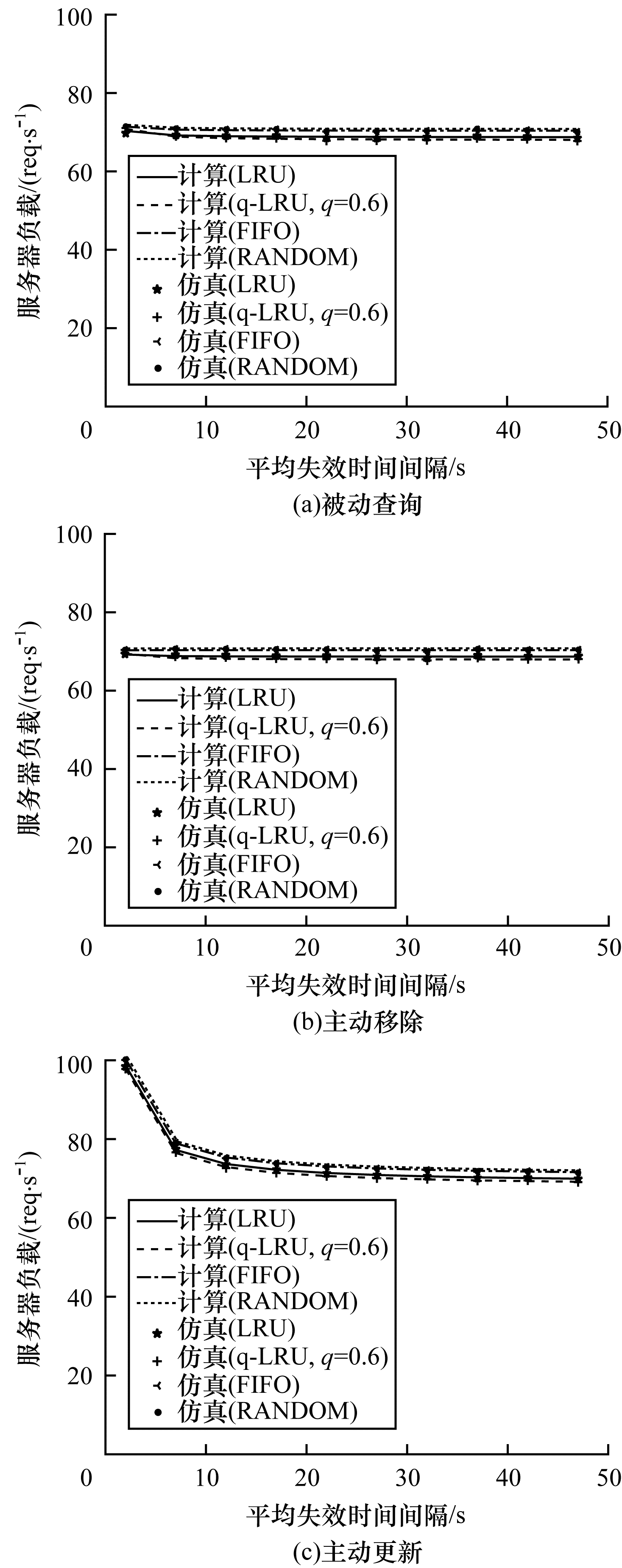
在图 8中，通过改变平均失效时间间隔分析这4种缓存替换策略下服务器负载的变化情况。在图 8（a）中最大误差为1.01%，在图 8（b）中最大误差为0.62%，在图 8（c）中最大误差为0.39%。在3种失效策略下，主动更新的服务器负载最大。在平均失效时间间隔比较小时，对主动更新策略下服务器负载影响很大，因为失效越频繁，服务器越繁忙，其他两种策略只和缓存未命中相关，在此场景下，平均失效时间间隔和服务器负载减小，但变化趋势很小。在平均失效时间间隔大于2 s时，LRU或q-LRU的性能总是优于FIFO和RANDOM，且此时q-LRU是最优策略。在平均失效时间间隔小于2 s时，是一种快速更新的行为，在实际环境中并不常见，此时FIFO或RANDOM更为合适，因为缓存替换的行为也需要时间，如果替换的时间相较于失效时间间隔不是足够小，则用户很难请求到最新的内容。

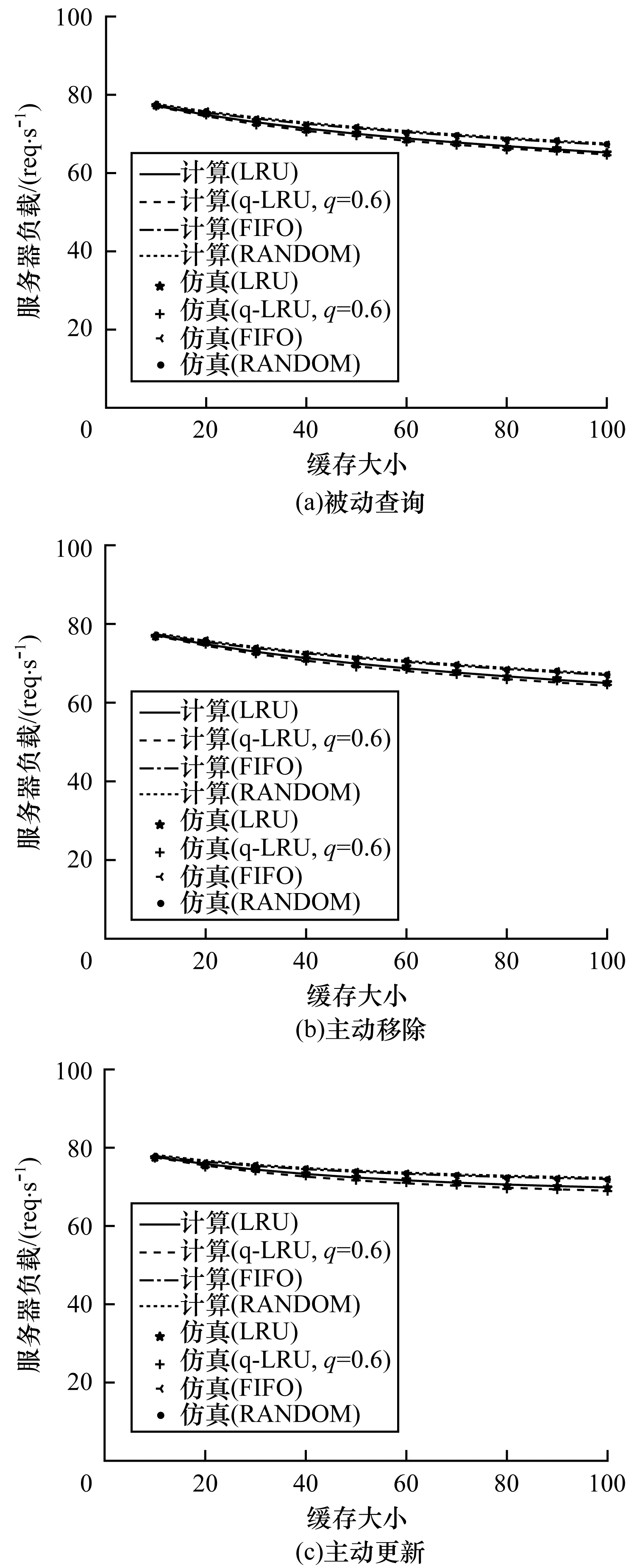
图 9给出了4种缓存替换策略下服务器负载随着缓存大小的变化情况。在图 9（a）中最大误差为0.60%，在图 9（b）中最大误差为0.69%，在图 9（c）中最大误差为0.53%。在缓存较大时，FIFO和RANDOM具有相同的性能，但服务器负载总是高于LRU或q-LRU。从服务器负载的角度来看，在缓存较大时，q-LRU策略下服务器负载最低，此时q-LRU是最优策略。在缓存较小时，很多流行的内容没有被缓存下来，因此服务器负载较大，此时4种缓存替换策略均会产生较高的服务器负载，可以选用实现更为简单的FIFO或RANDOM策略。

4 结束语

本文构建缓存强一致性通用分析模型，并给出3种缓存强一致性策略下缓存命中率和服务器负载的计算方法。通过选取不同的缓存参数进行仿真实验，证明了通用分析模型具有较高的计算精确度，并且根据通用分析模型的计算方法，可在不同缓存参数或缓存场景下选取最优的缓存替换策略以取得最优的缓存性能。后续可将缓存强一致性通用分析模型拓展至更复杂的网络拓扑结构，进一步提高计算结果的精确度，同时在真实网络环境中部署缓存替换策略，基于通用分析模型选取合适的缓存参数，使缓存节点可在资源消耗较小时取得较优的缓存性能。