开放科学（资源服务）标志码（OSID）：

0 概述

情感的产生是一个生理和心理相互作用的过程，与感受、想法和行为有关^[1-2]。脑电（EEG）是一种典型的中枢神经生理信号^[3]，可以用来检测大脑对不同情绪状态的反应，为情绪识别提供更加客观和全面的信息，并且EEG数据具有时间分辨率高、成本低、易于获得和使用等特点^[4-5]。因此，EEG被广泛应用于大脑研究领域。

EEG主要通过构建脑网络来反映大脑的相互作用，目前已构建的脑网络主要分为功能性脑网络和因果脑网络2种。功能性脑网络^[6]主要反映网络中节点之间的连接关系，是研究大脑工作机制的重要渠道。文献[7]使用相位滞后指数（Phase Lag Index，PLI）在DEAP公共情绪数据集上构建了不同波段下的人脑EEG功能性脑网络进行情绪识别。因果脑网络^[8-9]研究主要针对脑功能网络中的有向信息流和因果属性，其反映节点之间的因果关系，可以更好地观察到情绪信息在不同脑区的流动方向，并从流动的方向来判断出因果关系。对于这2种脑网络而言，因果网络的研究更能反映出脑网络的变化，揭示情绪产生的机理。

格兰杰（Granger）因果检验因其简单性和易于实现性而成为计算时间序列之间因果关系的一种主流方法^[10]。文献[11]采用格兰杰因果关系构建因果连接脑网络，并提取了脑网络的连接密度和因果流来对5种情绪进行分类，文献[12]则采用格兰杰因果关系分析调查了Gamma波段的脑连接。但是格兰杰因果检验在计算时仅考虑2个时间序列之间的关系，没有考虑其他时间序列的影响。本文引入条件格兰杰因果检验（Conditional Granger Causality text，CGC）算法^[10]研究在其他通道信息影响下各通道之间的因果关系，找出在情绪产生过程中起到主要作用的脑区和通道，进而简化因果网络。在此基础上，将简化网络中节点之间的因果关系作为特征送入SVM和KNN分类器进行训练分类，验证本文方法的有效性。

1 因果脑网络计算方法 1.1 CGC算法

格兰杰因果检验原理为：在多元自回归（MVAR）模型中，如果时间序列Y的历史信息显著提高了时间序列X的预测准确性，则可以确定时间序列Y到X的格兰杰因果关系^[13]。但是此方法只适合分析2个时间序列之间的因果关系，一旦时间序列超过2个就不得不考虑其他时间序列的影响。本文利用CGC算法分析在其他时间序列影响下任意序列之间的因果关系的计算问题。

假设有3个时间序列$ {X}_{1}\left(t\right) $、$ {X}_{2}\left(t\right) $和$ {X}_{3}\left(t\right) $，在$ {X}_{3}\left(t\right) $存在的条件下，$ {X}_{1}\left(t\right) $和$ {X}_{2}\left(t\right) $的自回归模型为：

$ \left\{ {\begin{array}{*{20}{l}} {{{\rm{X}}_{1,t}} = \sum\limits_{j = 1}^m {{a_{11}}} {X_{1,t - j}} + {a_{13}}{X_{3,t - j}} + {\varepsilon _{1,t}}}\\ {{{\rm{X}}_{2,t}} = \sum\limits_{j = 1}^m {{a_{21}}} {X_{2,t - j}} + {a_{23}}{X_{3,t - j}} + {\varepsilon _{2,t}}} \end{array}} \right. $

(1)

$ {X}_{1}\left(t\right) $、$ {X}_{2}\left(t\right) $的联合回归模型为：

$ \left\{ {\begin{array}{*{20}{c}} {{X_{1, t}} = \sum\limits_{j = 1}^m {{a_{11}}} {X_{1, t - j}} + {a_{12}}{X_{2, t - j}} + {a_{13}}{X_{3, t - j}} + {\eta _{1, t}}}\\ {{X_{2, t}} = \sum\limits_{j = 1}^m {{a_{21}}} {X_{1, t - j}} + {a_{22}}{X_{2, t - j}} + {a_{23}}{X_{3, t - j}} + {\eta _{2, t}}} \end{array}} \right. $

(2)

其中：$ t=\mathrm{0, 1}, \cdots , n $；m为回归模型的阶数；$ {\varepsilon }_{i} $和$ {\eta }_{j} $为回归估计残差，它们的均值为0，且互不相关，方差分别表示为$ {\sigma }_{{\varepsilon }_{i}}^{2} $和$ {\sigma }_{{\eta }_{j}}^{2} $$ （i=\mathrm{1, 2}, j=\mathrm{1, 2}，3） $。由此，$ {X}_{2}\left(t\right) $对$ {X}_{1}\left(t\right) $的因果影响定义为：

$ {G}_{{X}_{2}\to \left.{X}_{1}\right|{X}_{3}}=\mathrm{l}\mathrm{n}\frac{{\sigma }_{{\varepsilon }_{1}}^{2}}{{\sigma }_{{\eta }_{1}}^{2}} $

(3)

如果式（3）所示等式的值大于0，则$ {\varepsilon }_{1} $ > $ {\eta }_{1} $，证明在$ {X}_{3}\left(t\right) $存在的条件下，$ {X}_{1}\left(t\right) $和$ {X}_{2}\left(t\right) $联合预测的误差小于$ {X}_{1}\left(t\right) $自身预测的误差，必然是因为$ {X}_{2}\left(t\right) $对$ {X}_{1}\left(t\right) $的预测，因此，在$ {X}_{3}\left(t\right) $存在的条件下，称$ {X}_{2}\left(t\right) $对$ {X}_{1}\left(t\right) $有因果作用；如果式（3）所示等式的值不大于0，则证明$ {X}_{2}\left(t\right) $对$ {X}_{1}\left(t\right) $无因果作用。

同理，在$ {X}_{3}\left(t\right) $存在的条件下，$ {X}_{1}\left(t\right) $对$ {X}_{2}\left(t\right) $的因果影响定义为：

$ {G}_{{X}_{1}\to \left.{X}_{2}\right|{X}_{3}}=\mathrm{l}\mathrm{n}\frac{{\sigma }_{{\varepsilon }_{2}}^{2}}{{\sigma }_{{\eta }_{2}}^{2}} $

(4)

1.2 介数计算公式

脑网络中节点的介数公式定义为：

$ {C_{\rm{B}}}\left( v \right) = \sum\limits_{{\rm{s}} \ne v \ne t \in V} {\frac{{{\sigma _{st}}\left( v \right)}}{{{\sigma _{st}}}}} $

(5)

其中：V表示网络中节点的总数目；$ {\sigma }_{st}\left(v\right) $表示经过$ v $的脑网络节点s到t的最短路径数；$ {\sigma }_{st} $表示s到t的最短路径数。从式（5）可以看出，$ {C}_{\mathrm{B}}\left(v\right) $反映了节点$ v $在因效网络中的重要程度，$ {C}_{\mathrm{B}}\left(v\right) $的值越大，代表节点$ v $越重要。

1.3 因果网络构建

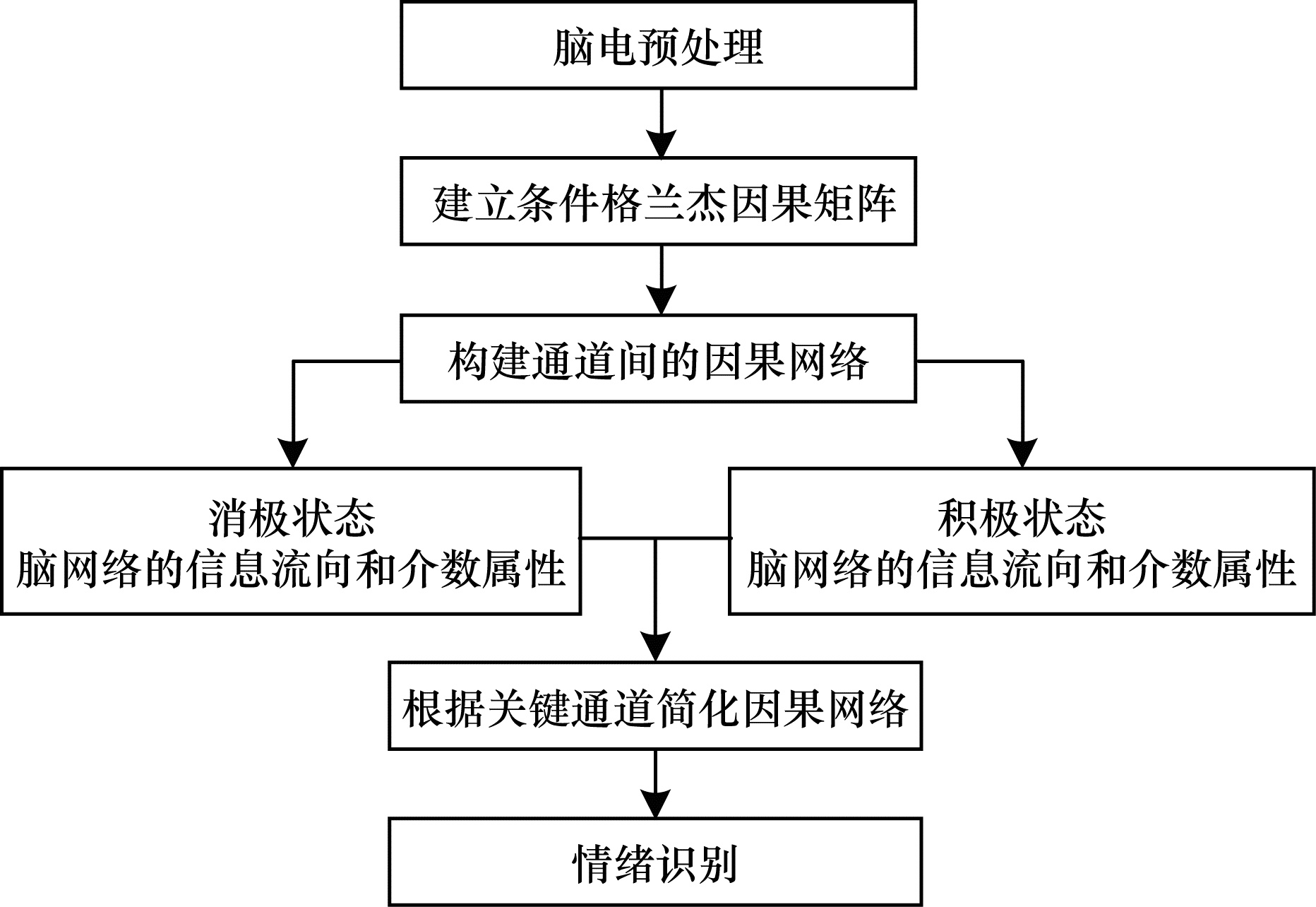
脑电预处理先对脑电信号的均值和平稳性进行处理，再利用计算得到的因果矩阵可视化构建因果网络，在不同情绪下对因果网络进行属性分析，主要包括通道之间信息的流向和介数属性。因果网络的情感状态分析方法流程如图 1所示。

2 实验设计 2.1 实验数据集

DEAP^[14]是人类情绪状态的公共数据集，其中记录了32位参与者（16位男性和16位女性）在观看40个带有不同情感标记的视频片段时的各种生理信号，参与者看完视频片段以后，对每一个视频在效价和唤醒的维度上划分1~9的等级。对收集到的脑电信号应用512 Hz采样和4.0~45 Hz的带通滤波器进行滤波。实验记录的EEG信号为63 s的数据，其中前3 s是记录的基线数据。由于本文的主要研究内容是用CGC计算脑电信号，因此选择大脑内部不同脑区中32个EEG的信号通道，另外8个通道是外围的生理信号，本文不做参考。

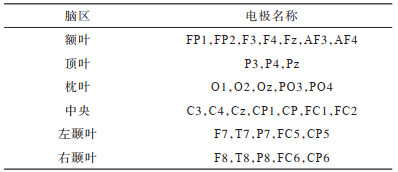
根据国际10-20脑电系统，可以将大脑划分为额叶、顶叶、枕叶、左颞叶、右颞叶、中央大脑区域6个区域。每个脑区对应不同的通道，表 1列出了实验所选择的6个脑区的32个通道，每个大脑区域位置的电极名称与DEAP情感数据集中对应的电极名称相同。

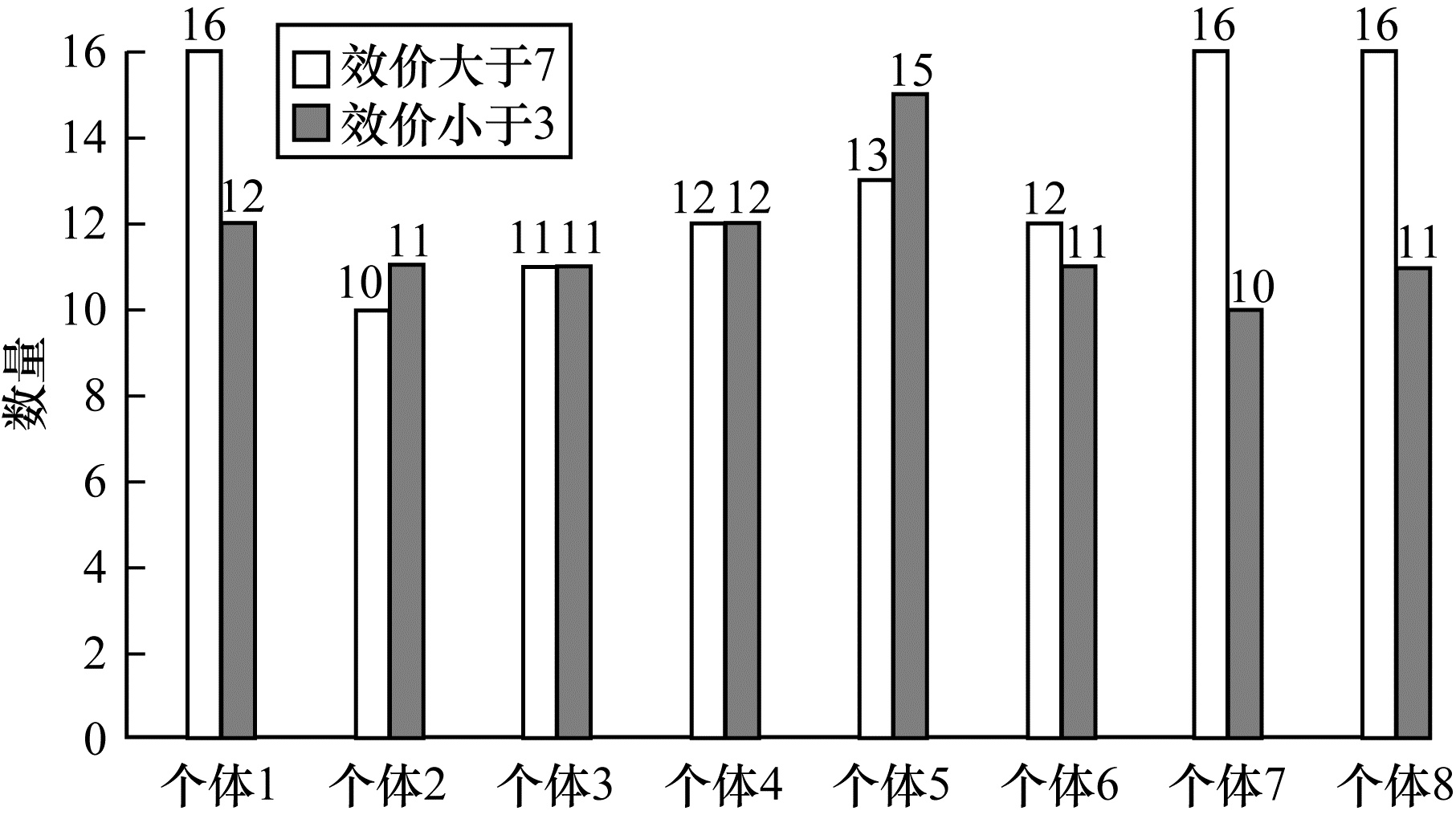
在实验预处理的过程中，删除前3 s的基线数据，仅保留剩余60 s的数据，同时将EOG伪影和尾迹从EEG信号中删除，然后根据参与者划分的标签选择数据。为避免中性数据的干扰并确保提供足够的数据，对个体和实验都进行筛选，在效价的维度上，将大于7的视为积极情绪，将小于3的视为消极情绪，根据划分的范围选择积极和消极的实验次数都大于9的个体^[15]。图 2显示了筛选的个体以及该个体对应的积极实验和消极实验的数量。

2.2 CGC矩阵

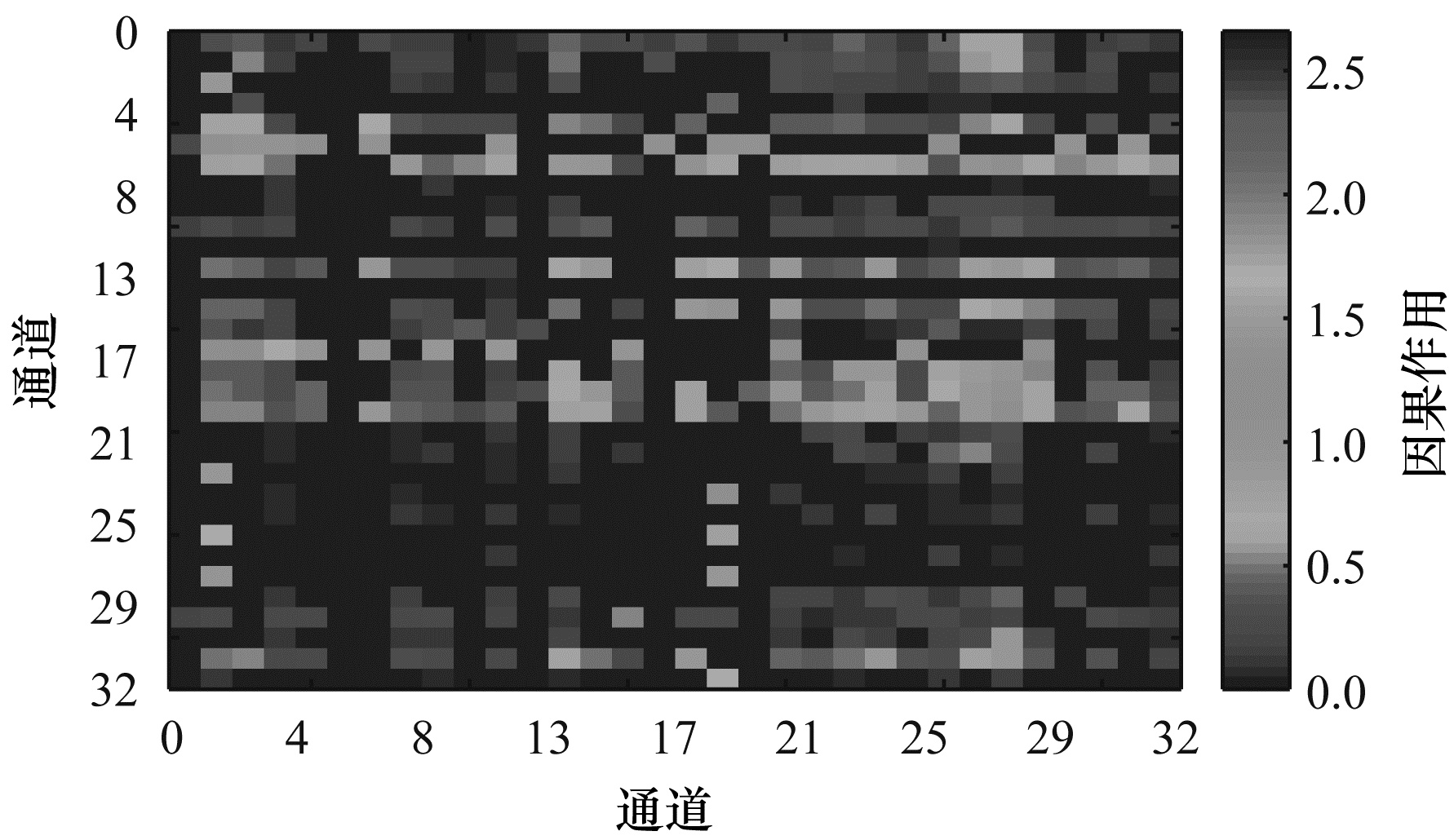
根据CGC计算的标准化流程^[16-17]，计算出每个个体在不同情绪下每次实验不同通道之间的因果关系。图 3和图 4分别显示个体的2次实验得到的因果关系所对应的因果关系矩阵，包括1次积极情绪状态下的实验和1次消极情绪状态下的实验，其中坐标轴代表所选的大脑内部的32个通道，最右侧数值代表通道之间的因果作用大小，数值越大，代表通道之间的因果作用越强烈。通过2幅图之间的对比可以看出：消极情绪状态下通道之间的因果作用强度要明显大于积极情绪状态下的因果作用强度，且消极情绪状态下通道之间的反应要明显大于积极状态下通道之间的反应，这说明消极情绪状态下通道之间的连接更复杂多样。

2.3 因果网络属性分析

利用上述计算得到的因果关系可视化构建因果网络，因为CGC计算得出的因果关系是一个确定的数值，所以在进行可视化之前先对因果数值进行二值化处理，将通道之间因果值大于0的设置为1，小于等于0的设置为0。在因果网络中，节点代表脑区的通道，边代表通道之间的因果作用。入/出度^{[8, 18]}和介数拓扑属性^[19-20]是衡量因果网络的2个重要指标。分析这2个重要指标的目的是找出网络中的关键通道。入/出度是从信息流向的角度对网络中通道的因果连接关系进行分析，通道的出度越多，表明该通道对其他通道的影响越大；通道的入度越多，表明该通道受其他通道的影响越多；入度和出度越多，则表明此通道更活跃，在网络中的地位越高。介数拓扑属性描绘了通道或者通道之间的连接边在整个网络中的作用和影响力，介数高的通道往往位于网络中的重要位置。

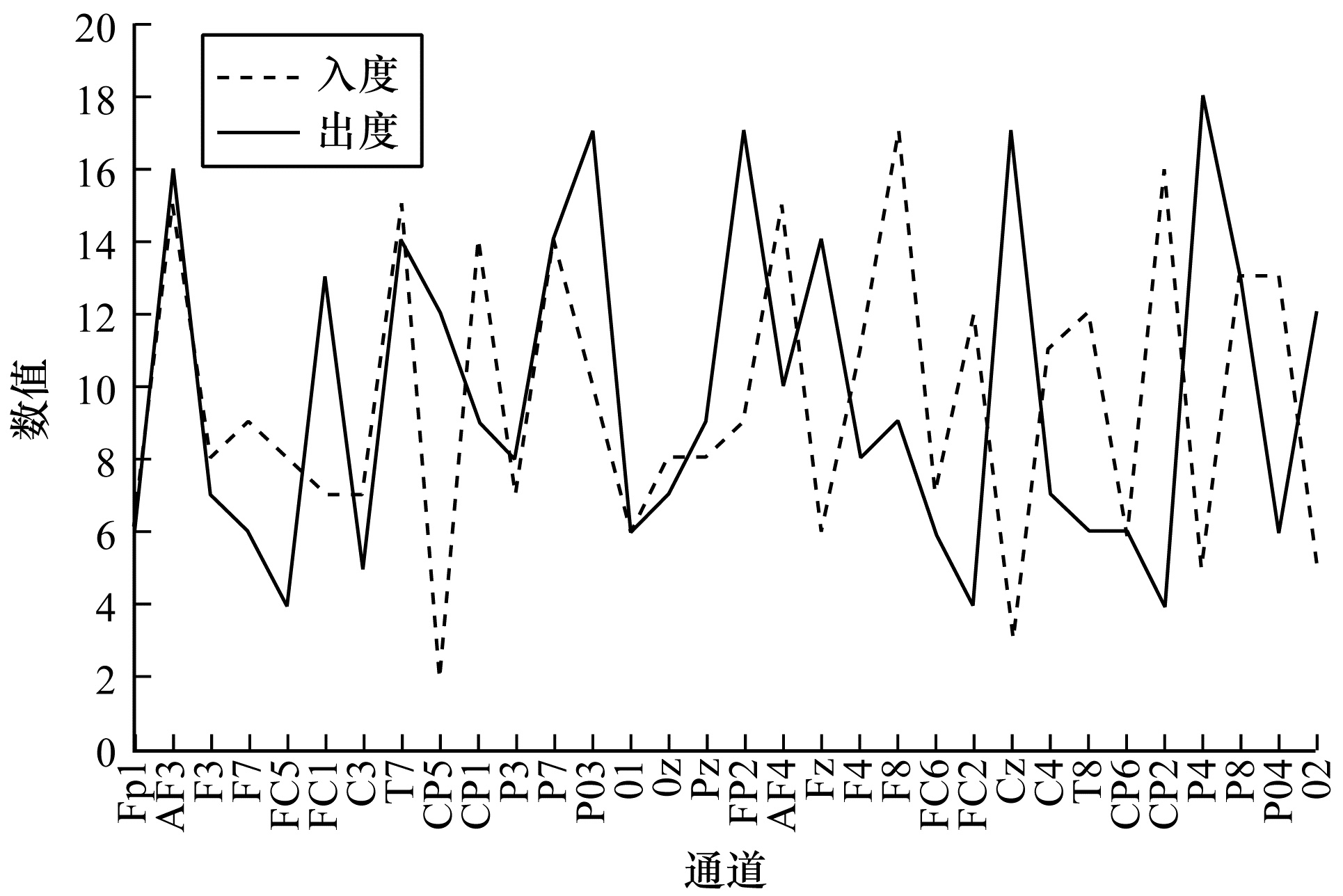
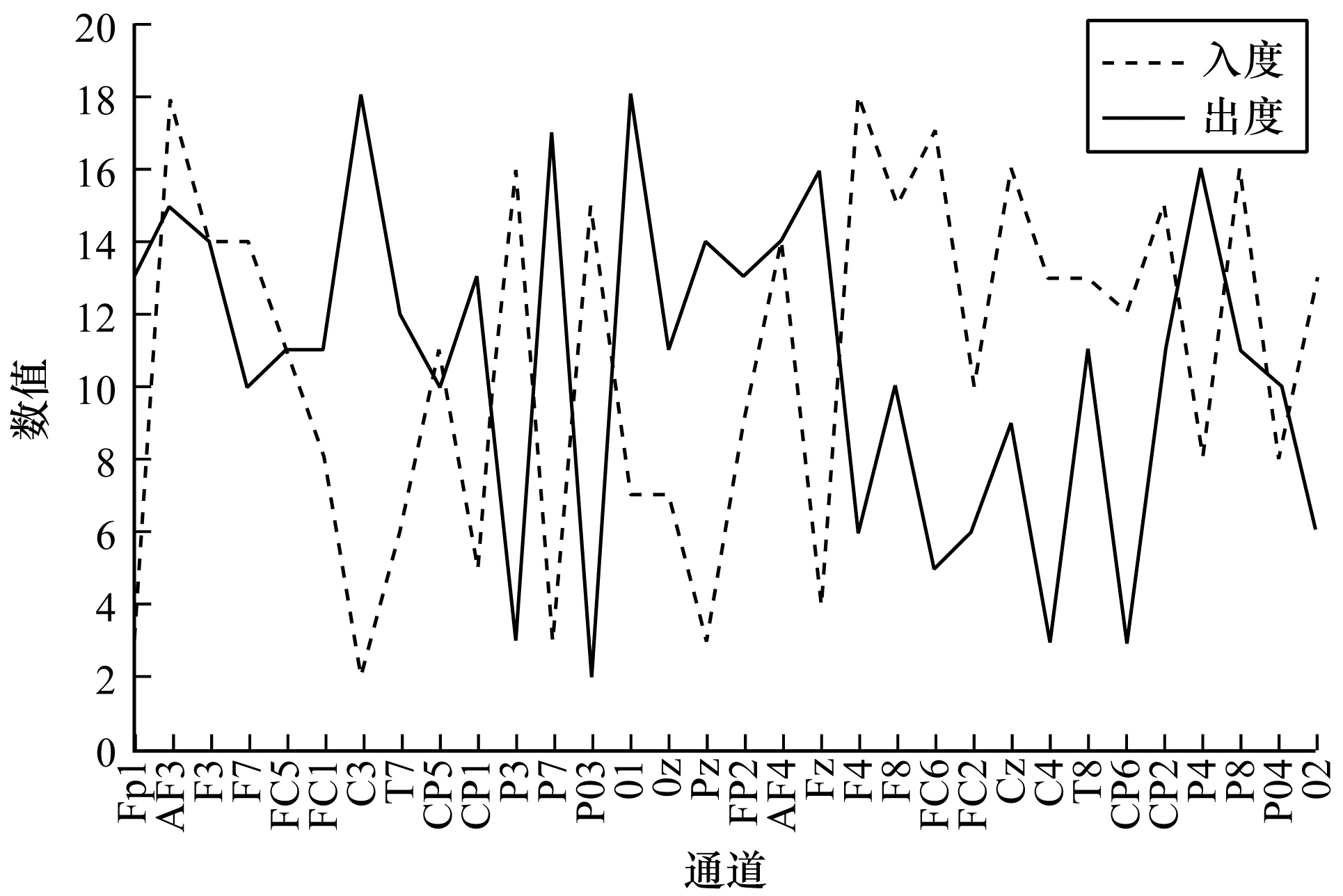
积极情绪和消极情绪下因果网络中节点的入度和出度分别如图 5和图 6所示。由计算可以得出消极情绪下通道入度和出度的数目大于积极情绪下入度和出度的数目，这表明消极情绪下大脑区域形成的网络更复杂，信息交互更活跃，这一点与上文分析一致。此外，2种情绪下通道AF3、AF4、FP1、FP2、T7、P8、F8、P7、PO3、PO4、F4、F3的入度和出度数目都较多，说明这些通道对其他通道或者是受到其他通道的影响较多，在情绪的产生过程中起到主要作用。因此，可以初步认为这些通道是因果网络中的关键通道。

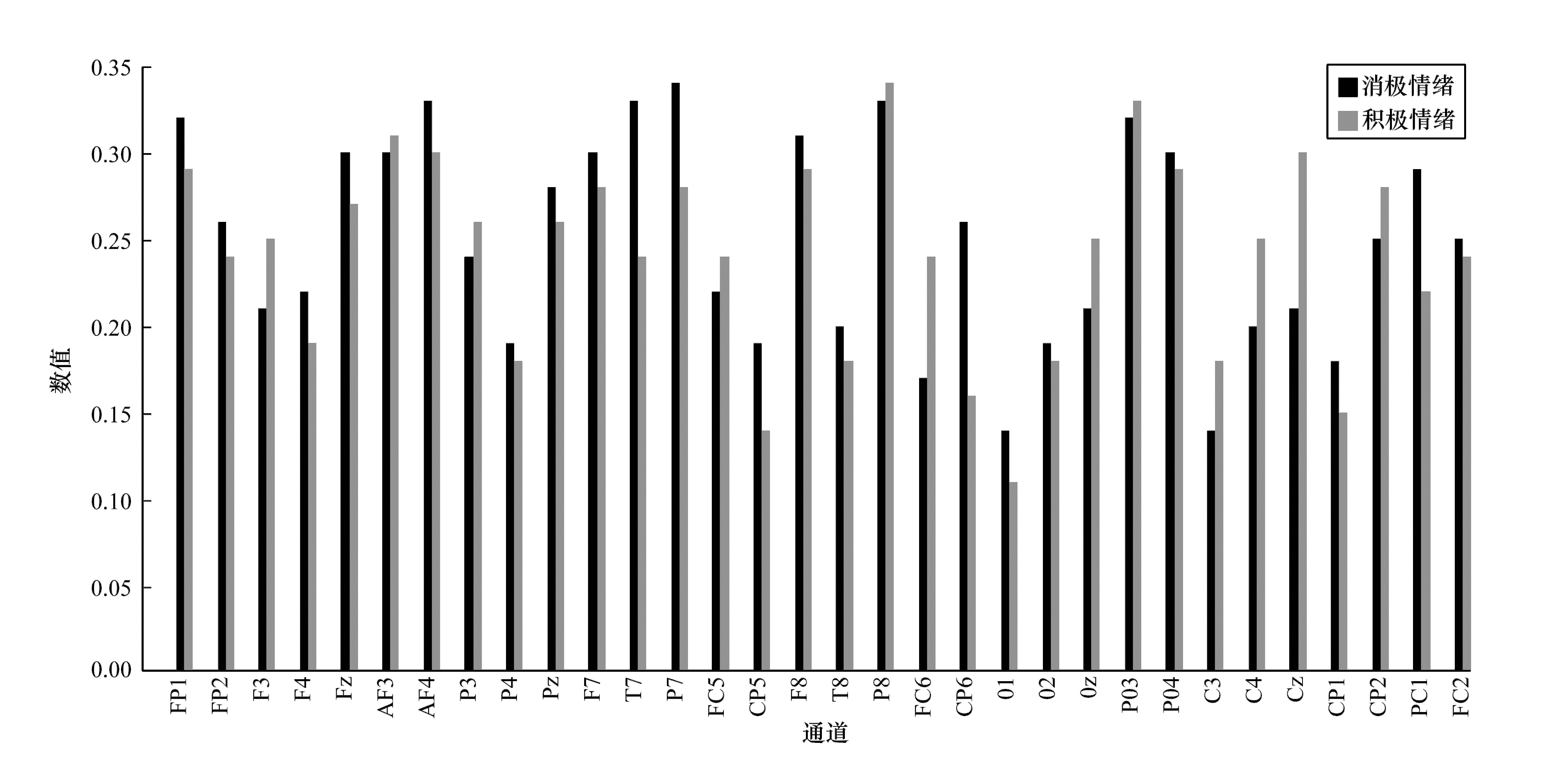
为得到不同情绪下因果网络中的关键通道，分别计算网络中通道的介数拓扑属性。图 7描绘了被试者在积极和消极2种情绪状态下因果网络的介数拓扑属性，介数的值越大，通道在因果网络的地位越高。可以看出：积极情绪状态下因果网络中介数较高的通道为AF3、AF4、FP1、FP2、P8、P7、PO4、F3，消极情绪状态下介数较高的通道为AF3、AF4、FP1、FP2、T7、F8、PO3、PO4。通过分析比较可以看出，即使在不同情绪下，因果网络的关键通道也基本一致，因此，不同情绪状态下所构建的因果网络的相似度很高。由此可见，通道AF3、AF4、FP1、FP2、T7、P8、F8、P7、Pz、PO3、PO4、F3、F4在因果网络中的地位较高，可将这些通道归为网络中的关键通道。

通过入度和出度的分析，可以得出因果网络中的关键通道为AF3、AF4、FP1、FP2、T7、P8、F8、P7、PO3、PO4、F4、F3；通过对介数拓扑属性的分析，可以得出因果网络中的关键通道为AF3、AF4、FP1、FP2、T7、P8、F8、P7、Pz、PO3、PO4、F3、F4。由此可以看出，对网络的2种属性分析得到的关键通道基本一致，取2次属性分析关键通道的并集作为最终选取的关键通道，因此，最终选取的关键通道为AF3、AF4、FP1、FP2、T7、P8、F8、P7、Pz、PO3、PO4、F3、F4。可以看出，关键通道主要位于脑区中的额叶、颞叶和枕叶，由此判断这些脑区在情绪产生的过程中起到主要作用，这个结果与多数已有研究结果相同^[21-22]。在简化因果网络的过程中，本文只保留与关键通道相连接的边和通道，因为这些通道为关键通道，在因果网络中起到重要作用，保留与这些通道相连接的边可反映出网络的主要特征。图 8是个体简化网络之后的因果连接网络，个体包括1次积极实验和1次消极实验。

3 有效性验证

为验证简化得到的因果网络，将节点之间的因果连接关系作为一种特征进行情绪识别，使用SVM和KNN对数据进行训练和分类。实验的个体共有8个，为了将全部的数据都应用于训练和分类，对实验数据采用8倍交叉验证，以平均识别率作为最终的识别精度。实验结果表明，本文方法构建的基于多通道脑电信号的因果网络平均识别精度分别为75.3%和78.4%，整体识别率较高，表明CGC算法是一种有效的计算时间序列间因果关系的方法，由此证明本文方法的有效性。

4 结束语

本文提出一种面向多通道脑电信号的因果网络情绪识别方法。利用条件格兰杰因果检验算法得到不同情绪下大脑内部各通道之间的因果关系，以此构建因果网络，并使用简化的因果网络进行情绪分类。实验结果表明，本文方法能够对不同的情绪进行有效分类。后续将去除多余的EEG通道，而只选取关键通道计算其间的因果关系，进一步提高分类精度。