2. 中国科学院大学, 北京 100049;
3. 北京航空航天大学 软件学院, 北京 100191;
4. 中国原子能科学研究院, 北京 102413
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Software, Beihang University, Beijing 100191, China;
4. China Institute of Atomic Energy, Beijing 102413, China
开放科学(资源服务)标志码(OSID):
在科学计算和工程应用领域中,很多实际问题的求解通常可以转换为求解线性代数方程组
一些学者基于机器学习方法构建SpMV算法生成库。李佳佳等[14]提出一个SMAT自动调优器,对于一个给定的稀疏矩阵,SMAT结合矩阵特征选择并从DIA、ELL、CSR、COO等4种格式中返回最优的存储格式。SEDAGHATI等[15]构建一个决策模型,实现对给定目标平台上的稀疏矩阵自动选择最优存储格式。BENATIA等[16]采用SVM方法来解决存储格式选择问题。NISA等[17]结合决策树和SVM两种方法,实现一个存储格式预测模型。ZHAO等[18-19]考虑运行时预测开销以及格式转换开销的影响,设计回归模型以及基于神经网络的时间序列预测模型,有效捕获了开销以及格式预测和转换对整体程序性能的影响。ZHAO等[20]将深度学习方法引入SpMV的最优稀疏矩阵存储格式选择中,提出Late-merging卷积神经网络(Convolutional Neural Network,CNN)结构,有效地将深度学习方法应用于高性能计算问题,但该模型缺乏对体系结构参数的考虑。上述方法主要用于稀疏矩阵存储格式选择,并不适用于SpMV性能预测。对于SpMV,由于输入的特征数据来源于稀疏矩阵和体系结构参数,数据含义以及表示形式与图像处理网络中的输入数据不同,因此图像处理领域中的CNN网络结构不再适用,需要设计新的CNN网络来满足SpMV运算时间预测的需求。
本文构建一个SpMV性能预测模型,将稀疏矩阵的特征以及硬件平台的特征作为输入、SpMV运算时间作为输出。设计CNN网络结构,对各部分特征输入分别独立进行特征处理。引入特征融合模块,将特征融合延迟到CNN网络后期,使CNN网络更好地适应SpMV的输入表示形式,并使用稀疏矩阵集合进行实验验证。
1 基于CNN的SpMV运算时间预测模型 1.1 模型构建SpMV运算时间预测模型为三通道独立CNN模型,网络添加了特征融合模块,如图 1所示。该模型主要由双通道稀疏矩阵特征融合以及稀疏矩阵特征与体系结构特征融合两部分组成,每个部分的作用如下:

|
Download:
|
| 图 1 特征融合CNN模型结构 Fig. 1 Structure of feature fusion CNN model | |
1)双通道稀疏矩阵特征融合。考虑到稀疏矩阵的表示以及CNN具备提取矩阵特征的能力,本文设计双通道稀疏矩阵特征融合模块,获取稀疏矩阵的特征。通过直方采样算法从稀疏矩阵中提取出行特征矩阵以及列特征矩阵,采用特征后融合的方法,将它们分别输入各自的卷积神经网络中,在后期进行线性拼接融合,并输入至全连接层,进而得到稀疏矩阵的融合特征。
2)稀疏矩阵特征与体系结构特征融合。同样采用特征后融合的方法,首先将融合后的稀疏矩阵特征与体系结构参数特征分别使用BN(Batch Normalization)层[21]规范化后进行特征融合,得到稀疏矩阵与体系结构参数的融合特征,然后经过Softmax函数,最后输出四分类的预测值。
在图像处理领域,对一幅给定RGB图像,每个通道中的第i个元素都对应原始图像的第i个像素。在本文所研究的问题中,由于稀疏矩阵采用直方采样算法提取特征,行特征矩阵和列特征矩阵在数值上具有不同的统计意义,即一个是对行的直方统计,另一个是对列的直方统计,因此并没有图像处理中点对点的对应关系[20]。基于上述考虑,特征融合模块将对来自稀疏矩阵的特征矩阵以及来自运行平台的体系结构参数特征分别进行处理,在网络后期将两者特征融合,避免了多类别特征过早融合导致特征提取时造成的相互干扰,同时降低了算法复杂度。
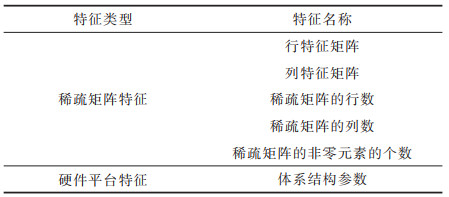
1.2 特征数据的选取和构建SpMV实际运行的时间与多种因素有关,例如矩阵的规模大小、矩阵的非零元素个数、运行平台的体系结构参数等。在构建模型时,单一特征通常只侧重于某一方面,为了提高模型的可靠性和准确性,采取特征融合的方法来兼顾多种特征的信息。为此,本文选取并构建SpMV运算时间预测的多类别输入特征,将SpMV数据特征分为两类,即稀疏矩阵特征和硬件平台特征,如表 1所示。
|
下载CSV 表 1 输入特征信息 Table 1 Input feature information |
稀疏矩阵特征包括行特征矩阵、列特征矩阵,以及稀疏矩阵的行数、列数、非零元素的个数。其中,对于稀疏矩阵,采用直方采样算法对原稀疏矩阵分别进行行直方采样以及列直方采样,从而得到行特征矩阵以及列特征矩阵。稀疏矩阵的行数和列数表征了稀疏矩阵的规模大小,对于规模很小的稀疏矩阵,执行SpMV自动调优的耗时较短,对其进行时间预测的意义较小。因此,本文实验剔除了规模较小的矩阵,即行数或列数小于100的矩阵。
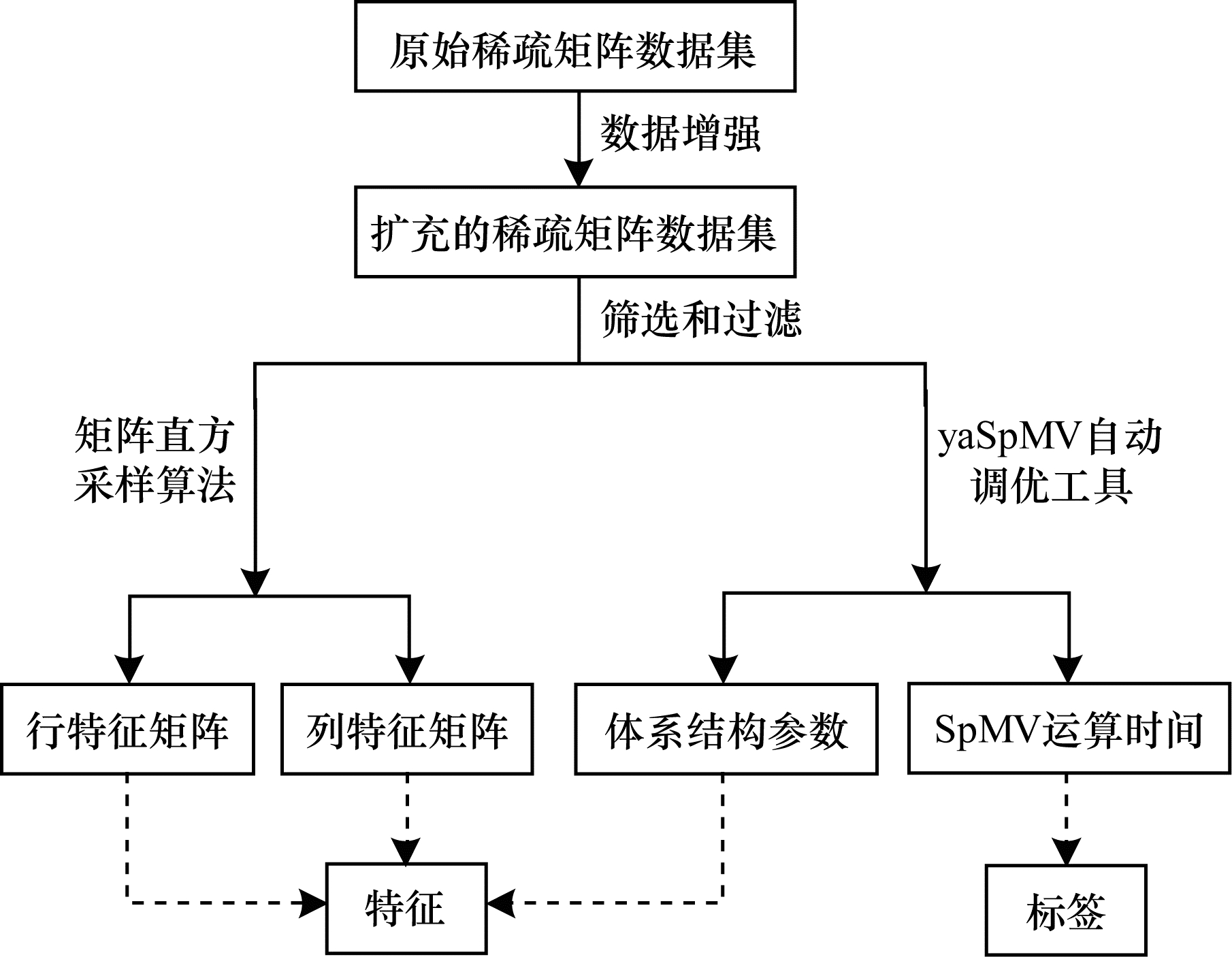
在选定模型的输入特征后,需要进行数据采集以及数据预处理,构建完整的特征数据集。适当的数据预处理能够提高整个预测模型的准确性,图 2给出了数据预处理的过程,其中,实线表示数据预处理的流程,虚线表示模型的特征数据和标注数据。由于CNN网络需要大量数据作为训练样本,进而获得样本间的知识,因此应用数据增强技术来获取足量数据。首先,对原始稀疏矩阵进行转置,对现有的数据进行扩充产生更多训练数据,以便模型学习到更多矩阵特征。其次,对扩充后的数据进行筛选和过滤,包括处理无效数据、过滤不符合要求的数据等。最后,采用直方采样算法提取稀疏矩阵的行特征以及列特征,并借助yaSpMV[10]工具获取体系结构参数以及SpMV运算时间。
|
Download:
|
| 图 2 数据预处理过程 Fig. 2 Process of data preprocessing | |
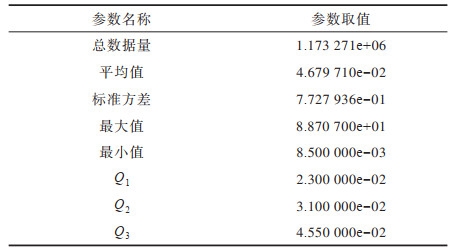
基于深度学习的模型训练需要海量的标注数据。本文使用箱形图[22]统计时间信息,箱形图能够显示出一组数据的最大值、最小值、中位数以及上下四分位数,可以用来反映数据分布的中心位置和散布范围,并且可以直观地识别批量数据中的异常值。在箱形图中,异常值被定义为小于
|
下载CSV 表 2 基于箱形图的时间统计信息 Table 2 Time statistics based on box plot |
为使数据类别划分尽可能均匀,实验采用
| $ \mathrm{Class}=\left\{\begin{array}{l0, 0}\le t < {Q}_{1}\\ 1, {Q}_{1}\le t < {Q}_{2}\\ 2, {Q}_{2}\le t < {Q}_{3}\\ 3, {Q}_{3}\le t < {Q}_{3}+1.5{I}_{\mathrm{IQR}}\end{array}\right. $ | (1) |
其中:SpMV运算时间在[0,
1)对原始稀疏矩阵数据进行预处理,提取稀疏矩阵的特征,得到特征矩阵,包括行特征矩阵和列特征矩阵。
2)获取硬件平台的体系结构参数组合,构建多类别特征数据集,同时对每一组参数设置执行SpMV运算,得到对应的SpMV运算时间,作为训练标签。
3)设计基于卷积神经网络的模型结构,利用步骤1、步骤2中得到的特征数据和标签组成数据集,输入模型中进行训练,不断进行参数优化调整,直至得到训练好的模型。
4)使用新的稀疏矩阵,经过数据预处理得到特征数据,输入训练好的模型中得到预测结果。
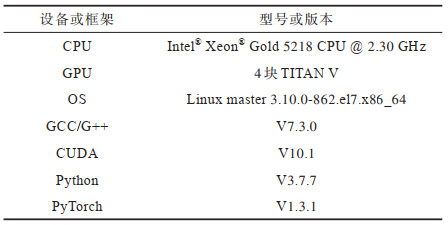
2 实验与结果分析为验证本文特征融合CNN模型的准确性和有效性,实验选择佛罗里达稀疏矩阵数据集[23]进行验证,选用格式为MM格式[24],获取并扩充得到稀疏矩阵文件1 538个。实验平台相关信息如表 3所示。
|
下载CSV 表 3 实验平台相关信息 Table 3 Experimental platform related informations |
本文特征融合CNN模型采取将稀疏矩阵特征与体系结构参数特征先分别卷积池化再进行融合的模型进行处理,旨在消除输入特征之间的相互干扰。为验证该模型的有效性,建立一个对比模型,记为非特征融合CNN模型。在该模型中,稀疏矩阵特征与体系结构参数特征在网络后期直接融合,这与图 1所展现的特征先消融再融合的结构有着本质区别。
对于两个模型,将预处理得到的数据按10∶1的比例分为训练集和验证集,数据量信息如表 4所示。模型均在相同的训练集以及验证集上进行实验。由于数据量较大,如果直接将训练数据输入预测模型进行训练,每轮迭代时间较长,参数更新缓慢,因此采用梯度下降法中的mini-batch训练方法进行小批量训练,结合反向传播算法优化参数,降低内存负载,提高训练速度。模型训练参数设置如下:损失函数为CrossEntropyLoss,优化器为optim.Adam,学习率为1e-2,共训练50批次,每批次数据量为1 024。

|
下载CSV 表 4 数据集划分 Table 4 Dataset division |
选取以下评价指标对特征融合CNN三通道独立CNN模型进行预测性能分析:
1)Loss值。使用平均绝对误差(Mean Absolute Error,MAE)值表示Loss值,MAE计算公式如下:
| $ {M}_{\mathrm{MAE}}=\frac{1}{n}\sum\limits_{i=1}^{n}\left|{y}_{i}-{y}_{i}^{\mathrm{\text{'}}}\right| $ | (2) |
其中:
2)ACC值。使用ACC值作为准确率的值,ACC计算公式如下:
| $ {A}_{\mathrm{ACC}}=\frac{{C}_{\mathrm{true}}}{{C}_{\mathrm{all}}}\times 100\mathrm{\%} $ | (3) |
其中:
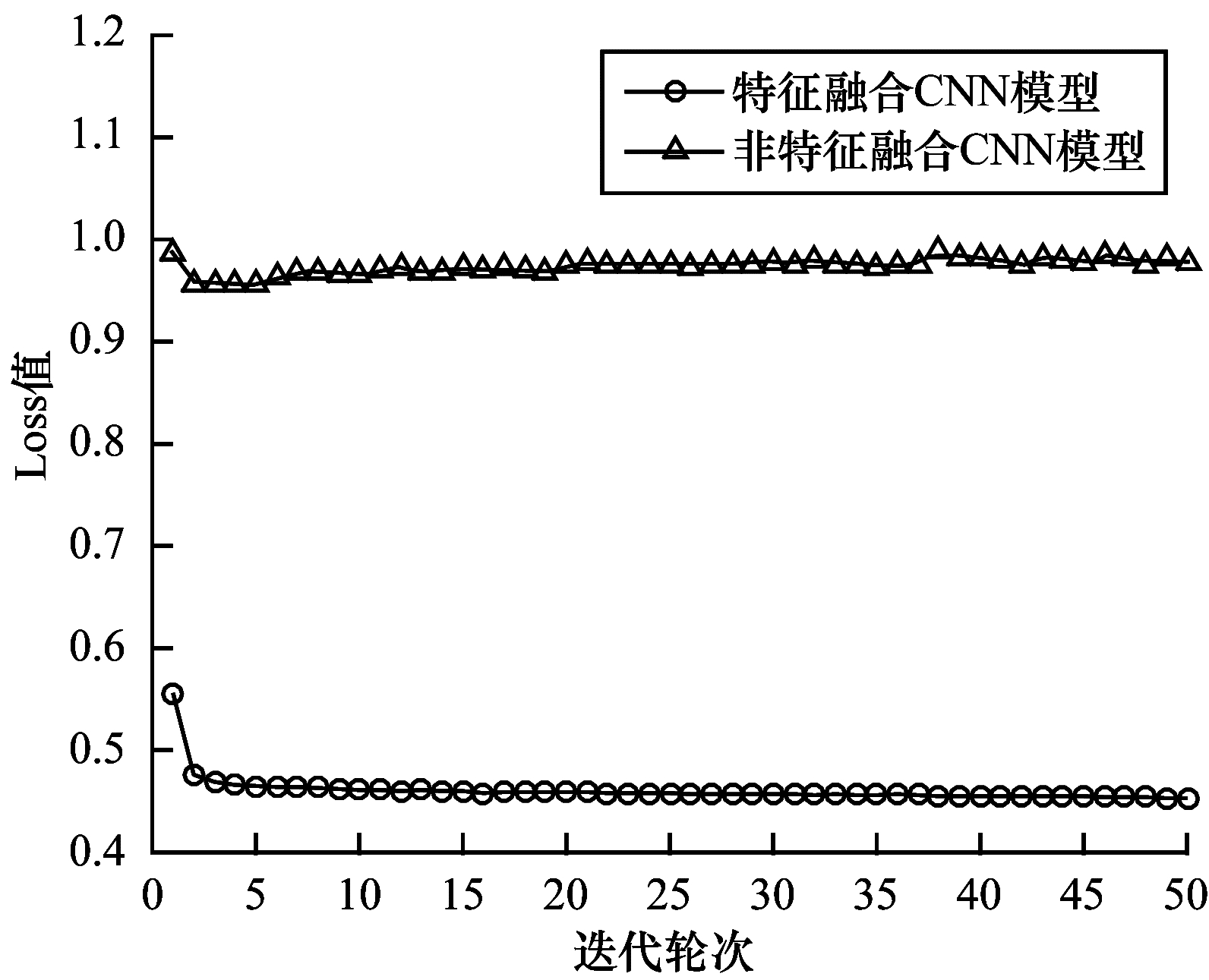
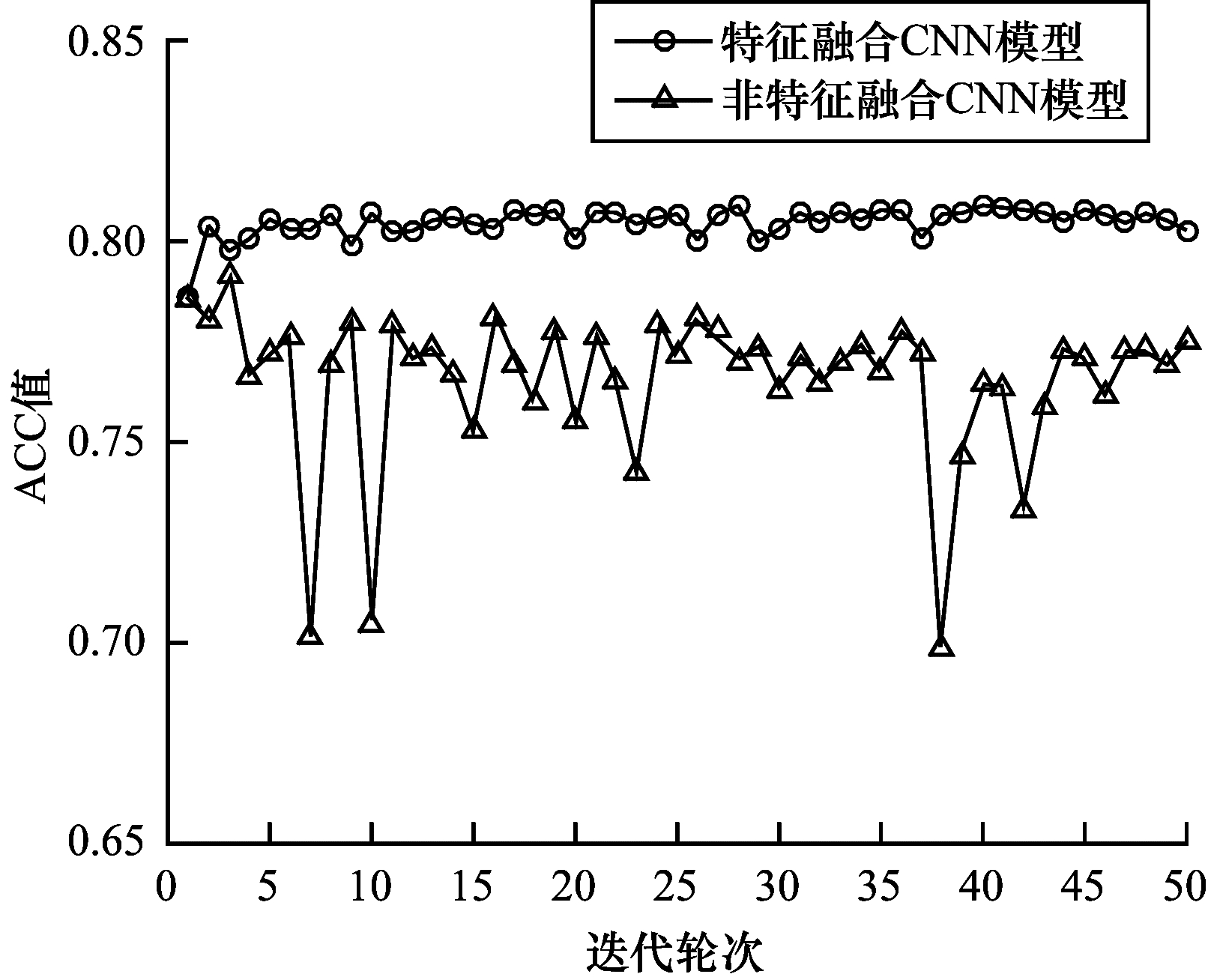
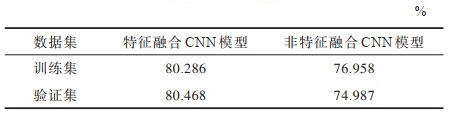
图 3给出了未添加特征融合模块的非特征融合CNN模型以及添加了特征融合模块的三通道独立CNN模型的Loss值随迭代轮次的变化趋势图。从图 3中可以看出,特征融合CNN模型比非特征融合CNN模型的收敛速度更快,收敛效果更好。图 4给出了两个模型的ACC值随迭代轮次的变化趋势图,两个模型在训练集以及验证集上的平均准确率如表 5所示。可见,特征融合CNN模型在收敛过程中的预测准确率更高,表现出更好的泛化能力,说明本文对不同特征之间关联性的考虑及处理使得特征提取更加全面多样且层次性更强,从而进一步提升了预测准确率。
|
Download:
|
| 图 3 特征融合CNN模型与非特征融合CNN模型的Loss值对比 Fig. 3 Comparison of Loss values between feature fusion CNN model and non-feature fusion CNN model | |
|
Download:
|
| 图 4 特征融合CNN模型与非特征融合CNN模型的ACC值对比 Fig. 4 Comparison of ACC values between feature fusion CNN model and non-feature fusion CNN model | |
|
下载CSV 表 5 模型平均预测准确率对比 Table 5 Comparison of average prediction accuracy between models |
预测SpMV的运算时间有利于加快SpMV自动调优速度。本文建立基于深度学习的SpMV运算时间预测模型,结合稀疏矩阵的行特征、列特征以及运行平台的体系结构参数等因素,分类别对SpMV的运算时间进行预测。实验结果表明,基于特征融合CNN的SpMV运算时间预测模型的预测准确率较高,运行速度较快,适合处理不同特点的稀疏矩阵。后续将对SpMV自动调优过程中的每组调优参数均进行运算时间预测,从而寻得耗时最短的调优参数组合,以达到快速自动调优的目的。
| [1] |
李亿渊, 薛巍, 陈德训, 等. 稀疏矩阵向量乘法在申威众核架构上的性能优化[J]. 计算机学报, 2020, 43(6): 1010-1024. LI Y Y, XUE W, CHEN D X, et al. Performance optimization for sparse matrix-vector multiplication on Sunway architecture[J]. Chinese Journal of Computers, 2020, 43(6): 1010-1024. (in Chinese) |
| [2] |
VUDUC R, DEMMEL J W, YELICK K A, et al. Performance optimizations and bounds for sparse matrix-vector multiply[C]//Proceedings of 2002 ACM/IEEE Conference on Supercomputing. Washington D.C., USA: IEEE Press, 2002: 1-35.
|
| [3] |
BELL N, GARLAND M. Implementing sparse matrix-vector multiplication on throughput-oriented processors[C]//Proceedings of 2009 ACM Conference on High Performance Computing Networking, Storage and Analysis. New York, USA: ACM Press, 2009: 1-11.
|
| [4] |
CHOI J W, SINGH A, VUDUC R W. Model-driven autotuning of sparse matrix-vector multiply on GPUs[C]//Proceedings of the 15th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. New York, USA: ACM Press, 2010: 115-126.
|
| [5] |
KOURTIS K, KARAKASIS V, GOUMAS G, et al. CSX: an extended compression format for SpMV on shared memory systems[C]//Proceedings of the 16th ACM Symposium on Principles and Practice of Parallel Programming. New York, USA: ACM Press, 2011: 247-256.
|
| [6] |
LIU W F, VINTER B. CSR5: an efficient storage format for cross-platform sparse matrix-vector multiplication[C]//Proceedings of the 29th ACM on International Conference on Supercomputing. New York, USA: ACM Press, 2015: 339-350.
|
| [7] |
LIU W F, VINTER B. Speculative segmented sum for sparse matrix-vector multiplication on heterogeneous processors[J]. Parallel Computing, 2015, 49: 179-193. DOI:10.1016/j.parco.2015.04.004 |
| [8] |
SU B Y, KEUTZER K. clSpMV: a cross-platform OpenCL SpMV framework on GPUs[C]//Proceedings of the 26th ACM international conference on Supercomputing. New York, USA: ACM Press, 2012: 353-364.
|
| [9] |
XIE B W, ZHAN J F, LIU X, et al. CVR: efficient vectorization of SpMV on X86 processors[C]//Proceedings of 2018 International Symposium on Code Generation and Optimization. New York, USA: ACM Press, 2018: 149-162.
|
| [10] |
YAN S G, LI C, ZHANG Y Q, et al. yaSpMV: yet another SpMV framework on GPUs[C]//Proceedings of the 19th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. New York, USA: ACM Press, 2014: 107-118.
|
| [11] |
袁娥, 张云泉, 刘芳芳, 等. SpMV的自动性能优化实现技术及其应用研究[J]. 计算机研究与发展, 2009, 46(7): 1117-1126. YUAN E, ZHANG Y Q, LIU F F, et al. Automatic performance tuning of sparse matrix-vector multiplication: implementation techniques and its application research[J]. Journal of Computer Research and Development, 2009, 46(7): 1117-1126. (in Chinese) |
| [12] |
VUDUC R, DEMMEL J W, YELICK K A. OSKI: a library of automatically tuned sparse matrix kernels[J]. Journal of Physics: Conference Series, 2005, 16: 521-530. |
| [13] |
WILLIAMS S, OLIKER L, VUDUC R, et al. Optimization of sparse matrix-vector multiplication on emerging multicore platforms[J]. Parallel Computing, 2009, 35(3): 178-194. DOI:10.1016/j.parco.2008.12.006 |
| [14] |
李佳佳, 张秀霞, 谭光明, 等. 选择稀疏矩阵乘法最优存储格式的研究[J]. 计算机研究与发展, 2014, 51(4): 882-894. LI J J, ZHANG X X, TAN G M, et al. Study of choosing the optimal storage format of sparse matrix vector multiplication[J]. Journal of Computer Research and Development, 2014, 51(4): 882-894. (in Chinese) |
| [15] |
SEDAGHATI N, MU T, POUCHET L N, et al. Automatic selection of sparse matrix representation on GPUs[C]//Proceedings of the 29th ACM on International Conference on Supercomputing. New York, USA: ACM Press, 2015: 99-108.
|
| [16] |
BENATIA A, JI W X, WANG Y Z, et al. Sparse matrix format selection with multiclass SVM for SpMV on GPU[C]//Proceedings of the 45th International Conference on Parallel Processing. Washington D.C., USA: IEEE Press, 2016: 496-505.
|
| [17] |
NISA I, SIEGEL C, RAJAM A S, et al. Effective machine learning based format selection and performance modeling for SpMV on GPUs[C]//Proceedings of 2018 IEEE International Parallel and Distributed Processing Symposium Workshops. Washington D.C., USA: IEEE Press, 2018: 1056-1065.
|
| [18] |
ZHAO Y, ZHOU W J, SHEN X P, et al. Overhead-conscious format selection for SpMV-based applications[C]//Proceedings of 2018 IEEE International Parallel and Distributed Processing Symposium. Washington D.C., USA: IEEE Press, 2018: 950-959.
|
| [19] |
ZHOU W J, ZHAO Y, SHEN X P, et al. Enabling runtime SpMV format selection through an overhead conscious method[J]. IEEE Transactions on Parallel and Distributed Systems, 2020, 31(1): 80-93. DOI:10.1109/TPDS.2019.2932931 |
| [20] |
ZHAO Y, LI J J, LIAO C H, et al. Bridging the gap between deep learning and sparse matrix format selection[C]//Proceedings of the 23rd ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. New York, USA: ACM Press, 2018: 94-108.
|
| [21] |
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift[C]//Proceedings of the 32nd International Conference on International Conference on Machine Learning. New York, USA: ACM Press, 2015: 448-456.
|
| [22] |
WILLIAMSON D F, PARKER R A, KENDRICK J S. The box plot: a simple visual method to interpret data[J]. Annals of Internal Medicine, 1989, 110(11): 916-921. DOI:10.7326/0003-4819-110-11-916 |
| [23] |
DAVIS T A, HU Y F. The university of Florida sparse matrix collection[J]. ACM Transactions on Mathematical Software, 2011, 38(1): 1-25. |
| [24] |
BOISVERT R F, POZO R, REMINGTON K A. The matrix market exchange formats[EB/OL]. [2020-11-15]. https://www.researchgate.net/publication/213880672_The_Matrix_Market_Exchange_Format_Initial_Design.
|
 2022, Vol. 48
2022, Vol. 48

 ,
,