2. 广州大学 网络空间先进技术研究院, 广州 510006
2. Cyberspace Institute of Advanced Technology, Guangzhou University, Guangzhou 510006, China
开放科学(资源服务)标志码(OSID): 
随机森林具有良好的准确性和高效性,被认为是性能最优的分类算法之一。文献[1]在121个数据集上对179个分类器进行评估,在所得实验结果中随机森林表现最好。然而,这121个数据集中大多数据规模较小,在数据规模较大的数据集上,随机森林的表现一般不如AdaBoost(Adaptive Boosting)等boost算法[2]。虽然存在上述问题,但是随机森林算法十分简单,可并行化,训练时间远低于boost算法且不容易过拟合[3],因此,其仍是当今最流行的分类算法之一。
文献[4]通过使用多个特征评估度量来降低决策树间的相关性而非决策树的准确性,同时使用加权平均进行预测,在分类数据集上其预测结果较好。文献[5]通过复杂的动态集成方法进行预测,设计一种提高随机森林在某些数据集上预测性能的方法,实验结果表明,在27个分类数据集中,该方法能改善12个数据集中随机森林的预测表现。文献[6]在随机选择K个划分特征的基础上,通过随机选择划分结点来进一步降低决策树间的相关性并提高随机森林的预测表现,实验结果表明,在12个分类数据集中,该方法能够显著改善5个数据集中随机森林的预测表现。文献[7]通过袋外(out-of-bag)预测误差对决策树的预测进行加权,在10个噪声数据集上该方法取得了较好的性能表现。文献[8]提出一种不放回的抽样方法,其提高了算法效率,并在7个数据集上提高了预测准确性。文献[9]提出一种对特征子集加权抽样的方法,该方法提高了与分类相关的属性的抽样概率,在高维数据上取得了较好的性能表现。文献[10]通过PCA(Principle Component Analysis)对每个决策树的输入特征随机分组进行旋转预处理,以降低决策树间的相关性并提高随机森林的性能,实验结果表明,在33个分类数据集中,该方法能够显著改善10个数据集中随机森林的预测表现。文献[11]通过LDA(Linear Discriminative Analysis)为每个分裂结点选择倾斜的分裂方向,使决策树的决策边界倾向坐标轴,该方法同样降低了决策树间的相关性,在一些数据集上取得了更好的表现。文献[12]通过Householder QR分解对每个决策树的输入特征进行随机旋转,类似于文献[10],其提高了随机森林的性能表现。文献[13]通过在每个分裂结点随机抽样一个稀疏矩阵,利用该矩阵对结点的输入特征进行旋转,在旋转后的稀疏特征空间中搜索最佳划分结点,该方法提高了随机森林的准确性。文献[14]通过拓展特征空间的方式,为每个决策树的输入特征随机生成部分新特征,其能降低决策树间的相关性,且未显著降低决策树的准确性,实验结果表明,在36个分类数据集中,该方法能够明显改善8个数据集中随机森林的预测表现。
上述方法大多在构建决策树时通过某些方式注入随机性,这会降低决策树间的相关性,从而提高随机森林的预测表现。在数据规模较大时,注入随机性的方式并不能显著降低决策树间的相关性,同时又因为牺牲了决策树的准确性,使得随机森林及其改进算法的性能改善效果有限,其预测表现一般不如AdaBoost等boost算法。因此,本文提出一种基于out-of-bag预测的改进算法,将随机森林的out-of-bag预测概率视为特征,将其与原始特征相结合,重新训练随机森林。out-of-bag预测概率能够改善决策树的划分,有效提高决策树的准确性,从而提升随机森林的预测准确性。由于out-of-bag预测概率会增大决策树间的相关性,因此本文利用文献[14]所提方法来降低由out-of-bag预测带来的决策树相关性,且不显著降低决策树的准确性,从而保证随机森林的预测性能。
1 相关工作 1.1 随机森林随机森林是当今最流行的分类器之一[1],其在bootstrap的基础上,通过随机选择特征子集来分裂决策树的结点,进一步为决策树注入随机性,从而降低决策树间的相关性,提高预测的准确性[15]。
对于数据集D={(xi,yi),i=1,2,…,m},其中,xi和yi分别表示第i个样本的特征向量和类别,随机森林的训练过程如下(其中,T和k均为预先设定好的超参数):
t从1到T:
1)从数据集D中有放回地抽样得到m个样本的数据集Dt,未被抽样到的样本组成数据集Dt-oob。
2)在数据集Dt上,训练一棵无剪枝的决策树ft。在训练过程中,对于决策树中的每个结点,通过随机选择k个特征来对结点进行划分,直到结点内的样本类别都相同或只有一个样本为止。
最终,随机森林通过平均所有决策树的输出来获得最终输出,即:
| F(x)=1TT∑t=1ft(x) | (1) |
在抽样得到的数据集Dt中,不重复的样本大约占63.2%,剩下大约占36.8%的Dt-oob被称为out-of-bag样本。显然以ft预测Dt-oob是无偏的,因此可以用ft对Dt-oob预测的平均结果作为对Dt的预测。对于Dt中的样本x,其预测为:
| F(x)=T∑t=1ft(x)I(x∈Dt−oob)T∑t=1I(x∈Dt−oob) | (2) |
其中:I为指示函数。
1.2 空间扩展文献[14]为了降低决策树间的相关性,提出一种随机组合的特征空间扩展方法。对于每个决策树,其输入特征由特征本身加上特征的随机组合,每个决策树的输入特征都不相同,从而降低了决策树间的相关性。同时,由于特征的量纲不同且一些特征间存在相关性,生成的特征中会有部分特征对决策树的贡献和原特征相同,甚至表现更好,因此扩展空间方法不会显著降低决策树的准确性。
1.3 AdaBoostAdaBoost以其优秀的泛化性能而受到学术界的关注[16-17]。AdaBoost通过确定性的方式更新样本的权重,使新的决策树更加关注之前分类错误的样本,从而提高了最终的泛化能力。AdaBoost的输出由T个决策树的输出加权组成,即:
| F(x)=T∑t=1αtft(x) | (3) |
其中:αt为每轮迭代产生的权重。
假设经过t-1轮迭代,Ft-1(x)是经过t-1轮迭代得到的结果模型:
| Ft−1(x)=α1f1(x)+α2f2(x)+⋅⋅⋅+αt−1ft−1(x) | (4) |
则在第t轮迭代中,需要得到αt、ft(x)和Ft(x):
| Ft(x)=Ft−1(x)+αtft(x) | (5) |
为了能够进一步提高泛化性能,需要使Ft(x)在损失函数L上最小,即联合优化αt和ft(x)使损失函数L最小:
| minαt,ftm∑i=1L(yi,Ft−1(xi)+αtft(xi)) | (6) |
其中:L为度量类别y和模型Ft(x)之间差异的损失函数。
2 随机森林改进算法 2.1 改进理论理论1 随机森林的泛化误差上界为:
| PPE∗=ˉρ1−s2s2 | (7) |
其中:PPE*为泛化误差;
为了提高随机森林的预测表现,大多数改进方法通过牺牲单个决策树的准确性来降低决策树间的相关性,即以降低s为代价来降低
理论2 令T为一个在有l个实数值特征的数据的基础上构建的二元决策树,共有N个内部结点,则有
理论3 令H是一组函数,其取值在{-1,1}范围,其VC-dimension为d,则对于任意δ,至少有1-δ的概率,式(8)对所有h∈H成立。
| R(h)≤ˆRS(h)+√2ln(em/d)m/d+√ln(1/δ)2m | (8) |
其中:S为m个样本的训练集;R(h)表示泛化风险;
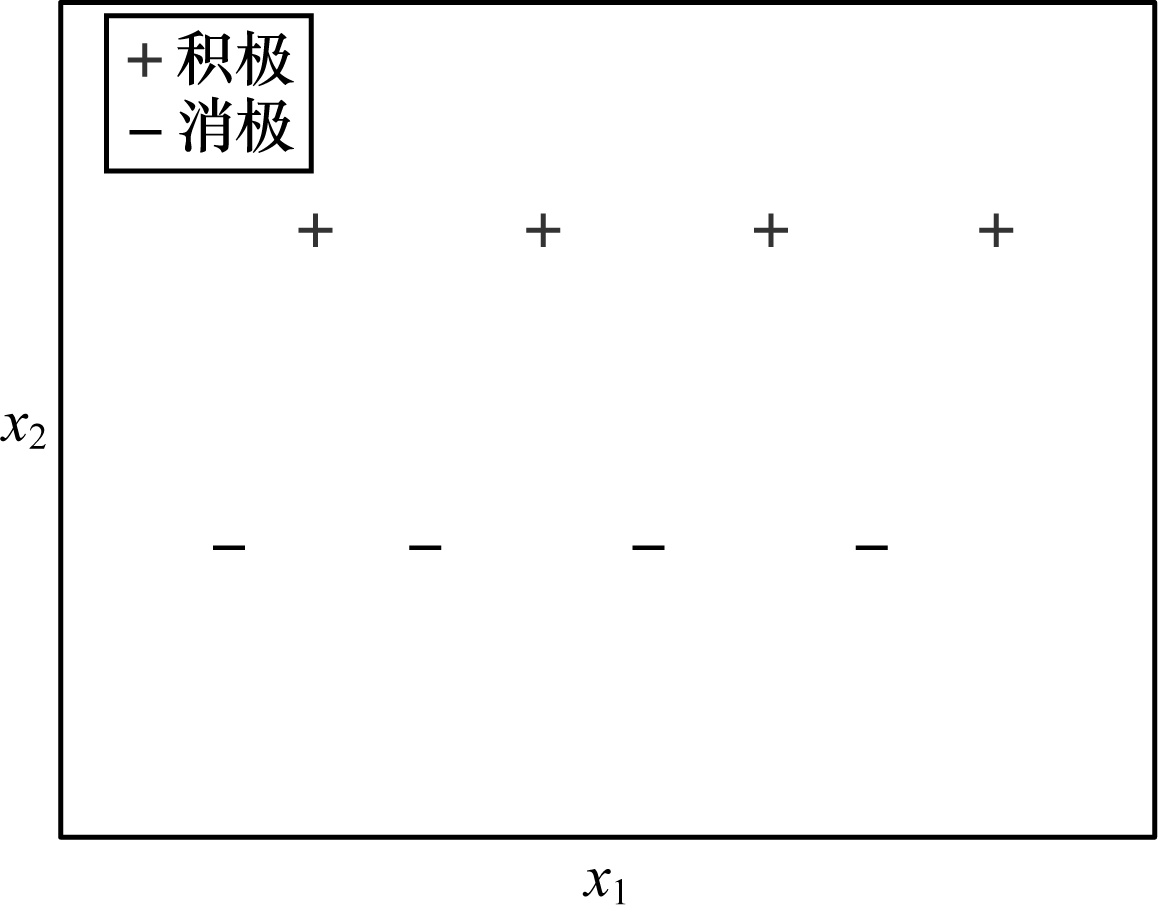
在决策树的构建过程中,同目标类别y较相关的特征会产生较少的叶子结点,不太相关的特征会产生较多的叶子结点,而且较相关的特征产生的叶子结点能够得到更小的经验风险。如图 1所示,决策树在特征x2上只会产生2个叶子结点,而在特征x1上会产生8个叶子结点,且特征x2上的经验风险明显小于x1。由于决策树中只有度为0和度为2的结点,因此决策树内部结点的数量N2与叶子结点的数量N0的关系为N2=N0-1。受此启发,如果能够构造一些较相关的特征来帮助构建决策树,那么不仅能够降低决策树的经验风险,还能降低决策树的VC-dimension,从而提高决策树的准确性。
|
Download:
|
| 图 1 特征与目标间相关性的直观表示 Fig. 1 Visual representation of the correlation between features and targets | |
以随机森林的out-of-bag预测概率作为特征有以下2个优点:
1)随机森林的准确率高于单个决策树,对于二分类问题,仅使用预测概率就能使决策树的经验风险接近随机森林的经验风险,对于多分类问题,预测概率也能有效降低决策树的经验风险,同时有效减少决策树的内部结点。
2)通过out-of-bag估计得到预测概率仅需非常小的代价,在随机森林的训练阶段即可得到预测概率且其是无偏的,而通过交叉预测得到预测概率不仅十分耗时,得到的结果也是有偏的。
以随机森林的out-of-bag预测概率作为构造的特征,与原始特征相结合并重新训练随机森林,能够显著提高单个决策树的准确性s,从而提高随机森林的准确性。但是不可避免的,准确性的提升会提高决策树间的相关性,即提高了
为了解决上述问题,本文通过文献[14]提出的扩展空间算法,使随机森林中的每个决策树构建在不同的训练数据上,从而在不显著降低决策树准确性s的情况下,降低决策树间的相关性
本文利用out-of-bag预测概率作为新的特征来构建决策树,从而降低决策树的VC-dimension以及经验风险和泛化风险,最终提高决策树的准确性s和随机森林的预测性能。基于out-of-bag预测的改进算法描述如下所示:
算法1 基于out-of-bag预测的改进算法
输入 训练集Xtrain,测试集Xtest,训练集的目标类别Ytrain,Random Forest的算法A
输出 测试集的预测概率ptest
1.以算法A在(Xtrain,Xtest)上训练得到分类器C和out-of-bag预测概率,即:
2.以分类器C得到测试集的预测概率,即:
3.将poob、ptest分别与Xtrain、Xtest相结合,即:
4.重新训练得到分类器C,即:
5.输出测试集的预测概率
算法1需额外训练一个随机森林,其时间复杂度为
由于决策树准确性s的提高,会使决策树间的预测更加相同,从而提高决策树间的相关性
算法2 基于out-of-bag预测和扩展空间的改进算法1
输入 训练集Xtrain,测试集Xtest,训练集的目标类别Ytrain,Random Forest的算法A,Random Forest中决策树的算法L,随机种子函数S
输出 测试集的预测概率ptest
1.同算法1,有
2.同算法1,有
3. t从1到T:
1)
2)训练得到决策树ft,即
3)
4)
4.输出测试集的预测概率
算法3 扩展特征空间算法E
输入 数据X,随机种子seed
输出 扩展的数据Xe
1.获取X的特征数量,即:
2.随机生成2个不同的特征索引序列并将其合并,即:
3.分别得到indices中奇数位置的索引inds1={ }和偶数位置的索引inds2={ },即:
1)i从1到n:
4.以inds1和inds2对X做扩展操作,得到并返回扩展后的数据Xe,即:
算法3即为文献[14]提出的扩展特征空间算法,本文使用文献[14]中表现最好的相减操作。扩展空间算法等价于通过以2个特征为1组的方式,将n个特征随机划分为
| M=K∏i=1(n−2i+2)!2!(n−2i)!/K!=n!(2!)KK! | (9) |
其中:K=
算法2也需额外训练一个随机森林,其时间复杂度为
在算法1和算法2的训练过程中,out-of-bag预测概率的准确性越高,对随机森林的提升效果就越好。out-of-bag预测虽然是无偏的,但对于其中的每个样本,大约只有37.8%的决策树会对其作出预测。相比于测试集的全部决策树预测,两者之间的准确性会有所差异。为了降低这部分差异,本文将算法1和算法2产生的out-of-bag预测概率相结合,通过加法融合来提高out-of-bag预测概率的准确性,减少其与测试集预测之间的差异。上述过程的算法描述如下:
算法4 基于out-of-bag预测和扩展空间的改进算法2
输入 训练集Xtrain,测试集Xtest,训练集的目标类别Ytrain,Random Forest的算法A,Random Forest中决策树的算法L,随机种子函数S
输出 测试集的预测概率ptest
1.同算法1,有
2.同算法1,有
3.t = 1,2,…,T:
1)
2)训练得到决策树ft及其out-of-bag预测概率,即:
3)
4)
4.得到扩展空间随机森林的out-of-bag预测概率及其对测试集的预测概率,即:
5.对上述概率做平均,即:
6.同算法2,有
7.同算法2,输出
算法4相比算法2又需要额外训练一个随机森林,其时间复杂度为
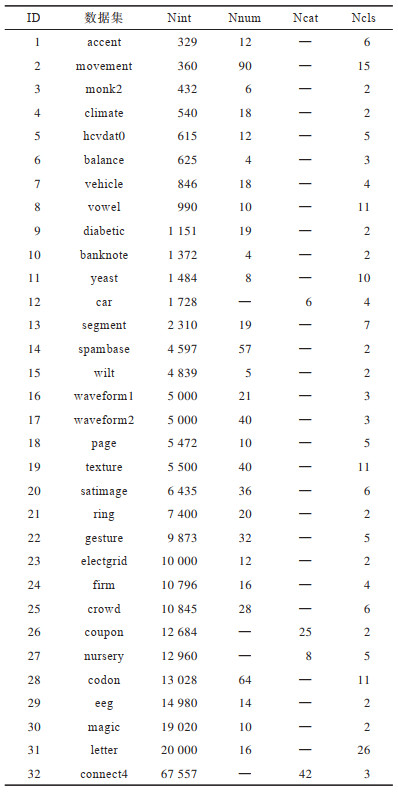
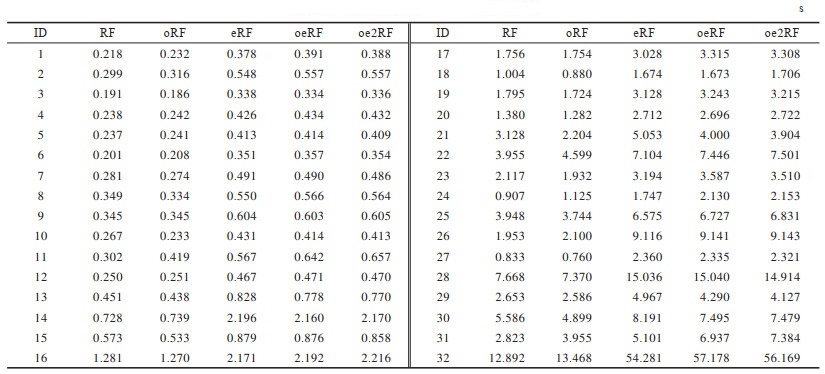
本文收集32个分类数据集,这些数据集全都来自UCI机器学习数据库[20],数据集的统计特性如表 1所示。其中:Nint表示样本的数量;Nnum表示数值特征数量;Ncat表示类别特征数量;Ncls表示类别数量。这些数据集的样本数量在329~67 557之间,特征数量在4~90之间,类别数量在2~26之间。每个数据集都只含数值特征或类别特征,表中的“—”表示没有该类型的特征。有些数据集存在缺失值,需要对其进行填充:对于类别特征的缺失,本文使用最常见的特征值对其进行填充;对于数值特征的缺失,本文使用文献[21]提出的序列回归填充方法对其进行填充。
|
下载CSV 表 1 实验数据集统计信息 Table 1 Experimental datasets statistics |
本文以RF表示原始随机森林,以oRF表示算法1改进的随机森林,以eRF表示文献[14]提出的扩展随机森林,以oeRF表示算法2改进的随机森林,以oe2RF表示算法4改进的随机森林。同时还将本文算法与AdaBoost类算法,具体为文献[22]提出的Multi-AdaBoost算法(以BT表示)进行对比。
对于超参数,由于随机森林和AdaBoost都是树模型,本文将两者的决策树数量都设为100,只调整决策树的深度,以5折交叉验证网格搜索的方式选择最佳的树深。上述模型均使用文献[23]中的scikit-learn机器学习库。
4 实验结果及分析 4.1 实验度量本文使用准确率(acc)作为模型性能的评估度量。除此之外,由于随机森林的性能与s、
1)决策树准确率的平均值(atc)。以单个决策树对测试集预测准确率的平均来表示单个决策树的准确性。
2)决策树kappa的平均值(kapp)。文献[24]以kappa值来度量2个分类器预测之间的一致性,显然其还可以用来度量决策树间的相关性。对于c个类,kappa定义在2个分类器预测的c×c混淆矩阵M上[10]。以N表示样本的总数量,则2个分类器之间的kappa值为:
| kkappa=∑kMkk−AABC1−AABC | (10) |
| AABC=∑k(∑sMksN)×(∑sMskN) | (11) |
其中:Mks表示其中一个分类器预测样本为k而另一个分类器预测样本为s的数量。在随机森林中共有T个决策树,因此,需要度量T(T-1)/2次kappa的值并对其做平均。
3)决策树out-of-bag准确率的平均值(abc)。以单个决策树对out-of-bag样本预测准确率的平均来近似表示决策树的经验风险。
4)决策树中叶子结点数量的平均值(node)。由理论2可知,决策树的VC-dimension与实值特征数量、内部结点数量有关,但实值特征数量要经过log处理,因此,决策树的VC-dimension主要受内部结点数量影响,而决策树内部结点数量又与叶子结点数量有关,因此,本文以决策树叶子结点数量来近似表示决策树的VC-dimension。
4.2 实验结果本文随机地将80%的样本划分为训练集,将剩下的20%样本划分为测试集。由于数据集规模的不同,该划分过程重复的次数也不同。对于样本数量小于1 500的数据集,该划分重复30次;对于样本数量大于等于1 500而小于8 000的数据集,该划分重复20次;对于样本数量大于等于8 000的数据集,该划分重复10次。本文使用校正的paired t-test对实验结果做显著性检验[25]。对于2个不同的数据集划分,2个训练集之间至少有75%的部分相同,容易出现Type Ⅰ类错误[26]。因此,本文使用校正的paired t-test,将显著性水平设为95%。
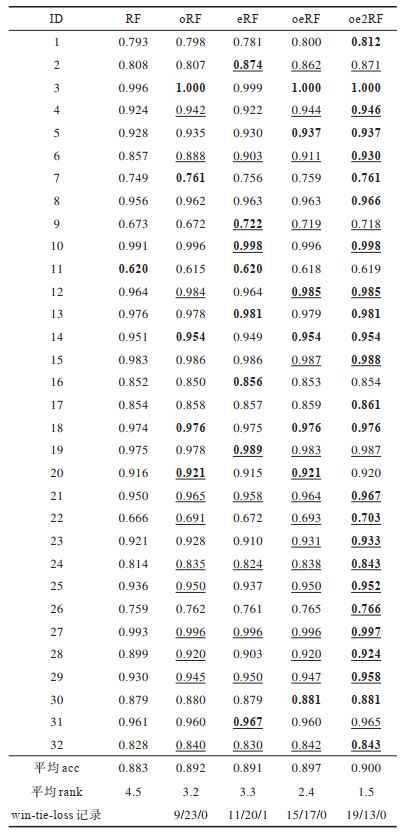
实验结果如表 2所示,其中,加粗表示该模型的预测acc最高,下划线表示该模型的预测结果显著优于RF,“×”表示该模型的预测结果显著劣于RF,表格倒数第3行表示模型的平均acc,倒数第2行表示模型的平均rank,倒数第1行表示模型相较于RF的显著性win-tie-loss记录。从表 2可以看出,本文方法和文献[14]方法都能提高RF的预测性能,其中表现最好的是本文提出的oe2RF模型,在32个数据集中,oe2RF能够获得最高的平均acc以及最低的平均rank,能够在19个数据集上显著优于RF。
|
下载CSV 表 2 模型预测性能比较 Table 2 Comparison of prediction performance of models |
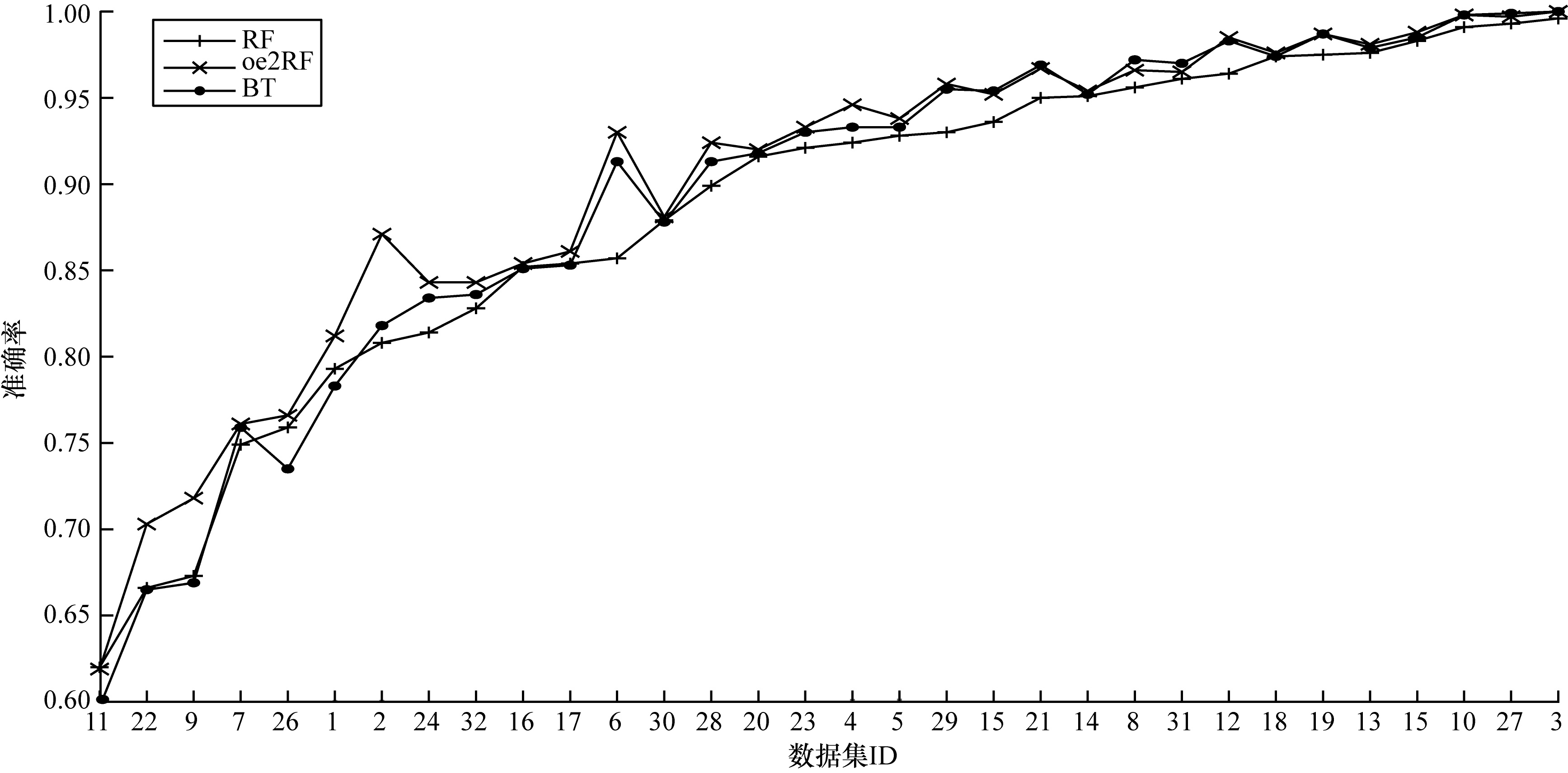
本文还对比了oe2RF与RF、BT的性能差异,对比结果如图 2所示。从图 2可以看出,BT性能优于RF,而oe2RF能获得比BT更优的性能表现。
|
Download:
|
| 图 2 oe2RF与RF、BT的性能对比 Fig. 2 Performance comparison of oe2RF with RF and BT | |
各模型的平均训练时间如表 3所示,其中训练时间指各模型最终额外训练的随机森林的训练时间,总训练时间可由表中数据相加得到。例如,oRF总训练时间=RF训练时间+oRF训练时间,eRF总训练时间=eRF训练时间。显然,各个模型最终额外的训练时间开销大致符合2.2节中额外训练的随机森林的算法时间复杂度分析,其中部分波动是由于:1)out-of-bag预测有效减少了决策树中叶子结点的数量,这会降低训练时间,例如,在ID为10和21的数据集上,oRF的训练时间小于RF;2)在扩展特征空间时,每次生成n个特征需要时间复杂度为O(mn)的时间开销,这会提高训练时间,例如,在ID为26和32的数据集上,由于2个数据集的特征均为类别特征,训练时需要对其进行one-hot编码,编码后的特征数量较多,对其进行空间扩展会带来较多的额外时间开销。
|
下载CSV 表 3 模型平均训练时间 Table 3 Models average training time |
本文方法对RF的性能提升在于提高了单个决策树的准确性,同时由于提高决策树的准确性会使决策树间的相关性提高,因此本文借助文献[14]方法降低决策树间的相关性,且不显著降低决策树的准确性,从而较好地改善了RF的预测性能。
如图 3所示,图中的每个点代表一个数据集,横坐标表示各模型与RF在kapp上的差异,纵坐标表示各模型与RF在atc上的差异。从图 3可以看出:oRF能够大幅提高决策树的atc,但也会大幅提高决策树间的kapp;eRF能够在不显著降低决策树atc的情况下降低决策树间的kapp,图中部分atc和kapp提高的原因在于划分结点时特征子集的选择正比于特征数量,如果将特征子集数量设为固定值,将不会出现该情况;oeRF相比于oRF降低了kapp,也降低了atc,但相比于RF的kapp和atc提高了很多;oe2RF相比于oeRF提高了atc,略微提高了kapp,因此,其能够获得最好的性能表现。由图 3可知,本文方法能大幅提高单个决策树的准确性,符合理论2和理论3,其实验验证如图 4所示,横坐标表示各模型与RF在node上的差异,纵坐标表示各模型与RF在abc上的差异。从图 4可以看出:oRF、oeRF和oe2RF均能大幅提高决策树的abc,且同时降低决策树的node,从而提高了决策树的atc;eRF略微提高了决策树的abc,同时降低了决策树的node,其原因在于特征子集正比于特征数量,而且特征量纲的不同和特征间存在相关性,扩展特征空间时可能会产生部分较好的特征,有利于决策树划分,在固定特征子集大小时,这种情况很少发生。

|
Download:
|
| 图 3 各模型与RF在atc和kapp上的性能差异 Fig. 3 Performance difference between each model and RF on atc and kapp | |
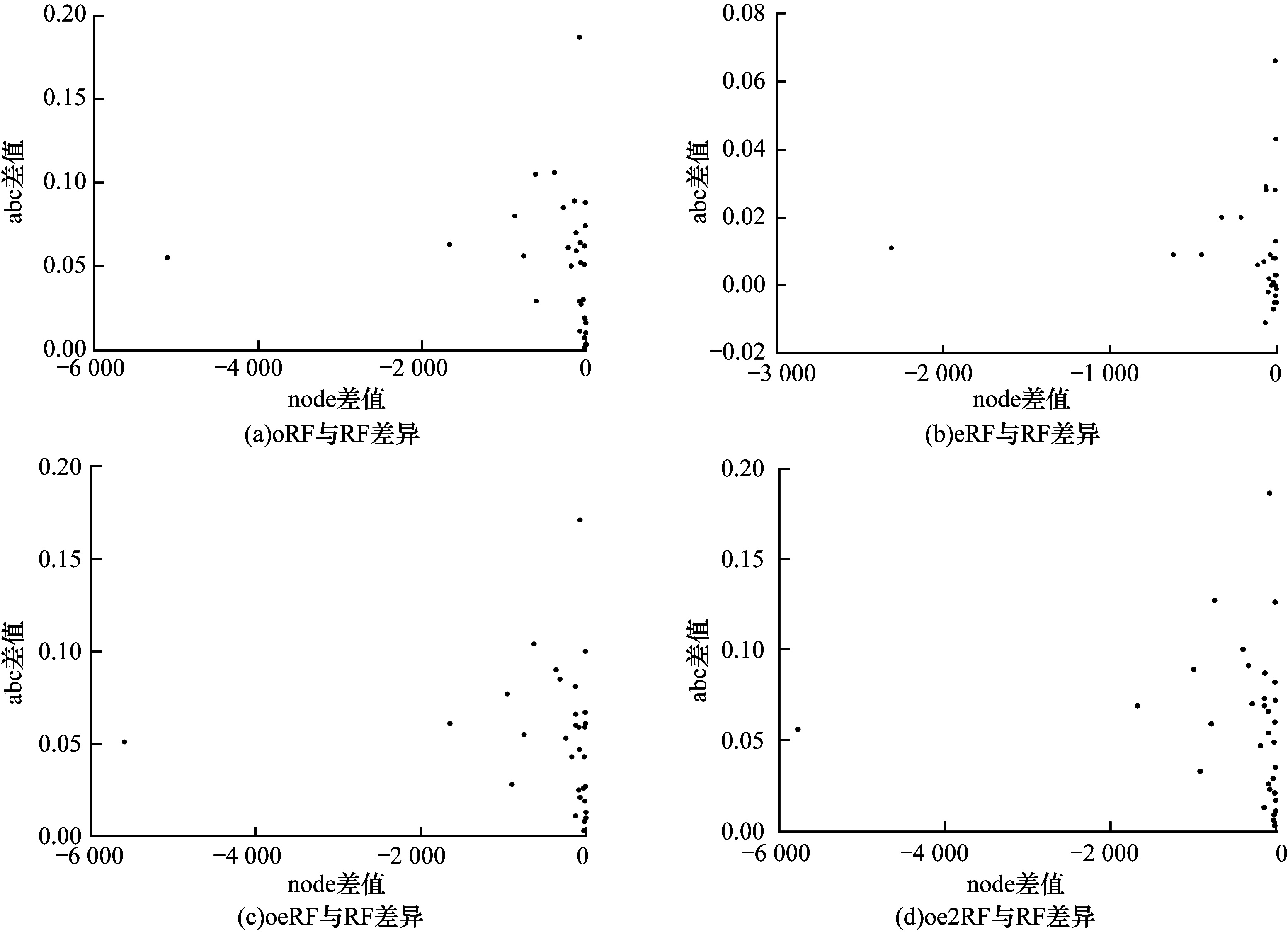
|
Download:
|
| 图 4 各模型与RF在决策树abc和node上的性能差异 Fig. 4 Performance difference between each model and RF on decision tree abc and node | |
多数已有预测方法牺牲单个决策树的准确性来提高随机森林的性能,本文通过out-of-bag预测概率提高单个决策树的准确性,同时利用文献[14]所提扩展空间方法降低决策树间的相关性,以有效改善随机森林的预测性能。在32个UCI分类数据集上的实验结果验证了该方法的有效性。后续将进一步提升决策树的准确性,同时利用数据旋转技术来降低决策树间的相关性,从而提高随机森林的准确性。
| [1] |
FERNÁNDEZ-DELGADO M, CERNADAS E, BARRO S, et al. Do we need hundreds of classifiers to solve real world classification problems?[J]. The Journal of Machine Learning Research, 2014, 15(1): 3133-3181. |
| [2] |
DIETTERICH T G. An experimental comparison of three methods for constructing ensembles of decision trees: bagging, boosting, and randomization[J]. Machine Learning, 2000, 40(2): 139-157. DOI:10.1023/A:1007607513941 |
| [3] |
方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32-38. FANG K N, WU J B, ZHU J P, et al. A review of technologies on random forests[J]. Statistics and Information Forum, 2011, 26(3): 32-38. (in Chinese) |
| [4] |
ROBNIK-ŠIKONJA M. Improving random forests[C]//Proceedings of European Conference on Machine Learning. Berlin, Germany: Springer, 2004: 359-370.
|
| [5] |
TSYMBAL A, PECHENIZKIY M, CUNNINGHAM P. Dynamic integration with random forests[C]//Proceedings of European Conference on Machine Learning. Berlin, Germany: Springer, 2006: 801-808.
|
| [6] |
GEURTS P, ERNST D, WEHENKEL L. Extremely randomized trees[J]. Machine Learning, 2006, 63(1): 3-42. DOI:10.1007/s10994-006-6226-1 |
| [7] |
LI H B, WANG W, DING H W, et al. Trees weighting random forest method for classifying high-dimensional noisy data[C]//Proceedings of 2010 IEEE International Conference on E-Business Engineering. Washington D.C., USA: IEEE Press, 2010: 160-163.
|
| [8] |
李慧, 李正, 佘堃. 一种基于综合不放回抽样的随机森林算法改进[J]. 计算机工程与科学, 2015, 37(7): 1233-1238. LI H, LI Z, SHE K. An improved random forest algorithm based on comprehensive sampling without replacement[J]. Computer Engineering and Science, 2015, 37(7): 1233-1238. (in Chinese) |
| [9] |
XU B, HUANG J Z, WILLIAMS G, et al. Classifying very high-dimensional data with random forests built from small subspaces[J]. International Journal of Data Warehousing and Mining, 2012, 8(2): 44-63. DOI:10.4018/jdwm.2012040103 |
| [10] |
RODRIGUEZ J J, KUNCHEVA L I, ALONSO C J. Rotation forest: a new classifier ensemble method[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(10): 1619-1630. DOI:10.1109/TPAMI.2006.211 |
| [11] |
MENZE B H, KELM B M, SPLITTHOFF D N, et al. On oblique random forests[C]//Proceedings of Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, Germany: Springer, 2011: 453-469.
|
| [12] |
BLASER R, FRYZLEWICZ P. Random rotation ensembles[J]. The Journal of Machine Learning Research, 2016, 17(1): 126-151. |
| [13] |
TOMITA T M, BROWNE J, SHEN C, et al. Sparse projection oblique randomer forests[EB/OL]. [2021-10-05]. https://arxiv.org/pdf/1506.03410v6.pdf.
|
| [14] |
AMASYALI M F, ERSOY O K. Classifier ensembles with the extended space forest[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 26(3): 549-562. |
| [15] |
BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [16] |
FREUND Y, SCHAPIRE R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55(1): 119-139. DOI:10.1006/jcss.1997.1504 |
| [17] |
BARTLETT P, FREUND Y, LEE W S, et al. Boosting the margin: a new explanation for the effectiveness of voting methods[J]. The Annals of Statistics, 1998, 26(5): 1651-1686. |
| [18] |
LEBOEUF J S, LEBLANC F, MARCHAND M. Decision trees as partitioning machines to characterize their generalization properties[J]. Advances in Neural Information Processing Systems, 2020, 33: 10-13. |
| [19] |
MOHRI M, ROSTAMIZADEH A, TALWALKAR A. Foundations of machine learning[M]. Cambridge, USA: MIT Press, 2018.
|
| [20] |
BLAKE C. UCI repository of machine learning databases[EB/OL]. [2021-10-05]. http://www.ics.uci.edu/~mlearn/MLRepository.html.
|
| [21] |
RAGHUNATHAN T E, LEPKOWSKI J M, VAN HOEWYK J, et al. A multivariate technique for multiply imputing missing values using a sequence of regression models[J]. Survey Methodology, 2001, 27(1): 85-96. |
| [22] |
HASTIE T, ROSSET S, ZHU J, et al. Multi-class adaboost[J]. Statistics and Its Interface, 2009, 2(3): 349-360. DOI:10.4310/SII.2009.v2.n3.a8 |
| [23] |
PEDREGOSA F, VAROQUAUX G, GRAMFORT A, et al. Scikit-learn: machine learning in Python[J]. The Journal of Machine Learning Research, 2011, 12: 2825-2830. |
| [24] |
MARGINEANTU D D, DIETTERICH T G. Pruning adaptive boosting[EB/OL]. [2021-10-05]. https://web.engr.oregonstate.edu/~tgd/publications/ml97-pruning-adaboost.pdf.
|
| [25] |
NADEAU C, BENGIO Y. Inference for the generalization error[J]. Machine Learning, 2003, 52(3): 239-281. DOI:10.1023/A:1024068626366 |
| [26] |
DEMŠAR J. Statistical comparisons of classifiers over multiple data sets[J]. The Journal of Machine Learning Research, 2006, 7: 1-30. |
 2022, Vol. 48
2022, Vol. 48 图 1
图 1


