2. 中国科学技术大学 信息科学技术学院, 合肥 230026
2. School of Information Science and Technology, University of Science and Technology of China, Hefei 230026, China
开放科学(资源服务)标志码(OSID):
近年来,机器人应用逐渐从工业领域向国防军事、医疗康复、助老助残、居家服务等领域迅速拓展[1]。RGB-D相机可采集场景中的彩色图和深度图,获取视野内任意目标三维点云,被广泛应用于智能协作机器人以感知周围环境[2]。智能协作机器人在进入未知环境时,依赖视觉系统感知动态工作空间定位目标,实现机械臂对目标对象的自主抓取回收作业[3]。获取机器人坐标系和相机坐标系之间的变换关系,即手眼标定,是机器人进行视觉伺服作业的前提[4]。关于视觉系统与其他坐标系之间的标定方法,近年来受到了学者们的广泛关注并取得了一定的研究成果。手眼标定方法主要分为需要标定物和不需要标定物两类。文献[5-7]介绍了不需要标定物的手眼标定方法,标定过程复杂、干扰因素多。在基于标定物的传统方法中,机器人末端携带标定物,通过相机拍摄标定物多组不同姿态获得标定方程。文献[8-9]将传统标定板作为标定件,通过在多个坐标系之间的转换,求解齐次矩阵方程。在标定时需要高精度的标定板[10-11],且保持标定板位于相机视野范围内,但机器人的运动范围较有限。文献[12-14]利用激光跟踪仪或三轴跟踪仪进行手眼标定,复杂的辅助标定设备增加了手眼标定的难度和成本。文献[15-17]采用立体视觉获取空间点坐标计算手眼转换矩阵,标定精度仍有很大的提升空间。
针对RGB-D相机与机器人坐标系的手眼标定问题,本文提出基于目标检测的机器人手眼标定方法,将3D打印球作为标定件夹持在机械手末端工具中心点(Tool Center Point,TCP),使用改进的yolov3目标检测神经网络实时检测与定位标定球在相机坐标系下的3D位置,计算并得到抓取机器人的末端TCP在机器人本体坐标系与相机坐标系之间的转换关系。
1 相机成像模型RGB-D相机可获得彩色图和深度图,其中深度图由物体在像平面的像素坐标u、v及其到像平面的距离d构成。利用小孔成像原理对相机进行建模[18],根据其内参矩阵k将二维像素坐标系下的点P(u,v)投影到三维相机坐标系{C}空间中。
| $ \boldsymbol{k}=\left[\begin{array}{ccc}f/{d}_{x}& 0& {u}_{0}\\ 0& f/{d}_{y}& {v}_{0}\\ 0& 0& 1\end{array}\right] $ | (1) |
| $ {}^{P}{D}_{z}\left[\begin{array}{c}{P}_{u}\\ {P}_{v}\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_{x}& 0& {u}_{0}\\ 0& {f}_{y}& {v}_{0}\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{}^{P}{C}_{x}\\ {}^{P}{C}_{y}\end{array}\\ {}^{P}{C}_{z}\end{array}\right] $ | (2) |
其中:f为相机焦距,单位为mm;dx和dy为像元尺寸,单位为mm;u0和v0表示主点与图像中心点的偏离程度;
若在相机内参矩阵k已知的情况下,则将像素坐标系{P}下的点P(u,v)投影到相机坐标系{C}下的空间点坐标
| $ \left\{\begin{array}{l}{}^{P}{C}_{x}=\frac{({P}_{u}-{u}_{0}){}^{P}{D}_{z}}{{f}_{x}}\\ {}^{P}{C}_{y}=\frac{({P}_{v}-{v}_{0}){}^{P}{D}_{z}}{{f}_{y}}\\ {}^{P}{C}_{z}={}^{P}{D}_{z}\end{array}\right. $ | (3) |
在本文方法中,3D打印球被夹持在机械手末端TCP,如图 1所示。获取标定球的彩色图像后,从彩色图中检测并提取标定球的球心位置。霍夫变换圆形等传统特征检测只能从简单背景中提取圆形特征,不能在实际环境、机械手夹持遮挡等复杂情况下检测标定球。基于卷积神经网络的目标检测网络能自动学习目标特征,从图片中提取目标对象[19]。因此,本文利用改进的yolov3目标检测神经网络[20]检测并定位标定球。

|
Download:
|
| 图 1 标定球夹持在机械手末端的示意图 Fig. 1 Schematic diagram of the calibration ball clamped at the end of the manipulator | |
基于yolov3的标定球检测模型如图 2所示,作为标定球检测器实现对标定球的检测定位,以获取标定球在像素坐标系下的成像的圆心坐标

|
Download:
|
| 图 2 基于yolov3的标定球检测模型 Fig. 2 Detection model based on yolov3 for calibration ball | |
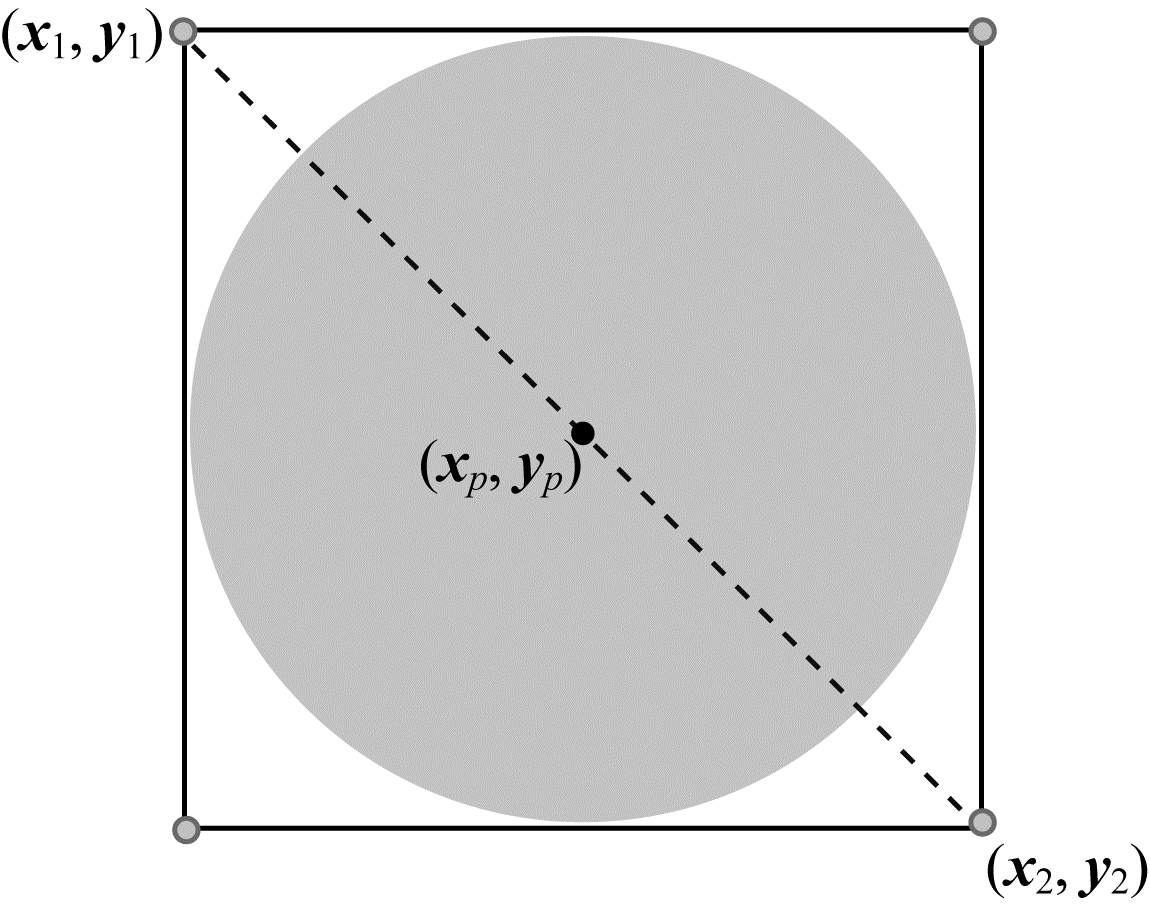
采集150张不同尺寸的标定球夹持在机械手末端的图片,制作单一类别球的小规模数据集。利用数据增强方式扩增数据集训练神经网络可增强网络模型的泛化能力与鲁棒性。通过在一定范围内随机改变图像亮度、对比度和色域度,以及在一定范围内随机对图像进行缩放、宽高扭曲和水平翻转,对采集的150张图像的数据集通过数据集扩充10倍后进行训练,部分数据集图像如图 3所示。采用PASCAL VOC格式标注数据集,左上角(x1,y1)与右下角(x2,y2)两点标注格式如图 4所示,标注中心点(xP,yP)为左上角和右下角两点的中点,计算公式如式(4)所示:
| $ \left\{\begin{array}{l}{\boldsymbol{x}}_{P}=({\boldsymbol{x}}_{1}+{\boldsymbol{x}}_{2})/2\\ {\boldsymbol{y}}_{P}=({\boldsymbol{y}}_{1}+{\boldsymbol{y}}_{2})/2\end{array}\right. $ | (4) |

|
Download:
|
| 图 3 部分数据集图像 Fig. 3 Part of the dataset images | |
|
Download:
|
| 图 4 数据集标注格式 Fig. 4 Dataset annotation format | |
训练改进的yolov3模型,将数据增强后的数据集随机按8∶2比例分成训练集和测试集,训练时Batch size设置为8,初始学习率设置为0.001,每一轮衰减系数设置为0.95,共训练50个epoch。训练完成后将网络权重模型在测试集中进行测试,若预测并输出标定球的定位框与标签框的交并比(Intersection over Union,IOU)大于0.5,则为检测成功,在测试集中得到98.3%的检测成功率。
在实验过程中,正常的室内光照强度为150 Lux,对采集的图片加入干扰处理,测试检测模型的鲁棒性。对正常情况下采集的多组图片,调节亮度变化范围为[-70%,+70%]、对比度变化范围为0.0~0.3、三通道色域扭曲范围为[-30%,+30%]以及随机缩放范围为0.2~2.0。经过处理后得到100组带干扰的图片送入模型进行标定球检测,标定球检测成功率为98%,部分检测结果如图 5所示。通过网络输出定位框,由式(4)计算标定球成像的圆心像素坐标。

|
Download:
|
| 图 5 部分标定球检测结果 Fig. 5 Part of the detection results of the calibration ball | |
标定球被夹持在机械手末端的中心,即球心与机械手末端的TCP重合。使用训练后的改进yolov3目标检测神经网络模型检测提取标定球在像素坐标系下的球心坐标,结合RGB-D相机获取的球心像素点对应的深度值,由式(3)计算得到标定球球心在相机坐标系下的三维坐标,将手眼标定问题转换为求解相机坐标系与机器人基坐标系之间的映射矩阵。相机坐标系与机器人基坐标系之间的映射矩阵计算如下:
| $ {}_C^B \boldsymbol{H}=\left[\begin{array}{cc} {}_C^B \boldsymbol{R}& {}_C^B \boldsymbol{{\rm T}}\\ 0& 1\end{array}\right] $ | (5) |
| $ \left[\begin{array}{c}{}^{P}{B}_{x}\\ {}^{P}{B}_{y}\\ {}^{P}{B}_{z}\\ 1\end{array}\right]=\left[\begin{array}{cc} {}_C^B \boldsymbol{R}& {}_C^B \boldsymbol{T}\\ 0& 1\end{array}\right]\left[\begin{array}{c}{}^{P}{C}_{x}\\ {}^{P}{C}_{y}\\ {}^{P}{C}_{z}\\ 1\end{array}\right] $ | (6) |
其中:
在标定时,控制机械臂在相机视野中随机移动n个点,利用上述方法获得标定球在相机坐标系的三维坐标和对应点在机器人基坐标系下的坐标。记录标定球在相机坐标系和机器人坐标系下一一对应的点集:相机坐标系Ci={c1,c2,…,cn}和机器人基坐标系Bi={b1,b2,…,bn}。使用奇异值分解(Singular Value Decomposition,SVD)方法求解两个坐标系之间转换矩阵的最小二乘解[21]。计算相机坐标系{C}到机器人坐标系{B}映射的旋转矩阵
| $ ( {}_C^B \boldsymbol{R}, {}_C^B \boldsymbol{T})=\underset{\boldsymbol{R}, \boldsymbol{T}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\sum\limits _{1}^{n}{‖( {}_C^B \boldsymbol{R}{C}_{i}+ {}_C^B \boldsymbol{T})-{B}_{i}‖}^{2} $ | (7) |
1)计算标定球在相机坐标系和机器人坐标系下的两个点集的重心,如式(8)所示:
| $ \left\{\begin{array}{l}\stackrel{-}{B}=\frac{1}{n}\sum\limits _{i=1}^{n}{B}_{i}\\ \stackrel{-}{C}=\frac{1}{n}\sum\limits _{i=1}^{n}{C}_{i}\end{array}\right. $ | (8) |
2)计算两个点集中的每个点减去重心后的平移数据,如式(9)所示:
| $ {x}_{i}={C}_{i}-\stackrel{-}{C}, {y}_{i}={B}_{i}-\stackrel{-}{B}, i=\mathrm{1, 2}, \cdots , n $ | (9) |
3)计算X和Y的协方差矩阵S,其中X和Y由向量xi、yi构成,如式(10)所示:
| $ \boldsymbol{S}=\boldsymbol{X}{\boldsymbol{Y}}^{\mathrm{T}} $ | (10) |
4)对S进行奇异值分解,计算出旋转矩阵,如式(11)所示:
| $ \begin{array}{l}\boldsymbol{S}=\boldsymbol{U}\boldsymbol{\Sigma }{\boldsymbol{V}}^{\mathrm{T}}\\ {}_C^B \boldsymbol{R}=\boldsymbol{V}\left(\begin{array}{ccc}1& & \\ & \ddots & \\ & & \mathrm{d}\mathrm{e}\mathrm{t}\left(\boldsymbol{V}{\boldsymbol{U}}^{\mathrm{T}}\right)\end{array}\right){\boldsymbol{U}}^{\mathrm{T}}\end{array} $ | (11) |
5)由旋转矩阵计算平移向量,如式(12)所示:
| $ {}_C^B \boldsymbol{T}=\stackrel{-}{B}- {}_C^B \boldsymbol{R}\stackrel{-}{C} $ | (12) |
通过仿真实验验证本文提出的基于目标检测的机器人手眼标定方法的有效性。实际的机器人坐标系{B}与相机坐标系{C}之间的手眼变换关系
在仿真实验中,设定机器人坐标系{B}和RGB-D相机坐标系{C}之间的刚体旋转Rx(45°)、Ry(-30°)、Rz(60°)和平移X(850 mm)、Y(1 200 mm)、Z(1 350 mm)。Rx、Ry、Rz分别表示绕x轴、y轴和z轴旋转,因此两个坐标系的转换关系旋转矩阵
| $ {}_C^B {\boldsymbol{R}}_{T}=\left[\begin{array}{rrr}0.433 \ 2& -0.789 \ 1& 0.435 \ 4\\ 0.750 \ 2& 0.048 \ 0& -0.659 \ 4\\ 0.499 \ 4& 0.612 \ 3& 0.612 \ 8\end{array}\right] $ | (13) |
| $ {}_C^B {\boldsymbol{T}}_{T}={\left[\begin{array}{ccc}850& 1 \ 200& 1 \ 350\end{array}\right]}^{\mathrm{T}} $ | (14) |
在仿真过程中,设定3D打印球在机械手末端的夹持误差为-5~5 mm的随机误差,相机坐标系{C}下TCP在X、Y、Z各个方向的检测误差是均值为0、标准差为1.5的正态随机误差。在机器人坐标系{B}下随机采集100个标定点作为TCP在机器人坐标系下的点集
利用在机器人坐标系{B}下采集TCP的点集
| $ {}_C^B {\boldsymbol{R}}_{\mathrm{s}\mathrm{i}\mathrm{m}}=\left[\begin{array}{rrr}0.432 \ 8& -0.789 \ 5& 0.434 \ 9\\ 0.749 \ 9& 0.047 \ 6& -0.659 \ 8\\ 0.500 \ 0& 0.611 \ 7& 0.612 \ 7\end{array}\right] $ | (15) |
| $ {}_C^B {\boldsymbol{T}}_{\mathrm{s}\mathrm{i}\mathrm{m}}={\left[\begin{array}{ccc}844.98& 1 \ 203.94& 1 \ 352.26\end{array}\right]}^{\mathrm{T}} $ | (16) |
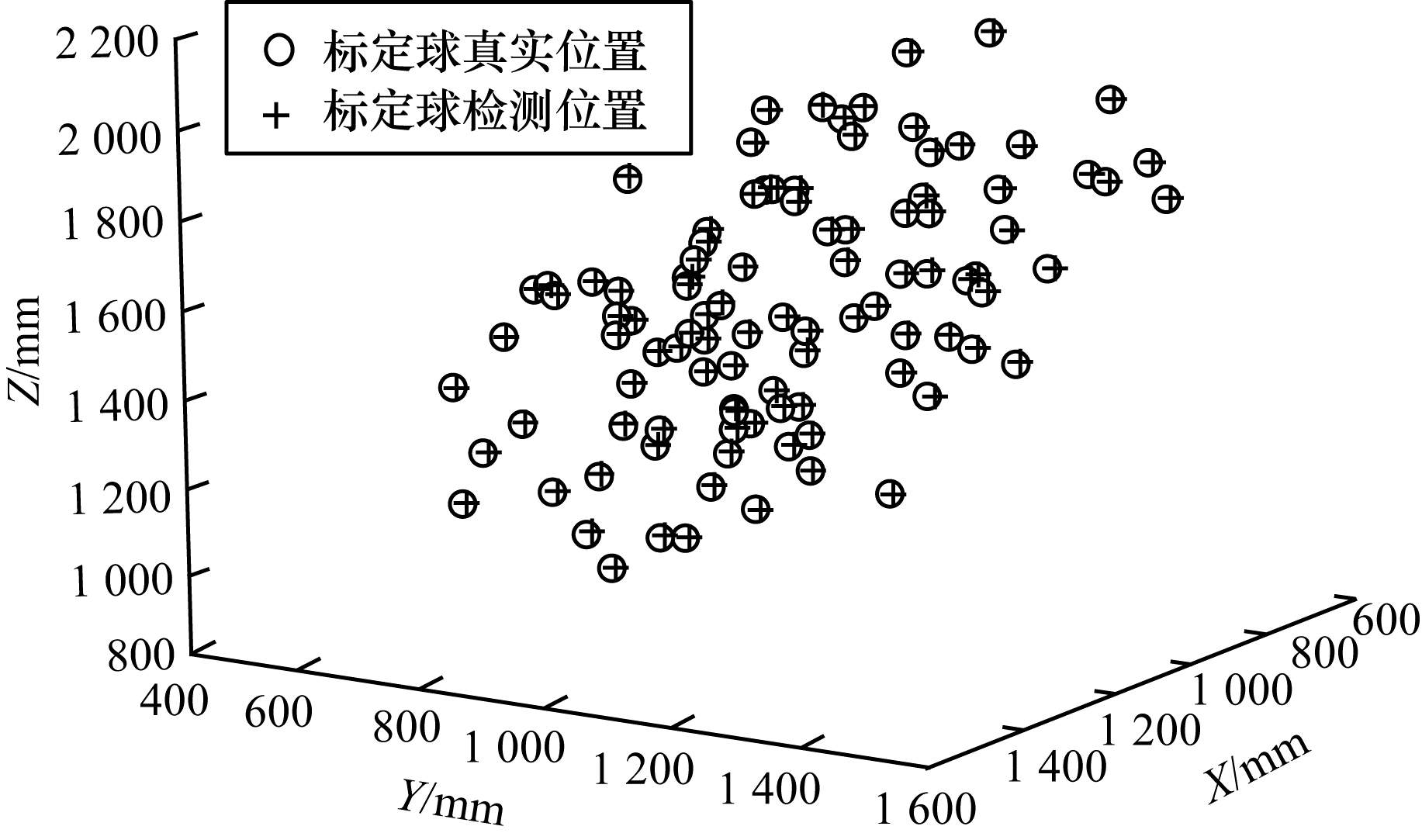
图 6给出了在相机坐标系{C}下的标定球理论点集
|
Download:
|
| 图 6 相机坐标系中的标定结果 Fig. 6 Calibration results in the camera coordinate system | |
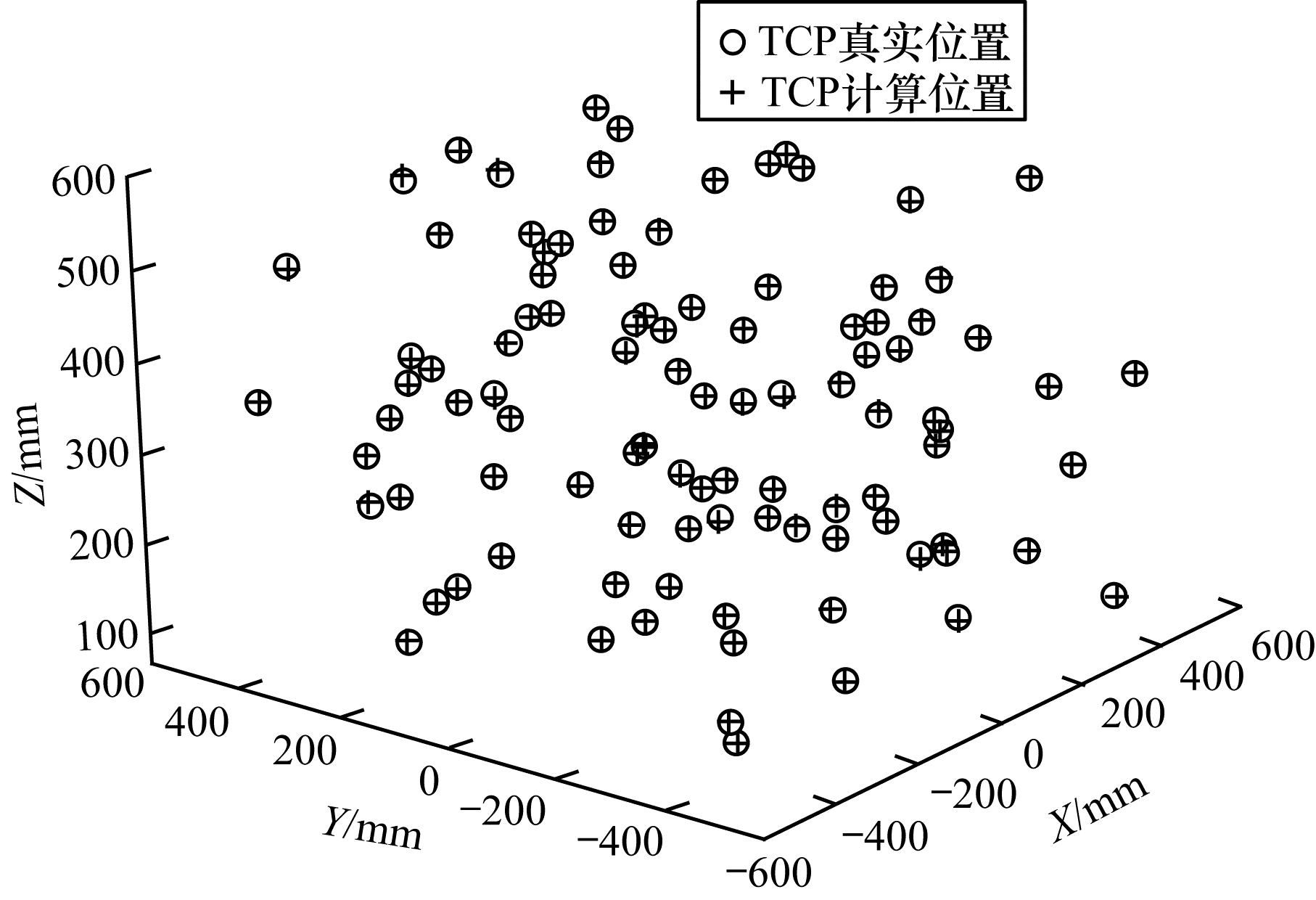
|
Download:
|
| 图 7 机器人坐标系中的标定结果 Fig. 7 Calibration results in the robot coordinate system | |
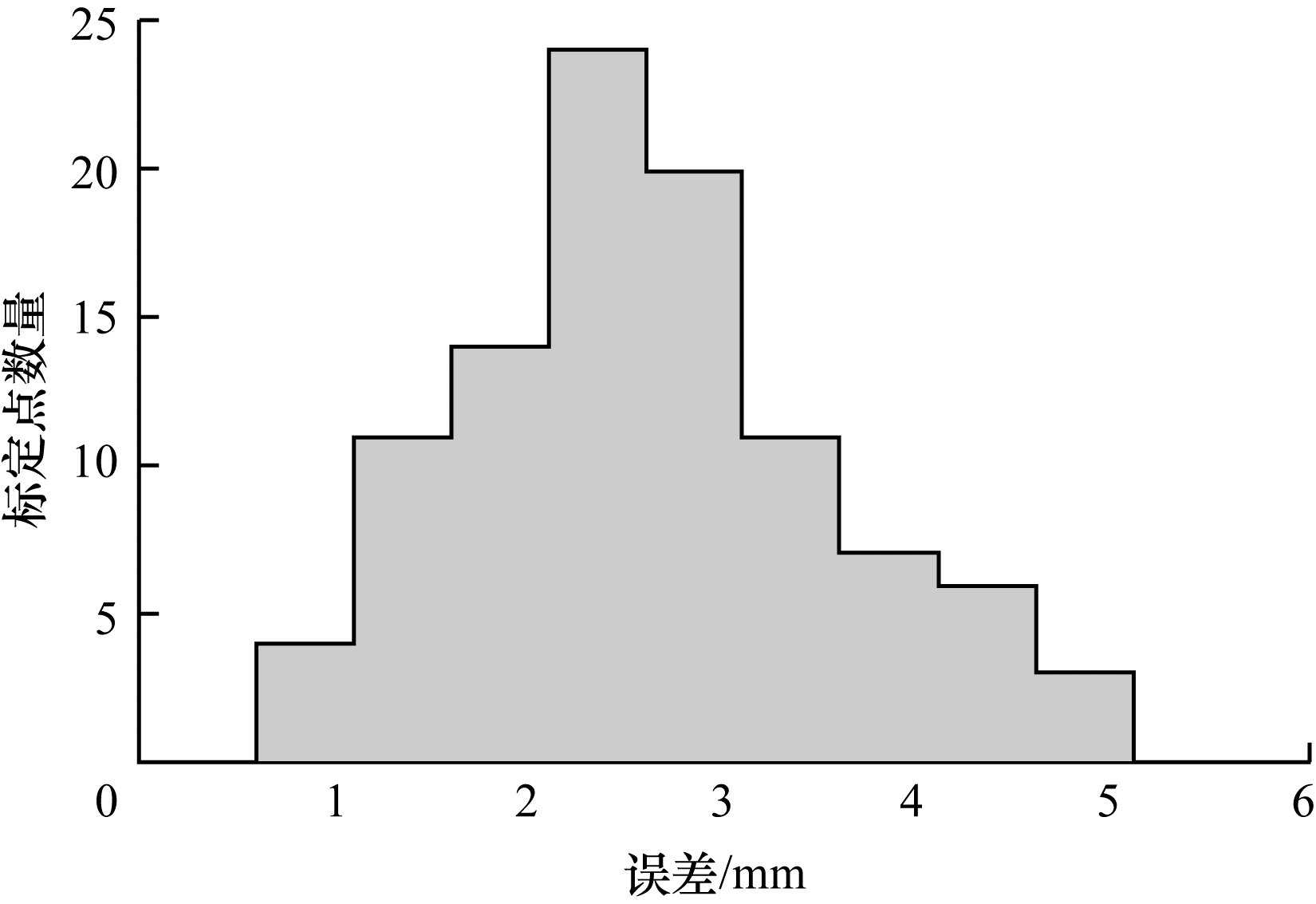
从仿真结果可看出,通过奇异值分解得到旋转矩阵和平移向量与标定量设定值基本一致。为进一步分析标定精度,定义标定误差:利用求得的标定结果,将相机坐标系下的点转换到机器人坐标系下,转换后的点与对应机械手末端TCP之间的欧氏距离为标定误差。该定义没有去除TCP在相机中的检测误差和标定球在机械手末端的夹持误差,因此为复合误差,用于间接分析标定精度。仿真实验得到的标定误差分布如图 8所示,标定误差整体成正态分布,误差均值为2.63 mm,误差方差为0.92 mm,验证了本文提出的基于目标检测的机器人手眼标定方法的有效性。
|
Download:
|
| 图 8 标定误差分布 Fig. 8 Calibration error distribution | |
利用末端安装有Robotiq85机械手的6自由度UR5机械臂和Intel RealSense D415深度相机搭建手眼系统,如图 9所示。算法运行环境为Windows10、Pytorch1.4.0、Python3.7,CPU为i5-6200,GPU为GeForce 940M 2 GB显存。上位机通过网口与UR5控制机箱通信与机械臂运动,获取机械手末端TCP在机器人坐标系下的坐标,利用Intel RealSense D415的PyRealSense2包,获得相机内参矩阵k信息,通过USB接口读取相机的彩色图和深度图。

|
Download:
|
| 图 9 手眼标定实验设置 Fig. 9 Experiment setting of hand-eye calibration | |
使用直径为3 cm标定球夹持在UR5机械臂Robotiq85机械手末端,控制机械臂在相机视野中移动。在移动过程中,利用改进的yolov3网络从RGB-D相机返回的彩色图中检测标定球的球心坐标

|
Download:
|
| 图 10 标定误差均值与标定点数量的关系 Fig. 10 The relationship between the mean value of calibration errors and the number of calibration points | |
训练后的改进yolov3标定球检测模型权重占用192 MB的内存空间,网络模型对416×416像素单张图片预测输出标定球球心坐标的平均耗时为167.6 ms。采集标定数据后,利用50组标定数据计算标定结果的旋转矩阵和平移向量最高耗时小于2 ms。
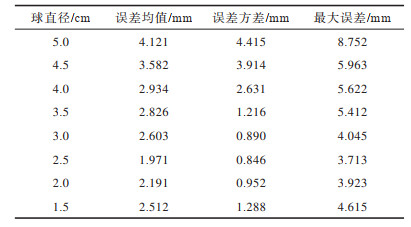
4.3 标定球检测实验标定球被夹持在机械手末端,通过目标检测网络检测标定球位置进行手眼标定。当使用不同尺寸的标定球进行标定实验时,会得到不同精度的标定结果。为获得精度较高的标定结果,需找到最佳尺寸的标定球,分别测试8种不同直径的标定球,得到不同的标定误差,如表 1所示。在实验中,标定球直径太大或太小都会使最终的标定误差增大。标定球直径过大容易引起较大的夹持误差,使标定误差增大;标定球直径过小,容易引起较大的检测误差,使标定误差增大。实验结果表明,在仿真中设定的误差分布情况与实际系统中直径为3.0~3.5 cm的标定球的误差结果较接近。与其他直径的标定球相比,直径为2.5 cm的标定球的误差均值、最大误差、误差方差均最小。
|
下载CSV 表 1 不同直径标定球的误差结果 Table 1 Error results of calibration balls with different diameters |
在上述两个测试实验的基础上,利用直径为2.5 cm的标定球重新进行标定实验,在机器人运动范围内随机选取40个采样点作为标定点,记录机器人机械手末端TCP在机器人坐标系的坐标和标定球球心在相机坐标系下的坐标,求得手眼关系转换矩阵
| $ {}_C^B \boldsymbol{R}=\left[\begin{array}{rrr}0.097 \ 9& -0.995 \ 1& -0.005 \ 5\\ -0.995 \ 1& -0.097 \ 8& -0.004 \ 1\\ 0.003 \ 5& 0.005 \ 9& -0.999 \ 9\end{array}\right] $ | (17) |
| $ {}_C^B \boldsymbol{T}={[-733.39, -\mathrm{104.53, 1} \ 041.97]}^{\mathrm{T}} $ | (18) |
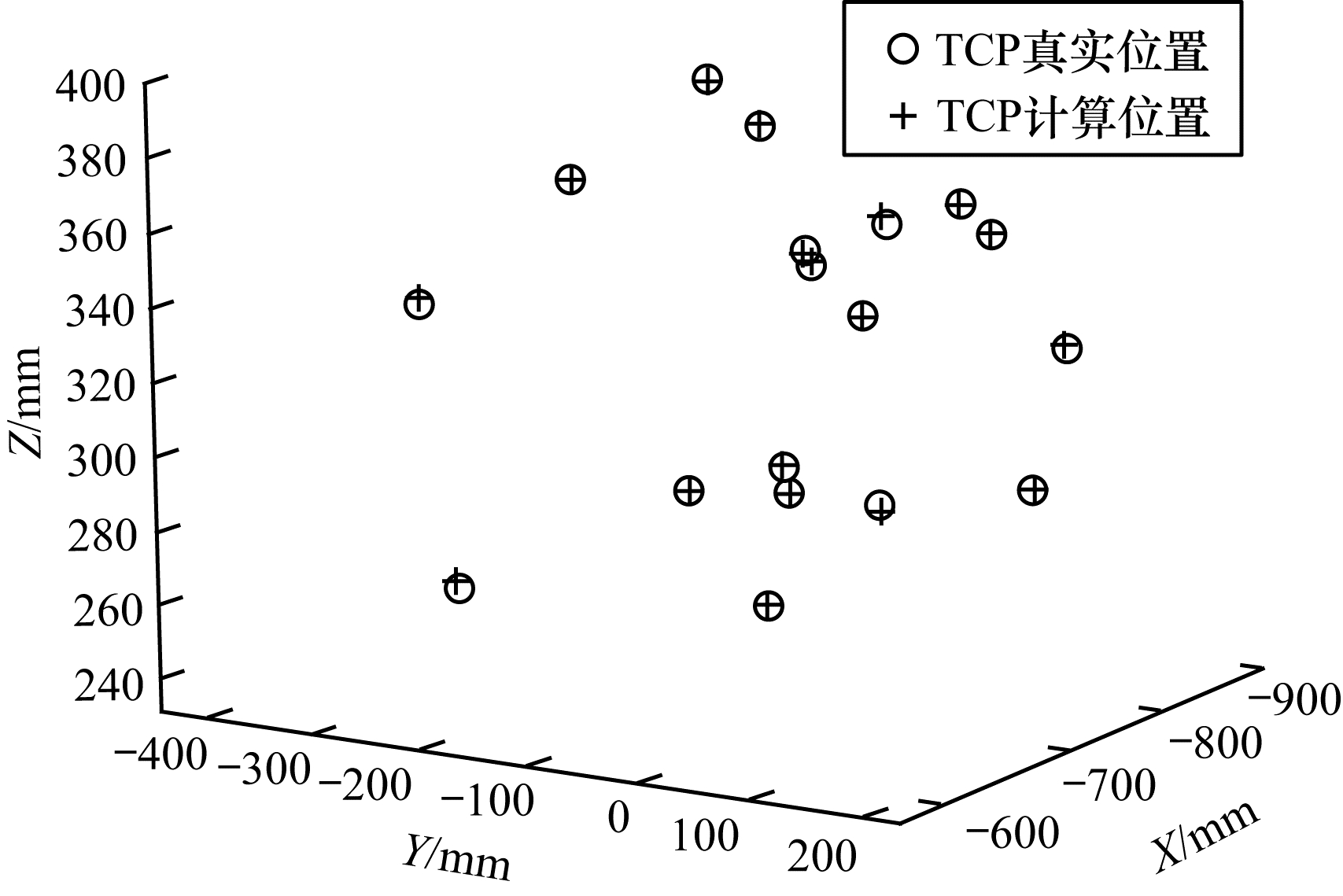
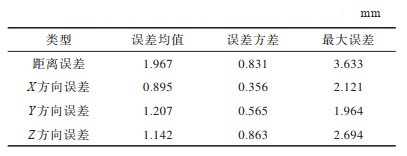
通过控制机器人使标定球在机器人运动范围内选取20个采样点作为验证点,如图 11所示。使用式(17)和式(18)的标定结果,由式(6)将RGB-D相机检测标定球在相机坐标系下的坐标转换到机器人坐标系下,转换后的空间点坐标与从机器人控制器返回的机械手末端TCP坐标进行对比,求出各点转化后的距离误差均值和X、Y、Z方向的误差结果如表 2所示。在本文实验环境下使用最佳直径2.5 cm的标定球得到的标定结果,转换后机器人坐标系下空间点的距离误差均值为1.967 mm,在X、Y、Z各方向上的误差均值为0.895 mm、1.207 mm、1.142 mm,最大误差和误差方差均较稳定。
|
Download:
|
| 图 11 验证点空间分布 Fig. 11 Spatial distribution of verification points | |
|
下载CSV 表 2 验证点误差结果 Table 2 Error results of verification points |
本文提出基于目标检测的机器人手眼标定方法,将3D打印球作为标定件,通过改进的yolov3目标检测神经网络对标定球进行检测定位,可在较复杂的环境中实现对标定球的提取,从而完成机械手末端TCP在相机坐标系与机器人坐标系之间的标定,避免了多个坐标系之间的复杂转换。实验结果表明,基于该方法转换后的空间点位置误差在2 mm以内,标定精度较高。下一步将分析标定求解算法及标定球的夹持安装精度、yolov3标定球检测精度等对最终标定精度的影响。
| [1] |
徐青青. 基于机器视觉的工业机器人智能分拣系统设计[J]. 仪表技术与传感器, 2019(8): 92-95, 100. XU Q Q. Design of intelligent sorting system for industrial robot based on machine vision[J]. Instrument Technique and Sensor, 2019(8): 92-95, 100. (in Chinese) |
| [2] |
XIAO H Z, LI Z J, YANG C G, et al. RGB-D sensor-based visual target detection and tracking for an intelligent wheelchair robot in indoors environments[J]. International Journal of Control, Automation and Systems, 2015, 13(3): 521-529. DOI:10.1007/s12555-014-0353-4 |
| [3] |
丁吉祥, 杜姗姗. 基于针孔模型与相机空间操作的机械臂视觉定位方法[J]. 计算机工程, 2015, 41(12): 317-320. DING J X, DU S S. Vision positioning method of robot manipulator based on pin-hole model and camera space manipulation[J]. Computer Engineering, 2015, 41(12): 317-320. (in Chinese) |
| [4] |
CHANG W C. Robotic assembly of smartphone back shells with eye-in-hand visual servoing[J]. Robotics and Computer-Integrated Manufacturing, 2018, 50: 102-113. DOI:10.1016/j.rcim.2017.09.010 |
| [5] |
陈梅, 车尚岳. 无标定视觉伺服机器人跟踪控制策略研究[J]. 控制工程, 2019, 26(6): 1055-1059. CHEN M, CHE S Y. Research on tracking control strategy of uncalibrated robot visual servo system[J]. Control Engineering of China, 2019, 26(6): 1055-1059. (in Chinese) |
| [6] |
HELLER J, HAVLENA M, SUGIMOTO A, et al. Structure-from-motion based hand-eye calibration using L∞ minimization[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2011: 3497-3503.
|
| [7] |
PACHTRACHAI K, ALLAN M, PAWAR V, et al. Hand-eye calibration for robotic assisted minimally invasive surgery without a calibration object[C]//Proceedings of International Conference on Intelligent Robots and Systems. Washington D.C., USA: IEEE Press, 2016: 2485-2491.
|
| [8] |
李巍, 吕乃光, 董明利, 等. 凸松弛全局优化机器人手眼标定[J]. 计算机应用, 2017, 37(5): 1451-1455. LI W, LÜ N G, DONG M L, et al. Robot hand-eye calibration by convex relaxation global optimization[J]. Journal of Computer Applications, 2017, 37(5): 1451-1455. (in Chinese) |
| [9] |
QIU S W, WANG M M, KERMANI M R. A new formulation for hand-eye calibrations as point-set matching[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(9): 6490-6498. DOI:10.1109/TIM.2020.2967958 |
| [10] |
ZHAO Z J. Hand-eye calibration using convex optimization[C]//Proceedings of 2011 IEEE International Conference on Robotics and Automation. Washington D.C., USA: IEEE Press, 2011: 2947-2952.
|
| [11] |
WU J, SUN Y X, WANG M M, et al. Hand-eye calibration: 4-D procrustes analysis approach[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(6): 2966-2981. DOI:10.1109/TIM.2019.2930710 |
| [12] |
WU L, REN H L. Finding the kinematic base frame of a robot by hand-eye calibration using 3D position data[J]. IEEE Transactions on Automation Science and Engineering, 2017, 14(1): 314-324. DOI:10.1109/TASE.2016.2517674 |
| [13] |
毕德学, 王欣亮, 刘志芳, 等. 机器人工具和相机位姿标定的新方法[J]. 仪器仪表学报, 2019, 40(1): 101-108. BI D X, WANG X L, LIU Z F, et al. New method for robot tool and camera pose calibration[J]. Chinese Journal of Scientific Instrument, 2019, 40(1): 101-108. (in Chinese) |
| [14] |
SHARIFZADEH S, BIRO I, KINNELL P. Robust hand-eye calibration of 2D laser sensors using a single-plane calibration artefact[J]. Robotics and Computer-Integrated Manufacturing, 2020, 61: 101823. DOI:10.1016/j.rcim.2019.101823 |
| [15] |
刘常杰, 班荣兴, 郭寅, 等. 基于双目视觉机器人TCP校准方法研究[J]. 红外与激光工程, 2015, 44(6): 1912-1917. LIU C J, BAN R X, GUO Y, et al. Calibration method of TCP based on stereo vision robot[J]. Infrared and Laser Engineering, 2015, 44(6): 1912-1917. (in Chinese) |
| [16] |
WU L, WANG J L, QI L, et al. Simultaneous hand-eye, tool-flange, and robot-robot calibration for comanipulation by solving the problem[J]. IEEE Transactions on Robotics, 2016, 32(2): 413-428. DOI:10.1109/TRO.2016.2530079 |
| [17] |
杜惠斌, 宋国立, 赵忆文, 等. 利用3D打印标定球的机械臂与RGB-D相机手眼标定方法[J]. 机器人, 2018, 40(6): 835-842. DU H B, SONG G L, ZHAO Y W, et al. Hand-eye calibration method for manipulator and RGB-D camera using 3D-printed ball[J]. Robot, 2018, 40(6): 835-842. (in Chinese) |
| [18] |
徐昀泽, 赵汝进, 马跃博, 等. 一种用于鱼眼镜头的线性标定方法[J]. 计算机工程, 2019, 45(12): 196-200. XU Y Z, ZHAO R J, MA Y B, et al. A linear calibration method for fisheye lens[J]. Computer Engineering, 2019, 45(12): 196-200. (in Chinese) |
| [19] |
GIRSHICK R. Fast R-CNN[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2015: 1440-1448.
|
| [20] |
REDMON J. FARHADI A. Yolov3: an incremental improvement[C]//Proceedings of 2018 IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2018: 1-6.
|
| [21] |
SORKINE-HORNUN O, RABINOVICH M. Least-squares rigid motion using SVD[EB/OL]. [2020-12-12]. https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Least-squares+rigid+motion+using+SVD&btnG.
|
 2022, Vol. 48
2022, Vol. 48

 ,
,