2. 中国科学技术大学 计算机科学与技术学院, 合肥 230022
2. School of Computer Science and Technology, University of Science and Technology of China, Hefei 230022, China
开放科学(资源服务)标志码(OSID): 
无线传感器网络(Wireless Sensor Network,WSN)[1]由许多能量受限的传感器节点构成,一般用来完成环境感知和数据收集任务。传感器节点能量有限且难以维护,通常部署在水下、森林深处、火山口等人类无法到达的地方。因此,能量对于传感器节点而言至关重要,能量的使用效率直接决定了WSN的生命周期。
为了降低传感器节点的能量消耗,WSN中通常引入醒睡机制,即节点周期性地在醒睡模式之间进行切换[2],只有当节点处于醒模式下才可正常通信,而处于睡眠模式的节点则无法与邻居节点进行通信,但是会大幅降低能量的消耗。
WSN中通常有2种介质访问控制(Medium Access Control,MAC)协议,即同步MAC协议和异步MAC协议。在同步MAC协议中,所有节点都在同一时刻醒来,发送节点可以直接将数据发送给接收节点而不需要等待;在异步MAC协议中,发送节点往往会花费很长时间等待接收节点醒来然后才能发送数据,这将大幅增加发送节点的等待时延。
为了解决异步WSN中发送节点等待时延过长的问题,节点一般从邻居节点中选择多个节点作为候选转发节点。当发送节点有数据要进行发送时,从醒来的候选转发节点中选择一个作为接收节点,这将减少发送节点的等待时延。这种选择多接收节点构成转发节点集的方法的时延性能远优于单接收节点方法,但是其对路由算法也提出了更高的要求,如果处理不当,不仅不会取得性能上的提升,还会造成更多的能量消耗,原因是:存在候选节点集大小问题,当候选节点集过小时,将不能很好地减少发送节点的等待时延,当候选节点集过大时,会提高多接收节点出现的概率,即多个候选节点同时醒来,这将产生过多的冗余数据包从而消耗节点的能量;存在候选转发节点的选择问题,由于评估选择算法的不合理导致一些不好的节点被选择加入至候选转发集中,当数据包经过这些节点转发时会使得网络性能下降,例如,数据包通过离sink位置较远的节点进行转发会导致路由路径变长,端到端延迟和转发数据包所需能耗提升;数据包通过低能量节点转发会导致该节点过早地因能量耗尽而无法继续工作等。
由以上分析可知,候选转发节点的评估与选择对网络性能影响较大。为了更好地对节点进行评估,选择更合理的候选转发节点集,本文基于层次分析法(Analytic Hierarchy Process,AHP)和模糊推理系统(Fuzzy Inference System,FIS),提出一种DAF(Dynamic evaluation algorithm based on AHP and FIS)算法,该算法在网络运行的过程中根据节点信息使用FIS动态构建AHP中的成对比较矩阵,从而实现对邻居节点的动态评分。
1 相关工作为了降低传感器节点的能耗、提高WSN的生命周期,研究人员提出很多MAC层和路由层协议。
文献[3]提出一个异步MAC协议B-MAC,当发送节点有数据包要发送时,会先发送一个前导码包给邻居节点,询问它们的状态信息,处于醒模式下的邻居节点会接收该前导码包并发回一个ACK确认包,发送节点在接收到这些ACK之后会从中选择一个节点作为接收节点并将数据包转发给该节点,如果没有邻居节点醒来,即发送节点接收不到ACK,则会不间断地发送前导码包。文献[4]提出另一种异步MAC协议X-MAC,相较于B-MAC,X-MAC发送的前导码包较短。文献[5]提出BoX-MAC,该协议通过共享物理层和数据链路层的信息来减少节点的能量消耗从而提高网络性能。
文献[6]基于ETX(Expected Transmission Count)提出一种路由参数EDC(Expected Duty Cycled wake-ups),其表示到达sink节点所需要的平均醒睡周期数,EDC越小的节点表示离sink越近,且只有当网络拓扑发生变化时EDC才会改变。发送节点会选择EDC较小的节点作为转发节点,因此,这些节点往往会因为接收过多的数据包而导致能量消耗比其他节点更快。
文献[7]在EDC的基础上考虑节点的剩余能量,剩余能量越高的节点越有可能被选择作为接收节点,EDC较小的节点会因为其剩余能量较低而被选择作为接收节点的优先级降低,因此,其能均衡网络负载并提高网络生命周期。
在文献[8]中,数据包被节点接收后不会被立即转发,若在短时间内有新的数据包被接收,则该节点会将这些数据包进行融合之后再发送,通过减少发送次数来节省能耗,但是这对数据融合算法提出了较高的要求,当网络数据传输率较低时,往往在网络性能上表现不佳。
文献[9]提出一种自适应路由协议AOR(Adaptive Opportunistic Routing),其采用分区方案来提高网络的吞吐量,即根据节点和汇聚节点之间的位置关系,将整个网络分成不同的区域,每个区域拥有不同的优先级。但是,由于区域划分的计算量较大且无法实现动态计算,因此在网络拓扑发生动态变化时,无法准确地将不同位置的节点划入不同的区域中,从而导致网络性能下降。
文献[10]采用和AOR类似的分区思想,提出一种新的路由协议算法OR-AHaD(an Opportunistic Routing algorithm with Adaptive Harvesting-aware Duty Cycling)。该算法可根据节点的位置信息进行区域划分,同时结合节点自身剩余能量调整休眠周期的占空比(Duty Cycle),综合各因素后确定不同节点的优先级和候选节点集。但是,该算法对数据传输所需要的代价评估往往不够准确,导致其在丢包率上性能表现相对较差。
文献[11]提出方向分布、传输距离分布、垂直距离分布、剩余能量分布这4种分布,通过参数控制4种分布的权重,最终计算出每个节点的得分。同时,为每个节点定义一个矩形范围,称为CZ(Candidates Zone),只有CZ中的节点才可被选择作为转发节点。但是,该网络性能在很大程度上受到参数的影响,在网络运行过程中,参数不可动态改变,因此,很难在网络运行之前确定合理的分布权重参数。
文献[12]为了提高WSN路由算法的灵活性,提出一种新的路由算法FRCA,在该算法中,节点的转发概率取决于多个部分,包括影响网络性能的物理量、基本的数学函数以及路由参数,通过调整各个部分的参数权重,最终计算出节点的路由度量,在节点转发数据包时用该度量来进行接收节点的选择。但是,针对不同的网络应用来调整一组合适的路由参数非常困难,且当网络拓扑发生变化时该算法不能在运行过程中进行参数调整。
节点评估算法的性能在很大程度上受到WSN动态性的影响,如由新旧节点的替换带来的网络拓扑变化、由节点移动引起的相对位置信息变化以及由收发数据包带来的剩余能量信息变化等。因此,一个性能较好的路由协议应该具有一定的动态性来适应WSN网络信息的动态变化。本文提出一种节点动态评估算法DAF,节点以剩余能量、距离和角度为评估准则对邻居节点进行动态评分。具体地,当某节点发现邻居节点关于某准则状态值发生变化时,使用FIS来动态构建AHP中的成对比较矩阵,然后使用AHP来计算每个邻居节点的评分,根据该评分选择候选转发节点以及接收节点。DAF使得发送节点可以根据邻居节点的信息变化来动态更新候选转发节点集,通过及时加入评分较高的节点并移出评分较低的节点来提高网络性能。
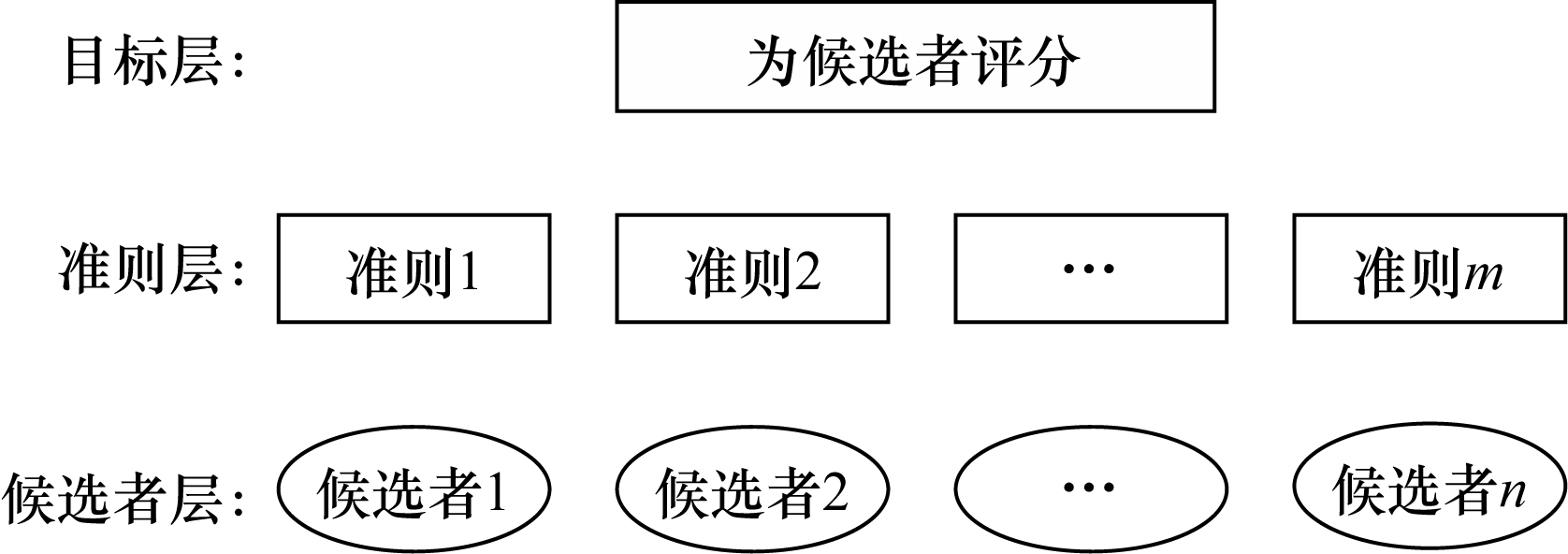
2 技术介绍 2.1 层次分析法AHP[13]是根据网络系统理论和多目标综合评价方法提出的一种层次权重决策分析方法。一般而言,AHP将目标、准则和候选者按不同层次进行聚集组合,形成一个多层次的分析结构模型,如图 1所示。
|
Download:
|
| 图 1 AHP结构 Fig. 1 The structure of AHP | |
为了计算准则相对于目标的权重,AHP需要预先构建一个成对比较矩阵,该矩阵主对角元素全为1,其余元素关于主对角元素互为倒数。假设有m个准则,则该成对比较矩阵是一个m维方阵,其形式如式(1)所示:
| $ \left[\begin{array}{cccc}{a}_{11}& {a}_{12}& \cdots & {a}_{1m}\\ \begin{array}{l}{a}_{21}\\ ⋮\end{array}& \begin{array}{l}{a}_{22}\\ ⋮\end{array}& \begin{array}{l}\cdots \\ \end{array}& \begin{array}{l}{a}_{2m}\\ ⋮\end{array}\\ {a}_{m1}& {a}_{m2}& \cdots & {a}_{mm}\end{array}\right] $ | (1) |
矩阵元素

|
下载CSV 表 1 矩阵元素取值及其含义 Table 1 Values of matrix elements and their meanings |
假设有n个候选者,则该部分共有m个成对比较矩阵,每个矩阵都是n维方阵。按照上述求解方法,决策者需要预先构建这m个成对比较矩阵,然后分别求解m个矩阵的最大特征值对应的特征向量,将所有特征向量按列合并后组成一个新的n×m维矩阵,该矩阵表示所有候选者相对于所有准则的权重,其中,第k列表示所有候选者相对于第k个准则的权重。
将上述计算所得n×m维矩阵点乘2.1.1节所得m维列向量,得到一个n维列向量,该向量每一维度数值表示对应候选者相对于目标的总评分。
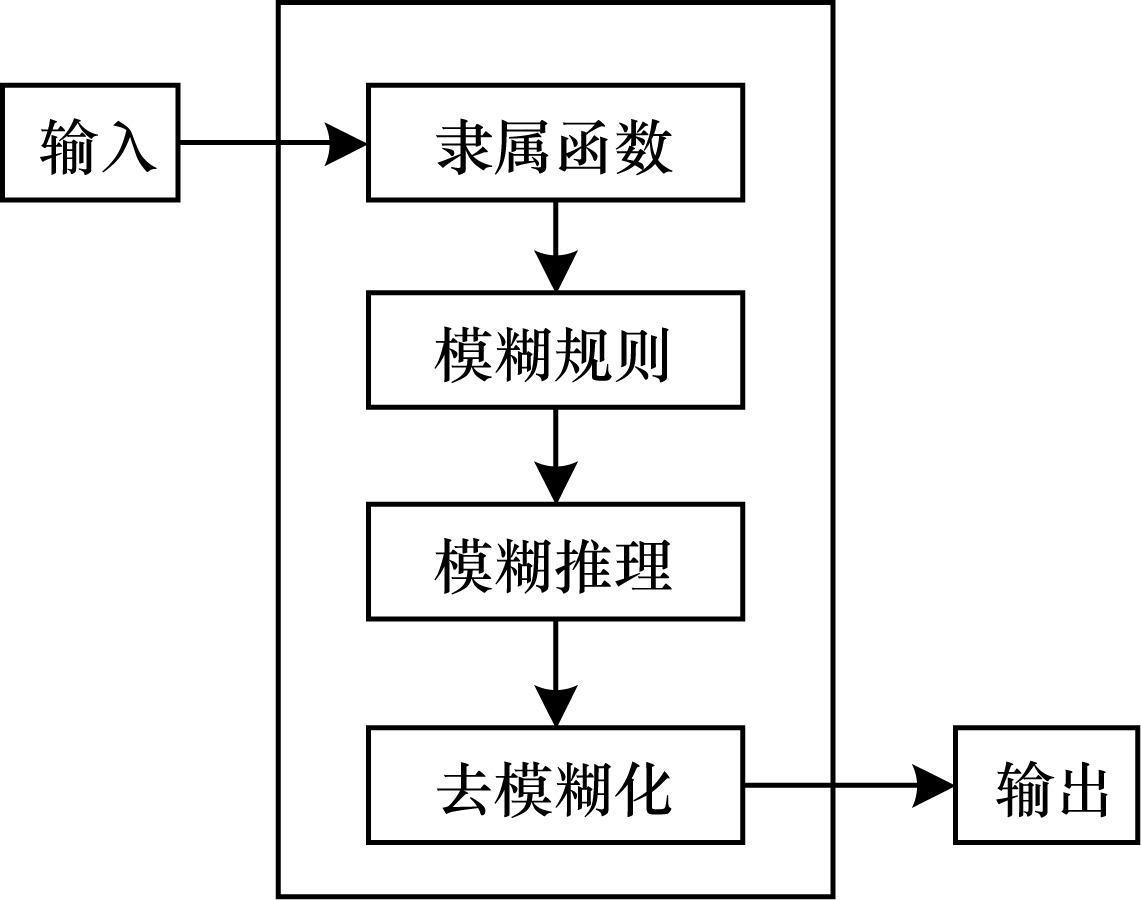
2.2 模糊推理系统FIS[14]通过将一系列清晰的输入值模糊化,基于自定义模糊规则得到模糊输出,再将模糊输出去模糊化得到一个清晰的输出值,如图 2所示。FIS中有2个重要的概念,即隶属函数和模糊规则。
|
Download:
|
| 图 2 FIS结构 Fig. 2 The structure of FIS | |
一个模糊集合可以用一个语言变量来表述,对于某个特定的数值,其属于某模糊集合的隶属度就用隶属函数来表示。一般地,隶属函数的值域范围为0~1,定义域包括输入变量的所有取值。模糊集合、隶属函数和输入变量之间的关系如式(2)所示:
| $ A=\{x, {\mu }_{A}\left(x\right)|x\in X\} $ | (2) |
其中:A表示模糊集合;x是输入变量;
在一般情况下,一个具有2个前提条件的模糊规则形式如式(3)所示:
| $ \begin{array}{l} 如果:x属于A且y属于B\\ 那么:z属于C \end{array} $ | (3) |
其中:“如果”后面的内容称为前提;“那么”后面的内容称为结论。x和y均是输入变量,z是输出量,“x属于A”表示x属于A的隶属度,即
1)评估前提的隶属度。
2)确定模糊输出。
计算复合前提的隶属度,首先要计算每个前提的隶属度,然后根据规则中的连接词(“且”“或”“非”)使用不同的方法求解复合前提的隶属度。在模糊逻辑中,结论的隶属度与前提的隶属度保持一致。一个模糊推理系统一般有多条模糊规则,所有模糊规则并行执行,都会产生一个模糊输出。将所有模糊输出聚合后形成一个模糊输出集,再通过使用去模糊化方法即可求得一个清晰的输出值,该输出值就是整个模糊推理系统的输出。
3 DAF算法节点从邻居节点中选择合适的候选转发节点并在需要发送数据时选择其中一个节点作为接收节点,这是一个多目标决策问题(Multiple Criteria Decision Making,MCDM)[15]。AHP在解决多目标决策问题时具有简单高效的优势,因此,本文在WSN中引入AHP来解决与节点相关的决策问题。
应用AHP的关键在于成对比较矩阵的构建,其构建特性具有一定的局限性:首先,成对比较矩阵需要决策者根据自己的主观判断或喜爱偏好来构建,这往往会因为决策者个人问题导致无法做出合理的判断;其次,成对比较矩阵的构建需要人为干预,因此,在系统运行中无法完成矩阵构建。
FIS能够使系统或控制器如同一个经验丰富的专家或专业的操作员,因此,本文通过在WSN中引入FIS,使传感器节点能够像人类一样思考,使得AHP中成对比较矩阵的构建可以在无人为干涉的条件下由传感器节点独立完成。通过为FIS自定义合适的模糊隶属函数和模糊规则,使得矩阵的构建不仅可以基于专家建议和意见,还可以在WSN运行过程中动态完成。
DAF算法首先使用AHP确定准则之间的权重,其次在评估不同准则下的邻居节点时,使用FIS动态构建AHP中的成对比较矩阵,具体表现为:将节点信息作为FIS的输入,用FIS的输出来替代矩阵中的元素值。本文所使用的符号及解释如表 2所示。

|
下载CSV 表 2 符号含义 Table 2 Symbolic meaning |
为了更好地评估邻居节点,本文定义3个影响网络性能的准则,其归一化方法及含义如表 3所示。

|
下载CSV 表 3 准则信息 Table 3 Criterion information |
结合实验数据和经验分析,本文构建准则的成对比较矩阵如式(4)所示,行(列)标依次表示剩余能量、距离和角度。求解矩阵最大特征值对应的特征向量,归一化之后得到准则权重向量
| $ \boldsymbol{A}=\left(\begin{array}{ccc}1& 2& 3\\ 1/2& 1& 2\\ 1/3& 1/2& 1\end{array}\right) $ | (4) |
本文通过构建AHP成对比较矩阵,计算成对比较矩阵最大特征值对应的特征向量,以评估邻居节点。为了能够动态评估邻居节点,需要实现成对比较矩阵动态构建,本文使用FIS的输出来代替成对比较矩阵的元素值,从而实现矩阵动态构建。
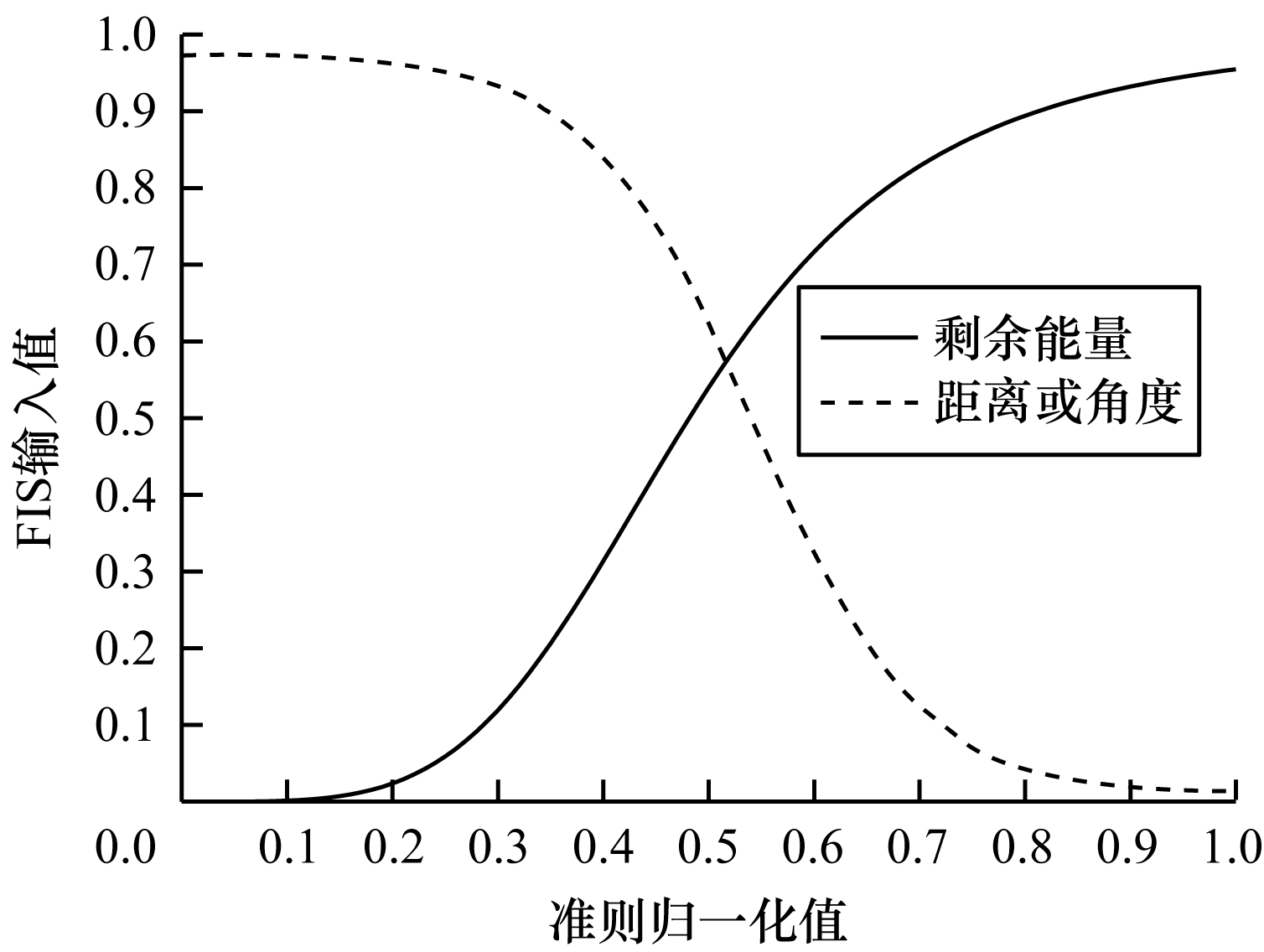
3.2.1 FIS输入值为了使用同一套FIS来构建不同准则的成对比较矩阵,本文在获取FIS输入值时需要对不同准则的归一化值进行处理,目的是屏蔽FIS输入值对应的物理意义。剩余能量越多的节点重要性越大,相反地,距离越远、角度越大的节点重要性越小。通过实验数据和理论分析,本文使用插值法进行函数拟合,如式(5)、式(6)所示,其中,式(5)的自变量是剩余能量归一化值,式(6)的自变量是距离或角度的归一化值,函数图像如图 3所示。
| $ \begin{array}{l}\stackrel{-}{\mathit{\Phi} }\left(x\right)=V\cdot \frac{{x}^{n}}{{k}^{n}+{x}^{n}}\\ k=0.48, n=4.23, V=0.99, x={E}_{{n}_{ij}}/{E}_{i}\end{array} $ | (5) |
| $ \begin{array}{l}\stackrel{-}{\mathit{\Psi} }\left(x\right)={a}_{1}+\frac{{a}_{1}-{a}_{2}}{1+{\mathrm{e}}^{(x-{x}_{1})/{x}_{2}}}, ({a}_{1}=0.97, {x}_{1}=0.54, x={d}_{{n}_{ij}}/R)\\ \mathrm{或}({a}_{2}=0.08, {x}_{2}=0.07, x={\alpha }_{{n}_{ij}}\cdot 2/\mathrm{\pi })\end{array} $ | (6) |
|
Download:
|
| 图 3 FIS不同准则下的输入值 Fig. 3 FIS input values under different criteria | |
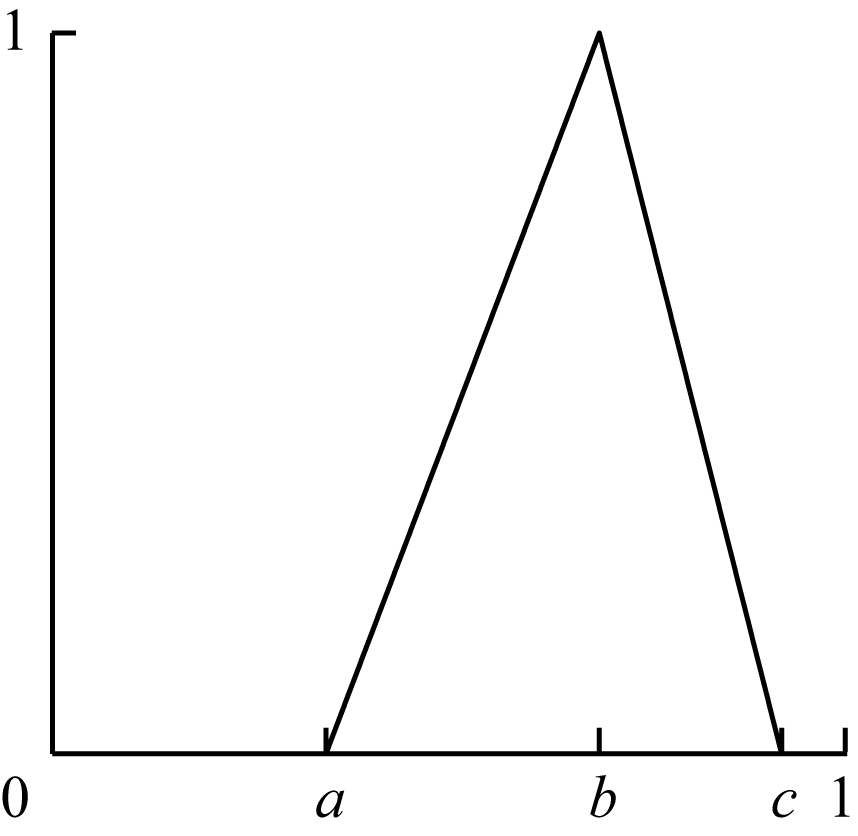
Triangular函数[16]是最简单且常用的模糊隶属函数,其函数图像主要由3个点构成,形成一个三角形,又称为三角形函数。Triangular函数表达如式(7)所示,图像如图 4所示。
| $ \mu \left(x\right)=\left\{\begin{array}{l}(x-a)/(b-a)\text{,}a\le x < b\\ (c-x)/(c-b)\text{,}b\le x < c\\ 0\text{,}\mathrm{其}\mathrm{他}\end{array}\right. $ | (7) |
|
Download:
|
| 图 4 三角形模糊隶属函数 Fig. 4 Triangular fuzzy membership function | |
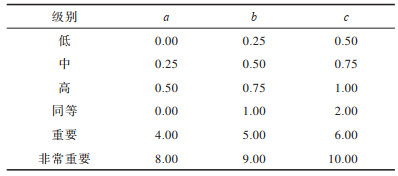
考虑到Triangular函数设计简单、计算高效等特点,本文使用该函数来定义输入和输出隶属函数。其中:输入隶属函数表示“合适度”,共有“低”“中”“高”3个级别;输出隶属函数表示“重要性”,包括“同等”“重要”“非常重要”3个级别。输入和输出隶属函数的参数设置如表 4所示。
|
下载CSV 表 4 输入输出隶属函数参数设置 Table 4 Input and output membership function parameters setting |
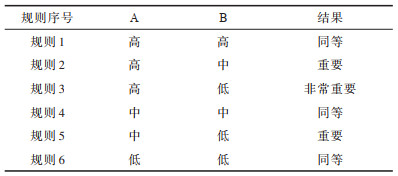
本文使用Mamdani模糊推理系统[17],模糊规则如表 5所示,每个规则前提由2个部分组成,通过“且”进行连接。去模糊化方法使用重心法CoG(Center-of-Gravity)[18],该方法计算简单且易于理解,已成为一种常用的去模糊化方法。重心法通过求解一个x值,使得过该值的垂线可将模糊集合平分为2个面积相等的部分,如式(8)所示:
| $ {x}^{*}=\frac{\int x{\mu }_{c}\left(x\right)\mathrm{d}x}{\int {\mu }_{c}\left(x\right)\mathrm{d}x} $ | (8) |
其中:
|
下载CSV 表 5 模糊规则 Table 5 Fuzzy rules |
构造不同准则对应的成对比较矩阵均使用表 5所示的模糊规则,且每次将2个节点中数值较大的节点作为A,较小的节点作为B。通过该模糊系统得到的输出值表示A相对于B的重要性,B相对于A的重要性利用成对比较矩阵的互反性求得。例如在构建剩余能量矩阵时,规则2被翻译为:如果节点A的剩余能量“合适度”是“高”且节点B的剩余能量“合适度”是“中”,那么针对剩余能量准则而言,节点A相对于节点B是“重要”的。
3.3 算法描述以构建关于剩余能量准则的成对比较矩阵为例,用FIS输出值代替矩阵某元素值的求解过程如算法1所述,基于算法1,节点使用DAF动态评估邻居节点的过程如算法2所述。
算法1 求解剩余能量成对比较矩阵元素对
输入 2个邻居节点的剩余能量
输出 剩余能量准则成对比较矩阵中的元素对
1.归一化剩余能量值
2.通过式(5)获得FIS输入值
3.如果
4.那么用FIS的输出值代替
5.否则将FIS的输出值代替
算法2 节点使用DAF动态评估邻居节点
输入 节点
输出
1.获得准则之间的权重
2.归一化所有邻居节点在不同准则下的值
3.利用算法1构建所有准则的成对比较矩阵
4.计算所有成对比较矩阵的最大特征值对应的特征向量
5.将所有特征值归一化后合并成一个新的矩阵
6.将步骤5中的矩阵点乘步骤1中的权重向量
7.得到列向量,即为所有邻居节点的评分
4 实验结果与分析 4.1 仿真设置和参数默认值本文使用文献[19]中所提供的仿真平台,在实验过程中,节点按照圆形拓扑随机部署,sink节点位于网络中心,且拥有无限的能量,数据包由节点循环生成。每个节点的初始能量相同且有限,通信范围相同且不变,节点各自选择一个随机的时间点周期性地在醒睡2种模式下切换,默认醒1 s,睡2 s。节点的坐标通过基于RSSI(Received Signal Strength Indicator)测距模型[20]获得。通信模型采用FSPM(Free Space Propagation Model)[21],该模型假设节点的通信范围是一个以节点为圆心、以通信范围为半径的圆,处于圆内的节点都可正确接收信息。能量模型采用FORM(First Order Radio Model)[22],传输一个k bit长度的数据包所需的能耗如式(9)所示,接收一个k bit长度的数据包所需的能耗如式(10)所示。其余默认参数配置如表 6所示。
| $ {E}_{T}\left({d}_{i, j}, k\right)=\left\{\begin{array}{l}k{E}_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}}+k{\xi }_{\mathrm{a}\mathrm{m}\mathrm{p}}{d}_{i, j}^{2}, {d}_{i, j} < {d}_{*}\\ k{E}_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}}+k{\xi }_{\mathrm{f}\mathrm{s}}{d}_{i, j}^{4}, {d}_{i, j} > {d}_{*}\end{array}\right. $ | (9) |
| $ {E}_{R}\left(k\right)=k{E}_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}} $ | (10) |
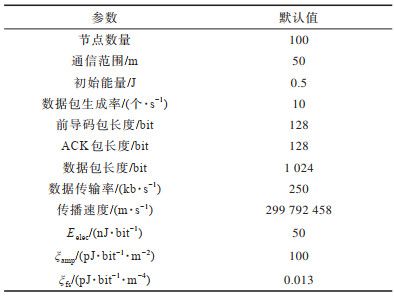
|
下载CSV 表 6 实验默认参数配置 Table 6 Experiment default parameters configuration |
1)ORW算法中使用的路由参数是EDC,每个节点都有属于自己的EDC且仅当网络拓扑发生变化时节点的EDC值才会被重新计算。发送节点每次从醒来的邻居节点中选择一个EDC值最低的节点作为转发节点,因此,EDC值较低的节点会因为转发过多的数据包而导致能耗较高。
2)ORR算法在EDC的基础上考虑节点的剩余能量,提出新的路由参数FS(Forwarder Score)。同时为了限制候选转发节点集的大小,sink节点会周期性地收集所有邻居节点的信息,然后计算出一个最大值n作为所有节点的候选转发节点集最大值,该过程通常会消耗较多的能量。
4.2.2 评估标准本文使用以下性能指标作为算法的评估标准:
1)生命周期,表示第一个节点耗尽其初始能量时网络生成的数据包总数。
2)能量消耗,表示当sink节点收集一定数量的数据包时网络消耗的总能量。
3)平均冗余传输,表示每发送一个数据包所产生的平均冗余数据包。
4.3 结果分析本文通过改变不同的参数值分别进行实验。在生命周期实验中,将数据包大小设置为1 024 Byte,在能量消耗及平均冗余传输实验中,sink节点接收数据包数量被固定为3 000。
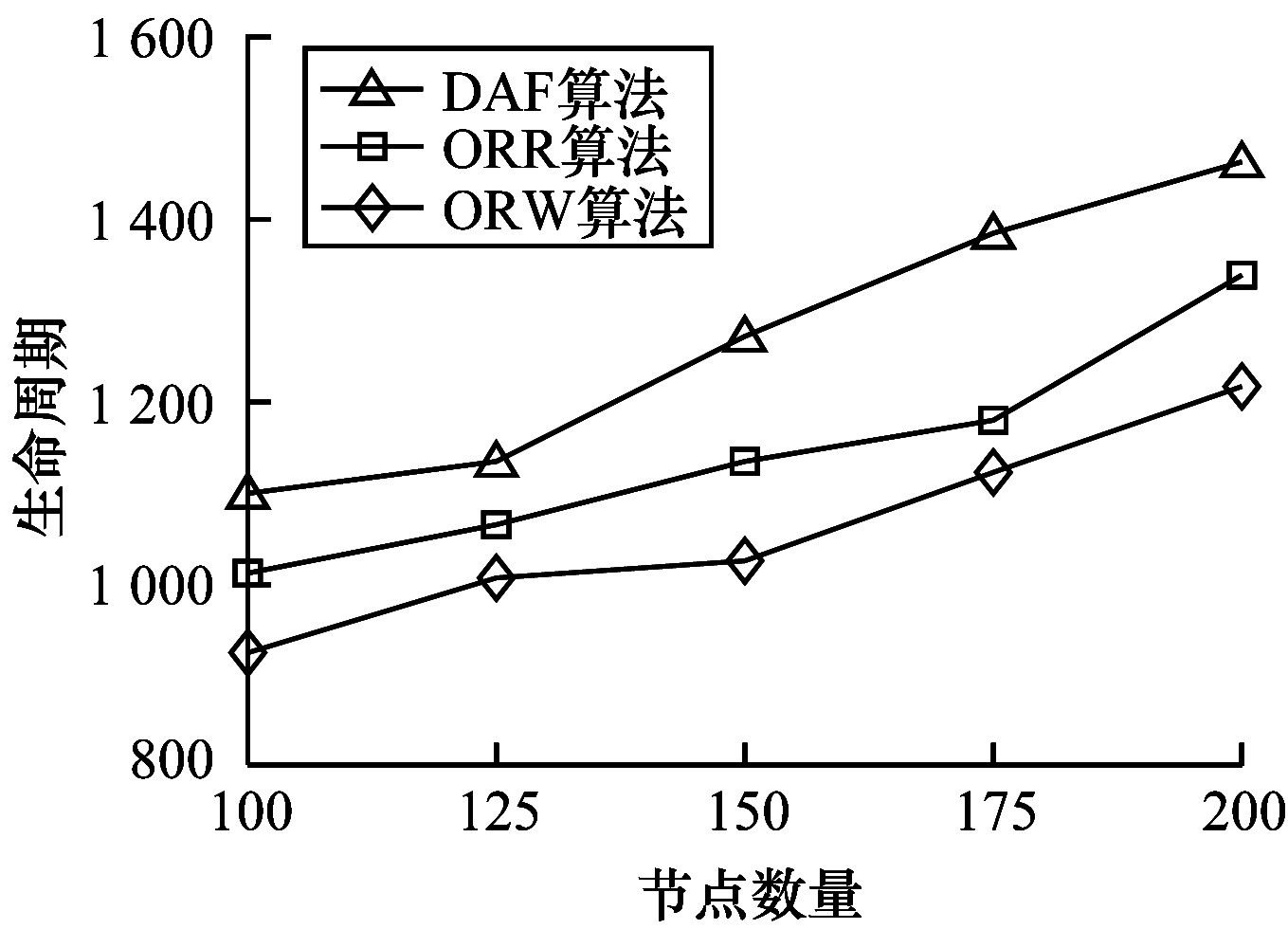
4.3.1 节点数量对算法性能的影响将节点数量从100依次增加到200,其他默认参数设置不变,实验结果如图 5~图 7所示。
|
Download:
|
| 图 5 生命周期随节点数量的变化情况 Fig. 5 Life cycle changes with the number of nodes | |
|
Download:
|
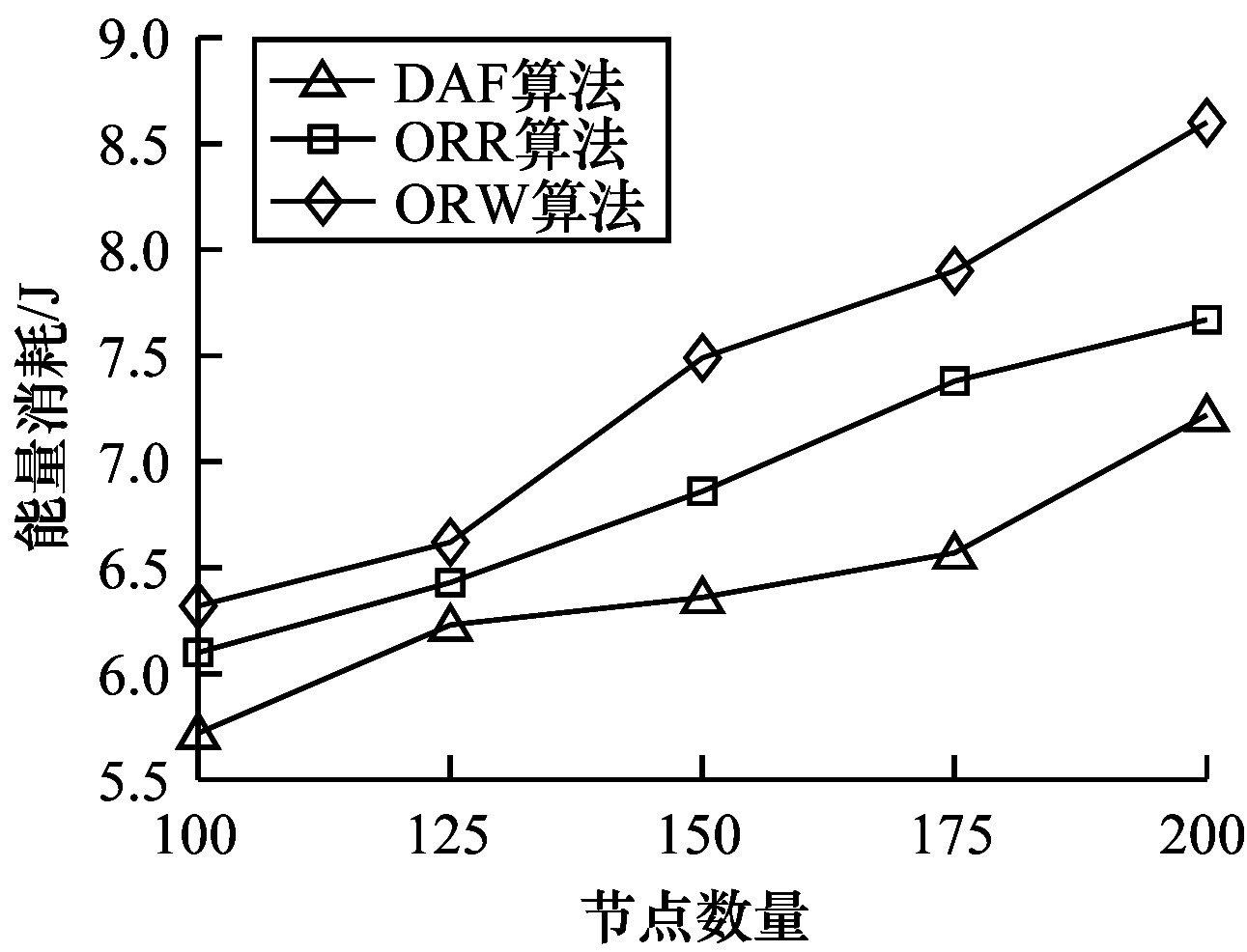
| 图 6 能量消耗随节点数量的变化情况 Fig. 6 Energy consumption changes with the number of nodes | |
|
Download:
|
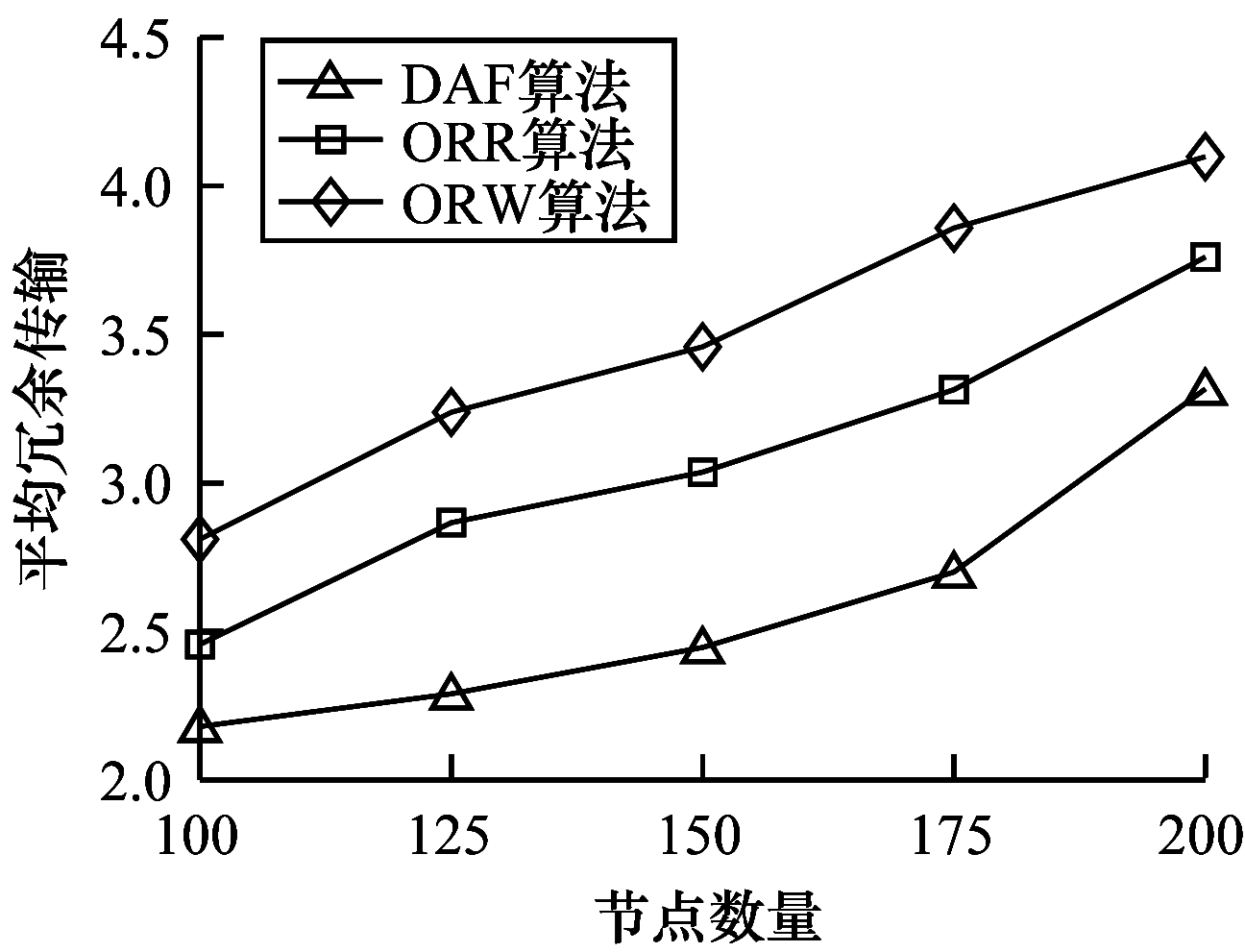
| 图 7 平均冗余传输随节点数量的变化情况 Fig. 7 Average redundant transmission changes with the number of nodes | |
由图 5可知,网络生命周期随节点数量增加而增加。节点数量增加导致网络密度增加,节点间的平均距离缩短,节点间单跳传输能耗降低,因此,网络生命周期延长。DAF基于预确定的评估准则,节点优先发送数据给那些剩余能量高、距离近、角度小的节点,因此其性能表现最好。由图 6可知,网络的能量消耗随着节点数量增加而增加。网络密度增加,导致数据包跳数增加,因此,每个数据包消耗的平均总能耗增加,即网络的总能耗增加。DAF保证了路由路径尽可能地向sink靠近,降低了路由的偏离程度,因此其性能更佳。由图 7可知,平均冗余传输随着节点数量增加而增加。网络密度增加,邻居节点数量增加,节点的候选转发节点集也随之增加,发送节点在选择转发节点的过程中产生了更多的冗余数据包。DAF通过动态地为节点进行评分,从而有效减少了平均冗余传输。
4.3.2 醒睡周期对算法性能的影响在本次实验中,节点醒周期被固定为1 s,睡周期从1 s依次增加到5 s,其他默认参数设置不变,实验结果如图 8~图 10所示。
|
Download:
|
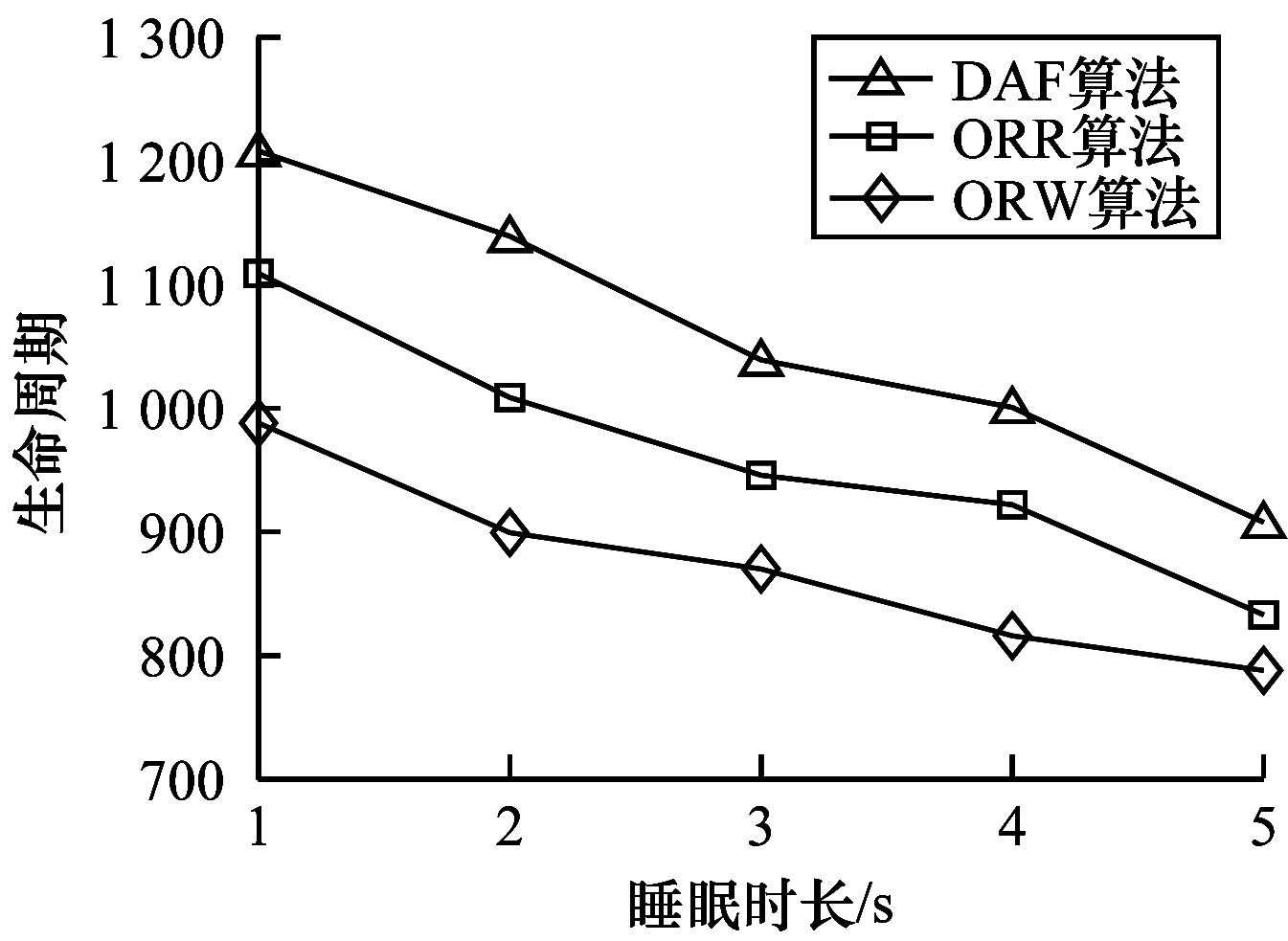
| 图 8 生命周期随节点睡眠时长的变化情况 Fig. 8 Life cycle changes with node sleep duration | |
|
Download:
|
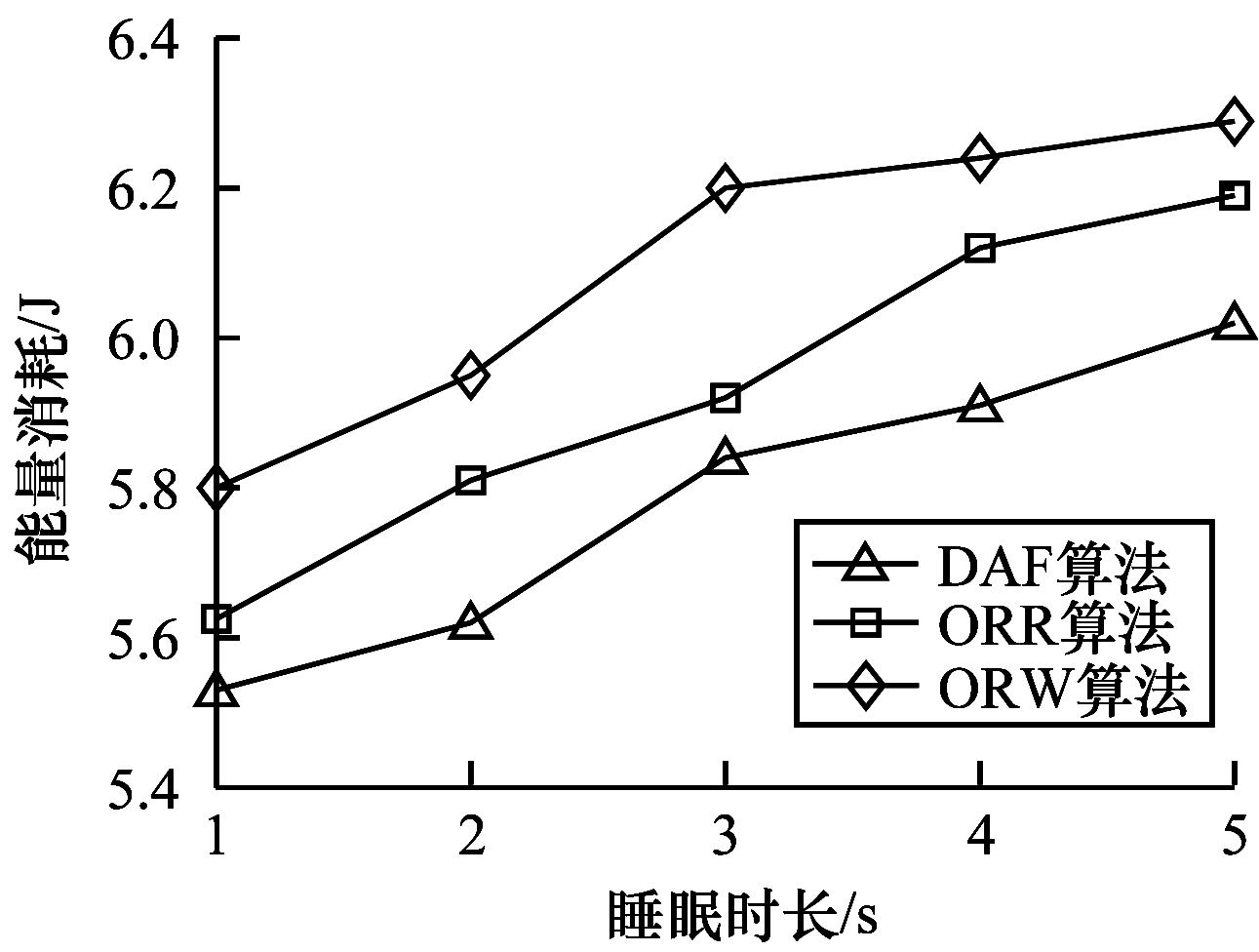
| 图 9 能量消耗随节点睡眠时长的变化情况 Fig. 9 Energy consumption changes with node sleep duration | |
|
Download:
|
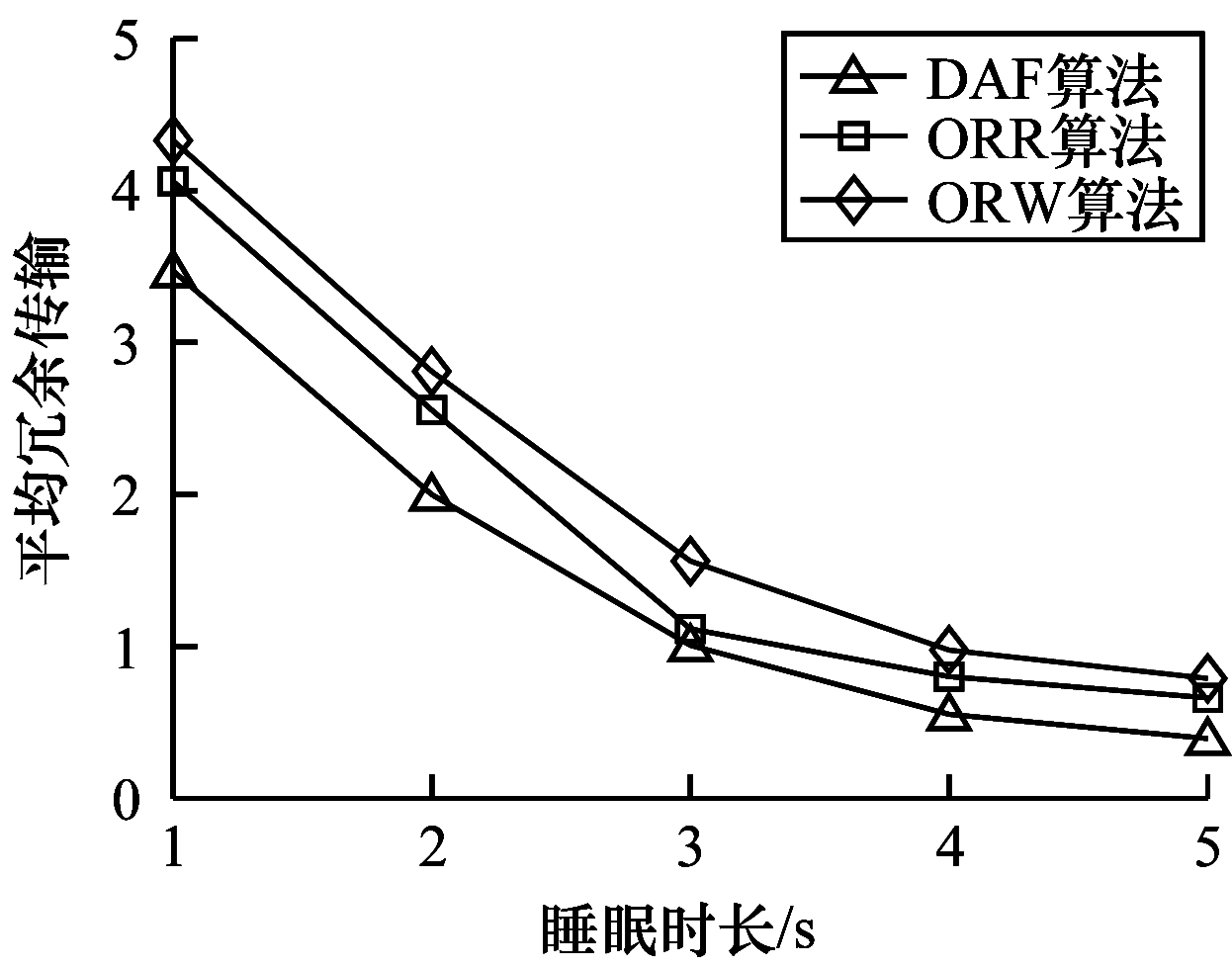
| 图 10 平均冗余传输随节点睡眠时长的变化情况 Fig. 10 Average redundant transmission changes with node sleep duration | |
由图 8可知,生命周期随睡眠时长的增加而减少。发送节点在发送数据包之前会不停地发送前导码包,随着节点的睡眠周期延长,发送节点用于发送前导码包的能耗越来越多,导致网络的生命周期减少。DAF通过动态更新候选转发节点集使得其性能较ORW和ORR更佳。由图 9可知,能量消耗随睡眠时长增加而增加。虽然能耗会因为冗余包减少而减少,但是能耗更多地浪费在发送前导码包上。DAF性能较优的理由如上所述。由图 10可知,平均冗余传输随睡眠时长增加而减少。多个节点同时醒来的概率随着睡眠时长的增加而减少,因此,减少了冗余数据包的产生。从实验结果来看,DAF在平均冗余传输指标上较ORW和ORR略优。
4.3.3 通信半径对算法性能的影响将节点通信半径从50 m依次增加到90 m,其他默认参数设置不变,实验结果如图 11~图 13所示。
|
Download:
|
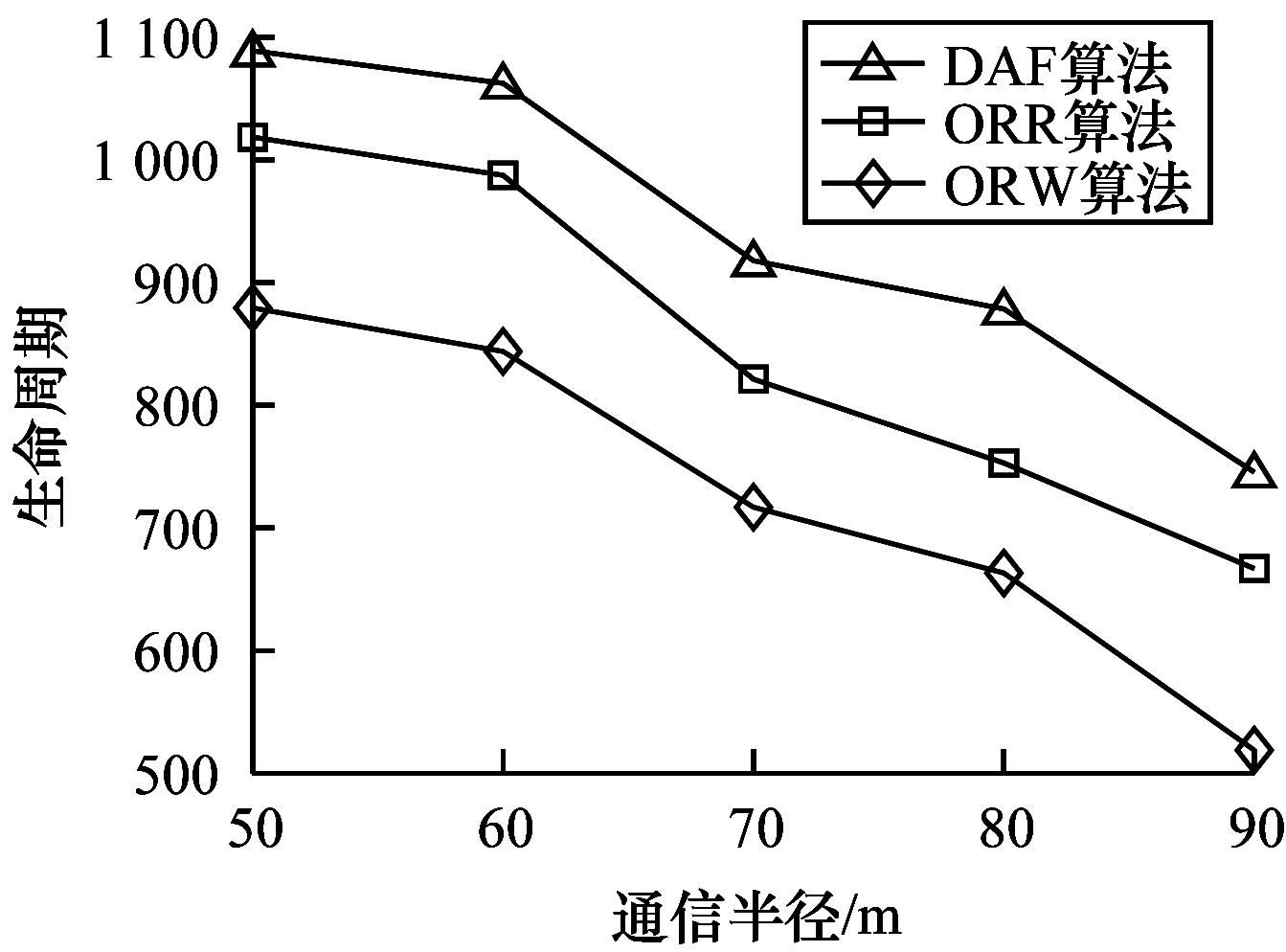
| 图 11 生命周期随通信半径的变化情况 Fig. 11 Life cycle changes with communication radius | |
|
Download:
|
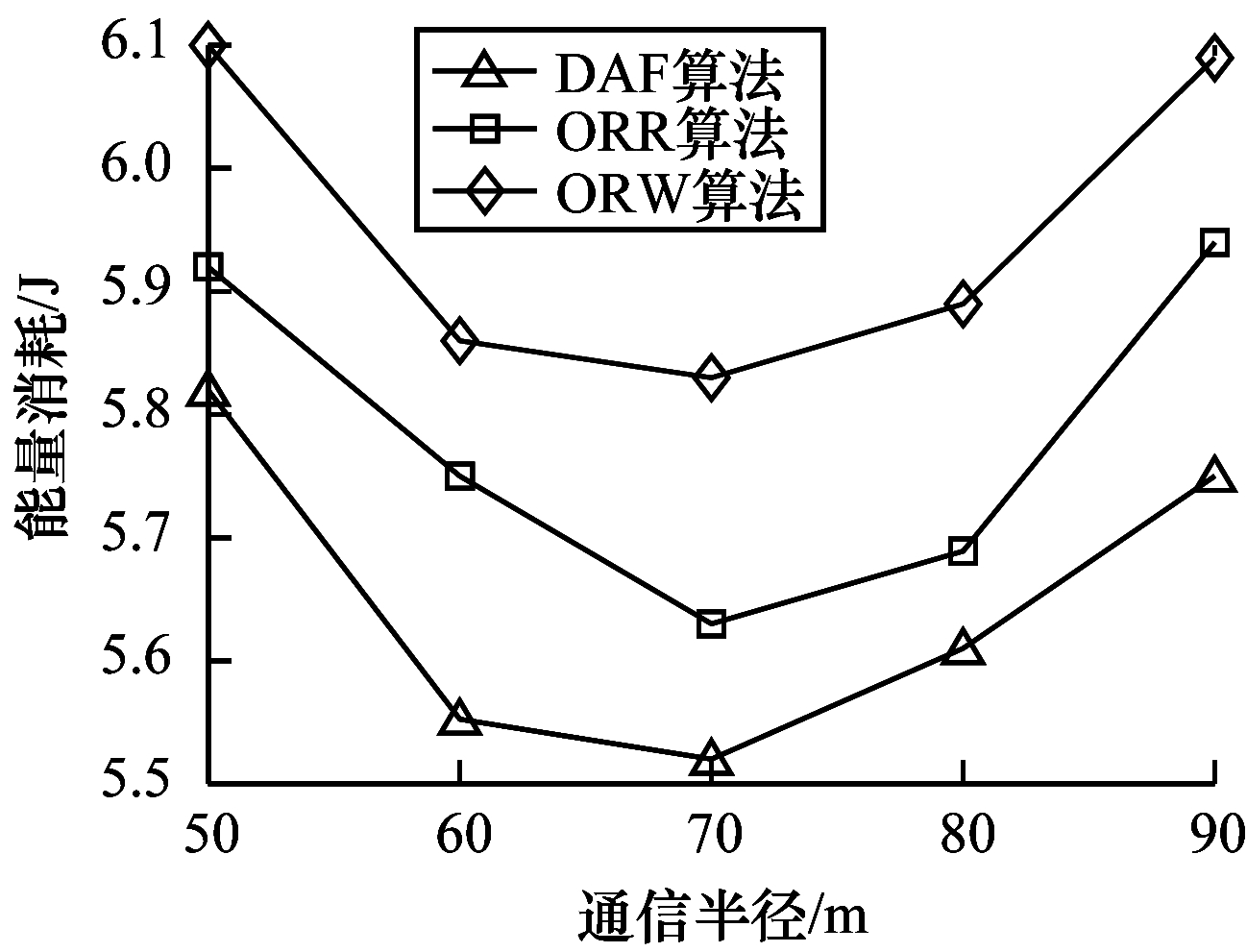
| 图 12 能量消耗随通信半径的变化情况 Fig. 12 Energy consumption changes with communication radius | |
|
Download:
|
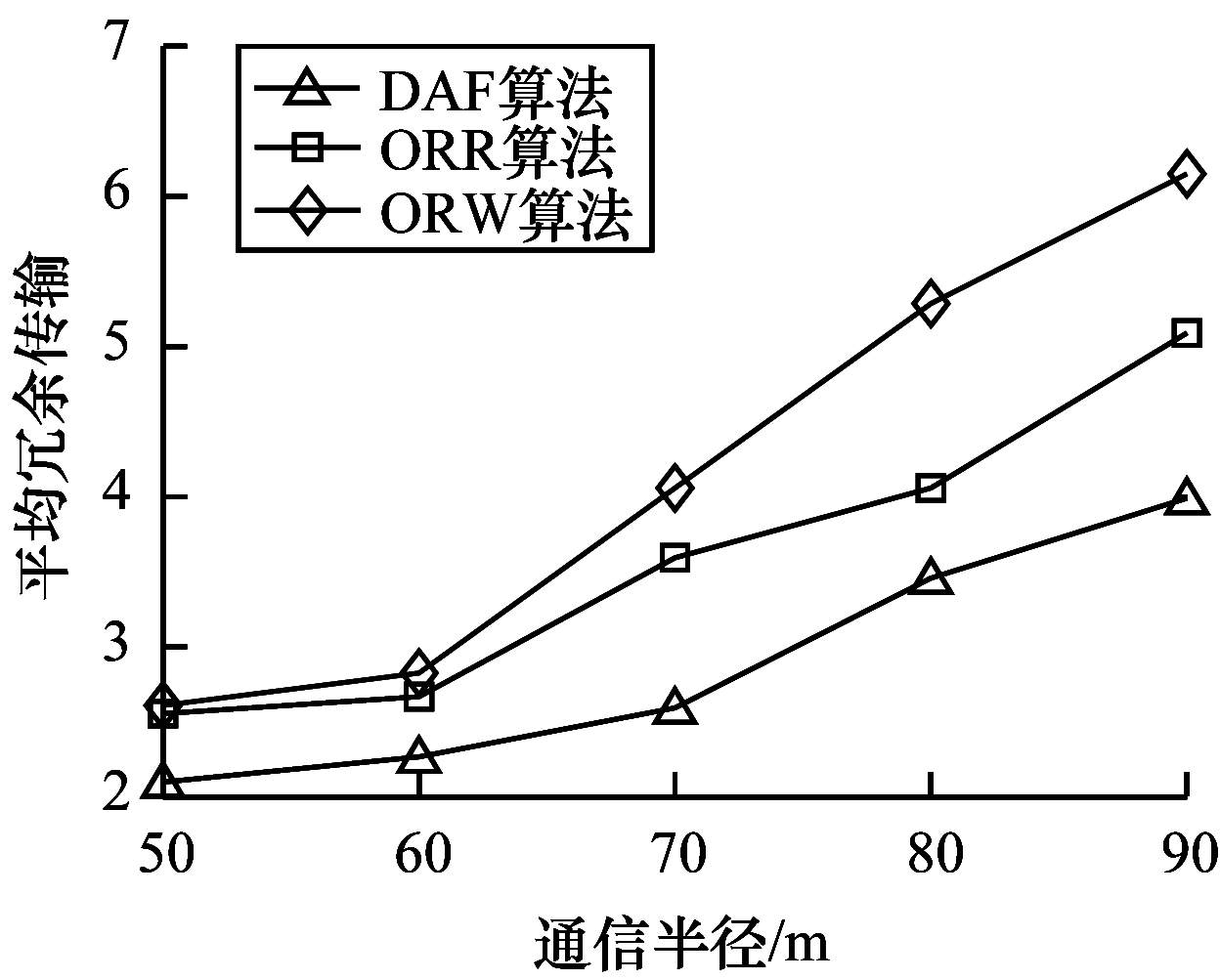
| 图 13 平均冗余传输随通信半径的变化情况 Fig. 13 Average redundant transmission changes with communication radius | |
由图 11可知,网络生命周期随通信半径增加而减少。通信半径增加,导致候选转发节点集中包含更远的候选转发节点,当数据包通过这些较远的节点进行转发时,单跳数据包能耗增加,因此,生命周期呈下降趋势。DAF通过距离准则评估邻居节点,从而在一定程度上避免了距离较远的邻居节点被选择加入候选转发节点集,因此,其单跳能耗更低,生命周期相对较长。
由图 12可知,能量消耗随通信半径增加而先降低后提高。随着通信半径的增加,数据包的跳数减少,能耗随着跳数的减少而减少,因此,先呈现下降趋势。但是,由于式(9)中的距离阈值,随着通信范围的继续增加,用于发送数据包的能耗大幅增加,使得能耗呈现上升趋势。DAF考虑距离标准,在一定程度上控制了数据包的单跳能耗,因此,其性能表现更佳。
由图 13可知,平均冗余传输随通信半径的增加而增加。通信半径的增加直接导致节点的候选转发节点集增加,因此,在发送数据包的过程中产生了更多的冗余数据包。DAF动态选择候选转发节点集,使得其性能优于ORW和ORR。
5 结束语在基于异步醒睡机制的WSN中,传感器节点通常会选择多个节点作为候选转发节点,任何一个醒来的候选转发节点均可进行数据路由。因此,候选节点的选择对网络性能有较大影响,动态路由算法可以很好地适应WSN中网络节点信息或拓扑结构实时变化的特性。本文提出一种动态评估邻居节点的路由算法DAF,在网络运行中根据节点信息并使用FIS动态构建AHP中的成对比较矩阵,从而选择出更合理的候选转发节点集。实验结果表明,与ORW和ORR算法相比,该算法能够有效提高网络生命周期,减少能量消耗和冗余数据包。下一步考虑在硬件上真实部署传感器网络,并在能量以及计算能力均不受限的WSN中进行路由算法设计。
| [1] |
BENSALEH M S, SAIDA R, KACEM Y H, et al. Wireless sensor network design methodologies: a survey[J]. Journal of Sensors, 2020(1): 1-13. |
| [2] |
DINH T, KIM Y, GU T, et al. An adaptive low-power listening protocol for wireless sensor networks in noisy environments[J]. IEEE Systems Journal, 2018, 12(3): 2162-2173. DOI:10.1109/JSYST.2017.2720781 |
| [3] |
YADAV R V S M N. Performance analysis of optimized medium access control for wireless sensor network[J]. IEEE Sensors Journal, 2010, 10(12): 1863-1868. DOI:10.1109/JSEN.2010.2049838 |
| [4] |
BUETTNER M, YEE G V, ANDERSON E, et al. X-MAC: a short preamble MAC protocol for duty-cycled wireless sensor networks[C]//Proceedings of the 4th International Conference on Embedded Networked Sensor Systems. Washington D. C., USA: IEEE Press, 2006: 307-320.
|
| [5] |
MOSS D, LEVIS P. BoX-MACs: exploiting physical and link layer boundaries in low-power networking[EB/OL]. [2021-02-05]. http://coronet2010.stanford.edu/pubs/sing-08-00.pdf.
|
| [6] |
GHADIMI E, LANDSIEDEL O, SOLDATI P, et al. Opportunistic routing in low duty-cycle wireless sensor networks[J]. ACM Transactions on Sensor Networks, 2014, 10(4): 1-39. |
| [7] |
SO J, BYUN H. Load-balanced opportunistic routing for duty-cycled wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2016, 16(7): 1940-1955. |
| [8] |
ARORA S, SINGH S. Node localization in wireless sensor networks using butterfly optimization algorithm[J]. Arabian Journal for Science and Engineering, 2017, 42(8): 3325-3335. DOI:10.1007/s13369-017-2471-9 |
| [9] |
EU Z A, TAN H P. Adaptive opportunistic routing protocol for energy harvesting wireless sensor networks[C]//Proceedings of 2012 IEEE International Conference on Communications. Washington D. C., USA: IEEE Press, 2012: 318-322.
|
| [10] |
BEHESHTIHA S S, TAN H P, SABAEI M. Opportunistic routing with adaptive harvesting-aware duty cycling in energy harvesting WSN[C]//Proceedings of the 15th International Symposium on Wireless Personal Multimedia Communications. Washington D. C., USA: IEEE Press, 2012: 90-94.
|
| [11] |
HAWBANI A, WANG X, ZHAO L, et al. Novel architecture and heuristic algorithms for software-defined wireless sensor networks[J]. IEEE/ACM Transactions on Networking, 2020, 28(6): 2809-2822. DOI:10.1109/TNET.2020.3020984 |
| [12] |
LIU P, WANG X, HAWBANI A, et al. FRCA: a novel flexible routing computing approach for wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2019, 19(11): 2623-2639. |
| [13] |
LEAL J E. AHP-express: a simplified version of the analytical hierarchy process method[J]. MethodsX, 2020, 7: 100748. DOI:10.1016/j.mex.2019.11.021 |
| [14] |
VILELA M, OLUYEMI G F, PETROVSKI A. Sensitivity analysis applied to fuzzy inference on the value of information in the oil and gas industry[J]. International Journal of Applied Decision Sciences, 2020, 13(3): 344-362. DOI:10.1504/IJADS.2020.108484 |
| [15] |
REN Y, ZHANG C, ZHAO F, et al. An MCDM-based multiobjective general variable neighborhood search approach for disassembly line balancing problem[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2018, 50(10): 3770-3783. |
| [16] |
KOSHELEVA O, KREINOVICH V. Why Triangular membership functions are often efficient in F-transform applications: relation to probabilistic and interval uncertainty and to Haar wavelets[C]//Proceedings of International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems. Berlin, Germany: Springer, 2018: 127-138.
|
| [17] |
MUDIA H. Comparative study of mamdani-type and sugeno-type fuzzy inference systems for coupled water tank[J]. Indonesian Journal of Artificial Intelligence and Data Mining, 2020, 3(1): 42-49. DOI:10.24014/ijaidm.v3i1.9309 |
| [18] |
NAIMI M, TAHAYORI H, SADEGHIAN A. A fast and accurate method for calculating the center of gravity of polygonal interval type-2 fuzzy sets[J]. IEEE Transactions on Fuzzy Systems, 2020, 29(6): 1472-1483. |
| [19] |
HAWBANI A, WANG X, ZHAO L, et al. Novel architecture and heuristic algorithms for software-defined wireless sensor networks[J]. IEEE/ACM Transactions on Networking, 2020, 28(6): 2809-2822. DOI:10.1109/TNET.2020.3020984 |
| [20] |
朱莉, 顾能华, 姚英彪, 等. 基于RSSI的WSN二维对数搜索定位算法[J]. 计算机工程, 2014, 40(4): 87-90, 95. ZHU L, GU N H, YAO Y B, et al. RSSI-based two-dimensional logarithmic search localization algorithm for WSN[J]. Computer Engineering, 2014, 40(4): 87-90, 95. (in Chinese) |
| [21] |
SANTI P. Topology control in wireless ad hoc and sensor networks[J]. ACM Computing Surveys, 2005, 37(2): 164-194. DOI:10.1145/1089733.1089736 |
| [22] |
HEINZELMAN W R, CHANDRAKASAN A, BALAKRISHNAN H. Energy-efficient communication protocol for wireless microsensor networks[C]//Proceedings of the 33rd Annual Hawaii International Conference on System Sciences. Washington D. C., USA: IEEE Press, 2000: 102-123.
|
 2022, Vol. 48
2022, Vol. 48
