开放科学(资源服务)标志码(OSID): 
近年来,卫星网络系统凭借其有效的全球无线覆盖能力和优秀的可扩展性受到广泛关注,卫星通信系统已经成为现代通信系统最重要的组成部分之一[1]。相较地球同步轨道(Geostationary Earth Orbit,GEO)卫星和中轨道(Medium Earth Orbit,MEO)卫星通信系统,拥有较低轨道高度的低轨(Low Earth Orbit,LEO)卫星网络具有星地链路时延低、传播损耗小等特点,但是,为了维持较低的轨道高度,其覆盖范围在地球表面上会快速变化,根据“铱星”通信系统,一颗卫星只能提供10 min左右的服务时间,而一个波束只能提供1~2 min的服务时间[2]。为了确保实时通信,终端需在LEO卫星或波束间频繁切换,这不仅增加了系统信令开销,也会提高终端的掉话率与呼叫中止率[3]。
目前,已经有许多学者对LEO卫星网络切换算法展开研究。从单目标决策属性出发,文献[4]在切换发生时选择“最近”的卫星进行接入,以减少传播延迟。文献[5-6]基于可视卫星的服务时长,选择具有最长服务时间的卫星,从而最小化切换次数。为实现不同的切换性能,文献[7-8]提出多属性综合加权的切换策略,它们综合考虑网络中的负载、接收信号强度、剩余服务时间等信息。文献[9]则利用熵权法将影响用户接入卫星的几个因素进行加权处理,从而将多目标优化问题转化为单目标优化问题。同时,研究人员还提出基于方案模型的判决决策,如文献[10-11]利用图论将切换视为在有向图中寻找最短路径的过程,根据不同的切换准则设置权重,以支持多种卫星的切换。文献[12-13]在满足负载等约束条件下,利用Q学习算法做出近似最优决策,以有效增加系统收益。文献[14]利用卷积神经网络提取不同用户间最佳决策的内在规律,减少了切换发生频率。文献[15]基于卫星星历提出一种预设卫星链的无缝切换方案,其能提供不间断的卫星通信服务。文献[16]提出以用户为中心的切换方案,通过在多个卫星中同时缓存用户数据来提高链路接入质量。文献[17]将博弈论引入LEO卫星切换决策中,联合考虑用户端收益以及卫星网络负载,当系统达到纳什均衡时其终端可以获取最大收益。
但是,目前针对LEO卫星通信系统的切换策略大多只考虑少量用户或均匀用户发生切换的场景。随着LEO卫星网络的快速发展,服务用户数量将大幅增加,其切换决策的成本也随之增大[18],尤其对于热点区域的地面用户群组,当用户聚集在一定范围内时,会出现批量用户并发发起切换的情况,导致网络中存在大量的请求报文并形成网络拥塞,极大地降低了网络性能。此外,诸多研究以单波束作为研究对象,但是在实践中以多波束卫星作为研究对象更具有工程意义。
在无线网络中,当同时切换的用户数较多时,先对用户进行分组可有效降低切换成本[19]。为此,本文提出一种基于用户分群的LEO卫星系统切换管理策略,将具有相似切换行为的用户分为一组,减少处理过程中的重复操作,以降低系统信令开销和平均切换时延同时提高切换成功率。
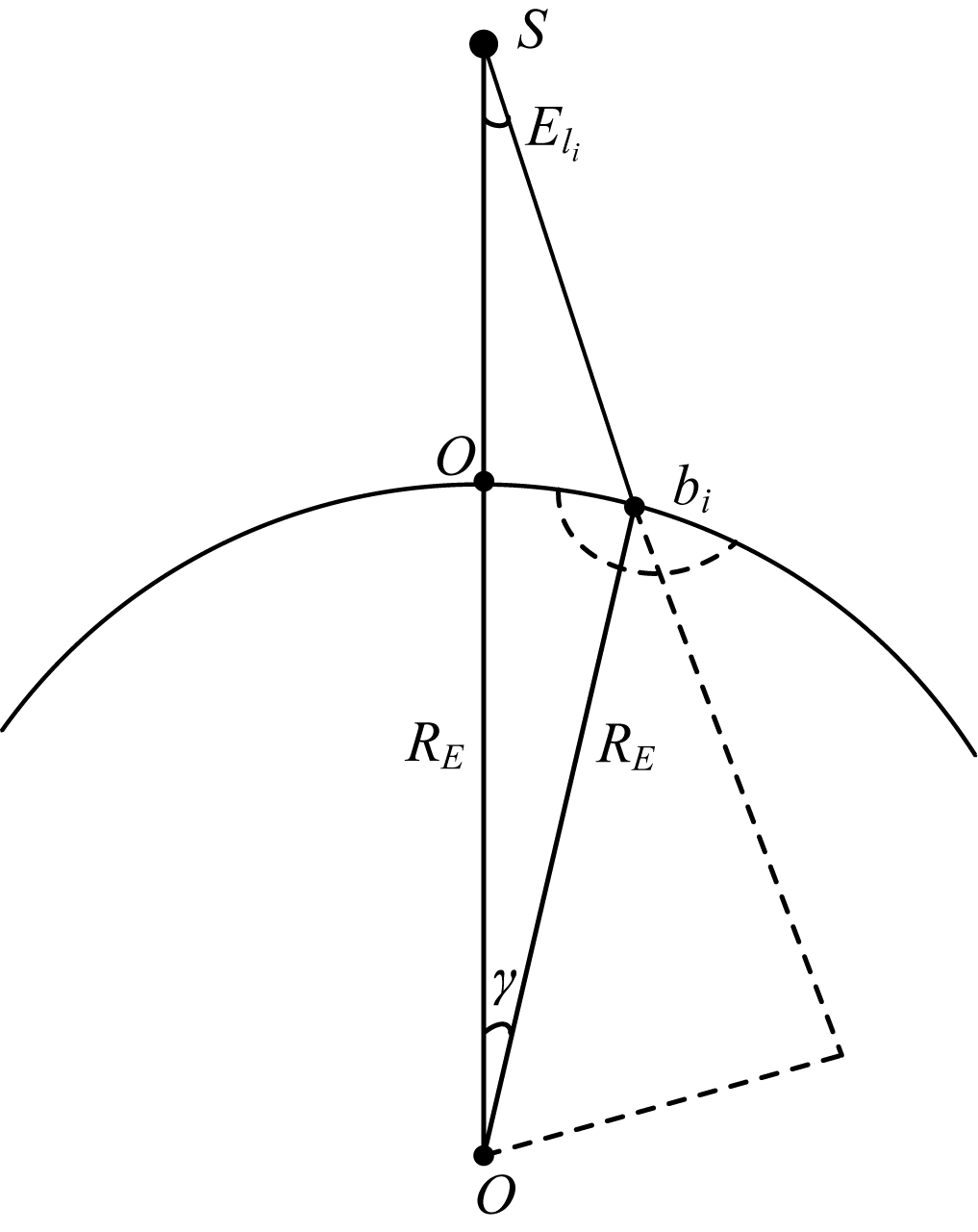
1 LEO多波束卫星星座场景本文以多波束LEO卫星为研究对象,如图 1所示,
| $ \mathrm{s}\mathrm{i}\mathrm{n}({E}_{{l}_{i}}+\gamma )=\frac{({R}_{E}+h)\mathrm{s}\mathrm{i}\mathrm{n}{E}_{{l}_{i}}}{{R}_{E}} $ | (1) |
则波束中心点到星下点的距离为:
| $ {o}_{{b}_{i}}={R}_{E}\gamma ={R}_{E}\left(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\frac{({R}_{E}+h)\mathrm{s}\mathrm{i}\mathrm{n}{E}_{{l}_{i}}}{{R}_{E}}-{E}_{{l}_{i}}\right) $ | (2) |
|
Download:
|
| 图 1 波束俯仰角与地心角的关系 Fig. 1 Relationship between beam pitch angle and geocentric angle | |
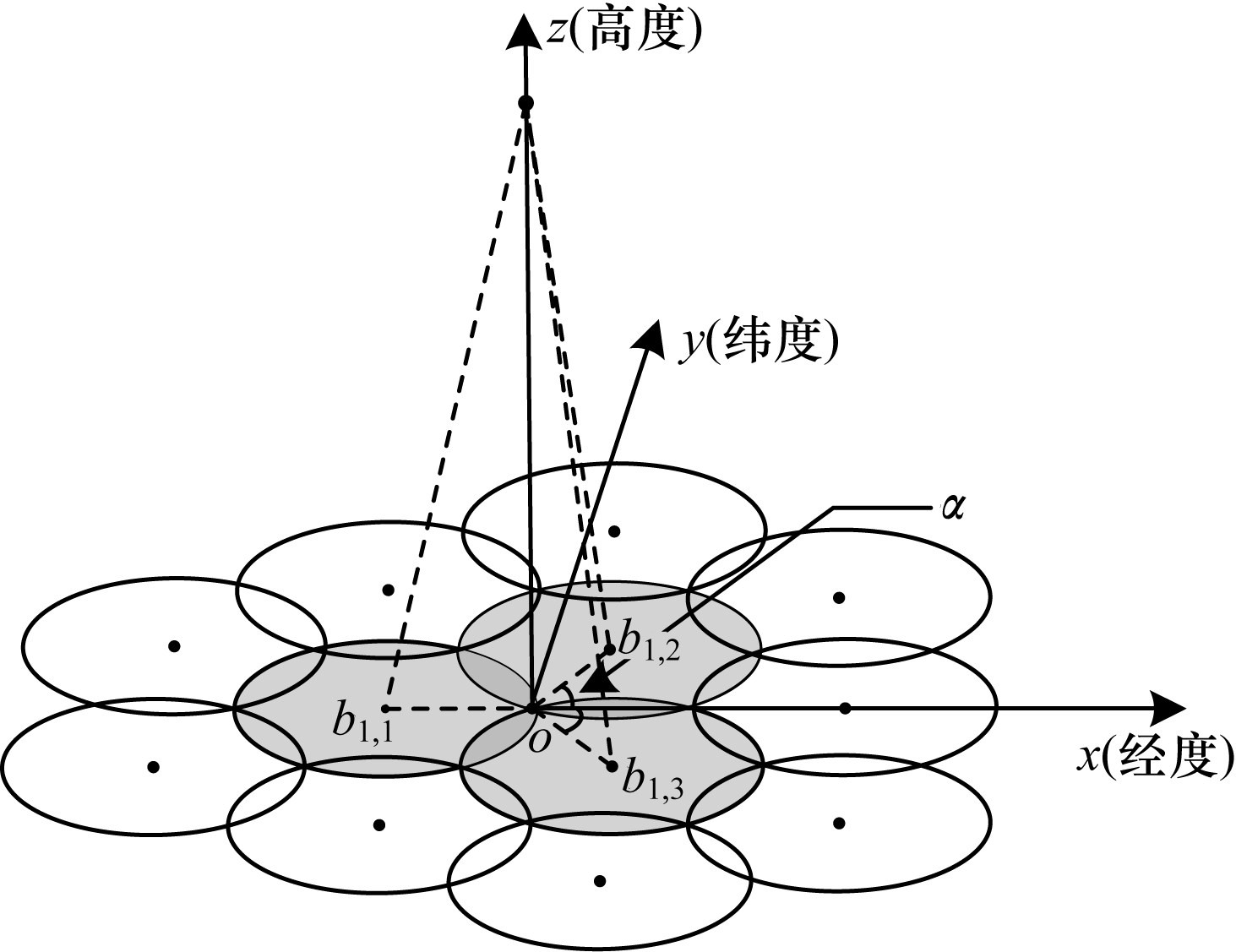
图 2所示为卫星多波束天线对地覆盖模型,在大地坐标系中,假设卫星位于
|
Download:
|
| 图 2 卫星多波束天线对地覆盖模型 Fig. 2 Ground coverage model of satellitemulti-beam antenna | |
1)先找到与星下点经度相同的中心波束,其余波束沿着中心波束绕星下点均匀分布,计算各波束中心点到星下点的距离
2)将上述距离投影到
3)根据星下点坐标
为了选择切换行为相似的用户,本文将切换触发时刻、最佳波束小区2个因素作为分群决策的属性。依据终端收到服务波束的参考信号接收功率(Reference Signal Received Power,RSRP)来判断是否需要进行切换。因此,需要预测接收信号强度来估计切换触发时刻,还需要在切换触发时刻下得到终端的邻区覆盖情况,根据邻区的可视时长进行排序,以得到最佳波束小区。
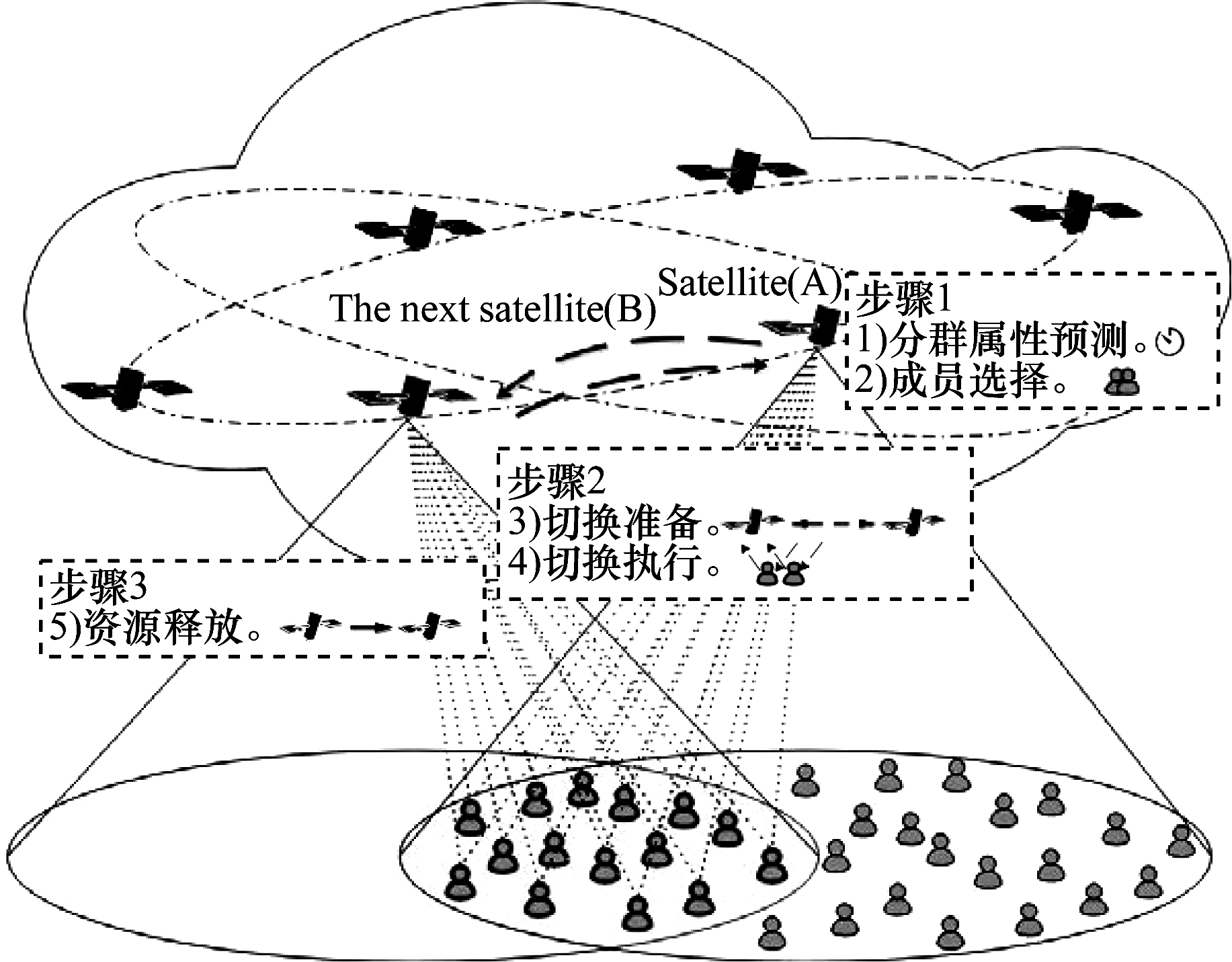
如图 3所示,基于用户分群技术的切换策略主要包括分群处理、群组切换和资源释放3个部分。当群首测量结果满足条件时触发切换流程,群首进入切换准备和执行阶段,当所有成员完成切换后,释放资源同时完成切换。为方便描述,用
|
Download:
|
| 图 3 基于用户分群的切换策略流程 Fig. 3 Handover strategy procedure based on user grouping | |
当信号强度低于分群触发阈值
用户终端在完成随机接入后,会周期性地接收并测量当前服务波束的RSRP,以用户终端收到服务波束的RSRP低于阈值的时刻作为切换触发时刻。定义
| $ {y}_{i}={\beta }_{0}+{\beta }_{1}{x}_{i}+{\beta }_{2}{x}_{i}^{2}, i=\mathrm{0, 1}, \cdots , n $ | (3) |
令
| $ \mathit{\boldsymbol{Y}}=\left(\begin{array}{c}{y}_{1}\\ {y}_{2}\\ {y}_{3}\end{array}\right)\text{,}\mathit{\boldsymbol{X}}=\left(\begin{array}{ccc}{x}_{10}& {x}_{11}& {x}_{12}\\ {x}_{20}& {x}_{21}& {x}_{22}\\ ⋮& ⋮& ⋮\\ {x}_{n0}& {x}_{n1}& {x}_{n2}\end{array}\right)\text{,}\mathit{\boldsymbol{\beta}}=\left(\begin{array}{c}{\beta }_{0}\\ {\beta }_{1}\\ {\beta }_{2}\end{array}\right)\text{,}\mathit{\boldsymbol{\epsilon }}=\left(\begin{array}{c}{\epsilon }_{0}\\ {\epsilon }_{1}\\ {\epsilon }_{2}\end{array}\right) $ | (4) |
其中:
采用广泛使用的最小二乘法估计拟合系数,使每个点到拟合线的铅直距离的平方和达到最小,即最小化误差平方和,误差平方和函数为:
| $ S\left(\boldsymbol{\beta}\right)={\boldsymbol{\epsilon }}^{\mathrm{T}}\boldsymbol{\epsilon }={(\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta })}^{\mathrm{T}}(\boldsymbol{Y}-\boldsymbol{X}\boldsymbol{\beta }) $ | (5) |
当
设切换触发阈值为
| $ {t}_{\mathrm{H}\mathrm{O}}=t+k\mathrm{\Delta }t $ | (6) |
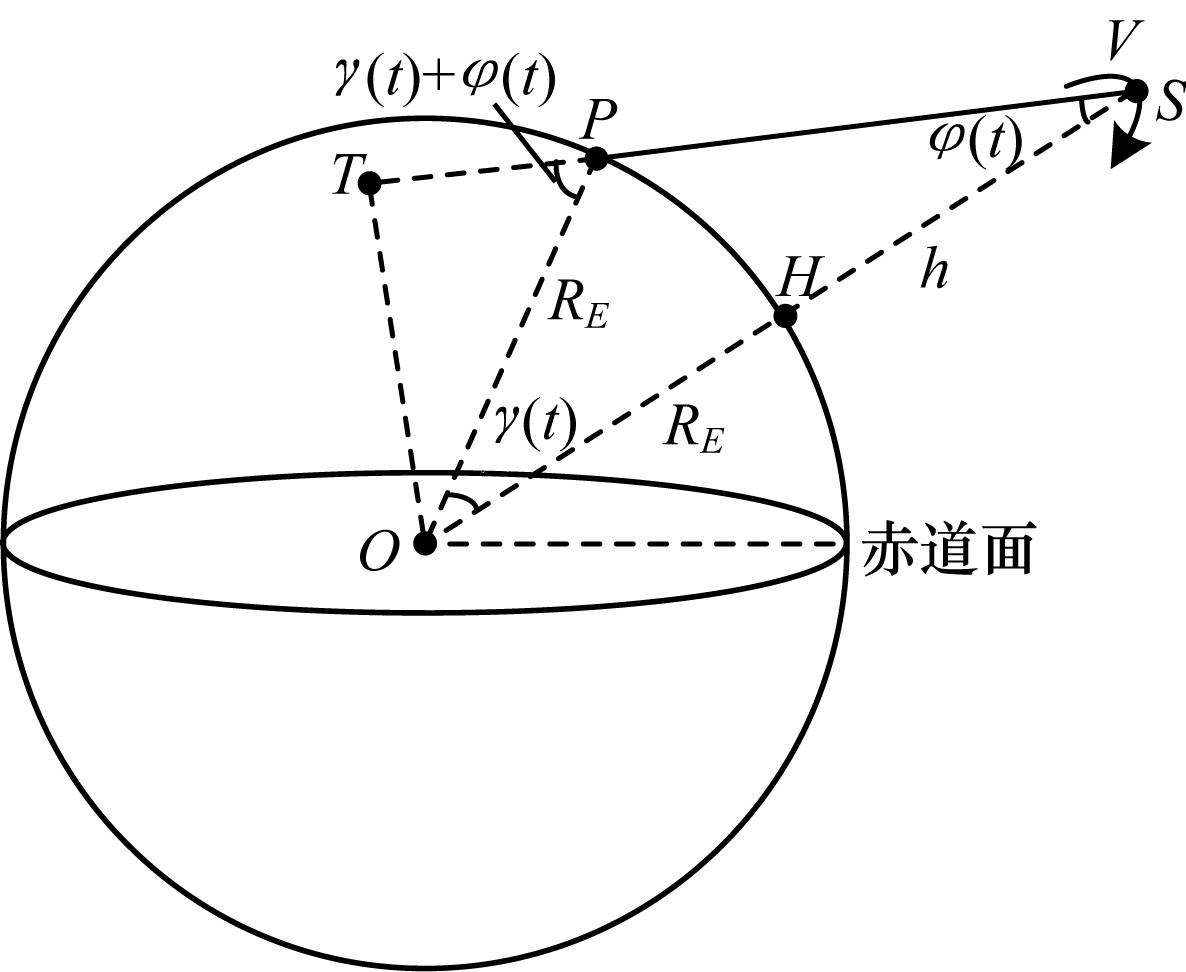
在切换时刻预测后,进一步计算切换触发时刻下终端的卫星覆盖情况,设单星的最大星下半俯仰角为
| $ {r}_{\mathrm{m}\mathrm{a}\mathrm{x}}={R}_{E}\left(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\frac{({R}_{E}+h)\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{R}_{E}}-{\phi }_{\mathrm{m}\mathrm{a}\mathrm{x}}\right) $ | (7) |
|
Download:
|
| 图 4 星下俯仰角与覆盖半径的关系 Fig. 4 Relationship between sub-satellite pitch angle and coverage radius | |
终端根据广播星历信息,得到
| $ {l}_{\mathrm{H}\mathrm{O}}=2{R}_{E}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\sqrt{\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\left(\frac{{s}_{j}-{u}_{j}}{2}\right)+\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\left(\frac{{s}_{w}-{u}_{w}}{2}\right)\mathrm{c}\mathrm{o}\mathrm{s}\,{s}_{j}\mathrm{c}\mathrm{o}\mathrm{s}\,{u}_{j}} $ | (8) |
对于
| $ B=\{{b}_{1}^{1}, {b}_{1}^{2}, \cdots , {b}_{1}^{N}, {b}_{2}^{1}, {b}_{2}^{2}, \cdots , {b}_{2}^{N}, \cdots , {b}_{m}^{1}, {b}_{m}^{2}, \cdots , {b}_{m}^{N}\} $ |
其中:
为了降低用户在通信过程中的掉话率,需要选择能够提供最大服务时长的卫星和波束[21]。本文针对多波束LEO卫星,提出一种波束空间关系模型,通过候选波束与用户的运动方向和速度,用波束的空间关系值来表征波束可视时长的大小关系。
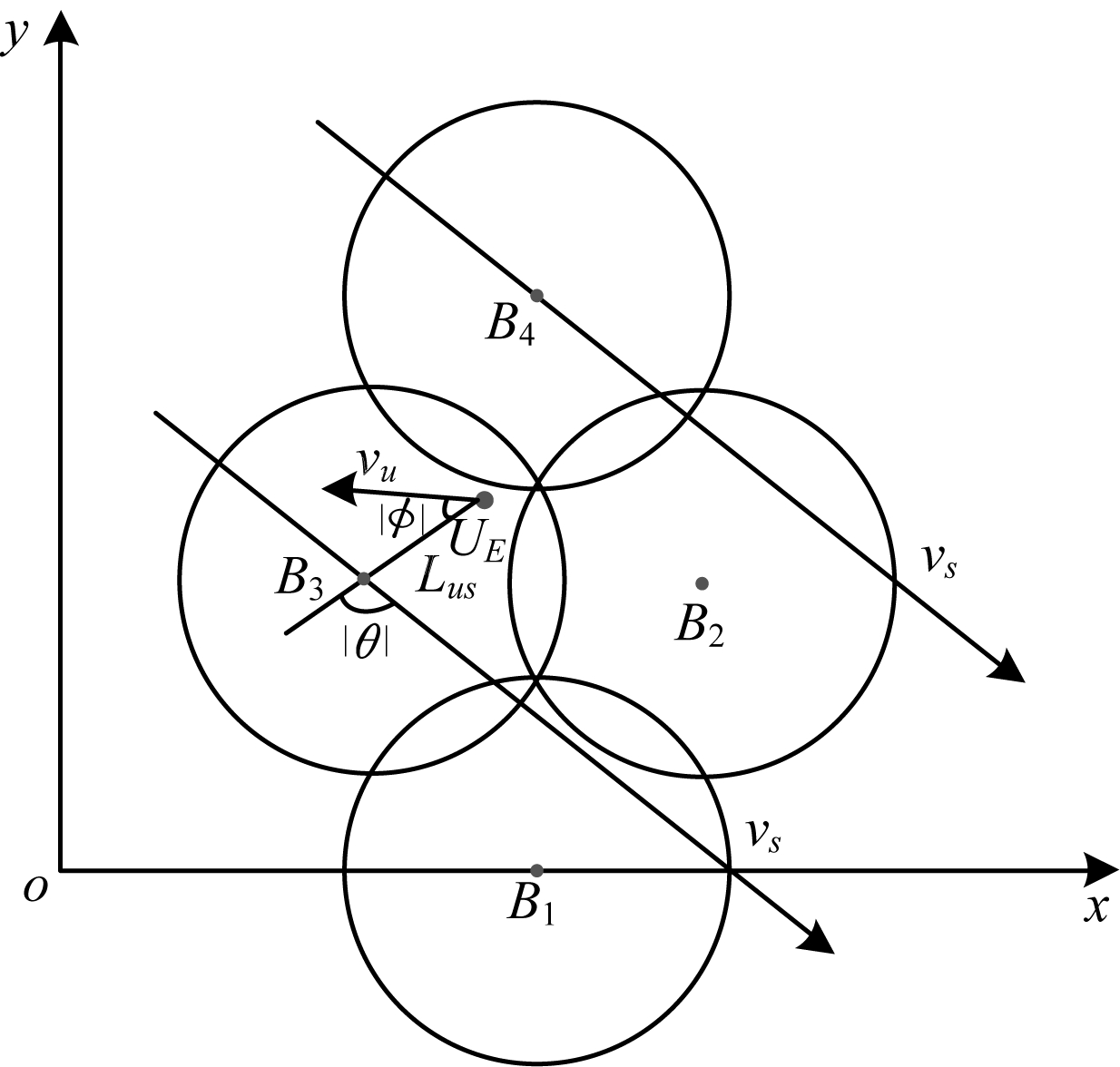
各波束的空间关系如图 5所示,
|
Download:
|
| 图 5 用户与波束的相对运动关系 Fig. 5 Relative motion relationship between the user and beam | |
首先定义相对方位角变化情况
| $ {P}_{a}=2+\frac{{P}_{\theta }+{P}_{\phi }}{2} $ | (9) |
其次定义相对距离变化情况
| $ {P}_{\mathrm{\Delta }D}=2-\frac{{d}_{us}{u}_{us}}{R({u}_{s}+{u}_{u})} $ | (10) |
其中:
通过归一化有效相对距离
| $ {P}_{D}=\left\{\begin{array}{l}1 , {d}_{us}\le R\\ \frac{R-{d}_{us}}{R}, {d}_{us} > R\end{array}\right. $ | (11) |
最后为了对波束空间关系进行全面评估,空间关系值
| $ \begin{array}{l}{P}_{us}={P}_{a}\times {P}_{d}=\left(2+\frac{\left|\theta \right|-\left|\phi \right|}{\mathrm{\pi }}\right)\cdot \\ \left(2-\frac{{d}_{us}({u}_{s}\mathrm{c}\mathrm{o}\mathrm{s}\theta -{u}_{u}\mathrm{c}\mathrm{o}\mathrm{s}\phi )}{R({u}_{s}+{u}_{u})}\right)\end{array} $ | (12) |
用户终端计算邻区候选集内各波束空间关系值
成员选择的目的是挑选出在切换触发时刻下处于切换边缘的一组用户,即同一群组内的成员,它们的切换时刻非常相似。设
为方便叙述,定义
步骤1 在初始状态时,任意用户还未加入任意一个群组,所有的
步骤2 提取出用户信息
步骤3 切换时刻的相似程度可以通过计算两两数据之间的“距离”来衡量。用户
步骤4 计算剩余所有保留用户与群首之间的切换时间差,按差值从小到大划分到该群中,其
步骤5 判断成员集合中所有用户的
步骤6 判断用户信息中
卫星会记录用户的状态信息,表明用户所处的切换状态,并随着切换的进行而不断更新状态信息。用户状态包含的字段如图 6所示,其中:

|
Download:
|
| 图 6 用户状态信息 Fig. 6 User status information | |
群首测量当前服务卫星与邻近卫星的RSRP,以判断是否要向卫星发送切换申请。假设卫星
当卫星
当
在等待一段时间后,
当
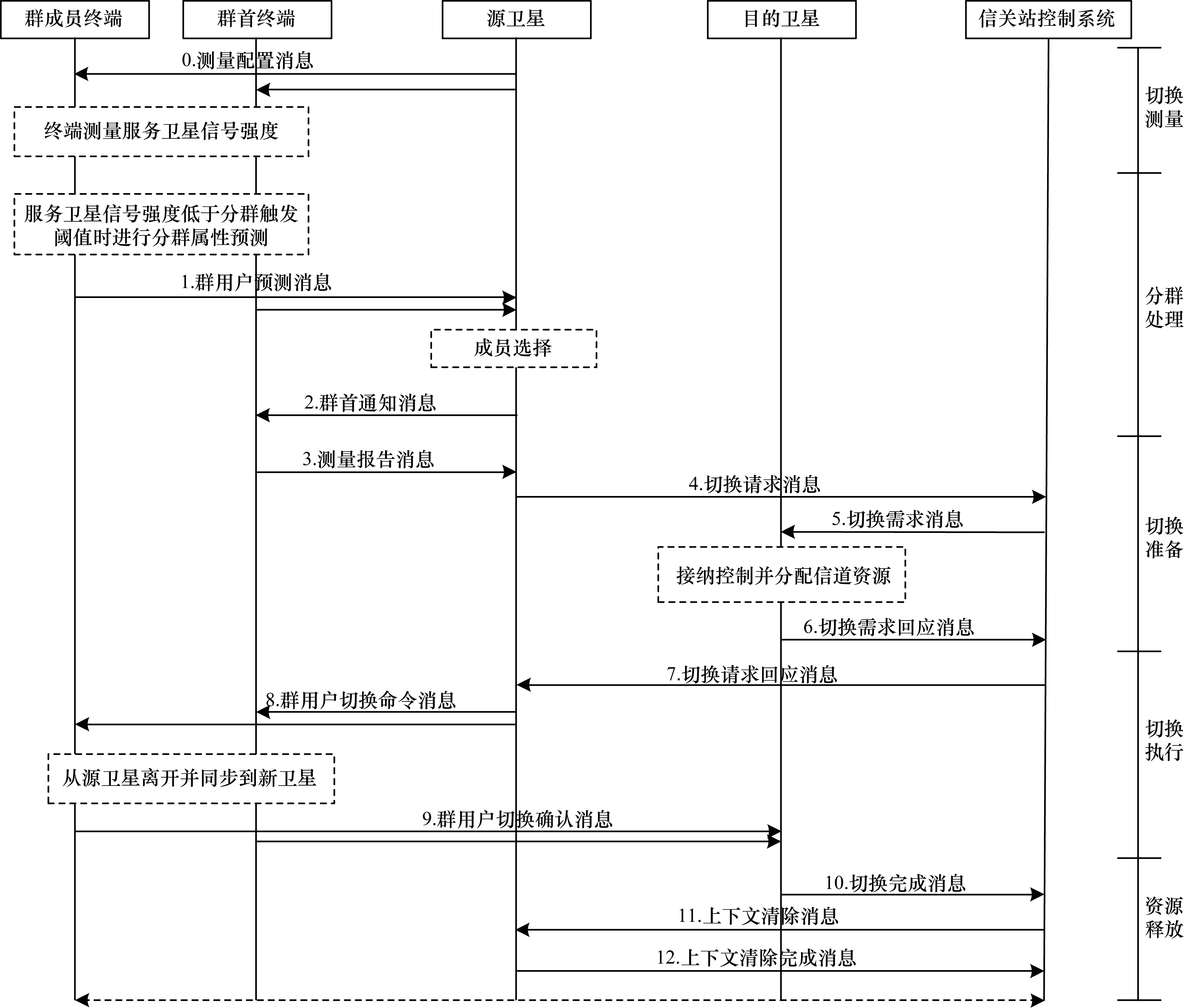
图 7所示为基于用户分群的切换信令交互流程,其中:切换测量阶段对应步骤0;分群处理阶段对应步骤1~步骤2;切换准备阶段对应步骤3~步骤6;切换执行阶段对应步骤7~步骤9;资源释放阶段对应步骤10~步骤12。
|
Download:
|
| 图 7 基于用户分群的切换信令交互流程 Fig. 7 Handover signaling interaction procedure based on user grouping | |
本文在仿真软件OPNET中搭建LEO卫星网络仿真平台,平台参考铱星星座,空间段共有66颗卫星,每颗卫星具备48个点波束,仿真中设置每个波束的信道数为80,地面段设有2个移动交换中心和1个网络控制中心,用户随机分布在一个
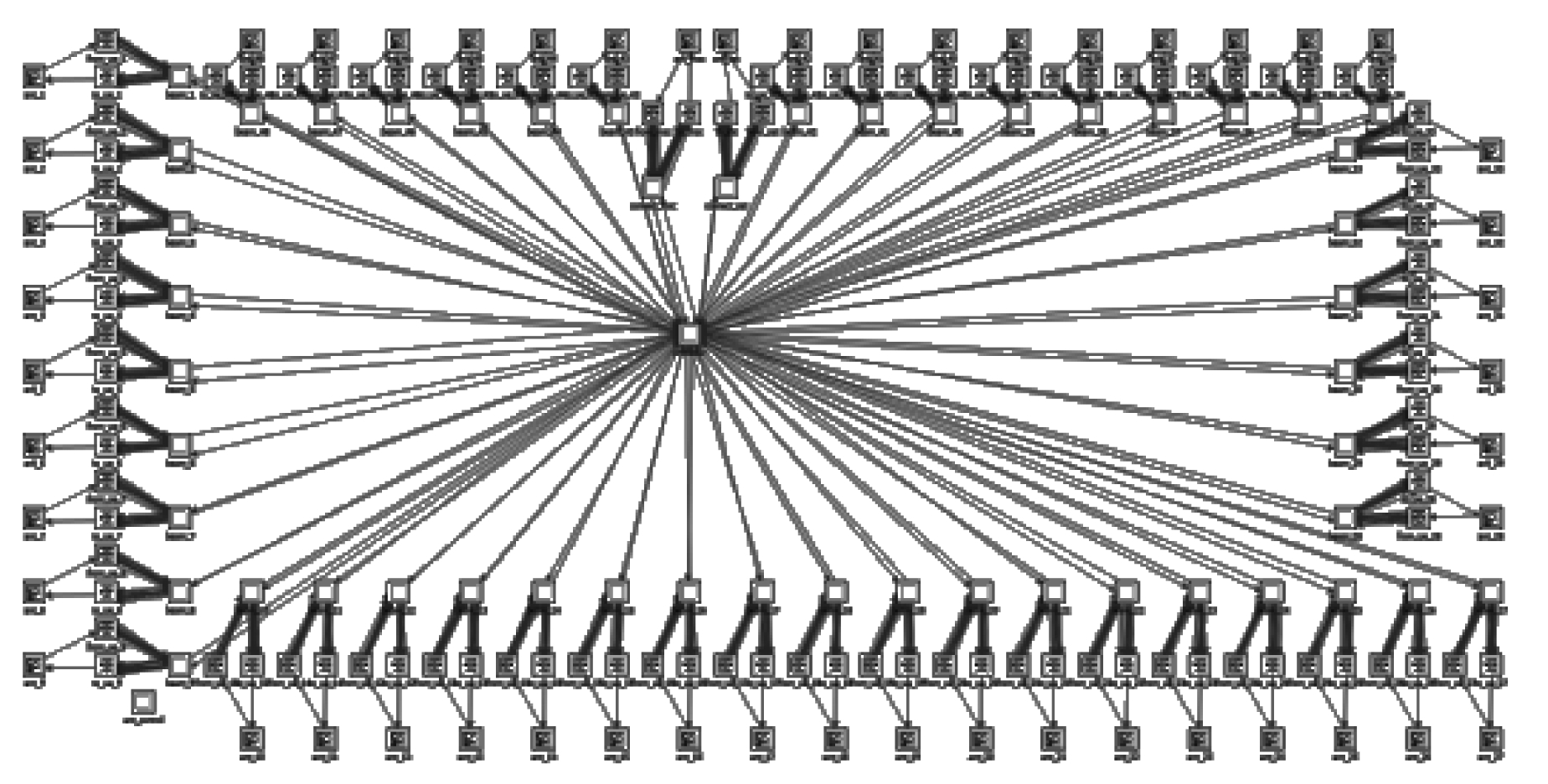
卫星节点模块由多波束模块、星间链路模块、馈电链路模块、中央处理器模块和天线模块组成,如图 8所示。多波束模块仿真多波束天线功能,每个点波束在地面形成一个波束小区,并按照一定的时间间隔向地面广播导频信息;星间链路模块负责信令和数据在星间链路的传递过程;馈电链路模块负责卫星检测信关站广播的导频信息;中央处理器模块负责各种信令处理;天线模块负责加载和动态更新多波束天线的空间指向。
|
Download:
|
| 图 8 卫星节点模型 Fig. 8 Satellite nodes model | |
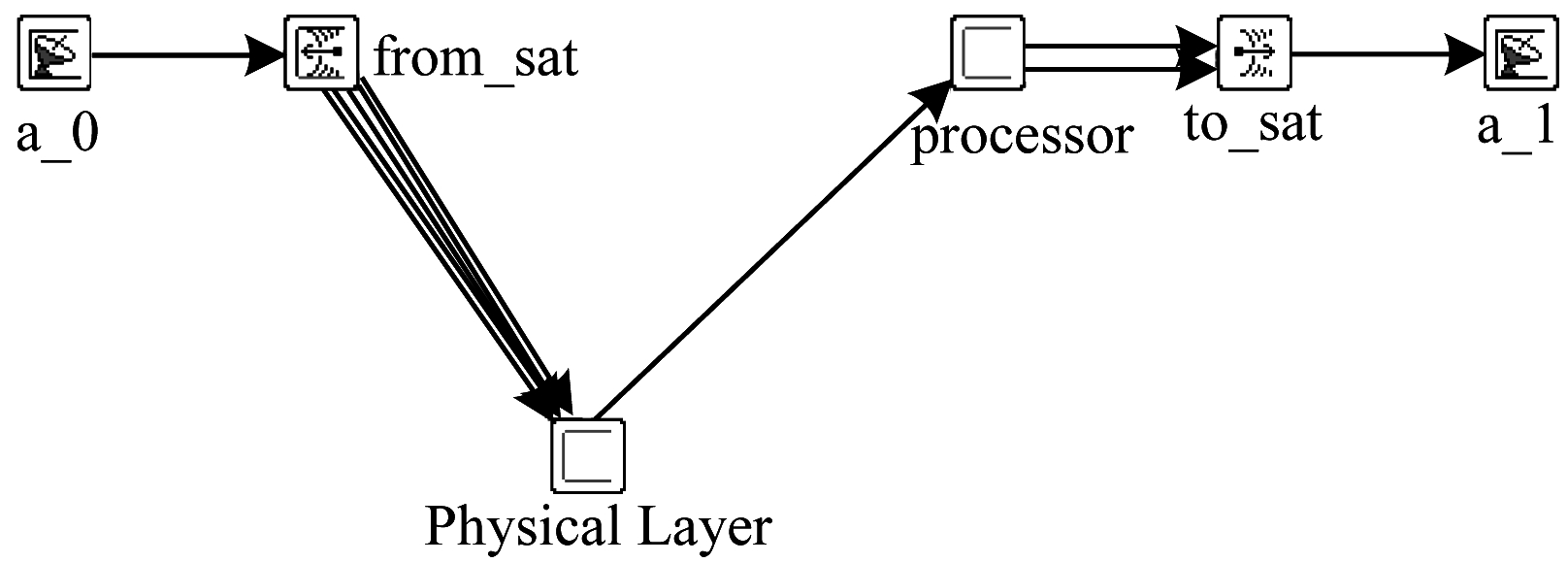
如图 9所示,用户终端由2个部分组成:一部分实现物理层的切换测量功能,将测量结果经过过滤后发送给上层;另一部分实现用户的接入、切换、信令收发等功能。系统参数设置如表 1所示。
|
Download:
|
| 图 9 用户终端节点模型 Fig. 9 User terminal nodes model | |
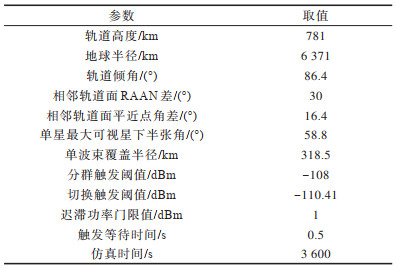
|
下载CSV 表 1 系统仿真参数设置 Table 1 System simulation parameters setting |
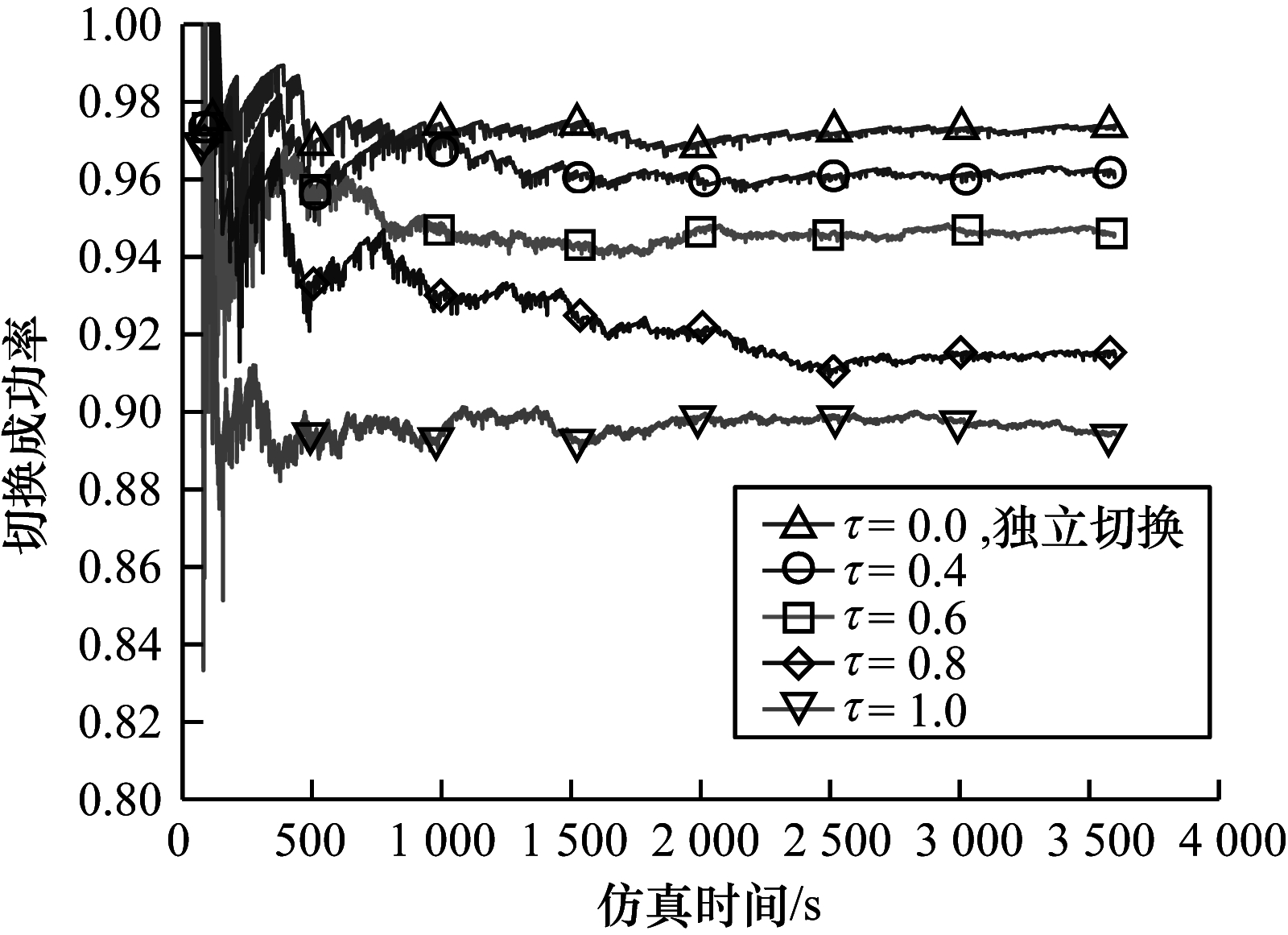
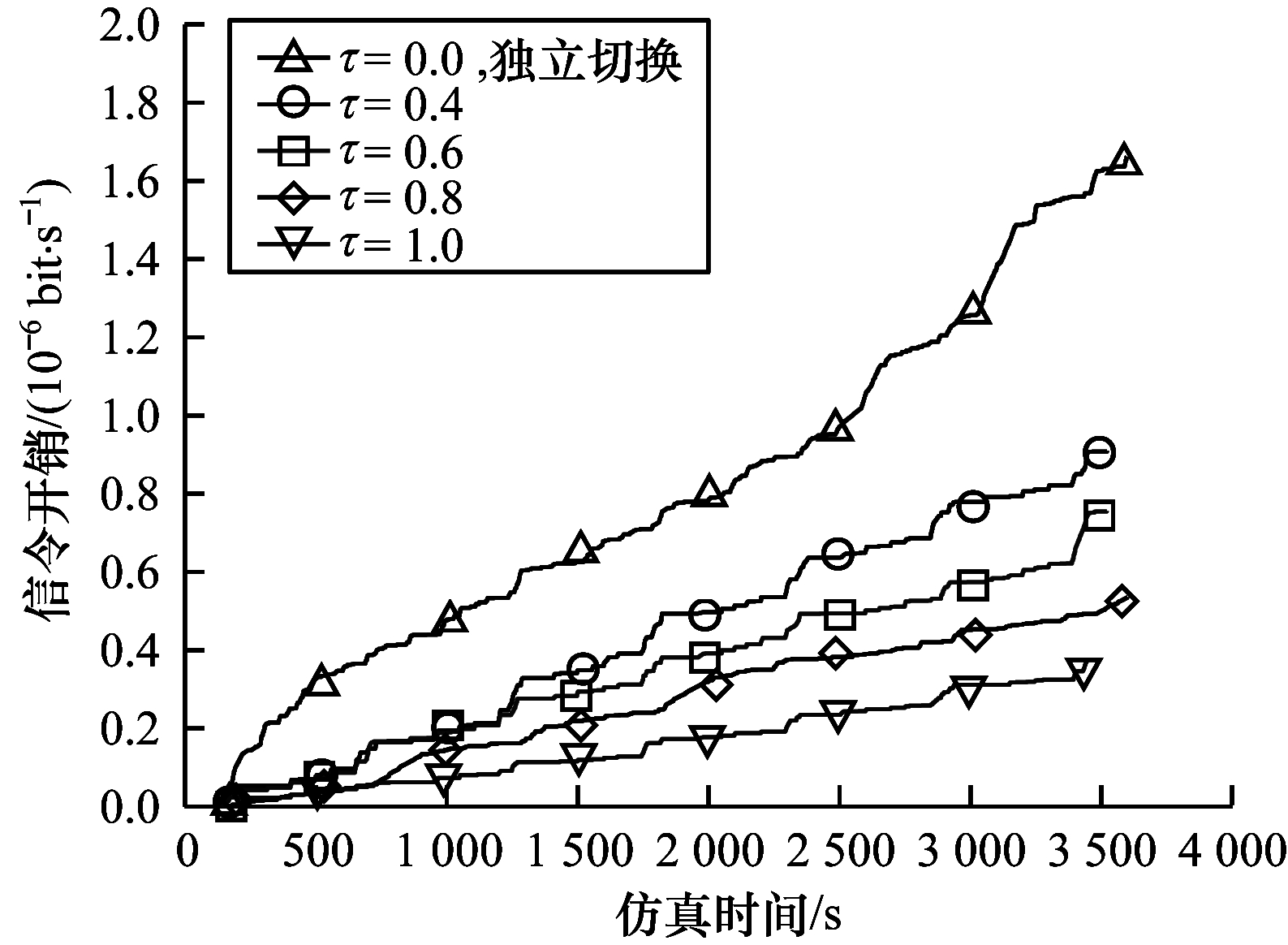
为了评估基于用户分群的切换管理策略的有效性,本文考虑的切换性能参数包括信令开销、切换成功率和切换时延。在切换过程中,需要在不同节点之间进行切换信令消息交互,所产生的开销称为信令开销[22],信令开销是衡量切换方案性能的重要指标,当网络发生频繁切换时,过多的信令开销会降低网络性能。同时,切换成功率越高说明切换策略越有效,切换时延越长说明更多的时间是在等待各种切换信令,不利于用户通信质量的维持。图 10、图 11分别比较在聚合调节参数
|
Download:
|
|
图 10 不同调节参数 |
|
|
Download:
|
|
图 11 不同调节参数 |
|
从图 10可以看出,随着仿真时间的进行,切换成功率刚开始有轻微波动但最终趋于一个稳定值,这表明本文所搭建的LEO卫星网络仿真平台能有效维持网络的稳定性。当
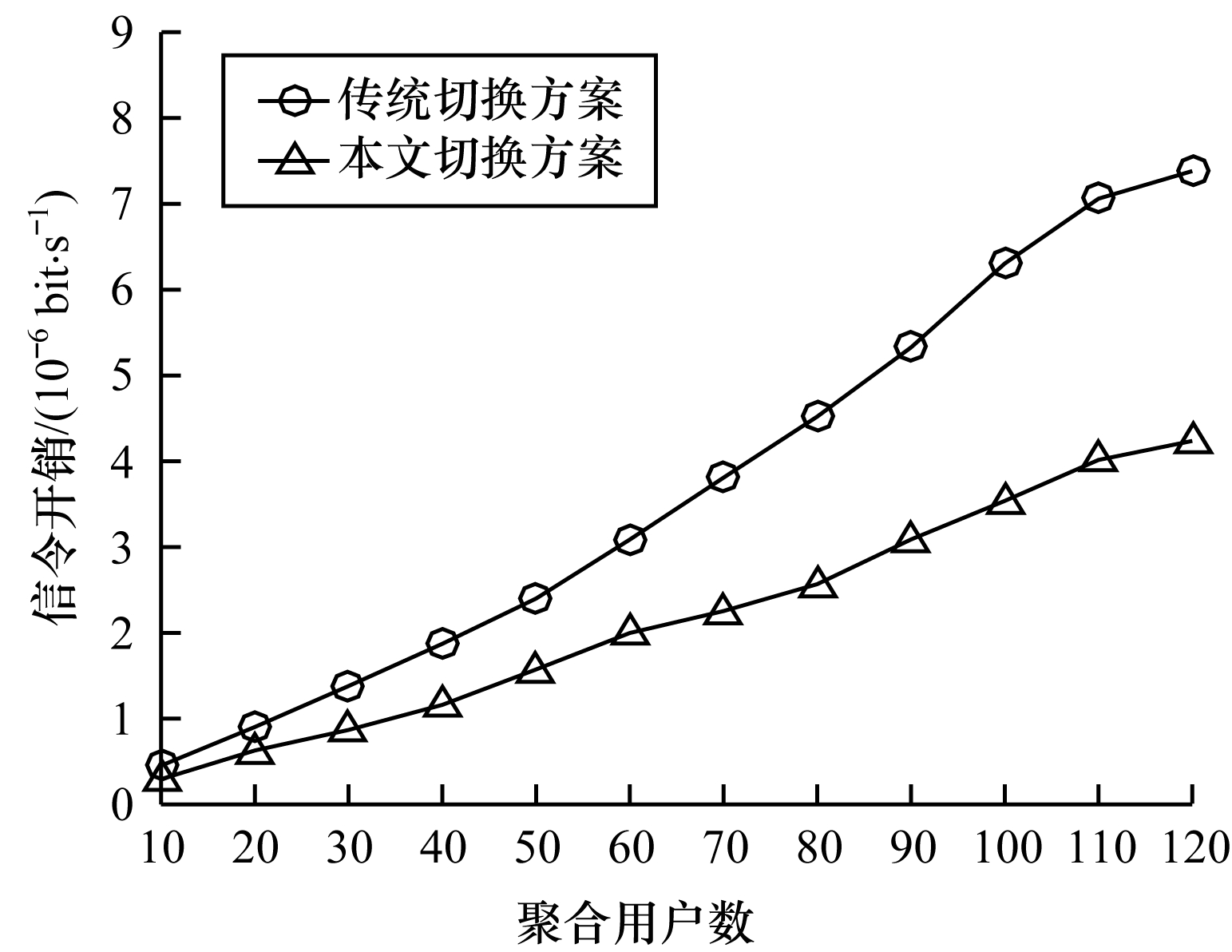
在卫星数量和仿真时间确定、聚合用户数量不同的场景下,对比传统用户独立切换方案和基于用户分群的切换方案,图 12所示为2种方案的系统信令开销对比。从图 12可以看出,随着聚合用户数量的增加,系统信令开销增大,由于本文切换方案将多个具有相似切换行为的用户聚合为一次切换,减少了切换请求发起的次数,降低了切换的成本,使得系统的信令开销小于传统方案,并且随着用户数量的增加,优化效果更加明显。
|
Download:
|
| 图 12 不同聚合用户数量下的信令开销比较 Fig. 12 Comparison of signaling overhead under different number of aggregated users | |
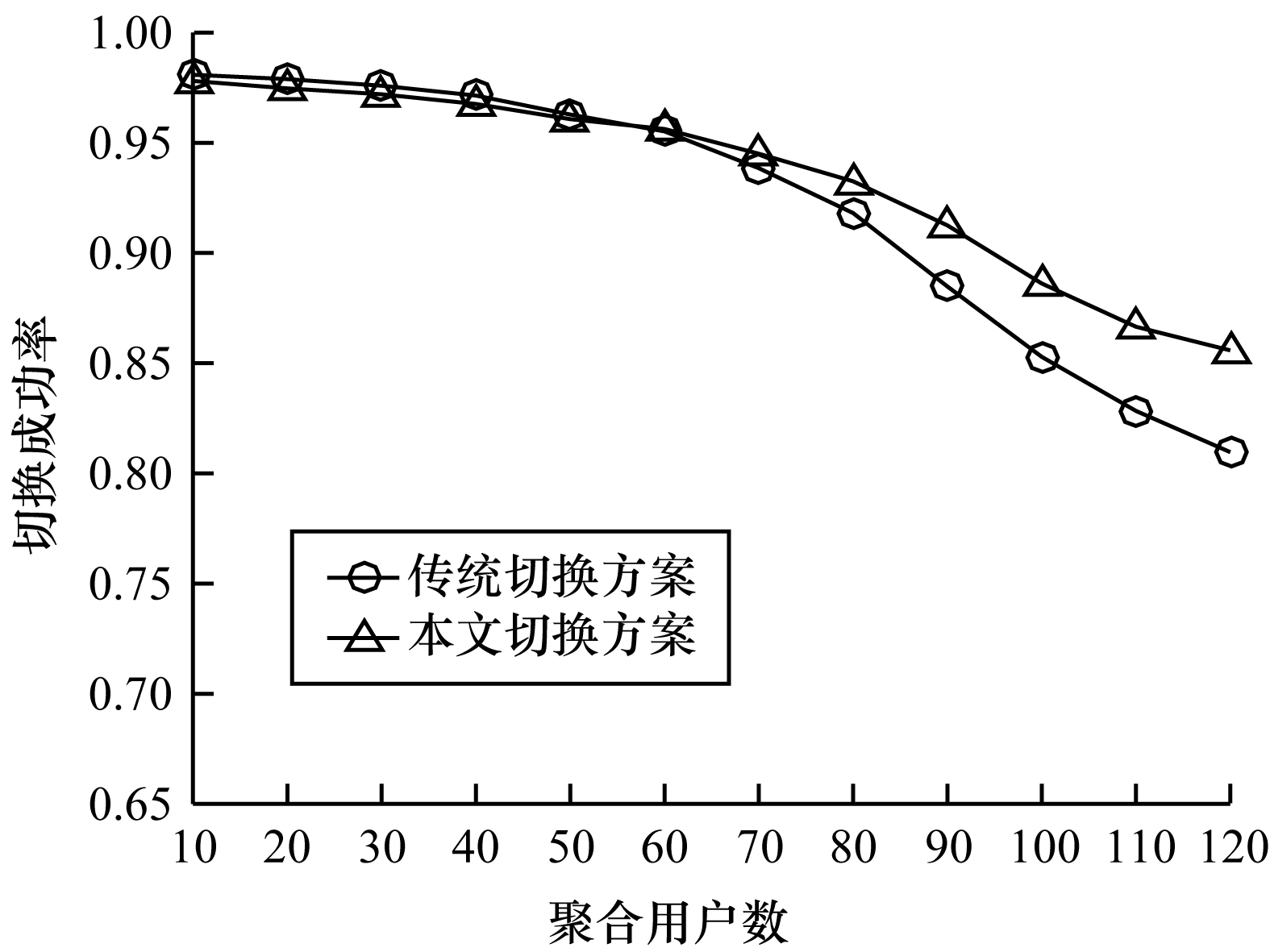
图 13所示为聚合用户数量与切换成功率的关系对比。从图 13可以看出,在用户数较少的情况下,2种方案切换成功率差异不大,这是因为当用户数量较少时,用户聚合程度低,存在独立切换的情况,加上此时信道资源充足,卫星发生拥塞的概率较小,所以在这种情况下2种方案的切换性能表现相似。随着用户数量的增加,卫星更容易发生拥塞,导致切换失败次数增加,使得2种方案的切换成功率都随之下降。但是随着用户数量的增加,本文切换方案的切换成功率逐渐优于传统方案,这是因为用户间的相关性变大,用户聚合程度逐渐变大,群首的切换状态逐渐与群成员相似,另一方面,节省的系统开销变多,能有效减少卫星发生拥塞的情况,从而减少切换失败发生次数,并且在信道资源不足的情况下,也能减缓系统性能恶化速度。综上所述,在聚合用户数量较多的场景下,本文基于分群技术的切换方案具有更好的性能。
|
Download:
|
| 图 13 不同聚合用户数量下的切换成功率比较 Fig. 13 Comparison of handover success rate under different number of aggregated users | |
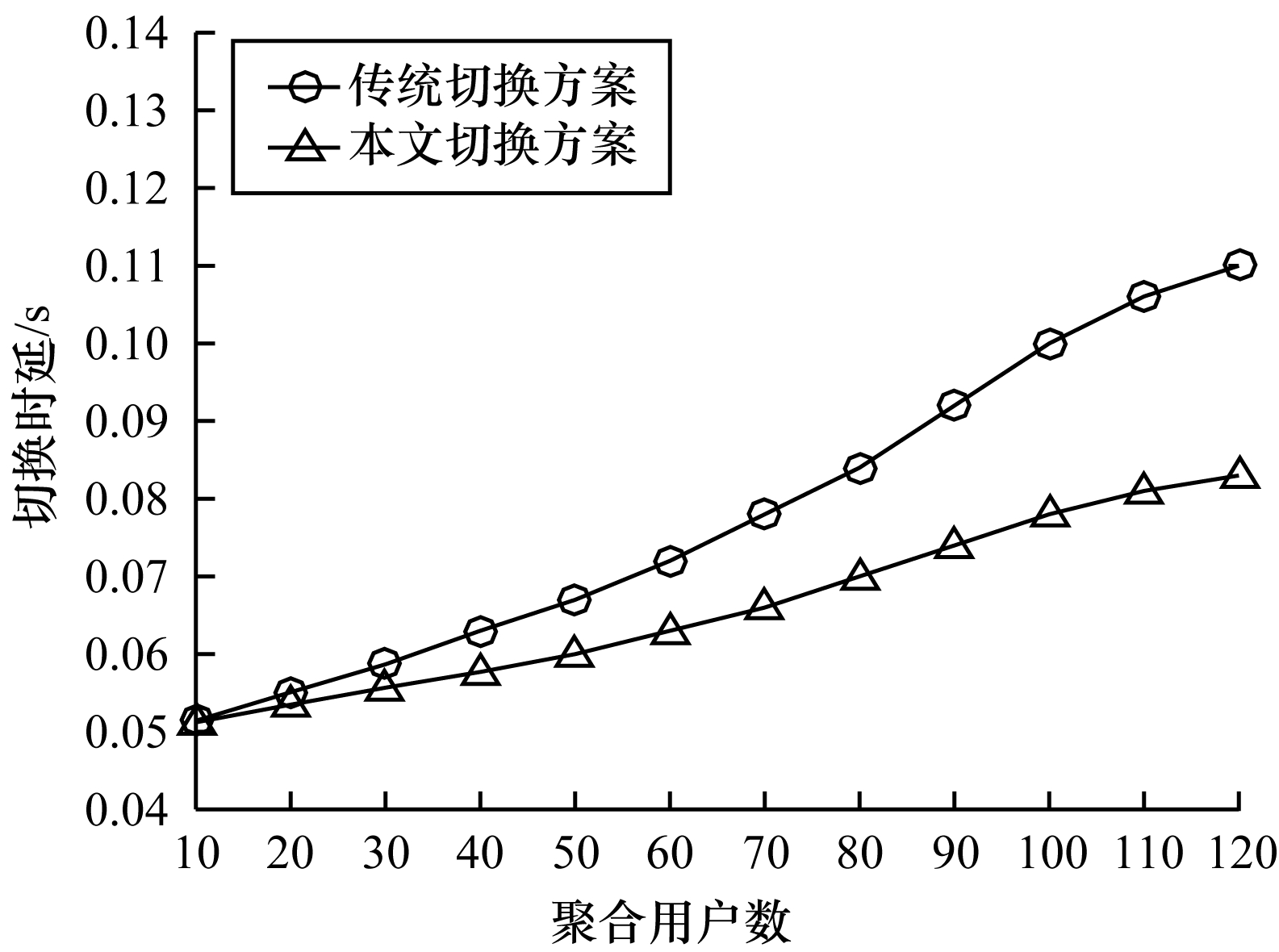
图 14所示为聚合用户数量与平均切换时延的关系。从图 14可以看出,传统切换方案的平均切换时延随着用户规模的增大而增加,原因是用户数量越多,系统中的信令开销越大,一方面导致网络拥塞,增加了排队等待处理时延,另一方面也增大了碰撞发生的概率,碰撞后产生退避增加了传输时延,两者结合会增加平均切换时延。而本文基于用户分群的切换方案将具有相似切换过程的多个用户切换聚合成一次切换,减少了切换请求发起次数和网络负载,从而降低了网络拥塞程度和平均切换时延。
|
Download:
|
| 图 14 不同聚合用户数量下的平均切换时延比较 Fig. 14 Comparison of average handover delay under different number of aggregated users | |
本文针对LEO卫星系统下的用户并发切换问题,提出一种基于用户分群的切换管理策略。在切换边缘选出一组具有相似切换行为的用户,用群首的切换代替群内成员的切换,以此降低切换成本。同时,从分群处理、群组切换、资源释放3个方面设计完整的切换流程和信令交互机制。仿真结果表明,相较传统用户独立切换方案,该切换管理策略能够减少处理过程中的重复操作,降低系统信令开销和平均切换时延,提高切换成功率,且用户聚集数目越多,性能提升越明显。下一步考虑引入高速动态终端切换技术,以提高本文策略的精确度。
| [1] |
LI T X, ZHOU H C, LUO H B, et al. SAT-FLOW: multi-strategy flow table management for software defined satellite networks[J]. IEEE Access, 2017, 5: 14952-14965. DOI:10.1109/ACCESS.2017.2726114 |
| [2] |
RAHMAN M, WALINGO T, TAKAWIRA F. Adaptive handover scheme for LEO satellite communication system[C]//Proceedings of AFRICON'15. Washington D. C., USA: IEEE Press, 2015: 1-5.
|
| [3] |
贺达健, 游鹏, 雍少为. LEO卫星通信网络的移动性管理[J]. 中国空间科学技术, 2016, 36(3): 1-14. HE D J, YOU P, YONG S W. Mobility management in LEO satellite communication networks[J]. Chinese Space Science and Technology, 2016, 36(3): 1-14. (in Chinese) |
| [4] |
DUAN C F, FENG J, CHANG H T, et al. A novel handover control strategy combined with multi-hop routing in LEO satellite networks[C]//Proceedings of 2018 IEEE International Parallel and Distributed Processing Symposium Workshops. Washington D. C., USA: IEEE Press, 2018: 845-851.
|
| [5] |
WU Z F, HU G Y, SEYEDI Y, et al. A simple real-time handover management in the mobile satellite communication networks[C]//Proceedings of the 17th Asia-Pacific Network Operations and Management Symposium. Washington D. C., USA: IEEE Press, 2015: 175-179.
|
| [6] |
MUSUMPUKA R, WALINGO T, SMITH J. Performance analysis of correlated handover service in LEO mobile satellite systems[J]. IEEE Communications Letters, 2016, 20(11): 2213-2216. DOI:10.1109/LCOMM.2016.2604311 |
| [7] |
黄飞. 低轨卫星通信接入与切换策略研究[D]. 成都: 电子科技大学, 2009. HUANG F. Research on access and handoff strategy in low earth orbit satellite communication[D]. Chengdu: University of Electronic Science and Technology of China, 2009. (in Chinese) |
| [8] |
MIAO J S, WANG P J, YIN H Q, et al. A multi-attribute decision handover scheme for LEO mobile satellite networks[C]//Proceedings of 2019 IEEE International Conference on Computer and Communications. Washington D. C., USA: IEEE Press, 2019: 938-942.
|
| [9] |
ZHANG S B, LIU A J, LIANG X H. A multi-objective satellite handover strategy based on entropy in LEO satellite communications[C]//Proceedings of 2020 IEEE International Conference on Computer and Communications. Washington D. C., USA: IEEE Press, 2020: 723-728.
|
| [10] |
WU Z F, JIN F L, LUO J X, et al. A graph-based satellite handover framework for LEO satellite communication networks[J]. IEEE Communications Letters, 2016, 20(8): 1547-1550. DOI:10.1109/LCOMM.2016.2569099 |
| [11] |
HU X, SONG H Y, LIU S J, et al. Velocity-ware handover prediction in LEO satellite communication networks[J]. International Journal of Satellite Communications and Networking, 2018, 36(6): 451-459. DOI:10.1002/sat.1250 |
| [12] |
熊丹妮, 李屹. 星地融合网络中基于Q学习的切换算法研究[J]. 通信学报, 2015, 36(9): 252-258. XIONG D N, LI Y. Q-learning based handoff algorithm for satellite system with ancillary terrestrial component[J]. Journal on Communications, 2015, 36(9): 252-258. (in Chinese) |
| [13] |
HE S X, WANG T Y, WANG S W. Load-aware satellite handover strategy based on multi-agent reinforcement learning[C]//Proceedings of GLOBECOM'20. Washington D. C., USA: IEEE Press, 2020: 1-6.
|
| [14] |
ZHANG C C, ZHANG N, CAO W, et al. An AI-based optimization of handover strategy in non-terrestrial networks[C]//Proceedings of 2020 ITU Kaleidoscope: Industry-Driven Digital Transformation. Washington D. C., USA: IEEE Press, 2020: 1-6.
|
| [15] |
ZHAO C, HUA N, LI J L, et al. Provisioning uninterrupted satellite communication services by Preset-Satellite-Chain(PSC)-based seamless handover[C]//Proceedings of Asia Communications and Photonics Conference. Beijing, China: [s. n. ], 2020: 213-216.
|
| [16] |
LI J, XUE K P, LIU J Q, et al. A user-centric handover scheme for ultra-dense LEO satellite networks[J]. IEEE Wireless Communications Letters, 2020, 9(11): 1904-1908. DOI:10.1109/LWC.2020.3007818 |
| [17] |
WU Y, HU G Y, JIN F L, et al. A satellite handover strategy based on the potential game in LEO satellite networks[J]. IEEE Access, 2019, 7: 133641-133652. DOI:10.1109/ACCESS.2019.2941217 |
| [18] |
HU H F, YUAN D M, LIAO M X, et al. Packet cache-forward method based on improved Bayesian outlier detection for mobile handover in satellite networks[J]. China Communications, 2016, 13(6): 167-177. DOI:10.1109/CC.2016.7513212 |
| [19] |
BHATTACHARYA S, DE D. An enhanced handover strategy for GSM-R technology[C]//Proceedings of 2012 International Conference on Computer and Communication Technology. Washington D. C., USA: IEEE Press, 2012: 227-232.
|
| [20] |
SCHUSS J J, UPTON J, MYERS B, et al. The IRIDIUM main mission antenna concept[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(3): 416-424. DOI:10.1109/8.768775 |
| [21] |
ALI I, AI-DHAHIR N, HERSHEY J E. Predicting the visibility of LEO satellites[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1183-1190. DOI:10.1109/7.805436 |
| [22] |
尹星, 吴国新, 董永强. 一种支持高速移动的网络预先切换方案[J]. 东南大学学报(自然科学版), 2015, 45(6): 1038-1045. YIN X, WU G X, DONG Y Q. A proactive handover scheme for high-speed network mobility[J]. Journal of Southeast University(Natural Science Edition), 2015, 45(6): 1038-1045. (in Chinese) |
 2022, Vol. 48
2022, Vol. 48
