开放科学(资源服务)标志码(OSID):
时间序列是指人们在观测事物的发展规律时,根据观测对象状态记录的一定时间范围内及一定量的有序样本。随着传感器技术和互联网技术的迅速发展,时间序列在各行各业中正以一种前所未有的速度产生和积累。比如:在生物医学领域[1],使用穿戴式设备监测使用者的体温数据、心率数据、血压数据等人体健康指标数据;在交通领域[2],使用传感器监测得到的交通流量数据;在金融领域[3],股票市场中实时产生的股票交易数据等。时间序列数据往往蕴藏着丰富的信息,对其进行分析建模能够帮助人们发现观察对象的本质或发展规律,从而为人们提供决策依据。
时间序列分类即通过构建分类模型来建模时间序列中的特征以实现对该时间序列的归类,是时间序列分析中的一个重要的研究分支,近年来被广泛运用到各个行业中。比如:在医疗行业,通过对心电图数据的建模分析,可以发现心脏是否存在异常[4];在网络安全领域,通过监测网络的流量情况,可以判断是否出现网络流量异常,从而及时做出相应的判断和决策[5]。
传统的时序分类方法主要通过分析时间序列间在时域、形状、变化趋势等方面的相似性,从而实现对时间序列的分类,这类方法的分类性能较大程度地受限于序列间的相似性度量方式[6]。而基于机器学习的方法则需要根据不同的业务场景精心设计特征提取规则,特征工程的优劣决定了模型性能的上限[7]。随着神经网络和深度学习的发展,相继出现了较多的基于深度学习的时序分类方法。这类方法无需事先对数据进行复杂的特征提取,是一种端到端的学习方法,因此适用范围较广。如文献[8]将FCN和ResNet运用到时间序列分类任务中,直接将原始时间序列作为FCN和ResNet的输入,取得了较好的分类效果。但是这类方法仅从时域上对时间序列进行建模,主要是捕获时间序列的局部形状特征,而忽视了时间序列中蕴含的长期趋势特征、周期性特征、季节性特征等。
针对上述的问题,本文提出一种基于自适应多级小波分解的时间序列分类方法AMWDNet。该方法使用自适应多级小波分解,提取多级低频特征和高频特征,对于各级的时频特征,使用长期时间模式提取模块和短期时间模式提取模块分别捕获时间序列中的全局变化模式和局部变化模式,并对各级的预测结果进行融合,作为最终的预测结果。
1 相关工作目前主流的时间序列分类方法主要分为四大类,包括基于距离的方法、基于特征的方法、基于集成学习的方法和基于深度学习的方法。
基于距离的方法是通过计算两个时间序列之间的距离作为时间序列之间的相似性度量,然后将获得的相似度作为分类器(常用的分类器有K近邻分类器、支持向量机等)的输入从而得到分类的结果。因此,如何定义出一种合适的距离度量是关键。常用的距离度量方法有欧氏距离[9]和动态时间规整(Dynamic Time Wraping,DTW)[10]。这类方法虽然计算简单、可解释性较强,但是其时间和空间复杂度较高,不适用于大数据环境下的分类场景,因而存在较大的局限性。
基于特征的方法是从原始时间序列中提取有效的特征,然后将提取到的特征作为分类器的输入从而得到分类的结果。文献[11]提出的模式袋(Bag of Patterns,BOP)模型使用符号近似估计(Symbolic Aggregate approXiamtion,SAX)[12]将原始时间序列转换为单词集合,并针对单词的出现频率进行统计,再计算出两个时间序列对应的单词出现频率之间的欧氏距离,最后使用最近邻分类器进行分类。与BOP方法不同,文献[13]提出的符号傅里叶近似(Symbolic Fourier Approximation,SFA)模型,首先使用离散傅里叶变换提取每个时间序列的频域信息,然后转换成单词集合。除了利用全局的时间序列进行特征的提取和构造外,还有利用局部的时间序列片段来构造特征向量的方法。基于辨识性子序列(shapelet)的方法是从原始时间序列中搜索出最具判别性的一段连续的子序列用来进行分类。文献[14]提出shapelet的概念,随后便吸引了大量学者,涌现出大量的改进方法[15-16]。基于特征的方法的泛化性能较低,一般需要针对具体的问题对时间序列进行合适的特征表示,再使用分类器进行分类。
基于集成的方法是使用多个分类器进行分类,然后对多个分类器的分类结果进行融合,从而得到最终的分类结果。文献[17]提出的EE(Elastic Ensembles)算法将11个使用了不同距离度量的最近邻分类器的分类结果相结合作为模型最终的分类结果。文献[18]提出的COTE算法集成了35个不同的分类器,最终的分类结果是各个分类器的分类结果的加权融合。
随着深度学习的发展,使得其被广泛地应用到时间序列分类任务中。基于深度学习的方法是通过一系列的非线性计算来提取出时间序列中隐藏的特征。这类方法不需要事先设计复杂的特征提取规则,所以研究人员即使不具备丰富的领域知识,也可以使用这类方法来解决某个业务场景中的时间序列分类问题。但现有的深度学习方法大都基于时域的角度来对时间序列进行建模,如FCN、ResNet等。然而,现实世界中采集到的时间序列往往同时包含长期趋势、季节变化、循环变化和随机变化,仅从时域的角度对时间序列进行特征表示,则会给神经网络的建模带来较大的难度。
为克服上述问题,本文提出基于自适应多级小波分解的时序分类方法,该方法能够自适应地提取多级时频特征,提升模型分类效果。
2 模型介绍 2.1 问题定义本节首先给出时间序列分类相关定义的形式化描述。
定义1(单变量时间序列) 时间序列是指在一段时间内对某个对象或系统进行观测而产生的按照时间先后顺序排列的数值型记录[6]。根据每一时刻观测的变量个数,可以将时间序列划分为单变量时间序列和多变量时间序列。假设在
定义2(单变量时间序列数据集) 给定一个包含
定义3(单变量时间序列分类) 单变量时间序列分类任务即在假设空间
| $ \underset{h\in \mathcal{H}}{\mathrm{m}\mathrm{i}\mathrm{n}}\frac{1}{N}\sum\limits_{i=1}^{N}\mathcal{L}({y}_{i}, h({\mathit{\boldsymbol{x}}}_{i}\left)\right) $ | (1) |
其中:
离散小波分解(Discrete Wavelet Transform,DWT)在数字信号处理、语音信号处理、模式识别等多个领域都得到了广泛的应用。DWT可以将原始输入时间序列分解为低频分量(反映趋势特征)和高频频率(反映局部细节特征)。Mallat算法[19]是实现离散小波分解的经典算法之一。Mallat算法由小波滤波器
| $ {\mathit{\boldsymbol{A}}}_{0}\left[\mathit{\boldsymbol{s}}\right(t\left)\right]=\mathit{\boldsymbol{s}}\left(t\right) $ | (2) |
| $ {\mathit{\boldsymbol{A}}}_{i}\left[\mathit{\boldsymbol{s}}\right(t\left)\right]=\sum\limits_{k}\mathit{\boldsymbol{H}}\left(2\right.t-k\left){\mathit{\boldsymbol{A}}}_{i-1}\right[\mathit{\boldsymbol{s}}\left(t\right)] $ | (3) |
| $ {\mathit{\boldsymbol{D}}}_{i}\left[\mathit{\boldsymbol{s}}\right(t\left)\right]=\sum\limits_{k}\mathit{\boldsymbol{G}}\left(2\right.t-k\left){\mathit{\boldsymbol{A}}}_{i-1}\right[\mathit{\boldsymbol{s}}\left(t\right)] $ | (4) |
其中:
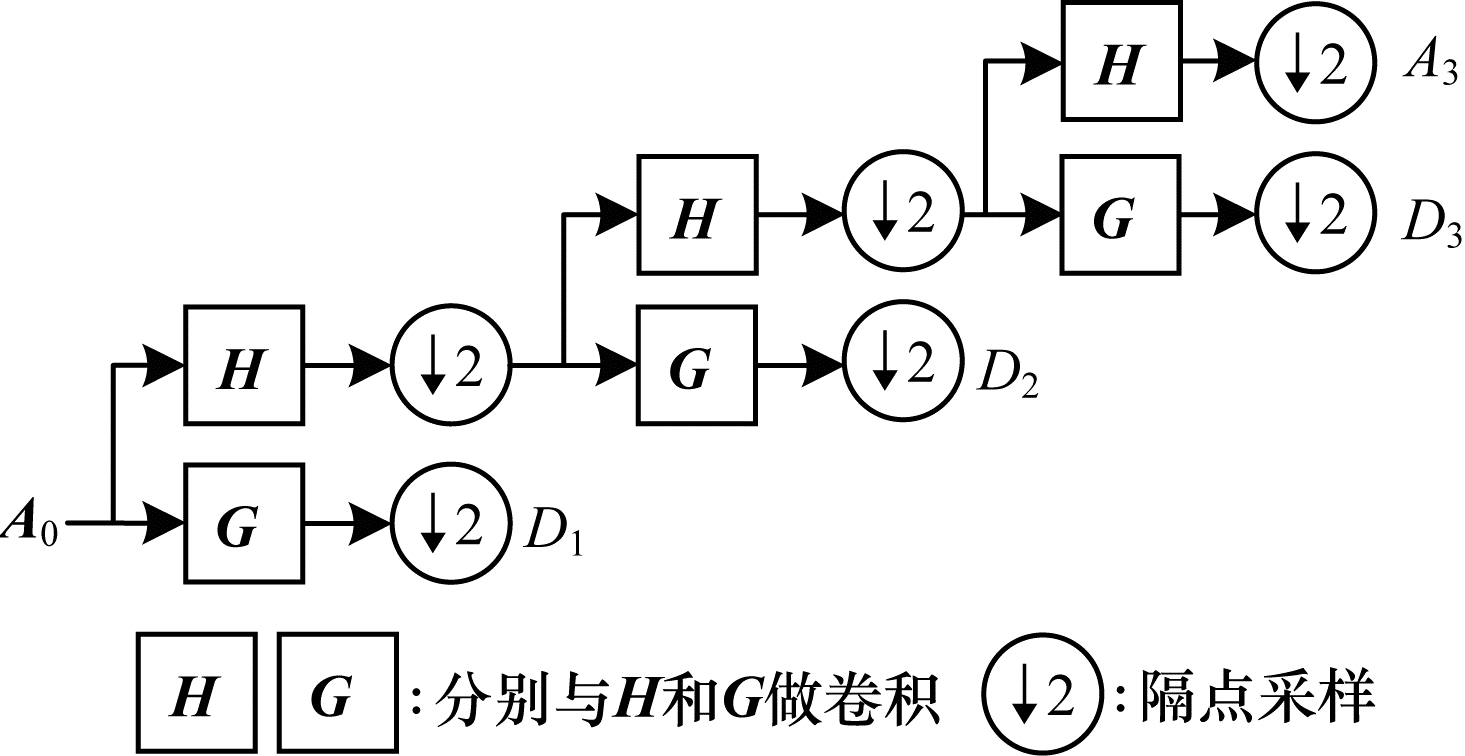
以一个时间序列
|
Download:
|
| 图 1 时间序列的Mallat三层分解过程 Fig. 1 Mallat three-level decomposition process of time series | |
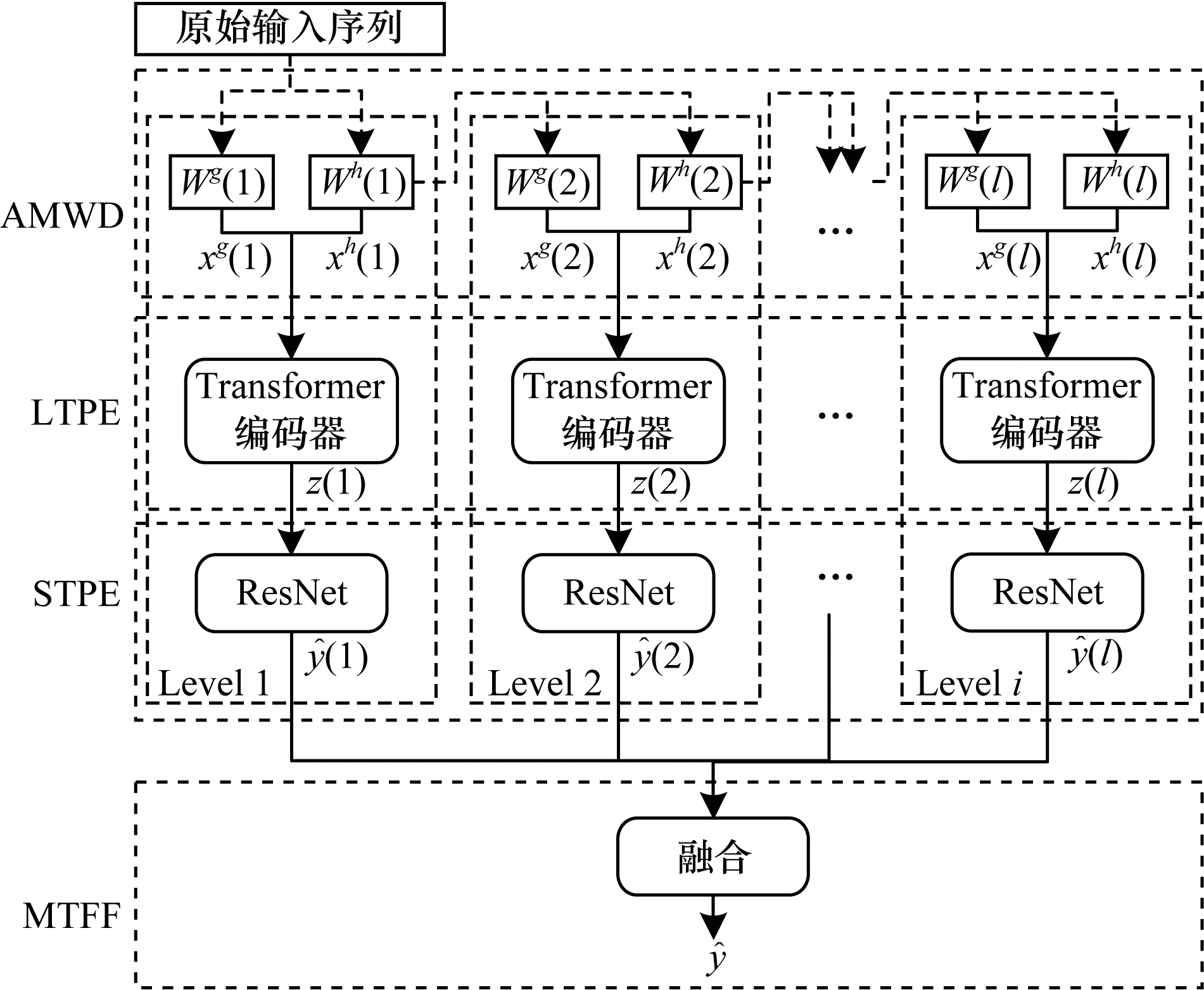
时间序列中蕴含着多种不同的特征模式,如局部的形状特征、全局的趋势变化特征、季节性特征等。这些特征在时域上相互杂糅,仅从时域上进行分析难以有效提取出存在于不同分辨率下的多种特征模式。因此,本文提出的AMWDNet模型首先通过对原始输入序列进行自适应多级小波分解,分解出多级的不同分辨率下的高频分量和低频分量,使得时间序列蕴含的多种特征模式得以显现。然后设计长期时间模式提取模块和短期时间模式提取模块,分别建模各级高频分量和低频分量中的长期趋势和短期波动。最后提出多级时频信息融合模块,对短期时间模式提取模块的输出结果进行融合,得到最终的分类结果。AMWDNet模型的整体结构如图 2所示,模型共包含4个模块:
|
Download:
|
| 图 2 AMWDNet模型总体结构 Fig. 2 Overall structure of AMWDNet model | |
1)自适应多级小波分解(Adaptive Multi-level Wavelet Decomposition,AMWD)模块。使用自适应的离散小波分解对原始时间序列进行分解,提取出多级的低频特征和高频特征。
2)长期时间模式提取(Long-term Temporal Patterns Extracting,LTPE)模块。使用Transformer[20]编码器捕获各级时频信息中的长期特征,即时间序列的全局变化模式。
3)短期时间模式提取(Short-term Temporal Patterns Extracting,STPE)模块。使用ResNet捕获短期特征,即时间序列的局部变化模式。
4)多级时频信息融合(Multi-level Time-Frequency information Fusion,MTFF)模块。对基于各级时频信息建模得到的分类结果进行融合,得到最终的分类结果。
本文提出的自适应多级小波分解方法能够将时域上相互杂糅的各种时序特征模式彼此分离,大幅降低了后续的建模难度,从而有效地提高了模型的分类性能。并且,多级时频信息的构建过程与神经网络紧密结合,无需人工提取特征,保留了深度学习端到端学习优点。同时,多级时频信息的提取还能根据数据进行自适应微调,提高了模型的鲁棒性。
2.3.1 自适应多级小波分解在时域上,时间序列的长期趋势、季节性、周期性和随机扰动同时存在,因此,从时域上对时间序列进行分析存在较高的难度。使用时频分析技术能够有效提取出时间序列中的时频信息,如小波变换的多分辨率分析,随着尺度由大到小,可以在各尺度上由粗到细地观察时间序列的不同特征。在大的尺度空间中,能够观察时间序列的整体变化模式和变化趋势;而在小的尺度空间中,可以观察时间序列的局部变化模型和形状特征。
为了能够同时从时域和频域上对时间序列进行分析建模,一种朴素的方法是先使用传统的时频分析方法(如Mallat方法)提取多级时频信息,再利用分类器对各级时频信息进行建模。这种方法虽然能够从不同的分辨率上分析时间序列中的多种特征模式,但是需要事先通过人工提取出时间序列中的多级时频信息。如果时频信息提取的过程不合理,会增加后续建模的难度,使得模型的分类性能较差。因此,本文使用自适应多级小波分解模块(AMWD)来自适应地提取原始序列中多级时频信息。自适应多级小波分解模块的思想是使用神经网络来近似地实现Mallat算法,使得多级时频信息的提取过程能够和后续的分类模型紧密结合,并通过反向传播算法共同训练参数,使得时频特征能够在分类模型学习的过程中根据数据的特点进行动态调整,提高模型的鲁棒性和泛化能力。
自适应多级小波分解的计算过程如式(5)~式(9)所示:
| $ {\mathit{\boldsymbol{x}}}^{h}\left(0\right)=\mathit{\boldsymbol{x}} $ | (5) |
| $ {\mathit{\boldsymbol{a}}}^{h}\left(i\right)={\mathit{\boldsymbol{W}}}^{h}\left(i\right){\mathit{\boldsymbol{x}}}^{h}(i-1)+{\mathit{\boldsymbol{b}}}^{h}\left(i\right) $ | (6) |
| $ {\mathit{\boldsymbol{a}}}^{g}\left(i\right)={\mathit{\boldsymbol{W}}}^{g}\left(i\right){\mathit{\boldsymbol{x}}}^{h}(i-1)+{\mathit{\boldsymbol{b}}}^{g}\left(i\right) $ | (7) |
| $ {\mathit{\boldsymbol{x}}}_{j}^{h}(i)=({\mathit{\boldsymbol{a}}}_{2j}^{h}(i)+{\mathit{\boldsymbol{a}}}_{2j-1}^{h}(i))/2 $ | (8) |
| $ {\mathit{\boldsymbol{x}}}_{j}^{g}(i)=({\mathit{\boldsymbol{a}}}_{2j}^{g}(i)+{\mathit{\boldsymbol{a}}}_{2j-1}^{g}(i))/2 $ | (9) |
其中:
为了能够运用神经网络近似地实现Mallat算法,本文使用已有的小波基来初始化滤波器矩阵
| $ {\mathit{\boldsymbol{W}}}^{h}\left(i\right)=\left[\begin{array}{ccccccc}{h}_{1}& {h}_{2}& \cdots & {h}_{K}& \varepsilon & \cdots & \varepsilon \\ \varepsilon & {h}_{1}& \cdots & {h}_{K-1}& {h}_{K}& \cdots & \varepsilon \\ \vdots & \vdots & & \vdots & \vdots & \vdots & \vdots \\ \varepsilon & \varepsilon & \cdots & {h}_{1}& \cdots & {h}_{K-1}& {h}_{K}\\ \vdots & \vdots & & \vdots & \vdots & \vdots & \vdots \\ \varepsilon & \varepsilon & \cdots & \cdots & \cdots & {h}_{1}& {h}_{2}\\ \varepsilon & \varepsilon & \cdots & \cdots & \cdots & \varepsilon & {h}_{1}\end{array}\right] $ | (10) |
| $ {\mathit{\boldsymbol{W}}}^{g}\left(i\right)=\left[\begin{array}{ccccccc}{g}_{1}& {g}_{2}& \cdots & {g}_{K}& \varepsilon & \cdots & \varepsilon \\ \varepsilon & {g}_{1}& \cdots & {g}_{K-1}& {g}_{K}& \cdots & \varepsilon \\ \vdots & \vdots & & \vdots & \vdots & \vdots & \vdots \\ \varepsilon & \varepsilon & \cdots & {g}_{1}& \cdots & {g}_{K-1}& {g}_{K}\\ \vdots & \vdots & & \vdots & \vdots & \vdots & \vdots \\ \varepsilon & \varepsilon & \cdots & \cdots & \cdots & {g}_{1}& {g}_{2}\\ \varepsilon & \varepsilon & \cdots & \cdots & \cdots & \varepsilon & {g}_{1}\end{array}\right] $ | (11) |
其中:
虽然
时间序列中往往同时蕴含着长期时间模式(如变化趋势)和短期时间模式(如局部的形状特征)。近年来,Transformer在自然语言处理等领域取得成功,因而受到了广泛的关注。其在建模时间序列的长期依赖问题上,具有出色的表现[21],能够捕获全局特征。因此,本文的长期时间模式提取模块(LTPE)采用Transformer编码器来分别建模自适应多级小波分解模块提取得到的多级时频信息
| $ \mathit{\boldsymbol{z}}\left(i\right)=\mathrm{T}\mathrm{E}\left(\right[{\mathit{\boldsymbol{x}}}^{g}\left(i\right);{\mathit{\boldsymbol{x}}}^{h}\left(i\right)\left]\right) $ | (12) |
其中:
ResNet模型通过引入恒等变换缓解了深层网络难以训练的问题,在图像分类任务中得到广泛的应用。2017年,WANG等[8]将其应用于时间序列分类任务中,取得了较好的效果。并且,ResNet由多个卷积块组成,能够有效捕获局部特征。因此,本文的短期时间模式提取模块(STPE)采用ResNet来建模长期时间模式提取模块输出结果的局部特征。
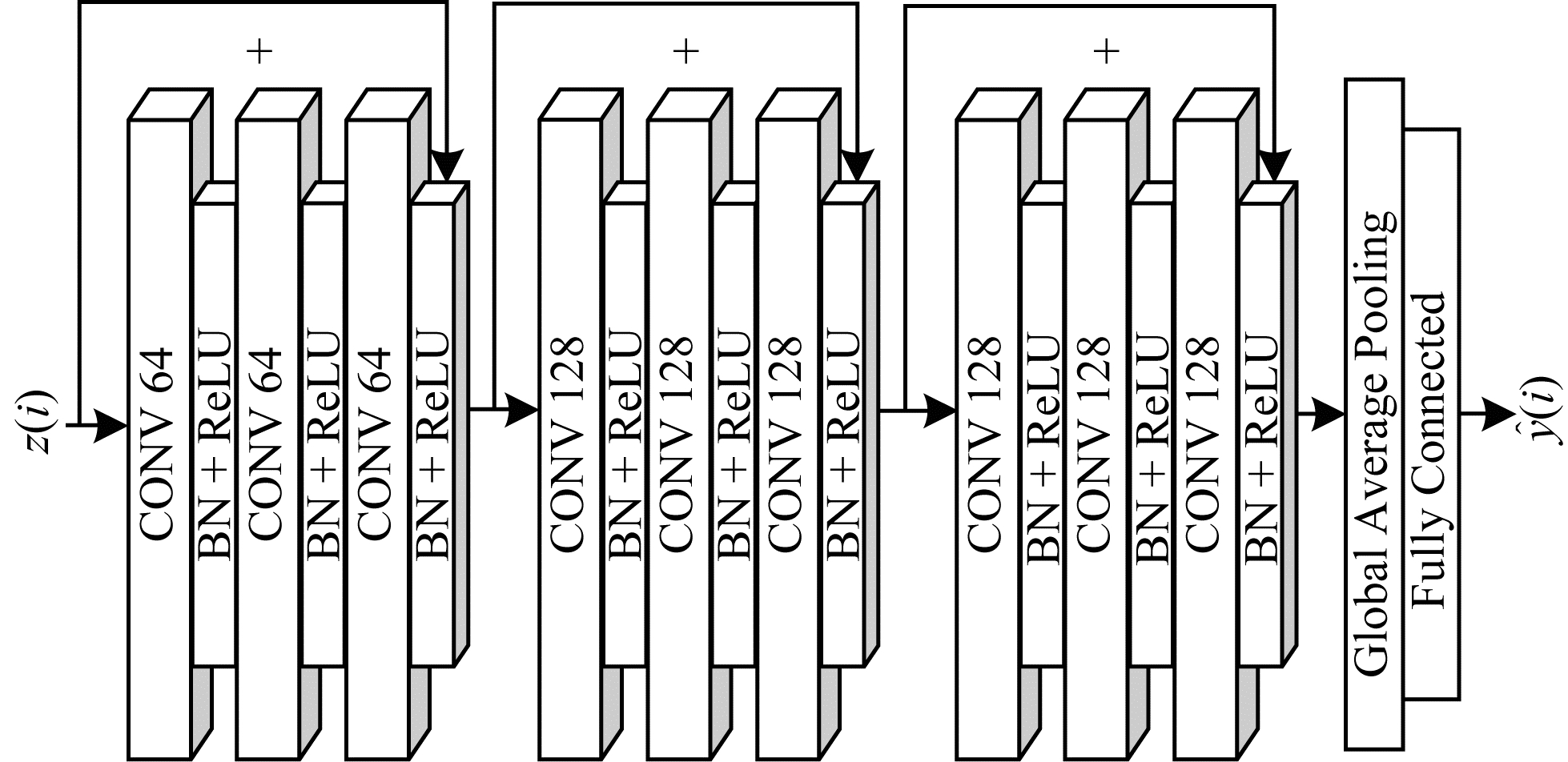
短期时间模式提取模块由3个残差模块、1个全局平均池化层和1个全连接层组成。与ResNet不同的是,短期时间模式提取模块最后没有使用softmax激活函数进行非线性变换,整体结构如图 3所示。
|
Download:
|
| 图 3 短期时间模式提取模块的整体结构 Fig. 3 Overall structure of short-term temporal pattern extraction module | |
多级时频信息融合模块作用于各级短期时间模式提取模块的输出结果之上,用于融合多级时频信息建模的结果。具体计算公式如下:
| $ {\widehat{\mathit{\boldsymbol{y}}}}^{f}=\sum\limits_{i=1}^{l}\mathit{\boldsymbol{w}}\left(i\right)\odot \widehat{\mathit{\boldsymbol{y}}}\left(i\right) $ | (13) |
其中:
各级建模的结果
| $ \widehat{\mathit{\boldsymbol{v}}}\left(i\right)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\widehat{\mathit{\boldsymbol{y}}}\right(i\left)\right) $ | (14) |
| $ {\widehat{\mathit{\boldsymbol{v}}}}^{f}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\widehat{\mathit{\boldsymbol{y}}}}^{f}\right) $ | (15) |
给定时间序列分类数据集
| $ \tilde{\mathcal{L}}\left(i\right)=-\frac{1}{N}\sum\limits_{n=1}^{N}{\mathit{\boldsymbol{v}}}_{n}^{T}l{n}_{}{\widehat{\mathit{\boldsymbol{v}}}}_{n}\left(i\right) $ | (16) |
其中:
定义在模型最后输出的分类结果
| $ {\tilde{\mathcal{L}}}^{f}=-\frac{1}{N}\sum\limits_{n=1}^{N}{\mathit{\boldsymbol{v}}}_{n}^{\mathrm{T}}\mathrm{l}\mathrm{n}{\widehat{\mathit{\boldsymbol{v}}}}_{n}^{f} $ | (17) |
则模型的最终训练目标是最小化损失函数如式(18)所示:
| $ \begin{array}{l}\mathcal{L}=\sum\limits_{i=1}^{l}\frac{i}{l}\tilde{\mathcal{L}}\left(i\right)+{\tilde{\mathcal{L}}}^{f}+\alpha \sum\limits_{i=1}^{l}{||{\mathit{\boldsymbol{W}}}^{h}\left(i\right)-{\widetilde {\mathit{\boldsymbol{W}}}}^{h}\left(i\right)||}_{F}^{2}+\\ \beta \sum\limits_{i=1}^{l}{||{\mathit{\boldsymbol{W}}}^{g}\left(i\right)-{\widetilde {\mathit{\boldsymbol{W}}}}^{g}\left(i\right)||}_{F}^{2}\end{array} $ | (18) |
其中:
在模型训练过程中,设置最大训练迭代轮数为10 000,并使用早停策略防止模型发生过拟合,当模型在验证集上的损失经过50轮迭代后仍然没有减少时就停止训练。同时,使用Adam优化算法(其中,超参数设置为
| $ lr\left(\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}\mathrm{s}\right)={d}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}^{-0.5}\cdot \mathrm{m}\mathrm{i}\mathrm{n}(\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}{\mathrm{s}}^{-0.5}, \mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}\mathrm{s}\cdot \mathrm{w}\mathrm{a}\mathrm{r}\mathrm{m}\mathrm{u}{\mathrm{p}}^{-1.5}) $ | (19) |
其中:
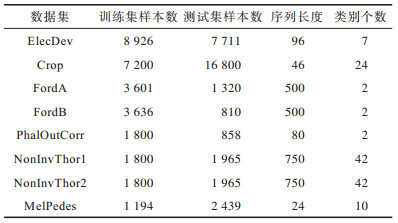
UCR[22]数据集仓库是时间序列分类任务常用的基准数据集,包含了来自不同领域的128个时间序列数据集。由于UCR数据集仓库中绝大部分的训练集和测试集的样本数据都较小,而本文提出方法是基于深度学习的方法,这类方法更适用于样本数目较大的数据集。因此,本文从中选取了8个训练集样本数目超过1 000的数据集进行实验。本文沿用UCR数据集仓库中原始的训练集、测试集划分,然后使用分层采样的方式从训练集中随机抽取20%的样本用于模型参数选择,其余80%的样本用于模型训练。8个数据集的详细信息如表 1所示。
|
下载CSV 表 1 数据集详细信息 Table 1 Dataset details |
通过选取8个基准方法与本文提出的AMWDNet进行对比实验,其中主要包括基于时域的方法、融合频域信息的方法和融合时频信息的方法。
1)多层感知机(MLP)[8],由三层前馈神经网络和softmax输出层组成,其中softmax输出层包括一层前馈神经网络和softmax激活函数。
2)全卷积神经网络(FCN)[8],由3个卷积块、全局平均池化(Global Average Pooling,GAP)层和softmax输出层组成,每个卷积块中包含卷积、批量归一化和ReLU激活3种运算。
3)编码网络(Encoder)[23],与FCN的结构相似,其不同之处在于Encoder将FCN中的GAP层替换为注意力机制。
4)残差网络(ResNet)[8],使用残差结构搭建的深层卷积网络,残差连接有效地缓解了深层神经网络在训练过程中可能发生的梯度消失或梯度爆炸问题。
5)多尺度卷积神经网络(MCNN)[24],通过恒等变换、下采样和平滑3种变换方式提取出时域和频域信息,分别使用3个卷积网络对3种变换方式提取出来的特征进行建模,最后经过拼接后输入到全连接层和softmax输出层中,得到序列样本属于各个类别的概率。
6)长短时记忆网络(LSTM)[25],循环神经网络的一种变体,通过使用输入门、遗忘门、输出门等门控机制来实现对细胞状态和隐藏状态的更新,能够有效捕获时间序列中的长期依赖关系。
7)门控循环单元(GRU)[26],是LSTM的一种变体。GRU相比于LSTM,其计算更加简单,仅使用更新门和重置门对隐藏状态的信息进行更新。虽然相比于LSTM,GRU的计算量和参数量都更少,但是其在许多任务中都能表现出和LSTM不相上下的建模能力。
8)多级小波分解网络(mWDN)[27],使用小波分解提取出多级时频特征之后,通过多个分类器进行分类。
本文采用时间序列分类任务中常用的分类准确率(Accuracy)衡量模型在单个数据集上的表现,具体公式如下:
| $ {A}_{\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}}=\frac{{N}_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}}{{N}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}} $ | (20) |
其中:
另外,使用平均排名衡量模型在多个数据集上的总体表现。平均排名是指模型在各个数据集上的表现排名的平均值,平均排名越小,说明模型在所有数据集上的整体表现越好。
3.3 实验环境与参数设置本文基于Pytorch深度学习框架实现AMWDNet。AMWDNet包含两类超参数:一类是涉及自适应多级小波分解模块,包括分别用于控制低通滤波器系数和高通滤波器系数微调程度的正则项系数
给定
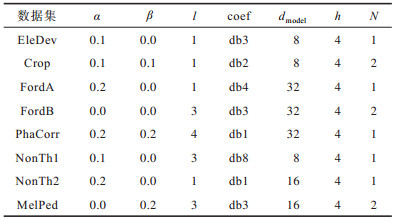
|
下载CSV 表 2 不同数据集的超参数设置 Table 2 Hyperparameter settings of different datasets |
实验针对各规模的数据集设置了不同的数据批处理大小,具体设置如表 3所示。
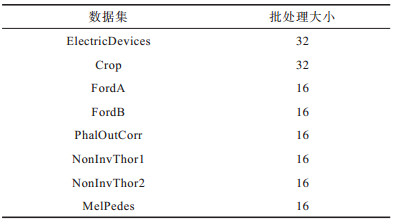
|
下载CSV 表 3 不同数据集的批处理大小 Table 3 Batch size of different datasets |
将本文提出的AMWDNet应用在UCR数据集仓库中的8个数据集上,并与8种基准方法进行分类性能的比较。
通过重复进行10次实验,计算出不同模型在各个数据集上的平均分类准确率,结果如表 4所示,其中粗体表示结果最优,下划线表示结果次优。
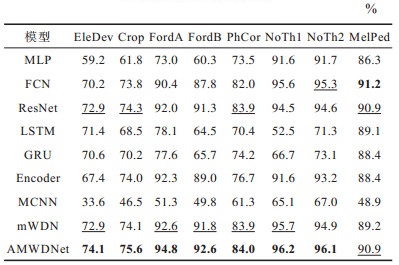
|
下载CSV 表 4 不同模型在各数据集上的平均分类准确率 Table 4 Average classification accuracy of different models on each dataset |
从整体实验结果来看,AMWDNet在7个数据集上取得最优结果,在1个数据集上取得次优结果,说明AMWDNet在不同的业务场景中都能表现出相当不错的分类性能,验证了AMWDNet的有效性和泛化性。
在MelPed数据集上,虽然AMWDNet的分类效果不如FCN,但是两者的差距较小。MelPed数据集记录了2017年墨尔本10个地点的行人统计数据,传感器每小时产生一个记录值。MelPed数据集中的样本序列长度仅为24,由于时间序列特征的时间跨度只有一天,很难反映出时间跨度更长的季节变化规律,比如以天、周、月为周期的变化特征。因此,在有限的时间区间内,时间序列包含的频域信息较少,降低了AMWDNet提取时间序列中的时频信息的有效性,导致AMWDNet在MelPed数据集上没有取得最高的准确率。
而在序列长度为500的FordA数据集上,AMWDNet相比其他结果最好的基准方法,其分类准确率的提升高达2.2%。说明在较长的时间区间内,AMWDNet能够有效地建模其中的时频信息,使得模型的分类性能得到了显著的提升。
为了更好地对比各个模型在8个数据集上的整体表现,对各模型的平均排名进行了统计,结果如图 4所示。
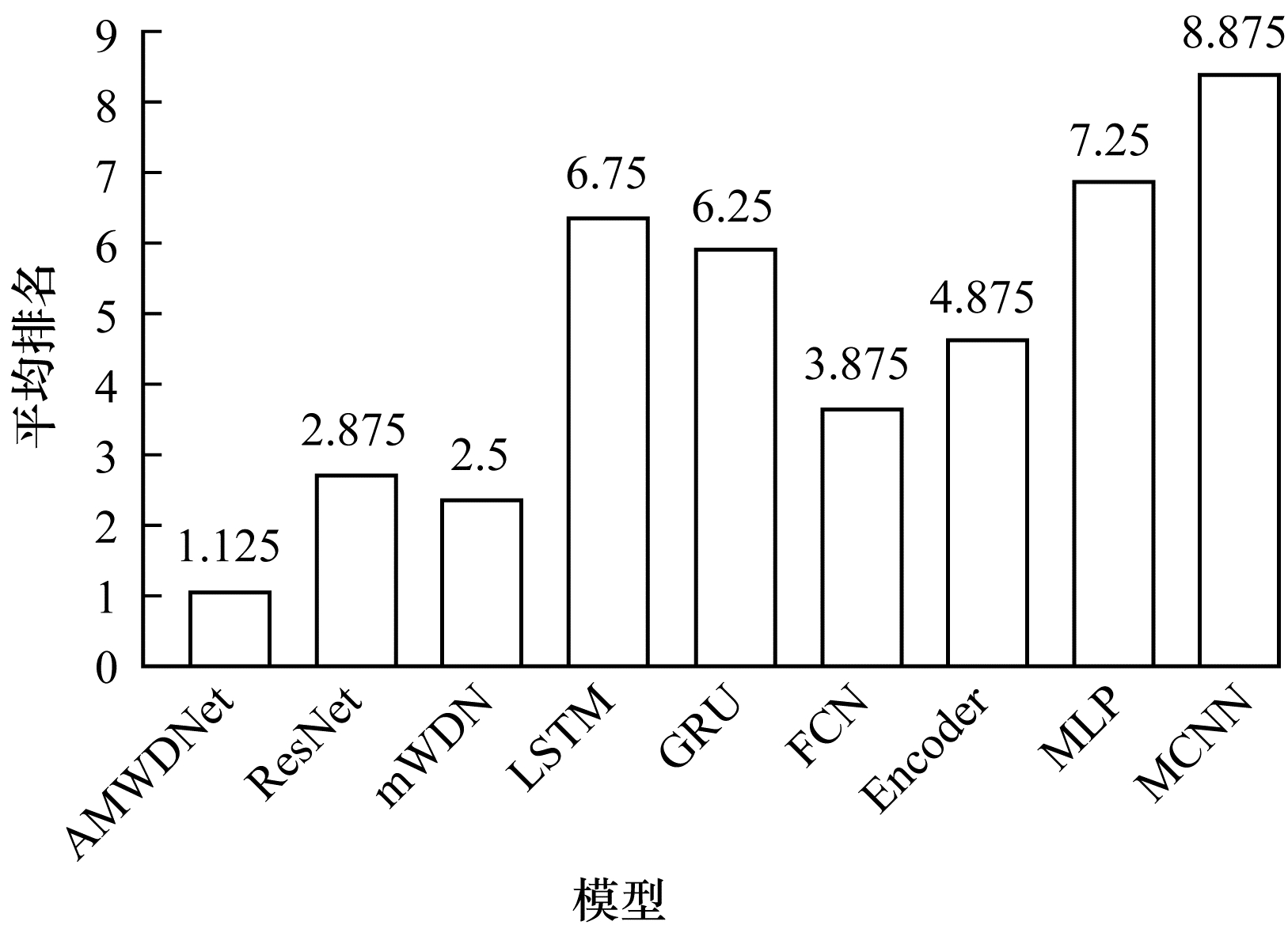
|
Download:
|
| 图 4 不同模型的平均排名 Fig. 4 Average rank of different models | |
从图 4可以看出:表现最好的两个方法是基于时频分析的方法AMWDNet和mWDN,证明了基于时频分析的方法的有效性和通用性;其次是基于局部特征提取的方法ResNet、FCN和Encoder;然后是基于全局特征提取的方法LSTM和GRU;而MLP和MCNN的表现最差。
当序列长度较长时,基于全局特征提取的方法LSTM和GRU,由于梯度消失等原因而导致模型难以训练,使得模型的分类性能大幅下降。而基于局部特征提取的方法ResNet、FCN和Encoder,三者的表现则更加鲁棒,因此在8个数据集上的总体表现比LSTM和GRU要好。但是这类方法仅在时域上对原始时间序列进行建模,无法分解出时间序列中包含的多种频率分量,使得建模难度较大,因此难以达到最佳的分类性能。
MCNN模型虽然也通过滑动平均提取了不同分辨率的时频信息,但是其提取时频信息的方法过于简单,无法有效地提取出具有显著区分度的时频特征,从而导致模型的分类性能较差。说明在对时间序列进行时频分析时,如果提取时频特征的方式不好,会对模型的分类性能带来较大影响,因此如何有效地提取时间序列中的时频信息十分关键。而AMWDNet模型通过自适应多级小波分解提取原始时间序列中的多级高频分量和低频分量,并且还对各级时频分量中的长期变化模式和短期变化模式进行了建模,因此在不同序列长度的分类任务中,都能达到几乎最佳的分类性能。
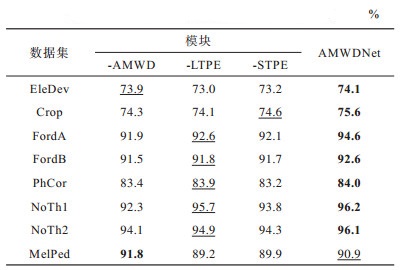
3.5 消融实验为了验证AMWDNet各个模块的效果,本文进行了消融实验,实验结果如表 5所示,其中粗体表示结果最优,下划线表示结果次优。
|
下载CSV 表 5 消融实验结果 Table 5 Results of ablation experiments |
在表 5中,“-AMWD”表示去掉自适应多级小波分解模块,仅使用Transformer和ResNet对原始输入序列进行建模。去掉自适应多级小波分解模块之后,在几乎所有数据集(除MelPed数据集外)上的分类准确率均有所下降,尤其是在样本序列长度较长的数据集上,分类准确率显著降低。如在序列长度为500的NonTh2数据集上,分类准确率下降了2个百分点,验证了自适应多级小波分解模块能有效提取时间序列中的多级时频信息,有助于提高模型整体分类性能,尤其在时间序列数据长度较长的场景中,自适应多级小波分解模块的贡献较大。
“-LTPE”表示去掉长期时间模式提取模块,使用自适应多级小波分解提取出多级时频信息后,再使用多个ResNet分别建模各级时频信息。去掉长期时间模式提取模块之后,在所有数据集上的效果都有所下降,证明时间序列的全局演变模式的建模能够有助于提高模型性能。
“-STPE”表示去掉短期时间模式提取模块,最后使用全局平均池化在时间维度上融合长期时间模式提取模块的输出结果。实验结果表明,即使建模了时间序列中的多级时频信息及全局变化模式,时间序列的局部形状模型的建模对时间序列分类任务仍然十分重要。
4 结束语在真实世界采集得到的时间序列数据往往同时存在长期趋势因素、季节性因素、周期性因素和随机变动因素,这些影响因素在时域上相互杂糅,如仅从时域上对其进行建模,难以达到较高的分类性能。为此,本文提出一种基于自适应多级小波分解的时序分类方法。将多级时频信息的提取过程嵌入到神经网络中,使得时频信息的提取能够根据数据进行自适应调整,并通过长期和短期时间模式提取模块有效地提取时间序列中的长期和短期时间特征。实验结果表明,该方法能够提高模型的整体分类性能。本文提出的方法只在单变量时间序列数据集上进行了对比实验,下一步将基于动态小波分解的思想,设计面向多变量的时间序列分类方法。
| [1] |
CABALLERO BARAJAS K L, AKELLA R. Dynamically modeling patient's health state from electronic medical records: a time series approach[C]//Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM Press, 2015: 69-78.
|
| [2] |
YU B, YIN H T, ZHU Z X. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting[C]//Proceedings of the 27th IEEE International Joint Conference on Artificial Intelligence. Washington D. C., USA: IEEE Press, 2018: 328-339.
|
| [3] |
KRISTJANPOLLER W, FADIC A, MINUTOLO M C. Volatility forecast using hybrid neural network models[J]. Expert Systems with Applications, 2014, 41(5): 2437-2442. DOI:10.1016/j.eswa.2013.09.043 |
| [4] |
YE C, KUMAR B V K V, COIMBRA M T. Heartbeat classification using morphological and dynamic features of ECG signals[J]. IEEE Transactions on Bio-Medical Engineering, 2012, 59(10): 2930-2941. DOI:10.1109/TBME.2012.2213253 |
| [5] |
卓勤政. 基于深度学习的网络流量分析研究[D]. 南京: 南京理工大学, 2018. ZHUO Q Z. Research on network traffic analysis based on deep learning[D]. Nanjing: Nanjing University of Science and Technology, 2018. (in Chinese) |
| [6] |
原继东. 时间序列分类算法研究[D]. 北京: 北京交通大学, 2016. YUAN J D. Research on time series classification[D]. Beijing: Beijing Jiaotong University, 2016. (in Chinese) |
| [7] |
谭振宁. 基于深度学习的时序预测和分类[D]. 广州: 华南理工大学, 2020. TAN Z N. Time series prediction and classification based on deep learning[D]. Guangzhou: South China University of Technology, 2020. (in Chinese) |
| [8] |
WANG Z G, YAN W Z, OATES T. Time series classification from scratch with deep neural networks: a strong baseline[C]//Proceedings of 2017 International Joint Conference on Neural Networks. Washington D. C., USA: IEEE Press, 2017: 1578-1585.
|
| [9] |
FALOUTSOS C, RANGANATHAN M, MANOLOPOULOS Y. Fast subsequence matching in time-series databases[J]. ACM SIGMOD Record, 1994, 23(2): 419-429. DOI:10.1145/191843.191925 |
| [10] |
SILVA D F, GIUSTI R, KEOGH E, et al. Speeding up similarity search under dynamic time warping by pruning unpromising alignments[J]. Data Mining and Knowledge Discovery, 2018, 32(4): 988-1016. DOI:10.1007/s10618-018-0557-y |
| [11] |
LIN J, KHADE R, LI Y. Rotation-invariant similarity in time series using bag-of-patterns representation[J]. Journal of Intelligent Information Systems, 2012, 39(2): 287-315. DOI:10.1007/s10844-012-0196-5 |
| [12] |
LIN J, KEOGH E, WEI L, et al. Experiencing SAX: a novel symbolic representation of time series[J]. Data Mining and Knowledge Discovery, 2007, 15(2): 107-144. DOI:10.1007/s10618-007-0064-z |
| [13] |
SCHÄFER P, HÖGQVIST M. SFA: a symbolic Fourier approximation and index for similarity search in high dimensional datasets[C]//Proceedings of the 15th International Conference on Extending Database Technology. Washington D. C., USA: IEEE Press, 2012: 516-527.
|
| [14] |
YE L X, KEOGH E. Time series shapelets: a new primitive for data mining[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM Press, 2009: 947-956.
|
| [15] |
LINES J, BAGNALL A. Time series classification with ensembles of elastic distance measures[J]. Data Mining and Knowledge Discovery, 2015, 29(3): 565-592. DOI:10.1007/s10618-014-0361-2 |
| [16] |
HILLS J, LINES J, BARANAUSKAS E, et al. Classification of time series by shapelet transformation[J]. Data Mining and Knowledge Discovery, 2014, 28(4): 851-881. DOI:10.1007/s10618-013-0322-1 |
| [17] |
RAKTHANMANON T, KEOGH E. Fast shapelets: a scalable algorithm for discovering time series shapelets[C]//Proceedings of 2013 SIAM International Conference on Data Mining. Philadelphia, USA: Society for Industrial and Applied Mathematics, 2013: 668-676.
|
| [18] |
BAGNALL A, LINES J, HILLS J, et al. Time-series classification with COTE: the collective of transformation-based ensembles[J]. IEEE Transactions on Knowledge and Data Engineering, 2015, 27(9): 2522-2535. DOI:10.1109/TKDE.2015.2416723 |
| [19] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need?[EB/OL]. [2021-02-10]. https://arxiv preprint arxiv:1706.03762.
|
| [20] |
MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693. DOI:10.1109/34.192463 |
| [21] |
LI S Y, JIN X Y, XUAN Y, et al. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting[EB/OL]. [2021-02-10]. https://arxiv.org/abs/1907.00235.
|
| [22] |
DAU H A, BAGNALL A, KAMGAR K, et al. The UCR time series archive[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(6): 1293-1305. DOI:10.1109/JAS.2019.1911747 |
| [23] |
SERRÀ J, PASCUAL S, KARATZOGLOU A. Towards a universal neural network encoder for time series[EB/OL]. [2021-02-10]. https://arxiv.org/abs/1805.03908.
|
| [24] |
CUI Z C, CHEN W L, CHEN Y X. Multi-scale convolutional neural networks for time series classification[EB/OL]. [2021-02-10]. https://arxiv.org/abs/160306995.
|
| [25] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [26] |
CHUNG J, GULCEHRE C, CHO K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[EB/OL]. [2021-02-10]. https://arxiv preprint arxiv:1412.3555.
|
| [27] |
WANG J Y, WANG Z, LI J F, et al. Multilevel wavelet decomposition network for interpretable time series analysis[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, USA: ACM Press, 2018: 2437-2446.
|
 2022, Vol. 48
2022, Vol. 48

