2. 西北大学 信息科学与技术学院,西安 710127
2. School of Information Science and Technology, Northwest University, Xi'an 710127, China
开放科学(资源服务)标志码(OSID):
云计算[1]是基于虚拟化技术和网格计算而发展起来的一种新兴计算模式,与网格计算相比,云计算的任务更具复杂性,在这种模式中,应用、数据和IT资源以服务的形式经过网络提供给用户使用,给用户带来诸多方便。近年来,越来越多的公司将应用部署在云端,这使得云数据中心的功耗波动更加剧烈,从而导致云数据中心资源利用率不平衡问题[2]。在负载快速增加时,从分配主机资源到使用主机资源的过程会产生时间延迟,在负载变化后分配资源时服务水平协议(Service Level Agreement,SLA)将遭到破坏。
为了给用户提供高性能的云服务,在云分布式控制系统中进行资源管理非常重要[3],它可以降低云数据中心能耗成本和二氧化碳排放量[4-5]。负载预测技术[6]是对云分布式控制系统进行资源管理的关键技术,其可以在不破坏SLA和不影响数据中心运行的前提下,通过对云数据中心的历史数据进行分析,以掌握负载数据的变化规律并准确预测下一时期的负载值,从而通过合理地分配云数据中心的资源来提高其资源利用率。
目前,针对时间序列的负载预测大多基于深度学习中的循环神经网络(Recurrent Neural Network,RNN)来进行建模,但是RNN在预测时间序列时存在梯度消失和梯度爆炸的问题。本文针对负载预测模型中存在的预测精度低、预测时间长的问题,提出一种组合预测模型GRU-LSTM,该模型结合门控循环单元(Gate Recurrent Unit,GRU)预测时间短、长短期记忆(Long-Short Term Memory,LSTM)预测精度高的优点,对云计算资源进行高效预测,从而提高云数据中心的资源利用率。
1 相关工作对云计算资源负载进行预测是一个典型的时间序列预测问题。目前,针对时间序列的预测方法主要分为基于机器学习的方法和基于深度学习的方法两类。
在基于机器学习的方法中,KHAIRALLA[7]提出一种混合模型,其将自回归移动平均模型(Auto-Regression and Moving Average Model,ARIMA)与支持向量机(Support Vector Machine,SVM)进行组合,然后对金融时间序列进行预测,并与人工神经网络(Artificial Neural Network,ANN)和SVM进行对比。BI等[8]提出一种小波分解与ARIMA的混合模型以对未来负荷进行预测,该模型通过SavitzkyGolay滤波平滑任务时间序列,并通过小波分解将其分解为多个分量,通过小波分解重构它们的预测结果,以估计到达任务数。但是,该模型可以通过使用更好的数据平滑算法来进一步提高其预测精度。LIU[9]利用支持向量回归(Support Vector Regression,SVR)建立0-1整数规划模型,将工作负载分类问题转化为任务分配问题,并提供在线解决方案。ZHONG[10]提出一种基于WSVM的预测算法,其利用小波分解对输入信号进行分解然后使用SVM完成预测,最后利用Google提供的集群公开数据集进行实验验证。GUPTA[11]提出一种基于分数差分的方法来捕捉时间序列数据的长相关性,并在Google提供的集群公开数据集上进行实验验证,结果表明,与非分数差分的方法相比,分数差分的方法具有更好的预测结果。
在基于深度学习的方法中,ZHANG[12]引入一种深度学习模型,利用规范多元分解来预测云负荷,并使用深度学习模型来学习虚拟机中复杂负载数据的重要特征,最后应用规范多元分解来压缩模型参数以提高训练效率。目前,针对时间序列的预测大多基于RNN来建模。文献[13]利用RNN对云计算资源负载进行预测,并使用Google提供的集群公开数据集进行实验来验证该方法的准确性,RNN的循环自回归结构能对时间序列进行很好地表示,但它在对时间序列进行预测时存在梯度消失和梯度爆炸的问题。因此,由RNN衍生出的LSTM网络被广泛应用于时间序列预测任务。SUDHAKAR[14]将LSTM与RNN进行组合,以对服务器未来的工作负载进行预测,并与ARIMA模型进行比较,结果表明,LSTM-RNN模型的预测精度高于ARIMA,同时也验证了组合预测模型的预测精度高于单一预测模型,但由于LSTM与RNN都含有较多参数,因此预测时间较长。文献[15]提出一种改进的LSTM预测模型GSO-LSTM,利用该模型对云主机负载进行预测,并通过实验验证了利用萤火虫智能优化(Glowworm Swarm Optimization,GSO)算法对LSTM进行优化具有可行性。文献[16]提出一种组合预测模型ARIMA-LSTM,以对云平台资源进行预测,并利用CRITIC数据融合对误差值进行预测,实验结果表明,该预测模型的预测精度优于单一预测模型。CHEN[17]对LSTM采用集成学习的思想,通过丰富模型的输入维度来解决由于缺乏历史数据而无法建模的问题,但是,由于模型的输入维度增加,导致该方法训练时间较长。在使用LSTM对时间序列进行预测时,增加网络层数也可以取得更好的预测结果。文献[18-19]分别提出Refined LSTM与Stacked LSTM预测模型(Refined LSTM、Stacked LSTM均为多层网络结构),对电荷数据进行预测后得出结论,Refined LSTM与Stacked LSTM预测精度都优于LSTM。在对时间序列进行预测时,虽然LSTM在预测精度上优于其他单一预测模型,但是LSTM参数过多,导致预测时间较长。
作为LSTM的变体,GRU在对时间序列进行预测时,由于减少了一个门而使得预测时间变短。GUO等[20]提出GRU和自相关分析相结合的多步预测方法,仿真分析结果表明,所提GRU预测模型在进行负载预测时预测时间得到优化。对于一些特定的时间序列问题,采用时间卷积网络(Temporal Convolutional Network,TCN)进行建模也可以取得很好的效果。文献[21]利用TCN对几个真实世界的数据集进行实验,结果表明,TCN对于点预测和概率预测具有较好的效果,但是对于长时间预测的效果较差。
现有的预测模型通常是单一预测模型,或者是一些基于集成学习的组合预测模型[22]。单一预测模型虽然在预测时间上优于组合预测模型,但预测精度明显低于组合预测模型。而现有的一些组合预测模型预测精度虽然高于单一预测模型,但是预测精度相对也较低且没有考虑预测时间的问题。为提高云平台负载的预测精度和预测效率,本文结合GRU与LSTM各自的预测优势,提出一种基于GRU与LSTM的组合预测模型,以对云平台资源负载进行预测。
2 负载预测模型 2.1 问题描述本文主要对云计算资源的负载情况进行预测。假设云计算原始资源负载序列值为xt={x1,x2,…,xn},其中,xt为t时刻集群的负载情况。将CPU利用率和内存(mem)利用率的负载值进行组合后作为新的输入,原因是这2个指标可以最直接地体现集群在某个时刻的负载情况,也是使用随机森林算法[23]进行特征选择后得分最高的2个指标。设置步长为k,从原始资源负载序列值xt中选取前k个时刻的数据作为负载预测模型的输入向量z={zn-k,…,zn-2,zn-1},通过负载预测模型训练后得到k+1时刻集群的负载情况。
云环境中工作负载存在一定的依赖关系,每个时刻的负载情况都和之前时刻的负载情况有着十分密切的联系,当历史值越接近当前时刻t的值,它们之间的关系就越密切。对于模型选择而言,长距离的依赖信息可以提供趋势信息,不能完全忽略掉,为了更好地利用过去的负载数据,需要对历史数据进行有选择地保留和丢弃。LSTM中的遗忘门可以控制进入当前时刻的历史信息量以及需要被舍弃的信息量。因此,本文模型选择LSTM以及与LSTM具有相似网络结构的GRU。
2.2 LSTMLSTM作为一种改进的RNN,其继承了RNN模型的优点,并且利用独特的门结构有效解决了RNN中的梯度爆炸和梯度消失问题,因此,LSTM可以有效处理长时间序列问题,并已经成功应用于语音识别、图像描述、自然语言处理等领域。相较RNN和GRU,LSTM模型的拟合和预测精度总体较高,但是,由于LSTM参数过多导致其训练过程耗时较长。
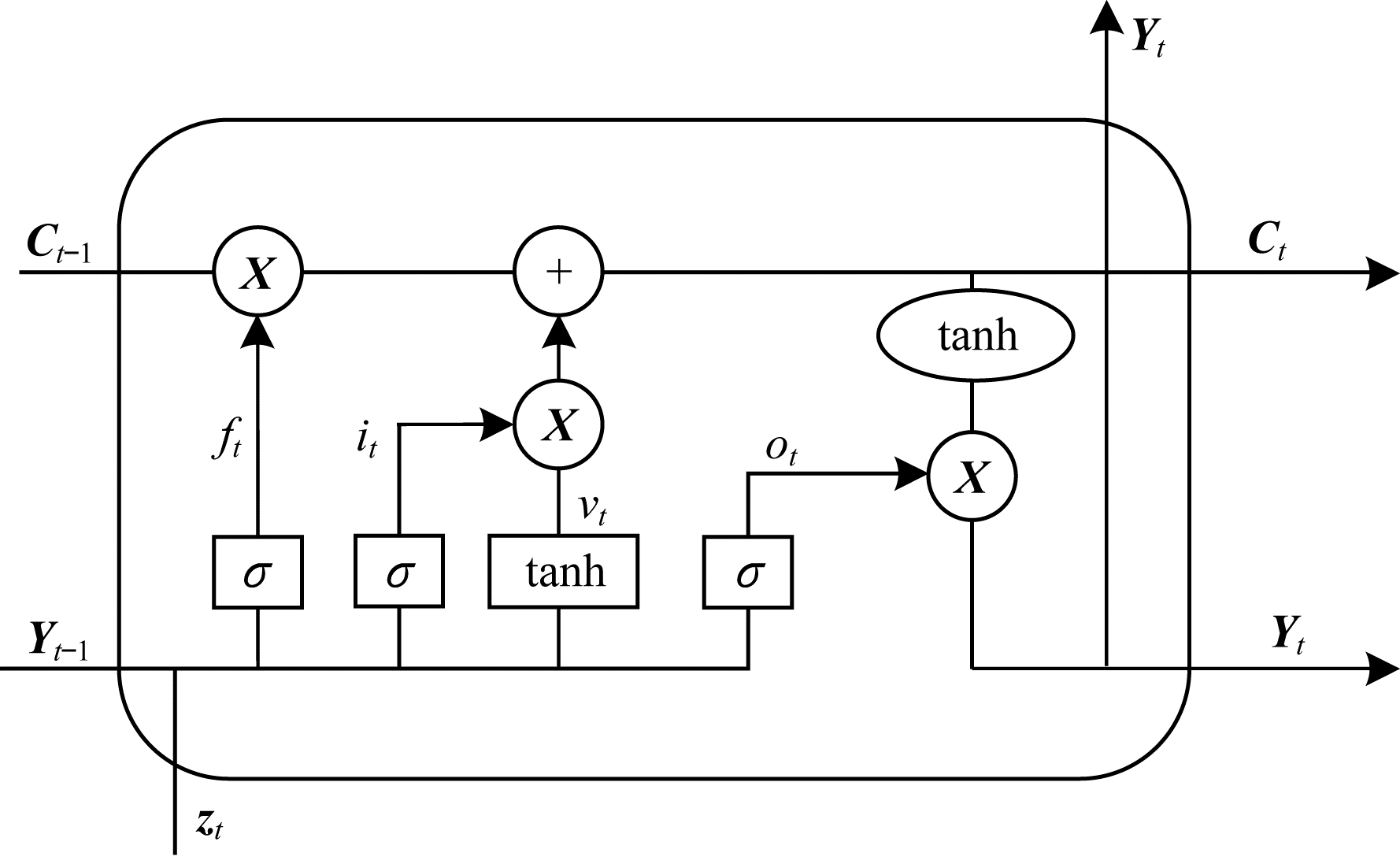
LSTM由多个循环单元组成,通过更新神经元状态信息,使用输入门、输出门、遗忘门来控制历史信息的权重从而存储过去的信息。基于LSTM的移动云主机t时刻负荷预测模型的单元结构如图 1所示。
|
Download:
|
| 图 1 LSTM单元结构 Fig. 1 Unit structure of LSTM | |
在图 1中:Ct-1为前一时刻神经元的状态;Yt-1为前一时刻神经元的输出;Zt为当前时刻的输入。
遗忘门决定上一时刻的单元状态Ct-1有多少可以保留到当前时刻Ct,遗忘门的输入包括前一时刻的输出Yt-1和当前时刻的负载Zt,最后通过最左边的激活函数sigmoid得到ft,计算如式(1)所示:
| $ {f}_{t}=\sigma ({\boldsymbol{W}}_{f}\cdot [{\boldsymbol{Y}}_{t-1}, {\boldsymbol{Z}}_{t}]+{\boldsymbol{b}}_{f}) $ | (1) |
| $ \sigma \left(z\right)=\frac{1}{1+{\mathrm{e}}^{-z}} $ | (2) |
其中:Wf是遗忘门的权重矩阵;bf表示偏差向量;σ表示激活函数sigmoid;ft表示最后一层神经元被遗忘的概率,取值范围为[0, 1],0表示完全丢弃,1表示完全保留。
输入门决定Zt中哪些新的输入可以存储在神经元中,神经元主要分为it和vt,其计算方法分别如式(3)和式(4)所示:
| $ {i}_{t}=\sigma ({\boldsymbol{W}}_{i}\cdot [{\boldsymbol{Y}}_{t-1}, {\boldsymbol{Z}}_{t}]+{\boldsymbol{b}}_{i}) $ | (3) |
| $ {v}_{t}=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}({\boldsymbol{W}}_{c}\cdot [{\boldsymbol{Y}}_{t-1}, {\boldsymbol{Z}}_{t}]+{\boldsymbol{b}}_{c}) $ | (4) |
| $ \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(z\right)=\frac{{\mathrm{e}}^{z}-{\mathrm{e}}^{-z}}{{\mathrm{e}}^{z}+{\mathrm{e}}^{-z}} $ | (5) |
其中:Wi 和Wc是输入门的权重矩阵;bi和bc为偏差向量。it和vt表示当前需要保留的负载信息的比例,其与前一时刻保留的神经元状态相加,生成更新后的神经元状态信息Ct,计算方法如式(6)所示:
| $ {\boldsymbol{C}}_{t}={f}_{t}\cdot {\boldsymbol{C}}_{t-1}+{i}_{t}\cdot {v}_{t} $ | (6) |
输出门控制神经元状态的输出并将状态转移到下一个神经元,输出门ot的计算方法如式(7)所示:
| $ {o}_{t}=\sigma ({\boldsymbol{W}}_{o}\cdot [{\boldsymbol{Y}}_{t-1}, {\boldsymbol{Z}}_{t}]+{\boldsymbol{b}}_{o}) $ | (7) |
其中:Wo为输出门的权重矩阵;bo为偏差向量;Yt为当前时刻神经元的输出。通过最后一层的计算得到最终的负载预测值,如式(8)所示:
| $ {\boldsymbol{Y}}_{t}={o}_{t}\cdot \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left({\boldsymbol{C}}_{t}\right) $ | (8) |
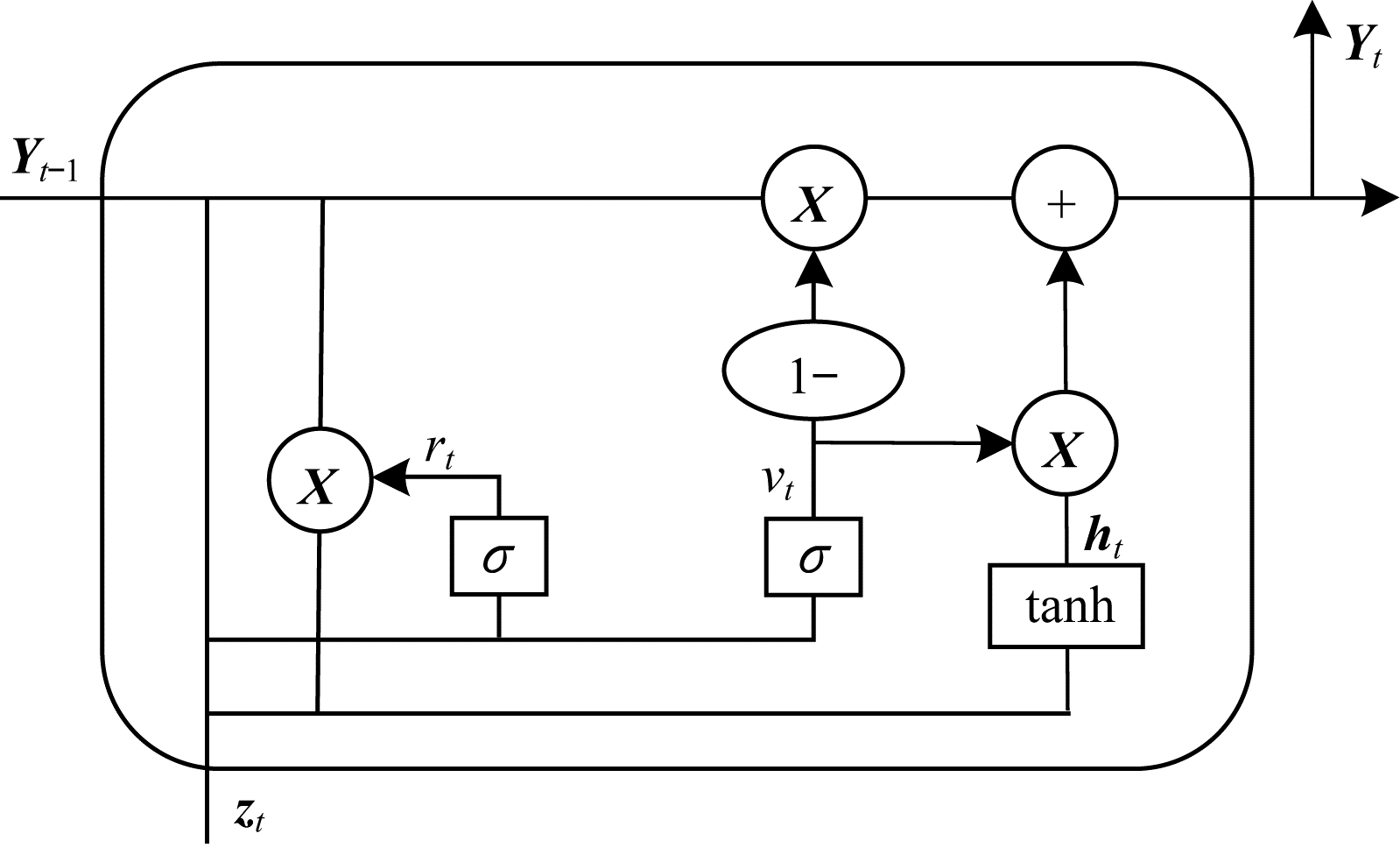
GRU作为LSTM的一种变体,也可以有效地解决RNN中的梯度爆炸和梯度消失问题。与LSTM相比,GRU的结构更为简单,其将遗忘门和输入门合并为一个更新门。由于GRU减少了一个门,矩阵乘法变少,因此当训练数据量很大时可以节省大量的时间,GRU网络结构如图 2所示。
|
Download:
|
| 图 2 GRU网络结构 Fig. 2 GRU network structure | |
在图 2中:Zt为当前时刻的输入;Yt-1为上一时刻的输出;Yt为当前时刻的输出。GRU有2个门:
1)第一个门为更新门vt,其决定有多少历史信息可以继续传递给未来,即更新门vt决定是否将隐藏状态更新为新状态。从功能上看,GRU的更新门vt类似于LSTM的输出门,更新门vt的计算方法如式(9)所示:
| $ {v}_{t}=\sigma ({\boldsymbol{W}}_{v}\cdot [{\boldsymbol{Y}}_{t-1}, {\boldsymbol{Z}}_{t}]+{\boldsymbol{b}}_{v}) $ | (9) |
其中:Wv为更新门的权重矩阵;bv为偏差向量。
2)第二个门为重置门rt,其主要功能是确定有多少历史信息不能传递到下一个状态,类似于LSTM中遗忘门和输入门的组合。重置门rt的计算方法如式(10)所示:
| $ {r}_{t}=\sigma ({\boldsymbol{W}}_{r}\cdot [{\boldsymbol{Y}}_{t-1}, {\boldsymbol{Z}}_{t}]+{\boldsymbol{b}}_{r}) $ | (10) |
其中:Wr为重置门的权重矩阵;br为偏差向量。
计算出更新门vt和重置门rt后,GRU将计算候选隐藏状态ht。候选隐藏状态ht计算方法如式(11)所示:
| $ {\boldsymbol{h}}_{t}=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}({\boldsymbol{W}}_{h}\cdot [{r}_{t}\cdot {\boldsymbol{Y}}_{t-1}, {\boldsymbol{Z}}_{t}]+{\boldsymbol{b}}_{h}) $ | (11) |
其中:Wh为对应的权重参数;bh为对应的偏差参数。从式(11)可以看出:当重置门rt的值接近0时,重置门对应的候选隐藏状态值也为0,即丢弃上一时刻的隐藏状态;当重置门rt的值接近1时,表示保留上一时刻的隐藏状态。因此,重置门的作用是有选择地丢弃与预测无关的历史信息。
最后,t时刻GRU的输出Yt的计算方法如式(12)所示:
| $ {\boldsymbol{Y}}_{t}=(1-{v}_{t})\cdot {\boldsymbol{Y}}_{t-1}+{v}_{t}\cdot {\boldsymbol{h}}_{t} $ | (12) |
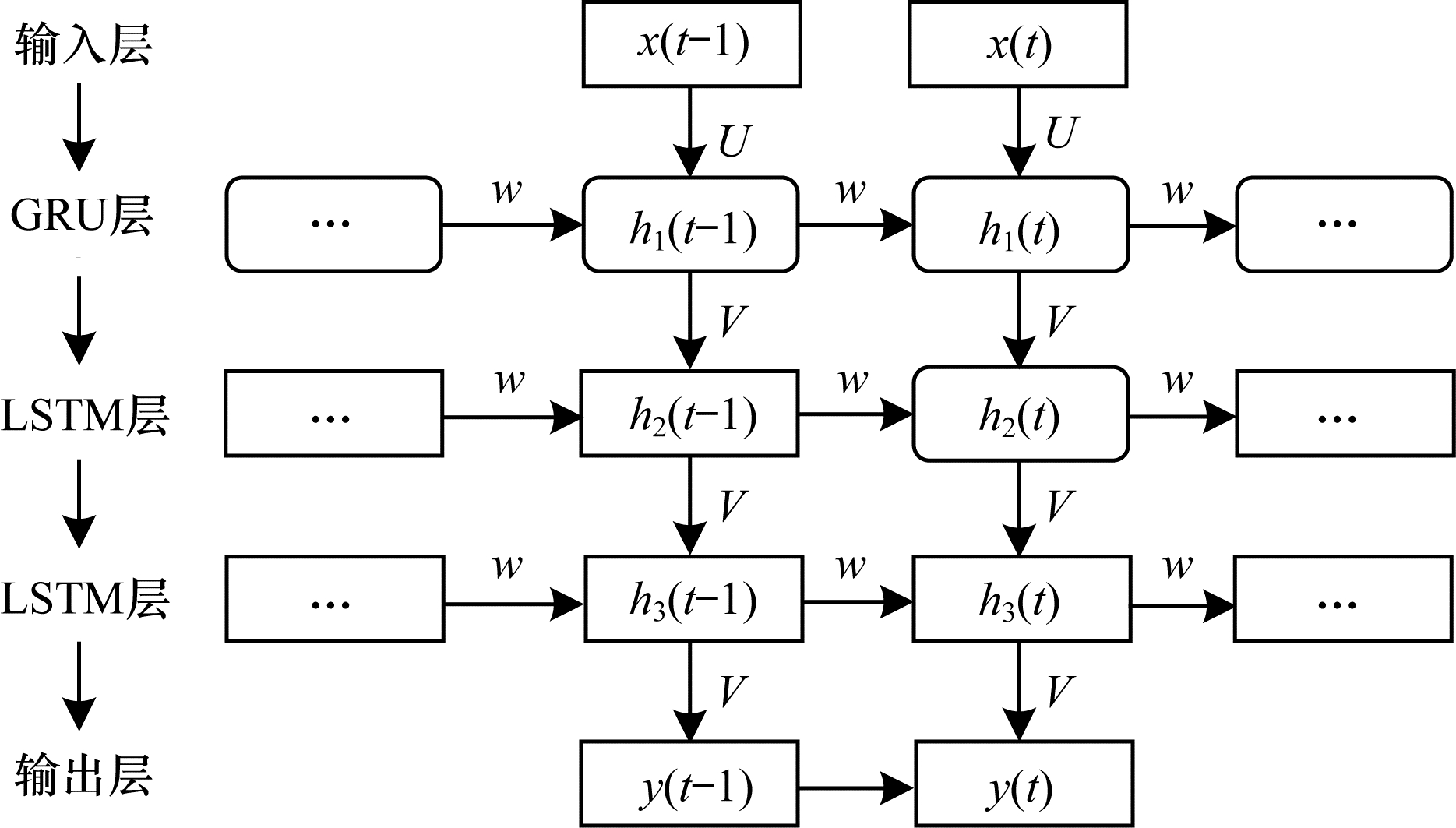
综合考虑预测精度和预测时间2个方面的因素,本文建立一种基于GRU与LSTM的组合预测模型,以对云计算资源负载进行预测。组合预测模型网络结构如图 3所示。
|
Download:
|
| 图 3 组合预测模型网络结构 Fig. 3 Network structure of combined forecasting model | |
本文组合预测模型的网络结构包括3层:第一层网络结构采用GRU,由于GRU的网络结构简单,参数少,更易收敛,因此在训练数据时GRU训练速度快,可以减少训练时间,但是,GRU的预测精度低于LSTM;第二层和第三层网络结构均采用LSTM,LSTM参数较多,预测精度更高,并且双层LSTM的预测精度优于单层LSTM。
2.5 模型评价标准本文采用平均绝对误差(Mean Absolute Error,MAE)、平均绝对值百分比误差(Mean Absolute Percentage Error,MAPE)、均方误差(Mean Squared Error,MSE)、均方根误差(Root Mean Square Error,RMSE)、决定系数(R2)作为模型的性能评估标准。预测时间主要以模型的训练时间作为评价标准。在对模型进行泛化实验时,采用可释方差得分(explanied_variance_score,简写为S)对模型的拟合程度进行评价。各指标的计算方法如下:
| $ {M}_{\mathrm{M}\mathrm{A}\mathrm{E}}=\dfrac{1}{n}\sum\limits_{i=1}^{n}|{y}_{i}-{\widehat{y}}_{i}| $ | (13) |
| $ {M}_{\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}}=\dfrac{1}{n}\sum\limits_{i=1}^{n}\left|\frac{{y}_{i}-{\widehat{y}}_{i}}{{y}_{i}}\right|\times 100\mathrm{\%} $ | (14) |
| $ {M}_{\mathrm{M}\mathrm{S}\mathrm{E}}=\dfrac{1}{n}\sum\limits_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i}{)}^{2} $ | (15) |
| $ {R}_{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}=\sqrt{\dfrac{1}{n}\sum\limits_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i}{)}^{2}} $ | (16) |
| $ {\mathrm{R}}^{2}=1-\frac{\sum\limits_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i}{)}^{2}}{\sum\limits_{i=1}^{n}({y}_{i}-{\stackrel{-}{y}}_{i}{)}^{2}} $ | (17) |
| $ S=1-\frac{\mathrm{V}\mathrm{a}\mathrm{r}\{{y}_{i}-{\widehat{y}}_{i}\}}{\mathrm{V}\mathrm{a}\mathrm{r}\left\{{y}_{i}\right\}} $ | (18) |
其中:n为负载预测值个数;
为了验证本文负载预测模型的预测性能,使用阿里云2018年发布的集群公开数据集Cluster-trace-v2018[24]进行实验。Cluster-trace-v2018包括大约4 000台机器在8天内的资源使用情况,本文实验使用其中1台机器在8天内的资源使用情况,共3 300条数据记录,选取前80%的数据作为训练集,后20%的数据作为测试集。本文对数据集进行如下处理:
1)缺失值处理。利用均值填充法进行缺失值处理。
2)标准化处理[25]。为了提高神经网络的收敛速度、迭代求解速度以及预测精度,采用式(19)(Min-Max归一化)对训练集的2 600个数据进行标准化处理:
| $ {X}_{t}^{\mathrm{*}}=\frac{{X}_{t}-{X}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{X}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{X}_{\mathrm{m}\mathrm{i}\mathrm{n}}} $ | (19) |
其中:
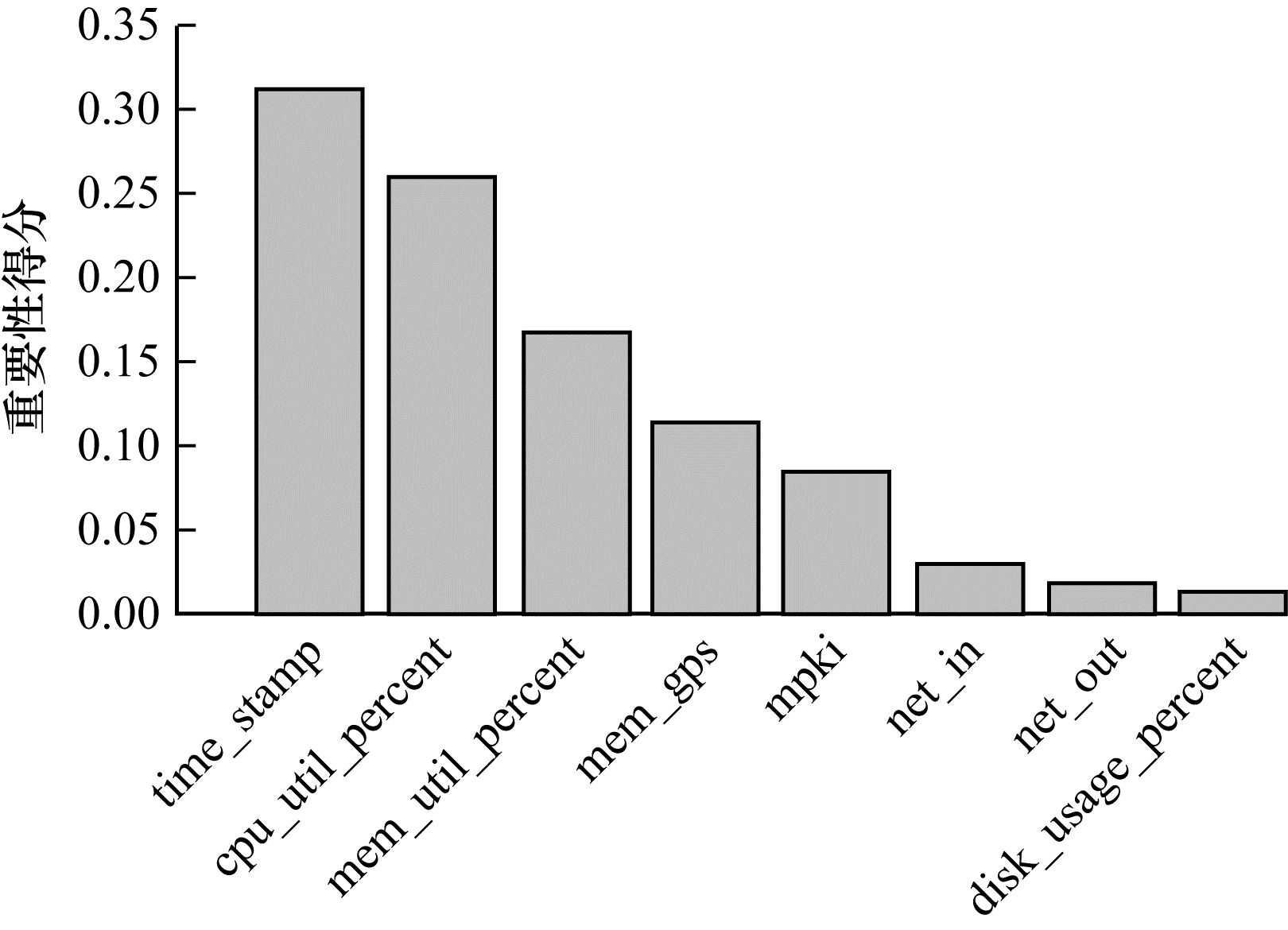
3)特征选择。特征选择可以从原始数据特征集中选出若干个具有代表性的特征子集,这不仅可以实现数据降维,还可以提升在该特征子集上所构建的回归模型的性能。随机森林算法通过特征随机置换前后误差分析,计算每个特征的重要性得分,得分越高,特征越重要,与其他特证选择算法相比,随机森林算法不仅能体现特征间的相互作用,而且还具有准确性高、鲁棒性好等优点[26]。因此,本文使用随机森林算法进行特征选择,特征选择结果如图 4所示,横坐标为特征。
|
Download:
|
| 图 4 特征选择结果 Fig. 4 Feature selection results | |
从图 4可以看出,CPU利用率和mem利用率是除时间特征之外经过特征选择后得分最高的2个特征,因此,本文实验选择CPU利用率和mem利用率的组合值作为云平台资源的负载值。负载值的计算公式如下:
| $ \boldsymbol{W}={\boldsymbol{W}}_{1}\cdot {L}_{1}+{\boldsymbol{W}}_{2}\cdot {L}_{2} $ | (20) |
其中:W为组合后的原始负载值;W1和W2分别代表CPU负载值和mem负载值;L1和L2分别代表CPU和mem的权重参数。本文根据特征的得分指数比例,设置L1为0.6,L2为0.4。
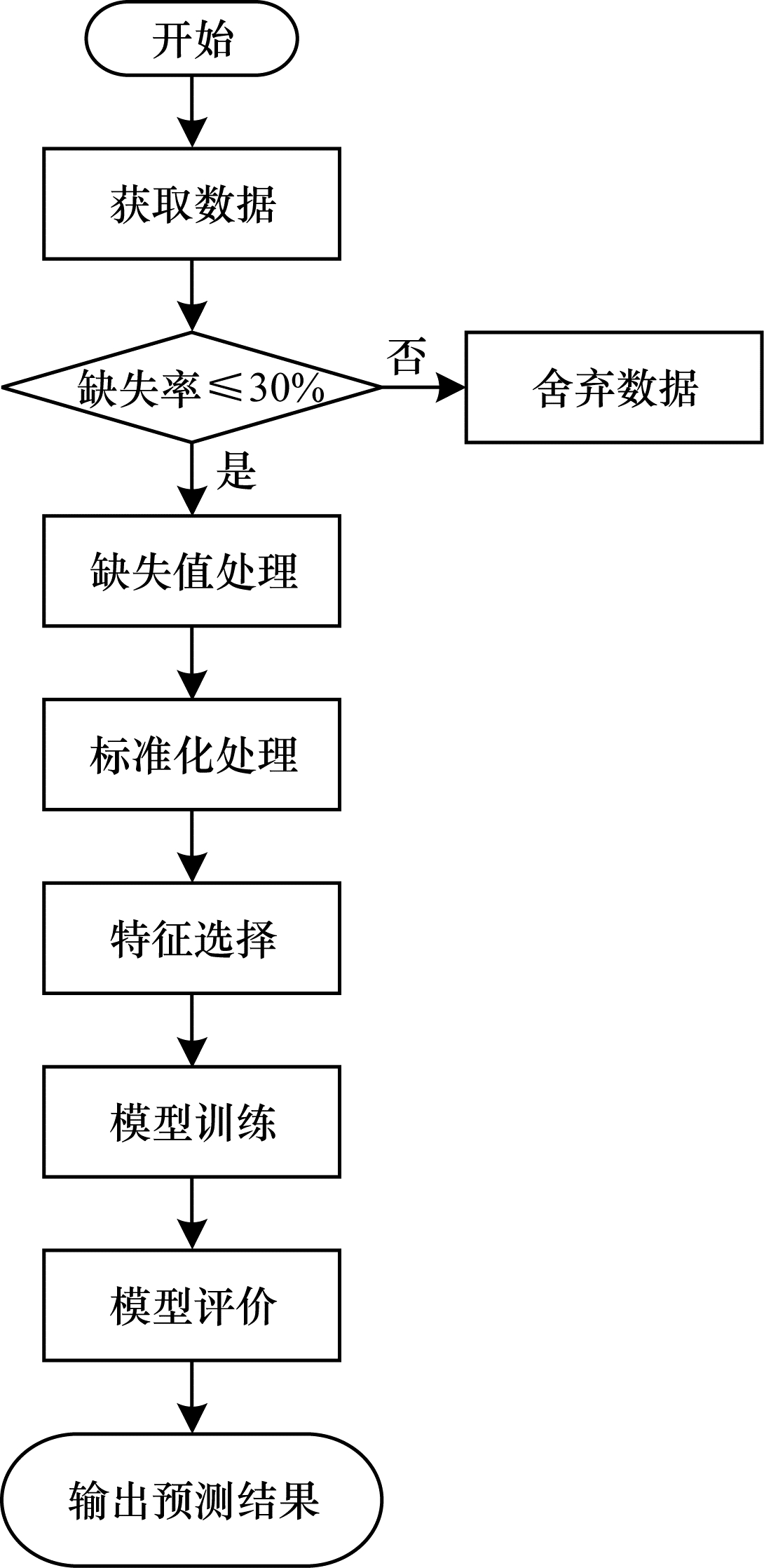
3.2 实验过程本文实验是一个单步预测过程,预测流程如图 5所示。
|
Download:
|
| 图 5 预测流程 Fig. 5 Procedure of prediction | |
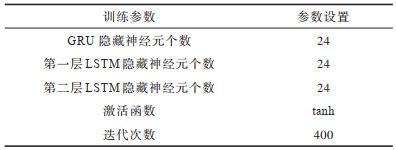
在获取数据后,首先对原始数据进行缺失值和标准化处理,当原始数据缺失率大于30%时,舍弃该条数据,若缺失率小于等于30%,则使用均值填充法对缺失值进行填充,并将填充后的数据通过归一化方法进行标准化处理,利用随机森林算法对标准化后的数据进行特征选择,根据特征的重要程度将特征选择后得到的特征数据加入权重参数进行组合,将组合后的负载值输入GRU-LSTM组合预测模型进行训练,设置步长为12(根据前12个数据来预测第13个数据)。最后,使用5个评价标准对模型性能进行评价,同时输出模型预测结果。预测模型参数设置如表 1所示。
|
下载CSV 表 1 参数设置 Table 1 Parameters setting |
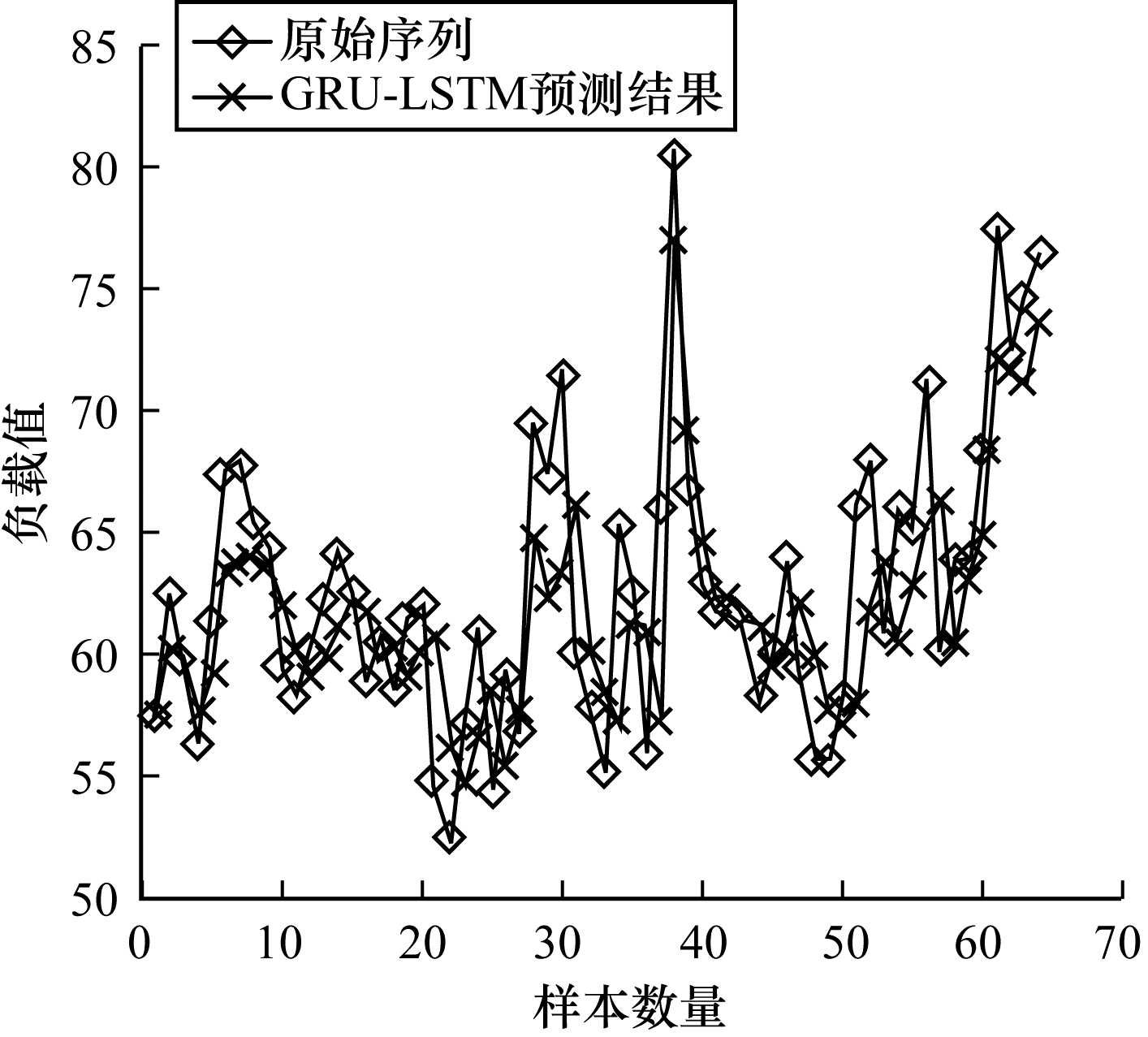
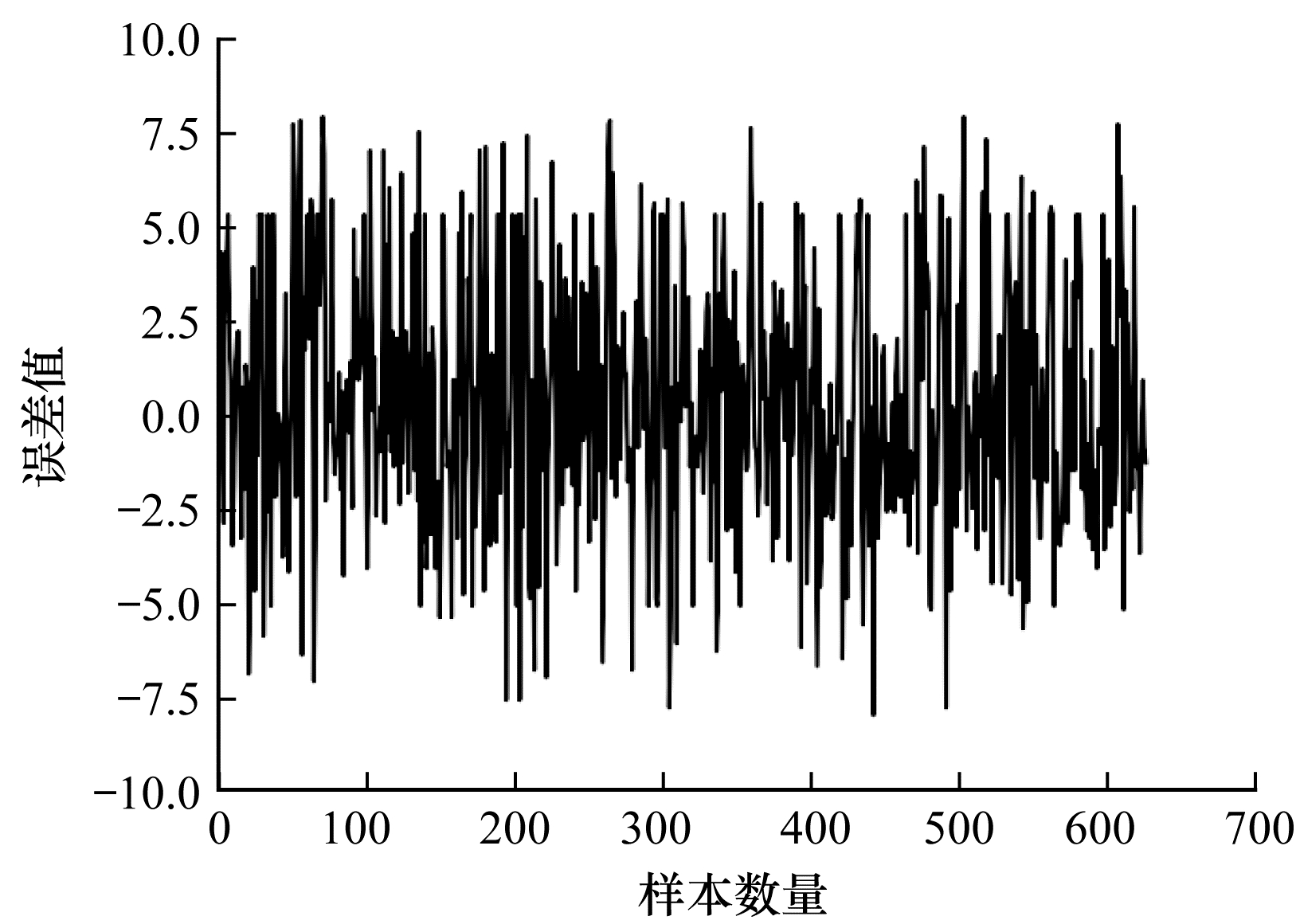
模型预测结果(64个样本)如图 6所示,从图 6可以看出,本文所提GRU-LSTM组合预测模型的预测结果与原始序列的趋势基本一致。从图 7可以看出(640个样本),本文GRU-LSTM模型经过训练后得到的预测数据与真实数据的误差大多集中在-5.0~5.0之间,误差较小,因此,该组合预测模型预测精度较高。
|
Download:
|
| 图 6 GRU-LSTM模型的预测结果 Fig. 6 Prediction results of GRU-LSTM model | |
|
Download:
|
| 图 7 GRU-LSTM预测误差结果 Fig. 7 GRU-LSTM prediction error results | |
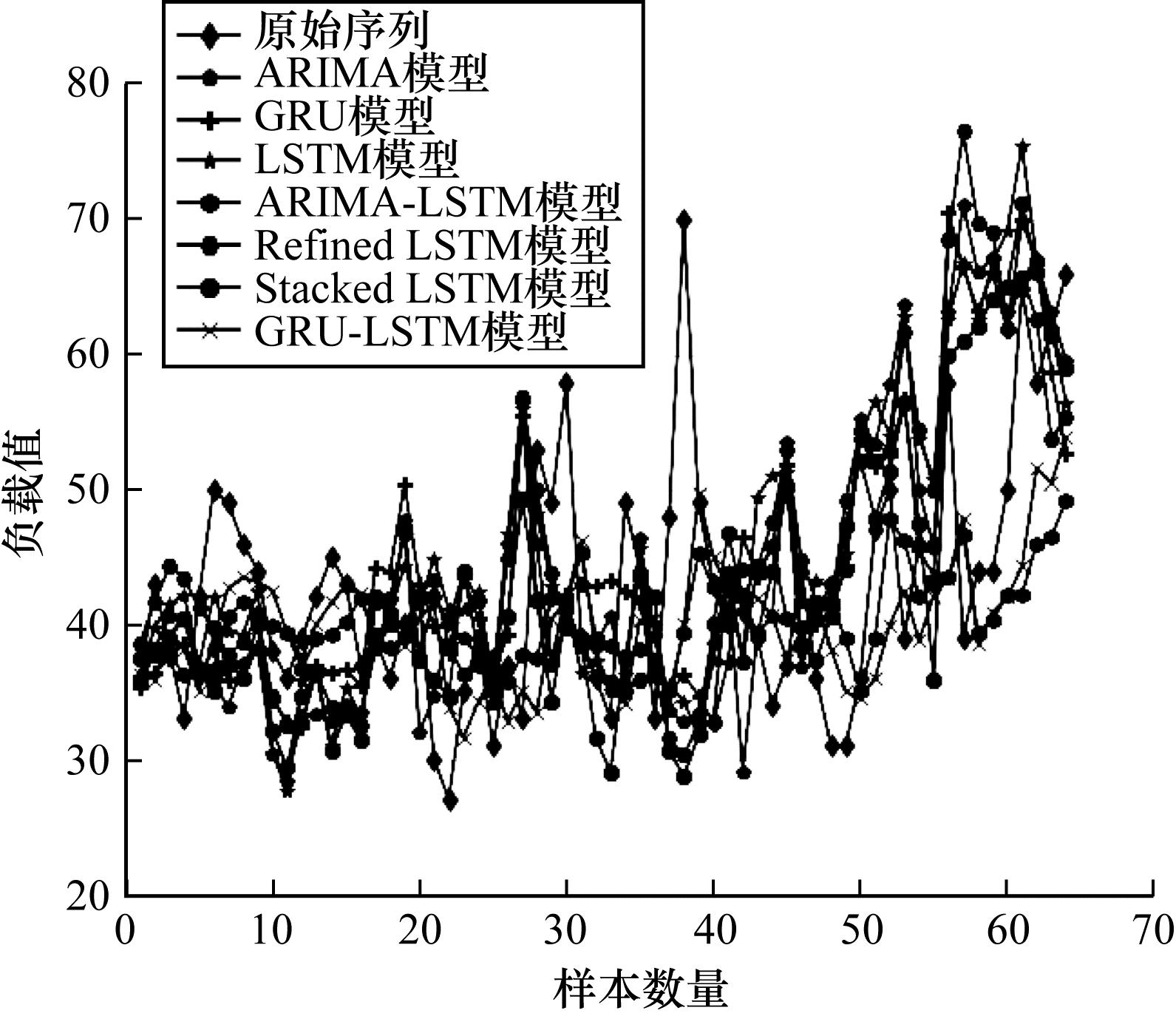
将本文模型与传统的单一负载预测模型ARIMA、GRU、LSTM进行对比,同时还与文献[16]提出的ARIMA-LSTM组合预测模型、文献[18]提出的Refined LSTM模型、文献[19]提出的Stacked LSTM模型进行实验对比。各模型的负载预测结果如图 8所示(64个样本),评价指标结果如表 2所示,最优结果加粗表示。
|
Download:
|
| 图 8 各模型的负载预测结果 Fig. 8 Load prediction results of each model | |
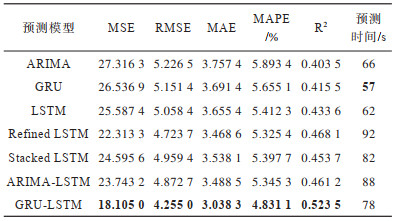
|
下载CSV 表 2 各模型的评价指标结果 Table 2 Evaluation index results of each model |
从图 8和表 2可以看出:相较传统的单一预测模型ARIMA、LSTM以及GRU,本文GRU-LSTM模型的预测精度较高,同时也验证了组合预测模型的预测精度要优于单一预测模型;相较组合预测模型ARIMA-LSTM、Refined LSTM和Stacked LSTM,本文模型的预测精度同样较高。虽然2层网络结构相比3层网络结构减少了参数,但是这在一定程度上削弱了模型的学习能力。本文所提GRU-LSTM模型结合GRU训练速度快、LSTM预测性能好的优点,在预测精度和预测时间上取得性能提升。
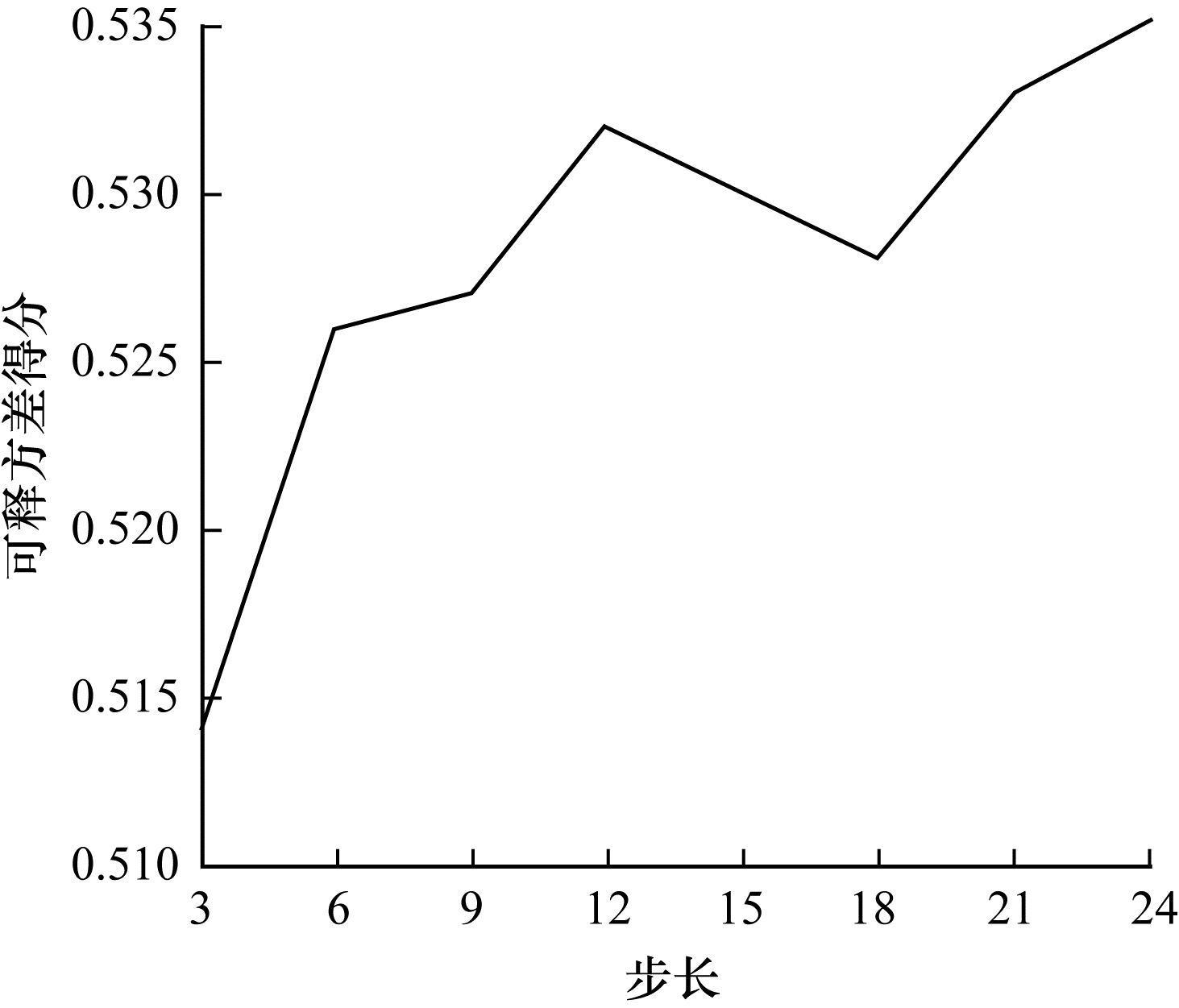
为了对模型的泛化能力进行验证,设置不同的步长重复进行实验,使用explanied_variance_score作为评价标准,结果如图 9所示。
|
Download:
|
| 图 9 不同步长下的可释方差得分结果 Fig. 9 explanied_variance_score results under different steps | |
通过图 9可以看出,GRU-LSTM组合预测模型的可释方差得分介于0.510~0.535之间,即该组合模型在不同的步长情况下均可以有效地对云计算资源负载值进行预测,其具备一定的泛化能力。
4 结束语针对目前负载预测模型预测精度低且预测时间长的问题,本文提出一种基于LSTM与GRU的组合预测模型GRU-LSTM,以对云计算资源负载情况进行预测。在阿里云平台发布的集群公开数据集上进行实验,结果表明,相较ARIMA、LSTM等模型,该负载预测模型具有较高的预测精度以及较短的预测时间,同时具有一定的泛化能力,将该模型应用到实际的云平台中,可以解决目前资源利用率不平衡的问题。下一步考虑通过优化算法寻找模型的最优参数,或对数据进行降噪处理,以提升本文模型的预测精度。此外,探索多变量和长时间序列的内在关联性并解决深度神经网络对输入变化不敏感的问题,也是今后的研究方向。
| [1] |
BOLIN J, YANG M K. Cloud computing: cost, security, and performance[C]//Proceedings of 2018 ACMSE Conference. New York, USA: ACM Press, 2018: 1.
|
| [2] |
MASDARI M, NABAVI S S, AHMADI V. An overview of virtual machine placement schemes in cloud computing[J]. Journal of Network and Computer Applications, 2016, 66: 106-127. DOI:10.1016/j.jnca.2016.01.011 |
| [3] |
MASDARI M, SALEHI F, JALALI M, et al. A survey of PSO-based scheduling algorithms in cloud computing[J]. Journal of Network and Systems Management, 2017, 25(1): 122-158. DOI:10.1007/s10922-016-9385-9 |
| [4] |
SINGH S, CHANA I. A survey on resource scheduling in cloud computing: issues and challenges[J]. Journal of Grid Computing, 2016, 14(2): 217-264. DOI:10.1007/s10723-015-9359-2 |
| [5] |
SHAO G L, CHEN J M. A load balancing strategy based on data correlation in cloud computing[C]//Proceedings of the 9th International Conference on Utility and Cloud Computing. New York, USA: ACM Press, 2016: 364-368.
|
| [6] |
MASDARI M, KHOSHNEVIS A. A survey and classifi-cation of the workload forecasting methods in cloud computing[J]. Cluster Computing, 2020, 23(4): 2399-2424. DOI:10.1007/s10586-019-03010-3 |
| [7] |
KHAIRALLA M A, NING X. Financial time series forecasting using hybridized support vector machines and ARIMA models[C]//Proceedings of 2017 International Conference on Wireless Communications, Networking and Applications. New York, USA: ACM Press, 2017: 94-98.
|
| [8] |
BI J, ZHANG L B, YUAN H T, et al. Hybrid task prediction based on wavelet decomposition and ARIMA model in cloud data center[C]//Proceedings of IEEE International Conference on Networking, Sensing and Control. Washington D.C., USA: IEEE Press, 2018: 1-6.
|
| [9] |
LIU C H, LIU C C, SHANG Y L, et al. An adaptive prediction approach based on workload pattern discrimination in the cloud[J]. Journal of Network and Computer Applications, 2017, 80: 35-44. DOI:10.1016/j.jnca.2016.12.017 |
| [10] |
ZHONG W, ZHUANG Y, SUN J, et al. The cloud computing load forecasting algorithm based on wavelet support vector machine[C]//Proceedings of the Australasian Computer Science Week Multiconference. New York, USA: ACM Press, 2017: 1-5.
|
| [11] |
GUPTA S, DILEEP A D, GONSALVES T A. Fractional difference based hybrid model for resource prediction in cloud network[C]//Proceedings of the 15th International Conference on Network, Communication and Computing. New York, USA: ACM Press, 2016: 93-97.
|
| [12] |
ZHANG Q C, YANG L T, YAN Z, et al. An efficient deep learning model to predict cloud workload for industry informatics[J]. IEEE Transactions on Industrial Informatics, 2018, 14(7): 3170-3178. DOI:10.1109/TII.2018.2808910 |
| [13] |
ZHANG W S, LI B, ZHAO D H, et al. Workload prediction for cloud cluster using a recurrent neural network[C]//Proceedings of International Conference on Identification, Information and Knowledge in the Internet of Things. Washington D.C., USA: IEEE Press, 2016: 104-109.
|
| [14] |
SUDHAKAR C, KUMAR A R, SIDDARTHA N, et al. Workload prediction using ARIMA statistical model and long short-term memory recurrent neural networks[C]//Proceedings of International Conference on Computing, Power and Communication Technologies. Washington D.C., USA: IEEE Press, 2018: 600-604.
|
| [15] |
ZHANG Z H, ZHU W, ZHONG W, et al. Load forecasting model of mobile cloud computing based on glowworm swarm optimization LSTM network[C]//Proceedings of the 7th International Conference on Information Technology: IoT and Smart City. Washington D.C., USA: IEEE Press, 2019: 113-119.
|
| [16] |
林涛, 冯竞凯, 郝章肖, 等. 基于组合预测模型的云计算资源负载预测研究[J]. 计算机工程与科学, 2020, 42(7): 1168-1173. LIN T, FENG J K, HAO Z X, et al. Cloud computing resource load prediction based on combined prediction model[J]. Computer Engineering & Science, 2020, 42(7): 1168-1173. (in Chinese) |
| [17] |
CHEN L, YU H H, TONG L, et al. Research on load forecasting method of distribution transformer based on deep learning[C]//Proceedings of the 7th IEEE International Conference on Cyber Security and Cloud Computing. Washington D.C., USA: IEEE Press, 2020: 228-233.
|
| [18] |
TANG D D, LI C, JI X H, et al. Power load forecasting using a Refined LSTM[C]//Proceedings of the 11th International Conference on Machine Learning and Computing. Washington D.C., USA: IEEE Press, 2019: 104-108.
|
| [19] |
YUAN C M, XIU T, LOU T Y. Probabilistic long-term load forecasting based on Stacked LSTM[C]//Proceedings of the 4th International Conference on Mathematics and Artificial Intelligence. Washington D.C., USA: IEEE Press, 2019: 80-84.
|
| [20] |
GUO J Y, WANG Z J, CHEN H W. On-line multi-step prediction of short term traffic flow based on GRU neural network[C]//Proceedings of the 2nd International Conference on Intelligent Information Processing. Washington D.C., USA: IEEE Press, 2017: 1-6.
|
| [21] |
CHEN Y T, KANG Y F, CHEN Y X, et al. Probabilistic forecasting with temporal convolutional neural network[J]. Neurocomputing, 2020, 399: 491-501. DOI:10.1016/j.neucom.2020.03.011 |
| [22] |
SHETTY J, SHOBHA G. An ensemble of automatic algorithms for forecasting resource utilization in cloud[C]//Proceedings of Future Technologies Conference. Washington D.C., USA: IEEE Press, 2016: 301-306.
|
| [23] |
DEVIAENE M, TESTELMANS D, BORZÉE P, et al. Feature selection algorithm based on random forest applied to sleep apnea detection[C]//Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Washington D.C., USA: IEEE Press, 2019: 2580-2583.
|
| [24] |
CHENG Y, ANWAR A, DUAN X J. Analyzing Alibaba's co-located datacenter workloads[C]//Proceedings of IEEE International Conference on Big Data. Washington D.C., USA: IEEE Press, 2018: 292-297.
|
| [25] |
蔡亮, 周泓岑, 白恒, 等. 基于多层BiLSTM和改进粒子群算法的应用负载预测方法[J]. 浙江大学学报(工学版), 2020, 54(12): 2414-2422. CAI L, ZHOU H C, BAI H, et al. Application load forecasting method based on multi-layer bidirectional LSTM and improved PSO algorithm[J]. Journal of Zhejiang University(Engineering Science), 2020, 54(12): 2414-2422. (in Chinese) |
| [26] |
董兰芳, 张军挺. 基于深度学习与随机森林的人脸年龄与性别分类研究[J]. 计算机工程, 2018, 44(5): 246-251. DONG L F, ZHANG J T. Research on face age and gender classification based on deep learning and random forest[J]. Computer Engineering, 2018, 44(5): 246-251. (in Chinese) |
 2022, Vol. 48
2022, Vol. 48
