2. 南方海洋科学与工程广东省实验室, 广东 珠海 519080;
3. 澳门大学 计算机与信息科学系, 澳门 999078;
4. 北京科技大学 计算机与通信工程学院, 北京 100083
2. Southern Marine Science and Engineering Guangdong Laboratory, Zhuhai, Guangdong 519080, China;
3. Department of Computer and Information Science, University of Macau, Macao 999078, China;
4. School of Computer and Communication Engineering, University of Science and Technology Beijing, Beijing 100083, China
开放科学(资源服务)标志码(OSID):
推荐系统是数据挖掘和机器学习领域最重要的应用之一,它能够帮助平台用户缓解信息过载的问题,并在电商平台、音乐网站等许多网页应用中挑选出有价值的信息。在大部分推荐系统中用户的行为序列是按照时间排列的,并且呈现出匿名性和大数据量的特征。为了预测用户在下一时刻的行为信息,基于会话序列的推荐通过挖掘用户历史行为中的序列顺序特征信息,从而学习用户的喜好[1]。会话序列是指在一段时间间隔内的由用户点击而产生的项目序列,而基于会话序列的推荐能捕捉到序列内部的依赖关系对序列预测的重要性[2]。用户在某一个会话序列中通常有着一个共同的目的,如购买下装衣物;而用户在不同序列之间的行为特性可能关联性不大,如在别的会话中用户的目的是购买手机配件等。
鉴于其较高的实际价值,基于会话序列的推荐在近年来得到了研究人员很大的关注,并且出现了许多具有良好效果的研究成果。早期的算法主要基于马尔科夫链和循环神经网络(Recurrent Neural Networks,RNN)。随着近期图神经网络(Graph Neural Networks,GNN)的兴起并且在许多下游任务中有着较好的表现[3-4],有研究人员将GNN应用到了基于会话序列推荐中[5-6]。尽管这些基于GNN的算法有着较好的表现,但是这些算法也存在以下问题:忽略了点击序列中重复出现的项目,多次出现的项目与其他项目的重要程度是不同的,这些项目在一定程度上能够体现用户偏好信息;在生成项目的向量表示时没有较好地利用会话序列图中的结构信息,只考虑项目之间的方向性还有所欠缺,引入项目之间的无向关系能够更好地学习用户的行为信息。
为解决以上问题,本文提出一种基于复杂结构信息的图神经网络序列推荐算法。利用带注意力的图卷积网络和门控图神经网络,分别提取序列图中项目之间的无向结构信息与有向结构信息,并引入注意力机制建模项目之间的复杂转换,从而得到项目隐含向量,根据隐含向量利用注意力网络结合会话的全局信息与局部信息,生成准确的会话向量表示。
1 相关工作 1.1 传统推荐算法早期的基于邻域建模算法在用户不匿名的推荐场景中使用最邻近算法进行会话序列预测[7-9],需要测量项目之间或者会话之间的相似度。DAVIDSON等[7]提出一种通过项目共同出现的模式来计算项目之间相似度的算法,并根据待预测会话序列中的项目推荐最有可能跟其共同出现的项目。PARK等[9]提出一种将会话序列转换成向量的算法,然后计算会话向量之间的余弦相似度。DIAS等[8]基于PARK的研究提出用聚类算法将稀疏会话向量转换为稠密向量,然后再计算稠密向量之间的余弦相似度,但它受到数据稀疏性的影响,且没有考虑到会话向量内部项目之间的复杂转换关系。
而基于马尔科夫链的算法可以更好地获得序列中顺序信息。最简单的基于马尔科夫链的算法利用训练集中项目的转换频率来计算得到转换矩阵[10],但不能应对那些在训练集中没出现过的转换关系。FPMC算法[11]通过一种张量分解的算法将转换矩阵进行分解,从而解决了该问题。另外一种解决算法是马尔科夫隐嵌入[12],首先把项目映射到欧式空间中,然后通过计算项目之间的欧式距离从而估算项目之间的转换概率。因为状态空间存在着数据爆炸的问题,基于马尔科夫链的算法多数都只考虑了用户点击序列对连续项目之间的单向转换,导致会话中的其他项目被忽略。
1.2 基于深度学习的算法循环神经网络(RNN)对会话序列有着强大的建模能力,能很好地解决基于马尔科夫链算法的不足。GRU4Rec[13]是一个基于RNN的会话序列推荐算法,它的原理是将多个GRU层堆叠在一起。受计算机视觉和自然语言处理领域中非常流行的注意力机制启发,LI等[14]采用带注意力的混合编码算法对用户的序列行为和目标进行建模,并且实验证明了学习到的序列表现结果十分有效。因此,后续基于RNN的工作都融入了注意力的机制[15-17]。
近几年图神经网络在许多任务中都有着较好的表现[18],也有一些研究人员将图神经网络引入到基于会话序列的推荐中。SR-GNN[4]将会话序列建模为不带权重的有向会话图,图中的边代表项目之间的转换关系,然后利用门控图神经网络(Gated Graph Neural Networks,GGNN)在有边相连的节点间进行信息的传播。XU等[6]在SR-GNN的基础上利用GGNN来提取局部信息,并且用自注意力网络来捕获远距离项目之间的全局依赖关系。上述算法证明,对于基于会话序列的推荐,GNN是一个值得研究的方向。
本文的主要贡献如下:
1)利用会话序列建立会话图。根据会话图的邻接关系,利用图卷积网络提取图中的无向结构信息,通过门控图神经网络提取图中的有向结构信息,最后对中间项目隐含向量通过线性变换得到最终的项目隐含向量。
2)在提取会话图中的结构信息时,给会话序列中出现的重复点击项目分配更高的注意力,并在生成项目隐含向量时引入注意力机制,根据项目间依赖的程度修改相应项目的权重系数。
3)进行大量的实验并在3个公开数据集上证明了该算法比现有的算法表现更优。
2 算法描述与模型框架 2.1 公式化描述基于会话序列的推荐旨在根据用户当前的会话序列数据给出用户下个时刻点击项目的预测,而在该过程中完全不依赖用户的长期偏好信息。
在基于会话序列的推荐中,令
对基于会话序列的推荐,首先从历史会话序列的信息中构建有向会话序列图。GCN和GNN分别能提取会话图中项目转换的无向结构信息和有向结构信息,并相应地生成精确的项目隐含向量。而后将得到的项目隐含向量输入到注意力网络中,同时考虑会话的全局信息与局部信息,从而构造出更可靠的会话表示,并以此推断下一次的点击项目。
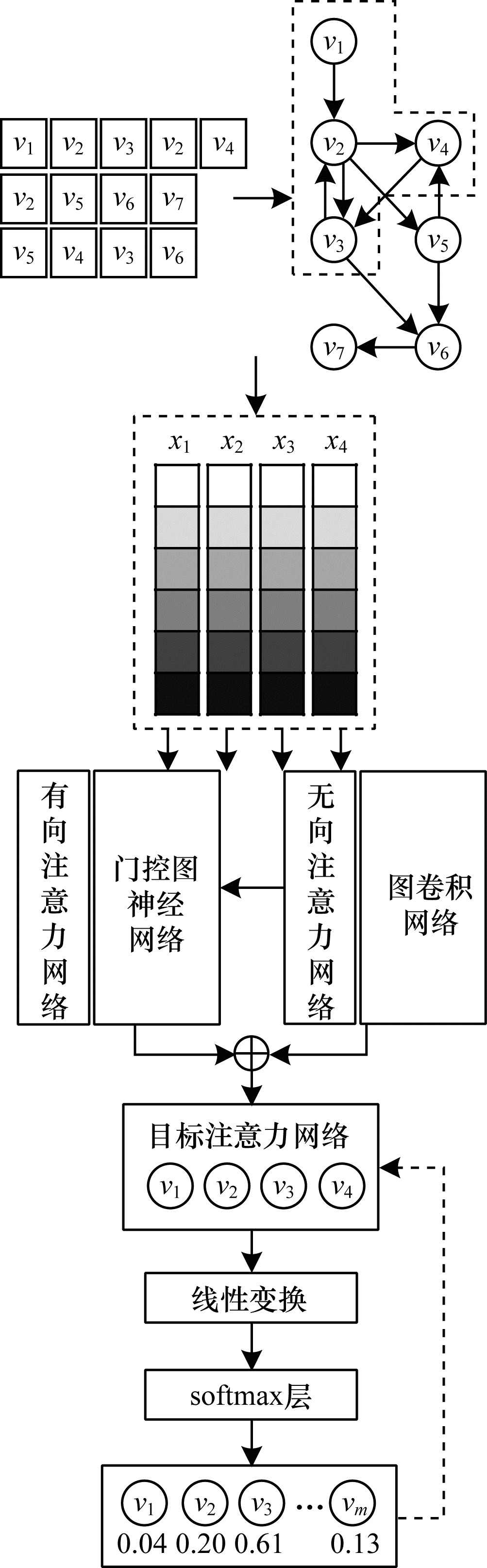
模型的整体框架如图 1所示。首先将每个会话序列
|
Download:
|
| 图 1 本文模型总体框架 Fig. 1 Overall framework of the proposed method | |
在建立好会话图
本文采用文献[19]算法构建图卷积网络(GCN)。会话图
与卷积神经网络(CNN)和多层感知机(MLP)类似,GCN在多层结构中对于每个节点的特征
| $ {\boldsymbol{H}}^{\left(0\right)}=\boldsymbol{X} $ | (1) |
层数为
特征传播是GCN和MLP之间的本质区别。在每层的最开始,每个节点
| $ {\stackrel{-}{\boldsymbol{h}}}_{i}^{\left(k\right)}\leftarrow \frac{1}{{d}_{i}+1}{\boldsymbol{h}}_{i}^{\left(k\right)}+\sum\limits_{j=1}^{n}\frac{{a}_{ij}}{\sqrt{({d}_{i}+1)({d}_{j}+1)}}{\boldsymbol{h}}_{j}^{(k-1)} $ | (2) |
上述的更新公式可以用整个图的简单矩阵操作来简化。
| $ \boldsymbol{S}={\tilde{\boldsymbol{D}}}^{-\frac{1}{2}}\tilde{\boldsymbol{A}}{\tilde{\boldsymbol{D}}}^{-\frac{1}{2}} $ | (3) |
| $ \tilde{\boldsymbol{S}}=\alpha (\boldsymbol{S}+\boldsymbol{I}-\boldsymbol{S}\odot \boldsymbol{I})+\beta \boldsymbol{I} $ | (4) |
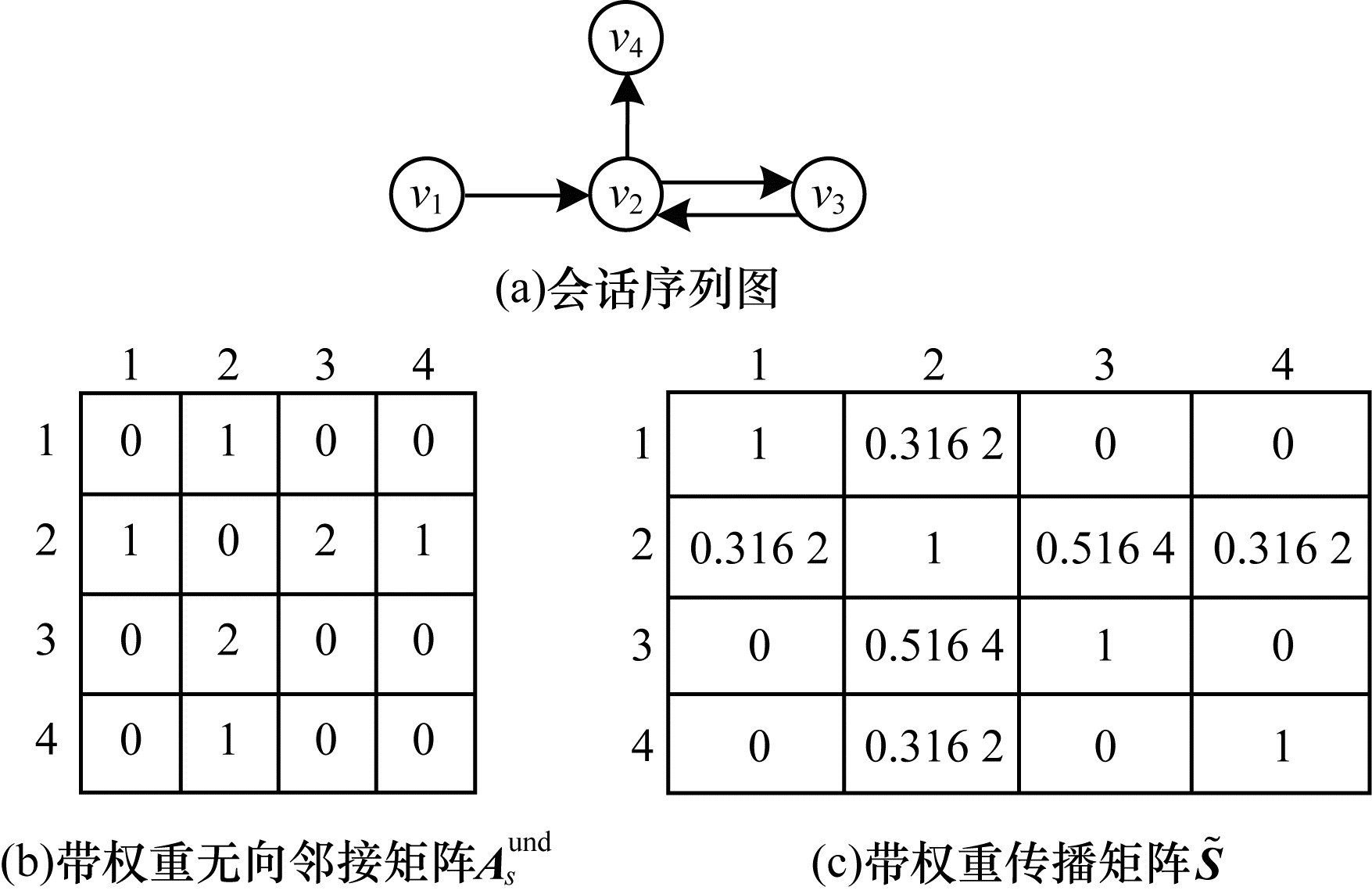
其中:
|
Download:
|
|
图 2 会话序列图与其对应的带权重无向邻接矩阵 |
|
因此,式(2)的等价更新形式就可以变成一个对于所有节点的简单稀疏矩阵相乘:
| $ {\tilde{\boldsymbol{H}}}^{\left(k\right)}=\tilde{\boldsymbol{S}}{\boldsymbol{H}}^{(k-1)} $ | (5) |
上述步骤沿着图上边对节点的隐含向量表示进行局部平滑,将GCN作为特征预处理算法对特征进行传播后,使得节点能够吸收相邻节点的带注意力信息,并最终使得局部相连的节点能够有相似的预测表现[20]。
2.3.2 带注意力的有向结构信息本文根据文献[21]构建模型GGNN。对于会话图
| $ {\boldsymbol{a}}_{i}^{\left(t\right)}={\widehat{\boldsymbol{A}}}_{i:}[{\boldsymbol{h}}_{{v}_{1}}^{(t-1)}, {\boldsymbol{h}}_{{v}_{2}}^{(t-1)}, \cdots , {\boldsymbol{h}}_{{v}_{n}}^{(t-1)}{]}^{\mathrm{T}}\boldsymbol{T}+\boldsymbol{b} $ | (6) |
| $ {\boldsymbol{z}}_{i}^{t}=\sigma ({\boldsymbol{W}}_{z}{\boldsymbol{a}}_{t}^{\left(t\right)}+{\boldsymbol{U}}_{z}{\boldsymbol{h}}_{{v}_{i}}^{(t-1)}) $ | (7) |
| $ {\boldsymbol{r}}_{i}^{t}=\sigma ({\boldsymbol{W}}_{r}{\boldsymbol{a}}_{t}^{\left(t\right)}+{\boldsymbol{U}}_{r}{\boldsymbol{h}}_{{v}_{i}}^{(t-1)}) $ | (8) |
| $ {\boldsymbol{h}}_{{v}_{i}}^{\left(t\right)}=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}({\boldsymbol{W}}_{o}{\boldsymbol{a}}_{i}^{\left(t\right)}+{\boldsymbol{U}}_{o}({\boldsymbol{r}}_{i}^{t}\odot {\boldsymbol{h}}_{{v}_{i}}^{(t-1)}\left)\right) $ | (9) |
| $ {\boldsymbol{h}}_{{v}_{i}}^{\left(t\right)}=(1-{\boldsymbol{z}}_{i}^{t})\odot {\boldsymbol{h}}_{{v}_{i}}^{(t-1)}+{\boldsymbol{z}}_{i}^{t}\odot {\boldsymbol{h}}_{{v}_{i}}^{\left(t\right)} $ | (10) |
其中:
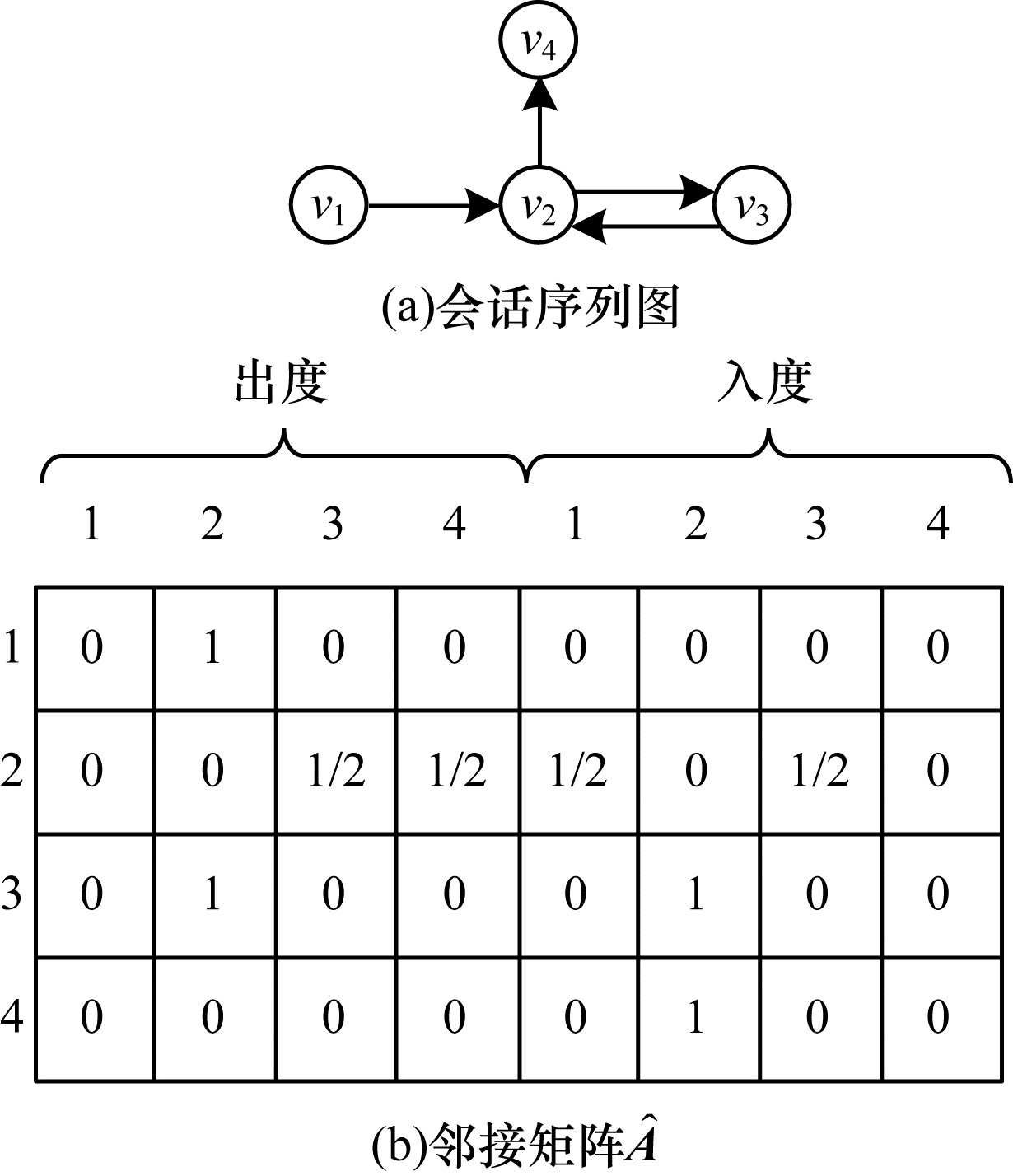
矩阵
|
Download:
|
|
图 3 会话序列图与其对应的邻接矩阵 |
|
所以,对于每个会话图
在经过图卷积网络(GCN)和门控图神经网络(GGNN)的信息处理后,分别得到
为了平衡带注意力的无向结构信息与有向结构信息的比例,采用式(11)进行控制:
| $ \boldsymbol{H}=\gamma \widehat{\boldsymbol{H}}+(1-\gamma )\widehat{\boldsymbol{H}} $ | (11) |
其中:
在得到每个项目的向量表示后,进一步构建目标向量,从而能在考虑到目标项目的前提下对历史行为的相关性进行分析,目标项目是指所有待预测的候选项目。因为在实际应用场景中,用户得到的推荐项目只匹配其一小部分的兴趣,所以利用文献[22]提出的目标注意力模型来计算目标会话中所有项目对目标项目的注意力得分。
本文利用局部目标注意力模型来计算会话
| $ {\beta }_{i, t}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({e}_{i, t}\right)=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\boldsymbol{h}}_{{v}_{t}}^{\mathrm{T}}\boldsymbol{W}{\boldsymbol{h}}_{{v}_{i}}\right)}{\sum\limits_{j=1}^{m}\mathrm{e}\mathrm{x}\mathrm{p}\left({\boldsymbol{h}}_{{v}_{t}}^{\mathrm{T}}\boldsymbol{W}{\boldsymbol{h}}_{{v}_{i}}\right)} $ | (12) |
其中:
在式(12)中,会话中的项目与候选目标分别匹配,并且用带权重矩阵
对于每个会话序列
| $ {\boldsymbol{s}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}^{t}=\sum\limits_{i=1}^{{s}_{n}}{\beta }_{i, t}{\boldsymbol{h}}_{{v}_{t}} $ | (13) |
最终得到基于目标注意力的向量
本文利用会话s中涉及到的项目向量进一步地探索用户的短期和长期喜好,从而得到会话中的局部向量与全局向量,并综合2.4.1节中计算得出的基于目标注意力的向量生成最终的会话向量。
首先是局部向量,在一个会话序列
| $ {\boldsymbol{s}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}={\boldsymbol{h}}_{{v}_{{s}_{n}}} $ | (14) |
对于全局向量,将用户的长期偏好定义为全局向量
| $ {\boldsymbol{\alpha }}_{i}={\boldsymbol{q}}^{\mathrm{T}}\sigma ({\boldsymbol{W}}_{1}{\boldsymbol{h}}_{{v}_{{s}_{n}}}+{\boldsymbol{W}}_{2}{\boldsymbol{h}}_{{v}_{i}}+\boldsymbol{c}) $ | (15) |
| $ {\boldsymbol{s}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}=\sum\limits_{i=1}^{{s}_{n}}{\boldsymbol{\alpha }}_{i}{\boldsymbol{h}}_{{v}_{i}} $ | (16) |
其中:
最后对于前面得到局部向量、全局向量和基于目标注意力的向量,将三者进行拼接并利用线性转换得到会话序列
| $ {\boldsymbol{s}}_{h}={\boldsymbol{W}}_{3}[{\boldsymbol{s}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}^{t};{\boldsymbol{s}}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}};{\boldsymbol{s}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}] $ | (17) |
其中:权重参数
在得到每个会话序列
| $ {\widehat{\boldsymbol{z}}}_{i}={\boldsymbol{s}}_{h}^{\mathrm{T}}{\boldsymbol{h}}_{{v}_{i}} $ | (18) |
然后通过softmax函数,获得模型的输出向量
| $ \widehat{\boldsymbol{y}}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\widehat{\boldsymbol{z}}}_{i}\right) $ | (19) |
其中:
对于每个会话图
| $ L\left(\widehat{\boldsymbol{y}}\right)=-\sum\limits_{i=1}^{m}{\boldsymbol{y}}_{i}lo{g}_{a}\left({\widehat{\boldsymbol{y}}}_{i}\right)+\left(1\right.-{\boldsymbol{y}}_{i})lo{g}_{a}\left(1\right.-{\widehat{\boldsymbol{y}}}_{i}) $ | (20) |
其中:
最后使用基于时间的反向传播(BPTT)算法来训练提出的模型。值得注意的是,在基于会话序列的推荐场景中,多数会话都是相对较短的序列。为了防止过拟合的出现,采用较小的训练次数是比较适宜的。
3 实验结果与分析本节介绍使用的数据集、数据预处理策略和评价指标,将提出算法与其他算法进行比较,最后在不同的实验设置下给出模型的详细分析。
3.1 数据集和数据预处理本文选择在实际应用中两个有代表性的数据集来评估所提出算法,数据集分别是RecSys Challenge 2015发布的公开数据集Yoochoose和CIKM Cup 2016发布的公开数据集Diginetica。Yoochoose数据集包含了电子购物平台上6个月内的用户点击流,而Diginetica数据集中只包含了交易成功的数据,即用户的购买流。
为了公平比较,本文遵循文献[14, 23]的预处理算法,在两个数据集中将长度为1的会话序列和总出现次数小于5次的项目滤去,同时遵循文献[1]的预处理算法,将长度大于20的会话序列滤去。因为一个会话序列如果长度过长,那么用户的主要目的在项目转换间很有可能已经发生了改变,后续的推荐如果基于若干目的中的一个进行推荐,则很难达到精准预测的效果。经过上述处理,最终在Yoochoose数据集中得到了7 897 532条会话和37 470个项目,在Diginetica数据集中得到了185 517条会话和43 093个项目。对于训练集和测试集的划分,在Yoochoose数据集中选择最后一天的数据作为测试集,在Diginetica数据集中则选择最后一个星期的数据进行测试,剩余的数据则作为训练集输入模型。由于Yoochoose训练集规模过于庞大,遵循文献[14, 23]的做法,将Yoochoose训练数据中距离测试集时间最近的1/64和1/4部分的数据划分出来作为训练数据。
和文献[24]的策略相同,本文进一步通过切分输入序列数据来生成对应的序列和标签。对于输入会话序列
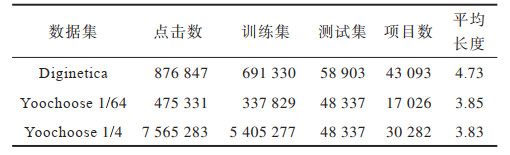
数据集具体情况如表 1所示。
|
下载CSV 表 1 实验数据集统计结果 Table 1 Statistical results of experimental datasets |
本文采用在基于会话序列的推荐中常用的两个度量标准作为算法的评价指标:
1)P@20(Precision)。是一种被广泛使用的预测精度的度量标准,它代表了算法推荐结果的前20项中正确推荐的比例。
2)MRR@20(Mean Reciprocal Rank)。是算法推荐结果中正确推荐项目的倒数排名均值。当真实结果在算法的推荐排位中超过20时,对应的倒数排名为0,MMR度量标准是一种考虑了推荐顺位的算法,较大的MRR值代表了在推荐列表中真实结果位于排名列表的顶部,这也证明了推荐系统的有效性。
3.3 参数设置根据文献[4, 14, 22-23],本文在两个数据集中均将隐含向量的维度设置为
为了评估所提算法的性能,将其与会话序列推荐问题的现有算法中有代表性的算法进行比较,即POP、S-POP、Item-KNN、BPR-MF、FPMC、GRU4Rec、RepeatNet、NARM、STAMP、SR-GNN、TAGNN。
1)POP和S-POP算法的策略是分别在训练集和当前会话序列中推荐前
2)Item-KNN[25]推荐与当前会话序列项目相似的项目,其中相似度定义为会话向量之间的余弦相似度。
3)BPR-MF[26]是一种基于贝叶斯后验优化的个性化排序算法,它通过随机梯度下降优化成对项目排序的目标函数。
4)FPMC[11]是一种基于马尔科夫链的序列推荐算法。
5)GRU4Rec[13]使用循环神经网络来对用户序列进行建模。
6)RepeatNet[16]在重复消费的场景下将常规神经推荐算法与新的重复推荐机制集成在一起。
7)NARM[14]使用带有注意力机制的循环神经网络来捕捉用户的主要意图和序列行为特征。
8)STAMP[23]利用自注意力机制捕捉用户在当前会话序列中的大致意图和最后一次点击行为的兴趣点所在。
9)SR-GNN[4]通过使用门控图神经网络来捕捉项目转换之间的关系。
10)TAGNN[20]在使用图神经网络模型的基础上利用注意力网络捕捉会话序列中的项目与目标项目的相似程度。
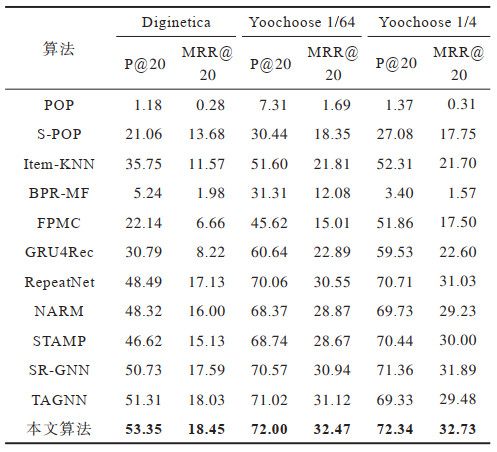
各算法在P@20和MRR@20这2个指标上的性能表现如表 2所示,其中加粗数字为最佳结果。本文提出算法能够灵活地在会话图上构建项目之间的联系,并且提取其中带注意力的有向结构信息和无向结构信息,使得后续目标注意力的学习能够更加准确,并且综合用户在会话中的全局兴趣和局部兴趣给出最后的推荐。由表 2中的实验数据可以看出,本文算法在3个数据集上的2个指标上都获得了最好的表现结果,这也证明了所提算法的有效性。
|
下载CSV 表 2 不同算法实验结果对比 Table 2 Comparison of experimental results of different algorithms |
从表 2可以看出:传统推荐算法如POP和S-POP在基于会话序列的问题上表现不尽如人意,因为其忽略了用户在当前会话中的偏好,仅考虑了前
与传统算法不同,基于深度学习的算法在所有数据集上的结果都有更好的表现。GRU4Rec是一种基于循环神经网络的算法,它的表现结果优于大部分传统算法,与一部分传统算法达到相近的程度。这说明了循环神经网络对于序列数据有着一定的建模能力。然而GRU4Rec主要聚焦在对会话序列进行建模,无法捕获会话中的用户偏好,其后出现的算法如NARM和STAMP都对GRU4Rec有着显著的提升。NARM显式地捕获用户在会话中的主要偏好,而STAMP利用注意力机制考虑用户的短期兴趣,也优于GRU4Rec。RepeatNet通过考虑用户的重复点击行为达到了较好的预测效果,这说明对用户的行为习惯进行建模具有一定的重要性。RepeatNet相比NARM与STAMP提升有限,可能是因为仅通过项目特征来对用户的重复点击习惯进行建模是不充分的,且基于RNN的结构无法捕获会话内的一些共同的依赖关系。
基于图神经网络的算法将每个会话序列都构建成一张子图,并且通过图神经网络对会话中的所有项目进行编码。SR-GNN和TAGNN比所有基于RNN的模型有着更好的结果。SR-GNN利用门控图神经网络来学习会话序列内项目之间的依赖关系,TAGNN进一步利用注意力机制挖掘会话内的项目与目标项目之间的依赖关系。然而,这些算法都完全根据会话图的有向关系进行学习,而没有综合考虑会话图中的无向关系,因为会话序列中物品和物品之间的关系有时往往不是单向的关系而是双向的,利用无向的结构信息能够捕获到物品之间更加全面的关系,且它们都忽视了会话序列中出现的重复点击特征,从直觉上来讲一个序列中重复出现项目的重要性应当是更大的。此外,在实际推荐场景中项目和项目之间的关联程度是多变的,而这些算法对于会话内项目和项目之间的依赖关系采用的是平均化算法,不能通过权重或者注意力的算法体现出某一项目对其他项目的依赖程度。
本文提出算法相比其他算法表现都要更优。具体而言,在3个数据集上,对于P@20,相对表现最佳的相关算法有3.55%、1.38%、1.37%的相对提升,对于MRR@20,对表现最佳的相关算法有1.92%、4.34%、2.63%的相对提升。本文算法能够很好地提取会话图中的结构信息,先后利用图卷积网络和门控图神经网络对图中的无向结构信息和有向结构信息进行提取,并将两者进行线性组合从而达到向量的精准表示。考虑到会话序列中的重复点击项目,通过注意力网络提高重复信息的权重,同时通过增加自环和矩阵操作提高会话图中节点的自我信息比例,使得节点不容易受到其他节点的噪声干扰。根据项目与项目之间不同的依赖关系,利用注意力网络分配不同的权重,从而使得网络能够生成精确的向量表示。
3.5 消融实验本文提出的算法能够灵活地捕捉会话图中的结构信息和项目之间的关系。为了验证模型中各组成成分的实际作用,设置了几种模型变体进行消融实验。在实验环节中选择SR-GNN[4]作为对比的基准算法,实验中的数据以对比SR-GNN的相对提升百分比的形式展示。
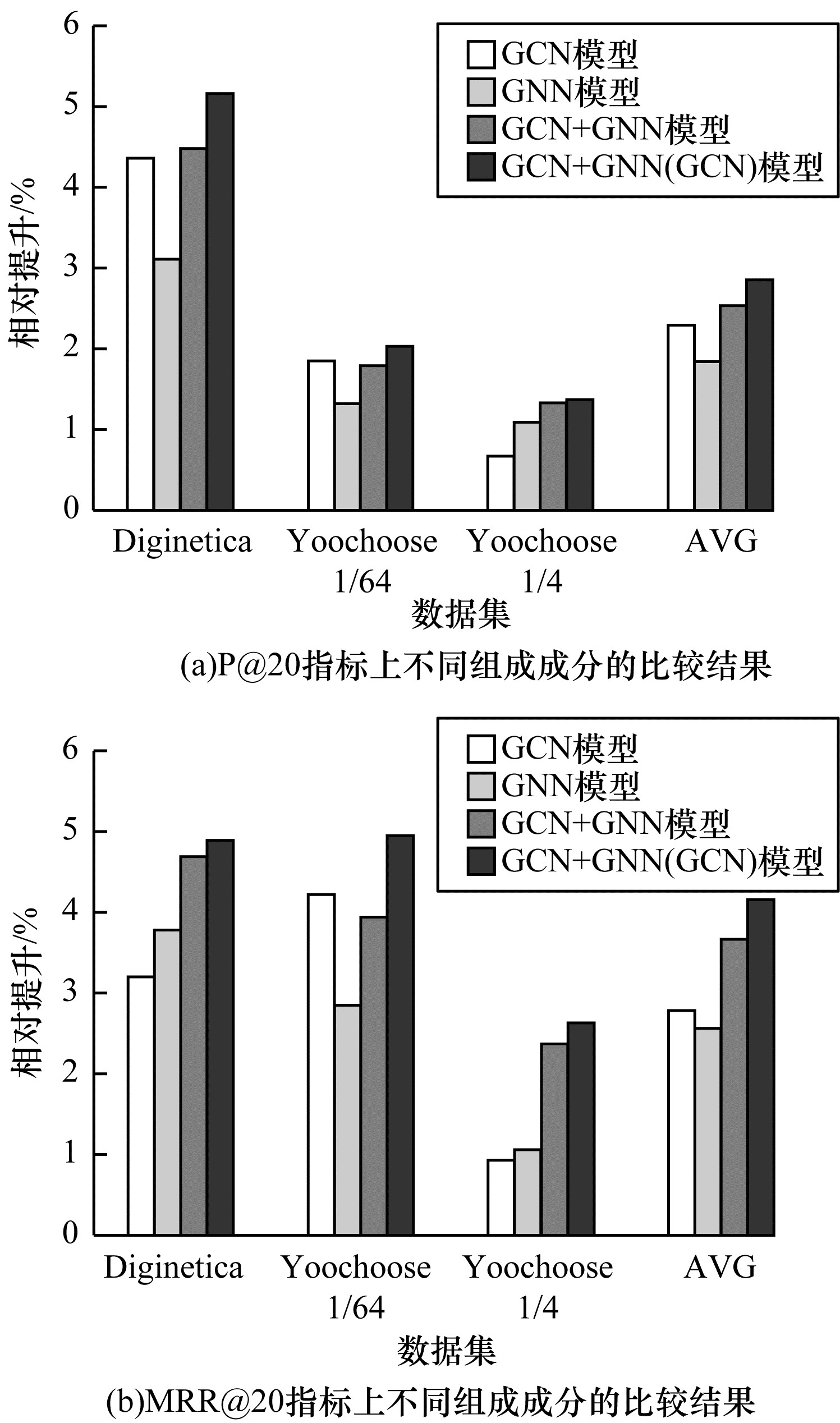
本文进行以下有向结构信息和无向结构信息的组合分析:1)GCN,只提取会话图中的无向结构信息;2)GNN,只提取会话图中的有向结构信息;3)GCN+GNN,将随机初始向量同时输入到两个神经网络中,然后把模型输出结果进行线性组合;4)GCN+GNN(GCN),首先将随机初始向量输入到GCN中,然后把GCN模型的输出向量作为GNN模型的输入,最后将2个模型的输出结果进行线性组合。实验对比结果如图 4所示,其中AVG代表4种组合条件在3个数据集上的平均表现。
|
Download:
|
| 图 4 不同结构信息的实验结果 Fig. 4 Experimental results of different structural information | |
从图 4可以看出,综合有向结构信息与无向结构信息的GCN+GNN(GCN)模型在3个数据集的2个指标P@20、MRR@20上都取得了最佳的结果,这证明了综合考虑有向结构信息和无向结构信息的重要性。图 4中平均数据AVG还显示了单独考虑无向结构信息相比单独考虑有向结构信息表现更加优异。从单个数据集的表现上可以看出,在Yoochoose 1/4数据集和Diginetica数据集的MRR@20指标上,考虑有向结构信息表现稍好于无向结构信息。这一定程度上反映了在基于会话序列的推荐中用户的偏好与项目之间的联系、项目之间的转换方向在不同的场景下有着不同的重要程度,但平均而言还是无向结构信息更重要。这说明在基于会话序列推荐的场景下用户在项目之间的转换方向虽然值得考虑,但还是需要重点考虑用户浏览的项目之间的联系,才能更好地学习到用户的偏好。而比前两者更好的做法是综合考虑有向结构信息和无向结构信息,图 4中GCN结合GNN的方法在3个数据集的综合表现及平均表现AVG上,基本都要比单独使用GCN或GNN的表现要好。而其中GCN+GNN的方法中2个网络模型的输入数据都是随机嵌入向量,而GCN+GNN(GCN)的方法中GNN模型的输入是经过GCN模型提取无向结构信息的向量,这说明了相比直接使用随机向量,先对无向结构信息进行提取而后再进行有向结构信息的提取能够得到更精准表示的嵌入向量。
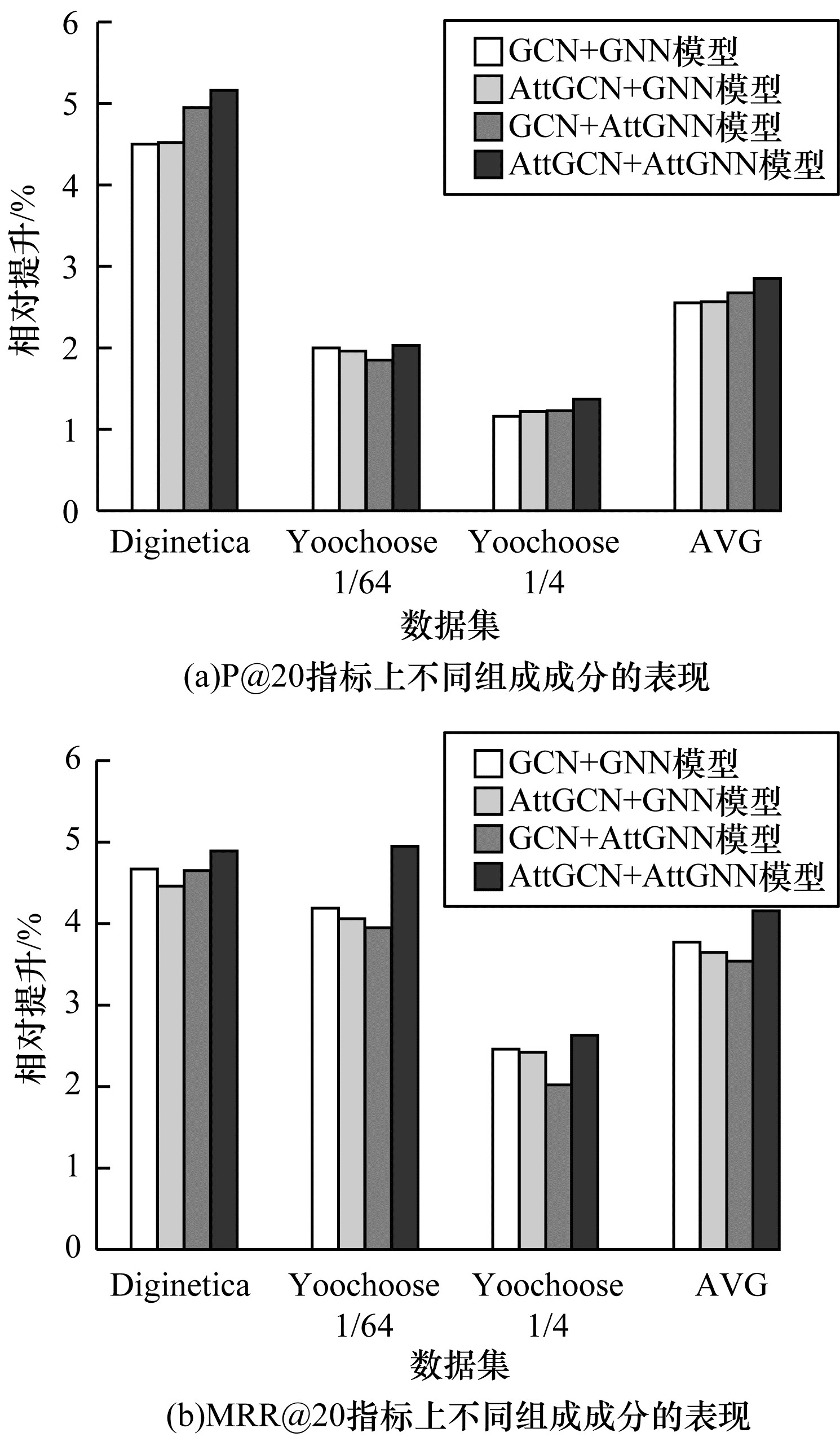
本文进行重复点击注意力信息和项目间依赖关系的组合分析如下:1)GCN+GNN,不考虑重复点击注意力信息和项目间不同的依赖关系;2)AttGCN+GNN,只在GCN中考虑重复点击项目的注意力信息;3)GCN+AttGNN,只在GNN中考虑项目之间不同程度的依赖关系;4)AttGCN+AttGNN,同时在GCN中融合重复点击的注意力信息和在GNN中融合带注意力的项目依赖关系。实验结果如图 5所示。
|
Download:
|
| 图 5 不同注意力信息组成成分的实验结果 Fig. 5 Experimental results of different attention information composition | |
从图 5可以看出,综合考虑重复点击注意力信息和项目间依赖关系的AttGCN+AttGNN在3个数据集的2个指标上均取得了最佳的实验结果,这说明重复点击行为和项目间的依赖关系在基于会话序列的推荐中有一定的重要性。根据图 5(a),单独考虑重复点击注意力和项目间关系的注意力比不考虑任何注意力信息的GCN+GNN要有更好的表现,综合考虑两者的AttGCN+AttGNN效果最佳,说明了注意力信息确实能够使得重要的信息尽可能地保留并得到更加精准表现的嵌入向量。根据图 5(b),虽然综合考虑两种注意力的AttGCN+AttGNN仍能获得最佳的实验表现,但是单独考虑两者注意力其中之一的表现会略差于不考虑任何注意力信息的GCN+GNN的表现,即单独使用注意力信息虽然能够提高推荐结果的精确率,但是对推荐排名的预测效果并不好。可能是向量在输入GCN和GNN模型时,如果一个模型考虑了注意力而另一个模型没有考虑,那么2个模型中邻接矩阵的表现模式也就没有统一,导致向量在两个模型之间输入输出时不能同时利用注意力保留结构信息,反而使得结构信息因为注意力模式不一致受到干扰,所以最后没有生成精准表示的嵌入向量,即不能在预测阶段计算出每个项目准确的预测得分。
4 结束语在基于会话序列的推荐场景中,用户的重复点击行为和图结构信息都能在不知用户历史偏好的情况下很好地预测出用户的行为。本文提出一种基于有向与无向信息同注意力相融合的图神经网络序列推荐算法。利用GCN与GNN模型提取会话序列图中的有向结构信息与无向结构信息并进行线性组合,在2个模型的内部引入注意力机制,对用户的重复点击和项目之间的复杂转换信息进行有效提取,使得生成的会话向量在推荐过程中预测更准确。在3个数据集上的实验结果表明,该算法精度优于目前现有的算法,并验证了注意力机制和复杂的结构信息的有效性。下一步将在研究复杂图结构的基础上,寻找更好的隐含向量表现方式和向量组合方式,提高会话序列推荐的准确率。
| [1] |
CHEN T W, WONG R C W. Handling information loss of graph neural networks for session-based recommendation[C]//Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM Press, 2020: 1172-1180.
|
| [2] |
CHENG Z Y, SHEN J L, ZHU L, et al. Exploiting music play sequence for music recommendation[C]//Proceedings of IEEE IJCAIʼ17. Washington D. C., USA: IEEE Press, 2017: 3654-3660.
|
| [3] |
QIU R H, LI J J, HUANG Z, et al. Rethinking the item order in session-based recommendation with graph neural networks[C]//Proceedings of the 28th ACM International Conference on Information and Knowledge Management. New York, USA: ACM Press, 2019: 579-588.
|
| [4] |
WU S, TANG Y Y, ZHU Y Q, et al. Session-based recommendation with graph neural networks[EB/OL]. [2021-02-20]. https://arxiv.org/abs/1811.00855.
|
| [5] |
王健宗, 孔令炜, 黄章成, 等. 图神经网络综述[J]. 计算机工程, 2021, 47(4): 1-12. WANG J Z, KONG L W, HUANG Z C, et al. Survey of graph neural network[J]. Computer Engineering, 2021, 47(4): 1-12. (in Chinese) |
| [6] |
XU C F, ZHAO P P, LIU Y C, et al. Graph contextualized self-attention network for session-based recommendation[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao, China: [s. n. ], 2019: 3940-3946.
|
| [7] |
DAVIDSON J, LIEBALD B, LIU J N, et al. The YouTube video recommendation system[C]//Proceedings of the 4th ACM Conference on Recommender Systems. New York, USA: ACM Press, 2010: 293-296.
|
| [8] |
DIAS R, FONSECA M J. Improving music recommendation in session-based collaborative filtering by using temporal context[C]//Proceedings of the 25th IEEE International Conference on Tools with Artificial Intelligence. Washington D. C., USA: IEEE Press, 2013: 783-788.
|
| [9] |
PARK S E, LEE S, LEE S G. Session-based collaborative filtering for predicting the next song[C]//Proceedings of the 1st ACIS/JNU International Conference on Computers, Networks, Systems and Industrial Engineering. Washington D. C., USA: IEEE Press, 2011: 353-358.
|
| [10] |
SHANI G, BRAFMAN R I, HECKERMAN D. An MDP-based recommender system[EB/OL]. [2021-02-20]. https://arxiv.org/ftp/arxiv/papers/1301/1301.0600.pdf.
|
| [11] |
RENDLE S, FREUDENTHALER C, SCHMIDT-THIEME L. Factorizing personalized Markov chains for next-basket recommendation[C]//Proceedings of the 19th IEEE Inter-national Conference on World Wide Web. Washington D. C., USA: IEEE Press, 2010: 811-820.
|
| [12] |
CHEN S, MOORE J L, TURNBULL D, et al. Playlist prediction via metric embedding[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM Press, 2012: 714-722.
|
| [13] |
HIDASI B, KARATZOGLOU A, BALTRUNAS L, et al. Session-based recommendations with recurrent neural networks[EB/OL]. [2021-02-20]. https://arxiv.org/abs/1511.06939.
|
| [14] |
LI J, REN P J, CHEN Z M, et al. Neural attentive session-based recommendation[C]//Proceedings of 2017 ACM Conference on Information and Knowledge Management. New York, USA: ACM Press, 2017: 1419-1428.
|
| [15] |
CHEN T W, WONG R C W. Session-based recommendation with local invariance[C]//Proceedings of 2019 IEEE International Conference on Data Mining. Washington D. C., USA: IEEE Press, 2019: 994-999.
|
| [16] |
REN P J, CHEN Z M, LI J, et al. RepeatNet: a repeat aware neural recommendation machine for session-based recommendation[C]//Proceedings of AAAI Conference on Artificial Intelligence. [S. 1. ]: AAAI Press, 2019: 4806-4813.
|
| [17] |
SONG J, SHEN H, OU Z J, et al. ISLF: interest shift and latent factors combination model for session-based recommendation[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao, China: [s. n. ], 2019: 5765-5771.
|
| [18] |
呼延康, 樊鑫, 余乐天, 等. 图神经网络回归的人脸超分辨率重建[J]. 软件学报, 2018, 29(4): 914-925. HUYAN K, FAN X, YU L T, et al. Graph based neural network regression strategy for facial image super-resolution[J]. Journal of Software, 2018, 29(4): 914-925. (in Chinese) |
| [19] |
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. [2021-02-20]. https://arxiv.org/abs/1609.02907.
|
| [20] |
WU F, ZHANG T Y, SOUZA A H J, et al. Simplifying graph convolutional networks[EB/OL]. [2021-02-20]. https://arxiv.org/abs/1902.07153.
|
| [21] |
LI Y J, TARLOW D, BROCKSCHMIDT M, et al. Gated graph sequence neural networks[EB/OL]. [2021-02-20]. https://arxiv.org/abs/1511.05493.
|
| [22] |
YU F, ZHU Y Q, LIU Q, et al. TAGNN: target attentive graph neural networks for session-based recommendation[C]//Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM Press, 2020: 1921-1924.
|
| [23] |
LIU Q, ZENG Y F, MOKHOSI R, et al. STAMP: short-term attention/memory priority model for session-based recommendation[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, USA: ACM Press, 2018: 1831-1839.
|
| [24] |
TAN Y K, XU X X, LIU Y. Improved recurrent neural networks for session-based recommendations[C]//Proceedings of the 1st IEEE Workshop on Deep Learning for Recommender Systems. Washington D. C., USA: IEEE Press, 2016: 17-22.
|
| [25] |
SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web. Washington D. C., USA: IEEE Press, 2001: 285-295.
|
| [26] |
RENDLE S, FREUDENTHALER C, GANTNER Z, et al. BPR: Bayesian personalized ranking from implicit feedback[EB/OL]. [2021-02-20].https://arxiv.org/abs/1205.2618.
|
 2022, Vol. 48
2022, Vol. 48

 ,
,