2. 西安邮电大学 无线网络安全技术国家工程实验室, 西安 710121
2. National Engineering Laboratory for Wireless Security, Xi'an University of Posts & Telecommunications, Xi'an 710121, China
开放科学(资源服务)标志码(OSID):
密码算法在加密设备上进行实现,加密设备在执行算法的过程中不可避免地会泄露不同形式的物理信息,例如能量消耗、电磁辐射、声音等,这些信息统称为侧信道信息。侧信道攻击是密码学研究的热点方向,自从KOCHER在1996年提出计时攻击思想以来[1],研究人员提出了大量侧信道攻击方法,例如差分能量分析攻击[2]、碰撞攻击[3]、相关能量分析攻击[4]、模板攻击[5]等。随着侧信道攻击方法的出现,与其相关的能量迹定位方法[6]和侧信道信息泄露评估方法[7-8]也陆续被提出。侧信道分析攻击能够从物理信道泄露的能量消耗等物理信息中获取密码设备运算时与密钥相关的中间值信息,并且能够分段恢复较长的密钥,对加密设备造成了很大的安全威胁。
碰撞攻击是侧信道攻击中的一种,关注的是加密设备在加密或解密过程中算法中间值是否存在碰撞,即是否出现相同的中间值,可以从泄露能量中有效地提取密钥相关信息。2003年,SCHRAMM等[3]提出针对数据加密标准(Data Encryption Standard,DES)的侧信道碰撞攻击。2004年,SCHRAMM等[9]又提出针对高级加密标准(Advanced Encryption Standard,AES)的列混合变换输入字节的碰撞检测攻击方法。2007年,BOGDANOV[10]提出针对AES的线性碰撞攻击,该方法改进了SCHRAMM等提出的针对AES的碰撞检测攻击。在实际应用中,为了抵抗侧信道攻击[11-12],加密设备[13-14]一般会采取一系列的对策,掩码技术[15-16]就是其中一种。2010年,MORADI等[17]提出一种能够识别使用掩码技术的AES算法S盒间碰撞的方法。2011年,CLAVIER等[18]利用重用掩码的特点,建立不同的S盒间带掩码数据的碰撞关系。2012年,BOGDANOV等[19]提出一种将DPA和侧信道碰撞攻击相结合的攻击方法,大幅提高了碰撞攻击效率。2019年,NIU等[20]提出一种能抵抗3种典型掩码方案的碰撞攻击思路,利用掩码和被掩码数据处理方式相同的特点,选择AES的列混合变换作为攻击点并实现了很好的攻击效果;DING等[21]提出自适应选择明文碰撞攻击,通过建立能量迹欧氏距离与中间值汉明距离的联系,用能量迹泄露的距离信息减小密钥候选值空间;ZHENG等[22]提出基于假设检测的侧信道碰撞攻击,利用假设检测方法确定一个合理的碰撞阈值,该方法提高了碰撞检测的成功率。
文献[18]提出的改进型相关性碰撞攻击需要预先确定1个碰撞阈值,通过比较2段能量迹之间的相关系数和碰撞阈值之间的大小关系来确定是否发生碰撞,阈值的准确性会影响碰撞检测的成功率,进而影响攻击的成功率。该攻击方法只能利用能量迹中发生碰撞的信息,未发生碰撞的信息会被忽略。文献[21]提出的自适应选择明文碰撞攻击在攻击之前需要攻击者拥有一个和目标设备相同的设备用于建立攻击模板,实施复杂且具有一定的局限性。由以上分析可知:文献[18, 21]中提出的方法都需要控制每次加密的明文,在攻击者不能操作和目标设备相同的设备并且只能获得一定数量的随机明文和对应能量迹的情况下,这2种方法均会失效。
本文基于重用掩码AES算法任意2个S盒之间输入的汉明距离和欧式距离之间的关系[21],提出一种高效的随机明文碰撞攻击方法。该方法无需预先确定碰撞阈值及建立攻击模板,即可有效利用能量迹中未发生碰撞的信息。此外,该方法属于随机明文攻击方法,因此当攻击者不能对目标设备进行操作时也可实施攻击。
1 相关工作 1.1 汉明重量模型汉明重量模型[5]是指设备泄露的能量与被处理数据的汉明重量相关,计算公式如下:
| $ {t}_{q}={s}_{q}\mathrm{H}\mathrm{W}\left(x\right)+{r}_{q} $ | (1) |
其中:
重用掩码方案在AES算法加密的每一轮中仅产生2个随机掩码值,在同一轮中16个S盒的输入用同一掩码,16个S盒的输出用同一掩码,也就是在一轮中只需要预计算1个新的S盒置换表
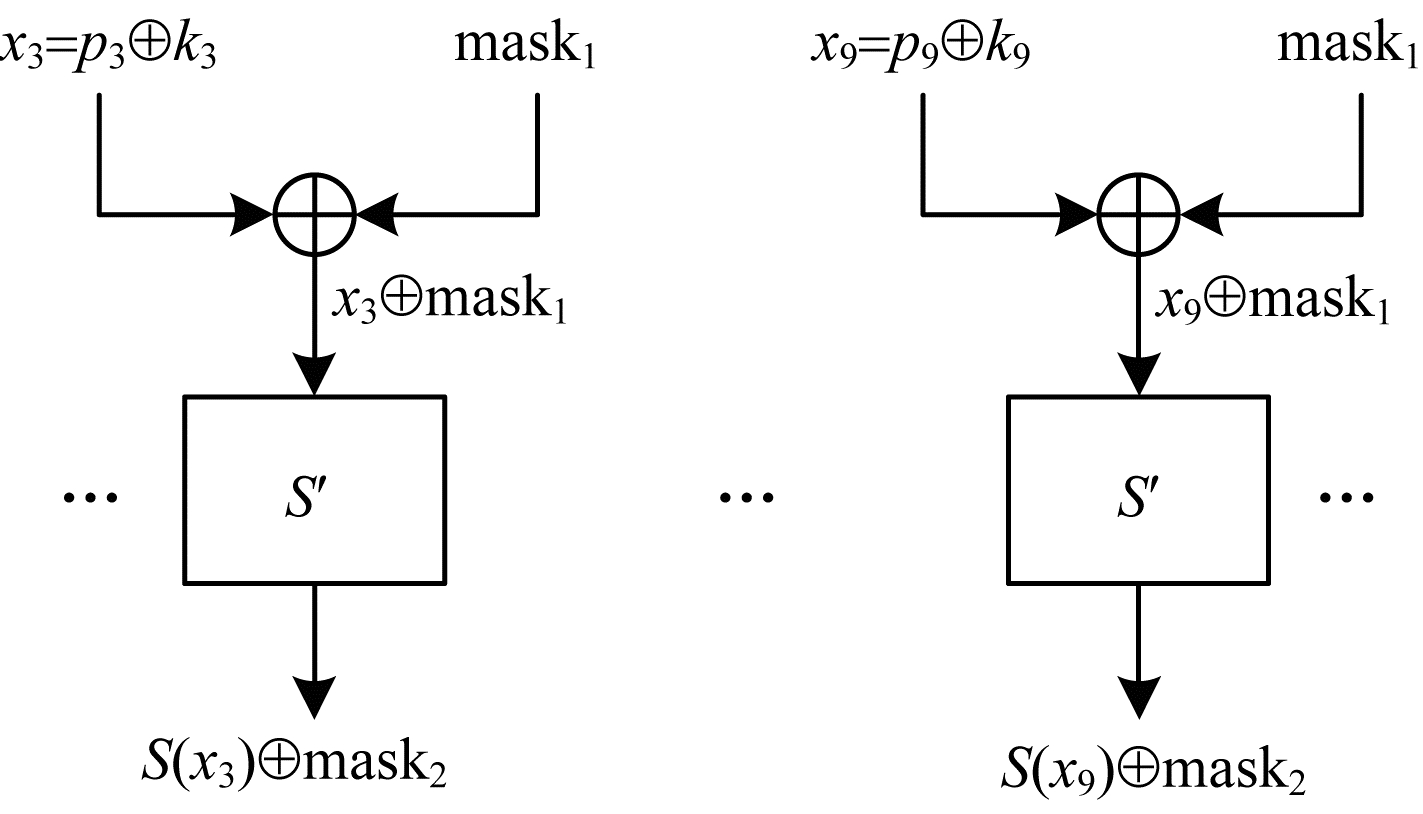
|
Download:
|
| 图 1 重用掩码方案框图 Fig. 1 Block diagram of reused mask scheme | |
汉明距离是指使用重用掩码的AES算法同一轮加密中2个S盒的输入之间的汉明距离。如图 2所示,2个不同的S盒
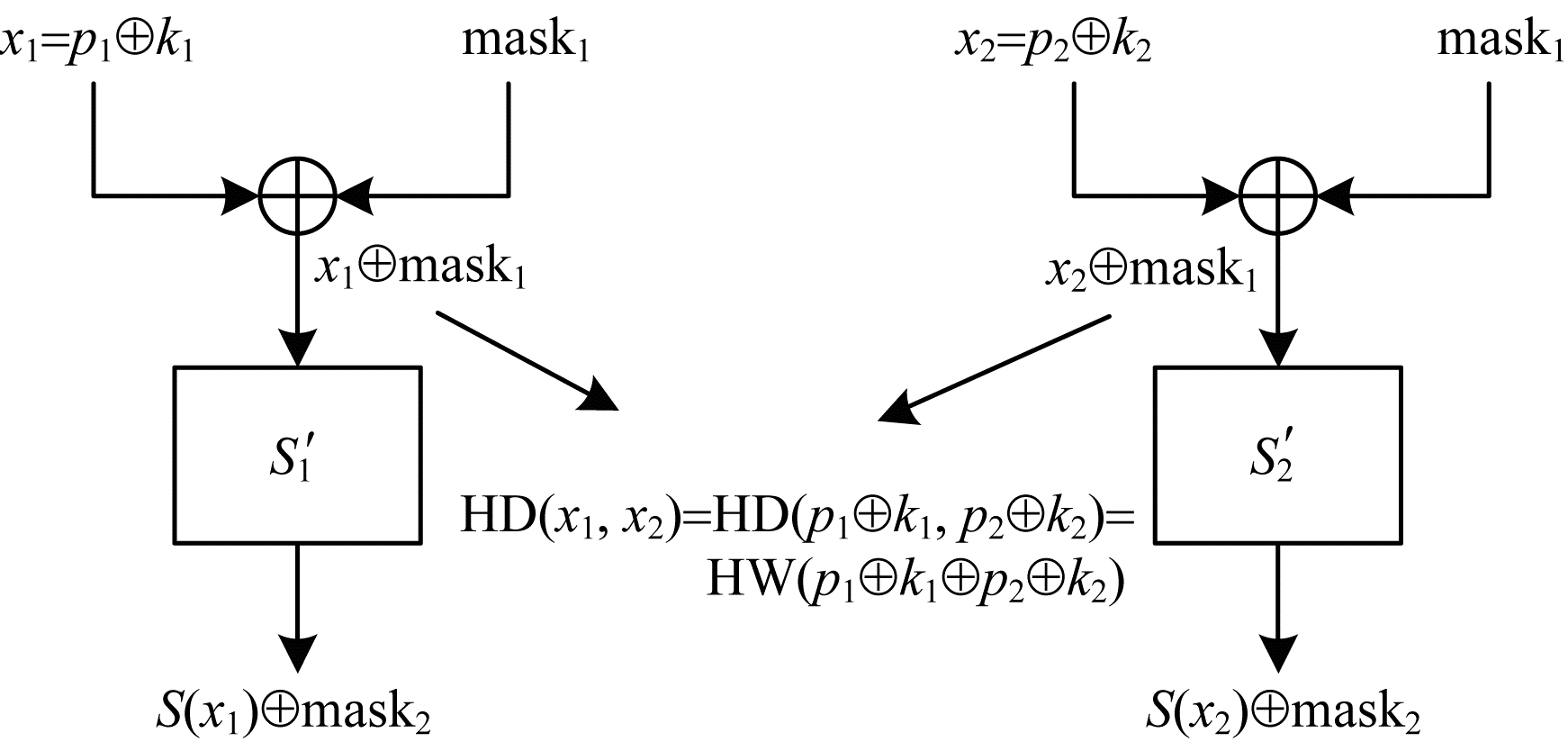
|
Download:
|
| 图 2 汉明距离示意图 Fig. 2 Schematic diagram of Hamming distance | |
欧氏距离计算以前2个S盒为例,对1个明文加密,采集其对应的能量迹,将能量迹中对应于图 2中处理数据
| $ \mathrm{E}\mathrm{D}({x}_{1}, {x}_{2})=\sum\limits _{q=1}^{l}({t}_{1, q}-{t}_{2, q}{)}^{2} $ | (2) |
其中:
在本文中,如果没有特殊说明,则汉明距离均指使用重用掩码的AES算法同一轮加密中2个不同S盒的输入之间的汉明距离,欧氏距离均指同一轮加密中2个不同S盒的输入位置所对应2段能量迹间的累积距离。
1.4 汉明距离和欧式距离之间的关系在使用重用掩码的AES算法中,对于2个不同的S盒
对同一
| $ {\xi }_{{{\mathit{\Delta}} }_{\mathrm{h}\mathrm{d}}}=\frac{1}{N}\sum\limits_{j=1}^{N}\sum\limits_{q=1}^{l}({t}_{1, q}^{\left(j\right)}-{t}_{2, q}^{\left(j\right)}{)}^{2} $ | (3) |
其中:
| $ {\xi }_{{{\mathit{\Delta}} }_{\mathrm{h}\mathrm{d}}}=2{\sigma }^{2}l+{{\mathit{\Delta}} }_{\mathrm{h}\mathrm{d}}\cdot \sum\limits_{q=1}^{l}{s}_{q}^{2} $ | (4) |
其中:
由此可见,欧氏距离的均值和汉明距离之间满足线性关系。
2 攻击原理 2.1 欧式距离归类使用猜测的汉明距离将欧氏距离进行归类,通过某个明文分别与256个密钥异或值求得256个猜测的汉明距离,利用这256个猜测的汉明距离分别与该明文对应的欧氏距离进行归类。
假设某个随机明文的前2个字节分别为
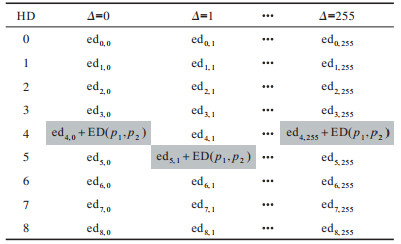
|
下载CSV 表 1 明文字节p1和p2对应欧氏距离归类后的结果 Table 1 Results of Euclidean distance classification of plaintext bytes p1 and p2 |
为方便归类结果的分析,使用式(5)来描述式(4)中汉明距离和欧式距离均值之间的线性关系。
| $ y=ax+b $ | (5) |
其中:x表示实际的汉明距离;y表示x对应的欧氏距离的均值;

|
下载CSV 表 2 汉明距离和欧氏距离均值的对应关系 Table 2 Relationship between Hamming distance and the mean of Euclidean distance |
2个明文字节的异或值是1个8 bit数据,对于1个8 bit的数据,共有

|
下载CSV 表 3 不同的d所求得的相关系数 Table 3 Correlation coefficients obtained for different values of d |
通过式(6)计算2个长度为n的向量X和Y之间的相关系数:
| $ \rho =\frac{\sum\limits_{i=1}^{n}({x}_{i}-\stackrel{-}{x})\cdot ({y}_{i}-\stackrel{-}{y})}{\sqrt{\sum\limits_{i=1}^{n}({x}_{i}{-\stackrel{-}{x})}^{2}}\cdot \sqrt{\sum\limits_{i=1}^{n}({y}_{i}{-\stackrel{-}{y})}^{2}}} $ | (6) |
其中:
从表 3中可以看出,在理论情况下,只有
|
Download:
|
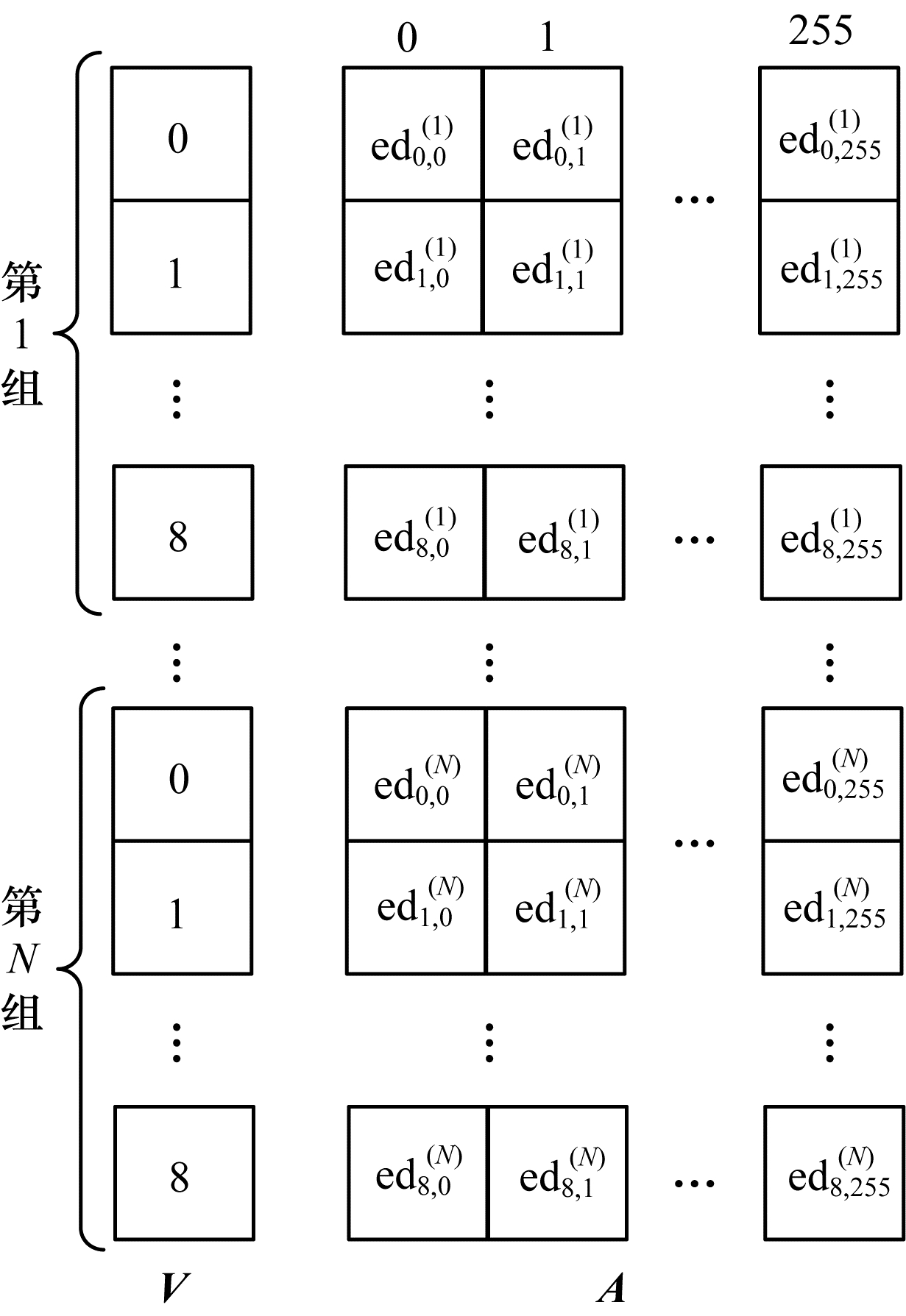
| 图 3 欧氏距离的分组归类 Fig. 3 Grouping and classification of Euclidean distance | |
为验证在实际情况下由于d的不同对相关系数的影响,在噪声标准差
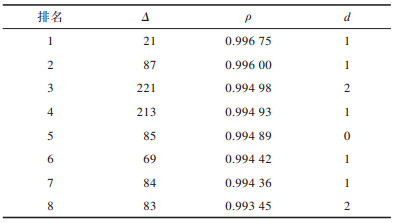
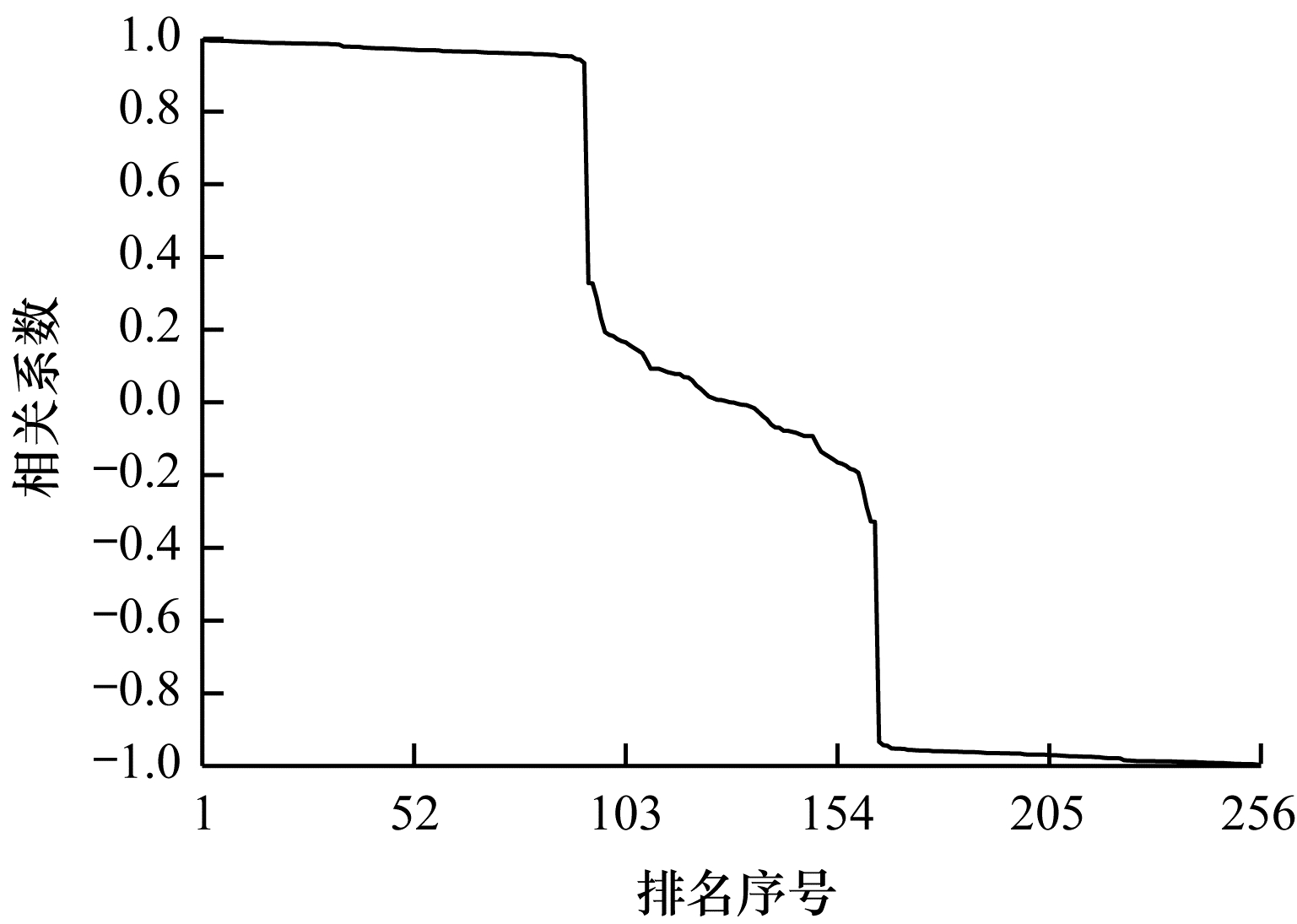
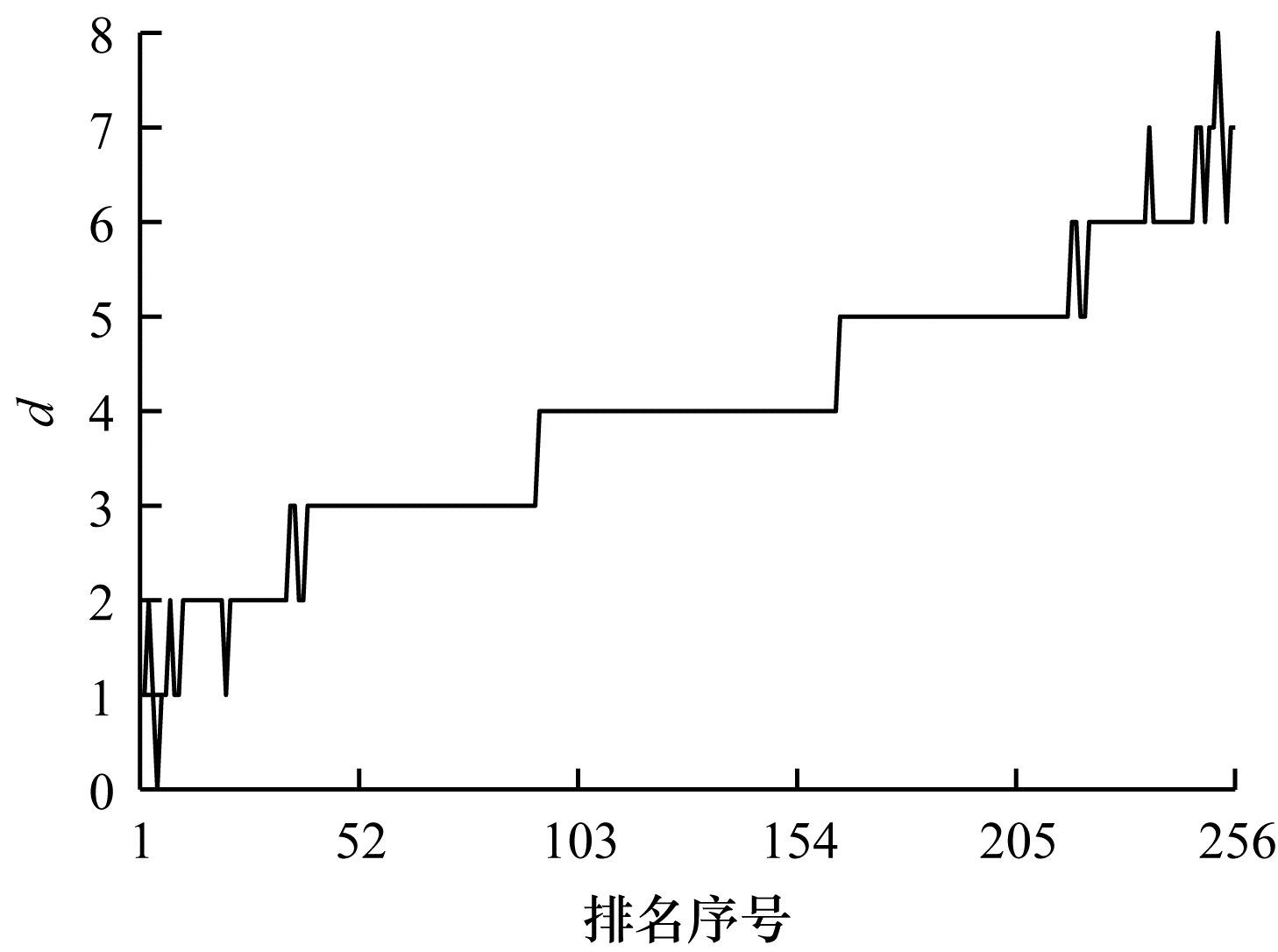
表 4给出了排名前8的猜测密钥异或值,可以看出这些值对应的d都很小。图 4给出了所有猜测密钥异或值对应求得的相关系数,可以看出:排名前93个密钥异或值对应相关系数接近于1且递减,对应于d为0、1、2、3的情况;从排名93开始相关系数突然变小,排名93到164对应于d为4的情况,相关系数接近于0;排名164到256的相关系数接近于-1,对应于d为5、6、7、8的情况。图 5给出了这256个排序后的密钥异或值所对应的d,可以看出:排名前10的密钥异或值所对应的d比较小,为0、1、2;当
|
下载CSV 表 4 排名前8的猜测密钥异或值所对应的相关系数 Table 4 Correlation coefficients corresponding to the top 8 guessed key XOR value |
|
Download:
|
| 图 4 归类分析后不同排名对应的相关系数 Fig. 4 Correlation coefficients corresponding to different rankings after classification analysis | |
|
Download:
|
| 图 5 归类分析后不同排名对应的d值 Fig. 5 d values corresponding to different rankings after classification analysis | |
以上结果验证了在实际情况中,d的不同会对相关系数造成影响,且根据相关系数对猜测密钥异或值排序后的前10个值所对应的d比较小,正确的密钥异或值排名会比较靠前。基于以上结论,可以首先通过归类分析法将正确密钥异或值所在范围缩小,然后本文攻击方法利用排名靠前的密钥异或值所对应的d比较小的特点提出投票法,从中进一步得到正确异或值。
3 攻击方法设计 3.1 实验平台介绍采用ChipWhisperer[23]平台作为实验平台,所有实验均使用该平台采集的能量迹,然后用MATLAB对能量迹进行分析。ChipWhisperer是一个开源平台,用于对硬件设备的安全性进行研究。如图 6所示,该平台包含主控板(左)和目标板(右)2个模块。主控板用于采集和传输能量消耗,同时用来实现PC和实验板的数据传输以及密码算法的下载。目标板实现对数据的加密。该平台对于研究人员而言具有低成本、易操作的优点。

|
Download:
|
| 图 6 ChipWhisperer实验平台示意图 Fig. 6 Schematic diagram of the ChipWhisperer experimental platform | |
实验板主要有2个对应的开源软件配合使用,分别是Capture和Analyzer,前者用于加载加密算法、控制明密文以及捕获能量迹,后者提供了一些分析能量迹的脚本。图 7给出了Capture软件能量迹采集示意图。

|
Download:
|
| 图 7 Capture软件能量迹采集示意图 Fig. 7 Schematic diagram of Capture software energy trace acquisition | |
不同的实验设备所对应的能量迹具有不同的噪声标准差,本文使用的平台噪声标准差
本文方法的攻击过程包括线上能量迹采集阶段和线下数据分析阶段,具体攻击流程如下:
步骤1 加密M个随机明文,采集对应的M条能量迹,并记录这M个随机明文。
步骤2 将M个明文和M条能量迹分成N组,每组包含
步骤3 将每条能量迹中对应于处理16个S盒输入的部分截取出来并对齐。
步骤4 对每条能量迹求第1个S盒和第2个S盒之间的欧氏距离,然后进行归类,并将归类后的矩阵拼接,得到如图 3所示的结果。
步骤5 求矩阵A中每个位置的均值,计算向量V和求均值后的矩阵A中每一列的相关系数,根据相关系数将猜测密钥异或值进行降序排序。
步骤6 用投票法将排序后排名前n的密钥异或值进行投票,筛选出票数最少的密钥异或值,该值是前2个密钥字节
步骤7 重复步骤4到步骤6,对第1个S盒和另外14个S盒进行归类分析,最终得到如等式(7)所示的第1个密钥字节和其他15个密钥字节之间的线性关系,从而将密钥空间从
| $ \left\{\begin{array}{c}{k}_{1}\mathrm{⊕}{k}_{2}={{\mathit{\Delta}} }_{\mathrm{1, 2}}\\ {k}_{1}\mathrm{⊕}{k}_{3}={{\mathit{\Delta}} }_{\mathrm{1, 3}}\\ \vdots \\ {k}_{1}\mathrm{⊕}{k}_{16}={{\mathit{\Delta}} }_{\mathrm{1, 16}}\end{array}\right. $ | (7) |
步骤8 遍历第1个密钥字节,从剩下的候选密钥中得到正确密钥。
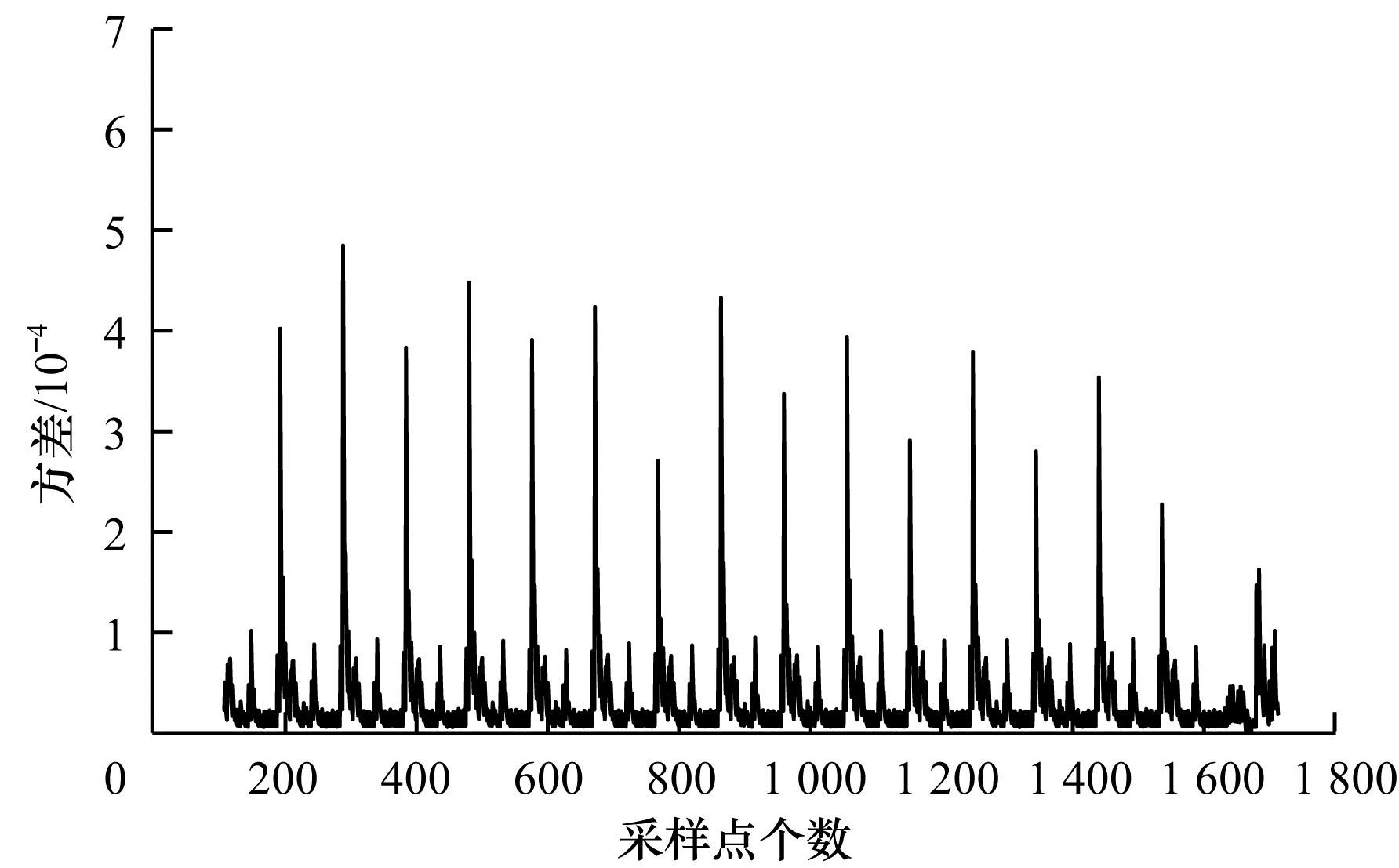
3.3 针对前2个S盒的攻击为验证本文方法的可行性,将对使用重用掩码方法的AES-128算法进行攻击,攻击的目标点是第1轮加密中前2个S盒的输入位置。在对采集的能量迹进行统计分析之前,需要将每条能量迹所对应16个S盒操作部分截取出来,如图 8所示。由于第1轮中的16个S盒操作的实现方式相同且依次执行,因此通过方差检测可以清晰地区分出16个S盒操作在能量迹中的位置。在确定16个S盒的位置后,对区间内的点进行攻击尝试,最终找到合适的8个采样点。不失一般性,在噪声标准差
|
Download:
|
| 图 8 AES加密的第1轮方差检测结果 Fig. 8 Results of the first round variance test of AES encryption | |
表 5给出了实施欧氏距离归类分析并根据相关系数排序后排名1到排名8的结果,可以看出这8个猜测密钥异或值
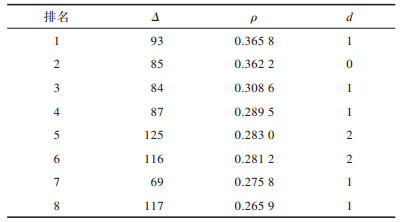
|
下载CSV 表 5 前2个S盒归类分析排序后的结果 Table 5 Results of classification analysis and sorting of the first two S-boxes |
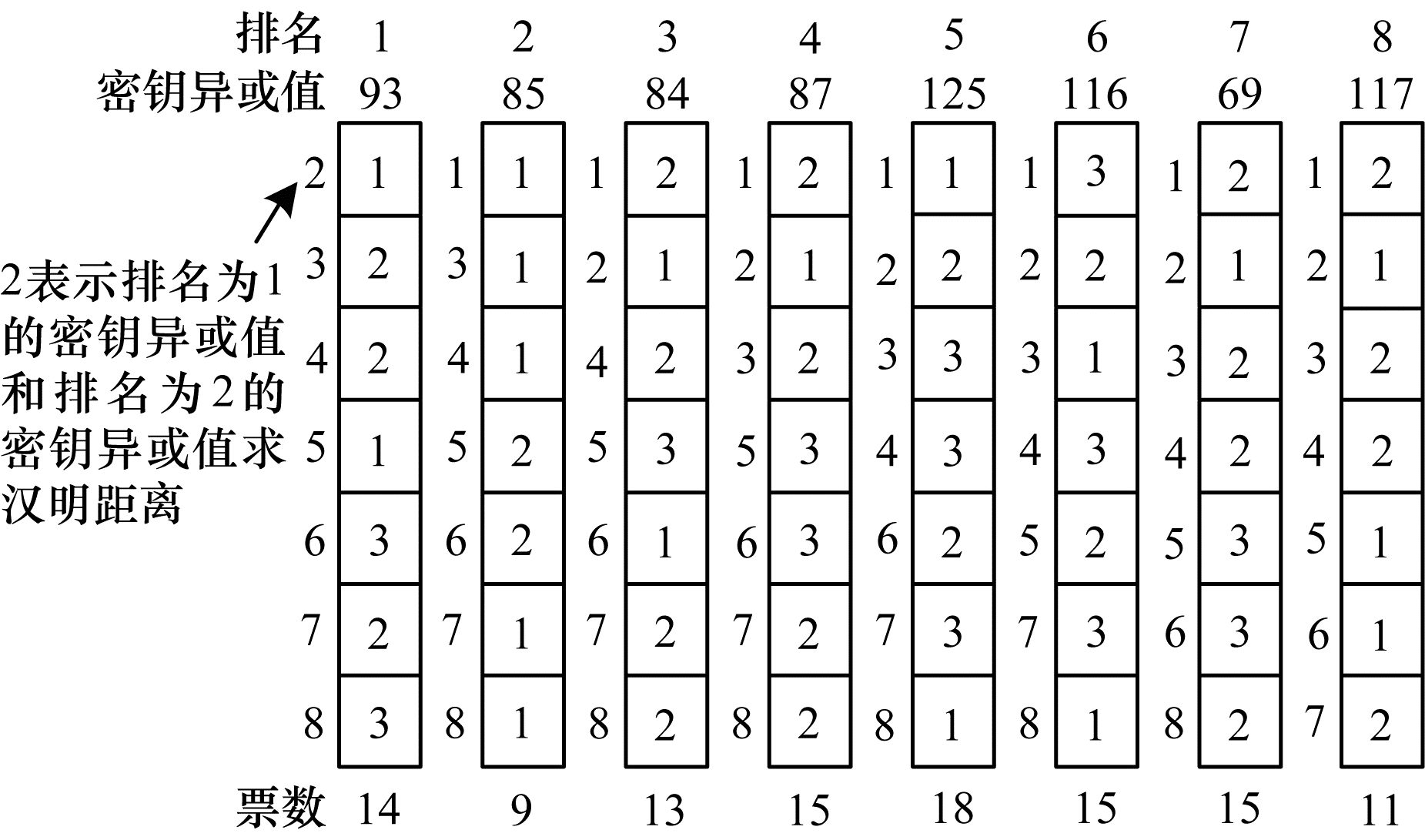
|
Download:
|
| 图 9 排名前8的猜测密钥异或值投票结果 Fig. 9 Results of the voting for the top 8 guessed key XOR value | |
为分析本文方法的效率,实验针对重用掩码AES-128算法加密的第1轮实施大量攻击后,统计成功率随着加密次数的变化曲线。在实际攻击中,控制明文分组为30,通过改变每个分组中随机明文的个数来统计成功率。为与其他方法进行对比,在相同的实验环境下实施另外3种攻击方法并统计其成功率。
图 10、图 11分别给出了本文方法与文献[18, 21]方法在不同的噪声环境下的攻击成功率对比。文献[18]中提出针对重用掩码AES算法的改进型相关性碰撞攻击(Improved Collision-Correlation Attack,ICCA),该攻击方法的成功率曲线对应图 10、图 11中的ICCA方法。文献[21]提出自适应选择明文碰撞攻击,使用最小二乘法(Least Square Method,LSM)和中心矩积法(Central Moment Product,CMP)这2种方法来计算2段能量迹的差,并利用自修正(Self-Correction,SC)错误机制,大幅提升了成功率,该攻击方法的成功率曲线对应图 10、图 11中的SC_LSM和SC_CMP方法。
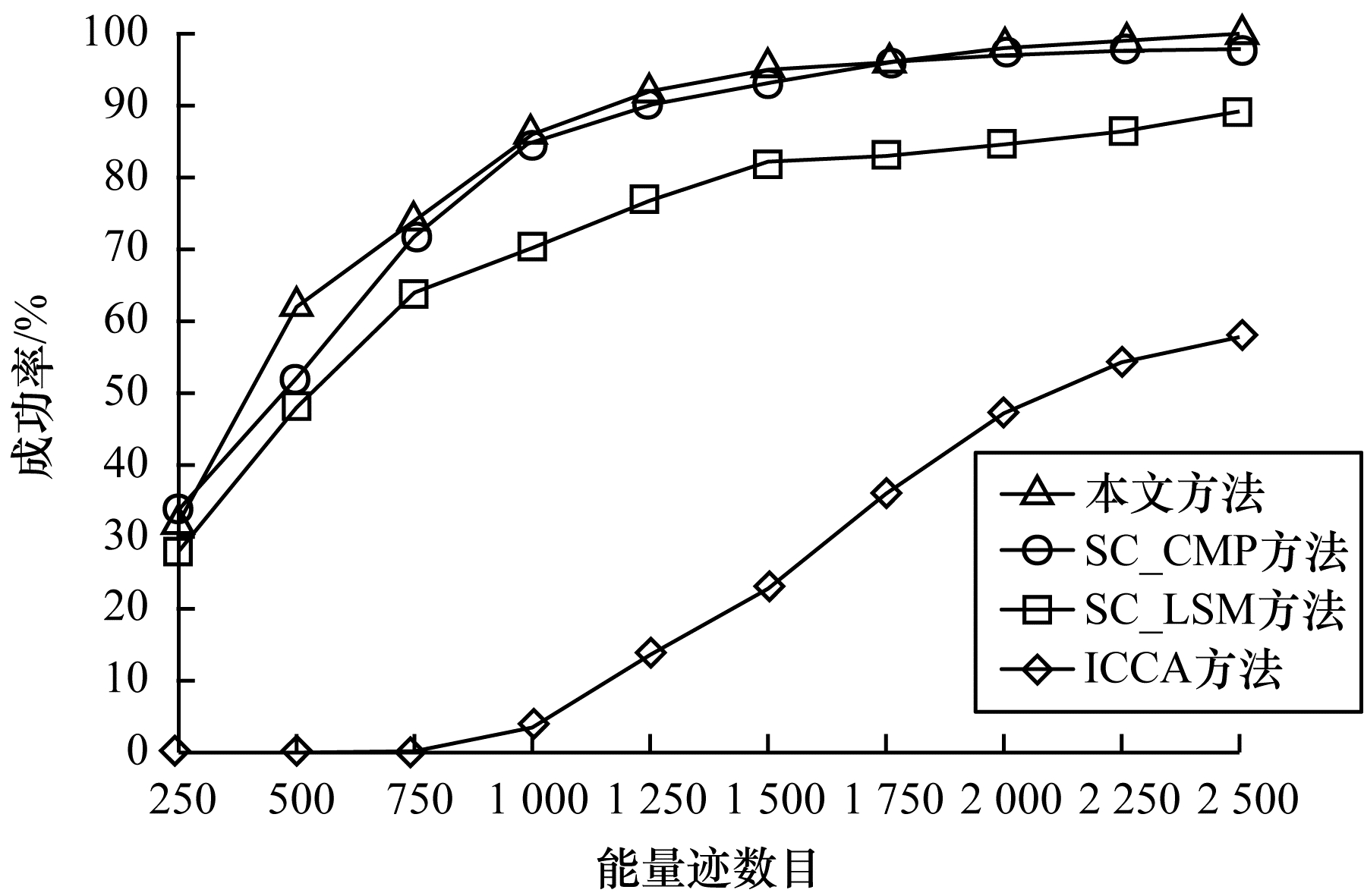
|
Download:
|
|
图 10 针对重用掩码方案的攻击成功率对比( |
|
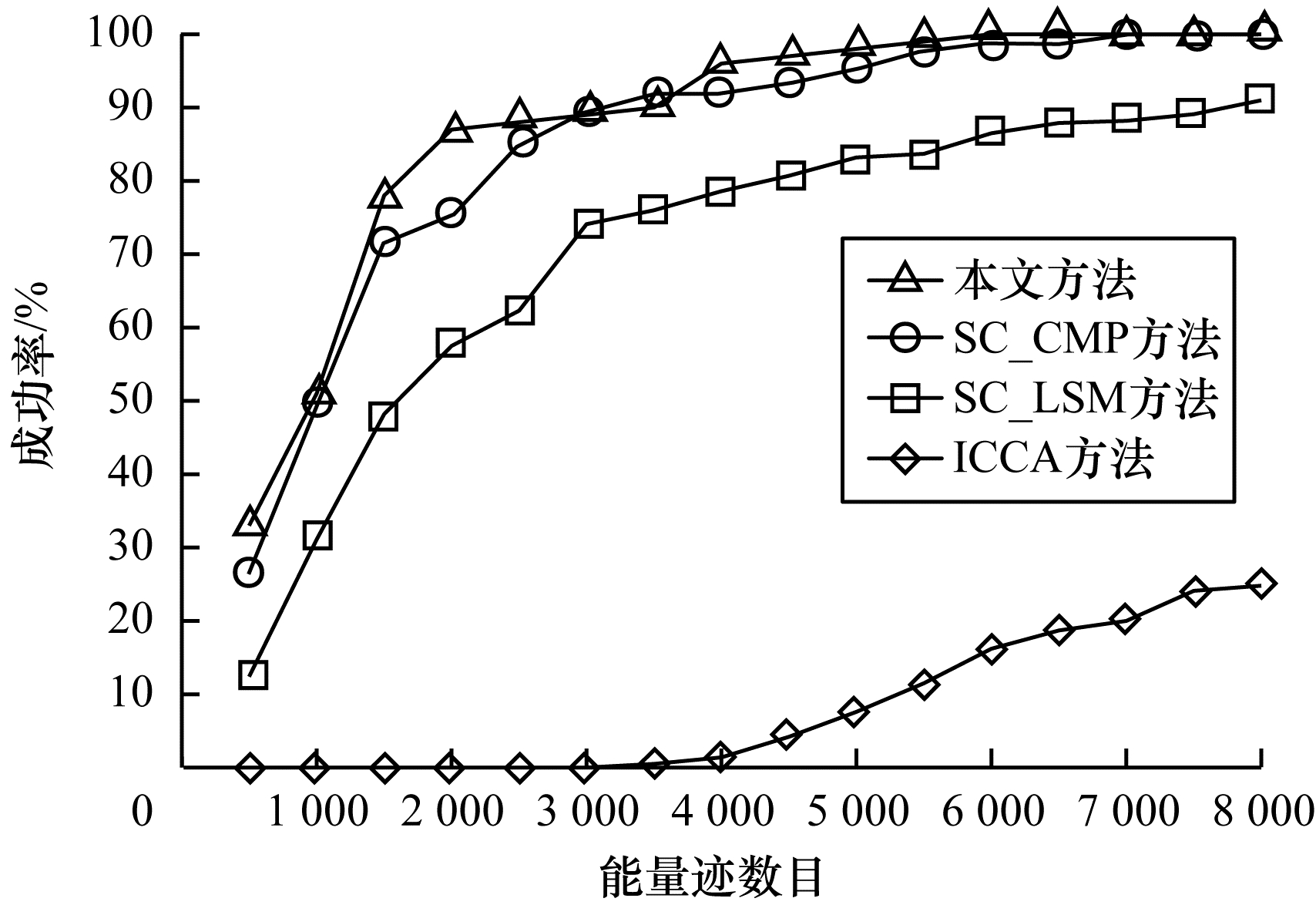
|
Download:
|
|
图 11 针对重用掩码方案的攻击成功率对比( |
|
从图 10、图 11可以看出:在噪声标准差σ为0.002 9时,若要达到95%的成功率,则本文方法需要约1 600条能量迹,其他3种方法中成功率最高的SC_CMP方法也需要约1 600条能量迹;在噪声标准差σ为0.006时,若要达到95%的成功率,则本文方法需要约4 000条能量迹,其他3种方法中成功率最高的SC_CMP方法需要约5 000条能量迹。
由此可见,本文方法相比于SC_CMP方法,成功率的优势并不明显,但相比于其他3种方法,除了不需要预先确定碰撞阈值及预先计算攻击模板外,最大的优势在于明文的随机性。当不允许攻击者操作与目标设备相同的设备且只可获得一定数量的随机明文和其对应能量迹时,其他3种方法就无法实施攻击,因为文献[18, 21]方法需要对选择明文进行加密,在攻击过程中需要对明文进行一定的控制,本文方法只需要获得一定数量的随机明文和其对应能量迹就可实施攻击,不需要攻击者主动控制明文,所以不会受到此因素的影响。
表 6从无需碰撞阈值、无需攻击模板、攻击过程简单、对重用掩码方案具有高效性、可利用未发生碰撞的信息、攻击者能够不操作目标设备等6个方面对本文方法和文献[18, 21-22]方法进行对比,其中,√表示具备该性能优势,×表示不具备该性能优势。由表 6可以看出,本文方法相比于已有方法具有一定的优势。

|
下载CSV 表 6 4种攻击方法的性能对比 Table 6 Performance comparison of four attack methods |
本文针对使用重用掩码技术的AES算法,提出一种高效的随机明文碰撞攻击方法。利用能量迹中未发生碰撞的信息,采用重用掩码AES算法S盒输入的汉明距离和欧式距离的关系,从256个密钥异或值中找出正确的密钥异或值。实验结果表明,与改进型相关性碰撞攻击、自适应选择明文碰撞攻击和基于假设检测的侧信道碰撞攻击方法相比,本文方法无需建立攻击模板及计算碰撞阈值,并且加密的是随机明文,实施简单。由于笔者通过分析发现采用多组明文进行实验可有效减少所需的明文总数,因此在后续工作中将研究明文组数对所需明文总数和成功率的具体影响,从而寻找到最优的明文组数。
| [1] |
KOCHER P C. Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems[C]//Proceedings of International Cryptology Conference on Advances in Cryptology. Berlin, Germany: Springer, 1996: 104-113.
|
| [2] |
KOCHER P, JAFFE J, JUN B. Differential power analysis[C]//Proceedings of International Cryptology Conference on Advances in Cryptology. Berlin, Germany: Springer, 1999: 388-397.
|
| [3] |
SCHRAMM K, WOLLINGER T, PAAR C. A new class of collision attacks and its application to DES[M]. Berlin, Germany: Springer, 2003.
|
| [4] |
BRIER E, CLAVIER C, OLIVIER F. Correlation power analysis with a leakage model[C]//Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin, Germany: Springer, 2004: 16-29.
|
| [5] |
CHARI S, RAO J R, ROHATGI P. Template attacks[C]//Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin, Germany: Springer, 2002: 13-28.
|
| [6] |
戴立, 胡红钢. 免触发信号的侧信道加解密区间定位方法[J]. 信息网络安全, 2019, 19(3): 43-51. DAI L, HU H G. Encryption and decryption interval locating method for non-trigger side-channel analysis[J]. Netinfo Security, 2019, 19(3): 43-51. (in Chinese) DOI:10.3969/j.issn.1671-1122.2019.03.006 |
| [7] |
王恺, 郭朋飞, 周聪, 等. 基于t检验的侧信道信息泄漏评估方法研究[J]. 信息网络安全, 2020, 20(10): 57-66. WANG K, GUO P F, ZHOU C, et al. Research on the assessment method of side channel information leakage based on t-test[J]. Netinfo Security, 2020, 20(10): 57-66. (in Chinese) DOI:10.3969/j.issn.1671-1122.2020.10.008 |
| [8] |
凌杭, 吴震, 杜之波, 等. 基于汉明重的EPCBC代数侧信道攻击[J]. 计算机工程, 2017, 43(8): 156-160, 168. LING H, WU Z, DU Z B, et al. Algebraic side channel attack against EPCBC based on hamming weight[J]. Computer Engineering, 2017, 43(8): 156-160, 168. (in Chinese) DOI:10.3969/j.issn.1000-3428.2017.08.026 |
| [9] |
SCHRAMM K, LEANDER G, FELKE P, et al. A collision-attack on AES[C]//Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin, Germany: Springer, 2004: 163-175.
|
| [10] |
BOGDANOV A. Improved side-channel collision attacks on AES[C]//Proceedings of International Workshop on Selected Areas in Cryptography. Berlin, Germany: Springer, 2007: 84-95.
|
| [11] |
MESSERGES T S. Securing the AES finalists against power analysis attacks[C]//Proceedings of International Workshop on Fast Software Encryption. Berlin, Germany: Springer, 2000: 150-164.
|
| [12] |
HERBST C, OSWALD E, MANGARD S. An AES smart card implementation resistant to power analysis attacks[C]//Proceedings of International Conference on Applied Cryptography and Network Security. Berlin, Germany: Springer, 2006: 239-252.
|
| [13] |
AKKAR M L, GIRAUD C. An implementation of DES and AES, secure against some attacks[C]//Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin, Germany: Springer, 2001: 309-318.
|
| [14] |
HUANG H, LIU L B, HUANG Q H, et al. Low area-overhead Low-Entropy Masking Scheme(LEMS) against correlation power analysis attack[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2019, 38(2): 208-219. DOI:10.1109/TCAD.2018.2802867 |
| [15] |
谭锐能, 卢元元, 田椒陵. 抗侧信道攻击的SM4多路径乘法掩码方法[J]. 计算机工程, 2014, 40(5): 103-108, 114. TAN R N, LU Y Y, TIAN J L. SM4 multi-path multiplicative masking method against side-channel attack[J]. Computer Engineering, 2014, 40(5): 103-108, 114. (in Chinese) DOI:10.3969/j.issn.1000-3428.2014.05.022 |
| [16] |
张翌维, 龚冰冰, 刘烈恩, 等. 抵御侧信道分析的AES双路径掩码方法[J]. 计算机工程, 2012, 38(13): 108-111. ZHANG Y W, GONG B B, LIU L E, et al. AES dual-path masking method for resisting side-channel analysis[J]. Computer Engineering, 2012, 38(13): 108-111. (in Chinese) |
| [17] |
MORADI A, MISCHKE O, EISENBARTH T. Correlation-enhanced power analysis collision attack[C]//Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin, Germany: Springer, 2010: 125-139.
|
| [18] |
CLAVIER C, FEIX B, GAGNEROT G, et al. Improved collision-correlation power analysis on first order protected AES[C]//Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems. Berlin, Germany: Springer, 2011: 49-62.
|
| [19] |
BOGDANOV A, KIZHVATOV I. Beyond the limits of DPA: combined side-channel collision attacks[J]. IEEE Transactions on Computers, 2012, 61(8): 1153-1164. DOI:10.1109/TC.2011.140 |
| [20] |
NIU Y C, ZHANG J W, WANG A, et al. An efficient collision power attack on AES encryption in edge computing[J]. IEEE Access, 2019, 7: 18734-18748. DOI:10.1109/ACCESS.2019.2896256 |
| [21] |
DING Y L, SHI Y, WANG A, et al. Adaptive chosen-plaintext collision attack on masked AES in edge computing[J]. IEEE Access, 2019, 7: 63217-63229. DOI:10.1109/ACCESS.2019.2916553 |
| [22] |
ZHENG D, JIA X, ZHANG M L. Hypothesis testing based side-channel collision analysis[J]. IEEE Access, 2019, 7: 104218-104227. DOI:10.1109/ACCESS.2019.2932036 |
| [23] |
O'FLYNN C, CHEN Z. ChipWhisperer: an open-source platform for hardware embedded security research[C]//Proceedings of International Workshop on Constructive Side-Channel Analysis and Secure Design. Berlin, Germany: Springer, 2014: 243-260.
|
 2022, Vol. 48
2022, Vol. 48
