2. 北方民族大学 图像图形智能处理国家民委重点实验室, 银川 750021;
3. 西北大学 信息科学与技术学院, 西安 710127
2. Key Laboratory of Image and Graphics Intelligent Processing of State Ethnic Affairs Commission, North Minzu University, Yinchuan 750021, China;
3. School of Information Science and Technology, Northwest University, Xi'an 710127, China
开放科学(资源服务)标志码(OSID):
最大团问题(Maximum Clique Problem,MCP)是图论中的一个经典问题,同时也是一类非确定性多项式(Non-deterministic Polynomial,NP)难问题,被广泛应用在故障诊断[1]、生物信息学[2]、计算机视觉[3]、社会网络分析[4]等领域。在社交网络问题中,团代表了紧密联系的团体,研究最大团及其松弛模型(Clique Relaxation,CR)能够对社会网络映射关系做出理论性分析[4]。在生物信息领域,比较蛋白质之间的结构相似度是生物领域的重要任务,由于蛋白质之间的结构相似可以通过氨基酸序列转化而来的匹配图近似模拟,因此在对比蛋白质结构问题中可以将其转化为最大团问题,并推测未知蛋白质功能[2]。所以,最大团问题具有较高的理论价值和现实意义。但随着最大团在真实世界的应用发展,部分领域在求解最大团问题时出现求解效率差、得不到最优解的情况。研究发现,与传统最大团研究测试用图例不同,真实世界所映射出的图模型通常为大规模无向图,这类图通常密度低,顶点数量巨大,并具有小世界属性[5]、幂律分布[6]、聚类[7]等共同的统计特征。因此,在此类大规模图模型中研究最大团具有重要意义。
为解决大规模最大团问题,研究人员利用大数据技术,使用MapReduce[8]、Pregel[9]等面向海量数据和密集型计算的并行处理框架求解大规模最大团问题。这些框架具有较好的容错性和可扩展性,且提供了简单的处理方法和功能强大的编程模型。
本文对大规模最大团问题研究算法进行分析,通过算法分类的方法总结各种算法的优点与不足,对主要算法进行对比分析,并提供未来解决方案与研究方向。
1 最大团问题定义及数学表示给定图
最大团问题也被称为最大独立集问题,独立集是指在图G中两两顶点之间没有边相连。顶点数最多的集合即为最大顶点独立集。当图G转化为
最大团问题作为一个组合优化问题,可以进行等价描述,整型规划问题的描述如下:
设
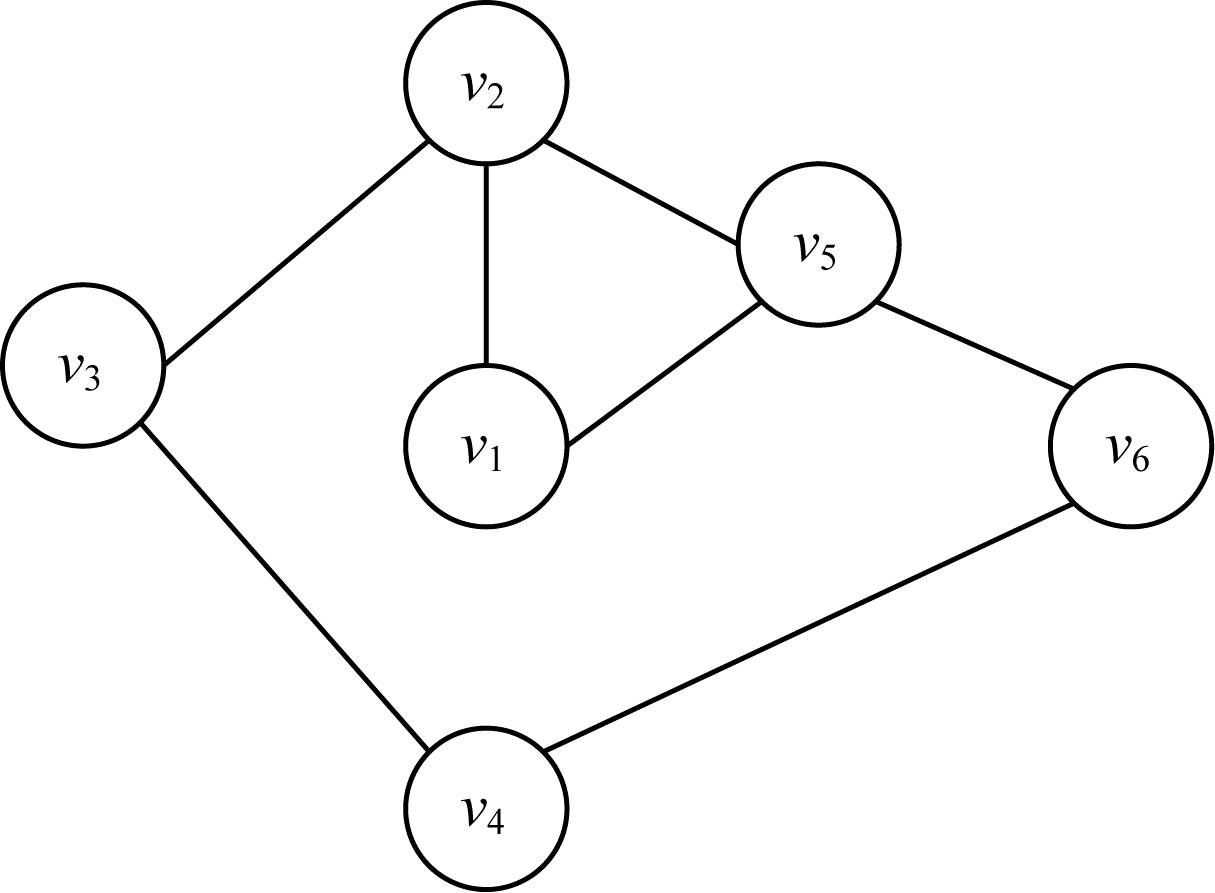
|
Download:
|
| 图 1 最大团为3的无向图 Fig. 1 Undirected graph with maximum clique 3 | |
求解最大团问题的常规算法大致分为3类:精确算法,启发式算法和分布式算法。
1)精确算法主要有枚举法[10]、回溯法[11]、分支限界法[12]等。这类算法能求得精确解,但时间复杂度相对较大[13]。例如HOSSEINIAN等[13]提出利用MCP的整数(线性)规划结合拉格朗日松弛技术,导出最大团的界,结合分支限界法得到一种新的精确算法。PLACHETTA等[12]指出分支限界法可满足求解器减少分支的需求,能够通过最大团与顶点覆盖的映射方法进行回溯求解。
2)启发式算法主要为遗传算法、蚁群算法、贪婪算法等。这类算法通过借鉴一些自然现象以及人类思维方式的指导来展开,对精确算法的时间复杂度进行了改善,但存在容易陷入局部最优及无法找到精确解[14]的缺点。例如BABKIN等[14]将遗传算法与禁忌搜索算法相结合来研究最大团问题,使种群多样性增加,加快跳出局部最优解并获得全局最优解。JI等[15]提出一种基于多目标蚁群算法和新的团表示方案来检测重叠社区。
3)分布式算法主要为最大积置信传播算法和m-tree算法,此类算法通过将最大团问题的线性规划方程,利用消息传递的分布式性质进行并行计算,从而缩短求解时间,提高算法效率。例如文献[16]提出一种改进的分布式最大权独立集算法,使用最大积信念传播算法框架,启发式地提出了一种相邻节点间交换信息的计算方法,使算法可以在环型无向图内进行消息传递与消息计算,弥补了置信传播算法求解此类问题在环形图中收敛困难的缺陷。表 1结合求解最大团问题的研究[17-19]给出了基于常规算法的最大团求解方法对比。
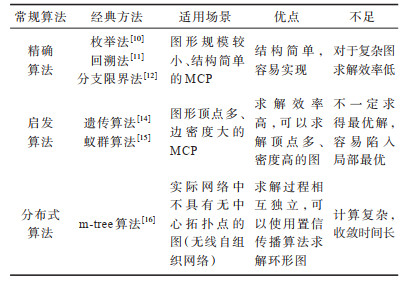
|
下载CSV 表 1 基于常规算法的最大团求解方法对比 Table 1 Comparison of maximum clique solution methods based on conventional algorithms |
传统最大团算法主要使用顶点数量在几千以内的随机生成图、人工构造图数据集以及以DIMACS和BHOSLIB为代表的中小规模标准测试数据集。而真实世界中大规模图例无论在顶点规模还是在图结构特征上均存在明显区别,因此传统求解最大团算法在大规模图例中并不适用。例如CBB[20]算法、MaxCLQ[21]算法、MMCQ[22]算法、IncMaxCLQ[23]等算法对DIMACS数据集中的图例有较好的效果,但难以处理数量达到百万级的真实世界大规模图。针对大规模图例的MCP求解问题,由于数据量巨大且计算复杂,部分研究人员利用大数据计算平台与计算框架对图例进行简化预处理和并行搜索处理以提高求解效率。在求解大规模图例的MCP问题中,主要使用的大数据技术为MapReduce编程框架[24]、Spark分布式内存计算框架以及Hadoop分布式云计算平台[9]。图 2给出了利用MapReduce进行并行计算的流程。
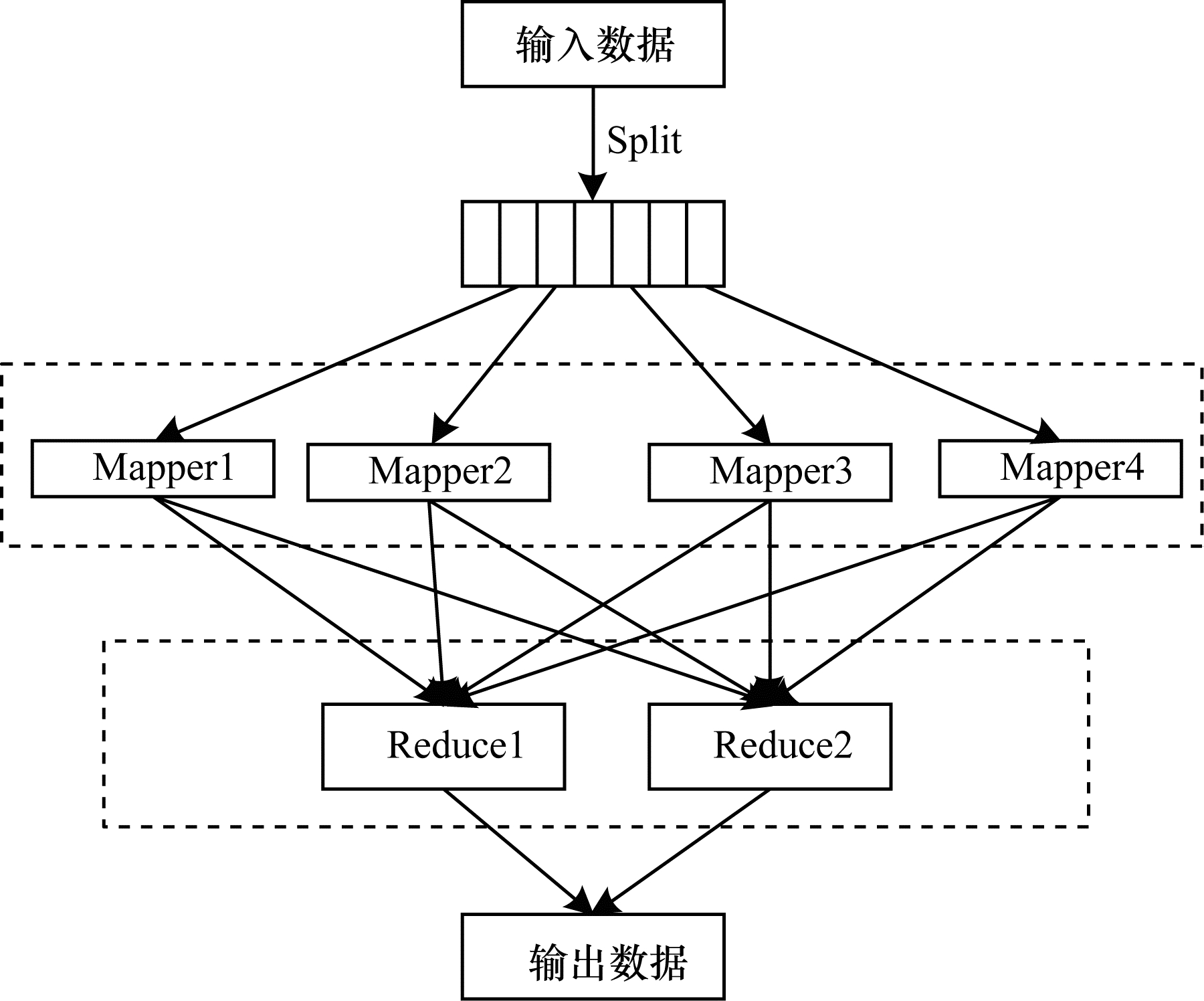
|
Download:
|
| 图 2 MapReduce并行调度流程 Fig. 2 MapReduce parallel scheduling process | |
在大数据背景下,将大数据计算平台与图划分方法相结合以求解大规模图例的最大团是一种有效的方法。所谓图划分方法就是通过将大规模图例划分为多个小规模的子图图例,使其他搜索算法可以精确快速求解的方法。图划分方法分为预处理阶段和搜索阶段2个阶段。如图 3所示为一般图划分求解大规模图例最大团的方案。
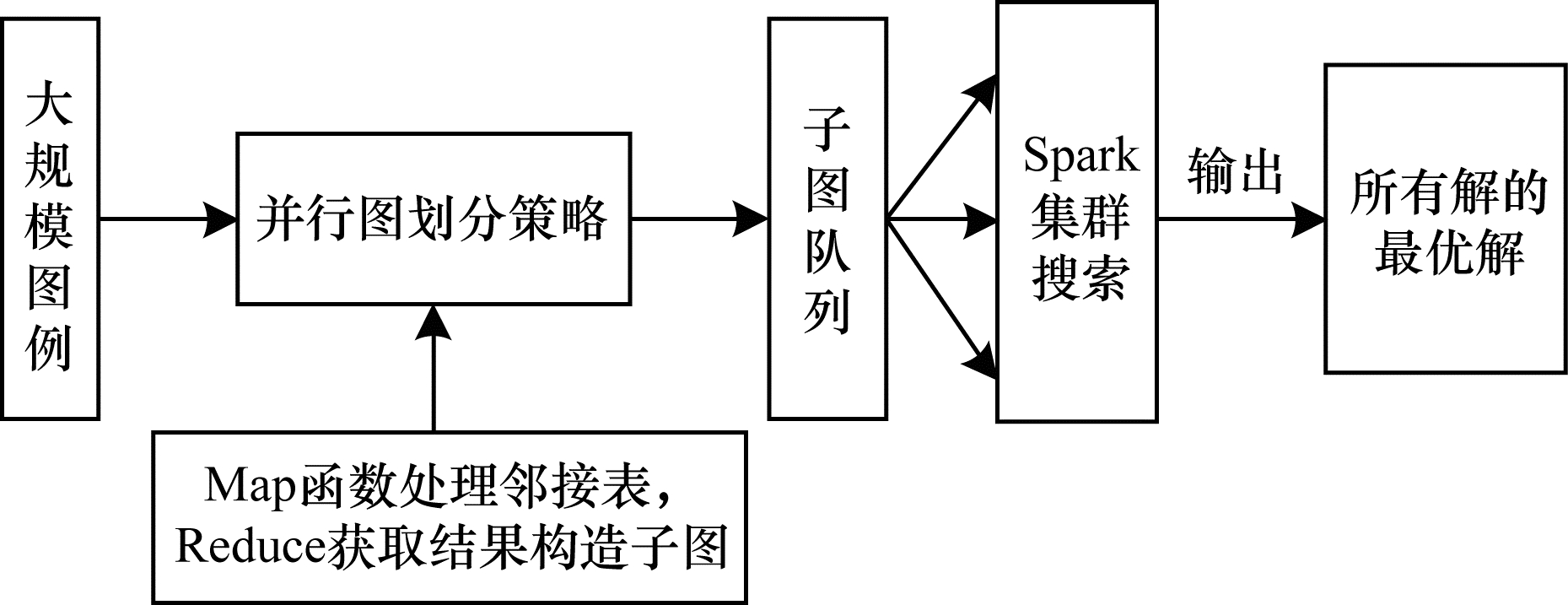
|
Download:
|
| 图 3 一般图划分求解大规模图例的方案 Fig. 3 Scheme for solving large-scale graph by dividing general graph | |
为解决传统模式下求解大规模图例最大团过程中存在的存储大规模图例问题与单机处理图数据问题,文献[25]提出一种基于MapReduce的计算方法,通过图着色进行子图划分,并使用分支定界法独立计算不同分区的最大团数并选出最优解。图划分作为求解的关键一步,划分后的子图是否有利于求解直接影响搜索速率。针对子图划分的改进,文献[26]提出一种新的多图层划分求解最大方法(Parallel Multilayer Graph Partitioning method for Solving Maximum Clique,PMGP_SMC)来提高求解效率,提出多图层划分(Multi-layer Graph Partitioning,MGP)算法,将MGP算法与Spark的GraphX图计算相结合,并基于大数据平台的并行计算方法提出并行多图层划分(Parallel MGP,PMGP)方法。
文献[27]针对大规模图例求解效率提出一种基于并行约束规划的最大团识别研究算法BMT,使用多层划分方法并加入任务时间预测函数,提出基于任务时间预测模型的并行图划分方法,该预测模型
| $ T\left(G\right)={\left(\sum\limits _{i=0}^{k}|G{|}^{i}\sum\limits _{j=0}^{k}{a}_{i, j}\rho {\left(G\right)}^{j}\right)}^{\left|G\right|(\rho {\left(G\right)}^{2}+b\rho (G)+c)} $ | (1) |
其中:k用来控制模型自由度,即泰勒函数展开级数;
BMT算法通过时间预测函数实现了2个需求:
1)有效图分割。将复杂图分割为更易求解的若干更小且独立子图,使Spark集群中计算节点可独立计算,降低通信开销。
2)保证各点负载均衡。通过预测时间模型估算求解时间,决定图分割的深度。将子图分配给Spark集群计算节点,每个计算节点采用约束规划的方法对分割产生的子问题分别进行建模和求解,实现最大团问题的并行化处理,提高大规模图例下的最大团问题求解速率。
对于子图中的局部搜索问题,文献[28]提出Random_BLS算法,通过联合局部搜索和自适应扰动策略来探索解空间,但算法的搜索多样性较差。文献[29]提出PBLS算法能够解决搜索不全面问题,提高算法搜索解的多样性,PBLS算法加入了惩罚因子,根据惩罚值与禁忌值对节点进行选择优化搜索阶段多样性。由于迭代次数固定,小规模子图和大规模子图求解时间相同,导致总求解速度慢。文献[27] 对PBLS算法进行改进,提出可以根据子图大小自动设定迭代次数的SPBLS算法,该算法使用迭代公式模型增加PBLS的灵活性,提高了算法的执行效率,使SPBLS算法根据子图规模自动设置迭代次数,从而降低总求解时间,提高求解效率。SPBLS算法的迭代公式模型如式(2)所示:
| $ I=T\left(\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}\left(-N/m\right)}-c\right) $ | (2) |
其中:T表示最大迭代数;N表示图中节点的个数;m是取值范围为10~100的常量;c是取值范围为在0~1的常量。当所求节点个数越多时,SPBLS求解最大团所需的次数越多,当求得的迭代次数为小数时,迭代次数向上取整。
上述措施主要针对图划分方法,对大规模图例的预处理和搜索子图进行改进,有效增强划分后子图的可搜索性,提高求解速率,避免了在求解过程的复杂缓慢计算。从本质上来说,对原始图例进行多次划分、利用大数据并行计算平台能显著降低算法的搜索时间复杂度[30],但也带来了计算平台固有的缺陷,在使用大数据技术求解最大团问题时,MapReduce并不总对求解有正面影响。当子图数量大且重复数据多时,需要多次的迭代进行求解,但MapReduce的多次调用需要消耗巨大的内存空间,因此不利于提高求解速率。为此,算法在改进时还应该考虑多层划分时多次迭代所使用的内存空间。当前有效的解决方法是使用Spark的GraphX这一类即使进行多次迭代,但耗费内存较小的并行计算平台进行多层划分[27],这类并行计算平台可以有效减少迭代次数,虽然增加了计算次数但相较于使用MapReduce进行多次迭代,求解速率更快。表 2所示为图划分方法的对比分析结果。

|
下载CSV 表 2 不同图划分方法的对比分析结果 Table 2 Comparative analysis results of different graph division methods |
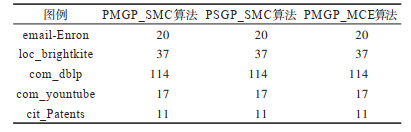
由表 3可知,PSGP_SMC算法与PMGP_SMC算法在求解精度上均能满足枚举算法PMGP_MCE所求得的精确解。
|
下载CSV 表 3 不同算法求解大规模图例最大团的结果对比 Table 3 Comparison of the results of solving the largest clique of large-scale graph with different algorithms |
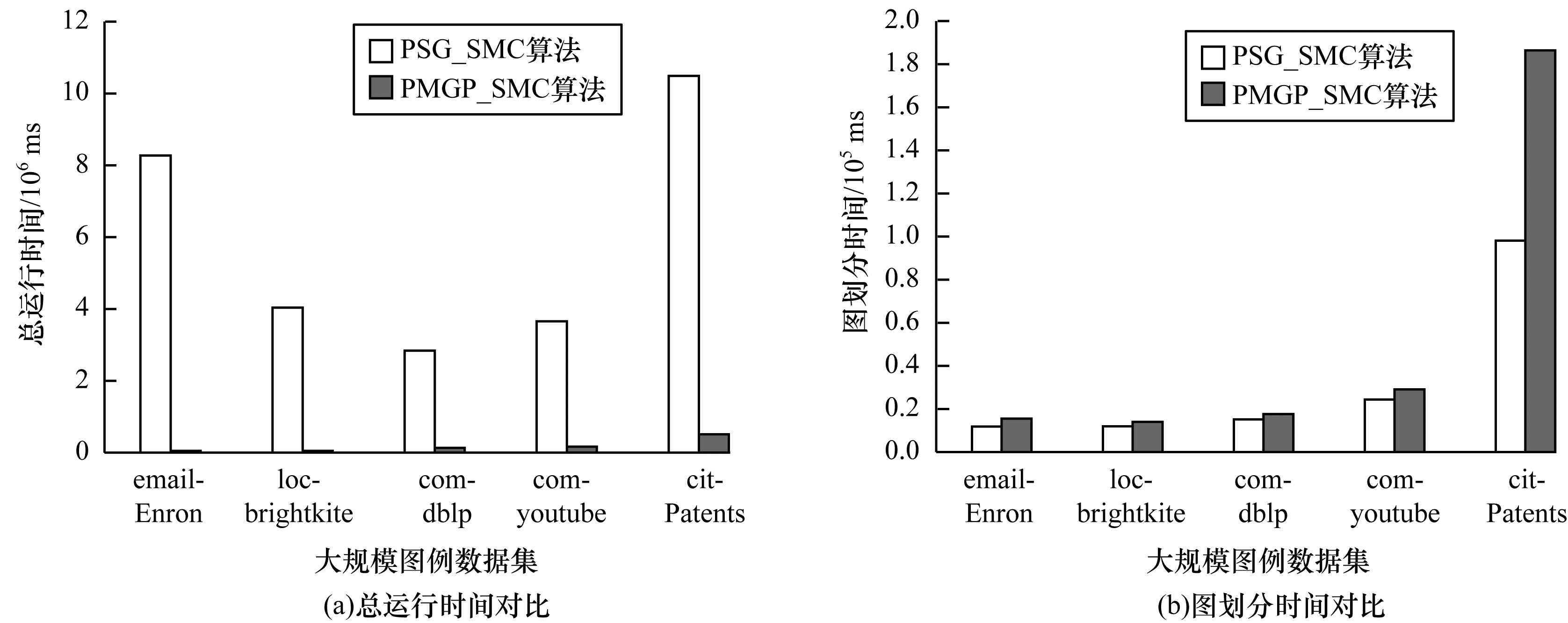
由图 4可知,PMGP_SMC算法在总运行时间上有明显优势,特别是在email-Enron中表现最为明显。结合总运行时间对比发现,在求解精度相同的条件下,图划分时间较长的PMGP_SMC算法的子图搜索时间远优于PSGP_SMC算法。这是由于多层图划分虽然耗费较多时间,但是所搜索到的子图更适合子图搜索,能够使子图快速求解。此外,自适应迭代函数针对使用图划分方法后产生较多子图的大规模图例有更高的求解速率。针对结合图划分方法,本文主要改进方向为如何使图划分后的子图得到更优解,以及如何在多个子图中快速求解。对于子图较多、求解较复杂的情况可以同时将2种计算方式布置在大数据并行计算平台中,从而提高求解速度。
|
Download:
|
| 图 4 不同算法的实验结果对比 Fig. 4 Comparison of experimental results of different algorithms | |
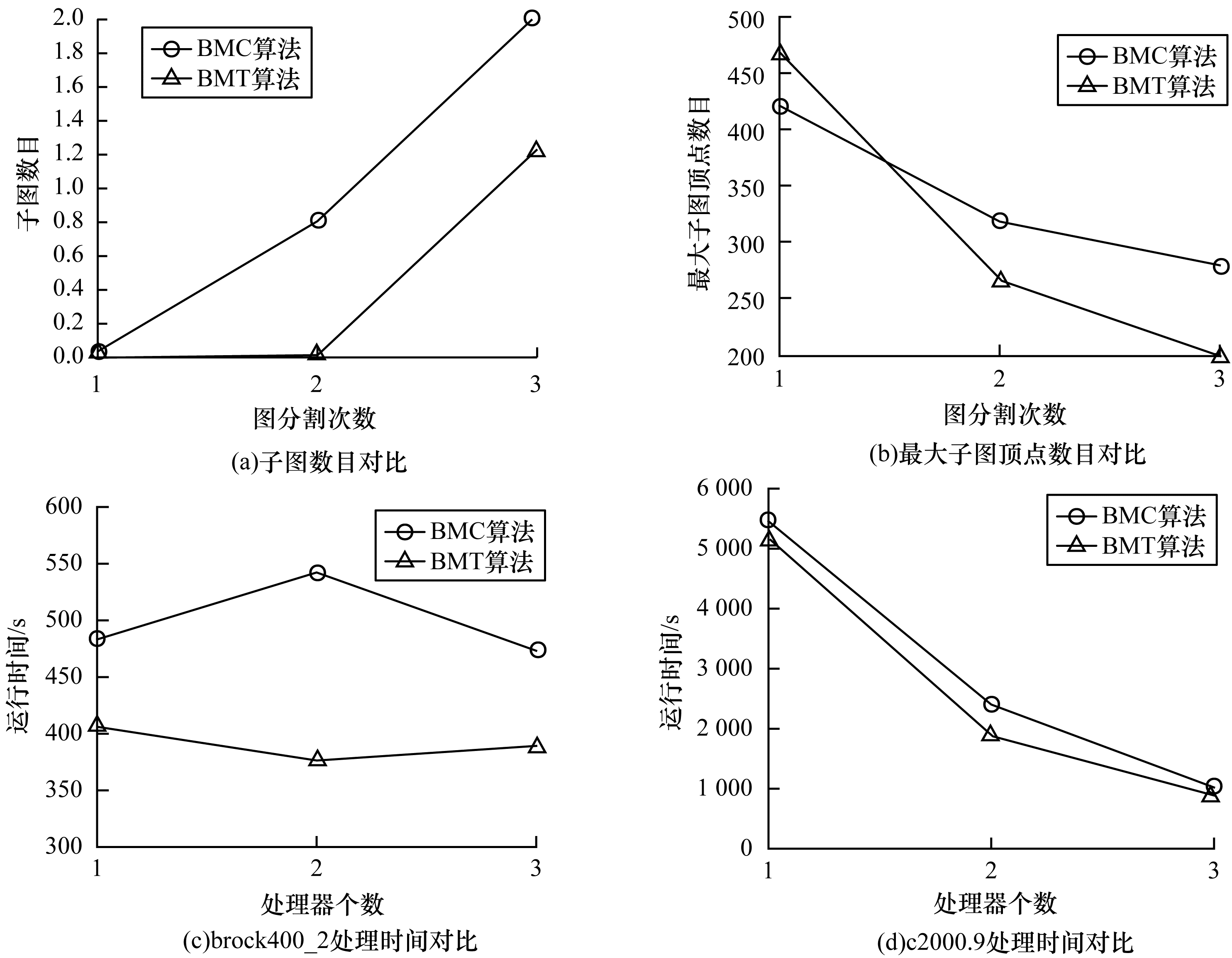
与BMC算法相比,BMT算法使用了多层图划分方法且启发式地提出了时间预测函数。由图 5(a)、图 5(b)可知,BMT算法在相同图分割次数下得到的子图数量较少,但是平均子图顶点数目小于BMC算法,说明BMT算法在相同分割条件下对图中求解最大团所连接的无效边有更好的删除效果。图 5(c)、图 5(d)展示了BMT算法分别使用了1、3、6这3种数量的处理器(4核16 GB内存,1个主节点,6个从节点)进行处理图划分,可以看出对大规模图例并行处理能够大幅缩短运行时间,而对小规模图例并不适合使用并行处理,因为处理器的增多无法带来求解速率的提升,且在高密度图中最少需要3层划分才能优于BMC算法。BMT算法对处理器有较高的要求,并且此次算法实验所使用的图例密度均为0.9的高密度图,且顶点数范围为125~1 500,泛化性较弱。
|
Download:
|
| 图 5 2种算法的实验结果对比 Fig. 5 Comparison of experimental results of two algorithm | |
k-core的概念由WATTS提出,并且指出k-core可用来帮助识别网络中紧密相连的组,以及可以表示结构性质和层次性质[32]。k-core算法通过逐渐递增k值来挖掘图中的最大团,同时也可以作为一种社会网络分析作用于中心性分析和社区检测。文献[33]根据网络分析问题提出一种共享内存算法,该算法用于多核平台的k-core分解,在求解大规模最大团问题上对图例类型有较好的泛化性。支限界法作为求解最大团问题最主流的算法,使用k-core缩小最大团上界并对候选集进行剪枝来提高求解速率。在分支限界法中,文献[34]提出一种针对大型稀疏图的快速并行最大团(Parallel Maximum Clique,PMC)算法。PMC算法在查询前利用启发式算法获得初始团,然后采用分支定界的方法,使用图着色方法与k-core结构估计最大团的上界,并搜索树剪枝。在并行搜索的过程中,根据搜索到的结果对最大团的上界和下界进行更新,使PMC算法在求解时可以缩小求解空间,提高求解速率。文献[35] 同样使用剪枝方法,利用k-core算法提出新的剪枝策略和搜索区域限制策略,该算法结合图着色的上界估计,将搜索区域限制在根据core值得到的每个子问题的顶点子集内,通过剪枝操作对无法形成比当前团更大的子问题进行删除,从而加快求解过程。但不足的是,该算法与PMC算法相比,所使用的图例规模不够大。对于现实世界的无标度网络图[36],文献[37]提出一种利用初始启发算法改进的搜索算法,该算法在得到初始团大小后,通过k-core算法结合剪枝策略减小图的尺寸,并基于贪婪算法对选定的顶点及其邻居节点进行图着色,提升搜索过程的求解速率。
由于core结构对于化简大规模图模型有显著效果,随着研究的发展,研究人员发现k-community对化简大规模图例有同样好的效果。针对这2种化简方法,文献[38]提出FC算法,利用2种团松弛结构,将网络实例减少到现有求解器可处理的尺寸,同时保持求解最优性。在团松弛的过程中,利用贪婪式启发算法求解最大团问的下界(
针对大规模稀疏图的特征,文献[39]描述了一种利用core算法对边界进行优化的分支定界求解稀疏图问题最大团的算法(Branch-and-Bound Maximum Clique algorithm of Sparse graphs Problem,BBMCSP),BBMCSP算法在预处理阶段可以在多项式时间内有效减少问题的规模,并在搜索阶段通过递归搜索求解最大团。与BBMCSP算法不同的是,PMC算法使用了一个辅助列表来存储不能作为解的一部分顶点,而BBMCSP算法则使用确定的核心数作为初始节点,只对根节点进行剪枝操作,使剩余节点可以通过core值来判断边界。新算法在递归搜索过程中利用并行性降低求解时间,且算法结构比PMC算法更清晰简单。
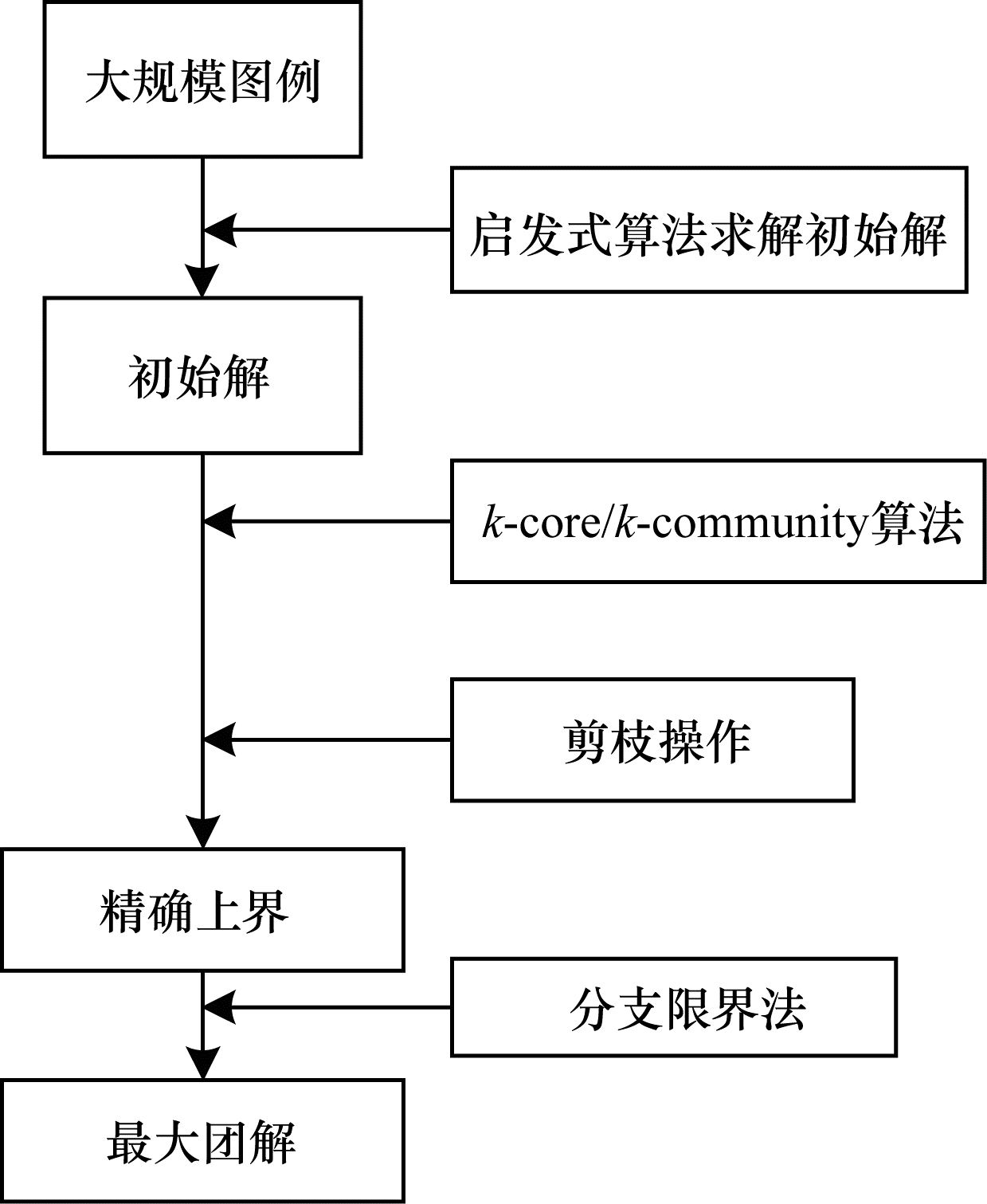
上述算法主要针对k-core算法对分支限界法进行了改进,有效增强了分支限界法的剪枝操作,显著减少了算法的搜素空间与搜索难度,避免了内存浪费。从本质上来说,使用分支限界法求解大规模最大团问题是对最优解无用顶点的冗余删除,即剪枝操作,为此使用k-core算法有助于分析图中顶点结构,从而快速剪枝。对于这一思路的相关操作,有研究人员使用k-community方法,同样取得了优异的剪枝效果。在求解过程中,k-community方法对密集图的处理效果低于图划分方法,但在大规模稀疏图中却表现优异。图 6为使用core算法求解大规模最大团问题的一般流程。
|
Download:
|
| 图 6 core算法求解大规模图例最大团问题的一般流程 Fig. 6 General process of core algorithm to solve the maximum clique problem of large scale graph | |
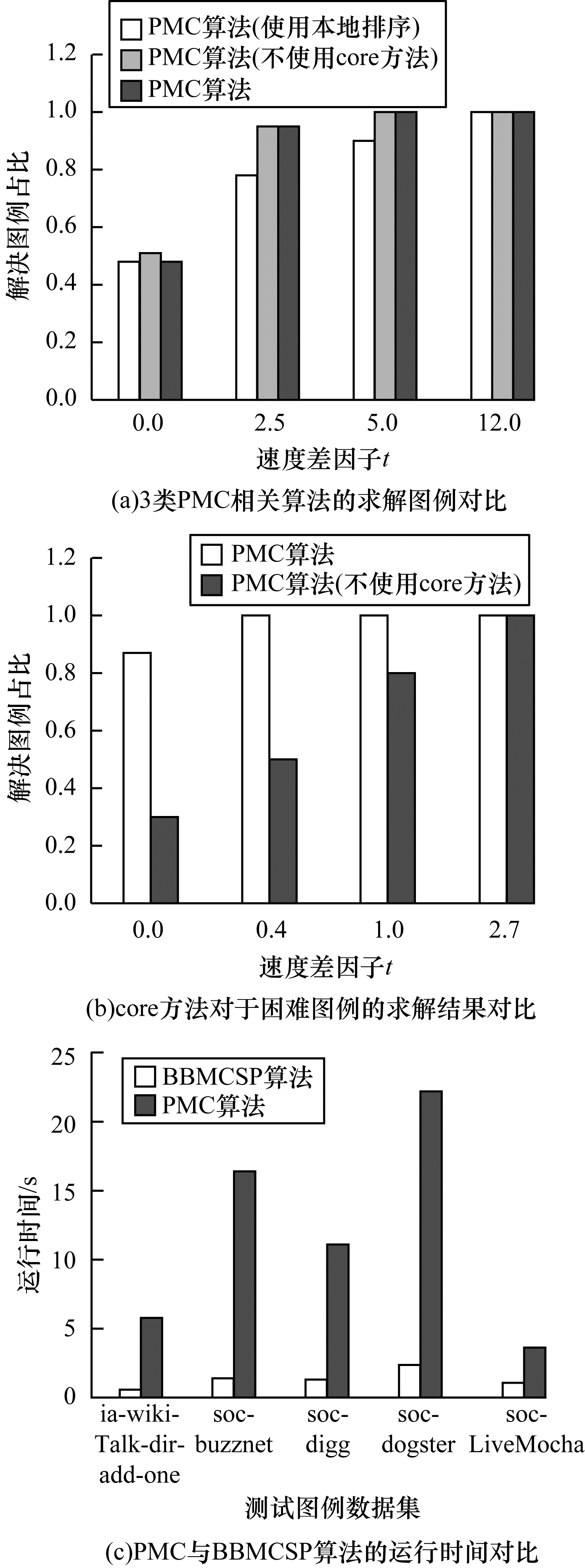
图 7(a)展示了在30个困难的社交和网络图例中分别使用完整算法、无core算法、无Degenerace排序算法的效果对比。由图 7(a)可知,完整算法与不使用core算法之间的差别很小,但完整算法与不使用Degeneracr排序算法有较大差别,当速度差因子为2.5时完整算法可以求解全部的难解图例,而不使用Degeneracr算法则只能求解大约78%的图例。这说明PMC算法有利于处理这类部分顶点度数大的社交与网络图例,并且在度数较大图中算法对于Degeneracr排序依赖性较大,对core算法依赖性较低。对于求解困难的并行DIMACS-Hard图例,从图 7(b)中可知完整算法与不使用core算法的求解效果相差巨大,当速度差因子为0.4时完整算法基本能够解决所有并行难解图例,而不使用core算法在速度差因子为2.7时才能全部求解并行难解图例,说明core算法在并行化计算求解难解图问题上效果更好。
|
Download:
|
| 图 7 不同算法的实验结果对比 Fig. 7 Comparison of experimental results of different algorithm | |
图 7(c)所示为BBMCSP算法和PMC算法在顶点为0~300万的测试图例中的对比结果。BBMCSP算法在初始解不相同的情况下的所有求解结果均优于PMC算法。其中在大规模数目点的soc-dogster中求解速度表现最好,算法求解效率比PMC算法高出数个量级。在具有相同初始解和不同初始解的平均情况下,BBMCSP算法比PMC算法效率提高了428倍。尤其是与具有相同初始解的BBMCSP算法相比,拥有不相同初始解的BBMCSP算法具有更高的求解效率[39]。与PMC算法对比发现,对于现实世界所对应的大规模稀疏图,BBMCSP算法的平均求解效率高于PMC算法。
3.3 大规模图例最大团问题的精确算法文献[40]提出在MapReduce框架下使用排序的并行枚举团(Parallel Enumeration of Cliques using Ordering,PECO)算法。PECO算法只枚举不重复的最大团,不添加已删除的重复最大团和非最大团,减少了重复搜索步骤。PECO算法提升求解效率的关键在于图的顶点总排序,可以使求解之前的工作分配均衡,并且消除处理器间的冗余工作。PECO算法提出了度排序、三角排序、字典排序和随机排序4种方法,在现实生活所映射的大规模稀疏图中基于度数排序和三角排序的表现最好,既减少了枚举时间,又有利于负载平衡。
在精确算法求解大规模稀疏图的最大团问题上,使用最多的方法为分支限界法,对于上界的求解最大团问题,文献[41]通过对最大团问题的转化,将最大团问题转化为同是NP难问题的MaxSAT问题进行上界估计[42],并提出针对大规模稀疏图的最大团(shot for Large MaxClique,LMC)算法。LMC算法由2个子程序构成,1个预处理程序Initialize和1个主查询程序SearchMaxClique。LMC使用单个预处理程序完成PMC算法和BBMCSP算法的3项任务,并对原始图G进行预处理,在搜索树第1层子图中调用Initialize程序进行预处理,改进顺序染色的上界,并估计准确度[43]。从程序的时间复杂度来比较,LMC算法的时间复杂度
在求解大规模的最大团问题上,并行计算是一个非常重要的方法。文献[45]提出一种基于并行核且使用watched方法的最大团求解算法BBMCW,该算法可以直接编码在内存中,通过使用2个新指针分别监视第1个和最后1个块位,有效地将集合操作限制在较少的顶点上,从而减少空位块操作的数量,降低性能损失并减少BBMCW算法的伪计算次数。此外,当图例的稀疏性较高时,BBMCW算法使用标准的顺序贪婪着色计算边界颜色,从而减少求解规模,增加求解时间。这种技术也可以应用在SAT领域,当子句的文字很少时,可以看作是稀疏的,从而提高求解速率。
在大规模图例求解最大团问题的算法中,需要对算法以及图例自身结构进行研究。2020年WALTEROs和BUCHANAN[46]发现一些大规模图例在满足某种关系时,最大团问题是好解的,有些则是难解的。已知
上述算法主要针对精确算法求解大规模图例最大团问题进行了补充,分别从3个角度使用精确算法对最大团问题进行分析。经典的分支限界法通过对与已给出的图结构进行分析,获取图结构信息以进行有效的剪枝操作,从而达到有效预处理的目的,提高求解速率。由于大多数精确算法都是基于图结构自身的分支定界法,近年来研究内容较多,算法更新改进较为困难。对于NP难问题的转移求解,LMC算法展示出了较好的效果。LMC算法将图结构信息转化为MaxSAT问题,对其进行冲突检测来推导上界估计,并启发式地给出了基于其他NP难问题的结构转化方法的求解算法。图着色、最大顶点独立集、顶点覆盖等问题对分析最大团问题也存在启发式的意义,但是NP难问题的转变仍是NP难问题,对于有效信息的转化利用则是问题的研究难点。对于图结构的相变研究,Main算法通过已发现的相变规律设计了更高效的算法,因此,构建相变表达式与分析相变技术是未来可以研究的重要方向。
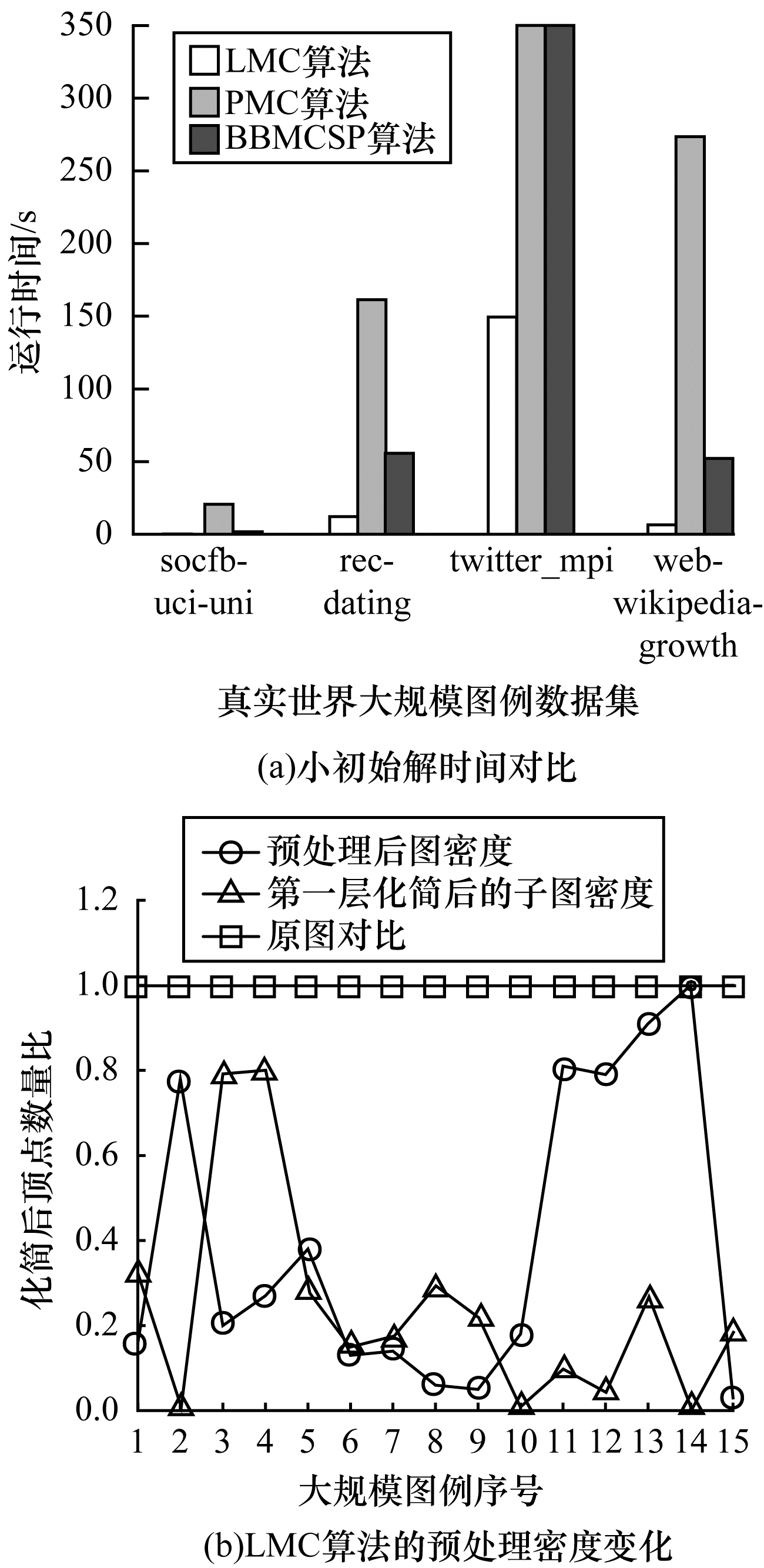
3.3.1 LMC算法结果分析图 8(a)所示为LMC算法与PMC算法、BBMCSP算法的搜索解对比结果。对比算法求解时间可知,无论LMC算法在初始解相同或是在小于其他两类算法的情况下,对大规模图例子图的搜索速度均优于其他两类算法。尤其是在图例twitter_mpi中,LMC的初始解小于其他两类算法,但求解时间为149.5 s,而其他两类算法则在5 h内无法找到正确解。说明MaxSAT方法在求解最大团问题上对于初始解的依赖性较低,有利于搜索最大团的上界估计。通过对原始图进行化简,子图中的顶点数显著降低,且当原图的密度较低时,如图 8(b)所示,子图第1层数目的化简与原始图顶点数目存在正相关的关系。但当原始图密度较高时,第1层化简的密度仍然很大,说明MaxSAT推理上界方法对求解大规模最大团问题有较好的效果,但在高密度图中预处理结果较差,求解时间不稳定。
|
Download:
|
| 图 8 不同算法在预处理阶段的结果对比 Fig. 8 Comparison of results of different algorithm in pretreatment stage | |
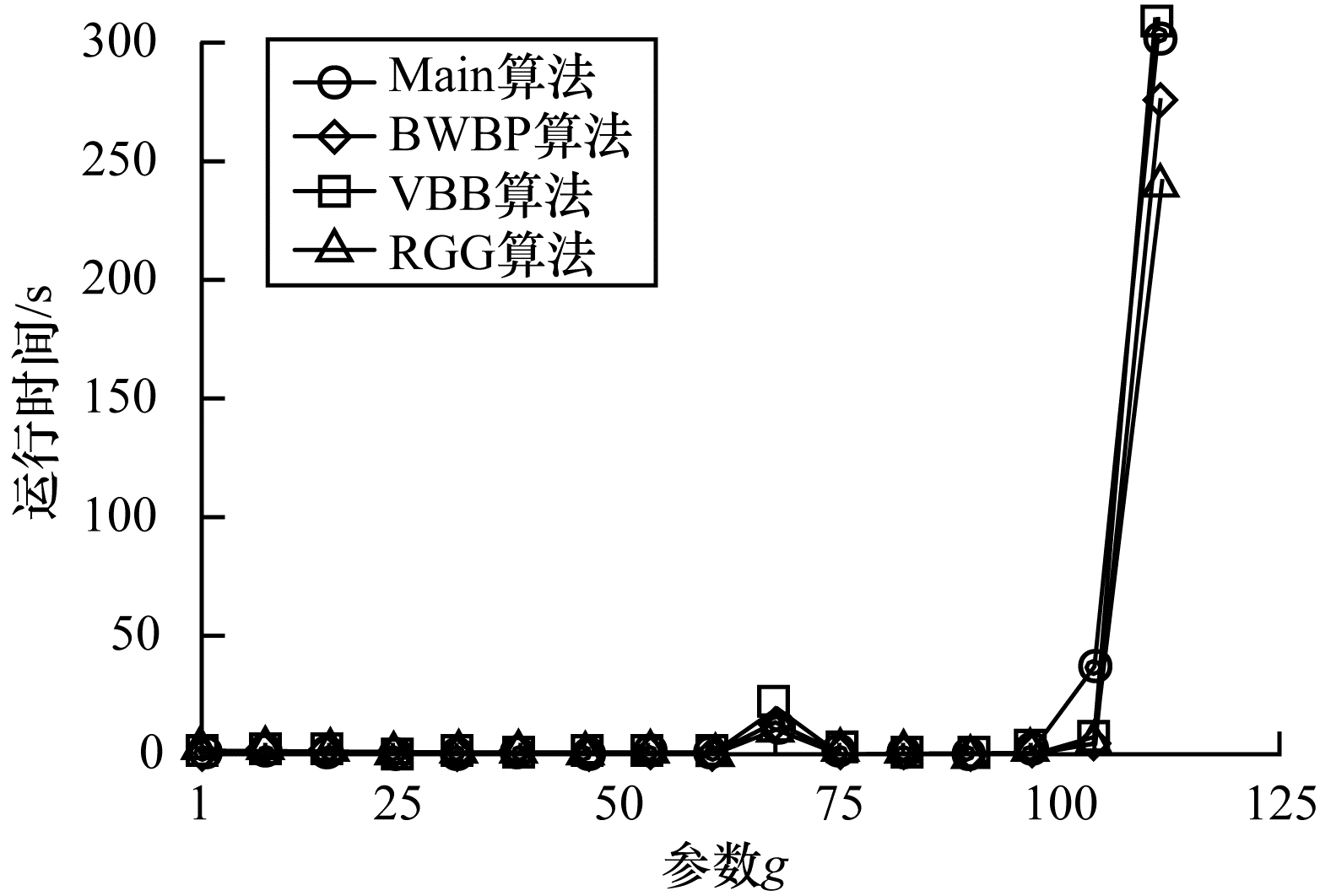
通过设置Main算法中不同核间距g[46]的大小,验证大规模图例中g对求解速度的影响,实验结果如图 9所示。由图 9可知,当g < 10时,求解速度最快;当g在10~100之间,求解速度适中;当g > 100后,求解较为困难。提出一个新的因素用来衡量图模型是否可解,并在实验结果中验证核间距的正确性,求得该图例是成为难解图结构的相变点。通过g在0~100之间的求解效率优于文中所提到的3类算法[46]可以看出顶点数与边数的大小无关,与图模型的结构相关,即无论顶点和边为多少,只要不接近所提出相变点位置的大规模最大团问题,就都是好解的。
|
Download:
|
|
图 9 参数 |
|
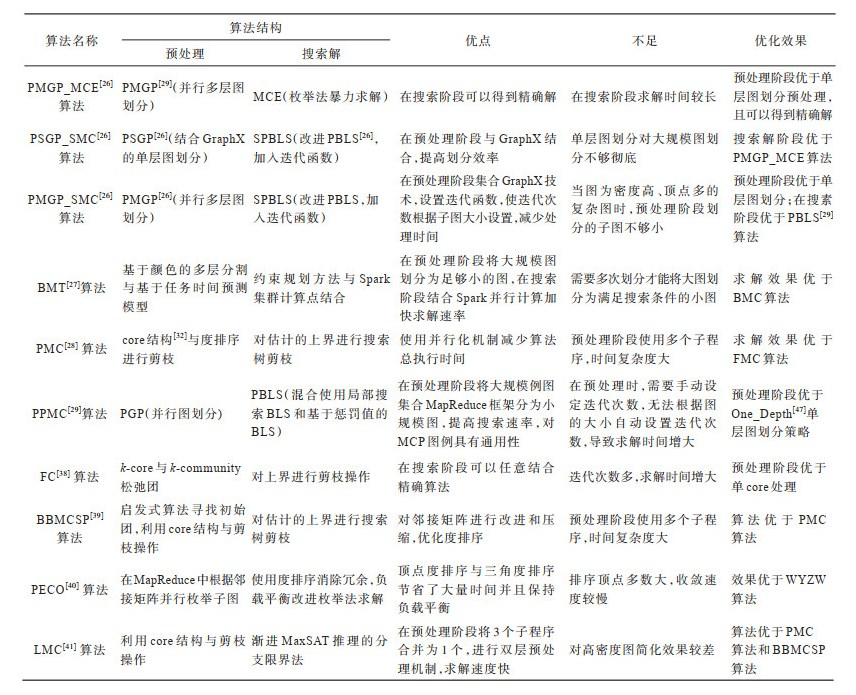
近年来,在求解图例规模大、计算复杂度高的最大团问题中涌现出了很多优秀的算法,在应用过程中展示了一定的优势,但也暴露出了一些自身的局限性,将这些算法进行总结分析,结果如表 4所示。
|
下载CSV 表 4 大规模图例的最大团问题算法的对比分析 Table 4 Comparative analysis of algorithms for maximum clique problem based on large-scale lgraph |
基于大规模图例求解最大团问题时需要先对原始图例进行预处理,将大规模图例转化为多个小规模子图或单个多剪枝化简图,使其有利于子图搜索解。为简化数据计算复杂度并增强计算效率,使用大数据并行计算平台进行多线程并行操作,逐步转化为可求解规模图例。
目前对于求解大规模图例最大团问题的主要创新点在预处理上,一般分为2种处理方式:
1)将大规模图例划分为多个小规模图例,主要基于单层图划分和多层图划分,且划分方法为图着色划分。单层图划分有较快的划分速度,能更大限度地保持原有图结构,但划分时间较长。多层划分则划分较慢但划分后的子图更利于搜索解,且在时间函数约束下更有利于求解密集图。由于大规模图例划分的复杂性和密集性,因此主要使用MapReduce方法进行并行计算获得多个子图。因为MapReduce方法不适用于多层图划分,所以采用更有利于图计算的Spark集群框架进行多层划分。
2)将大规模图例基于k-core进行剪枝操作,转化为小规模图例。k-core方法能够有效地反应图的度数和团数量的关系,有利于分支限界法的剪枝操作,化简大规模图,提高求解速率。对于分支限界法的研究,部分研究人员利用MaxSAT问题的子句冲突与最大团问题上界估计的关联关系,使用编码公式将最大团问题转化为最大可满足问题后,通过求解子句冲突集进行最大团的快速剪枝,从而提高上界精度与预处理速度,MaxSAT方法在大规模稀疏图中的处理效果提升显著。
5 未来展望本文旨在对近年来有关大规模图例求解最大团问题的研究进行了分析与综述,重点分析了各类算法的特点与优劣性。深度强化学习作为当前的研究热点,在解决组合优化问题上展示出了求解速度快、模型泛化能力强的优势,例如文献[48]利用GNN+RL方法求解图着色问题,文献[49]通过GNN+监督式训练求解最小支配集问题,文献[50]基于GNN+RL解决最小顶点覆盖集问题,均表现出显著的求解效果,与传统方法相比是一种全新的求解方式,也是一类新型的交叉学科[51]。虽然深度强化学习及其应用已经取得了一定进展,现有研究也展示出了在深度强化学习、解决图上组合和优化问题上的优势[52-53],但大规模组合优化问题的求解速度仍有待提高。因此,对基于深度强化学习方法解决经典组合优化问题的算法进行改进,扩大求解规模,使其可以解决大规模图例的难解问题是未来一个很好的研究方向[51]。
针对深度强化学习难以求解大规模图例最大团的问题、传统方法求解大规模图例最大团问题的数据计算量复杂问题、分支限界法中的上界精确推理问题以及图结构分析问题,有如下可借鉴技术:
1)使用分层式强化学习将大规模图例进行预处理,划分为多个可解子问题,并进行分层式学习策略,再将子问题进行组合,形成全局最优策略,从而解决大规模图例的最大团问题。
2)针对大规模图例的数据计算复杂问题,目前使用最多的是大数据平台下的分布式计算平台,该平台能够提高计算效率,但同时也带来一些不足,例如MapReduce多次迭代将消耗较多内存空间。针对内存消耗问题,可以结合量子计算方法对具有高复杂度的数据结构进行求解。量子计算根据量子力学叠加原理使量子信息单元的状态能够处于多种可能性的叠加状态,从而使量子信息处理从效率上相比于经典信息处理有更大的潜质[54]。此外,还可以将分布式计算平台应用于求解大规模数据结构的其他组合优化问题中。
3)针对分支限界法的上界精确推理问题,LMC算法在求解大规模图例最大团问题上效果良好。由于精确估计上界对分支定界法的求解速率有决定性影响[23],因此利用MaxSAT在编码后的图结构中进行寻找冲突子句从图,从而缩小最大团问题上界至关重要[44]。与MaxSAT问题相对,MinSAT问题的目标是确定一个命题公式的最少可满足子句数量,MaxSAT问题与最大团的上界紧密相连。所以,在下一步研究中,可以以MaxSAT求解最大团为启发,对MinSAT算法进行改进,使其有利于求解大规模图例的最大团问题[55]。
4)针对图结构分析问题,在Main算法中,研究人员启发式地提出度量图结构难度的参数g并作出了有效的说明与分析,验证了图结构难解度的相变点。对于图结构分析而言,树宽[56]与结构熵[57]均为分析图结构的有力工具。结构熵可以反映网络的动态复杂性,树宽则是在树分解阶段利用最大团的大小判断树的宽度,反映图的复杂性。这2种结构在一定条件下均反映最大团的结构与难解程度。对求解大规模图例的最大团问题,下一步可以通过对图结构进行研究,定义新的相变表达式,求得难解相变点,从图结构的角度分析最大团的求解难度,并设计相应结构算法,从而提高求解效率。
通过上述分析,基于大规模图例的最大团问题具有较大的研究空间与研究潜力,值得继续研究。
6 结束语求解大规模图例的最大团问题是将常规最大团理论应用于真实世界的关键方法,具有重要的研究意义。本文对基于常规图例求解最大团问题进行了简单的介绍与总结,对基于大规模图例求解最大团问题从算法分类的角度进行综述,详细介绍了将目前主流算法与大数据技术相结合的求解方法,阐述了各类算法的优点与不足。此外,分析了目前基于大规模复杂图例求解最大团问题的难点及解决方案,通过对算法进行对比分析发现,目前在计算优化和难解问题映射求解上仍有一定的进步空间。在求解大规模图例最大团问题中,下一步将继续研究结合分层深度强化学习的划分方法和分析图结构的相变方法。
| [1] |
黄包裕, 张永祥, 赵磊. 基于布谷鸟搜索算法和最大二阶循环平稳盲解卷积的滚动轴承故障诊断方法[J]. 机械工程学报, 2021, 57(9): 99-107. HUANG B Y, ZHANG Y X, ZHAO L. Research on fault diagnosis method based on cuckoo search algorithm and maximum second-order cyclostationary blind deconvolution[J]. Chinese Journal of Mechanical Engineering, 2021, 57(9): 99-107. (in Chinese) |
| [2] |
MENG X, XIANG J, ZHENG R, et al. DPCMNE: detecting protein complexes from protein-protein interaction networks via multi-level network embedding[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2021, 99: 12-19. |
| [3] |
YANG S, ZHANG L, QI J Q, et al. Learning motion-appearance co-attention for zero-shot video object segmentation[C]//Proceedings of IEEE/CVF International Conference on Computer Vision. Washington D. C., USA: IEEE Press, 2021: 1544-1553.
|
| [4] |
GSCHWIND T, IRNICH S, FURINI F, et al. A branch-and-price framework for decomposing graphs into relaxed cliques[J]. Informs Journal on Computing, 2021, 33(3): 1070-1090. DOI:10.1287/ijoc.2020.0984 |
| [5] |
ZHANG M X, LI L, HUA W, et al. Efficient 2-hop labeling maintenance in dynamic small-world networks[C]//Proceedings of the 37th International Conference on Data Engineering. Washington D. C., USA: IEEE Press, 2021: 133-144.
|
| [6] |
VASCONCELOS G L, MACÊDO A M S, DUARTE-FILHO G C, et al. Power law behaviour in the saturation regime of fatality curves of the COVID-19 pandemic[J]. Scientific Reports, 2021, 11(1): 1-12. DOI:10.1038/s41598-020-79139-8 |
| [7] |
ZHONG H N, MAHDAVI PAJOUH F, PROKOPYEV O A. Finding influential groups in networked systems: the most degree-central clique problem[J]. Omega, 2021, 101: 102262-102271. DOI:10.1016/j.omega.2020.102262 |
| [8] |
SHI J, DHULIPALA L, SHUN J L. Parallel clique counting and peeling algorithms[C]//Proceedings of SIAM Conference on Applied and Computational Discrete Algorithms. Philadelphia, USA: Society for Industrial and Applied Mathematics, 2021: 135-146.
|
| [9] |
BESTA M, KANAKAGIRI R, KWASNIEWSKI G, et al. SISA: set-centric instruction set architecture for graph mining on processing-in-memory systems[C]//Proceedings of the 54th Annual IEEE/ACM Conference on International Symposium on Microarchitecture. Washington D. C., USA: IEEE Press, 2021: 282-297.
|
| [10] |
JIN Y, XIONG B W, HE K, et al. On fast enumeration of maximal cliques in large graphs[J]. Expert Systems With Applications, 2022, 187: 115915-115923. DOI:10.1016/j.eswa.2021.115915 |
| [11] |
PARDALOS P M, XUE J. The maximum clique problem[J]. Journal of Global Optimization, 1994, 4(3): 301-328. DOI:10.1007/BF01098364 |
| [12] |
PLACHETTA R, VAN DER GRINTEN A. SAT-and-reduce for vertex cover: accelerating branch-and-reduce by SAT solving[C]//Proceedings of Workshop on Algorithm Engineering and Experiments. Philadelphia, USA: Society for Industrial and Applied Mathematics, 2021: 169-180.
|
| [13] |
HOSSEINIAN S, FONTES D B M M, BUTENKO S. A Lagrangian bound on the clique number and an exact algorithm for the maximum edge weight clique problem[J]. Informs Journal on Computing, 2020, 32(3): 747-762. DOI:10.1287/ijoc.2019.0898 |
| [14] |
BABKIN E, BABKINA T, DEMIDOVSKIJ A. Hybrid neural network and bi-criteria tabu-machine: comparison of new approaches to maximum clique problem[J]. International Journal of Big Data Intelligence, 2018, 5(3): 143-149. DOI:10.1504/IJBDI.2018.092660 |
| [15] |
JI P, ZHANG S X, ZHOU Z P. Overlapping community detection based on maximal clique and multi-objective ant colony optimization[C]//Proceedings of Chinese Control and Decision Conference. Washington D. C., USA: IEEE Press, 2020: 5164-5169.
|
| [16] |
杜鹏. 一种启发式的分布式最大独立集算法[J]. 南京邮电大学学报(自然科学版), 2013, 33(6): 18-23, 28. DU P. A heuristic distributed algorithm for the maximum weight independent set problem[J]. Journal of Nanjing University of Posts and Telecommunications (Natural Science), 2013, 33(6): 18-23, 28. (in Chinese) DOI:10.3969/j.issn.1673-5439.2013.06.004 |
| [17] |
WU Q H, HAO J K. A review on algorithms for maximum clique problems[J]. European Journal of Operational Research, 2015, 242(3): 693-709. DOI:10.1016/j.ejor.2014.09.064 |
| [18] |
SINGH K K, PANDEY A K. Survey of algorithms on maximum clique problem[J]. International Advanced Research Journal in Science, Engineering and Technology, 2015, 2(2): 18-20. |
| [19] |
FAKHFAKH F, TOUNSI M, MOSBAH M, et al. Algorithms for finding maximal and maximum cliques: a survey[C]//Proceedings of International Conference on Intelligent Systems Design and Applications. Berlin, Germany: Springer, 2017: 745-754.
|
| [20] |
NASIRIAN F, MAHDAVI PAJOUH F, BALASUNDARAM B. Detecting a most closeness-central clique in complex networks[J]. European Journal of Operational Research, 2020, 283(2): 461-475. DOI:10.1016/j.ejor.2019.11.035 |
| [21] |
LIU Y, LI C M, JIANG H, et al. A learning based branch and bound for maximum common subgraph related problems[C]//Proceedings of AAAI Conference on Artificial Intelligence. San Francisco, USA: AAAI Press, 2020, 34(3): 2392-2399.
|
| [22] |
MOHAMMADI N, KADIVAR M. NK-MaxClique and MMCQ: tow new exact branch and bound algorithms for the maximum clique problem[J]. IEEE Access, 2020, 8: 180045-180053. DOI:10.1109/ACCESS.2020.3028112 |
| [23] |
JIANG H, LI C M, LIU Y, et al. A two-stage maxsat reasoning approach for the maximum weight clique problem[C]//Proceedings of AAAI Conference on Artificial Intelligence. San Francisco, USA: AAAI Press, 2018: 159-165.
|
| [24] |
MALEKI N, RAHMANI A M, CONTI M. MapReduce: an infrastructure review and research insights[J]. The Journal of Supercomputing, 2019, 75(10): 6934-7002. DOI:10.1007/s11227-019-02907-5 |
| [25] |
XIANG J G, GUO C, ABOULNAGA A. Scalable maximum clique computation using MapReduce[C]//Proceedings of the 29th International Conference on Data Engineering. Washington D. C., USA: IEEE Press, 2013: 74-85.
|
| [26] |
顾军华, 霍士杰, 武君艳, 等. 求解最大团问题的并行多层图划分方法[J]. 计算机应用, 2018, 38(12): 3425-3432. GU J H, HUO S J, WU J Y, et al. Parallel multi-layer graph partitioning method for solving maximum clique problems[J]. Journal of Computer Applications, 2018, 38(12): 3425-3432. (in Chinese) DOI:10.11772/j.issn.1001-9081.2018040934 |
| [27] |
肖成龙, 聂紫阳, 王宁, 等. 基于并行约束规划的最大团识别研究[J]. 计算机工程, 2020, 46(4): 53-59, 69. XIAO C L, NIE Z Y, WANG N, et al. Research on maximum clique identification based on parallel constraint programming[J]. Computer Engineering, 2020, 46(4): 53-59, 69. (in Chinese) |
| [28] |
HASHEM I A T, ANUAR N B, MARJANI M, et al. MapReduce scheduling algorithms: a review[J]. The Journal of Supercomputing, 2020, 76(7): 4915-4945. DOI:10.1007/s11227-018-2719-5 |
| [29] |
GUO J J, ZHANG S Q, GAO X, et al. Parallel graph partitioning framework for solving the maximum clique problem using Hadoop[C]//Proceedings of the 2nd International Conference on Big Data Analysis. Washington D. C., USA: IEEE Press, 2017: 186-192.
|
| [30] |
ARFAT Y, SUMA S, MEHMOOD R, et al. Parallel shortest path big data graph computations of US road network using apache spark: survey, architecture, and evaluation[C]//Proceedings of Conference on Smart Infrastructure and Applications. Berlin, Germany: Springer, 2020: 185-214.
|
| [31] |
MUKHERJEE A P, TIRTHAPURA S. Enumerating maximal bicliques from a large graph using MapReduce[J]. IEEE Transactions on Services Computing, 2017, 10(5): 771-784. DOI:10.1109/TSC.2016.2523997 |
| [32] |
WATTS D J, STROGATZ S H. Collective dynamics of small-world networks[J]. Nature, 1998, 393: 440-442. DOI:10.1038/30918 |
| [33] |
KABIR H, MADDURI K. Parallel k-core decomposition on multicore platforms[C]//Proceedings of IEEE International Parallel and Distributed Processing Symposium Workshops. Washington D. C., USA: IEEE Press, 2017: 1482-1491.
|
| [34] |
ROSSI R A, GLEICH D F, GEBREMEDHIN A H. Parallel maximum clique algorithms with applications to network analysis[J]. SIAM Journal on Scientific Computing, 2015, 37(5): 589-616. DOI:10.1137/14100018X |
| [35] |
PELOFSKE E, HAHN G, DJIDJEV H. Solving large maximum clique problems on a quantum annealer[C]//Proceedings of International Conference on Quantum Technology and Optimization Problems. Berlin, Germany: Springer, 2019: 123-135.
|
| [36] |
YU Y, LEI Z Y, WANG Y R, et al. Improving dendritic neuron model with dynamic scale-free network-based differential evolution[J]. IEEE/CAA Journal of Automatica Sinica, 2022, 9(1): 99-110. DOI:10.1109/JAS.2021.1004284 |
| [37] |
JURSA A. Fast algorithm for finding maximum clique in scale-free networks[EB/OL]. [2021-09-12]. https://www.semanticscholar.org/paper/Fast-Algorithm-for-Finding-Maximum-Clique-in-Jursa/798fad2595830dfcae3d6c04075eb63c2977818b.
|
| [38] |
VERMA A, BUCHANAN A, BUTENKO S. Solving the maximum clique and vertex coloring problems on very large sparse networks[J]. Informs Journal on Computing, 2015, 27(1): 164-177. DOI:10.1287/ijoc.2014.0618 |
| [39] |
SAN SEGUNDO P, ARTIEDA J, BATSYN M, et al. An enhanced bitstring encoding for exact maximum clique search in sparse graphs[J]. Optimization Methods and Software, 2017, 32(2): 312-335. DOI:10.1080/10556788.2017.1281924 |
| [40] |
BATAGELJ V, ZAVERSNIK M. An O (m) algorithm for cores decomposition of networks[EB/OL]. [2021-09-12]. https://arxiv.org/abs/cs/0310049.
|
| [41] |
JIANG H, LI C M, MANYÀ F. Combining efficient preprocessing and incremental MaxSAT reasoning for MaxClique in large graphs[C]//Proceedings of the 22nd European Conference on Artificial Intelligence. [S. l. ]: IOS Press 2016: 939-947.
|
| [42] |
LI C M, JIANG H, XU R C. Incremental MaxSAT reasoning to reduce branches in a branch-and-bound algorithm for MaxClique[C]//Proceedings of International Conference on Learning and Intelligent Optimization. Berlin, Germany: Springer, 2015: 268-274.
|
| [43] |
SVENDSEN M, MUKHERJEE A P, TIRTHAPURA S. Mining maximal cliques from a large graph using MapReduce: tackling highly uneven subproblem sizes[J]. Journal of Parallel and Distributed Computing, 2015, 79: 104-114. |
| [44] |
LI C M, JIANG H, MANYÀ F. On minimization of the number of branches in branch-and-bound algorithms for the maximum clique problem[J]. Computers & Operations Research, 2017, 84: 1-15. |
| [45] |
SAN SEGUNDO P, LOPEZ A, PARDALOS P M. A new exact maximum clique algorithm for large and massive sparse graphs[J]. Computers & Operations Research, 2016, 66: 81-94. |
| [46] |
WALTEROS J L, BUCHANAN A. Why is maximum clique often easy in practice?[J]. Operations Research, 2020, 68(6): 1866-1895. DOI:10.1287/opre.2019.1970 |
| [47] |
EMAMZADEH ESMAEILI NEJAD A, ZOLGHADRI JAHROMI M, TAHERI M. Graph compression based on transitivity for neighborhood query[J]. Information Sciences, 2021, 576: 312-328. DOI:10.1016/j.ins.2021.06.050 |
| [48] |
YOLCU E, PÓCZOS B. Learning local search heuristics for boolean satisfiability[EB/OL]. [2021-09-12]. https://www.doc88.com/p-25629059165440.html?r=1.
|
| [49] |
LI Z W, CHEN Q F, KOLTUN V. Combinatorial optimization with graph convolutional networks and guided tree search[EB/OL]. [2021-09-12]. https://www.semanticscholar.org/paper/Combinatorial-Optimization-with-Graph-Convolutional-Li-Chen/d77c0e84972c256a8922b952b04330e369f65f09.
|
| [50] |
MANCHANDA S, MITTAL A, DHAWAN A, et al. Learning heuristics over large graphs via deep reinforcement learning[EB/OL]. [2021-09-12]. https://arxiv.org/abs/1903.03332.
|
| [51] |
李凯文, 张涛, 王锐, 等. 基于深度强化学习的组合优化研究进展[J]. 自动化学报, 2021, 47(11): 2521-2537. LI K W, ZHANG T, WANG R, et al. Research reviews of combinatorial optimization methods based on deep reinforcement learning[J]. Acta Automatica Sinica, 2021, 47(11): 2521-2537. (in Chinese) |
| [52] |
BACCIU D, CONTE A, GROSSI R, et al. K-plex cover pooling for graph neural networks[J]. Data Mining and Knowledge Discovery, 2021, 35(5): 2200-2220. DOI:10.1007/s10618-021-00779-z |
| [53] |
SUN Y, ERNST A, LI X D, et al. Generalization of machine learning for problem reduction: a case study on travelling salesman problems[J]. OR Spectrum, 2021, 43(3): 607-633. DOI:10.1007/s00291-020-00604-x |
| [54] |
王潮, 姚皓南, 王宝楠, 等. 量子计算密码攻击进展[J]. 计算机学报, 2020, 43(9): 1691-1707. WANG C, YAO H N, WANG B N, et al. Progress in quantum computing cryptography attacks[J]. Chinese Journal of Computers, 2020, 43(9): 1691-1707. (in Chinese) |
| [55] |
ARGELICH J, LI C M, MANYÀ F, et al. Clause tableaux for maximum and minimum satisfiability[J]. Logic Journal of the IGPL, 2019, 29(1): 7-27. |
| [56] |
GURSKI F, KOMANDER D, REHS C. How to compute digraph width measures on directed co-graphs[J]. Theoretical Computer Science, 2021, 855: 161-185. DOI:10.1016/j.tcs.2020.11.047 |
| [57] |
GEORGE R, SHUJAEE K, KERWAT M, et al. A comparative evaluation of community detection algorithms in social networks[J]. Procedia Computer Science, 2020, 171: 1157-1165. DOI:10.1016/j.procs.2020.04.124 |
 2022, Vol. 48
2022, Vol. 48

 ,
,